Multiobjective Gate Assignment Model Considering Carbon Emissions
Abstract
1. Introduction
2. Literature Review
2.1. Gate Assignment Models
2.2. Algorithms
3. Methodology
3.1. Multiobjective Gate Assignment Model
- (1)
- Improve the proportion of flights assigned to the contact gate
- (2)
- Reduce aircraft taxiing fuel consumption
- (3)
- Increase gate assignment robustness
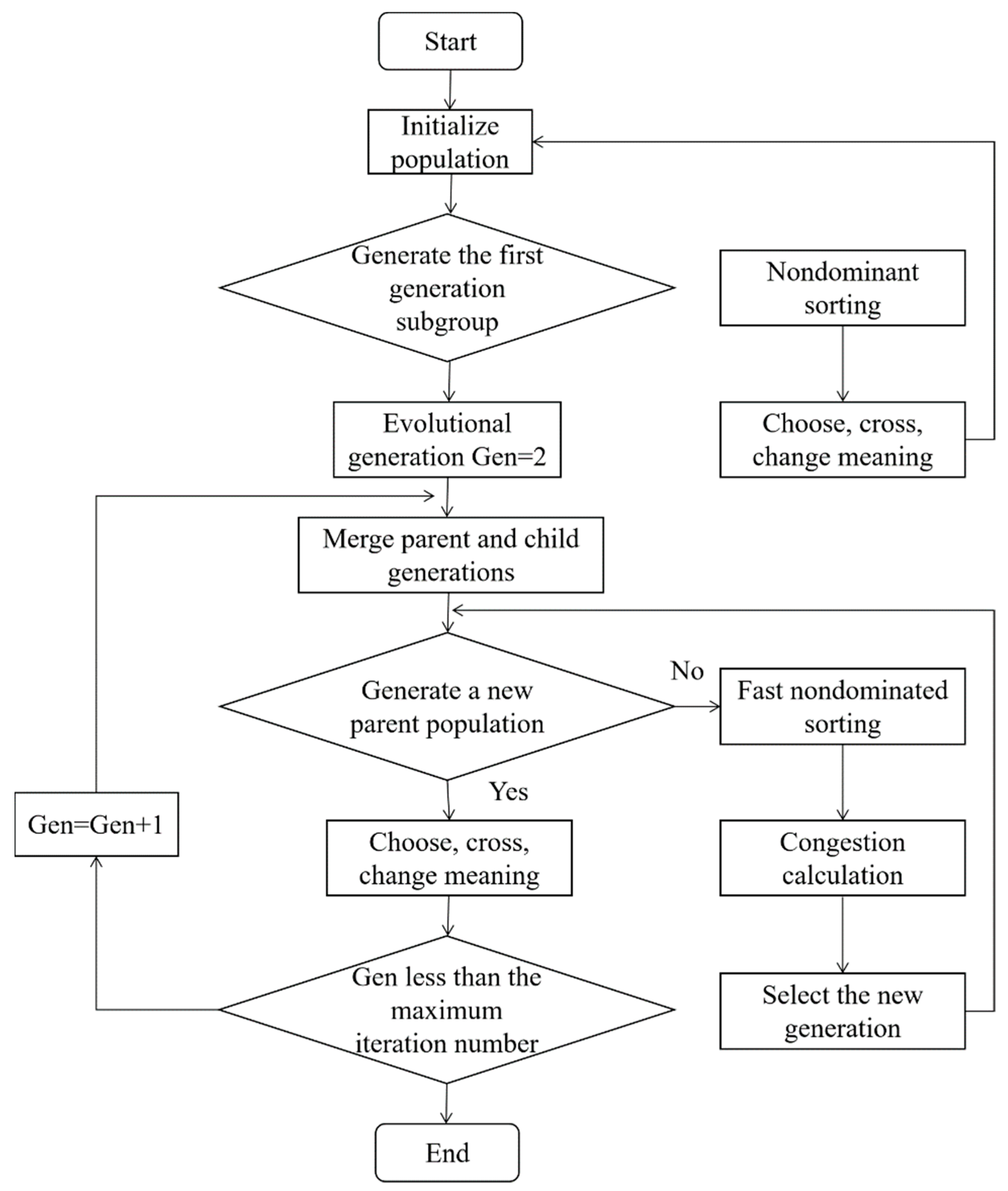
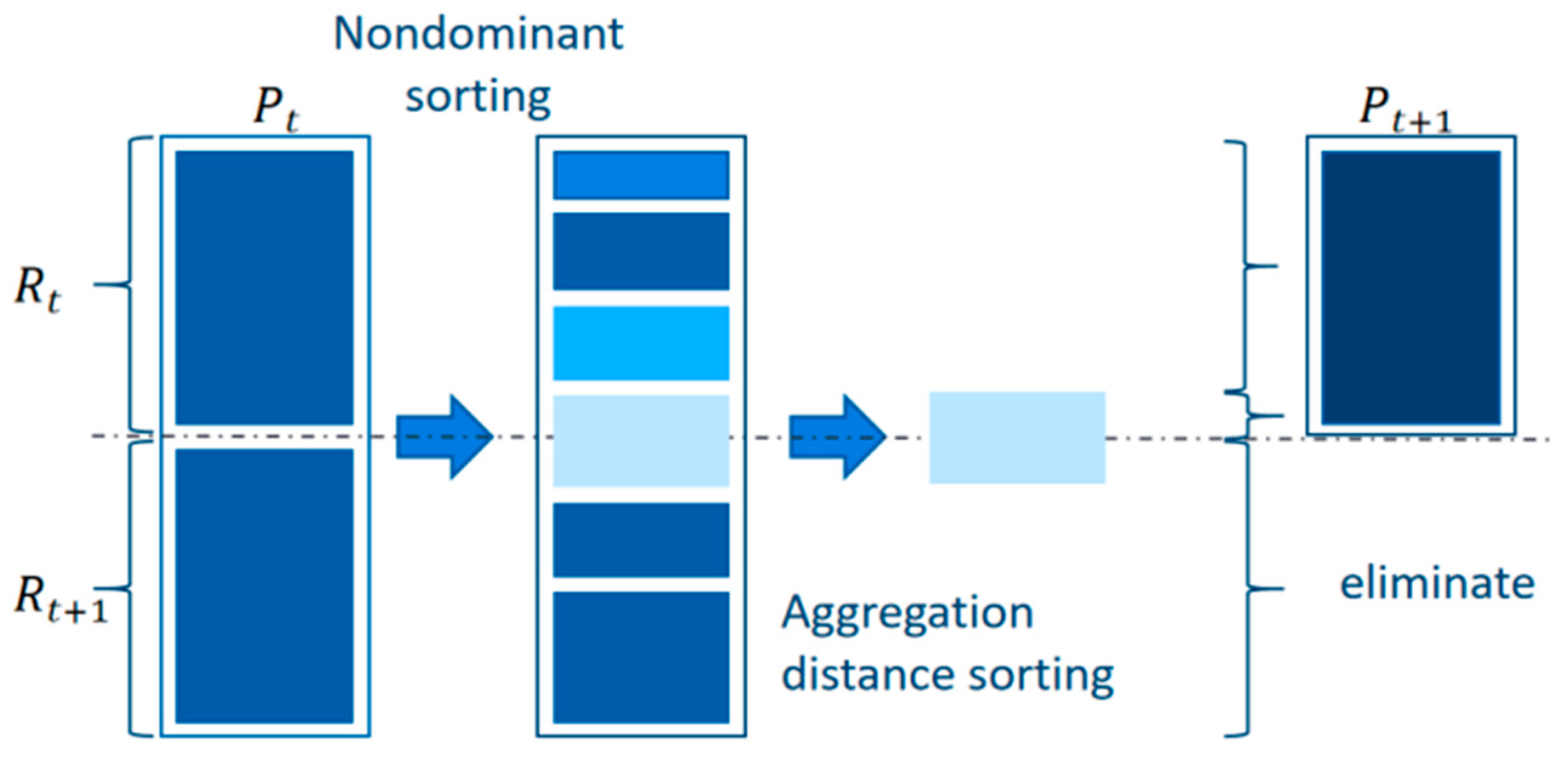
3.2. Algorithm
4. Experimental Results
4.1. Example Introduction
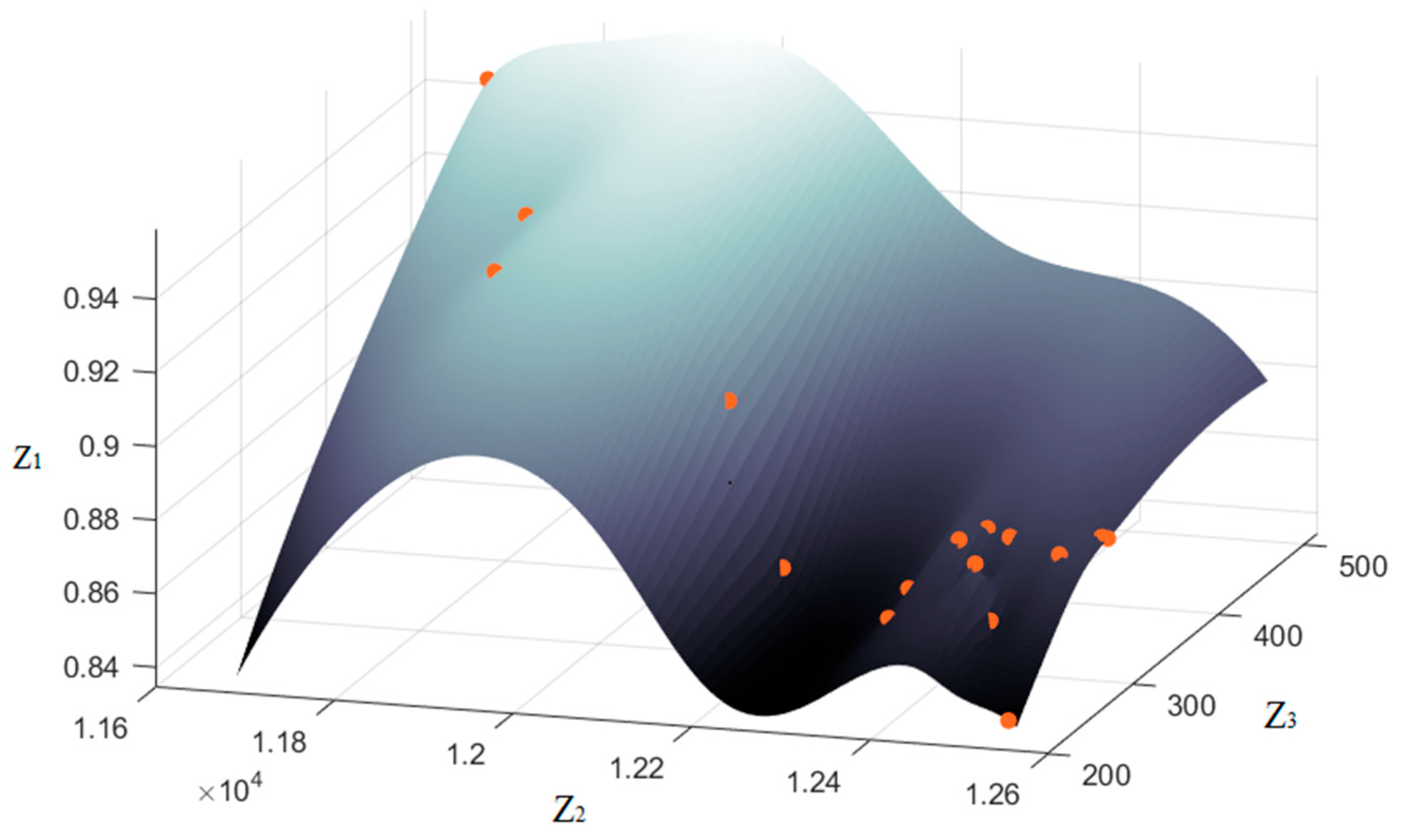
4.2. Results and Discussion
| Objective(s) | Z1 | Z2 | Z3 | Average Taxiing Fuel Consumption (kg) | Total Taxiing Carbon Emissions (kg) |
|---|---|---|---|---|---|
| OS | 85.29% | 12,401.44 | 284.42 | 182.37 | 57,555.16 |
| Z1 + Z2 | 94.12% | 11,670.32 | 515.66 | 171.62 | 54,162.01 |
| Z3 | 83.82% | 12,534.78 | 221.68 | 184.34 | 58,173.98 |
| Z1 + Z2 + Z3 | 92.65% | 11,851.36 | 334.57 | 174.28 | 55,002.22 |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Federal Aviation Administration Office of Environment and Energy. Aviation Emissions and Air Quality Handbook Version 3 Update 1; FAA: Washington, DC, USA, 2016.
- Long, J.L. Strategic thinking on developing new energy of air transport under low carbon economy. China Transp. Rev. 2013, 4, 9–13. [Google Scholar]
- Civil Aviation Administration of China. Outline of Action for the Construction of Four Types of Airports in China Civil Aviation; CAA: Beijing, China, 2020.
- Winther, M.; Kousgaard, U.; Ellermann, T.; Massling, A.; Ketzel, M. Emissions of NO x, particle mass and particle numbers from aircraft main engines, APU’s and handling equipment at Copenhagen Airport. Atmos. Environ. 2015, 100, 218–229. [Google Scholar] [CrossRef]
- Sznajderman, L.; RamírezDíaz, G.; Bernardi, C.A.D. Influence of the Apron Parking Stand Management Policy on Aircraft and Ground Support Equipment (GSE) Gaseous Emissions at Airports. Aerospace 2021, 8, 87. [Google Scholar] [CrossRef]
- Xue, Q.W.; Jiang, Y.; Lui, Z.L.; Zeng, L.Y. Gate Assignment Based on Airline Operation Cost and Fairness. Aeronaut. Comput. Technol. 2016, 46, 64–69. [Google Scholar]
- Shen, X.Y.; Yu, H.W. Research on multi-objective gate assignment based on aircraft matching degree. World Transp. Congr. 2018, 47, 445–457. [Google Scholar]
- Jiang, Y.; Hu, Z.T.; Tong, C.; Liu, Z.Y.; Chen, L.L.; Zhang, H.H. An Optimization Model for Gate Re-assignment under Flight Delays. J. Transp. Syst. Eng. Inf. Technol. 2020, 20, 185–190, 217. [Google Scholar]
- Yuan, Y.; Zhai, H.X.; Sun, C.L. Gate Assignment of Freight Flight Considering Efficiency Operation Support. J. Nanjing Univ. Aeronaut. Astronaut. 2021, 53, 934–940. [Google Scholar]
- Yan, P.; Yuan, Y. Joint Optimization of Flight Taxiing Path Planning and Gate Allocation. Control Eng. China 2021, 28, 464–470. [Google Scholar]
- Xiong, J.; Zhang, C. Airport Gate Assignment with Airplane Taxing Cost Analysis. J. Transp. Syst. Eng. Inf. Technol. 2010, 10, 165–170. [Google Scholar]
- Wang, X.T.; Tian, Y.; Wan, L.L.; Yang, Y. Research on Robustness of Gate Assignment Based on Column Generation Methods. J. Wuhan Univ. Technol. Transp. Sci. Eng. 2015, 39, 171–174, 179. [Google Scholar]
- Li, Q.W. Research on Optimization Models for Airport Gate Assignment Problem; Beijing Jiaotong University: Beijing, China, 2017. [Google Scholar]
- Daş, G.S. New Multi-Objective Models for the Gate Assignment Problem. Comput. Ind. Eng. 2017, 109, 347–356. [Google Scholar] [CrossRef]
- Genc, H.M.; Erol, O.; Eksin, I.; Berber, M.; Gueleryuez, B.O. A stochastic neighborhood search approach for airport gate assignment problem. Expert Syst. Appl. 2012, 39, 316–327. [Google Scholar] [CrossRef]
- Kumar, V.P.; Bierlaire, M. Multi-objective airport gate assignment problem in planning and operations. J. Adv. Transp. 2014, 48, 902–926. [Google Scholar] [CrossRef]
- Zheng, W.J.; Le, M.L.; Shao, J.J.; Li, T. Research on Assignment of Gate Assignment Based on Resource Utilization Efficiency. Aviat. Comput. Technol. 2019, 49, 70–73, 78. [Google Scholar]
- Marina, K.; Laura, L. Biofuels in aviation: Fuel demand and CO2 emissions evolution in Europe toward 2030. Transp. Res. Part D Transp. Environ. 2016, 46, 166–181. [Google Scholar]
- Wan, L. Research on the Optimization Method of Air Traffic Operation for Environmental Protection; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2015. [Google Scholar]
- Kuzu, S.L. Estimation and dispersion modeling of landing and take-off (LTO) cycle emissions from Atatürk International Airport. Air Qual. Atmos. Health 2017, 11, 153–161. [Google Scholar] [CrossRef]
- Gao, W.; Cui, Y.; Kang, D. Optimization of airport ground operation for energy conservation and emission reduction. J. Transp. Inf. Saf. 2019, 37, 128–135. [Google Scholar]
- Evertse, C.; Visser, H.G. Real-time airport surface movement planning: Minimizing aircraft emissions. Trans. Res. Part C Emerg. Technol. 2017, 79, 224–241. [Google Scholar] [CrossRef]
- Soltani, M.; Ahmadi, S.; Akgunduz, A.; Bhuiyan, N. An eco-friendly aircraft taxiing approach with collision and conflict avoidance. Transp. Res. Part C Emerg. Technol. 2020, 121, 102872. [Google Scholar] [CrossRef]
- Balakrishnan, H. Queuing Models of Airport Departure Processes for Emissions Reduction; American Institute of Aeronautics & Astronautics Guidance, Navigation, and Control Conference: Chicago, IL, USA, 2009. [Google Scholar]
- Li, N.; Zhang, H. Calculating aircraft pollutant emissions during taxiing at the airport. Acta Sci. Circumstantiae 2017, 37, 1872–1876. [Google Scholar]
- Zhang, H. Research on the Strategy of Aircraft Low Emission Taxiing on the Airports; Civil Aviation University of China: Tianjing, China, 2017. [Google Scholar]
- Lu, M.Y. Research on Jointed Scheduling Optimization of Busy Airport Taxiway and Gate; Civil Aviation Flight University of China: Tianjing, China, 2022. [Google Scholar]
- Tang, X.W.; Chen, Z.; Zhang, S.R.; Ye, D. Impact of Apron Spatial Configuration on Flight Departure Taxi Time at Busy Airports. J. Transp. Syst. Eng. Inf. Technol. 2022, 22, 309–317. [Google Scholar]
- Li, R.N.; Feng, X. Optimization of Flight Area Layout with Minimum Fuel Consumption Based on Improved Genetic Algorithm. J. Chongqing Jiaotong Univ. Nat. Sci. 2022, 10, 1–8. [Google Scholar]
- Gök, Y.S.; Padrón, S.; Tomasella, M.; Guimarans, D.; Ozturk, C. Constraint-based robust planning and scheduling of airport apron operations through simheuristics. Ann. Oper. Res. 2022, 320, 795–830. [Google Scholar] [CrossRef]
- Yin, S.; Han, K.; Ochieng, W.Y.; Sanchez, D.R. Joint apron-runway assignment for airport surface operations. Transp. Res. Part B 2022, 156, 76–100. [Google Scholar] [CrossRef]
- Wen, J.; Sun, H.; Xu, J.; Liang, Z.J. Study of the Gate Assignment in Airport Based on Fixed Job Scheduling Algorithm. Syst. Eng. 2004, 7, 102–106. [Google Scholar]
- Liu, J.L. Research on the Airport Gate Assignment Based on Difference Evolution Algorithm; Civil Aviation Flight University of China: Tianjing, China, 2022. [Google Scholar]
- Liu, J.L.; Wang, J.H.; Liang, H.J. Research on Parking Space Allocation Based on Genetic Algorithm. Comput. Inf. Technol. 2020, 28, 14–15, 56. [Google Scholar]
- Xu, S.M.; Jiang, Y.; Wang, H.; Chen, L.L. Multi-objective Gate Assignment Modeling and Simulation Based on NSGA-II. J. Nanjing Univ. Aeronaut. Astronaut. 2018, 50, 823–828. [Google Scholar]
- Liu, Z. Research on Optimization of Airport Gate Assignment Based on Column Generation; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2022. [Google Scholar]
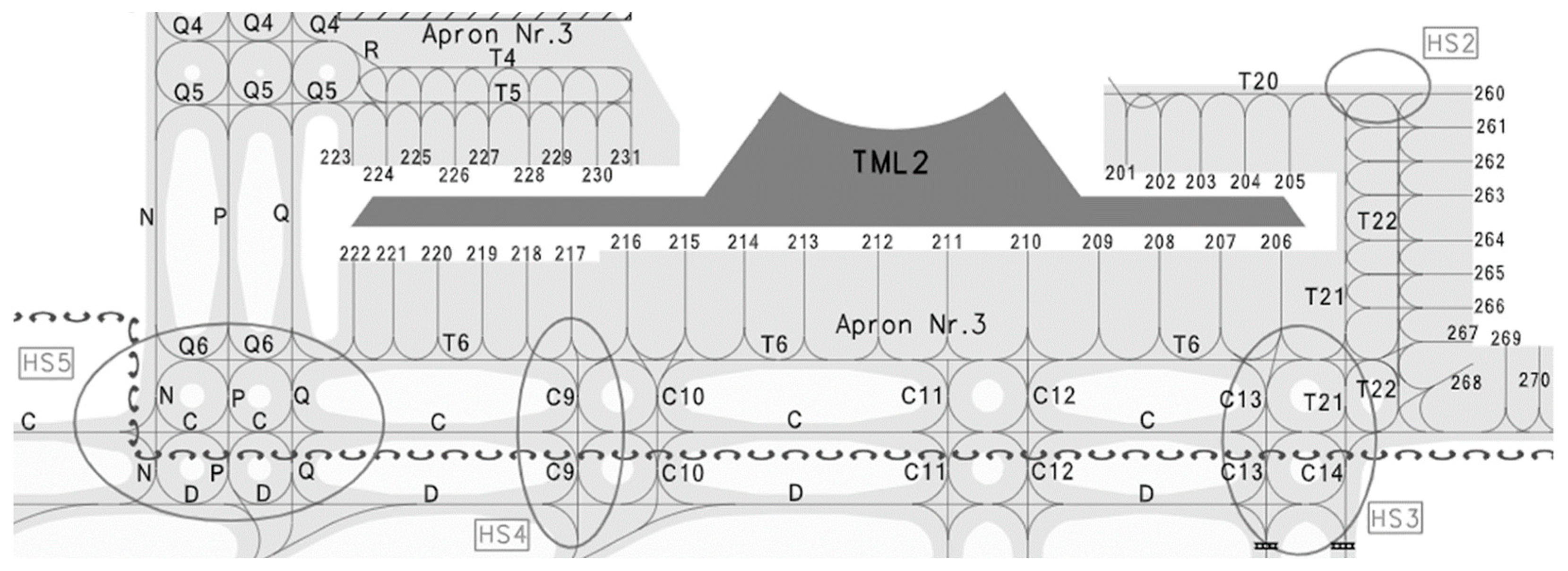
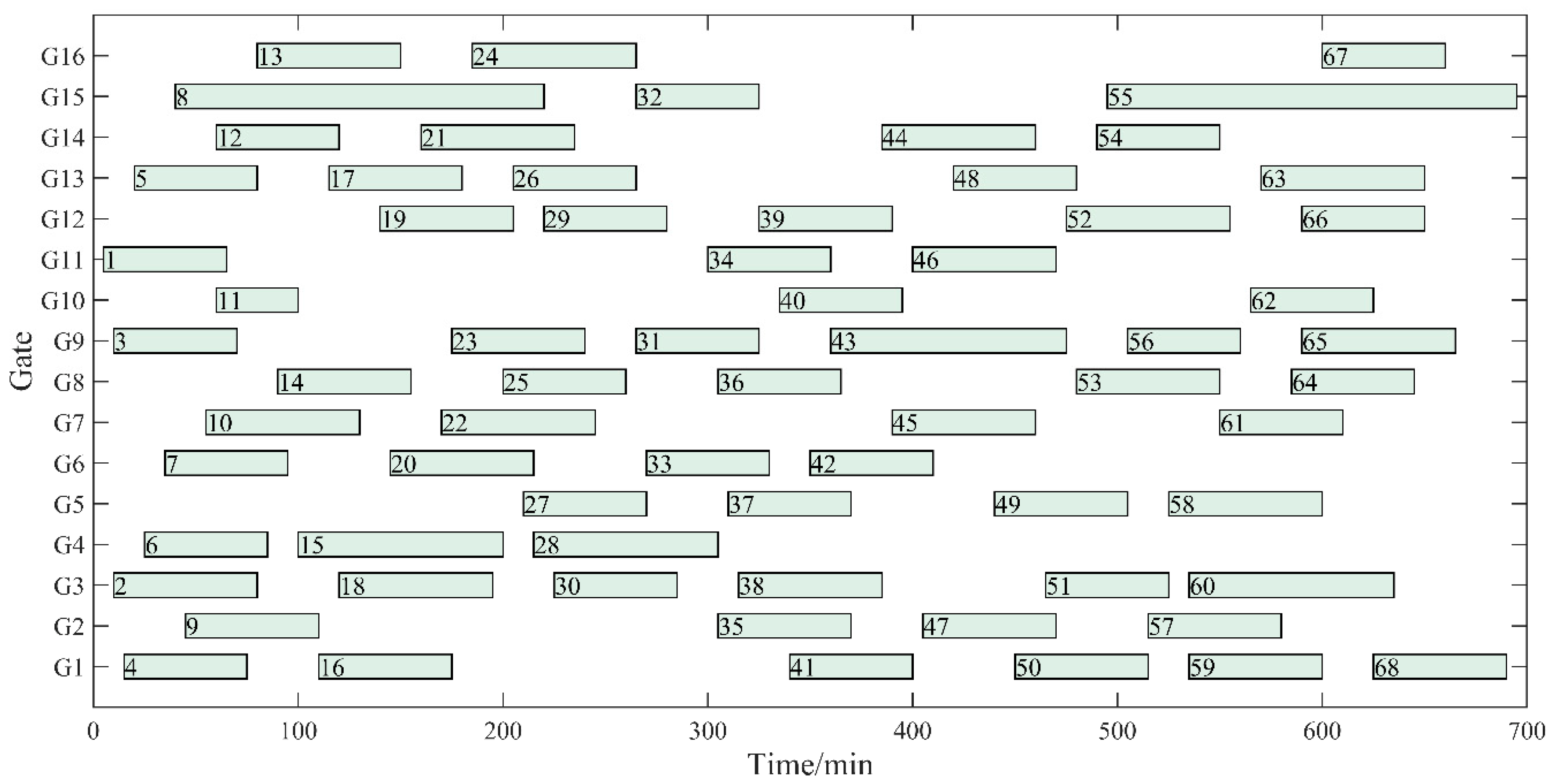
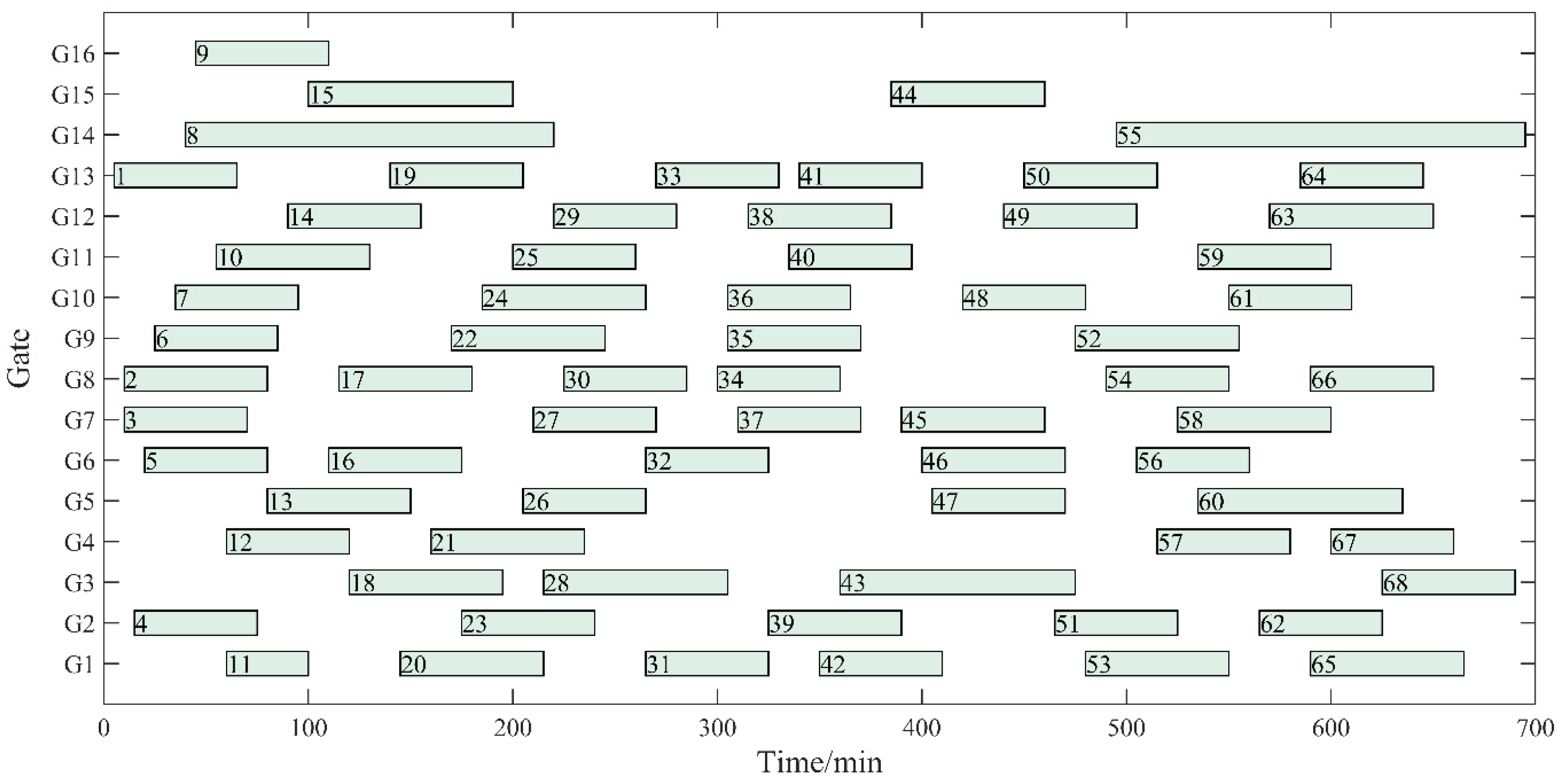
| Gate Number | Number | Gate Type | Gate Size | Arrival Taxiing Distance (m) | Departure Taxiing Distance (m) |
|---|---|---|---|---|---|
| 212 | G1 | Near | 3 | 1380 | 2450 |
| 213 | G2 | Near | 3 | 1440 | 2390 |
| 214 | G3 | Near | 3 | 1100 | 2330 |
| 215 | G4 | Near | 3 | 1000 | 2275 |
| 216 | G5 | Near | 3 | 920 | 2275 |
| 217 | G6 | Near | 2 | 860 | 1870 |
| 218 | G7 | Near | 2 | 920 | 1810 |
| 219 | G8 | Near | 2 | 980 | 1780 |
| 220 | G9 | Near | 2 | 1030 | 1730 |
| 221 | G10 | Near | 2 | 1100 | 1670 |
| 222 | G11 | Near | 2 | 1150 | 1580 |
| 223 | G12 | Near | 2 | 1000 | 1150 |
| 224 | G13 | Near | 2 | 1050 | 1320 |
| 266 | G14 | Far | 3 | 1980 | 2880 |
| 267 | G15 | Far | 3 | 1900 | 2950 |
| 269 | G16 | Far | 3 | 2100 | 3000 |
| Flight Pair Number | Arrival Flight Number | Arrival Time | Departure Flight Number | Departure Time | Aircraft Size | Engine | Engine Fuel Flow Rate (kg/s) |
|---|---|---|---|---|---|---|---|
| 1 | ZH9855 | 8:35 | ZH9856 | 9:35 | 2 | 2 | 0.109 |
| 9 | CZ6189 | 9:15 | CZ6189 | 10:20 | 2 | 2 | 0.138 |
| 18 | 3U8923 | 10:30 | 3U8924 | 11:45 | 3 | 2 | 0.228 |
| 21 | ZH9843 | 11:10 | ZH9844 | 12:25 | 3 | 2 | 0.270 |
| 52 | CZ6971 | 16:25 | CZ6972 | 17:45 | 2 | 2 | 0.109 |
| Aircraft Type | Engine | Engine Type | Engine Fuel Flow Rate (kg/s) |
|---|---|---|---|
| 32 N | 2 | LEAP-1A26CJ | 0.091 |
| A319 | 2 | CFM56-5B5/P | 0.102 |
| A320 | 2 | CFM56-5A3 | 0.104 |
| A321 | 2 | V2530-A5 | 0.138 |
| A322 | 2 | CFM56-5B4/P | 0.102 |
| A332 | 2 | CF6-80C2B4 | 0.228 |
| A333 | 2 | Trent 772B-60 | 0.270 |
| B737 | 2 | CFM56-3C-1 | 0.124 |
| B738 | 2 | CFM56-7B24/2 | 0.109 |
| B789 | 2 | GEnx-1B70/72/P2 | 0.201 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, Y.; Shao, Y.; Yuan, Q.; Jiang, Y. Multiobjective Gate Assignment Model Considering Carbon Emissions. Int. J. Environ. Res. Public Health 2023, 20, 3952. https://doi.org/10.3390/ijerph20053952
Shan Y, Shao Y, Yuan Q, Jiang Y. Multiobjective Gate Assignment Model Considering Carbon Emissions. International Journal of Environmental Research and Public Health. 2023; 20(5):3952. https://doi.org/10.3390/ijerph20053952
Chicago/Turabian StyleShan, Yixuan, Yuwei Shao, Qi Yuan, and Yu Jiang. 2023. "Multiobjective Gate Assignment Model Considering Carbon Emissions" International Journal of Environmental Research and Public Health 20, no. 5: 3952. https://doi.org/10.3390/ijerph20053952
APA StyleShan, Y., Shao, Y., Yuan, Q., & Jiang, Y. (2023). Multiobjective Gate Assignment Model Considering Carbon Emissions. International Journal of Environmental Research and Public Health, 20(5), 3952. https://doi.org/10.3390/ijerph20053952






