Discovering Geographical Flock Patterns of CO2 Emissions in China Using Trajectory Mining Techniques
Abstract
:1. Introduction
2. Materials and Methods
2.1. Basic Concepts
2.1.1. Bivariate Time Series
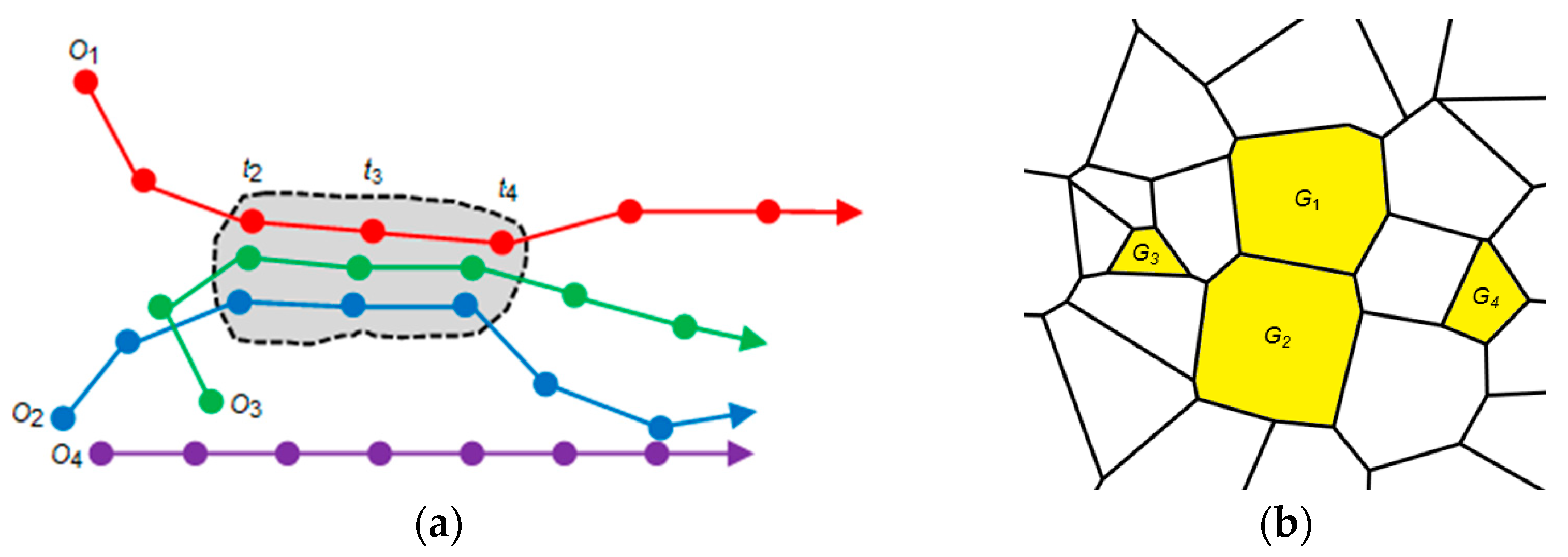
2.1.2. Attribute Trajectory
2.1.3. Geographical Flock
2.2. Study Area and Data
2.3. Methodology
2.3.1. Generating Attribute Trajectory Data
2.3.2. Generating STGs
2.3.3. Discovering Specific Types of Geographical Flock Patterns
3. Results and Discussion
3.1. Geographical Flock Patterns on the Province Level
3.1.1. The High–Low Attribute Values
3.1.2. The Extreme Number–Duration Values
3.2. Geographical Flock Patterns on the Geographical Region Level
3.2.1. The High–Low Attribute Values
3.2.2. The Extreme Number–Duration Values
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Zhao, X.; Jiang, Z.; Shao, S. How to achieve the 2030 CO2 emission-reduction targets for China’s industrial sector: Retrospective decomposition and prospective trajectories. Glob. Environ. Chang. 2017, 44, 83–97. [Google Scholar] [CrossRef]
- Rolnick, D.; Donti, P.L.; Kaack, L.H.; Kochanski, K.; Lacoste, A.; Sankaran, K.; Ross, A.S.; Milojevic-Dupont, N.; Jaques, N.; Waldman-Brown, A. Tackling climate change with machine learning. ACM Comput. Surv. 2022, 55, 1–96. [Google Scholar] [CrossRef]
- Abbas, A.; Zhao, C.; Waseem, M.; Ahmad, R. Analysis of energy input–output of farms and assessment of greenhouse gas emissions: A case study of cotton growers. Front. Environ. Sci. 2022, 725, 826838. [Google Scholar] [CrossRef]
- Elahi, E.; Khalid, Z.; Tauni, M.; Zhang, H.; Lirong, X. Extreme weather events risk to crop-production and the adaptation of innovative management strategies to mitigate the risk: A retrospective survey of rural Punjab, Pakistan. Technovation 2022, 117, 102255. [Google Scholar] [CrossRef]
- Elahi, E.; Khalid, Z. Estimating smart energy inputs packages using hybrid optimisation technique to mitigate environmental emissions of commercial fish farms. Appl. Energy 2022, 326, 119602. [Google Scholar] [CrossRef]
- Lahsen, M.; Ribot, J. Politics of attributing extreme events and disasters to climate change. Wiley Interdiscip. Rev. Clim. Chang. 2022, 13, e750. [Google Scholar] [CrossRef]
- IPCC. Intergovernmental Panel on Climate Change. 2022. Available online: https://www.ipcc.ch/sr15/ (accessed on 13 December 2022).
- Ren, L.; Zhou, S.; Peng, T.; Ou, X. A review of CO2 emissions reduction technologies and low-carbon development in the iron and steel industry focusing on China. Renew. Sustain. Energy Rev. 2021, 143, 110846. [Google Scholar] [CrossRef]
- Friedlingstein, P.; Jones, M.W.; O’Sullivan, M.; Andrew, R.M.; Bakker, D.C.; Hauck, J.; Le Quéré, C.; Peters, G.P.; Peters, W.; Pongratz, J. Global carbon budget 2021. Earth Syst. Sci. Data 2022, 14, 1917–2005. [Google Scholar] [CrossRef]
- Li, J.; Ho, M.S.; Xie, C.; Stern, N. China’s flexibility challenge in achieving carbon neutrality by 2060. Renew. Sustain. Energy Rev. 2022, 158, 112112. [Google Scholar] [CrossRef]
- Huang, Z.; Du, X. Toward green development? Impact of the carbon emissions trading system on local governments’ land supply in energy-intensive industries in China. Sci. Total Environ. 2020, 738, 139769. [Google Scholar] [CrossRef]
- Wen, L.; Yuan, X. Forecasting CO2 emissions in Chinas commercial department, through BP neural network based on random forest and PSO. Sci. Total Environ. 2020, 718, 137194. [Google Scholar] [CrossRef]
- Xuan, D.; Ma, X.; Shang, Y. Can China’s policy of carbon emission trading promote carbon emission reduction? J. Clean. Prod. 2020, 270, 122383. [Google Scholar] [CrossRef]
- Chen, X.; Lin, B. Towards carbon neutrality by implementing carbon emissions trading scheme: Policy evaluation in China. Energy Policy 2021, 157, 112510. [Google Scholar] [CrossRef]
- Ye, L.; Yang, D.; Dang, Y.; Wang, J. An enhanced multivariable dynamic time-delay discrete grey forecasting model for predicting China’s carbon emissions. Energy 2022, 249, 123681. [Google Scholar] [CrossRef]
- Cai, M.; Ren, C.; Shi, Y.; Chen, G.; Xie, J.; Ng, E. Modeling spatiotemporal carbon emissions for two mega-urban regions in China using urban form and panel data analysis. Sci. Total Environ. 2023, 857, 159612. [Google Scholar] [CrossRef]
- Liu, Z.; Deng, Z.; He, G.; Wang, H.; Zhang, X.; Lin, J.; Qi, Y.; Liang, X. Challenges and opportunities for carbon neutrality in China. Nat. Rev. Earth Environ. 2022, 3, 141–155. [Google Scholar] [CrossRef]
- Heil, M.T.; Selden, T.M. Carbon emissions and economic development: Future trajectories based on historical experience. Environ. Dev. Econ. 2001, 6, 63–83. [Google Scholar] [CrossRef]
- Silvestrini, A.; Veredas, D. Temporal aggregation of univariate and multivariate time series models: A survey. J. Econ. Surv. 2008, 22, 458–497. [Google Scholar] [CrossRef]
- Edinburgh, T.; Eglen, S.J.; Ercole, A. Causality indices for bivariate time series data: A comparative review of performance. ChaosCHAOS 2021, 31, 083111. [Google Scholar] [CrossRef]
- Zhang, L.; Weghe, N.V.D. Attribute trajectory analysis: A framework to analyse attribute changes using trajectory analysis techniques. Int. J. Geogr. Inf. Sci. 2018, 32, 1043–1059. [Google Scholar] [CrossRef]
- Benkert, M.; Gudmundsson, J.; Hübner, F.; Wolle, T. Reporting flock patterns. Comput. Geom. 2008, 41, 111–125. [Google Scholar] [CrossRef] [Green Version]
- Fort, M.; Sellares, J.A.; Valladares, N. A parallel GPU-based approach for reporting flock patterns. Int. J. Geogr. Inf. Sci. 2014, 28, 1877–1903. [Google Scholar] [CrossRef]
- Turdukulov, U.; Romero, A.; Huisman, O.; Retsios, V. Visual mining of moving flock patterns in large spatio-temporal data sets using a frequent pattern approach. Int. J. Geogr. Inf. Sci. 2014, 28, 2013–2029. [Google Scholar] [CrossRef] [Green Version]
- Sanches, D.E.; Alvares, L.O.; Bogorny, V.; Vieira, M.R.; Kaster, D.S. A top-down algorithm with free distance parameter for mining top-k flock patterns. In Proceedings of the 21st AGILE Conference on Geographic Information Science, Lund, Sweden, 12–15 June 2018; pp. 233–249. [Google Scholar]
- Zhang, T.; He, W.; Huang, J.; He, Z.; Li, J. Interactive visual analytics of moving passenger flocks using massive smart card data. Cart. Geogr. Inf. Sci. 2022, 49, 354–369. [Google Scholar] [CrossRef]
- Jeung, H.; Yiu, M.L.; Zhou, X.; Jensen, C.S.; Shen, H.T. Discovery of Convoys in Trajectory Databases. In Proceedings of the VLDB Endowment, Auckland, New Zealand, 23–28 August 2008; pp. 1068–1080. [Google Scholar]
- Yeoman, J.; Duckham, M. Decentralized detection and monitoring of convoy patterns. Int. J. Geogr. Inf. Sci. 2016, 30, 993–1011. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, H.; Li, J.; Chen, Y.; Yang, G.; Wang, J. BP-Model-based convoy mining algorithms for moving objects. Expert Syst. Appl. 2023, 213, 118860. [Google Scholar] [CrossRef]
- Gudmundsson, J.; Kreveld, M.V.; Speckmann, B. Efficient Detection of Patterns in 2D Trajectories of Moving Points. Geoinformatica 2007, 11, 195–215. [Google Scholar] [CrossRef] [Green Version]
- Solera, F.; Calderara, S.; Cucchiara, R. Learning to identify leaders in crowd. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015; pp. 43–48. [Google Scholar]
- Amornbunchornvej, C.; Berger-Wolf, T.Y. Mining and modeling complex leadership–followership dynamics of movement data. Soc. Netw. Anal. Min. 2019, 9, 58. [Google Scholar] [CrossRef]
- Kalnis, P.; Mamoulis, N.; Bakiras, S. On discovering moving clusters in spatio-temporal data. In Proceedings of the Advances in Spatial and Temporal Databases, Angra dos Reis, Brazil, 22–24 August 2005; pp. 364–381. [Google Scholar]
- Patel, D. On discovery of spatiotemporal influence-based moving clusters. ACM Trans. Intell. Syst. Technol. 2015, 6, 1–23. [Google Scholar] [CrossRef]
- Loglisci, C. Using interactions and dynamics for mining groups of moving objects from trajectory data. Int. J. Geogr. Inf. Sci. 2018, 32, 1436–1468. [Google Scholar] [CrossRef]
- Carbon Emission Accounts and Datasets for Emerging Economies. Available online: https://ceads.net (accessed on 1 September 2022).
- Zhang, P.; Li, H. Visually Exploring the Carbon Emissions in China from a Multi-Temporal Scale Perspective: A Case Study on the Province-Level CO2 Emissions. In Proceedings of the 29th International Conference on Geoinformatics, Beijing, China, 15–18 August 2022; pp. 1–6. [Google Scholar]



| Province | ID | Geographical Region | ID |
|---|---|---|---|
| Beijing | 1 | North China | 1 |
| Tianjin | 2 | ||
| Hebei | 3 | ||
| Shanxi | 4 | ||
| Inner Mongolia | 5 | ||
| Liaoning | 6 | Northeast China | 2 |
| Jilin | 7 | ||
| Heilongjiang | 8 | ||
| Shanghai | 9 | East China | 3 |
| Jiangsu | 10 | ||
| Zhejiang | 11 | ||
| Anhui | 12 | ||
| Fujian | 13 | ||
| Jiangxi | 14 | ||
| Shandong | 15 | ||
| Henan | 16 | Central China | 4 |
| Hubei | 17 | ||
| Hunan | 18 | ||
| Guangdong | 19 | South China | 5 |
| Guangxi | 20 | ||
| Hainan | 21 | ||
| Chongqing | 22 | Southwest China | 6 |
| Sichuan | 23 | ||
| Guizhou | 24 | ||
| Yunnan | 25 | ||
| Shaanxi | 26 | Northwest China | 7 |
| Gansu | 27 | ||
| Qinghai | 28 | ||
| Ningxia | 29 | ||
| Xinjiang | 30 |
| Criterion | Explanation | Type ID |
|---|---|---|
| The high–low attribute values | High X attribute value and high Y attribute value | A |
| High X attribute value and low Y attribute value | B | |
| Low X attribute value and high Y attribute value | C | |
| Low X attribute value and low Y attribute value | D | |
| The extreme number–duration values | Maximum number and longest duration | I |
| Maximum number and shortest duration | II | |
| Minimum number and longest duration | III | |
| Minimum number and shortest duration | IV |
| ID | Geographical Flock | Corresponding Provinces | Type ID |
|---|---|---|---|
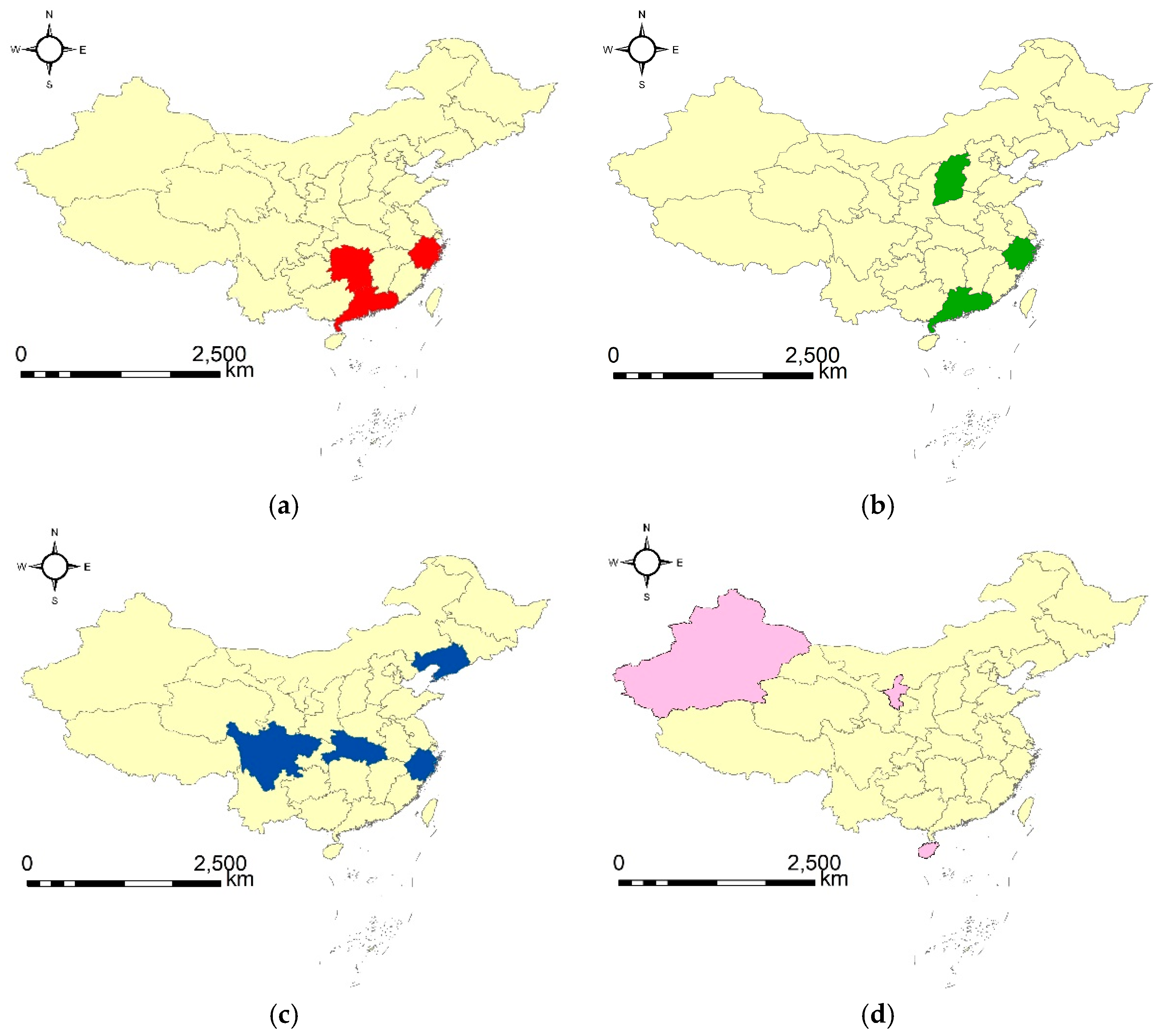
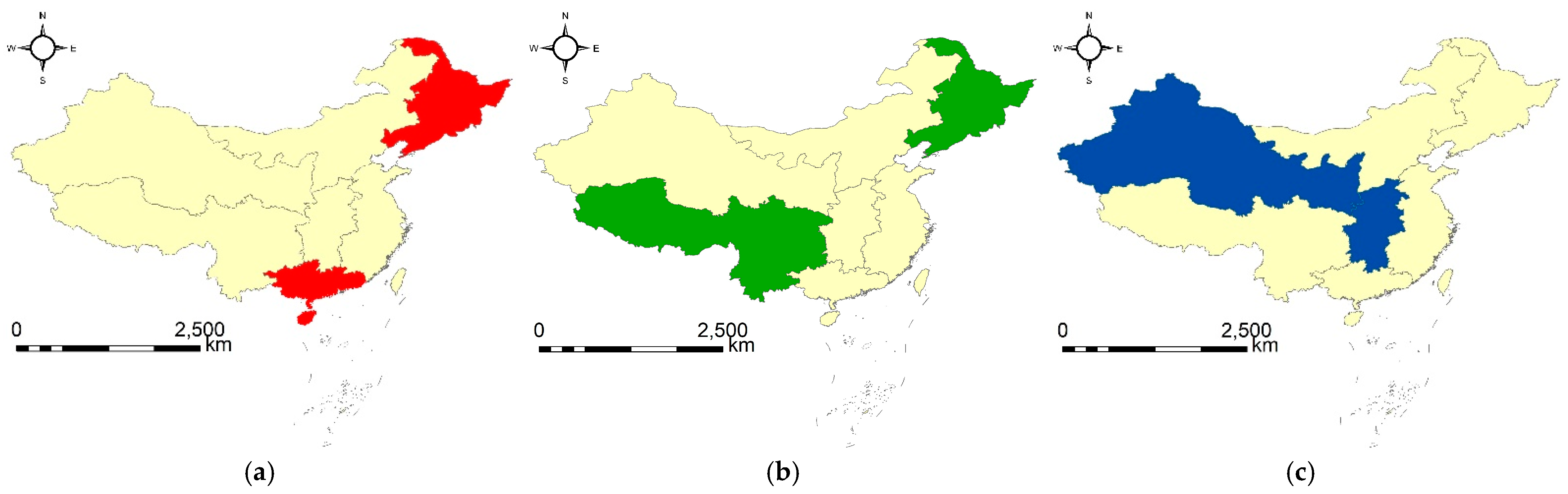
| 1 | {11, 18, 19}|[2012, 2014] | Zhejiang, Hunan, Guangdong | B |
| 2 | {4, 11, 19}|[2013, 2015] | Shanxi, Zhejiang, Guangdong | B |
| 3 | {6, 11, 17, 23}|[2014, 2016] | Liaoning, Zhejiang, Hubei, Sichuan | B |
| 4 | {21, 29, 30}|[2002, 2004] | Hainan, Ningxia, Xinjiang | C |
| ID | Geographical Flock | Corresponding Provinces | Type ID |
|---|---|---|---|
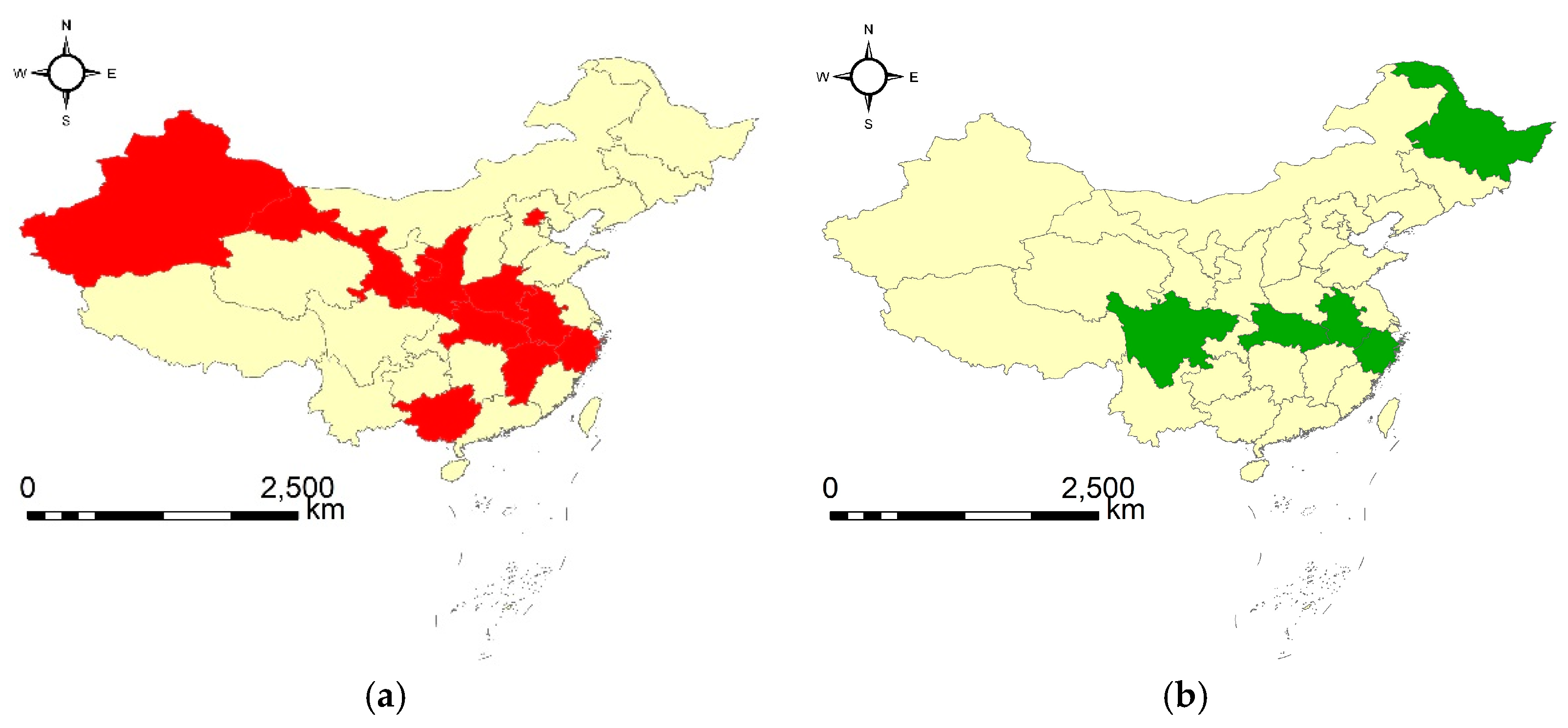
| 1 | {1, 4, 11, 12, 14, 16, 17, 20, 27, 30}|[1998, 2000] | Beijing, Shanxi, Zhejiang, Anhui, Jiangxi, Henan, Hubei, Guangxi, Gansu, Xinjiang | II |
| 2 | {8, 11, 12, 17, 23}|[2014, 2017] | Heilongjiang, Zhejiang, Anhui, Hubei, Sichuan | III |
| ID | Geographical Flock | Corresponding Provinces | Type ID |
|---|---|---|---|
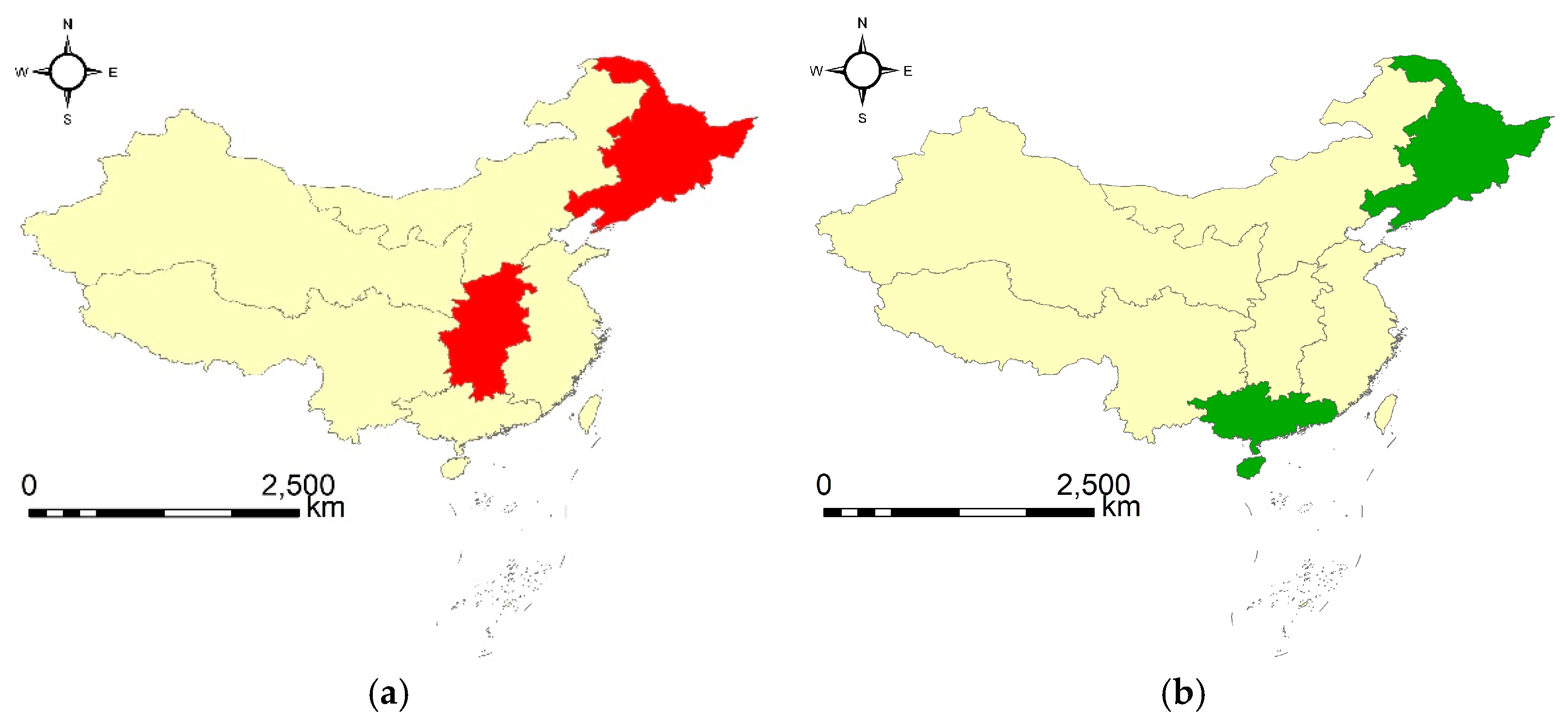
| 1 | {2, 4}|[2015, 2018] | Northeast China, Central China | B |
| 2 | {2, 5}|[2005, 2007] | Northeast China, South China | C |
| ID | Geographical Flock | Corresponding Provinces | Type ID |
|---|---|---|---|
| 1 | {2, 5}|[2005, 2008] | Northeast China, South China | I, III |
| 2 | {2, 6}|[2013, 2016] | Northeast China, Southwest China | I, III |
| 3 | {4, 7}|[2014, 2016] | Central China, Northwest China | II, IV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Miao, L.; Wang, F.; Li, X. Discovering Geographical Flock Patterns of CO2 Emissions in China Using Trajectory Mining Techniques. Int. J. Environ. Res. Public Health 2023, 20, 4265. https://doi.org/10.3390/ijerph20054265
Zhang P, Miao L, Wang F, Li X. Discovering Geographical Flock Patterns of CO2 Emissions in China Using Trajectory Mining Techniques. International Journal of Environmental Research and Public Health. 2023; 20(5):4265. https://doi.org/10.3390/ijerph20054265
Chicago/Turabian StyleZhang, Pengdong, Lizhi Miao, Fei Wang, and Xinting Li. 2023. "Discovering Geographical Flock Patterns of CO2 Emissions in China Using Trajectory Mining Techniques" International Journal of Environmental Research and Public Health 20, no. 5: 4265. https://doi.org/10.3390/ijerph20054265
APA StyleZhang, P., Miao, L., Wang, F., & Li, X. (2023). Discovering Geographical Flock Patterns of CO2 Emissions in China Using Trajectory Mining Techniques. International Journal of Environmental Research and Public Health, 20(5), 4265. https://doi.org/10.3390/ijerph20054265






