Particle Deposition in Large-Scale Human Tracheobronchial Airways Predicted by Single-Path Modelling
Abstract
:1. Introduction
2. Methods
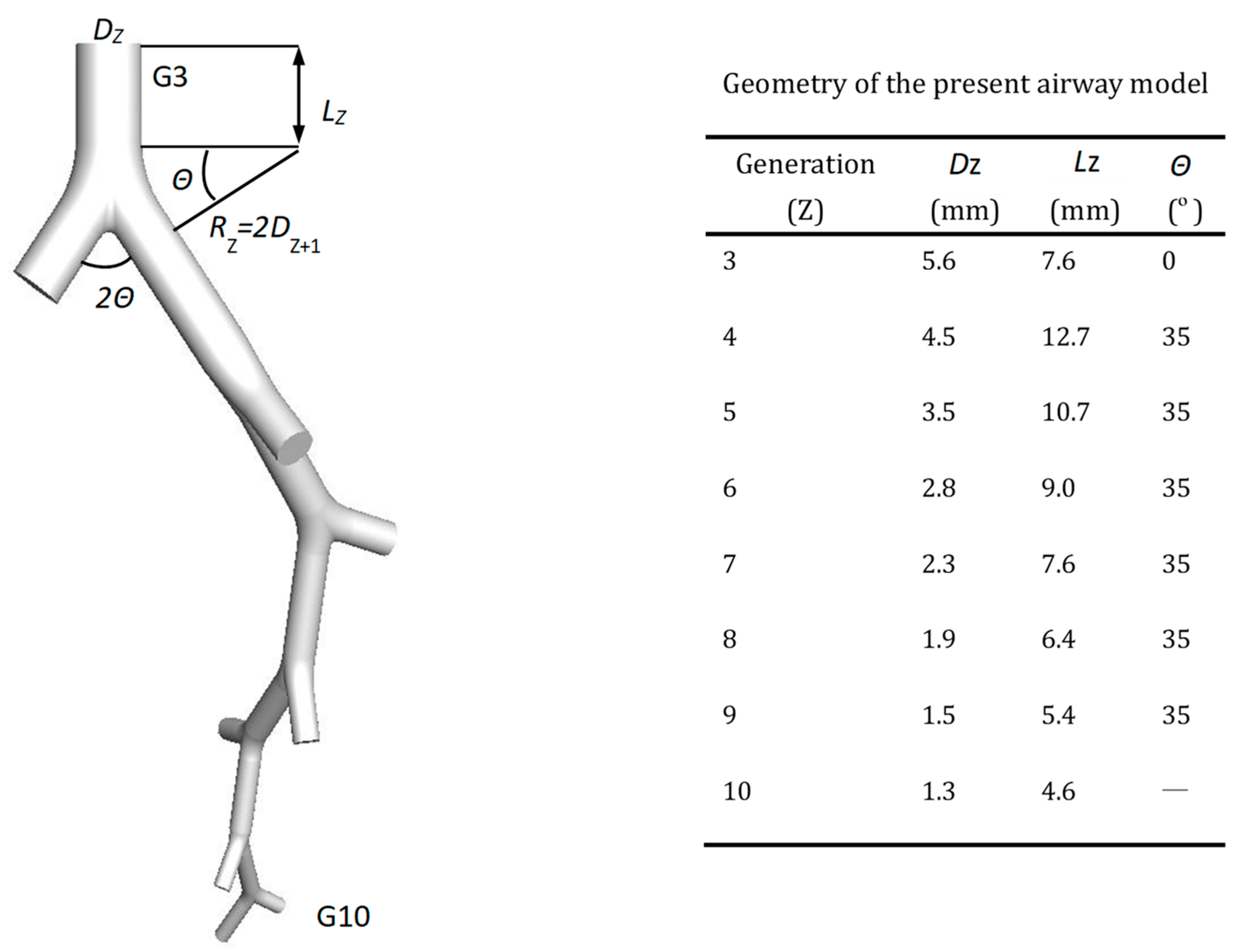
2.1. Truncated Airway Model
2.2. Governing Equations
2.3. Boundary Conditions
2.4. Particle Deposition Efficiency
2.5. Numerical Methods
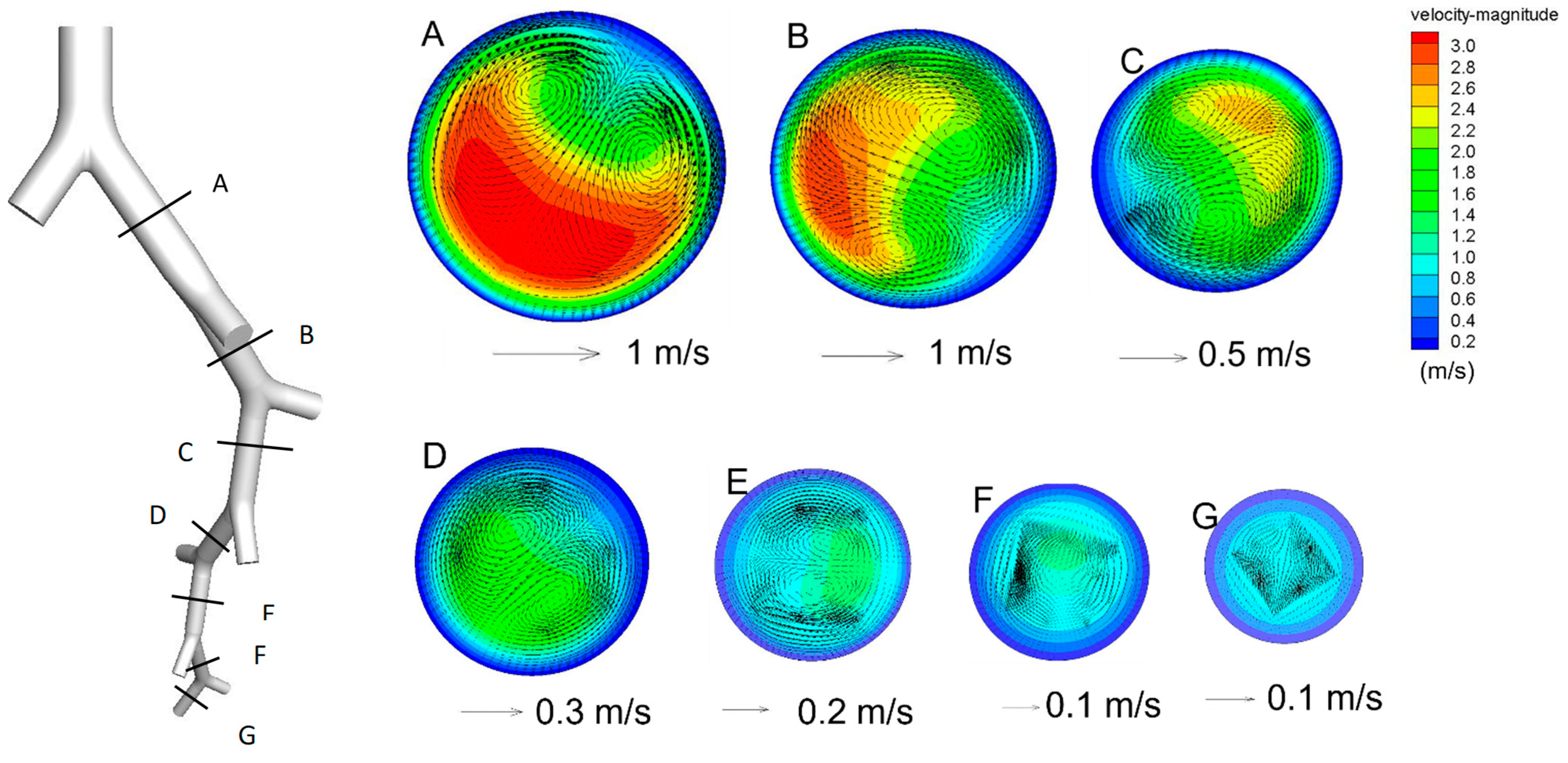
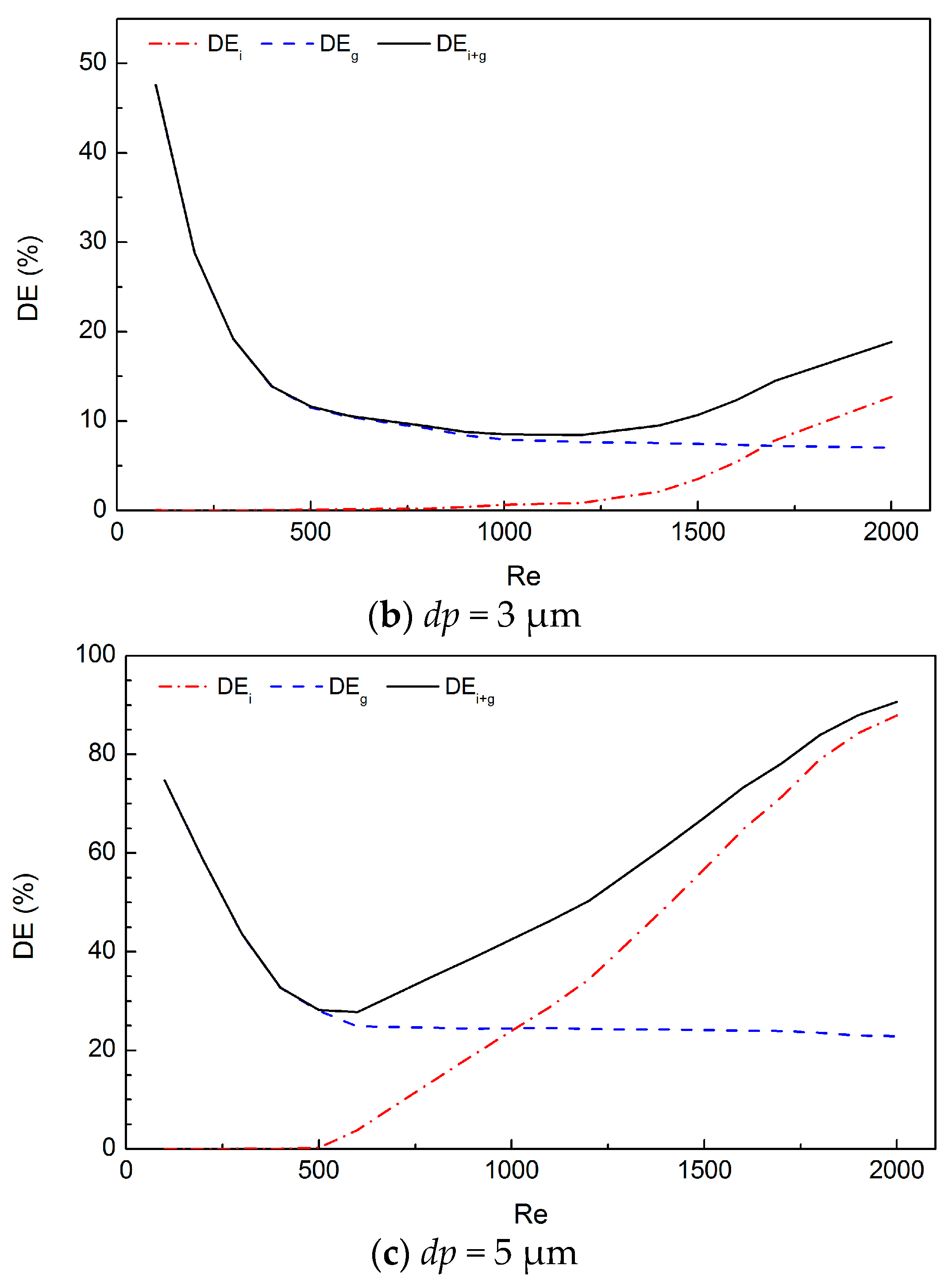
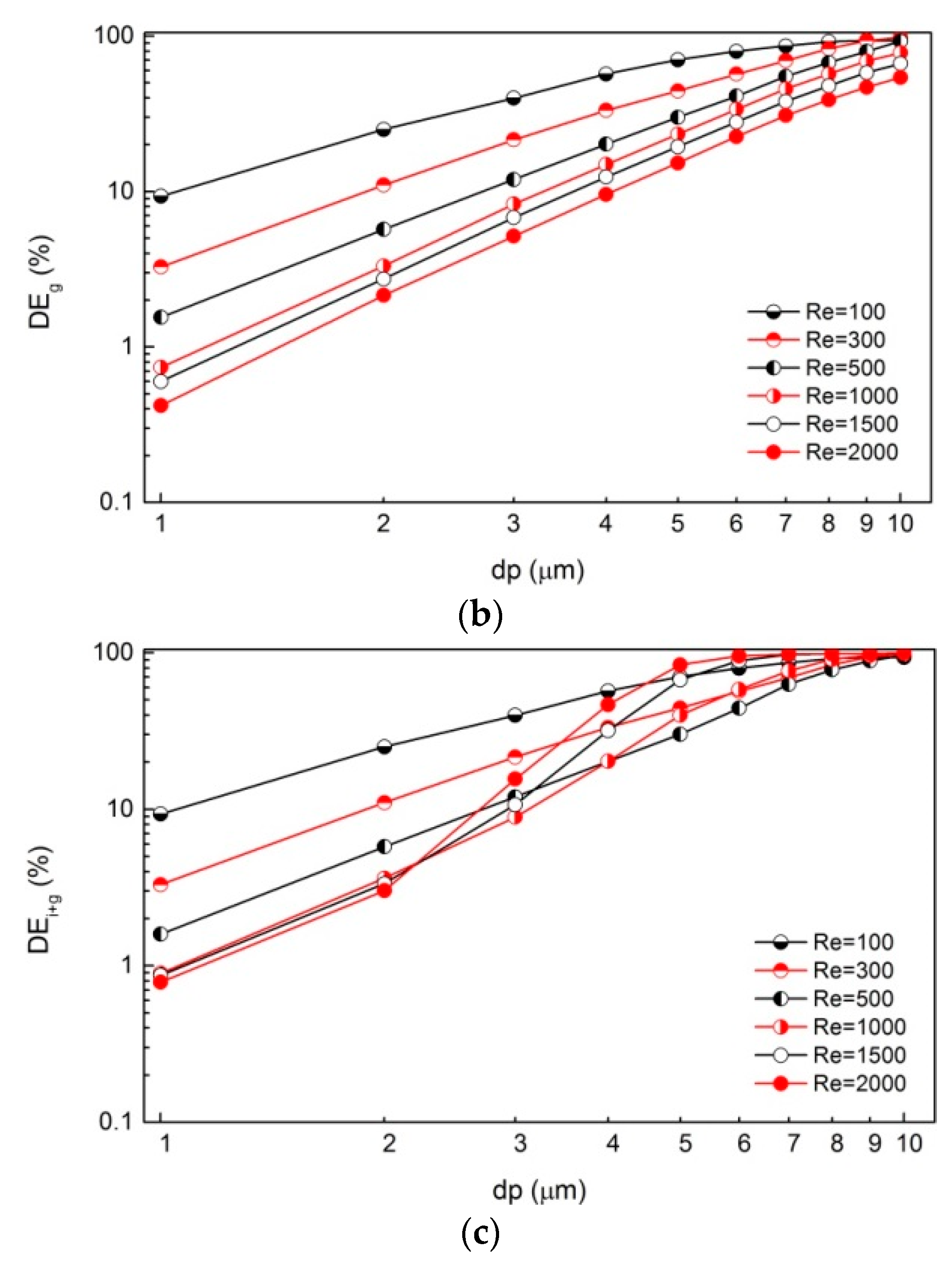
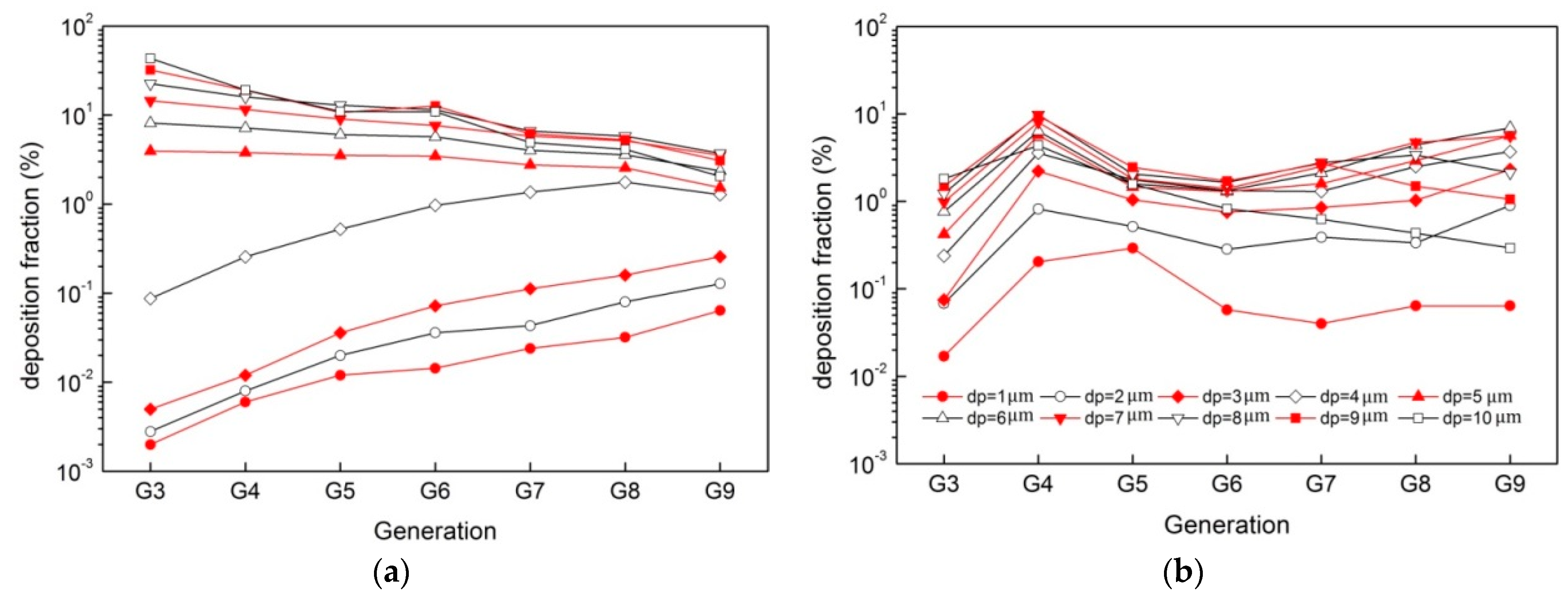
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wyzga, R.; Rohr, A.C. Long-term particulate matter exposure: Attributing health effects to individual PM components. J. Air Waste Manag. Assoc. 2015, 65, 523–543. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dockery, D. Health effects of particulate air pollution. Ann. Epidemiol. 2009, 19, 257–263. [Google Scholar] [CrossRef] [Green Version]
- Xue, T.; Zhang, Q. Associating ambient exposure to fine particles and human fertility rates in China. Environ. Pollut. 2018, 235, 497–504. [Google Scholar] [CrossRef]
- Achilleos, S.; Kioumourtzoglou, M.; Wu, C.; Schwartz, J.; Koutrakis, P.; Papatheodorou, S. Acute effects of fine particulate matter constituents on mortality: A systematic review and meta-regression analysis. Environ. Int. 2017, 109, 89–100. [Google Scholar] [CrossRef]
- Neuberger, M.; Schimek, M.; Horak, F.; Moshammer, H.; Kundi, M.; Frischer, T.; Gomiscek, B.; Puxbaum, H.; Hauck, H. Acute effects of particulate matter on respiratory diseases, symptoms and functions: Epidemiological results of the Austrian Project on Health Effects of Particulate Matter (AUPHEP). Atmos. Environ. 2004, 38, 3971–3981. [Google Scholar] [CrossRef]
- An, Z.; Jin, Y.; Li, J.; Li, W.; Wu, W. Impact of Particulate air pollution on cardiovascular health. Curr. Allergy Asthma Rep. 2018, 18, 15. [Google Scholar] [CrossRef] [PubMed]
- Scungio, M.; Stabile, L.; Rizza, V.; Pacitto, A.; Russi, A.; Buonanno, G. Lung cancer risk assessment due to traffic-generated particles exposure in urban street canyons: A numerical modelling approach. Sci. Total Environ. 2018, 631–632, 1109–1116. [Google Scholar] [CrossRef]
- Pope, C., III; Burnett, R.T.; Thun, M.J.; Calle, E.E.; Krewski, D.; Ito, K.; Thurston, G.D. Lung cancer, cardiopulmonary mortality, and long-term exposure to fine particulate air pollution. JAMA 2002, 287, 1132–1141. [Google Scholar] [CrossRef] [Green Version]
- Gao, P.; Hu, J.; Song, J.; Chen, X.; Ou, C.; Wang, H.; Sha, C.; Hang, J.; Xing, B. Inhalation bioaccessibility of polycyclic aromatic hydrocarbons in heavy PM2.5 pollution days: Implications for public health risk assessment in northern China. Environ. Pollut. 2019, 255, 113296. [Google Scholar] [CrossRef] [PubMed]
- Al-Hemoud, A.; Gasana, J.; Al-Dabbous, A.; Alajeel, A.; Al-Shatti, A.; Behbehani, W.; Malak, M. Exposure levels of air pollution (PM2.5) and associated health risk in Kuwait. Environ. Res. 2019, 179, 108730. [Google Scholar] [CrossRef]
- Prata, J.; da Costa, J.; Lopes, I.; Duarte, A.; Rocha-Santos, T. Environmental exposure to microplastics: An overview on possible human health effects. Sci. Total Environ. 2020, 702, 134455. [Google Scholar] [CrossRef] [PubMed]
- Thompson, J. Airborne Particulate Matter: Human Exposure and Health Effects. J. Occup. Environ. Med. 2018, 60, 392–423. [Google Scholar] [CrossRef] [PubMed]
- Ou, C.; Hu, S.; Luo, K.; Yang, H.; Hang, J.; Cheng, P.; Hai, Z.; Xiao, S.; Qian, H.; Xiao, S.; et al. Insufficient ventilation led to a probable long-range airborne transmission of SARS-CoV-2 on two buses. Build. Environ. 2022, 207, 108414. [Google Scholar]
- Fernández Tena, A.; Casan Clarà, P. Deposition of inhaled particles in the lungs. Arch. Bronconeumol. 2012, 48, 240–246. [Google Scholar] [CrossRef] [PubMed]
- Deng, Q.; Deng, L.; Miao, Y.; Guo, X.; Li, Y. Particle deposition in the human lung: Health implications of particulate matter from different sources. Environ. Res. 2019, 169, 237–245. [Google Scholar] [CrossRef]
- Ou, C.; Hang, J.; Deng, Q. Particle deposition in human lung airways: Effects of airflow, particle size, and mechanisms. Aerosol Air Qual. Res. 2020, 20, 2846–2858. [Google Scholar] [CrossRef]
- Chen, X.; Feng, Y.; Zhong, W.; Sun, B.; Tao, F. Numerical investigation of particle deposition in a triple bifurcation airway due to gravitational sedimentation and inertial impaction. Powder Technol. 2018, 323, 284–293. [Google Scholar] [CrossRef]
- Deng, Q.; Ou, C.; Chen, J.; Xiang, Y. Particle deposition in tracheobronchial airways of an infant, child and adult. Sci. Total Environ. 2018, 612, 339–346. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Kleinstreuer, C. Micron-particle transport, interactions and deposition in triple lung-airway bifurcations using a novel modeling approach. J. Aerosol Sci. 2014, 71, 1–15. [Google Scholar] [CrossRef]
- Comer, J.; Kleinstreuer, C.; Hyun, S.; Kim, C. Aerosol transport and deposition in sequentially bifurcating airways. J. Biomech. Eng. 2000, 122, 152–158. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; So, R.; Yang, J. The effect of inlet velocity profile on the bifurcation COPD airway flow. Comput. Biol. Med. 2006, 36, 181–194. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Zhang, Z. An Adjustable Triple-bifurcation unit model for air-particle flow simulations in human tracheobronchial airways. J. Biomech. Eng. 2008, 131, 021007. [Google Scholar] [CrossRef]
- Kolanjiyil, A.; Kleinstreuer, C. Nanoparticle mass transfer from lung airways to systemic regions—Part I: Whole-lung aerosol dynamics. J. Biomech. Eng. 2013, 135, 121003. [Google Scholar] [CrossRef]
- Nowak, N.; Kakade, P.; Annapragada, A. Computational fluid dynamics simulation of airflow and aerosol deposition in human lungs. Ann. Biomed. Eng. 2003, 31, 374–390. [Google Scholar] [CrossRef]
- Zhang, Z.; Kleinstreuer, C.; Kim, C. Airflow and nanoparticle deposition in a 16-generation tracheobronchial airway model. Ann. Biomed. Eng. 2008, 36, 2095–2110. [Google Scholar] [CrossRef] [PubMed]
- van Ertbruggen, C.; Hirsch, C.; Paiva, M. Anatomically based three-dimensional model of airways to simulate flow and particle transport using computational fluid dynamics. J. Appl. Physiol. 2005, 98, 970–980. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gemci, T.; Ponyavin, V.; Chen, Y.; Chen, H.; Collins, R. Computational model of airflow in upper 17 generations of human respiratory tract. J. Biomech. 2008, 41, 2047–2054. [Google Scholar] [CrossRef] [PubMed]
- Walters, D.; Luke, W. A Method for Three-dimensional Navier–Stokes simulations of large-scale regions of the human lung Airway. J. Fluids Eng. 2010, 132, 051101. [Google Scholar] [CrossRef]
- Walters, D.; Luke, W. Computational fluid dynamics simulations of particle deposition in large-scale, multigenerational lung models. J. Biomech. Eng. 2010, 133, 011003–011008. [Google Scholar] [CrossRef]
- Tian, G.; Longest, P.; Su, G.; Walenga, R.; Hindle, M. Development of a stochastic individual path (SIP) model for predicting the tracheobronchial deposition of pharmaceutical aerosols: Effects of transient inhalation and sampling the airways. J. Aerosol Sci. 2011, 42, 781–799. [Google Scholar] [CrossRef]
- Ou, C.; Li, Y.; Wei, J.; Yen, H.; Deng, Q. Numerical modeling of particle deposition in ferret airways: A comparison with humans. Aerosol Sci. Technol. 2017, 51, 477–487. [Google Scholar] [CrossRef] [Green Version]
- Weibel, E.; Cournand, A.; Richards, D. Morphometry of the Human Lung; Springer: Berlin/Heidelberg, Germany, 1963. [Google Scholar]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Yeh, H.; Schum, G. Models of human lung airways and their application to inhaled particle deposition. Bull. Math. Biol. 1980, 42, 461–480. [Google Scholar] [CrossRef]
- Longest, P.; Vinchurkar, S. Effects of mesh style and grid convergence on particle deposition in bifurcating airway models with comparisons to experimental data. Med. Eng. Phys. 2007, 29, 350–366. [Google Scholar] [CrossRef]
- Hyatt, R.; Wilcox, R. The pressure-flow relationships of the intrathoracic airway in man. J. Clin. Investig. 1963, 42, 29–39. [Google Scholar] [CrossRef]
- Tena, A.; Joaquín, F.; Eduardo, Á.; Pere, C.; Keith, W. Design of a numerical model of lung by means of a special boundary condition in the truncated branches. Int. J. Numer. Method Biomed. Eng. 2017, 33, e2830. [Google Scholar] [CrossRef] [PubMed]
- Farkas, Á.; Balásházy, I. Quantification of particle deposition in asymmetrical tracheobronchial model geometry. Comput. Biol. Med. 2008, 38, 508–518. [Google Scholar] [CrossRef]
- Inthavong, K.; Choi, L.; Tu, J.; Ding, S.; Thien, F. Micron particle deposition in a tracheobronchial airway model under different breathing conditions. Med. Eng. Phys. 2010, 32, 1198–1212. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Kleinstreuer, C.; Zhang, Z. Simulation of airflow fields and microparticle deposition in realistic human lung airway models. Part I: Airflow patterns. Eur. J. Mech. B Fluids. 2007, 26, 632–649. [Google Scholar] [CrossRef]
- Comer, J.; Kleinstreuer, C.; Kim, C. Flow structures and particle deposition patterns in double-bifurcation airway models. Part 2. Aerosol transport and deposition. J. Fluid Mech. 2001, 435, 55–80. [Google Scholar] [CrossRef]
- Zhang, Z.; Kleinstreuer, C. Transient airflow structures and particle transport in a sequentially branching lung airway model. Phys Fluids. 2002, 14, 862–880. [Google Scholar] [CrossRef]
- Rahimi-Gorji, M.; Gorji, T.; Gorji-Bandpy, M. Details of regional particle deposition and airflow structures in a realistic model of human tracheobronchial airways: Two-phase flow simulation. Comput. Biol. Med. 2016, 74, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Kleinstreuer, C.; Zhang, Z. Particle deposition in the human tracheobronchial airways due to transient inspiratory flow patterns. J. Aerosol Sci. 2007, 38, 625–644. [Google Scholar] [CrossRef]
- Hegedűs, C.; Balásházy, I.; Farkas, Á. Detailed mathematical description of the geometry of airway bifurcations. Respir. Physiol. Neurobiol. 2004, 141, 99–114. [Google Scholar] [CrossRef]
- Hofmann, W. Modelling inhaled particle deposition in the human lung—A review. J. Aerosol Sci. 2011, 42, 693–724. [Google Scholar] [CrossRef]
- Darquenne, C. Aerosol deposition in health and disease. J. Aerosol Med. Pulm. Drug Deliv. 2012, 25, 140–147. [Google Scholar] [CrossRef] [Green Version]
- Kleinstreuer, C.; Zhang, Z.; Kim, C. Combined inertial and gravitational deposition of microparticles in small model airways of a human respiratory system. J. Aerosol Sci. 2007, 38, 1047–1061. [Google Scholar] [CrossRef]
- Lee, J.; Goo, J.; Chung, M. Characteristics of inertial deposition in a double bifurcation. J. Aerosol Sci. 1996, 27, 119–138. [Google Scholar] [CrossRef]
- Longest, P.; Xi, J. Computational investigation of particle inertia effects on submicron aerosol deposition in the respiratory tract. J. Aerosol Sci. 2007, 38, 111–130. [Google Scholar] [CrossRef]
- Heyder, J. Deposition of inhaled particles in the human respiratory tract and consequences for regional targeting in respiratory drug delivery. Proc. Am. Thorac Soc. 2004, 1, 315–320. [Google Scholar] [CrossRef] [PubMed]
- Soni, B.; Aliabadi, S. Large-scale CFD simulations of airflow and particle deposition in lung airway. Comput. Fluids. 2013, 88, 804–812. [Google Scholar] [CrossRef]
- Fishler, R.; Ostrovski, Y.; Lu, C.; Sznitman, J. Streamline crossing: An essential mechanism for aerosol dispersion in the pulmonary acinus. J. Biomech. 2017, 50, 222–227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harrington, L.; Prisk, G.; Darquenne, C. Importance of the bifurcation zone and branch orientation in simulated aerosol deposition in the alveolar zone of the human lung. J. Aerosol Sci. 2006, 37, 37–62. [Google Scholar] [CrossRef]
- Balashazy, I.; Alfoldy, B.; Molnar, A.; Hofmann, W.; Szoke, I.; Kis, E. Aerosol drug delivery optimization by computational methods for the characterization of total and regional deposition of therapeutic aerosols in the respiratory system. Curr. Comput. Aided Drug Des. 2007, 3, 13–32. [Google Scholar] [CrossRef]
- Martonen, T.; Katz, I. Deposition patterns of aerosolized drugs within human lungs: Effects of ventilatory parameters. Pharm. Res. 1993, 10, 871–878. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Zhou, Y.; Su, W. Deposition of particles in human mouth-throat replicas and a USP induction port. J. Aerosol Med. Pulm. Drug Deliv. 2015, 28, 147. [Google Scholar] [CrossRef]
- Sul, B.; Wallqvist, A.; Morris, M.; Reifman, J.; Rakesh, V. A computational study of the respiratory airflow characteristics in normal and obstructed human airways. Comput. Biol. Med. 2014, 52, 130–143. [Google Scholar] [CrossRef]
- Xi, J.; Yuan, J.; Yang, M.; Si, X.; Zhou, Y.; Cheng, Y. Parametric study on mouth–throat geometrical factors on deposition of orally inhaled aerosols. J. Aerosol Sci. 2016, 99, 94–106. [Google Scholar] [CrossRef]
- Lai, T.; Morsi, S.; Das, S.; Owida, A. Numerical analysis of particle deposition in asymmetrical human upper airways under different inhalation cycles. J. Mech. Med. Biol. 2013, 13, 75–277. [Google Scholar] [CrossRef]
- Park, S.; Wexler, A. Size-dependent deposition of particles in the human lung at steady-state breathing. J. Aerosol Sci. 2008, 39, 266–276. [Google Scholar] [CrossRef]
- Phuong, N.; Yamashita, M.; Yoo, S.; Ito, K. Prediction of convective heat transfer coefficient of human upper and lower airway surfaces in steady and unsteady breathing conditions. Build. Environ. 2016, 100, 172–185. [Google Scholar] [CrossRef]
- Rahimi-Gorji, M.; Pourmehran, O.; Gorji-Bandpy, M.; Gorji, T. CFD simulation of airflow behavior and particle transport and deposition in different breathing conditions through the realistic model of human airways. J. Mol. Liq. 2015, 209, 121–133. [Google Scholar] [CrossRef]
- Zhang, Z.; Kleinstreuer, C. Effect of particle inlet distributions on deposition in a triple bifurcation lung airway model. J. Aerosol Med. 2001, 14, 13–29. [Google Scholar] [CrossRef] [PubMed]





| dp (μm) | Re = 500 | Re = 1000 | Re = 1500 | Re = 2000 |
|---|---|---|---|---|
| 1 | (0.72) | (0.72) | (0.79) | (0.79) |
| 2 | (0.36) | (0.42) | (0.49) | (0.43) |
| 3 | (0.01) | (0.19) | (0.41) | (0.55) |
| 4 | 0.22 | (0.20) | (0.50) | (0.61) |
| 5 | 0.37 | (0.26) | (0.55) | (0.57) |
| 6 | 0.19 | (0.23) | (0.45) | (0.42) |
| 7 | 0.02 | (0.22) | (0.34) | (0.28) |
| 8 | (0.06) | (0.20) | (0.23) | (0.16) |
| 9 | (0.10) | (0.14) | (0.13) | (0.10) |
| 10 | (0.10) | (0.10) | (0.07) | (0.06) |
| Mean relative error | (0.21) | (0.27) | (0.40) | (0.40) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, C.; Hang, J.; Hua, J.; Li, Y.; Deng, Q.; Zhao, B.; Ling, H. Particle Deposition in Large-Scale Human Tracheobronchial Airways Predicted by Single-Path Modelling. Int. J. Environ. Res. Public Health 2023, 20, 4583. https://doi.org/10.3390/ijerph20054583
Ou C, Hang J, Hua J, Li Y, Deng Q, Zhao B, Ling H. Particle Deposition in Large-Scale Human Tracheobronchial Airways Predicted by Single-Path Modelling. International Journal of Environmental Research and Public Health. 2023; 20(5):4583. https://doi.org/10.3390/ijerph20054583
Chicago/Turabian StyleOu, Cuiyun, Jian Hang, Jiajia Hua, Yuguo Li, Qihong Deng, Bo Zhao, and Hong Ling. 2023. "Particle Deposition in Large-Scale Human Tracheobronchial Airways Predicted by Single-Path Modelling" International Journal of Environmental Research and Public Health 20, no. 5: 4583. https://doi.org/10.3390/ijerph20054583
APA StyleOu, C., Hang, J., Hua, J., Li, Y., Deng, Q., Zhao, B., & Ling, H. (2023). Particle Deposition in Large-Scale Human Tracheobronchial Airways Predicted by Single-Path Modelling. International Journal of Environmental Research and Public Health, 20(5), 4583. https://doi.org/10.3390/ijerph20054583








