Early COVID-19 Pandemic Preparedness: Informing Public Health Interventions and Hospital Capacity Planning Through Participatory Hybrid Simulation Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Participatory Modeling to the COVID-19 Pandemic
2.1.1. Our Approach to Participatory Modeling: Purpose and Stakeholder Roles
2.1.2. Study Context and Background
2.2. Participatory Modeling Processes
- Establish initial buy-in via proof-of-concept modeling: We started developing proof-of-concept epidemiological models of COVID-19 transmission in late January 2020 to simulate the outbreak in China. The first version of the hybrid model presented in this study was completed in early February, before any COVID-19 cases were detected in Canada. This initial work was carried out by the academic modeling team led by N.O. [2]. The early work allowed us to quickly adapt the model to the Canadian context as the pandemic progressed. In addition, our team’s prior success in using participatory modeling for healthcare policy decisions in Saskatchewan [34] had built a solid foundation for collaboration, as many stakeholders were already familiar with dynamic modeling approaches and had worked with the modelers before. These two factors enabled us to act quickly. By 16 March 2020—just four days after the first confirmed COVID-19 case in Saskatchewan—we delivered our first presentation to stakeholders in the Saskatchewan Health Authority. We introduced the modeling approaches and presented early findings from the proof-of-concept COVID-19 modeling work. This meeting was crucial for gaining initial buy-in for using simulation modeling to guide rapid pandemic response. Drawing from experience in earlier participatory modeling work, we presented the modeling approaches in a less technical way and explained how these models could be used as a tool to simulate “what-if” intervention scenarios and make projections on epidemic curves under different assumptions to support decision-making. We clarified that the models were developed for making projections but not predictions. This distinction helped stakeholders understand the scope and purpose of these simulation models and avoided potential misinterpretation or misuse of the model results. This is crucial in the early stages when there were so many unknowns about COVID-19 transmission. The presentation included projections of epidemic curves under various intervention scenarios, including preliminary results of how enhanced contact tracing could help flatten the curve using an earlier version of the hybrid model presented in this study. Given that Saskatchewan was still in a very early stage of the COVID-19 pandemic, we highlighted both challenges and immediate actions that could be taken to mitigate the transmission. The initial modeling work drew significant interest among the stakeholders, leading to a follow-up presentation to the senior executive leadership team in Saskatchewan Health Authority on 19 March 2020.
- Assembling the modeling support team: The quick response and use of proof-of-concept COVID-19 models helped secure buy-in with the stakeholders. By the end of March 2020, the academic modeling team was seconded to the Saskatchewan Health Authority with the mandate to provide modeling support for the province’s pandemic response. The team was co-led by J.B. and N.O., with infectious disease modelers (including Y.T. and W.M.), data analysts, and additional analytical support from Saskatchewan Health Authority and Ministry of Health. Notably, three members of the team (Y.T., N.O., and J.B.) were also key members in earlier participatory modeling work [34], who had worked closely with stakeholders throughout the participatory modeling processes. The team lead (J.B.), who previously acted as the project champion and physician lead in earlier participatory modeling efforts [34], was the senior medical information officer for the health authority when this study was conducted. She played a key role in advocating for modeling approaches and interpreting modeling concepts and results in languages friendly to the stakeholders to facilitate knowledge translation. The team was in direct and frequent communication with decision-makers and public health officials.
- Problem conceptualization: The primary objective of the modeling team was to support the decision-makers in addressing the urgent decision-making needs. It is worth noting that the team developed several COVID-19 transmission models, using different modeling approaches, to address different objectives and policy questions [2]. The hybrid COVID-19 model presented in this study focused on addressing questions related to non-pharmaceutical public health interventions and hospital capacity planning in the early pandemic: (1) How many infections and deaths are expected under different intervention scenarios and model assumptions? (2) What are the estimated acute care resource needs? (3) What are the effects of non-pharmaceutical public health interventions (e.g., contact tracing, physical distancing, quarantine, and isolation) on those outcomes?
- Model implementation, model validation, and model use: The initial proof-of-concept hybrid model was continuously refined in response to policy requests posed by stakeholders. The model’s inputs and assumptions were reviewed and updated through a collaborative and iterative process. This included analyses of provincial epidemiological surveillance data, weekly scans of scientific evidence conducted by national and provincial research teams, and ongoing consultation with epidemiologists to update and review model inputs and results. This iterative process ensured that the hybrid model incorporated best estimates based on emerging evidence and new surveillance data. As the hybrid model was regularly adapted to reflect new evidence and evolving policy needs, we also conducted regular model validation through model verification, face validation, and cross-validation. Through routine meetings, the team leads presented model results in response to policy questions posed by decision-makers and medical health officers, while also addressing uncertainties and underlying model assumptions. The modeling results were also communicated to the general public through press briefings by the Saskatchewan Health Authority and the Ministry of Health on 28 April 2020 [38].
- Progress until June 2020: The hybrid model presented in this study was actively used until June 2020, playing a key role in informing public health decisions during the early stages of the pandemic. As decision-making shifted towards planning for gradual reopening, addressing the subsequent waves, understanding new variants, and preparing for vaccination rollout at the end of the year, the focus of modeling efforts evolved. Other simulation models were developed by the modeling support team and were continuously used to inform public health policies throughout these transitions [2].
2.3. The Hybrid Simulation Model
2.3.1. System Dynamics Sub-Model of COVID-19 Transmission
- Susceptible Individuals (): individuals who are susceptible to COVID-19 infection and not in quarantine.
- Quarantined Susceptible Individuals (): susceptible individuals who are quarantined.
- Non-isolated Exposed Individuals (): latently infected individuals who are not isolated.
- Isolated Exposed Individuals (): latently infected individuals who are isolated.
- Non-isolated Infectious Presymptomatic Individuals (): non-isolated infectious individuals who have not yet shown any symptoms of COVID-19 infection.
- Isolated Infectious Presymptomatic Individuals (): infectious presymptomatic individuals who are isolated.
2.3.2. Agent-Based Sub-Model of COVID-19 Disease Progression and Contact Tracing
2.3.3. Discrete-Event Simulation Sub-Model for COVID-19 Related Hospital Care
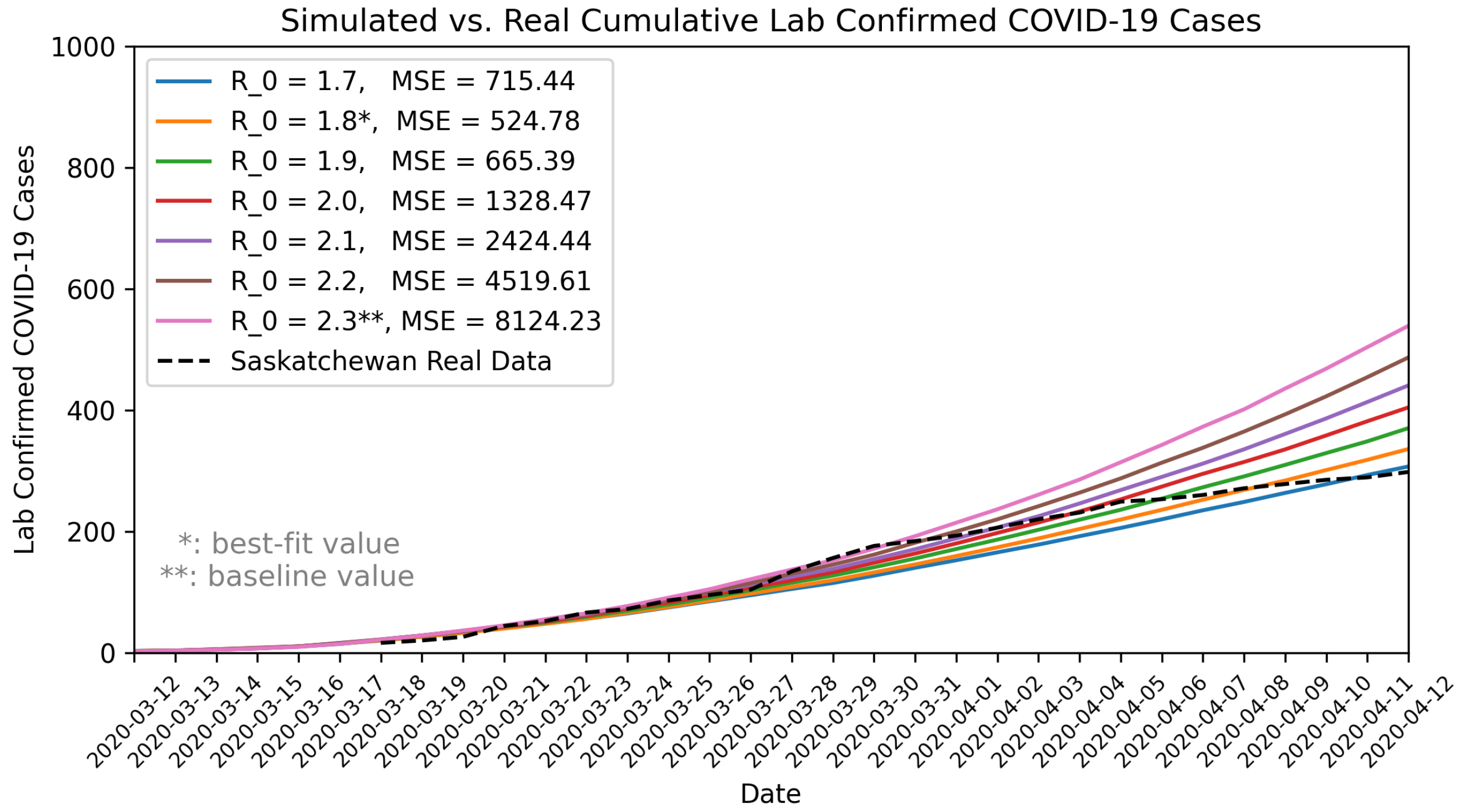
2.4. Model Validation
2.5. Intervention Scenarios
3. Results
3.1. Model Validation
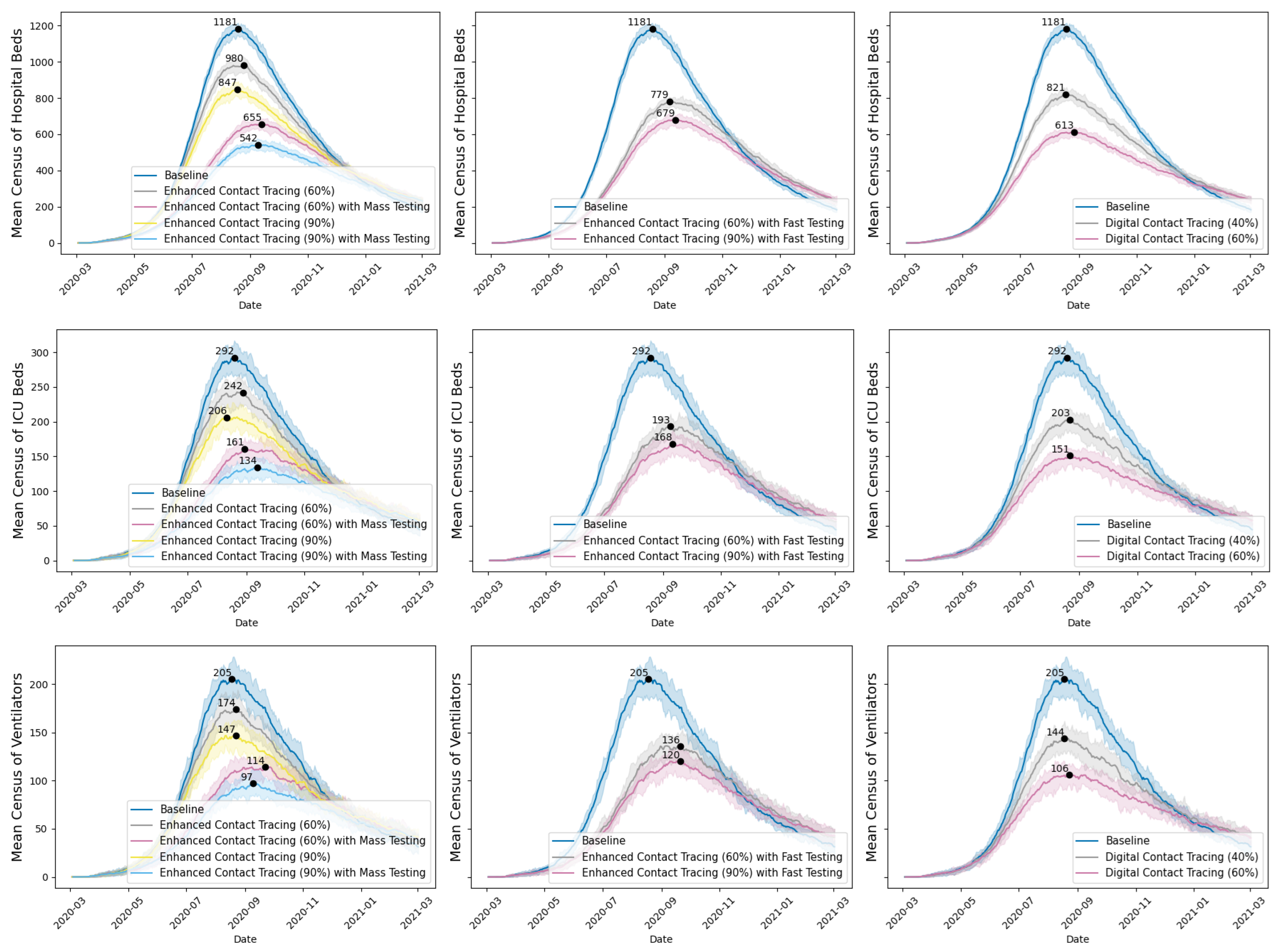
3.2. Simulation Results
3.3. Policy Responses
“in addition to ongoing testing, the Ministry of Health will deploy additional staff to the Saskatchewan Health Authority (SHA) to assist with contact tracing. This initiative is aimed at critical identification to better ensure cases are detected and followed up on in a timely manner, and to help prevent further transmission of COVID-19” [71,72].
On March 30, 2020, “the Saskatchewan Health Authority (SHA) already has up to 150 people involved in contact tracing. Over the coming days, 50 additional staff from across government will be moved into this key role. The need for additional resources will be assessed as the situation evolves.... Testing locations will continue to be expanded as demand warrants [73].
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Age Group | Age Group ID | Symptomatic Cases Requiring Hospitalization, % | Hospitalized Cases Requiring Intensive Care, % |
|---|---|---|---|
| 0 to 4 years | 1 | 0.1 | 5.0 |
| 5 to 9 years | 2 | 0.1 | 5.0 |
| 10 to 14 years | 3 | 0.3 | 5.0 |
| 15 to 19 years | 4 | 0.3 | 5.0 |
| 20 to 24 years | 5 | 1.2 | 5.0 |
| 25 to 29 years | 6 | 1.2 | 5.0 |
| 30 to 34 years | 7 | 3.2 | 6.3 |
| 35 to 39 years | 8 | 3.2 | 6.3 |
| 40 to 44 years | 9 | 4.9 | 6.3 |
| 45 to 49 years | 10 | 4.9 | 6.3 |
| 50 to 54 years | 11 | 10.2 | 12.2 |
| 55 to 59 years | 12 | 10.2 | 12.2 |
| 60 to 64 years | 13 | 16.6 | 27.4 |
| 65 to 69 years | 14 | 16.6 | 27.4 |
| 70 to 74 years | 15 | 24.3 | 43.2 |
| 75 to 79 years | 16 | 24.3 | 43.2 |
| 80 to 84 years | 17 | 27.3 | 43.2 |
| 85 to 89 years | 18 | 27.3 | 70.9 |
| 90 to 94 years | 19 | 27.3 | 70.9 |
| 95 to 99 years | 20 | 27.3 | 70.9 |
| 100 years and over | 21 | 27.3 | 70.9 |
References
- Nixon, K.; Jindal, S.; Parker, F.; Reich, N.G.; Ghobadi, K.; Lee, E.C.; Truelove, S.; Gardner, L. An evaluation of prospective COVID-19 modelling studies in the USA: From data to science translation. Lancet Digit Health 2022, 4, e738–e747. [Google Scholar] [CrossRef]
- Xia, Y.; Flores Anato, J.L.; Colijn, C.; Janjua, N.; Irvine, M.; Williamson, T.; Varughese, M.B.; Li, M.; Osgood, N.; Earn, D.J.D.; et al. Canada’s provincial COVID-19 pandemic modelling efforts: A review of mathematical models and their impacts on the responses. Can. J. Public Health 2024, 115, 541–557. [Google Scholar] [CrossRef] [PubMed]
- Waldner, D.; Harrison, R.; Johnstone, J.; Saxinger, L.; Webster, D.; Sligl, W. COVID-19 epidemiology in Canada from January to December 2020: The pre-vaccine era. Facets (Ott) 2021, 6, 760–822. [Google Scholar] [CrossRef]
- Knight, G.M.; Dharan, N.J.; Fox, G.J.; Stennis, N.; Zwerling, A.; Khurana, R.; Dowdy, D.W. Bridging the gap between evidence and policy for infectious diseases: How models can aid public health decision-making. Int. J. Infect. Dis. 2016, 42, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Heesterbeek, H.; Anderson, R.M.; Andreasen, V.; Bansal, S.; De Angelis, D.; Dye, C.; Eames, K.T.D.; Edmunds, W.J.; Frost, S.D.W.; Funk, S.; et al. Modeling infectious disease dynamics in the complex landscape of global health. Science 2015, 347, aaa4339. [Google Scholar] [CrossRef] [PubMed]
- Willem, L.; Verelst, F.; Bilcke, J.; Hens, N.; Beutels, P. Lessons from a decade of individual-based models for infectious disease transmission: A systematic review (2006–2015). BMC Infect. Dis. 2017, 17, 1–16. [Google Scholar] [CrossRef]
- Gerlee, P.; Jöud, A.; Spreco, A.; Timpka, T. Computational models predicting the early development of the COVID-19 pandemic in Sweden: Systematic review, data synthesis, and secondary validation of accuracy. Sci. Rep. 2022, 12, 13256. [Google Scholar] [CrossRef] [PubMed]
- Fone, D.; Hollinghurst, S.; Temple, M.; Round, A.; Lester, N.; Weightman, A.; Roberts, K.; Coyle, E.; Bevan, G.; Palmer, S. Systematic review of the use and value of computer simulation modelling in population health and health care delivery. J. Public Health Med. 2003, 25, 325–335. [Google Scholar] [CrossRef]
- Harper, A.; Mustafee, N.; Yearworth, M. The Issue of Trust and Implementation of Results in Healthcare Modeling and Simulation Studies. In Proceedings of the 2022 Winter Simulation Conference (WSC), Singapore, 11–14 December 2022; pp. 1104–1115. [Google Scholar] [CrossRef]
- Metcalf, C.J.E.; Lessler, J. Opportunities and challenges in modeling emerging infectious diseases. Science 2017, 357, 149–152. [Google Scholar] [CrossRef]
- Rutter, H.; Savona, N.; Glonti, K.; Bibby, J.; Cummins, S.; Finegood, D.T.; Greaves, F.; Harper, L.; Hawe, P.; Moore, L.; et al. The need for a complex systems model of evidence for public health. Lancet 2017, 390, 2602–2604. [Google Scholar] [CrossRef]
- Varallyay, N.I.; Langlois, E.V.; Tran, N.; Elias, V.; Reveiz, L. Health system decision-makers at the helm of implementation research: Development of a framework to evaluate the processes and effectiveness of embedded approaches. Health Res. Policy Syst. 2020, 18, 1–12. [Google Scholar] [CrossRef]
- Hare, M. Forms of participatory modelling and its potential for widespread adoption in the water sector. Environ. Pol. Gov. 2011, 21, 386–402. [Google Scholar] [CrossRef]
- Stave, K. Participatory System Dynamics Modeling for Sustainable Environmental Management: Observations from Four Cases. Sustain. Sci. Pract. Policy 2010, 2, 2762–2784. [Google Scholar] [CrossRef]
- Voinov, A.; Kolagani, N.; McCall, M.K.; Glynn, P.D.; Kragt, M.E.; Ostermann, F.O.; Pierce, S.A.; Ramu, P. Modelling with stakeholders—Next generation. Environ. Model. Softw. 2016, 77, 196–220. [Google Scholar] [CrossRef]
- Beall, A.M.; Ford, A. Reports from the Field: Assessing the Art and Science of Participatory Environmental Modeling. Int. J. Inf. Syst. Soc. Change 2010, 1, 72–89. [Google Scholar] [CrossRef]
- Freebairn, L.; Rychetnik, L.; Atkinson, J.A.; Kelly, P.; McDonnell, G.; Roberts, N.; Whittall, C.; Redman, S. Knowledge mobilisation for policy development: Implementing systems approaches through participatory dynamic simulation modelling. Health Res. Policy Syst. 2017, 15, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Tako, A.A.; Kotiadis, K. Participative simulation (Partisim): A Facilitated simulation Approach for Stakeholder Engagement. In Proceedings of the 2018 Winter Simulation Conference (WSC), Gothenburg, Sweden, 9–12 December 2018; pp. 192–206. [Google Scholar] [CrossRef]
- Richardson, G.P.; Andersen, D.F. Teamwork in group model building. Syst. Dyn. Rev. 1995, 11, 113–137. [Google Scholar] [CrossRef]
- Hovmand, P.S. Community Based System Dynamics; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Adams, S.; Rhodes, T.; Lancaster, K. New directions for participatory modelling in health: Redistributing expertise in relation to localised matters of concern. Glob. Public Health 2021, 17, 1827–1841. [Google Scholar] [CrossRef] [PubMed]
- Freebairn, L.; Atkinson, J.A.; Kelly, P.M.; McDonnell, G.; Rychetnik, L. Decision makers’ experience of participatory dynamic simulation modelling: Methods for public health policy. BMC Med. Inform. Decis. Mak. 2018, 18, 1–14. [Google Scholar] [CrossRef]
- Andersen, D.F.; Vennix, J.A.M.; Richardson, G.P.; Rouwette, E.A.J.A. Group model building: Problem structuring, policy simulation and decision support. J. Oper. Res. Soc. 2007, 58, 691–694. [Google Scholar] [CrossRef]
- Vennix, J.A.M. Group model-building: Tackling messy problems. Syst. Dyn. Rev. 1999, 15, 379–401. [Google Scholar] [CrossRef]
- Tako, A.A.; Kotiadis, K. PartiSim: A multi-methodology framework to support facilitated simulation modelling in healthcare. Eur. J. Oper. Res. 2015, 244, 555–564. [Google Scholar] [CrossRef]
- Tako, A.A.; Kotiadis, K. Facilitated conceptual modelling: Practical issues and reflections. In Proceedings of the 2012 Winter Simulation Conference (WSC), Berlin, Germany, 9–12 December 2012; pp. 1–12. [Google Scholar] [CrossRef]
- Tako, A.A.; Vasilakis, C.; Kotiadis, K. A participative modelling framework for developing conceptual models in healthcare simulation studies. In Proceedings of the 2010 Winter Simulation Conference, Baltimore, MD, USA, 5–8 December 2010; pp. 500–512. [Google Scholar] [CrossRef]
- Kotiadis, K.; Tako, A.A. Facilitated post-model coding in discrete event simulation (DES): A case study in healthcare. Eur. J. Oper. Res. 2018, 266, 1120–1133. [Google Scholar] [CrossRef]
- Frerichs, L.; Lich, K.H.; Dave, G.; Corbie-Smith, G. Integrating Systems Science and Community-Based Participatory Research to Achieve Health Equity. Am. J. Public Health 2016, 106, 215–222. [Google Scholar] [CrossRef]
- Augustsson, H.; Churruca, K.; Braithwaite, J. Re-energising the way we manage change in healthcare: The case for soft systems methodology and its application to evidence-based practice. BMC Health Serv. Res. 2019, 19, 1–11. [Google Scholar] [CrossRef]
- Hovmand, P.S. Group Model Building and Community-Based System Dynamics Process; Springer: New York, NY, USA, 2014. [Google Scholar]
- Seidl, R. A functional-dynamic reflection on participatory processes in modeling projects. Ambio 2015, 44, 750–765. [Google Scholar] [CrossRef] [PubMed]
- Freebairn, L.; Occhipinti, J.A.; Song, Y.J.C.; Skinner, A.; Lawson, K.; Lee, G.Y.; Hockey, S.J.; Huntley, S.; Hickie, I.B. Participatory Methods for Systems Modeling of Youth Mental Health: Implementation Protocol. JMIR Res. Protoc. 2022, 11, e32988. [Google Scholar] [CrossRef]
- Tian, Y.; Basran, J.; Stempien, J.; Danyliw, A.; Fast, G.; Falastein, P.; Osgood, N.D. Participatory Modeling with Discrete-Event Simulation: A Hybrid Approach to Inform Policy Development to Reduce Emergency Department Wait Times. Systems 2023, 11, 362. [Google Scholar] [CrossRef]
- Nguyen, T.; Graham, I.D.; Mrklas, K.J.; Bowen, S.; Cargo, M.; Estabrooks, C.A.; Kothari, A.; Lavis, J.; Macaulay, A.C.; MacLeod, M.; et al. How does integrated knowledge translation (IKT) compare to other collaborative research approaches to generating and translating knowledge? Learning from experts in the field. Health Res. Policy Syst. 2020, 18, 1–20. [Google Scholar] [CrossRef]
- Lawrence, L.M.; Bishop, A.; Curran, J. Integrated knowledge translation with public health policy makers: A scoping review. Healthc. Policy 2019, 14, 55–77. [Google Scholar] [CrossRef]
- Tian, Y.; Osgood, N.D.; Stempien, J.; Onaemo, V.; Danyliw, A.; Fast, G.; Osman, B.A.; Reynolds, J.; Basran, J. The impact of alternate level of care on access block and operational strategies to reduce emergency wait times: A multi-center simulation study. Can. J. Emerg. Med. 2023, 25, 608–616. [Google Scholar] [CrossRef]
- Government of Saskatchewan. New Pandemic Modelling Shows Improved Outlook for Saskatchewan. 2020. Available online: https://www.saskatchewan.ca/government/news-and-media/2020/april/28/updated-pandemic-modelling (accessed on 21 February 2022).
- Currie, C.S.M.; Fowler, J.W.; Kotiadis, K.; Monks, T.; Onggo, B.S.; Robertson, D.A.; Tako, A.A. How simulation modelling can help reduce the impact of COVID-19. J. Simul. 2020, 14, 83–97. [Google Scholar] [CrossRef]
- Brailsford, S.C.; Eldabi, T.; Kunc, M.; Mustafee, N.; Osorio, A.F. Hybrid simulation modelling in operational research: A state-of-the-art review. Eur. J. Oper. Res. 2019, 278, 721–737. [Google Scholar] [CrossRef]
- The AnyLogic Company. Simulation Modeling Software Tools & Solutions for Business. Available online: https://www.anylogic.com/ (accessed on 12 January 2020).
- Ma, S.; Zhang, J.; Zeng, M.; Yun, Q.; Guo, W.; Zheng, Y.; Zhao, S.; Wang, M.H.; Yang, Z. Epidemiological parameters of coronavirus disease 2019: A pooled analysis of publicly reported individual data of 1155 cases from seven countries. medRxiv 2020. [Google Scholar] [CrossRef]
- Li, R.; Pei, S.; Chen, B.; Song, Y.; Zhang, T.; Yang, W.; Shaman, J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science 2020, 368, 489–493. [Google Scholar] [CrossRef]
- Liang, J.; Yuan, H.Y.; Wu, L.; Pfeiffer, D.U. Estimating effects of intervention measures on COVID-19 outbreak in Wuhan taking account of improving diagnostic capabilities using a modelling approach. BMC Infect. Dis. 2021, 21, 424. [Google Scholar] [CrossRef] [PubMed]
- Xin, H.; Li, Y.; Wu, P.; Li, Z.; Lau, E.H.Y.; Qin, Y.; Wang, L.; Cowling, B.J.; Tsang, T.K.; Li, Z. Estimating the latent period of Coronavirus disease 2019 (COVID-19). Clin. Infect. Dis. 2022, 74, 1678–1681. [Google Scholar] [CrossRef]
- Ferretti, L.; Wymant, C.; Kendall, M.; Zhao, L.; Nurtay, A.; Abeler-Dörner, L.; Parker, M.; Bonsall, D.; Fraser, C. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science 2020, 368, eabb6936. [Google Scholar] [CrossRef]
- Roques, L.; Klein, E.K.; Papaïx, J.; Sar, A.; Soubeyrand, S. Using early data to estimate the actual infection fatality ratio from COVID-19 in France. Biology 2020, 9, 97. [Google Scholar] [CrossRef] [PubMed]
- Mossong, J.; Hens, N.; Jit, M.; Beutels, P.; Auranen, K.; Mikolajczyk, R.; Massari, M.; Salmaso, S.; Tomba, G.S.; Wallinga, J.; et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008, 5, e74. [Google Scholar] [CrossRef]
- Osgood, N.D.; Mahamoud, A.; Lich, K.H.; Tian, Y.; Al-Azem, A.; Hoeppner, V.H. Estimating the Relative Impact of Early-Life Infection Exposure on Later-Life Tuberculosis Outcomes in a Canadian Sample. Res. Hum. Dev. 2011, 8, 26–47. [Google Scholar] [CrossRef]
- Prem, K.; Cook, A.R.; Jit, M. Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLoS Comput. Biol. 2017, 13, e1005697. [Google Scholar] [CrossRef] [PubMed]
- Government of Saskatchewan. COVID-19: Additional Measures to Protect Saskatchewan Residents. Available online: https://www.saskatchewan.ca/government/news-and-media/2020/march/20/covid-19-update-march-20 (accessed on 22 May 2020).
- Tuite, A.R.; Fisman, D.N.; Greer, A.L. Mathematical modelling of COVID-19 transmission and mitigation strategies in the population of Ontario, Canada. CMAJ 2020, 192, E497–E505. [Google Scholar] [CrossRef] [PubMed]
- Google. COVID-19 Community Mobility Reports. Available online: https://www.google.com/covid19/mobility/ (accessed on 22 May 2020).
- Tindale, L.C.; Stockdale, J.E.; Coombe, M.; Garlock, E.S.; Lau, W.Y.V.; Saraswat, M.; Zhang, L.; Chen, D.; Wallinga, J.; Colijn, C. Evidence for transmission of COVID-19 prior to symptom onset. eLife 2020, 9, e57149. [Google Scholar] [CrossRef] [PubMed]
- Khalili, M.; Karamouzian, M.; Nasiri, N.; Javadi, S.; Mirzazadeh, A.; Sharifi, H. Epidemiological characteristics of COVID-19: A systematic review and meta-analysis. Epidemiol. Infect. 2020, 148, e130. [Google Scholar] [CrossRef]
- Hu, Z.; Song, C.; Xu, C.; Jin, G.; Chen, Y.; Xu, X.; Ma, H.; Chen, W.; Lin, Y.; Zheng, Y.; et al. Clinical characteristics of 24 asymptomatic infections with COVID-19 screened among close contacts in Nanjing, China. Sci. China Life Sci. 2020, 63, 706–711. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef] [PubMed]
- Murthy, S.; Archambault, P.M.; Atique, A.; Carrier, F.M.; Cheng, M.P.; Codan, C.; Daneman, N.; Dechert, W.; Douglas, S.; Fiest, K.M.; et al. Characteristics and outcomes of patients with COVID-19 admitted to hospital and intensive care in the first phase of the pandemic in Canada: A national cohort study. CMAJ Open 2021, 9, E181–E188. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Han, X.; Jiang, N.; Cao, Y.; Alwalid, O.; Gu, J.; Fan, Y.; Zheng, C. Radiological findings from 81 patients with COVID-19 pneumonia in Wuhan, China: A descriptive study. Lancet Infect. Dis. 2020, 20, 425–434. [Google Scholar] [CrossRef] [PubMed]
- Mizumoto, K.; Kagaya, K.; Zarebski, A.; Chowell, G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Euro Surveill. 2020, 25, 2000180. [Google Scholar] [CrossRef]
- Danis, K.; Epaulard, O.; Bénet, T.; Gaymard, A.; Campoy, S.; Botelho-Nevers, E.; Bouscambert-Duchamp, M.; Spaccaferri, G.; Ader, F.; Mailles, A.; et al. Cluster of Coronavirus disease 2019 (COVID-19) in the French Alps, February 2020. Clin. Infect. Dis. 2020, 71, 825–832. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Hu, B.; Hu, C.; Zhu, F.; Liu, X.; Zhang, J.; Wang, B.; Xiang, H.; Cheng, Z.; Xiong, Y.; et al. Clinical Characteristics of 138 Hospitalized Patients with 2019 Novel Coronavirus-Infected Pneumonia in Wuhan, China. JAMA 2020, 323, 1061–1069. [Google Scholar] [CrossRef] [PubMed]
- Richardson, S.; Hirsch, J.S.; Narasimhan, M.; Crawford, J.M.; McGinn, T.; Davidson, K.W.; the Northwell COVID-19 Research Consortium; Barnaby, D.P.; Becker, L.B.; Chelico, J.D.; et al. Presenting characteristics, comorbidities, and outcomes among 5700 patients hospitalized with COVID-19 in the New York City area. JAMA 2020, 323, 2052–2059. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; McGoogan, J.M. Characteristics of and Important Lessons From the Coronavirus Disease 2019 (COVID-19) Outbreak in China: Summary of a Report of 72 314 Cases From the Chinese Center for Disease Control and Prevention. JAMA 2020, 323, 1239–1242. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M. Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand. Technical Report, Imperial College London. 2020. Available online: http://hdl.handle.net/10044/1/77482 (accessed on 18 March 2020).
- Eddy, D.M.; Hollingworth, W.; Caro, J.J.; Tsevat, J.; McDonald, K.M.; Wong, J.B.; ISPOR-SMDM Modeling Good Research Practices Task Force. Model transparency and validation: A report of the ISPOR-SMDM Modeling Good Research Practices Task Force-7. Med. Decis. Mak. 2012, 32, 733–743. [Google Scholar] [CrossRef]
- Sy, K.T.L.; White, L.F.; Nichols, B.E. Population density and basic reproductive number of COVID-19 across United States counties. PLoS ONE 2021, 16, e0249271. [Google Scholar] [CrossRef] [PubMed]
- White, L.F.; Pagano, M. A likelihood-based method for real-time estimation of the serial interval and reproductive number of an epidemic. Stat. Med. 2008, 27, 2999–3016. [Google Scholar] [CrossRef]
- Obadia, T.; Haneef, R.; Boëlle, P.Y. The R0 package: A toolbox to estimate reproduction numbers for epidemic outbreaks. BMC Med. Inform. Decis. Mak. 2012, 12, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Shahroz, M.; Ahmad, F.; Younis, M.S.; Ahmad, N.; Kamel Boulos, M.N.; Vinuesa, R.; Qadir, J. COVID-19 digital contact tracing applications and techniques: A review post initial deployments. Transp. Eng. 2021, 5, 100072. [Google Scholar] [CrossRef]
- Government of Saskatchewan. 30 New Confirmed COVID-19 Cases in Saskatchewan. 2020. Available online: https://www.saskatchewan.ca/government/news-and-media/2020/march/28/covid-19-update-march-28 (accessed on 19 January 2024).
- Hunter, A. Staff Added to Trace COVID-19 Cases in Sask. As Province Approaches 10K Tests. 2020. Available online: https://www.cbc.ca/news/canada/saskatchewan/sask-covid19-tests-1.5515033 (accessed on 27 September 2024).
- Government of Saskatchewan. Saskatchewan Records First COVID-19 Deaths. 2020. Available online: https://www.saskatchewan.ca/government/news-and-media/2020/march/30/covid-19-update-march-30 (accessed on 19 January 2024).
- Kurz, L. Updated SHA Modelling Data Estimates Fewer Infections, Deaths from COVID-19. 2020. Available online: https://www.moosejawtoday.com/local-news/updated-sha-modelling-data-estimates-fewer-infections-deaths-from-covid-19-2290333 (accessed on 27 September 2024).
- Brailsford, S.C.; Harper, P.R.; Patel, B.; Pitt, M. An analysis of the academic literature on simulation and modelling in health care. J. Simul. 2009, 3, 130–140. [Google Scholar] [CrossRef]
- Pitt, M.; Monks, T.; Crowe, S.; Vasilakis, C. Systems modelling and simulation in health service design, delivery and decision making. BMJ Qual. Saf. 2016, 25, 38–45. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, J.A.M.; Wells, R.; Page, A.; Dominello, A.; Haines, M.; Wilson, A. Applications of system dynamics modelling to support health policy. Public Health Res. Pract. 2015, 25, e2531531. [Google Scholar] [CrossRef] [PubMed]
- Mohiuddin, S.; Busby, J.; Savović, J.; Richards, A.; Northstone, K.; Hollingworth, W.; Donovan, J.L.; Vasilakis, C. Patient flow within UK emergency departments: A systematic review of the use of computer simulation modelling methods. BMJ Open 2017, 7, e015007. [Google Scholar] [CrossRef]
- Taylor, S.J.E.; Eldabi, T.; Riley, G.; Paul, R.J.; Pidd, M. Simulation modelling is 50! Do we need a reality check? J. Oper. Res. Soc. 2009, 60, S69–S82. [Google Scholar] [CrossRef]
- Harper, P.R.; Pitt, M.A. On the Challenges of Healthcare Modelling and a Proposed Project Life Cycle for Successful Implementation. J. Oper. Res. Soc. 2004, 55, 657–661. [Google Scholar] [CrossRef]
- Moretto, N.; Comans, T.A.; Chang, A.T.; O’Leary, S.P.; Osborne, S.; Carter, H.E.; Smith, D.; Cavanagh, T.; Blond, D.; Raymer, M. Implementation of simulation modelling to improve service planning in specialist orthopaedic and neurosurgical outpatient services. Implement. Sci. 2019, 14, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Voinov, A.; Jenni, K.; Gray, S.; Kolagani, N.; Glynn, P.D.; Bommel, P.; Prell, C.; Zellner, M.; Paolisso, M.; Jordan, R.; et al. Tools and methods in participatory modeling: Selecting the right tool for the job. Environ. Model. Softw. 2018, 109, 232–255. [Google Scholar] [CrossRef]
- Freebairn, L.; Atkinson, J.A.; Osgood, N.D.; Kelly, P.M.; McDonnell, G.; Rychetnik, L. Turning conceptual systems maps into dynamic simulation models: An Australian case study for diabetes in pregnancy. PLoS ONE 2019, 14, e0218875. [Google Scholar] [CrossRef] [PubMed]
- Fox, G.J.; Barry, S.E.; Britton, W.J.; Marks, G.B. Contact investigation for tuberculosis: A systematic review and meta-analysis. Eur. Respir. J. 2013, 41, 140–156. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Osgood, N.D.; Al-Azem, A.; Hoeppner, V.H. Evaluating the effectiveness of contact tracing on tuberculosis outcomes in Saskatchewan using individual-based modeling. Health Educ. Behav. 2013, 40, 98S–110S. [Google Scholar] [CrossRef]
- Browne, C.; Gulbudak, H.; Webb, G. Modeling contact tracing in outbreaks with application to Ebola. J. Theor. Biol. 2015, 384, 33–49. [Google Scholar] [CrossRef]
- Aboushady, A.T.; Blackmore, C.; Nagel, A.; Janashvili, L.; Gexha, D.; Otorbaeva, D.; Bugaienko, N.; Pebody, R.; Hegermann-Lindencrone, M. Contact tracing in Austria, Georgia, Kyrgyzstan, Ukraine, and Kosovo† during the COVID-19 pandemic: Response review and good practices. Eur. J. Public Health 2024, 34, 387–393. [Google Scholar] [CrossRef] [PubMed]
- Cheng, V.C.C.; Siu, G.K.H.; Wong, S.C.; Au, A.K.W.; Ng, C.S.F.; Chen, H.; Li, X.; Lee, L.K.; Leung, J.S.L.; Lu, K.K.; et al. Complementation of contact tracing by mass testing for successful containment of beta COVID-19 variant (SARS-CoV-2 VOC B.1.351) epidemic in Hong Kong. Lancet Reg. Health West. Pac. 2021, 17, 100281. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiang, H.; Wang, Q.; Yang, M.; Chen, Y.; Jiang, Q. Use of contact tracing, isolation, and mass testing to control transmission of COVID-19 in China. BMJ 2021, 375, n2330. [Google Scholar] [CrossRef]
- Pozo-Martin, F.; Beltran Sanchez, M.A.; Müller, S.A.; Diaconu, V.; Weil, K.; El Bcheraoui, C. Comparative effectiveness of contact tracing interventions in the context of the COVID-19 pandemic: A systematic review. Eur. J. Epidemiol. 2023, 38, 243–266. [Google Scholar] [CrossRef]
- Mbwogge, M. Mass testing with contact tracing compared to test and trace for the effective suppression of COVID-19 in the United Kingdom: Systematic review. JMIRx Med. 2021, 2, e27254. [Google Scholar] [CrossRef]
- Juneau, C.E.; Briand, A.S.; Collazzo, P.; Siebert, U.; Pueyo, T. Effective contact tracing for COVID-19: A systematic review. Glob. Epidemiol. 2023, 5, 100103. [Google Scholar] [CrossRef] [PubMed]
- Peto, J.; Carpenter, J.; Smith, G.D.; Duffy, S.; Houlston, R.; Hunter, D.J.; McPherson, K.; Pearce, N.; Romer, P.; Sasieni, P.; et al. Weekly COVID-19 testing with household quarantine and contact tracing is feasible and would probably end the epidemic. R. Soc. Open Sci. 2020, 7, 200915. [Google Scholar] [CrossRef]
- Peto, J. COVID-19 mass testing facilities could end the epidemic rapidly. BMJ 2020, 368, m1163. [Google Scholar] [CrossRef] [PubMed]
- Powell, J.H.; Mustafee, N. Widening requirements capture with soft methods: An investigation of hybrid M&S studies in health care. J. Oper. Res. Soc. 2017, 68, 1211–1222. [Google Scholar] [CrossRef]
- Tian, Y. Agent-Based Modeling and System Dynamics Modeling on Transmission of Tuberculosis in Saskatchewan. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2011. [Google Scholar]
- Müller, J.; Kretzschmar, M. Contact tracing—Old models and new challenges. Infect. Dis. Model. 2021, 6, 222–231. [Google Scholar] [CrossRef]

| Parameter Name | Baseline Value | Plausible Range | Source a |
|---|---|---|---|
| Parameters used in System Dynamics Sub-model of COVID-19 Transmission | |||
| Mean latent period (l), day | 3.7 | (2–5.5) | [42,43,44,45] |
| Basic reproduction number () | 2.3 | (1.8–3.2) | [43,46,47] |
| Contacts per case per day (C) | 10 | (5–19) | [48,49,50] |
| Average duration of quarantine (), day | 14 | (10–14) | [51] |
| Reduction in exposure risk due to quarantine () | 0.64 | (0.64–0.9) | [52] |
| Reduction in infectivity for diagnosed isolated cases | 0.64 | (0.64–0.9) | [52] |
| Reduction in infectivity for undiagnosed isolated symptomatic individuals | 0.1 | (0.05–0.1) | Assumed |
| Reduction in infectivity for undiagnosed isolated asymptomatic individuals | 0.05 | (0.05–0.1) | Assumed |
| Proportion of contacts instantly quarantined or isolated () | 0.2 b | (0.1–0.3) | Assumed |
| Physical distancing level relative to pre-pandemic level () | 0.75 | (0.6–0.95) | [53] |
| Parameters used in Agent-based Sub-model of COVID-19 Disease Progression | |||
| Duration of infectiousness before symptom onset, day | 2 | (1–2.9) | [45,54,55] |
| Duration of infectiousness for mild or asymptomatic cases after pre-asym, day | 6.8 | (4–9.5) | [43,56] |
| Duration of infectiousness from symptom onset for severe cases, day | 5.9 | (3.2–7) | [43,54,56] |
| Duration from symptom onset to hospital admission for severe cases, day | 4 | (3–12) | [57,58] |
| Proportion of pre-symptomatic individuals who never develop symptoms | 0.3 | (0.17–0.4) | [59,60,61] |
| Parameters used in Discrete-event Simulation Sub-model of COVID-19 Related Hospital Patient Flow | |||
| Average length of stay for non-ICU inpatients c, day | 8 | (4.1–14) | [62,63] |
| Average pre-ICU length of stay for ICU inpatients, day | 3 | (0–3) | [57,62] |
| Average ICU length of stay for ICU inpatients c, day | 8 | (4–12) | [57,62] |
| Average post-ICU length of stay for ICU inpatients, day | 3 | (0–3) | [57,62] |
| Case fatality rate—ICU inpatients | 0.49 | (0.22–0.5) | [64] |
| Case fatality rate—non-ICU inpatients | 0.05 | (0.05–0.1) | [57,63] |
| Proportion of ICU inpatients requiring ventilation | 0.71 | (0.42–0.71) | [62] |
| Proportion of symptomatic cases requiring hospitalization by age group | – d | (0.01–0.27) | [65] |
| Proportion of hospitalized cases requiring ICU admission by age group | – d | (0.05–0.71) | [65] |
| Category | Target Population | Configured Parameters | Simulated Intervention Scenarios 1 | ||||
|---|---|---|---|---|---|---|---|
| Baseline | Enhanced CT | Enhanced CT with Fast Testing | Enhanced CT with Mass Testing | Digital CT | |||
| Physical Distancing | General population | Physical distancing start date | 3/18/2020 | ||||
| Physical distancing level relative to pre-pandemic (), % | 75 | ||||||
| Case Detection, Isolation, and Contact Tracing | Persistent asymptomatic cases | Time to test/isolation post-incubation, day | 4 | 3 | |||
| Case tested and isolated, % | 60 | 90 | |||||
| Confirmed cases traced, % | 30 | 60, 90 | 60, 90 | 60, 90 | |||
| Contacts traced with instant quarantine or isolation, % | 60 | ||||||
| Mild cases | Time to test/isolation after symptom onset, day | 3 | 2 | ||||
| Case tested and isolated, % | 70 | 90 | |||||
| Confirmed cases traced, % | 30 | 60, 90 | 60, 90 | 60, 90 | |||
| Contacts traced with instant quarantine or isolation, % | 60 | ||||||
| Severe cases | Time to test/isolation after symptom onset, day | 3 | 2 | ||||
| Case tested and isolated, % | 100 | ||||||
| Confirmed cases traced, % | 30 | 60, 90 | 60, 90 | 60, 90 | |||
| Contacts traced with instant quarantine or isolation, % | 60 | ||||||
| - | Conventional contact tracing start date | 3/12/2020 | |||||
| Digital Contact Tracing | Potentially exposed | Digital contact tracing start date | - | 3/30/2020 | |||
| Contacts instantly quarantined or isolated (), % | 20 | 40, 60 | |||||
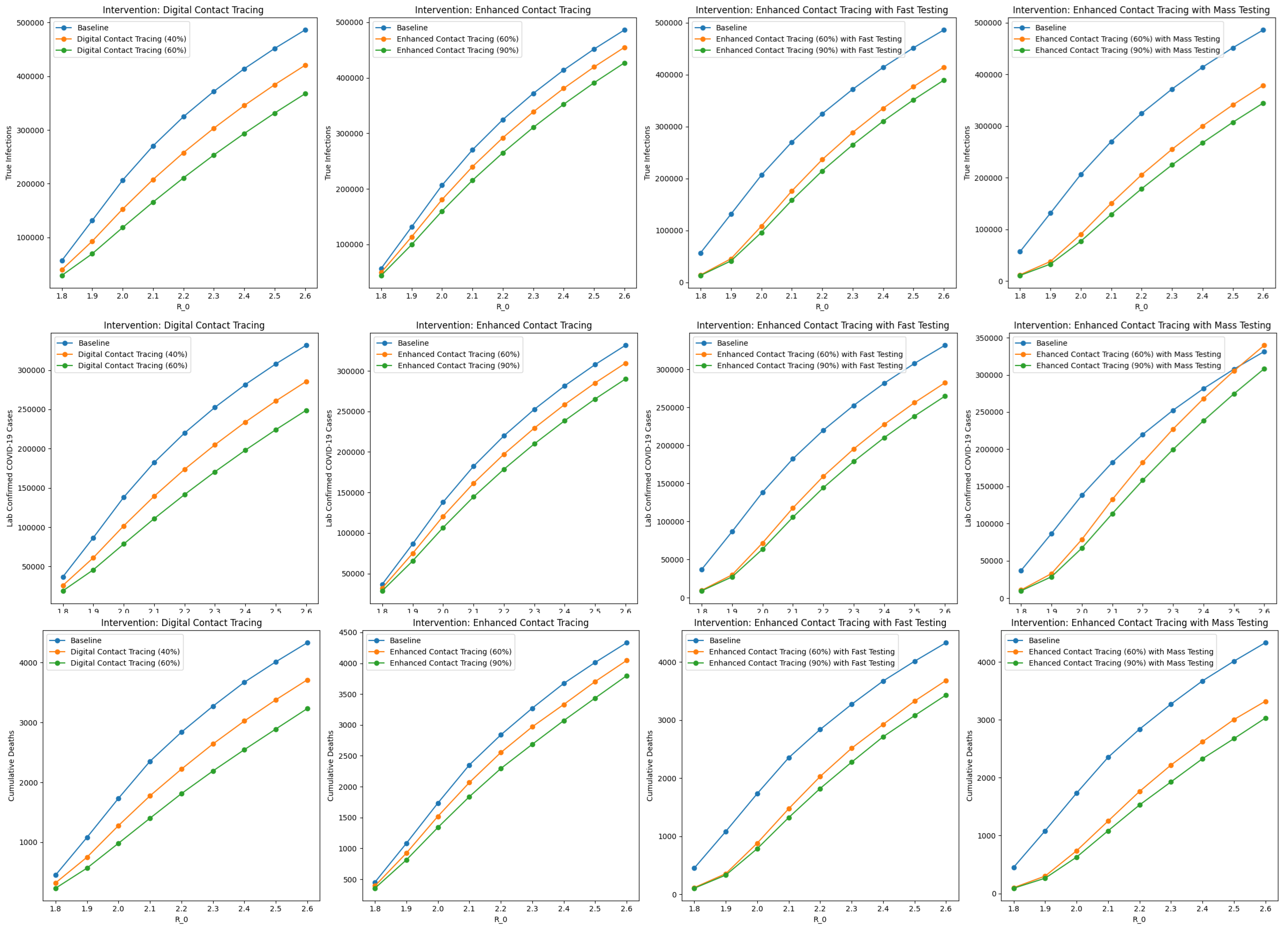
| Simulated Intervention Scenario | Scenario Name and Configuration | True Infections 1 | Confirmed COVID-19 Cases | Cumulative Deaths |
|---|---|---|---|---|
| Baseline | Baseline | 371,809 | 252,504 | 3271 |
| Enhanced Contact Tracing | Enhanced Contact Tracing (60%) | 338,623 | 229,383 | 2969 |
| Enhanced Contact Tracing (90%) | 310,612 | 209,926 | 2686 | |
| Enhanced Contact Tracing with Fast Testing | Enhanced Contact Tracing (60%) with Fast Testing | 288,638 | 195,246 | 2515 |
| Enhanced Contact Tracing (90%) with Fast Testing | 264,660 | 178,737 | 2275 | |
| Enhanced Contact Tracing with Mass Testing | Enhanced Contact Tracing (60%) with Mass Testing | 255,134 | 227,211 | 2218 |
| Enhanced Contact Tracing (90%) with Mass Testing | 224,838 | 199,751 | 1927 | |
| Digital Contact Tracing | Digital Contact Tracing (40%) | 303,211 | 204,862 | 2641 |
| Digital Contact Tracing (60%) | 253,343 | 170,485 | 2189 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Basran, J.; McDonald, W.; Osgood, N.D. Early COVID-19 Pandemic Preparedness: Informing Public Health Interventions and Hospital Capacity Planning Through Participatory Hybrid Simulation Modeling. Int. J. Environ. Res. Public Health 2025, 22, 39. https://doi.org/10.3390/ijerph22010039
Tian Y, Basran J, McDonald W, Osgood ND. Early COVID-19 Pandemic Preparedness: Informing Public Health Interventions and Hospital Capacity Planning Through Participatory Hybrid Simulation Modeling. International Journal of Environmental Research and Public Health. 2025; 22(1):39. https://doi.org/10.3390/ijerph22010039
Chicago/Turabian StyleTian, Yuan, Jenny Basran, Wade McDonald, and Nathaniel D. Osgood. 2025. "Early COVID-19 Pandemic Preparedness: Informing Public Health Interventions and Hospital Capacity Planning Through Participatory Hybrid Simulation Modeling" International Journal of Environmental Research and Public Health 22, no. 1: 39. https://doi.org/10.3390/ijerph22010039
APA StyleTian, Y., Basran, J., McDonald, W., & Osgood, N. D. (2025). Early COVID-19 Pandemic Preparedness: Informing Public Health Interventions and Hospital Capacity Planning Through Participatory Hybrid Simulation Modeling. International Journal of Environmental Research and Public Health, 22(1), 39. https://doi.org/10.3390/ijerph22010039






