Performance Enhancement of a Centrifugal Compressor by Designing a Tandem Cascade Diffuser

Abstract

The performance of a vane diffuser plays an important role in transforming the high kinetic energy into pressure energy at the impeller outlet of a centrifugal compressor. In this study, the performance enhancement of a centrifugal compressor is achieved by designing a tandem cascade diffuser. An optimum value of the total bending angle of a tandem cascade diffuser is obtained through numerical simulation. The total bending angle is defined as the angle between the tangent line of the front blade arc line at the leading edge point and the tangent line of the rear blade arc line at the trailing edge point. The range of the total bending angle increases from zero to 21°. The simulation results show that the variation of the total bending angle has a great impact on the performances of the compressor stage. The best performance is achieved by the 10° model, by which the minimum total pressure loss coefficient and the maximum static pressure recovery coefficient are obtained. The mechanism of performance improvement by choosing a reasonable total bending angle is that the separated flow zone in the diffuser is constrained and the distribution of radial velocity at the inlet and outlet of the diffuser is more uniformed. With the 10° model, the separated zone almost completely disappears in the diffuser and a distribution of more uniform radial velocity along the meridional section is obtained. Compared with the stage of the prototype with a single row of vane diffuser, the stage with the newly designed tandem vane diffuser (10° model) achieved performance improvement, the efficiency increased about 6%, and the total pressure ratio increased about 3.5% at the flow coefficient of 0.15.

1. Introduction

A centrifugal compressor is one of the most used turbomachineries which transfers the energy of gases at a high pressure. The kinetic energy discharged from the impeller outlet of centrifugal compressors is generally about 1/3 of the total energy input by the shaft. In order to make full use of this part of the energy, a radial diffuser is usually installed behind the outlet of the centrifugal impeller. A vane diffuser is widely used for this purpose since it has high efficiency around the design flow rate [1,2,3]. However, the flow discharged from the impeller outlet is generally largely distorted and is not uniform when entering the diffuser inlet, especially, at a flow rate lower than the design condition [4,5,6,7]. The design of the vane diffuser needs to be carried out carefully to consider the status of the complex flow discharged from the impeller for achieving a high-pressure recovery coefficient [8,9]. For high-pressure ratio centrifugal compressors, it is expected that a vane diffuser is able to undertake a higher load to enhance the performance of the centrifugal compressor stage [10,11]. Therefore, it is of great significance to design efficient vane diffusers for the centrifugal compressor stage.

A tandem cascade diffuser has been studied to improve the performance of centrifugal compressors in previous research. Senoo et al. tested a series of diffusers with backward curved centrifugal impellers, and demonstrated that a diffuser with a small-solidity cascade has a wide range of stable operations comparable to that of a vaneless diffuser, and the diffuser achieves considerably better pressure recovery [12]. Oh et al. [13] and Sakaguchi et al. did some research work on tandem cascade diffusers and obtained similar conclusions [14]. Saha and Roy [15,16] carried out a series of research on the new design method of low aspect ratio tandem cascade and the control ability of variable angle tandem cascade on non-design point flow. Conditional tandem cascades can maintain continuous flow deflection without separation over a wider range of angles of attack. Heinrich et al. conducted experiments with two tandem blade configurations with different load sharing on a 2D linear stator cascade test rig and compared them with a conventional single reference blade. The results showed that tandem vanes can reduce the total pressure loss and extend the operating range [17]. Further studies on the diffuser showed that the compressor can achieve the best performance when the relative circumferential position of the front and rear rows of blades is about 30%. Payyappalli and Shine conducted a numerical simulation of a two-dimensional axial flow tandem cascade for incompressible flow [18]. The research results showed that the tandem cascade layout has an optimal circumferential relative position and an optimal overlap degree and axial overlap with minimum loss is observed at zero axial overlap. In addition, the tandem cascade can accommodate a larger range of attack angle compared to a single-row cascade with the same equivalent chord length. Zhou et al. studied the tandem cascade diffuser for centrifugal compressors, and the results show that there is an optimal circumferential position between the front and rear rows of blades to minimize the loss of the diffuser [19,20]. Shan et al. carried out simulations on tandem cascades for six different percent pitches, and found that the total pressure recovery coefficient is increased if the vane geometry is carefully and reasonably designed [21]. Roy et al. conducted aerodynamic design and experimental studies on tandem cascades in low-speed axial compressors [22]. The study indicated that the tandem cascade is more affected by the circumferential distance than the axial distance. The results confirmed that tandem blades provide a very effective option to overcome the blade loading limitations. In order to study the flow structure on the end wall of the cascade, Böhle and Frey carried out a detailed numerical analysis and experimental study on the loss characteristics and flow field structure of a cascade vane diffuser under different chord length ratios and impact angles of the front and rear blades [23]. The results show that the flow topology of the cascade is obviously different from that of an ordinary single cascade.

These studies show that the use of tandem blades in the diffuser is an approach to enhance the performance of the compressor, which needs to consider the coordination between the blades to reduce the punching angle and to reduce the flow separation in the flow channel. Especially in the small flow condition, the internal flow of the diffuser will be separated first, which may induce a rotating stall at a low flow rate. The design should be done such that the separation zone in the vane passage is constrained. In recent years, several multidisciplinary comprehensive optimization methods [24,25,26,27] have also been employed in the design of centrifugal compressors for the purpose of achieving the best performance. Ju and Zhang developed a multi-objective optimization design method for a tandem compressor cascade at design and off design conditions, and were devoted to the gap geometry optimization in terms of the front and aft airfoil relative position, camber turning ratio, as well as the chord ratio [28,29]. The results show that the optimized all-better-than (ABT) tandem cascade has its design point performance significantly improved whereas the operation range slightly widened. It is also shown that a slight axial proximity and separation of the tandem airfoils are beneficial to widening the positive and negative operation range, respectively. Further, it is shown in the optimization design of impellers that the tandem impeller efficiency can be increased through reduced curvature of the blade profile at the inducer hub, S-shaped blade angle distribution at the inducer tip, and increased blade angle at the exducer tip near the leading edge. Cheng et al. integrated CFD technology and numerical optimization algorithms to comprehensively optimize the configuration parameters of the subsonic cascade, and summarized and verified the influence of chord-length ratio and corner ratio on the attack angle characteristics of a cascade [30]. In studies of compressor element performance and design, the exploration for achieving the best diffuser performance at a given impeller design is of great interest. Although a variety of geometric parameters jointly determine the performance of the tandem vane diffuser, it does not affect the analysis on the effect of a specific parameter alone on its performance.

In the present study, the general definition of the total bending angle of a tandem vane diffuser is given first, which includes the front row and the rear row blades. Then, a series of tandem vane diffusers are designed with the variation of the total bending angle. Numerical simulations are carried out to predict the performance of the compressor stage with these tandem vane diffusers. The effect of the total bending angle on the performance of the stage is discussed for the total pressure loss, the pressure recovery, the polytropic efficiency, and the stable operating range. The variation of the internal flow field with various total bending angles is analyzed to clarify the reason why a tandem vane diffuser is able to enhance the performance of the compressor stage. Finally, the research results show the optimum total bending angle to be 10°.

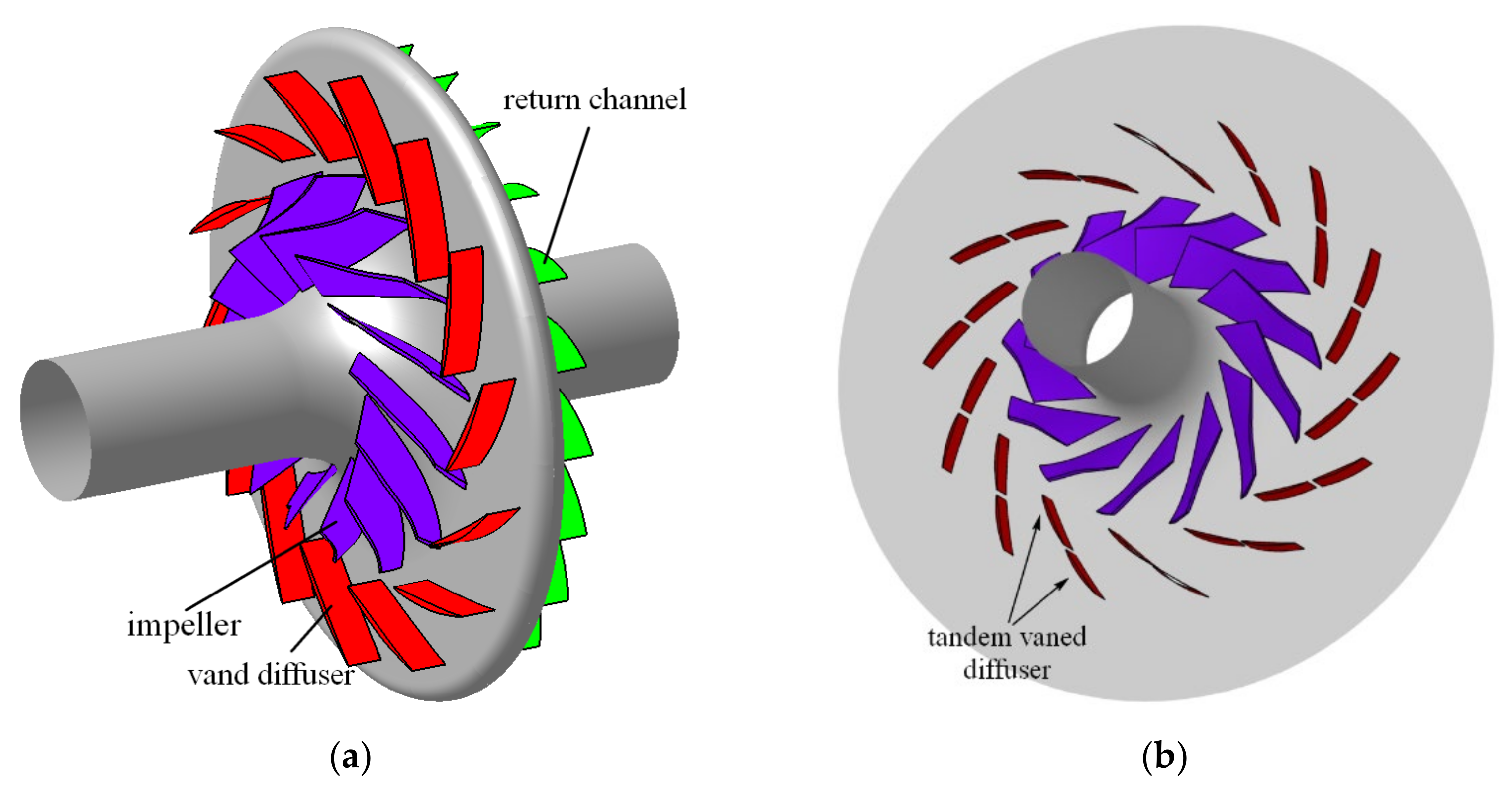
2. Computational Model and Numerical Method

2.1. Definition of Total Bending Angle of Tandem Vane Diffuser

In this study, the KY108 centrifugal compressor is employed as the prototype model, which is shown in Figure 1a. The stage is composed of the impeller, the vane diffuser with single row of blades, and a return channel. The number of the impeller blade is 13, the number of diffuser blade is 14, the rotational speed is 14,230 rpm, and the delivery medium is air. The detailed design parameters of the KY108 centrifugal compressor are given in reference [7]. In the newly designed vane diffuser, the impeller geometry is not changed, and the vane diffuser is replaced by tandem vane diffusers. The designs of the tandem vane diffusers are done with the following approaches: the blade profile of the original diffuser, the direction of the chord line, the leading edge, and the trailing edge point are fixed. The size of the blade is produced proportionally to the original blade, and the radial distance of the tandem blades is 0.1 times the original blade chord length, which is defined as the original mode of the tandem blade diffuser. The three-dimensional model is shown in Figure 1b. The angle between the tangent line of the front blade arc line at the leading edge point and the tangent line of the rear blade arc line at the trailing edge point is defined as the total bending angle, represented as θ_T.

Figure 2a is a schematic diagram of the total bending angle of the tandem blades. The rear blade rotates around the leading edge point for different total bending angles, as shown in Figure 2b. The total bending angle of the original single row of blades is 43.36° (now is replaced by 0° model below) and variations of tandem vane diffusers are obtained by increasing the angle of bending. Seven total bending angles are investigated in this paper, which are θ_T = 43.36°, 46.36°, 49.36°, 53.36°, 58.36°, 61.36°, and 64.36° (corresponding to the 0° model, 3° model, 6° model, 10° model, 15° model, 18° model, and 21° model, respectively).

2.2. Numerical Method

Numerical simulations of internal flow in the centrifugal compressor stages with a single row diffuser and tandem vane diffusers are carried out by NUMECA Fine/Turbo 9.1 which is a commercial software for solving viscous flow field calculation launched by Belgian NUMECA company for the international market. The three-dimensional Reynolds time-averaged Navier-Stokes equations are solved in the relative coordinate system. The system of equations is closed with the one-equation Spalart-Allmaras (S-A) turbulence model. Compared with the two-equation model, the S-A turbulence model has a smaller amount of storage and calculations as well as good calculation stability. The calculation grid near the wall does not need to be very fine, which is more suitable for engineering applications. The Jameson central difference scheme is used for spatial discretization. The multigrid method, variable time step size, and the residual smoothing method are used to accelerate iterative convergence. In order to ensure the conservation of mass, momentum, and energy, the rotational subsurface data transfer is based on the circumferential mean coupling hybrid plane method. The inlet boundary condition is set as the axial inlet, and the turbulent viscosity coefficient is 8 × 10⁻⁵ m²/s for a given total temperature and total pressure. The boundary condition at the outlet of the stage is given as a mass flow outlet or an average static pressure exit. The variations of flow coefficient for calculations are shown in

Table 1. Flow coefficient for the calculation of the performance of the compressor.

Number	1	2	3	4	5	6	7
Flow Coefficient	0.16768	0.15658	0.14997	0.14310	0.13554	0.12899	0.12090

. The working condition 4 is the design condition of the original single row diffuser. The minimum flow rate for the calculation is that the convergence of computation can be obtained with the calculation algorithm, from which the computation diverges. The flow coefficient $\phi$ is defined by the following equation,

$$\phi =\frac{4Q_m}{\pi {\rho }^{*}{U}_2{D}_2^2}$$

(1)

where $Q_m$ denotes the mass flow rate, ${\rho }^{*}$ is the mass density, $U_2$ is the circumferential velocity at the impeller exit, and $D_2$ is the outlet diameter of the impeller.

The convergence criteria are:

• Global residuals and block residuals decrease by at least three orders of magnitude.
• The relative error of flow rate at inlet and outlet is less than 0.02% and the pressure ratio converges to a fixed value or a small range of periodical oscillations occur in the range of ± 0.2%.

The model efficiency is calculated by using the data of the inlet parameters of the stage and the mean total pressure and total temperature which are circumferential mass averaged at the outlet of the diffuser. The pressure ratio refers to the ratio of the total pressure at the outlet of the diffuser to the total pressure at the inlet of stage.

Polytropic efficiency of stage

$${\eta }_{pol}=\frac{1}{\gamma /\left(\gamma -1\right)}\frac{\lg \left(p_{04}/p_{01}\right)}{\lg \left(T_{04}/T_{01}\right)}$$

(2)

Polytropic efficiency of impeller

$${\eta }_{pol}=\frac{1}{\gamma /\left(\gamma -1\right)}\frac{\lg \left(p_{02}/p_{01}\right)}{\lg \left(T_{02}/T_{01}\right)}$$

(3)

Total pressure ratio of diffuser

$${\pi }_D=\frac{p_{04}}{p_{03}}$$

(4)

where $p_{01}$ and $p_{02}$ are the total pressure at the inlet and outlet of the impeller, respectively, $p_{03}$ and $p_{04}$ are the total pressure at the inlet and outlet of the diffuser, respectively, $T_{01}$ and $T_{02}$ are the total temperature at the inlet and outlet of the impeller, respectively, $T_{04}$ is the total temperature at the diffuser exit and γ is the specific heat ratio.

The static pressure recovery coefficient and the total pressure loss coefficient are defined as follows, respectively,

$$C_{\mathrm{s}p}=\frac{p_4-p_3}{p_{03}-p_3},$$

(5)

$${\varsigma }_{tp}=\frac{p_{03}-p_{04}}{p_{03}-p_3},$$

(6)

where $p_3$ and $p_4$ are the static pressure at the inlet and outlet of the diffuser, respectively.

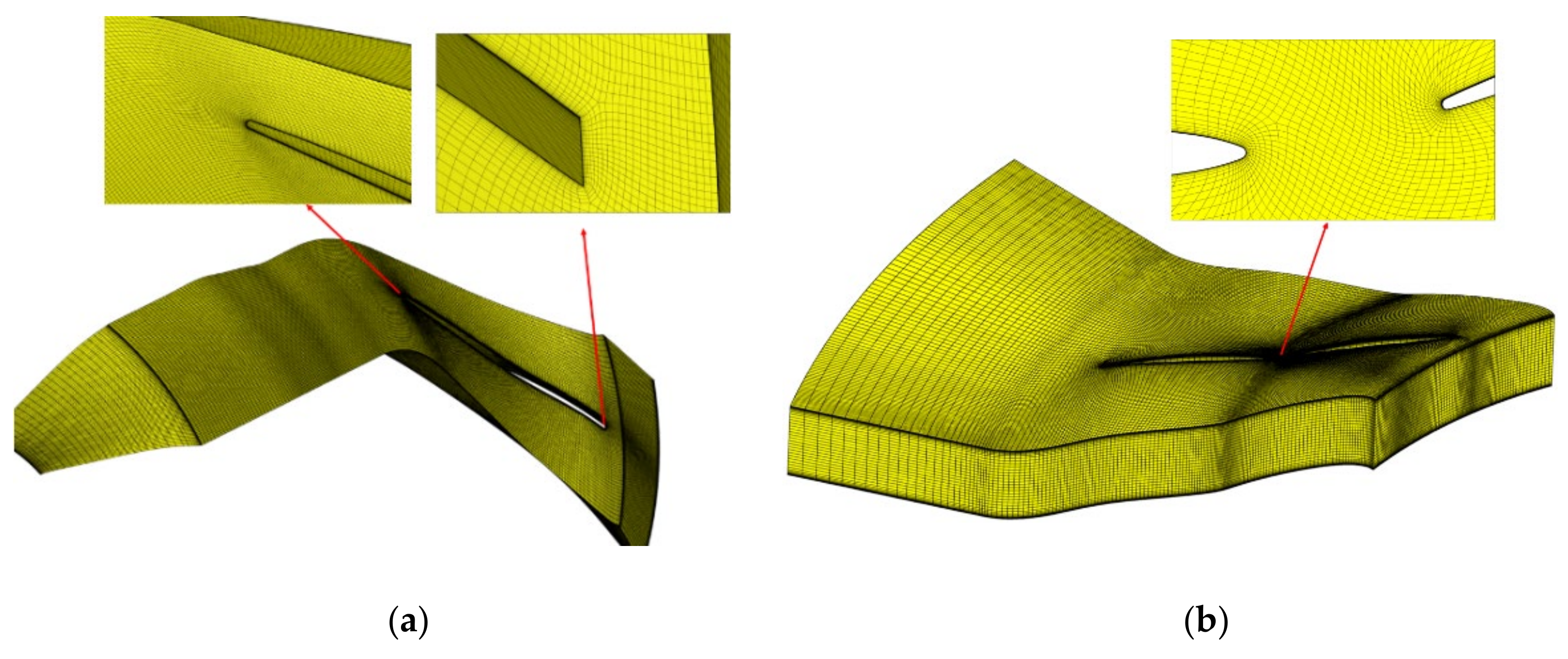
2.3. Computational Meshes and Grid Independence Verification

To effectively reduce the error caused by the artificial boundary condition applied by the inlet of the vane diffuser, the inlet boundary of the selected calculation area starts from the inlet of the impeller. The computational domain comprises two parts of the impeller and the diffuser. The computational grid is generated by the AutoGrid module, and the distance from the first layer grid node to the wall is 0.005 mm to meet the requirements of the wall condition in the S-A turbulence model ($y^{+}$ = 1~10). The impeller part adopts the same grid to process the tandem blade diffuser and the second row of blades as the splitter blades of the first row of blades, and the grid is generated as a whole. Grid-independent verification of the original model is performed using four sets of grids with 0.64 million, 1.27 million, 2.18 million, and 3.21 million elements. Figure 3 shows the grid-independence verification outcomes. When the number of elements is not less than 1.27 million, the relative error of the simulation results is less than 0.1%, indicating the number of elements has little effect on the accuracy of results. Considering the limitation of practical calculation conditions, the total number of elements in the final calculation is 2.18 million, with 1.11 million in the impeller and 1.07 million in the blade diffuser. One representative mesh corresponding to a tandem blade diffuser with a total bend angle of 43.36°, which is the 0° model, is shown in Figure 4.

In order to verify the accuracy and reliability of the numerical simulation results, the numerical simulation results for the KY108 model are compared with the experimental data provided by Shenyang blower (Group) Co., Ltd. (Shenyang, China). Figure 5 shows the comparison between the numerical simulation and the experimental results of polytropic efficiency and total pressure ratio. At the low flow conditions, the experimental value is slightly larger than the calculated value. With the increase of the flow rate, the gap between the two becomes smaller and the overall trend is consistent. The error is less than 2%, which meets the requirement of the calculation.

3. Calculation Results and Analysis

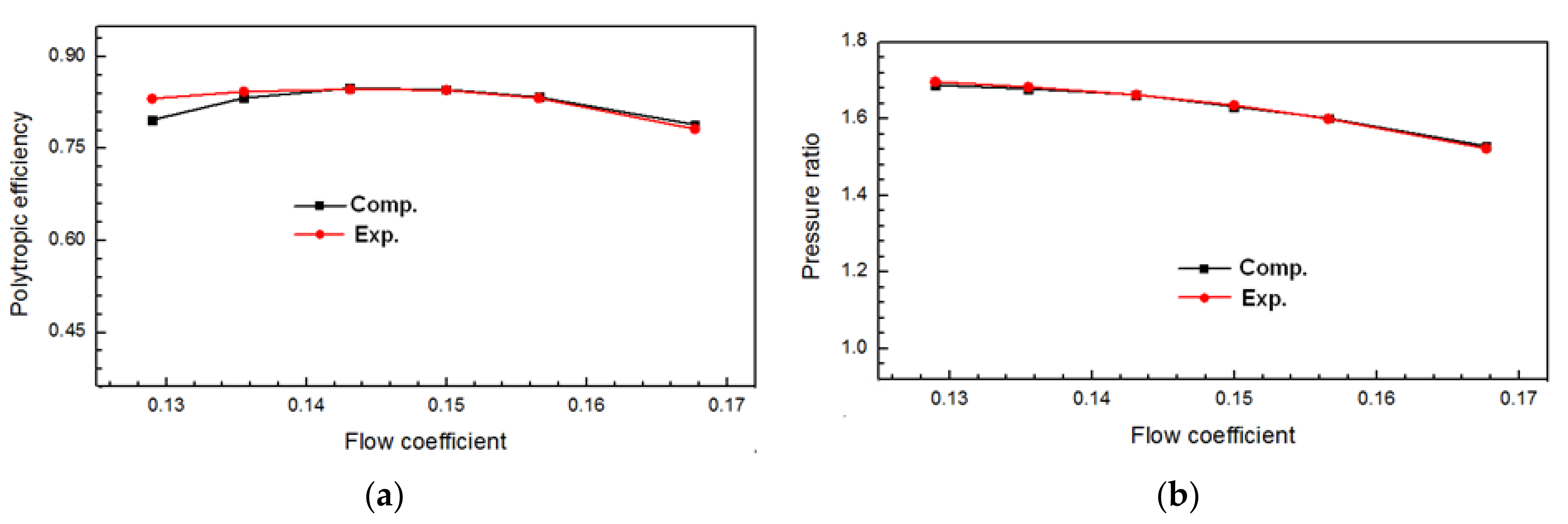
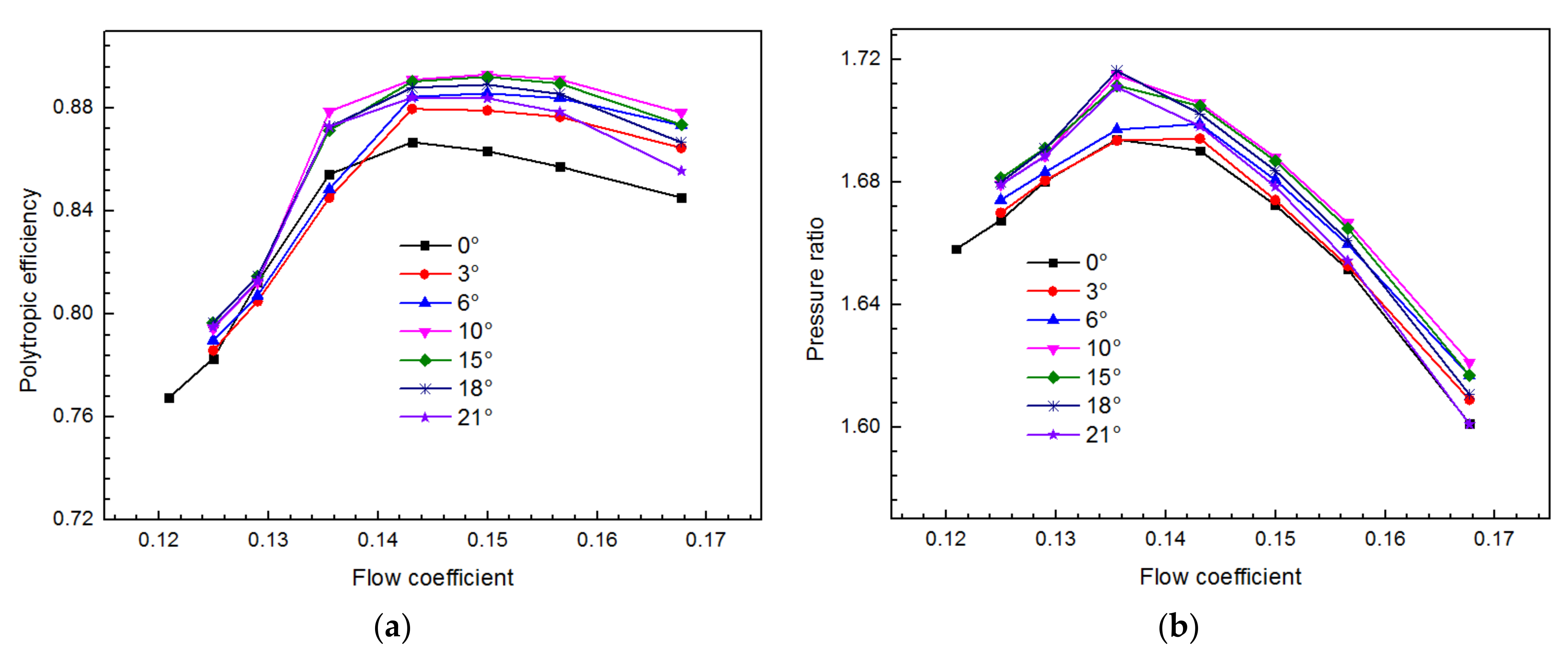
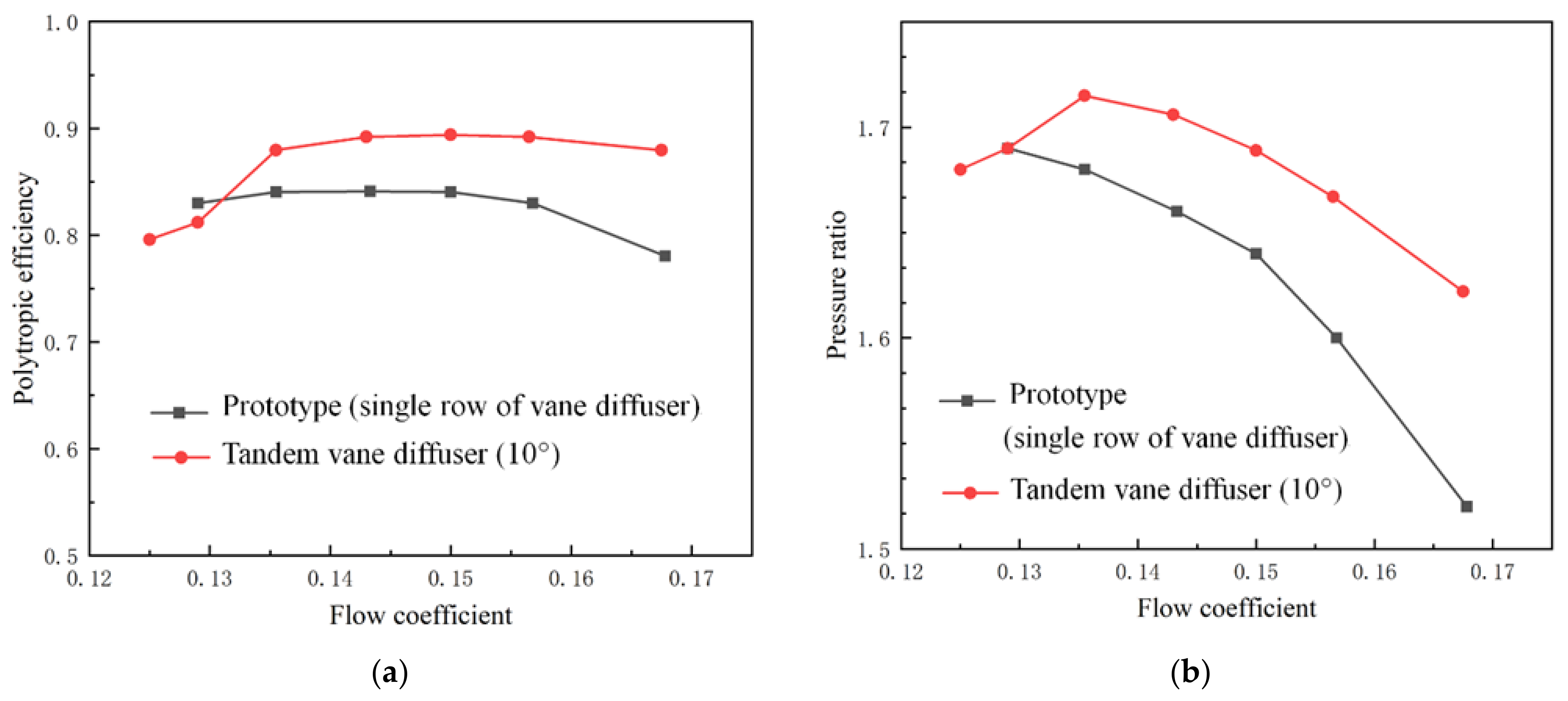
3.1. Analysis on Performance of Stage

Figure 6 shows the response of different total bend angles θ_T to centrifugal compressor performance. It can be seen from Figure 6a that θ_T can effectively change the performance curve of the stage. With the increase of the total bending angle of the model, the maximum efficiency position presents large variation. The variable efficiency of the 10° model is increased by four percentage points compared with the 0° model under working condition 5 ($\phi$ = 0.13554), which indicates that increasing the total bending angle can effectively widen the range of the model stage high efficiency. It can be seen from the total pressure ratio curve that with the increase of the total bending angle, the total pressure ratio increases in the range of the whole flow condition, and the maximum pressure ratio moves to the small flow range. However, when the increase of the total bending angle is greater than the 15° model, the efficiency and the pressure ratio decrease in the flow range above the design condition. The change of the total bending angle has an effect on the stable working range. Therefore, it is necessary to consider the balance between performance and stable range of work.

Figure 6b shows the performance comparison in different flow conditions of each scheme. Comparison is carried out for seven models of tandem vane diffusers. It is found that as the total bending angle increases, the model shows that the polytropic efficiency first increases and then decreases. Under the condition that the flow conditions of the impeller and the front vanes of the diffuser remain unchanged, the change of the installation angle of the rear vanes of the diffuser leads to the change of the incident angle, thereby changing the performance of the compressor. The efficiency corresponding to the 10° model reaches a maximum, and in the vicinity of surge condition, the 15° model reaches a maximum of efficiency. This shows that there is an optimum overall total bending angle to make the model efficiency reach the highest point.

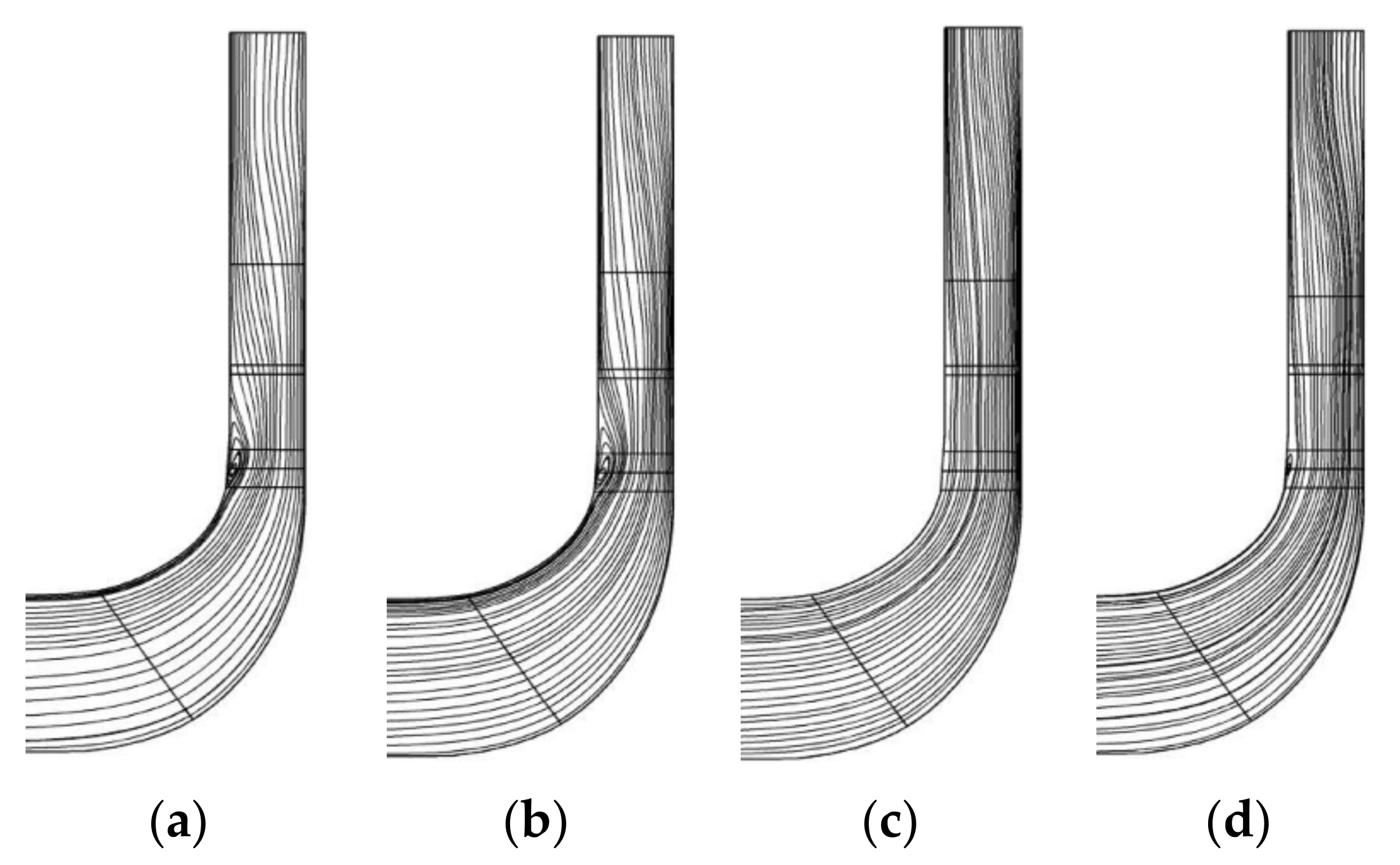
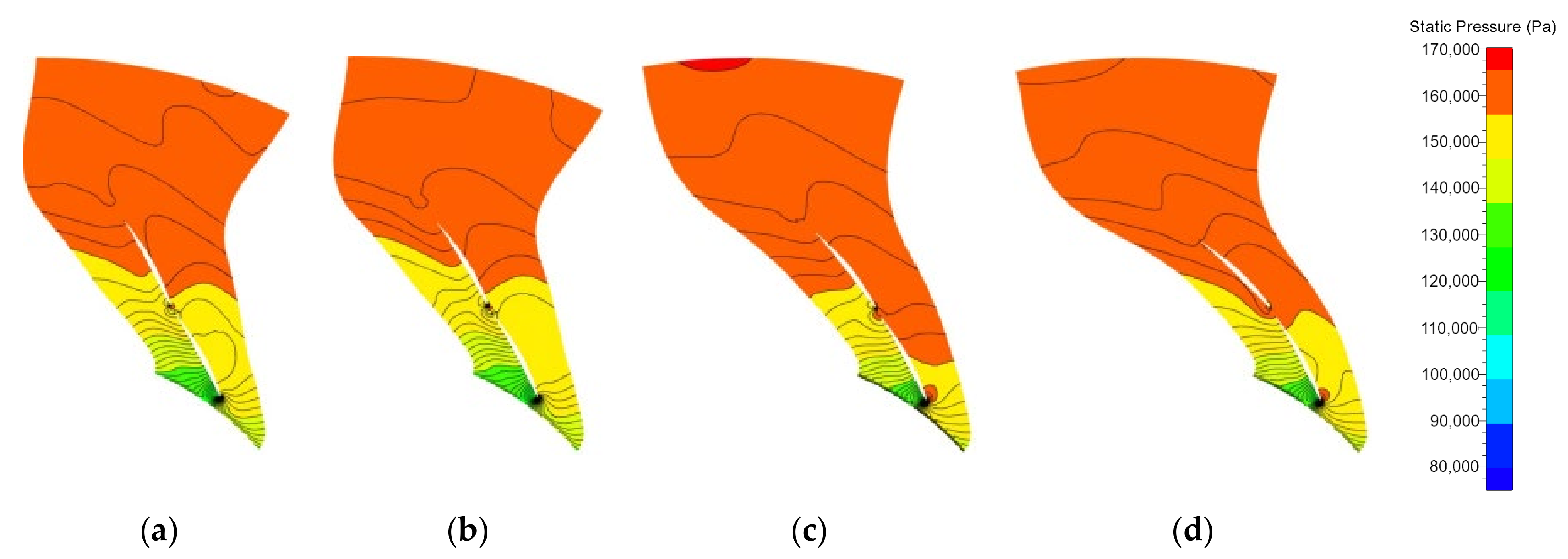
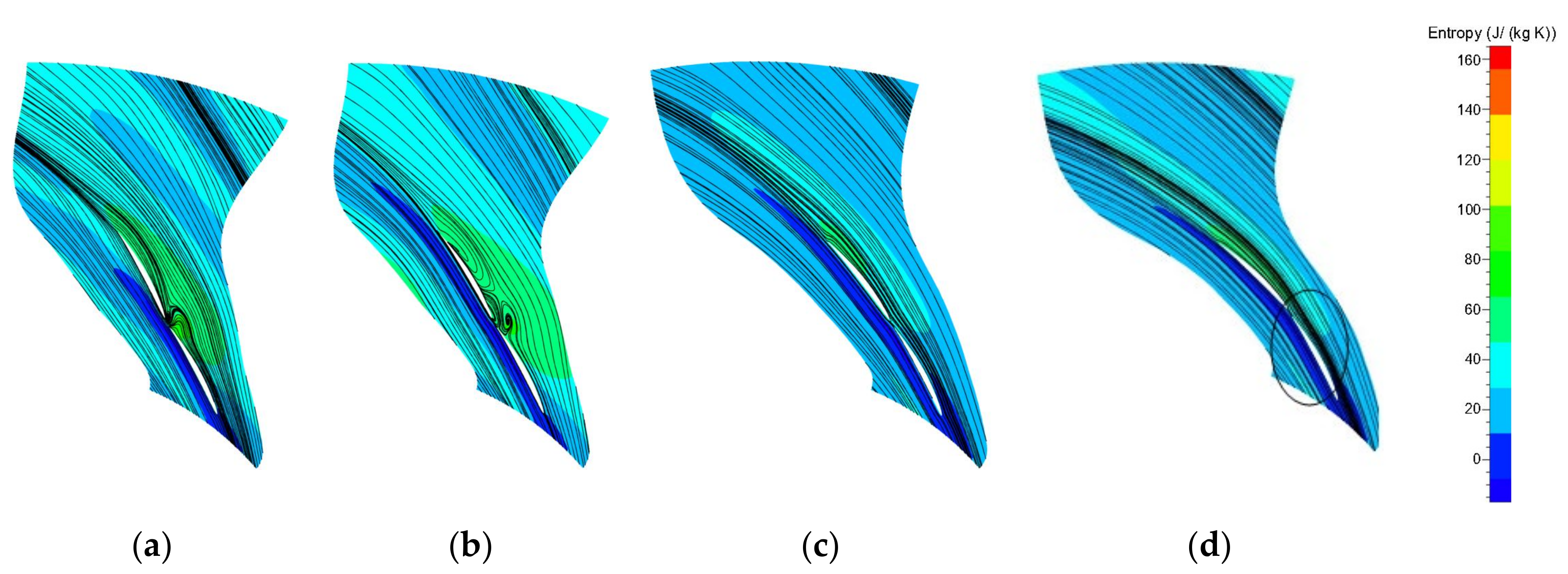
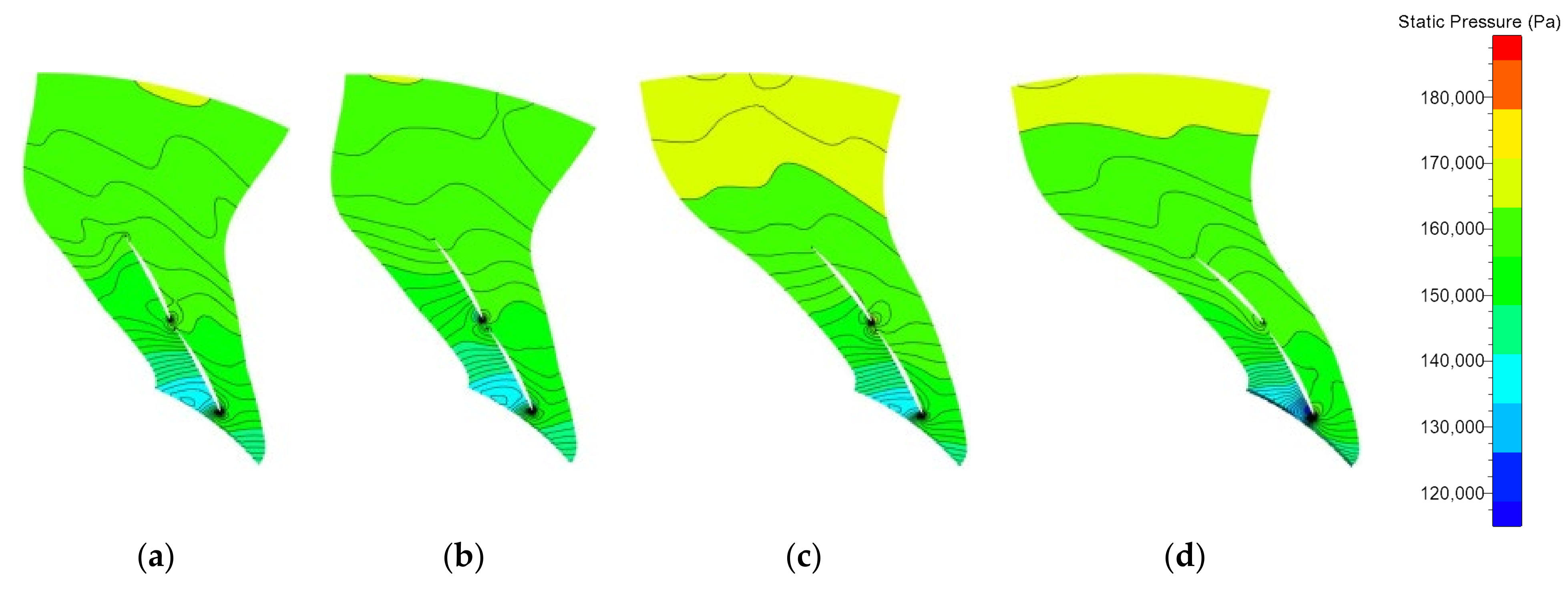
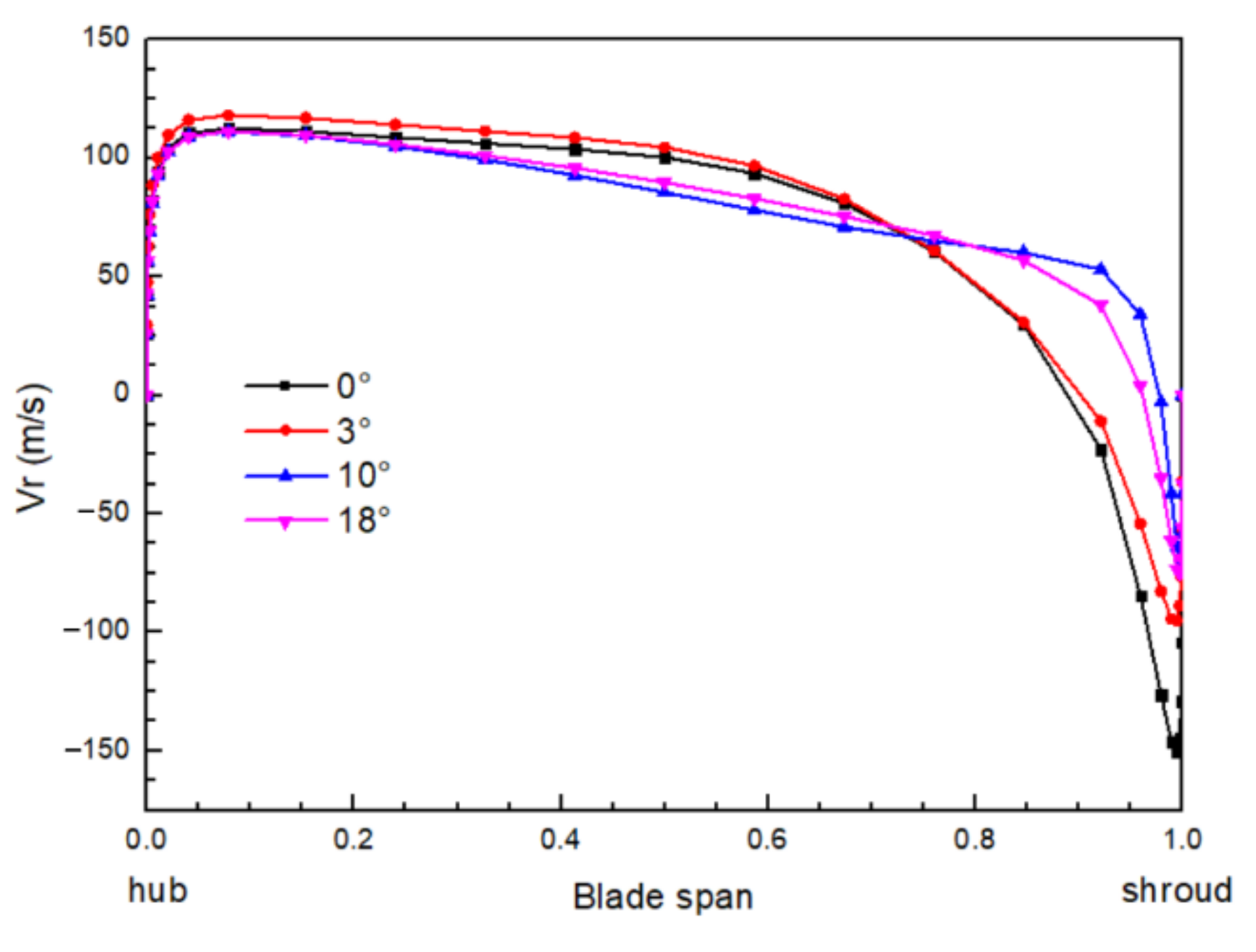
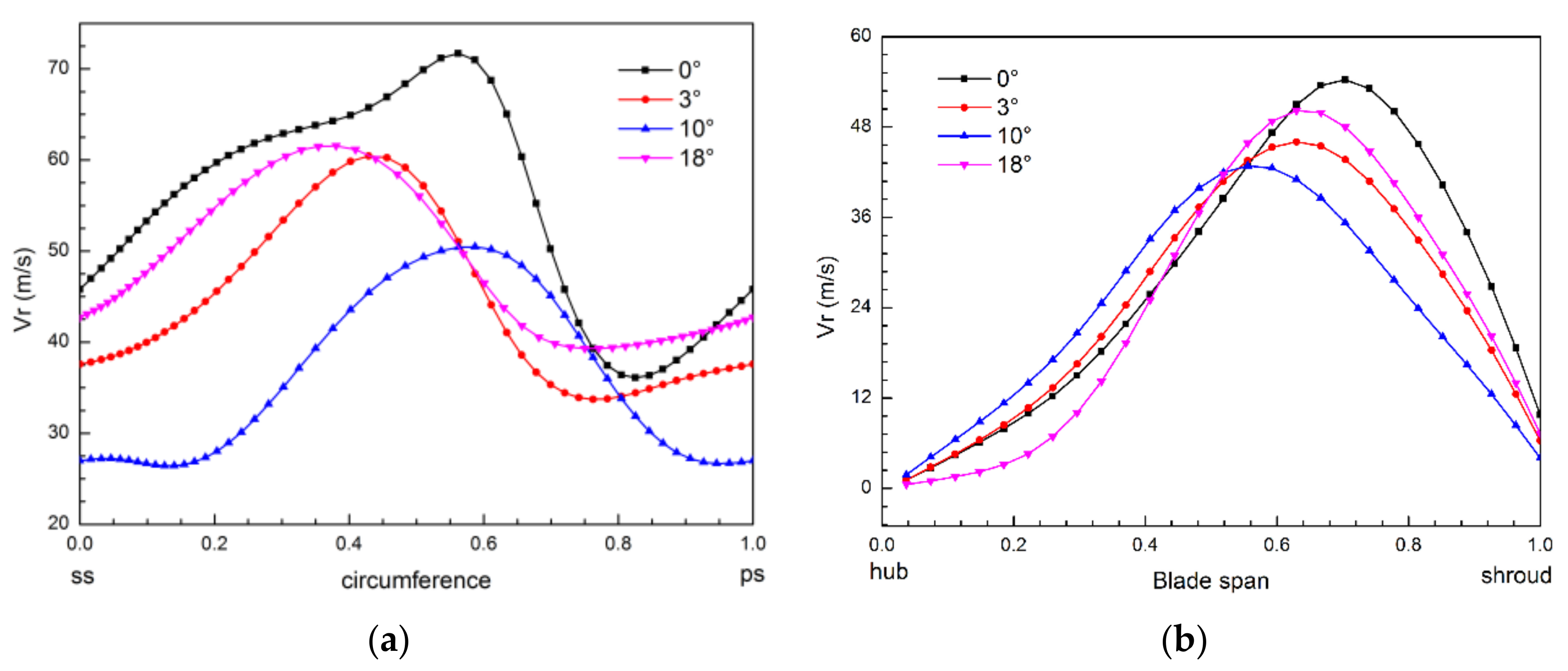
3.2. Analysis on Flow Field in the Diffuser at a Small Flow Rate

According to the performance analysis of centrifugal compressor in the previous section, under the condition of small flow rate (less than flow coefficient $\phi$ = 0.13554), the total bending angle has a great effect on the performance of the stage. In the following, the distribution of flow variables in each typical model under small flow condition is analyzed, and the influence of the total bending angle on the model stage performance of the centrifugal compressor is discussed.

Figure 7 and Figure 8 are the distributions of static pressure recovery coefficient and total pressure loss coefficient of the cascade blade diffuser with different total bending angles along the direction of the blade height, respectively. It can be seen from the graph that the static pressure recovery coefficient and total pressure loss coefficient of different models are similar along the longitudinal direction. The static pressure recovery coefficient increases slowly from the hub side to the shroud side, and the total pressure loss coefficient appears on the side of the near hub side and the near shroud side. The static pressure recovery coefficient of the 10° model increased by 15% compared with the original model, and the static pressure recovery coefficient of the 18° model increased compared with the original model of 5%. From Figure 9, it is found that the total pressure loss coefficient shows a gradual decrease from the hub side to a sharp rise near the shroud side. The larger loss occurs at the height below 5% and the greater height above 95%. The main reason is the severe friction produced by the wall effect. The total pressure loss for the 3° model and 0° model are significantly higher than those of other models. The 10° model has a lower total pressure loss coefficient along the height of the blade overall.

Figure 9 shows the meridian streamline diagram of the centrifugal compressor under small flow conditions. It can be seen from Figure 9a that there is a large separation zone between the impeller outlet and the diffuser inlet in the original model, especially near the shroud side of the impeller. This is because the jet-wake pattern is mainly located near the shroud area of the impeller outlet, which leads to the separation of flow from the wall at this position under the low velocity flow and the reverse pressure gradient effect, which results in the obvious deflection of the air flow away from the diffuser channel. Compared with Figure 9b it is found that the separation area of the shroud side increases significantly and the air flow deflection appears at the outlet position of the front row blade of the tandem blade diffuser. When further increasing the total bending angle as shown in Figure 9c, the reverse flow zone at the outlet of the impeller and the inlet of the diffuser is basically constrained and the airflow flows along the channel. Further continuing to increase the total bending angle as shown in Figure 9d, at the impeller outlet position, there is a small area of backflow zone. This shows that changing the total bending angle of the cascade blade diffuser can restrain the flow separation at the impeller outlet and the inlet position of the diffuser.

Figure 10 shows the entropy contour and streamline distribution at a 90% blade height (near the shroud side) for different cases. It can be seen from the diagram that the flow of airflow along the circumferential direction is obvious after the trailing edge of each model diffuser blade, which is mainly due to the influence of the wall surface. From the front edge of the front blade pressure side, the separation began to appear and extended to the position of 50% chord length. Due to the influence of the flow from the adjacent channels, the low speed fluid was sucked into the high speed fluid. A large swirl was formed in the channel and extended to 40% chord length of the rear blade. The circumferential flow at the inlet of diffuser weakens and there is no obvious flow separation in the front blade. There is a small separation area on the trailing edge of the pressure surface of the rear row blade.

Figure 11 shows the static pressure contour at a height of 90% of the blades in the diffuser channel. Compared with the four static pressure contours, it can be seen that the pressure surface of the front row blade of the 10° model increases greatly at the position of 50% chord length, and the high pressure region is obviously larger than that of other models. The pressure distribution is more uniform than those of other models, which indicates that the diffusing capacity of the 10° model is better than those of other models at the near cap position.

Figure 12 shows the streamline and entropy increase at 50% blade height in the diffuser channel. Figure 12a in the 0° model of the front pressure surface of the blade trailing edge of the recirculation zone, and the pressure of the rear blade existing on the surface of the boundary layer is thicker. Figure 12b shows that flow separation occurs near the blade pressure side for the 3° model. However, compared with that in the near shroud side, the separation and reverse flow regions at the trailing edge of the blade pressure surface of the front row are obviously reduced. At this cross section position, the flow in the diffuser channel of the 10° model and the 18° model is better, and there is no obvious flow separation on the blade surfaces. It can be seen from the entropy contour that the entropy increase of the 10° model and 18° model in this section is significantly lower than those of the 0° model and 3° model. It is verified that the total pressure loss coefficient of the 10° model and 18° model is significantly lower than those of the 0° model and the 3° model, and the coefficient of static pressure recovery is obviously larger than that of the 0° model and the 3° model.

Figure 13 shows the static pressure distribution at a 50% span for various total bending angles. It can be seen that the maximum static pressure increase is obtained in the case of the 10° model, which shows a more uniform pressure distribution in the diffuser channel and a high pressure zone behind the diffuser outlet, whereas for the other models, the distributions of static pressure in the diffuser channel are not uniform and are distorted within the rear row of blades.

Figure 14 shows the entropy contour and streamline distribution at 10% blade height (near the hub side) for different cases. It can be seen from the diagram that there is reverse flow in the suction side of the blade for the 0° model, and this is mainly due to the effect of the adverse pressure gradient. It can also be found that the entropy increase for the 0° and the 3° model is mainly in the areas behind the diffuser, and the entropy increase for the 18° model is mainly in the entry zone of the diffuser. For the 10° model, the entropy increase in the whole diffuser areas is the lowest.

Figure 15 shows the static pressure contour at height of 10% blades in the diffuser channel. Compared with the four static pressure contours, it can be seen that there is a low pressure area from the diffuser inlet to the suction surface position of the front row of diffuser, indicating that the inlet is impacted by high speed fluid from the impeller, whereas the 18° model is particularly severe and indicates a greater loss of the hub side diffuser inlet in the Figure 15d. The pressure distribution for the 10° model is more uniform than the others and it is high behind the blades, which indicates a high-pressure recovery.

Figure 16 shows the radial velocity distribution along the blade height at the diffuser inlet. It can be seen that the radial velocity distribution along the blade height at the diffuser inlet is not uniform, and it is high at the hub side and is low at the shroud side. The radial velocity at the shroud side is even negative. The distributions of the radial velocity at the diffuser outlet along the circumferential direction and along the vane height are shown in Figure 17. The abscissas of the Figure 17a,b are both dimensionless. It can be seen from Figure 17 that the radial velocity distribution at the outlet of the diffuser is greatly affected by different total bending angles. Most of the flow rate is concentrated near the suction side for 0° model, 3° model, and 18° model, whereas it is much improved with the 10° model. It can be seen from Figure 17b that the distribution of radial velocity along the blade height is not uniform, and the most uniform distribution is achieved by the 10° model. By comparing the radial velocity distribution along the blade height at the inlet and outlet position of the diffuser with different total angle models, it is found that the uneven distribution of radial velocity is greatly weakened by the variable-angle model of diffuser. At the same time, the reverse flow is restrained.

Figure 18 shows the relative velocity distribution at the cross section near the outlet of the front blade of the different total bending angle model. It can be seen that there is a high velocity wake on the suction side of the front row blade, and there is a low velocity region at the side of the pressure surface near the shroud. There is a high speed area near the hub side. Comparing the four graphs, it can be found that the low-speed range in Figure 18c is smaller, the relative velocity contour distribution is more uniform, the velocity gradient is small, the secondary flow loss is also small, and the energy loss due to incidence would be lower at the rear row blade. This is in agreement with the results of the flow analysis from entropy distributions.

To further analyze the effect of the total bending angle on the development of internal flow in diffuser, Figure 19 gives a comparison of the total pressure distribution between the 0° model and the 10° model diffuser at three cross-sections from the diffuser inlet (Section 1) to outlet (Section 3). For the 0° model, the location of the high-pressure region is not regular. At the diffuser inlet, it is located at the corner of hub/suction, whereas it moves to the corner of the shroud/suction at the diffuser outlet. For the 10° model, the location of the high pressure region is regular. At the diffuser inlet, it is located at the corner of the hub/suction, and it moves slightly to the middle of suction side at the middle and the outlet of the diffuser.

As discussed above, for the newly designed tandem vane diffusers, the one with the 10° model achieves the best performance and the internal flow is the most reasonable to obtain the pressure recovery and the total efficiency. Thus, the tandem vane diffuser with the 10° model is the optimum one in the present studies. The comparison of the performance of centrifugal compressor stages, between the prototype with single row of vane diffuser and the stage with new designed tandem vane diffuser of the 10° model is shown in Figure 20. It is found that both the polytropic efficiency and the total pressure are improved with the designed tandem vane diffuser in the whole range of flow rate except at a very low flow rate. It is seen that the efficiency is increased about 6% and the total pressure ratio is increased about 3.5% with the newly designed tandem vane diffuser at the design flow coefficient of 0.15.

4. Conclusions

In this paper, performance enhancement of a centrifugal compressor by designing a tandem cascade diffuser is carried out by numerical simulation. It is found that the total bending angle of the tandem cascade diffuser has a great effect on the performance and internal flow of the centrifugal compressor. The flow field in the centrifugal compressor with four typical total bending angles of the tandem cascade diffuser is analyzed in detail. The following conclusions are obtained:

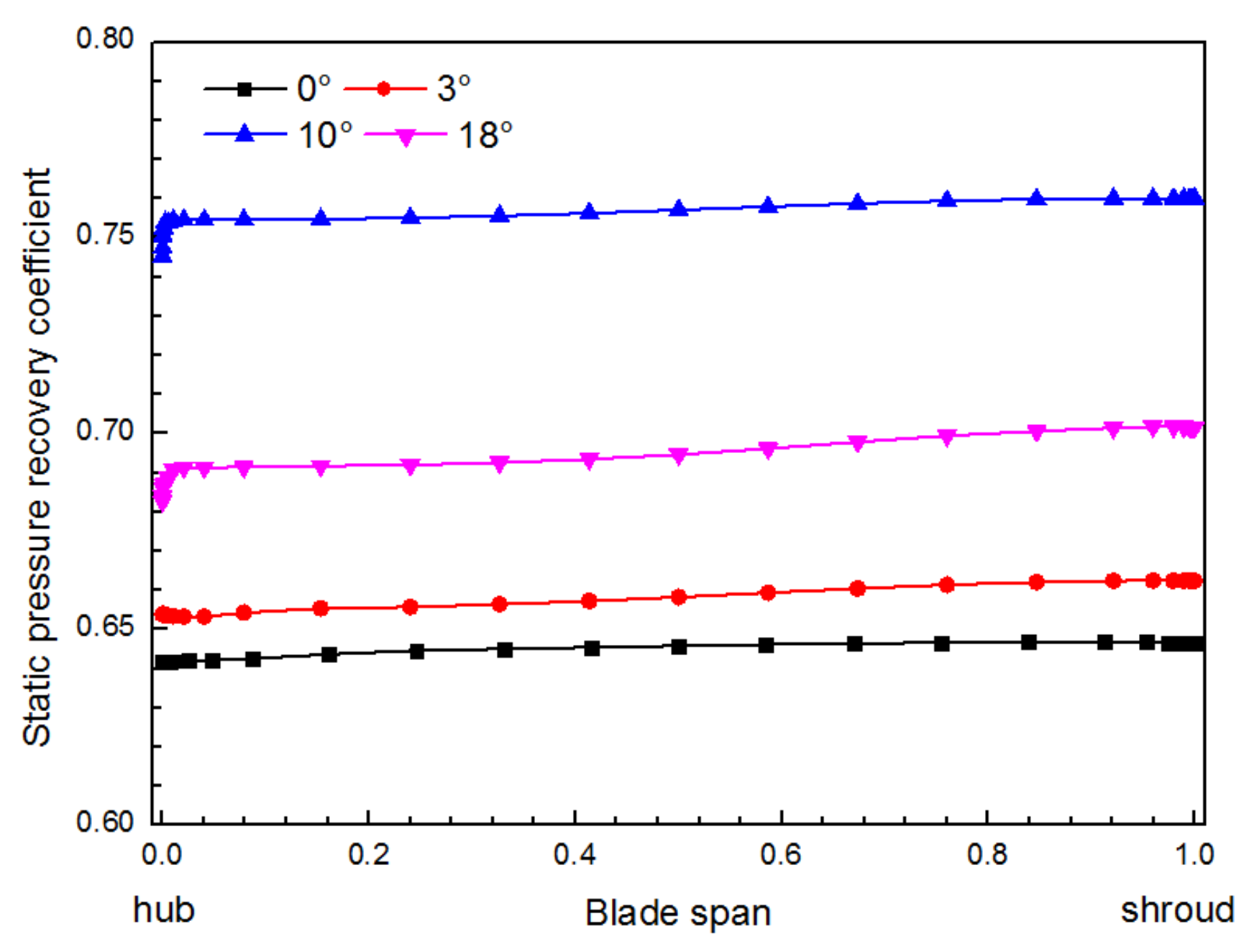
• The efficiency and pressure ratio of the compressor stage increases with the increase of the total bending angle of the tandem blade diffuser in a certain range. The results show that the optimal performance is obtained by the 10° model for the compressor studied.
• The analysis of the meridional flow field of the impeller-diffuser at the low flow condition reveals that the increase of the total bending angle in a reasonable range effectively reduces the separation area near the shroud side of the diffuser. The increase of the total bending angle improves the separation in the diffuser flow field, thus greatly increasing the static pressure recovery coefficient and reducing the total pressure loss coefficient in the whole range of blade heights.
• By analyzing the radial-circumferential sections of the diffuser, it is found that the increase of the total bending angle in a certain range improves the distribution of radial velocity in the diffuser inlet and outlet and the relative velocity distribution at the outlet of the front row blade.
• The minimum total pressure loss coefficient and the maximum static pressure recovery coefficient are achieved with the 10° model, and thus the optimum performance of the compressor is obtained at this value of the total bending angle.
• It is found that a proper increase in the total bending angle improves the performance of the compressor stage by significantly reducing the separation near the shroud and uniformly disturbing flow velocity at the impeller outlet and diffuser outlet. Sufficient increase of the total bending angle is necessary to produce beneficial effects, whereas excessive increasing will instead deteriorate the compressor’s performance.
• Compared with the stage of the prototype with single row of vane diffuser, the stage with newly designed tandem vane diffuser of the 10° model achieves the performance improvement, the efficiency increased about 6%, and the total pressure increased about 3.5% at the design flow coefficient of 0.15.