Communication Systems Performance at mm and THz as a Function of a Rain Rate Probability Density Function Model
Abstract
:1. Introduction
2. Rain Rate Statistics
3. Attenuation of RF Signal by Rain
4. Mathematical Model of Symbol Error Rate
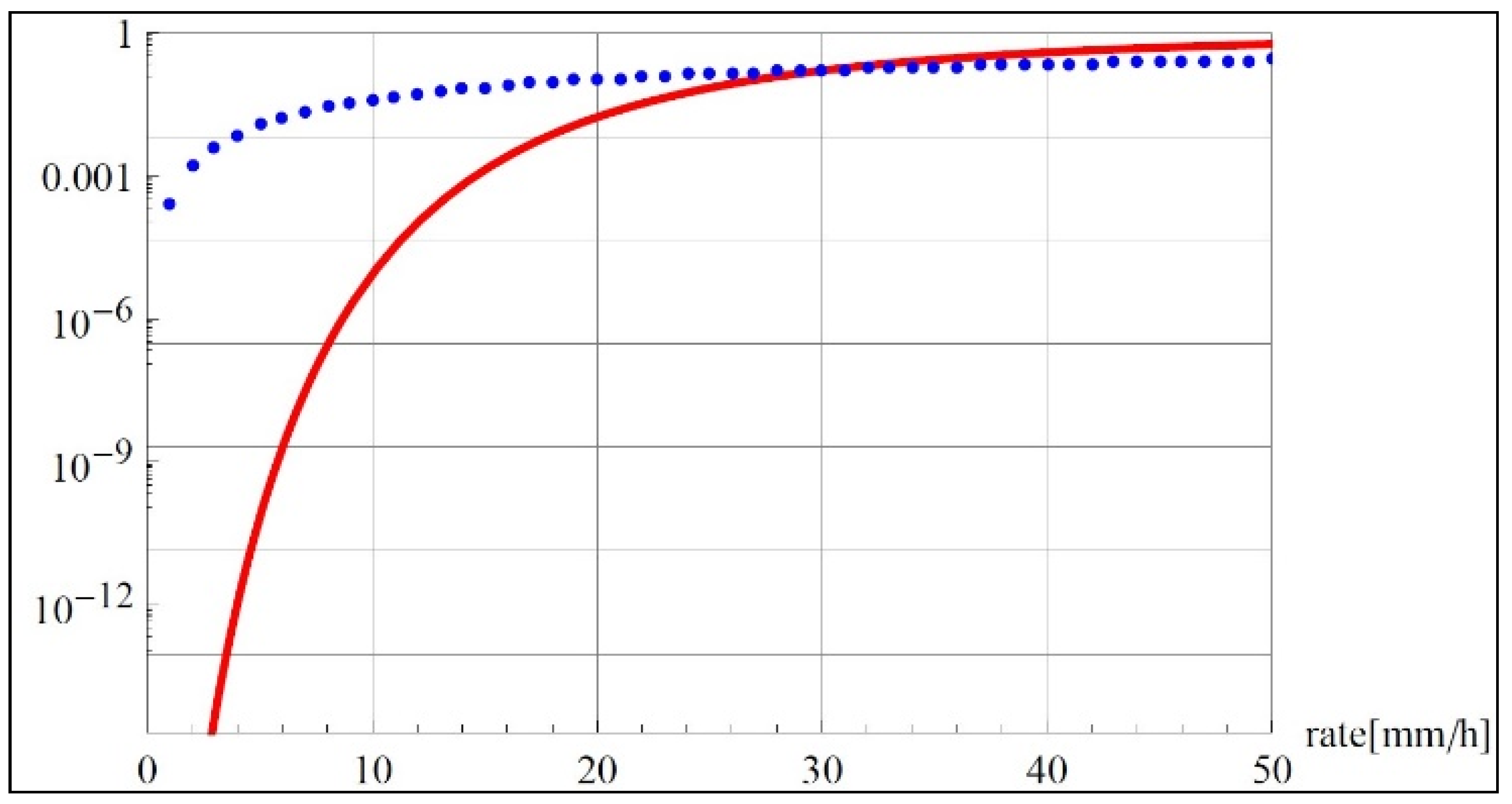
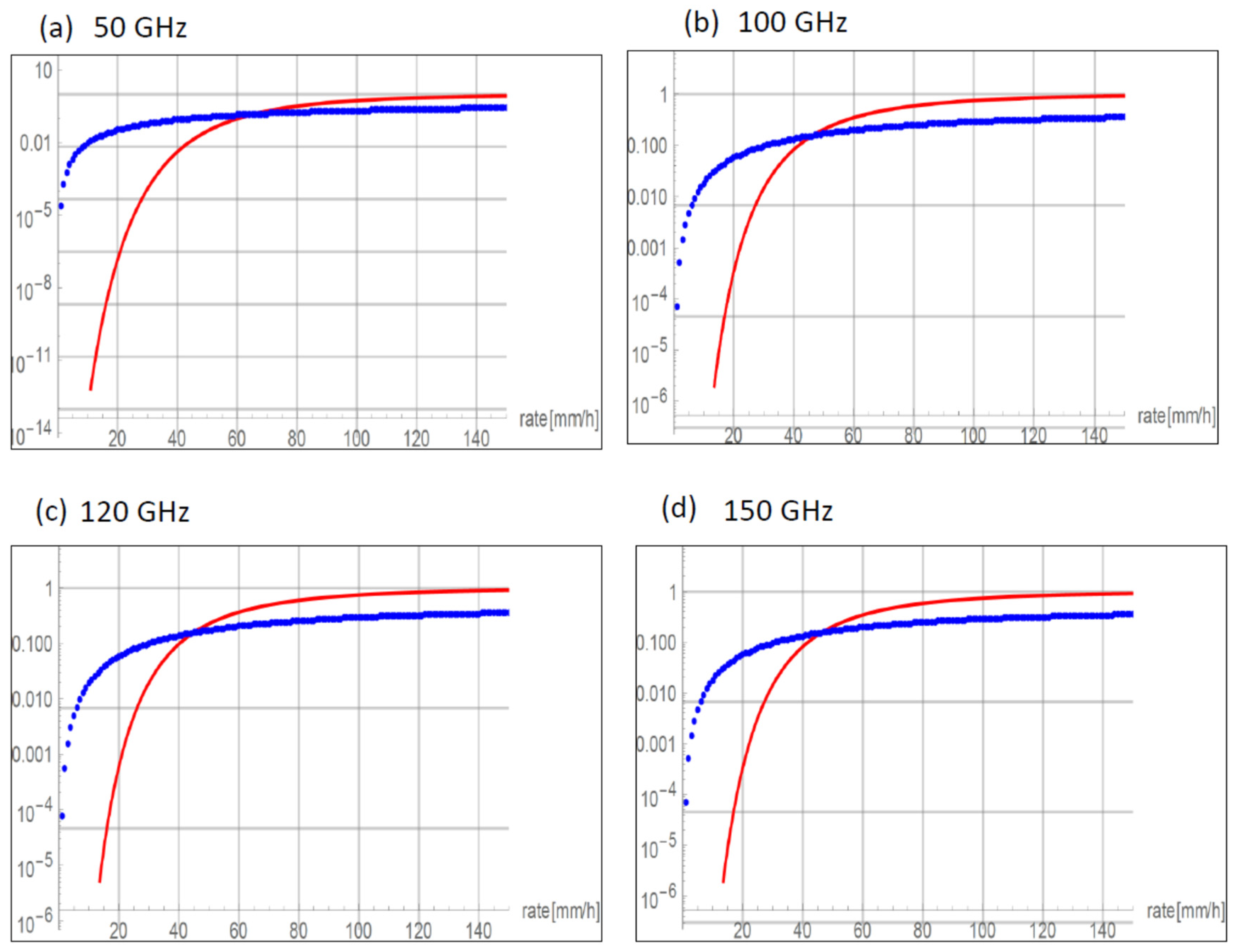
5. Rain Rate Statistics
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- FCC Opens Spectrum Horizons for New Services & Technologies. Available online: https://www.fcc.gov/document/fcc-opens-spectrum-horizons-new-services-technologies (accessed on 25 July 2022).
- Studies on the Use of Frequency Bands above 275 GHz by Land-Mobile and Fixed Service Applications. Available online: https://news.itu.int/studies-on-the-use-of-frequency-bands-above-275-ghz-by-land-mobile-and-fixed-service-applications/ (accessed on 25 July 2022).
- Moshirfatemi, F. Communicating at Terahertz Frequencies. 2017. Available online: https://pdxscholar.library.pdx.edu/cgi/viewcontent.cgi?article=4650&context=open_access_etds (accessed on 28 July 2022).
- Elayan, H.; Amin, O.; Shihada, B.; Shubair, R.M.; Alouini, M.S. Terahertz band: The last piece of RF spectrum puzzle for communication systems. IEEE Open J. Commun. Soc. 2019, 1, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Samsung Starts 6G Network Research at New Center. Available online: http://www.koreaherald.com/view.php?ud=20190604000610 (accessed on 25 July 2022).
- Move Over 5G, Japan Plans to Launch 6G by 2030, Says Report. Available online: https://www.livemint.com/technology/tech-news/move-over-5g-japan-plans-to-launch-6g-by-2030-says-report-11579590569894.html (accessed on 25 July 2022).
- Siles, G.A.; Riera, J.M.; Garcia-del-Pino, P. Atmospheric attenuation in wireless communication systems at millimeter and THz frequencies [wireless corner]. IEEE Antennas Propag. Mag. 2015, 57, 48–61. [Google Scholar] [CrossRef]
- Ishii, S.; Kinugawa, M.; Wakiyama, S.; Sayama, S.; Kamei, T. Rain attenuation in the microwave-to-terahertz waveband. Wirel. Eng. Technol. 2016, 7, 59–66. [Google Scholar] [CrossRef] [Green Version]
- Christofilakis, V.; Giorgos, T.; Spyridon, K.; Chronopoulos, A.; Sakkas, A.G.; Skrivanos, K.P.; Peppas, H.E.; Nistazakis, G.B.; Panos, K. Earth-to-earth microwave rain attenuation measurements: A survey on the recent literature. Symmetry 2020, 12, 1440. [Google Scholar] [CrossRef]
- Christofilakis, V.; Giorgos, T.; Christos, J.L.; Spyridon, K.; Chronopoulos, P.K.; Aristides, B.; Hector, E.N. A rain estimation model based on microwave signal attenuation measurements in the city of Ioannina, Greece. Meteorol. Appl. 2020, 27, e1932. [Google Scholar] [CrossRef]
- Giannetti, F.; Reggiannini, R.; Moretti, M.; Adirosi, E.; Baldini, L.; Facheris, L.; Vaccaro, A. Real-time rain rate evaluation via satellite downlink signal attenuation measurement. Sensors 2017, 17, 1864. [Google Scholar] [CrossRef]
- Korai, U.A.; Luini, L.; Nebuloni, R. Model for the prediction of rain attenuation affecting free space optical links. Electronics 2018, 7, 407. [Google Scholar] [CrossRef] [Green Version]
- Korai, U.A.; Luini, L.; Nebuloni, R.; Glesk, I. Statistics of attenuation due to rain affecting hybrid FSO/RF link: Application for 5G networks. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2022; pp. 1789–1792. [Google Scholar]
- Halder, T.; Adhikari, A.; Maitra, A. Rain attenuation studies from radiometric and rain DSD measurements at two tropical locations. J. Atmos. Sol.-Terr. Phys. 2018, 170, 11–20. [Google Scholar] [CrossRef]
- Singh, H.; Kumar, V.; Saxena, K.; Boncho, B.; Prasad, R. Proposed model for radio wave attenuation due to rain (RWAR). Wirel. Pers. Commun. 2020, 115, 791–807. [Google Scholar] [CrossRef]
- Samad, M.A.; Diba, F.D.; Choi, D.Y. A survey of rain attenuation prediction models for terrestrial links—Current research challenges and state-of-the-art. Sensors 2021, 21, 1207. [Google Scholar] [CrossRef]
- Specific Attenuation Model for Rain for Use in Prediction Methods, ITU Rec. ITU-R P.838-3, 2005. Available online: https://www.itu.int/rec/R-REC-P.838/en (accessed on 25 July 2022).
- Propagation Data and Prediction Methods Required for the Design of Earth-Space Telecommunication Systems. ITU Rec. ITU-R 618-12, 2015. Available online: https://www.itu.int/rec/R-REC-P.618/en (accessed on 25 July 2022).
- Time Series Synthesis of Tropospheric Impairments, ITU Rec. ITU-R P.1853-2, 2019. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-REC-P.1853-2-201908-I!!PDF-E.pdf (accessed on 25 July 2022).
- Norouzian, F.; Marchetti, E.; Gashinova, M.; Hoare, E.; Constantinou, C.; Gardner, P.; Cherniakov, M. Rain attenuation at millimeter wave and low-THz frequencies. IEEE Trans. Antennas Propag. 2019, 68, 421–431. [Google Scholar] [CrossRef]
- Ma, J. Terahertz Wireless Communication Through Atmospheric Atmospheric Turbulence and Rain. Master’s Thesis, New Jersey Institute of Technology, New Jersey, NJ, USA, 2016. [Google Scholar]
- Joss, J. The variation of raindrop size distributions at Locarno. Proc. Int. Conf. Cloud Physics. 1968, 49, 369–373. [Google Scholar]
- Utsunomiya, T.; Sekine, M. Rain attenuation at 103 GHz in millimeter wave Ranges. Int. J. Infrared Millim. Waves 2005, 26, 1651–1660. [Google Scholar] [CrossRef]
- Characteristics of Precipitation for Propagation Modelling, ITU Rec. ITU-R P.837-7, 2017. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-REC-P.837-7-201706-I!!PDF-E.pdf (accessed on 25 July 2022).
- Sauvageot, H. The probability density function of rain rate and the estimation of rainfall by area integrals. J. Appl. Meteorol. Climatol. 1994, 33, 1255–1262. [Google Scholar] [CrossRef]
- Luini, L.; Capsoni, C. MultiEXCELL: A New Rainfall Model for the Analysis of the Millimetre Wave Propagation Through the Atmosphere. In Proceedings of the 2009 3rd European Conference on Antennas and Propagation, Berlin, Germany, 23–27 March 2009; pp. 1946–1950. [Google Scholar]
- Mean Surface Temperature, ITU Rec. ITU-R 1510-1, 2017. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-REC-P.1510-1-201706-I!!PDF-E.pdf (accessed on 25 July 2022).
- Yaccop, A.H.; Yao, Y.D.; Ismail, A.F.; Badron, K.; Hasan, M.K. Refining Ku-band rain attenuation prediction using local parameters in tropics. Indian J. Sci. Technol. 2016, 9, 1–8. [Google Scholar] [CrossRef]
- Shrestha, S.; Choi, D.Y. Rain attenuation study over an 18 GHz terrestrial microwave link in South Korea. Int. J. Antennas Propag. 2019, 2019, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.H. Statistical behavior of rain attenuation. Bell Syst. Tech. J. 1973, 52, 557–581. [Google Scholar] [CrossRef]
- Cho, H.K.; Bowman, K.P.; North, G.R. A comparison of gamma and lognormal distributions for characterizing satellite rain rates from the tropical rainfall measuring mission. J. Appl. Meteorol. Climatol. 2004, 43, 1586–1597. [Google Scholar] [CrossRef]
- Lin, S.-H. A method for calculating rain attenuation distributions on microwave paths. Bell Syst. Tech. J. 1975, 54, 1051–1086. [Google Scholar] [CrossRef]
- Hansson, L. General characteristics of rain intensity statistics in the Stockholm area. Tele Swed. 1975, 27, 43–48. [Google Scholar]
- Hansson, L. General Characteristics of Rain Intensity Statistics in the Gothenburg Area. Rep. Usr. 1975, 75, 012. [Google Scholar]
- Harden, B.N.; Llewellyn-Jones, D.T.; Zavody, A.M. Investigations of attenuation by rainfall at 110 GHz in south-east England. Proc. Inst. Electr. Eng. 1975, 122, 6600–6604. [Google Scholar] [CrossRef]
- Sekine, M.; Ishii, S.; Hwang, S.I.; Sayama, S. Weibull raindrop-size distribution and its application to rain attenuation from 30 GHz to 1000 GHz. Int. J. Infrared Millim. Waves 2007, 28, 383–392. [Google Scholar] [CrossRef]
- Arnau, J.; Christopoulos, D.; Chatzinotas, S.; Mosquera, C.; Ottersten, B. Performance of the multibeam satellite return link with correlated rain attenuation. IEEE Trans. Wirel. Commun. 2014, 13, 6286–6299. [Google Scholar] [CrossRef]
- Matricciani, E. Probability distributions of rain attenuation obtainable with linear combining techniques in space-to-Earth links using time diversity. Int. J. Satell. Commun. Netw. 2018, 36, 220–237. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Dong, Y. Performance Analysis of Polar Codes against Rain Attenuation in Ka-band Satellite Communication. In Proceedings of the 2021 International Conference on Communications, Information System and Computer Engineering (CISCE) IEEE, Beijing, China, 14–16 May 2021; pp. 146–150. [Google Scholar]
- Proakis, J. Digital Communication, 2nd ed.; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Abramowitz, M.; Stegun, I.A.; Romer, R.H. Handbook of Mathematical Functions with Formulas, Graphs, And Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1964.
- Kedem, B.; Pfeiffer, R.; Short, D.A. Variability of space–time mean rain rate. J. Appl. Meteorol. 1997, 36, 443–451. [Google Scholar] [CrossRef]
- Feingold, G.; Zev, L. The lognormal fit to raindrop spectra from frontal convective clouds in Israel. J. Clim. Appl. Meteorol. 1986, 25, 1346–1363. [Google Scholar] [CrossRef] [Green Version]
- Kedem, B.; Long, S.C.; Gerald, R.N. Estimation of mean rain rate: Application to satellite observations. J. Geophys. Res. Atmos. 1990, 95, 1965–1972. [Google Scholar] [CrossRef]
- Harikumar, R.; Sampath, S.; Kumar, V.S. An empirical model for the variation of rain drop size distribution with rain rate at a few locations in southern India. Adv. Space Res. 2009, 43, 837–844. [Google Scholar] [CrossRef]
- Yuan, F.; Lee, Y.H.; Meng, Y.S.; Manandhar, S.; Ong, J.T. High-resolution ITU-R cloud attenuation model for satellite communications in tropical region. IEEE Trans. Antennas Propag. 2019, 67, 6115–6122. [Google Scholar] [CrossRef]
- Saunders, S.R.; Alejandro, A.-Z. Antennas and Propagation for Wireless Communication Systems; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
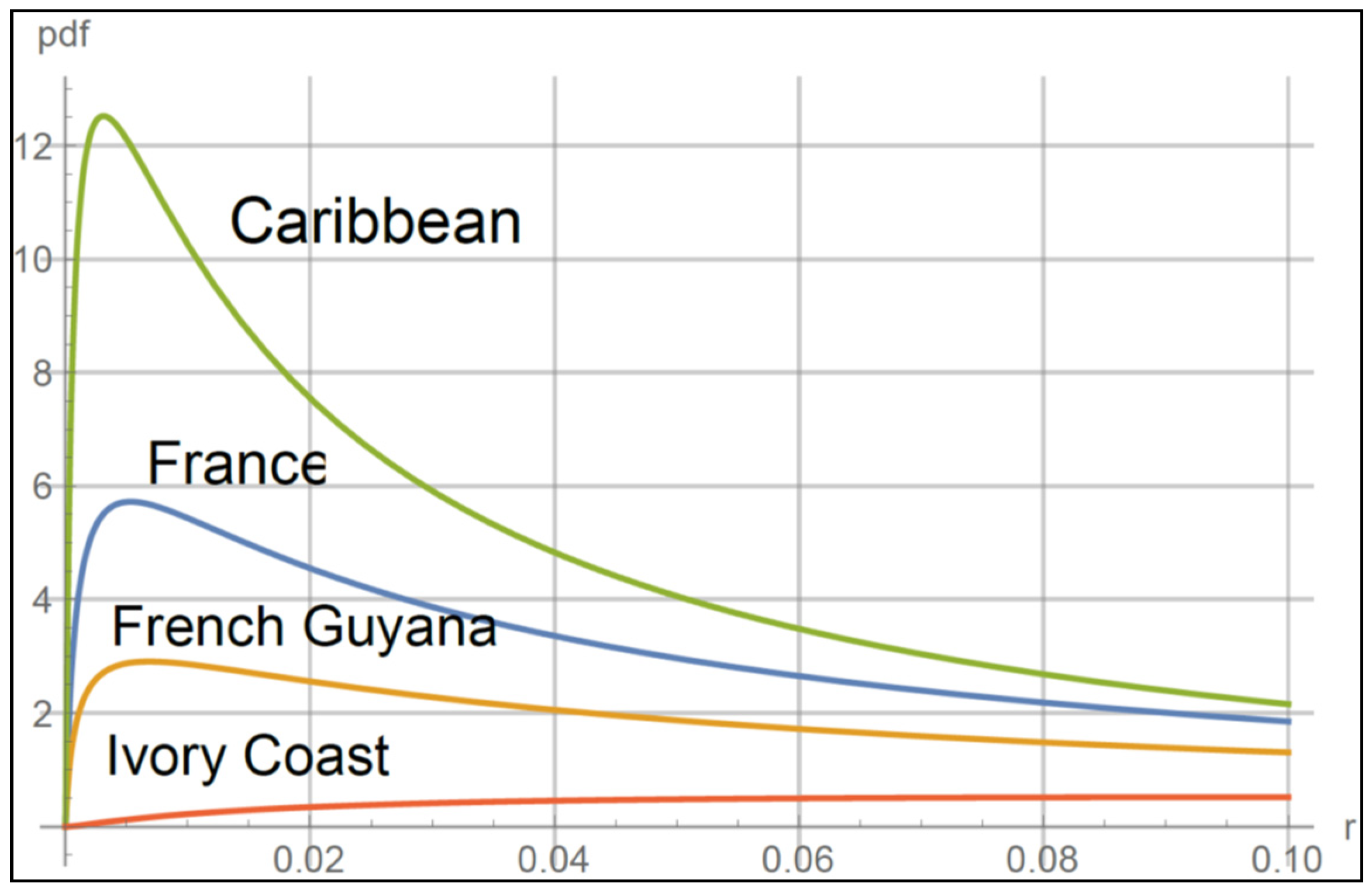
| Region | σ2R | σ2r | mR (mm/h) | mr (mm/h) |
|---|---|---|---|---|
| Southwest France | 2.38 | 1.95 | 0.63 | −1.43 |
| Ivory Coast | 108 | 1.74 | 4.81 | 0.7 |
| Caribbean | 23 | 2.12 | 1.77 | −0.49 |
| French Guyana (equatorial coastal) | 0.42 | 1.85 | 0.24 | −2.35 |
| mm Band | ||
| Freq (GHz) | k | α |
| 30 | 0.2347 | 0.931125 |
| 80 | 1.1686 | 0.706807 |
| 100 | 1.36755 | 0.678999 |
| Terahertz Band | ||
| Freq (THz) | k | α |
| 0.2 | 1.64105 | 0.636246 |
| 0.3 | 1.6286 | 0.6279 |
| 0.4 | 1.584 | 0.6259 |
| 0.7 | 1.4638 | 0.629948 |
| 0.8 | 1.4328 | 0.63245 |
| 1 | 1.38085 | 0.637598 |
| Error Probability | SNR Required for Classical Case (dB) | SNR Required (dB) | Difference (dB) |
|---|---|---|---|
| 10−4 | 26 | 23 | 3 |
| 10−5 | 26.5 | 24.8 | 1.7 |
| 10−6 | 27.8 | 26 | 1.8 |
| 10−7 | 28.4 | 27.4 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kupferman, J.; Arnon, S. Communication Systems Performance at mm and THz as a Function of a Rain Rate Probability Density Function Model. Sensors 2022, 22, 6269. https://doi.org/10.3390/s22166269
Kupferman J, Arnon S. Communication Systems Performance at mm and THz as a Function of a Rain Rate Probability Density Function Model. Sensors. 2022; 22(16):6269. https://doi.org/10.3390/s22166269
Chicago/Turabian StyleKupferman, Judy, and Shlomi Arnon. 2022. "Communication Systems Performance at mm and THz as a Function of a Rain Rate Probability Density Function Model" Sensors 22, no. 16: 6269. https://doi.org/10.3390/s22166269






