Critical Evaluation and Thermodynamic Optimization of the Cu-Zn, Cu-Se and Zn-Se Binary Systems
Abstract
:1. Introduction
2. Critical Review of the Experimental Literature Data
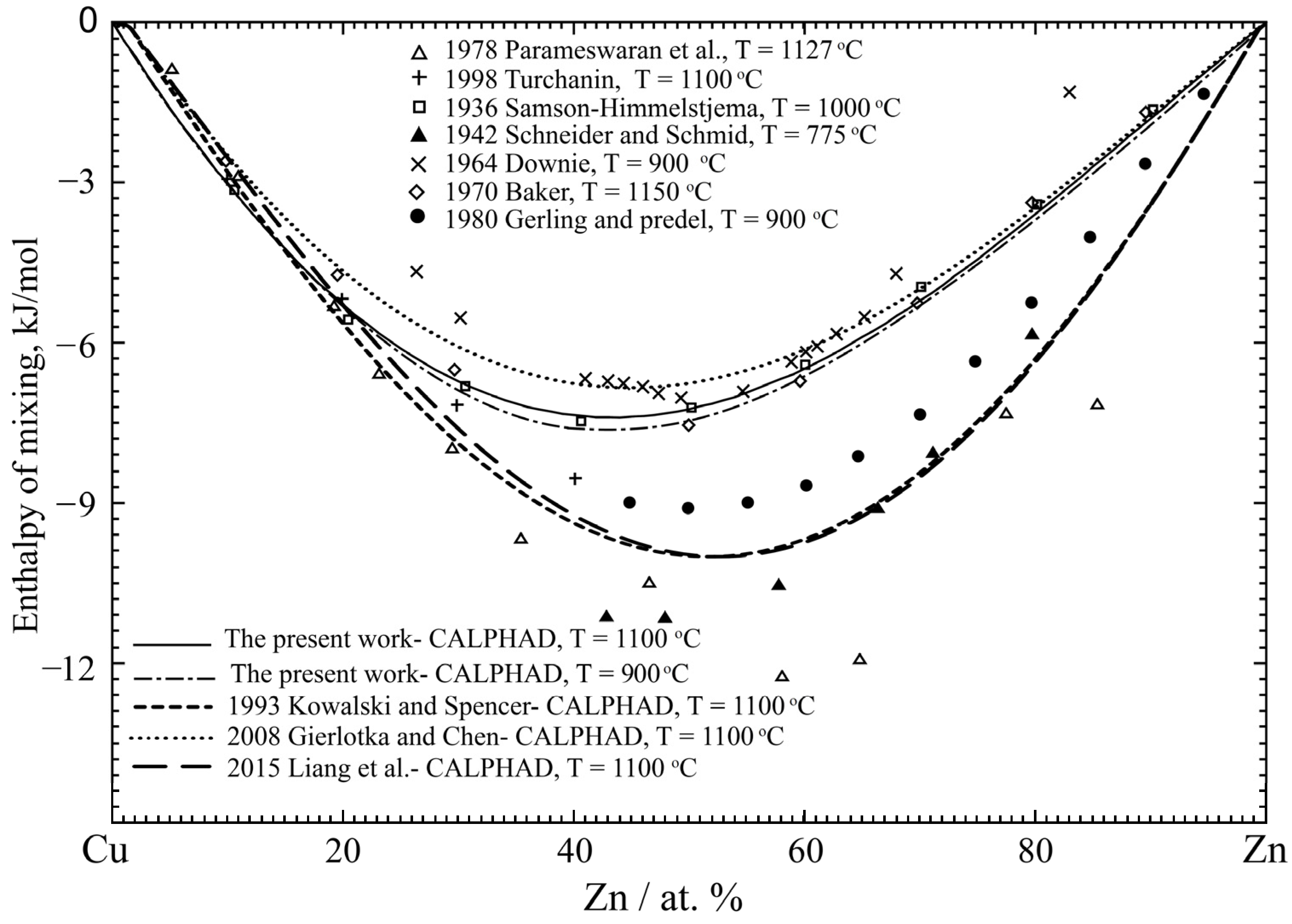
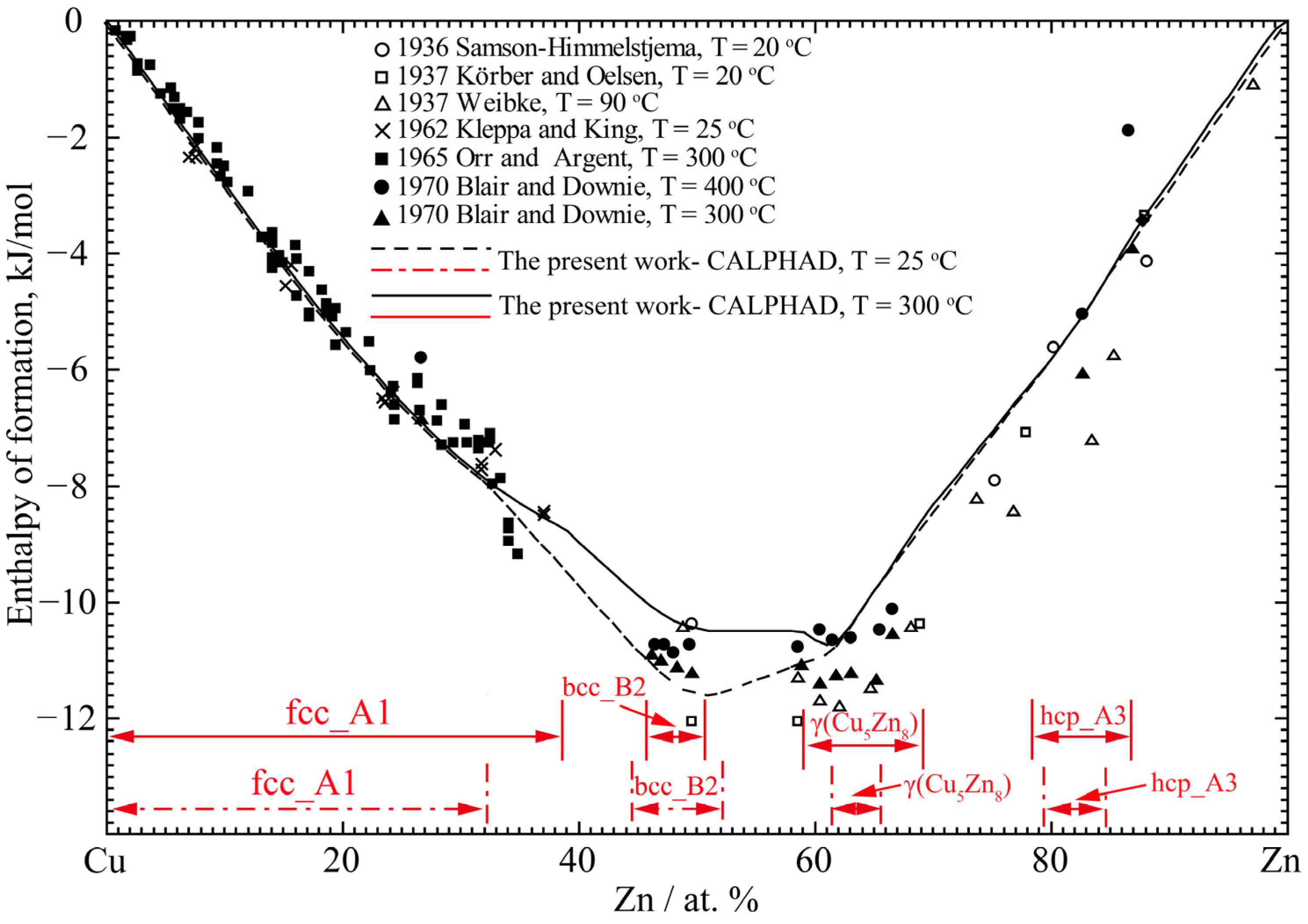
2.1. Cu-Zn Binary System
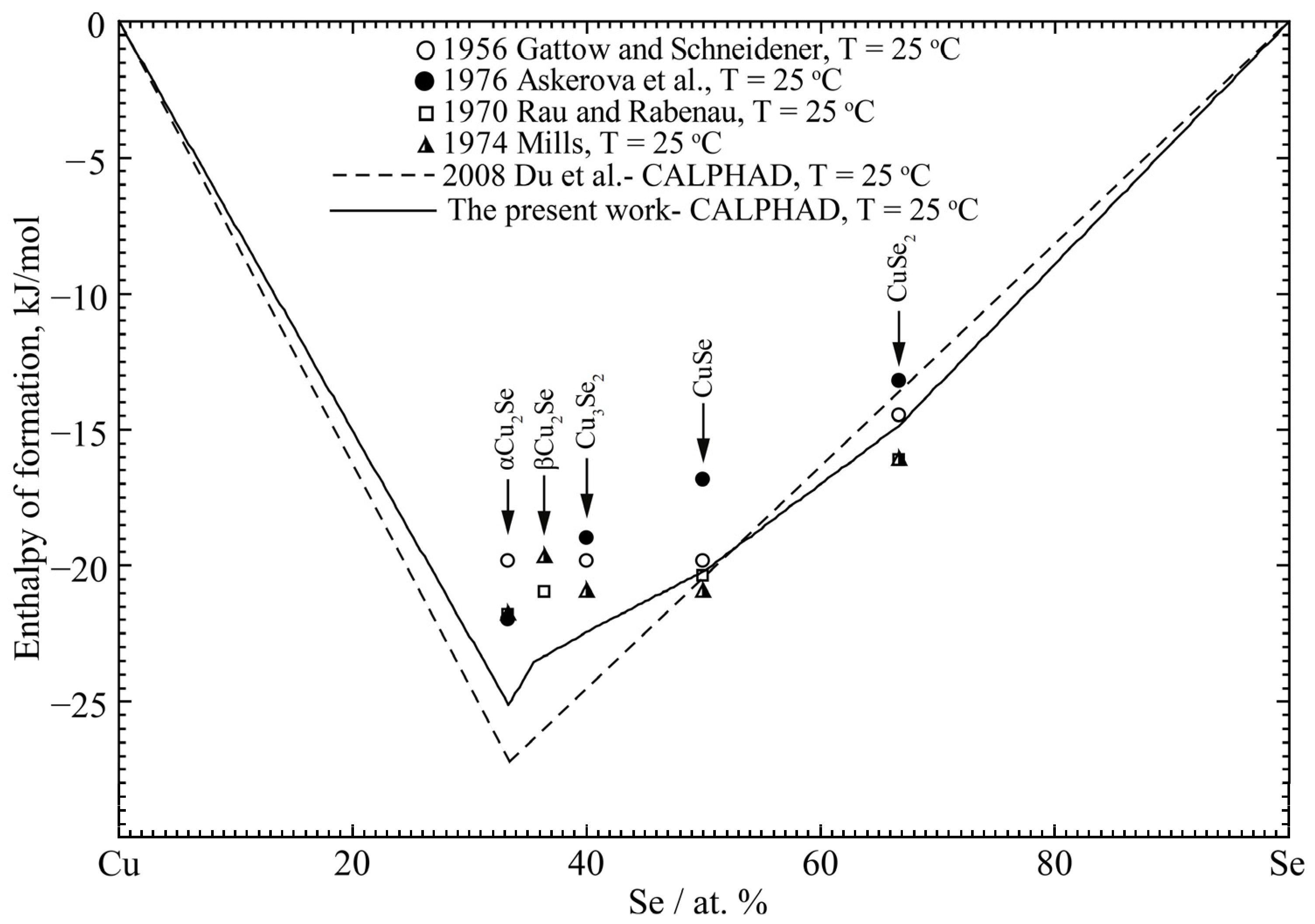
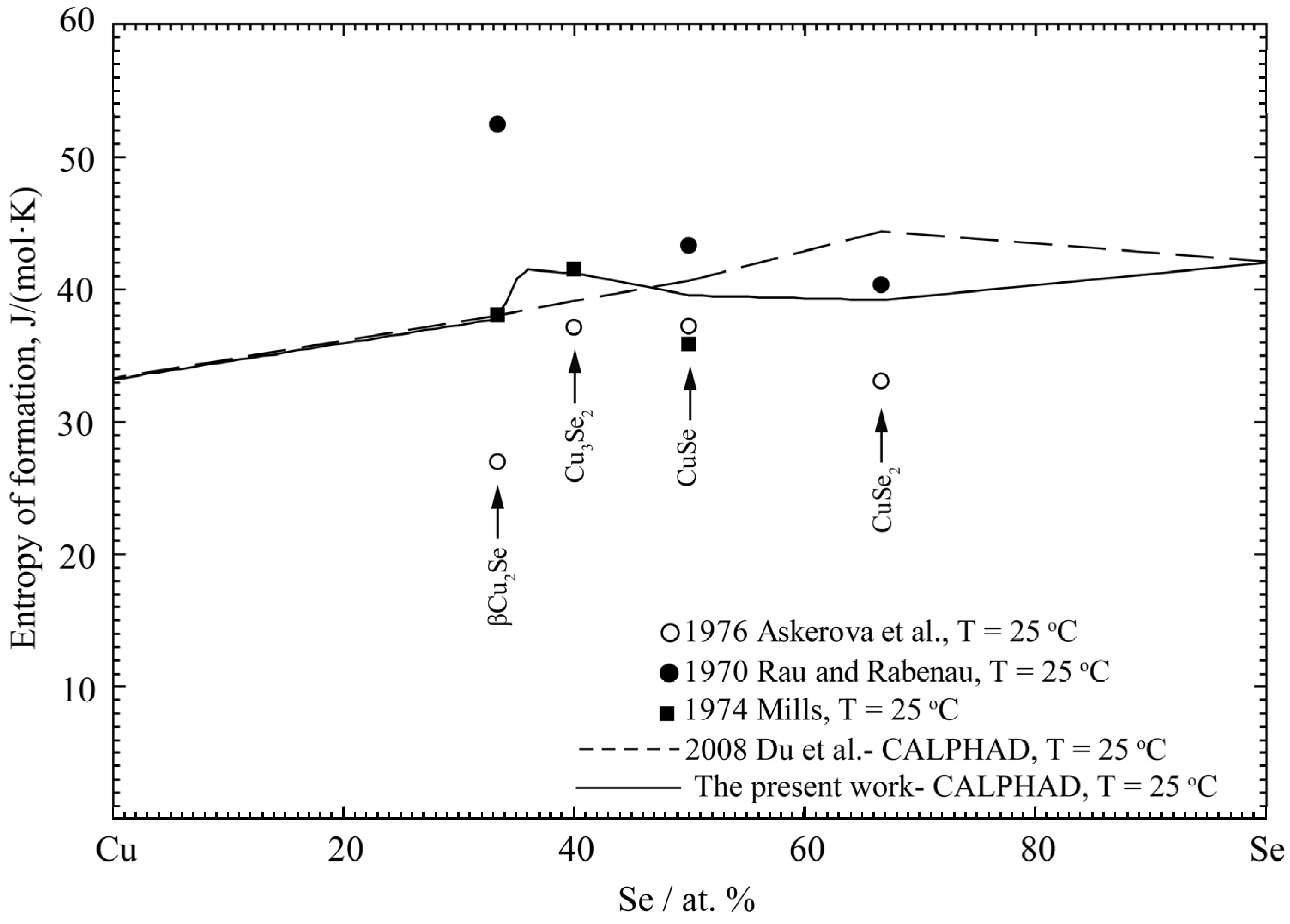
2.2. Cu-Se Binary System
2.3. Zn-Se Binary System
3. Thermodynamic Modeling
3.1. Liquid Phase
3.2. Solution Phases
3.3. Stoichiometric Intermetallic Compounds
4. Results and Discussion
4.1. Cu-Zn Binary System
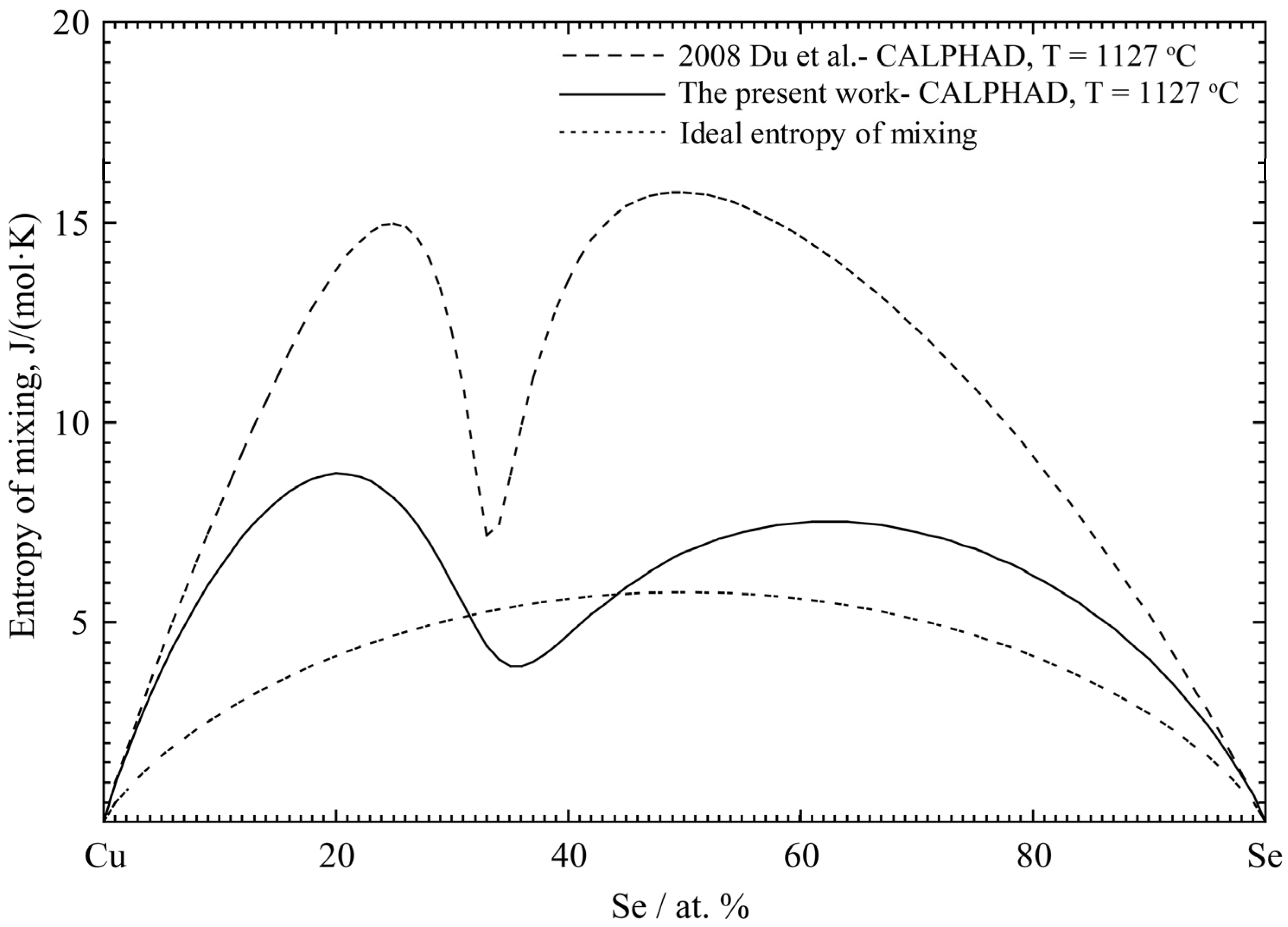
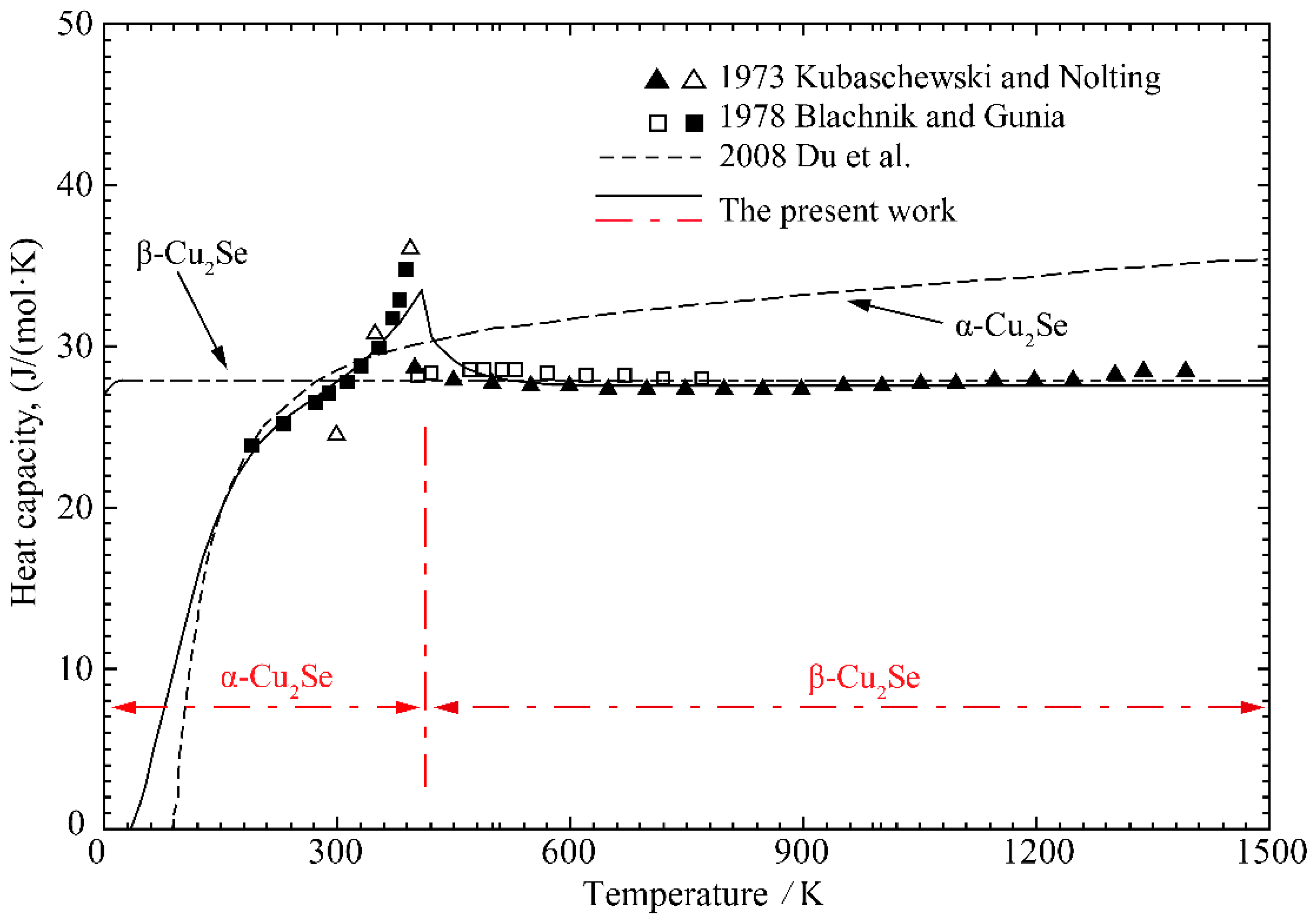
4.2. Cu-Se Binary System
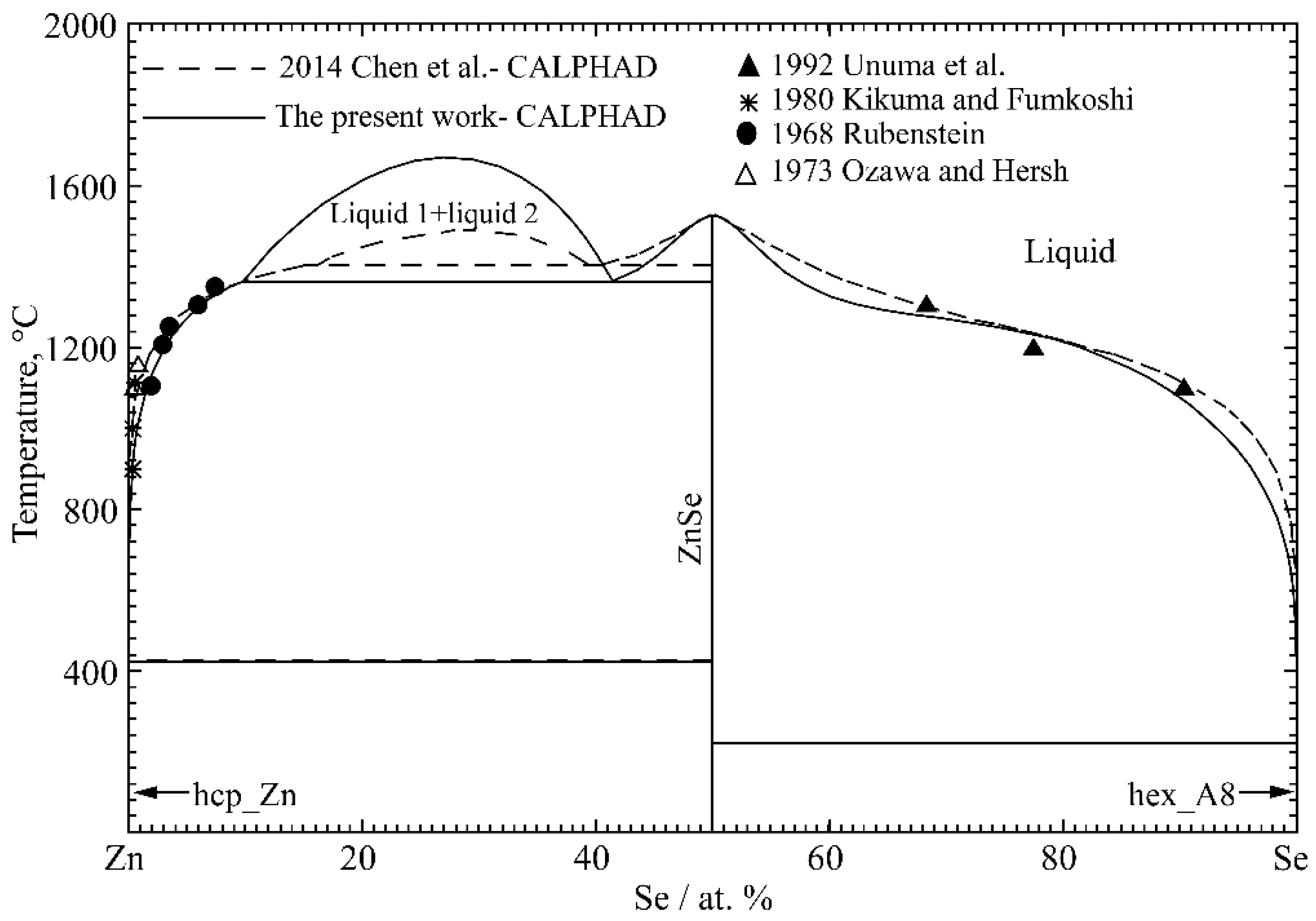
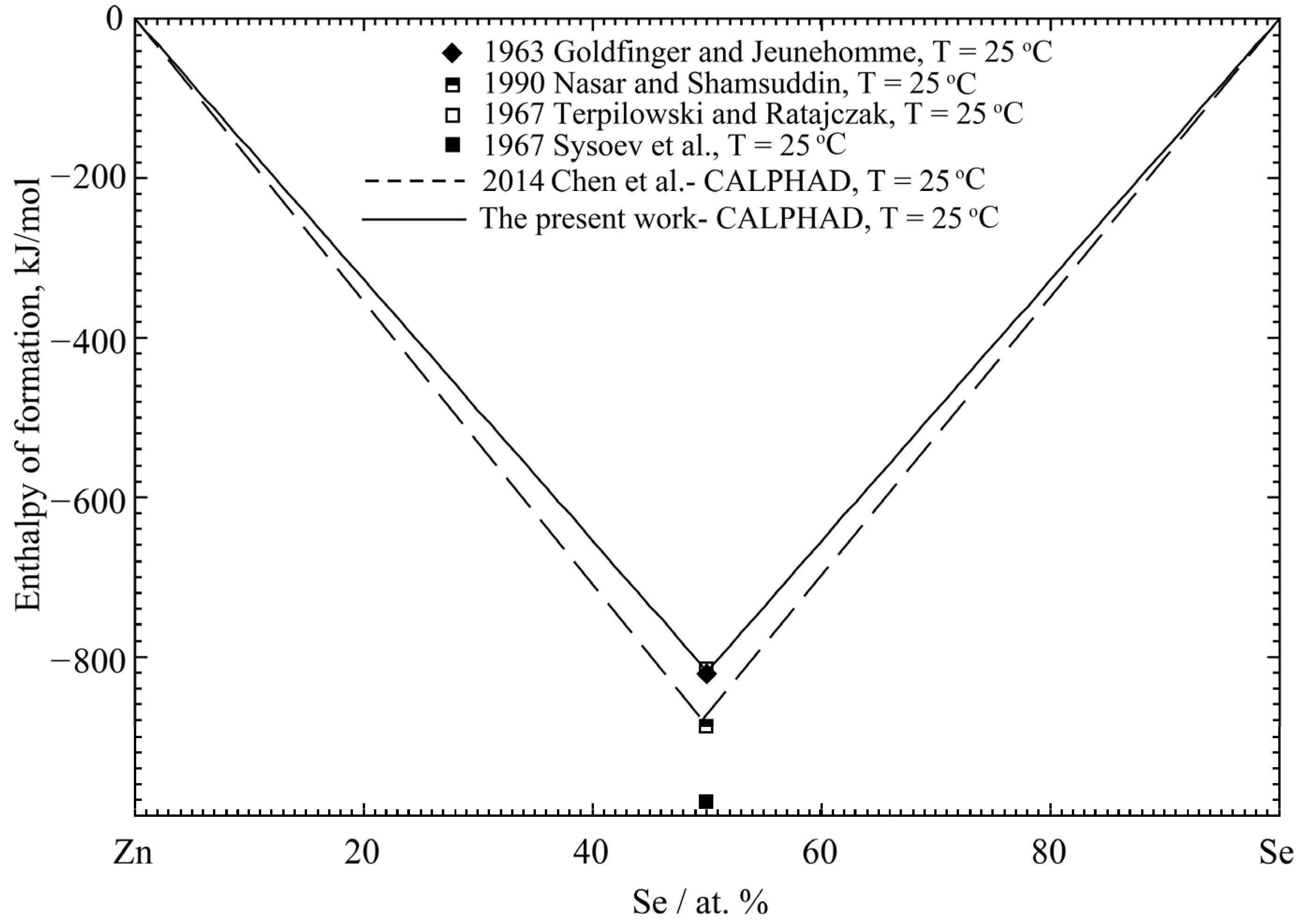
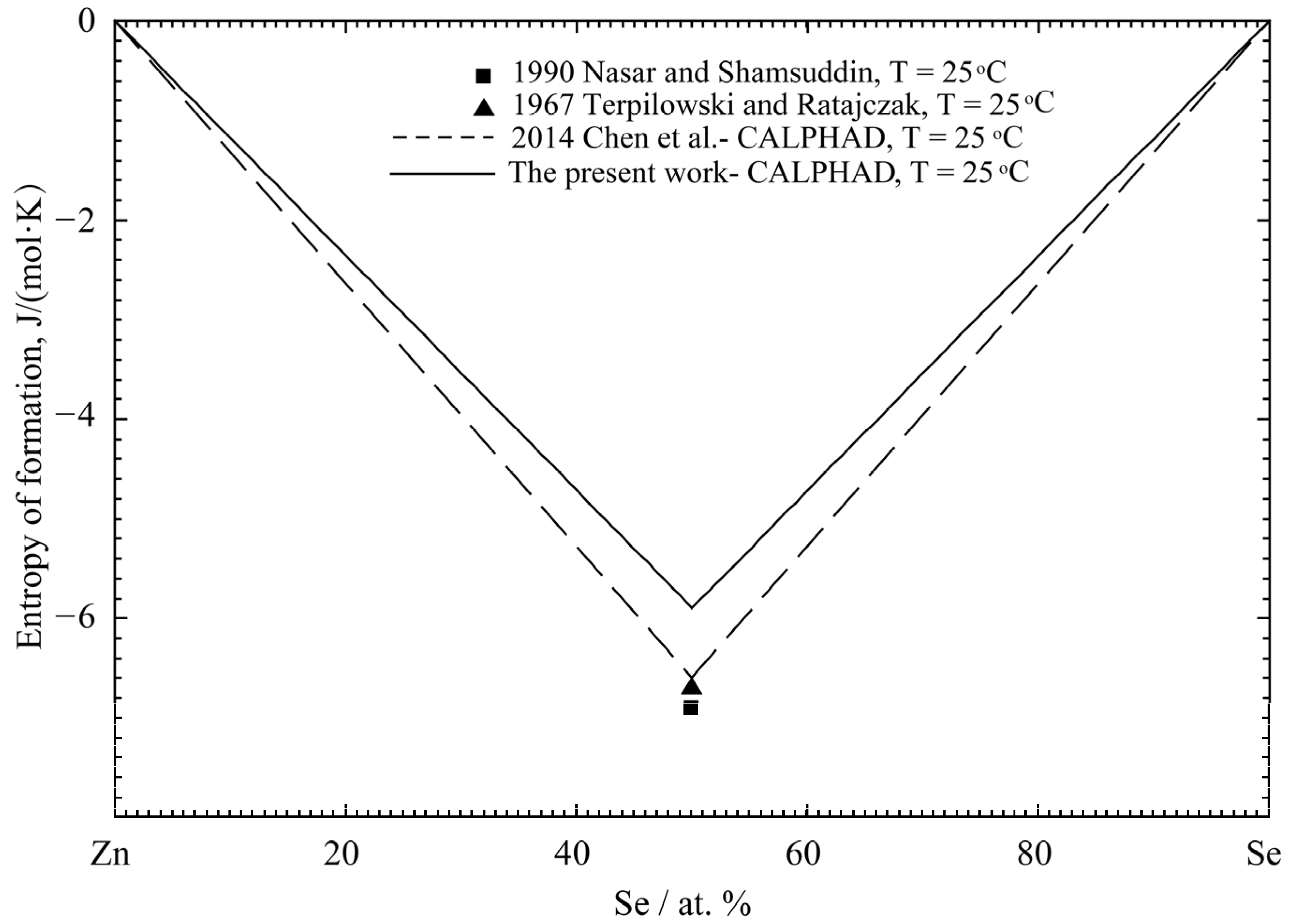
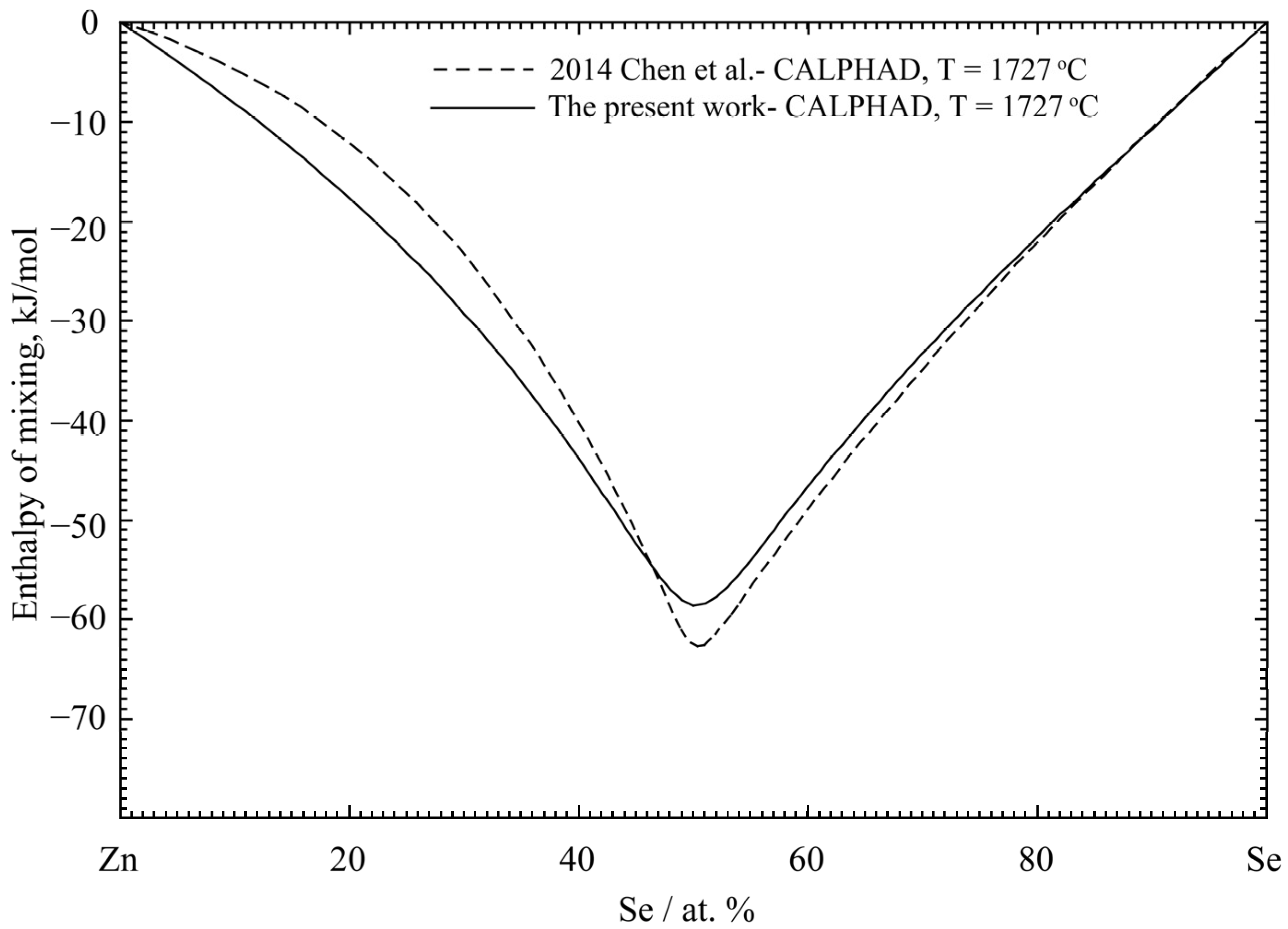
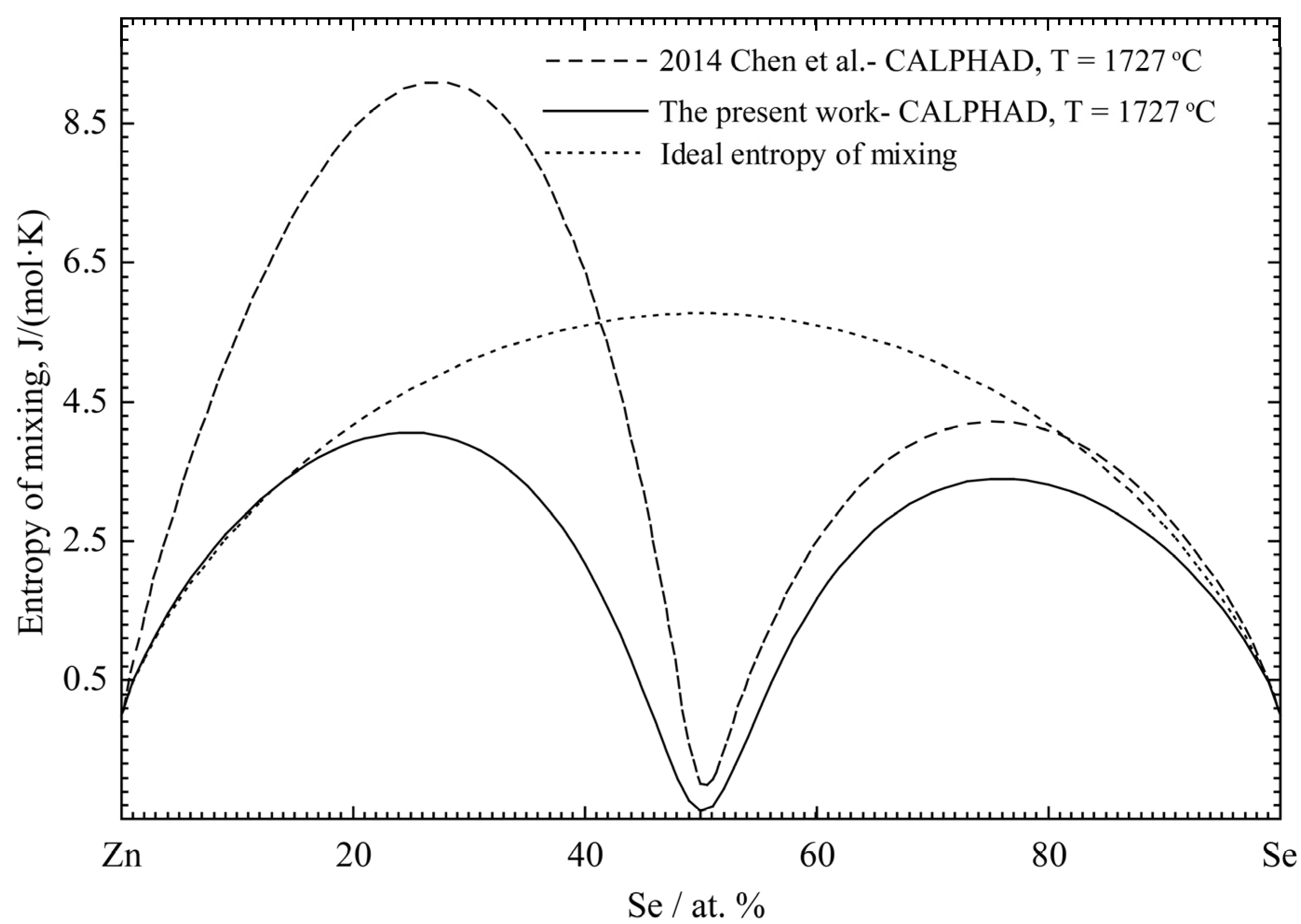
4.3. Zn-Se Binary System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Frederickson, C.J.; Koh, J.-Y.; Bush, A.I. The neurobiology of zinc in health and disease. Nat. Rev. Neurosci. 2005, 6, 449–462. [Google Scholar] [CrossRef] [PubMed]
- Seitz, J.M.; Durisin, M.; Goldman, J.; Drelich, J.W. Drelich Recent Advances in Biodegradable Metals for Medical Sutures: A Critical Review. Adv. Healthc. Mater. 2015, 4, 1915–1936. [Google Scholar] [CrossRef] [PubMed]
- Hernández, E.; Champagne, D.; Yilmazer, S.; Dikici, H.; Boehlert, B.; Hermawan, C.J.; Biomaterialia, H.J.A. Current status and perspectives of zinc-based absorbable alloys for biomedical applications. Acta Biomater. 2019, 97, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Mostaed, E.; Sikora-Jasinska, E.; Drelich, M.; Vedani, J.W.; Maurizio, V. Zinc-based alloys for degradable vascular stent applications. Acta Biomater. 2018, 71, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Venezuela, J.J.D.; Johnston, S.; Dargusch, M.S. The prospects for biodegradable zinc in wound closure applications. Acta Biomater. 2019, 8, 1900408. [Google Scholar] [CrossRef]
- Dambatta, M.; Kurniawan, D.; Izman, S.; Yahaya, B.; Hermawan, H. Review on Zn-Based Alloys As Potential Biodegradable Medical Devices Materials. In Applied Mechanics and Material; Trans Tech Publications Ltd.: New York, NY, USA, 2015; Volume 776, pp. 277–281. [Google Scholar]
- Katarivas Levy, G.; Goldman, J.; Aghion, E.J.M. The prospects of zinc as a structural material for biodegradable implants—A review paper. Biodegr. Metals 2017, 7, 402. [Google Scholar] [CrossRef]
- Čapek, J.; Jablonská, E.; Lipov, J.; Kubatík, T.F.; Vojtěch, D. Physics. Preparation and characterization of porous zinc prepared by spark plasma sintering as a material for biodegradable scaffolds. Mater. Chem. Phys. 2018, 203, 249–258. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, X.; Wang, T.; Xia, Y.; Cui, C. Mechanical properties and biodegradation of porous Zn-1Al alloy scaffolds. Mater. Lett. 2019, 247, 75–78. [Google Scholar] [CrossRef]
- Tang, Z.; Niu, J.; Huang, H.; Zhang, H.; Pei, J.; Ou, J.; Yuan, G. Potential biodegradable Zn-Cu binary alloys developed for cardiovascular implant applications. J. Mech. Behav. Biomed. Mater. 2017, 72, 182–191. [Google Scholar] [CrossRef]
- Xiao, X.; Liu, E.; Shao, J.; Ge, S. Advances on biodegradable zinc-silver-based alloys for biomedical applications. J. Appl. Biomater. 2021, 19, 22808000211062407. [Google Scholar] [CrossRef]
- Su, Y.; Cockerill, I.; Wang, Y.; Qin, Y.-X.; Chang, L.; Zheng, Y.; Zhu, D. Zinc-based biomaterials for regeneration and therapy. Trends Biotechnol. 2019, 37, 428–441. [Google Scholar] [CrossRef] [PubMed]
- Venezuela, J.; Dargusch, M. The influence of alloying and fabrication techniques on the mechanical properties, biodegradability and biocompatibility of zinc: A comprehensive review. Acta Biomater. 2019, 87, 1–40. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.; Xia, D.; Wu, S.; Zheng, Y.; Guan, Z.; Rau, J.V. A review on current research status of the surface modification of Zn-based biodegradable metals. Bioact. Mater. 2022, 7, 192–216. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Schille, C.; Schweizer, E.; Kimmerle-Müller, E.; Rupp, F.; Heiss, A.; Legner, C.; Klotz, U.E.; Geis-Gerstorfer, J.; Scheideler, L. Selection of extraction medium influences cytotoxicity of zinc and its alloys. Acta Biomater. 2019, 98, 235–245. [Google Scholar] [CrossRef]
- Li, H.; Yang, H.; Zheng, Y.; Zhou, F.; Qiu, K.; Wang, X. Design and characterizations of novel biodegradable ternary Zn-based alloys with IIA nutrient alloying elements Mg, Ca and Sr. Mater. Des. 2015, 83, 95–102. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Q.; Guo, T.; Li, S. Effect of Y Content on Properties of Extruded Zn-1.5Mg-xY Alloys for Medical Applications. Mater. Res. 2019, 22, 95–103. [Google Scholar] [CrossRef]
- Shi, Z.-Z.; Yu, J.; Liu, X.-F.; Zhang, H.-J.; Zhang, D.-W.; Yin, Y.-X.; Wang, L.-N. Effects of Ag, Cu or Ca addition on microstructure and comprehensive properties of biodegradable Zn-0.8Mn alloy. Mater. Sci. Eng. C 2019, 99, 969–978. [Google Scholar] [CrossRef]
- Chen, H.T.; Shi, Z.Z.; Liu, X.F. Microstructure and mechanical properties of extruded and caliber rolled biodegradable Zn-0.8Mn-0.4Ag alloy with high ductility. Mater. Sci. Eng. A 2020, 770, 138543. [Google Scholar] [CrossRef]
- Bednarczyk, W.; Kawałko, J.; Wątroba, M.; Bała, P. Achieving room temperature superplasticity in the Zn-0.5Cu alloy processed via equal channel angular pressing. Mater. Sci. Eng. A 2018, 723, 126–133. [Google Scholar] [CrossRef]
- Niu, J.; Tang, Z.; Huang, H.; Jia Pei, H.Z.; Yuan, G.; Ding, W. Research on a Zn-Cu alloy as a biodegradable material for potential vascular stents application. Mater. Sci. Eng. C 2016, 69, 407–413. [Google Scholar] [CrossRef]
- Fairweather-Tait, S.J.; Bao, Y.; Broadley, M.R.; Collings, R.; Ford, D.; Hesketh, J.E.; Hurst, R. Selenium in Human Health and Disease. Antioxid. Redox Signal. 2011, 14, 1337–1383. [Google Scholar] [CrossRef] [PubMed]
- Kipp, A.P.; Strohm, D.; Brigelius-Flohé, R.; Schomburg, L.; Bechthold, A.; Leschik-Bonnet, E.; Heseker, H. Revised reference values for selenium intake. J. Trace Elem. Med. Biol. 2015, 32, 195–199. [Google Scholar] [CrossRef] [PubMed]
- Gemma, F.-M.; Ana, N.-A.; Roberto, P.-B.; Eliseo, G. Selenium and coronary heart disease: A meta-analysis. Am. J. Clin. Nutr. 2006, 84, 762–763. [Google Scholar]
- Rederstorff, M.; Krol, A.; Lescure, A. Understanding the importance of selenium and selenoproteins in muscle function. Cell. Mol. Life Sci. 2006, 63, 52–59. [Google Scholar] [CrossRef] [PubMed]
- Shanu, A.; Groebler, L.; Kim, H.B.; Wood, S.; Weekley, C.M.; Aitken, J.B.; Harris, H.H.; Witting, P.K. Selenium Inhibits Renal Oxidation and Inflammation But Not Acute Kidney Injury in an Animal Model of Rhabdomyolysis. Antioxid. Redox Signal. 2013, 18, 756–769. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Y.; Luo, K.; Liu, Y.; Zhou, M.; Yan, S.; Shi, H.; Cai, Y. The protective effects of selenium on cadmium-induced oxidative stress and apoptosis via mitochondria pathway in mice kidney. Food Chem. Toxicol. 2013, 58, 61–67. [Google Scholar] [CrossRef]
- Joshi, D.; Mittal, D.K.; Shukla, S.; Srivastav, A.K.; Srivastav, S.K. N-acetyl cysteine and selenium protects mercuric chloride-induced oxidative stress and antioxidant defense system in liver and kidney of rats: A histopathological approach. J. Trace Elem. Med. Biol. 2014, 28, 218–226. [Google Scholar] [CrossRef]
- Persaud-Sharma, D.; Budiansky, N.; McGoron, A.J. Biocompatibility Assessment of Novel Bioresorbable Alloys Mg-Zn-Se and Mg-Zn-Cu for Endovascular Applications: In-Vitro Studies. J. Biomater. Tiss. Eng. 2013, 17, 25–43. [Google Scholar] [CrossRef]
- Saunders, N.; Miodownik, A.P. Calphad (Calculation of Phase Diagrams) A Comprehensive Guide; Pergamon: Oxford, UK, 1992. [Google Scholar]
- Jin, L.; Kang, Y.B.; Chartrand, P.; Fuerst, C.D.J.C. Thermodynamic evaluation and optimization of Al-La, Al-Ce, Al-Pr, Al-Nd and Al-Sm systems using the modified quasichemical model for liquids. Calphad 2011, 35, 30–41. [Google Scholar] [CrossRef]
- Hillert, M. The compound energy formalism. J. Alloys Compd. 2001, 320, 161–176. [Google Scholar] [CrossRef]
- Shepherd, E.S. The Constitution of Copper Zinc Alloys. J. Phys. Chem. C 1904, 8, 421–435. [Google Scholar] [CrossRef] [Green Version]
- Hoyt, S.L. On the Copper-rich Kalchoids (copper-tin-zinc-alloys). J. Inst. Met. 1913, 10, 235. [Google Scholar]
- Campbell, W. A note on the constitution of certain tin-bearing brasses. Master Thesis, Columbia University, New York, NY, USA, 1920. [Google Scholar]
- Bauer, O.; Hansen, M. Der Aufbau der Kupfer-Zinklegierungen; Springer: Berlin/Heidelberg, Germany, 1927. [Google Scholar]
- Ruer, R.; Kremers, K. Das System Kupfer-Link. Z. Anorg. Allg. Chem. 1929, 184, 193–231. [Google Scholar] [CrossRef]
- Schramm, J. Contribution to the Cu-Zn diagram. Prog. Mater. Sci. 1935, 14, 995–1001. [Google Scholar]
- Hansen, M. Handbook of Binary Alloys; Springer: Berlin, Germany, 1936. [Google Scholar]
- Raynor, G. The Cu-Sn Phase Diagram. Annot. Equilib. Diagr. Ser. 1944, 2, 4–5. [Google Scholar]
- Hansen, M.; Anderko, K. Constitution of Binary Alloys; McGraw-Hill: New York, USA, 1958. [Google Scholar]
- Massalski, T.; Okamoto, H.; Subramanian, D.; Kacprzak, L.; Scott, W. Binary Alloy Phase Diagrams; American Society for Metals: Park, OH, USA, 1986. [Google Scholar]
- Miodownik, A. Phase diagrams of binary copper alloys. ASM Int. 1994, 10, 487–496. [Google Scholar]
- Spencer, P. A thermodynamic evaluation of the Cu-Zn system. Calphad 1986, 10, 175–185. [Google Scholar] [CrossRef]
- Kowalski, M.; Spencer, P. Thermodynamic reevaluation of the Cu-Zn system. J. Phase Equilib. 1993, 14, 432–438. [Google Scholar] [CrossRef]
- Liang, H.; Chang, Y.A. A Thermodynamic Description for the Al-Cu-Zn System. J. Phase Equilib. 1998, 19, 25–37. [Google Scholar] [CrossRef]
- David, N.; Fiorani, J.; Vilasi, M.; Hertz, J. Thermodynamic reevaluation of the Cu-Zn system by electromotive force measurements in the zinc-rich part. J. Phase Equilib. 2003, 24, 240–248. [Google Scholar] [CrossRef]
- Gierlotka, W.; Chen, S. Thermodynamic descriptions of the Cu–Zn system. J. Mater. Res. 2008, 23, 258–263. [Google Scholar] [CrossRef]
- Wang, J.; Xu, H.; Shang, S.; Zhang, L.; Yong, D.; Zhang, W.; Liu, S.; Wang, P.; Liu, Z. Experimental investigation and thermodynamic modeling of the Cu-Si-Zn system with the refined description for the Cu-Zn system. Calphad 2011, 35, 191–203. [Google Scholar] [CrossRef]
- Liang, S.; Hsiao, H.; Fetzer, R. Thermodynamic assessment of the Al–Cu–Zn system, part I: Cu–Zn binary system. Calphad 2015, 51, 224–232. [Google Scholar] [CrossRef]
- Saunders, N. COST 507: Thermochemical database for light metal alloys. COST 1998, 168, 23–27. [Google Scholar]
- Bradley, A.; Gregory, C.I.X. A comparison of the crystal structures of Cu5Zn8 and Cu5Cd8. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1931, 12, 143–162. [Google Scholar] [CrossRef]
- Heidenstam, O.; Johansson, A.; Westman, S.; Larsen, C. A Redetermination of the Distribution of Atoms in Cu5Zn8, Cu5Cd8, and Cu9Al4. Acta Chem. Scand. 1968, 22, 653–661. [Google Scholar] [CrossRef]
- Gourdon, O.; Gout, D.; Williams, D.; Proffen, T.; Hobbs, S.; Miller, G. Atomic distributions in the gamma-brass structure of the Cu-Zn system: A structural and theoretical study. Inorg. Chem. 2007, 46, 251–260. [Google Scholar] [CrossRef] [PubMed]
- Sehubert, K.; Wall, E. Zur Kristallstruktur der δ-Hochtemperaturphase des Systems Kupfer-Zink. Int. J. Mater. Res. 1949, 40, 383–385. [Google Scholar] [CrossRef]
- Lenz, J.; Schubert, K. Über einige Leerstellen-und Stapelvarianten der Beta-Messing Strukturfamilie. Int. J. Mater. Res. 1971, 62, 810–816. [Google Scholar] [CrossRef]
- Degtyareva, V.F.; Afonikova, N.S. Simple metal binary phases based on the body centered cubic structure: Electronic origin of distortions and superlattices. J. Phys. Chem. Solids 2013, 74, 18–24. [Google Scholar] [CrossRef]
- Parameswaran, K.; Healy, G. A Calorimetric Investigation of the Copper-Zinc System. Metall. Trans. B 1978, 9, 657–664. [Google Scholar] [CrossRef]
- Turchanin, M. Enthalpies of formation of liquid copper alloys with 3d transition metals. Russ. Metall. 1998, 4, 29–38. [Google Scholar]
- Samson-Himmelstjerna, H.O. Heat capacity and heat of formation of molten alloys. Z. Metallkd. 1936, 28, 197. [Google Scholar]
- Schneider, A.; Schmid, H. Die Dampfdrucke des Zinks und Cadmiums über ihren binären flüssigen Legierungen mit Kupfer, Silber und Gold. Metalldampfdrucke III. Z. Für Elektrochem. Ber. Der Bunsenges. Für Phys. Chem. 1942, 48, 627–639. [Google Scholar]
- Everett, L.H.; Jacobs, P.W.M.; Kitchener, J.A. The activity of zinc in liquid copper-zinc alloys. Acta Metall. 1957, 5, 281–284. [Google Scholar] [CrossRef]
- Downie, D. Thermodynamic and structural properties of liquid zinc/copper alloys. Acta Metall. 1964, 12, 875–882. [Google Scholar] [CrossRef]
- Azakami, T.; Yazawa, A. Thermodynamic Studies of Liquid Copper Alloys. III. Activities of Zinc and Cadmium in Liquid Copper-Base Alloys. J. I. Min. Metal. 1968, 84, 1663–1668. [Google Scholar]
- Solovev, S.; Knyazev, M.; Ivanov, Y.; Vanyukov, A. Mass spectrometric study of partial characteristics of zinc in copper-zinc system. Ind. Lab. (USSR) 1979, 45, 841–844. [Google Scholar]
- Sugino, S.; Hagiwara, H. Activity of Zinc in Molten Copper and Copper-Gold Alloys. J. Jpn. Inst. Met. 1986, 50, 186–192. [Google Scholar] [CrossRef]
- Leitgebel, W. Uber das Sieden einiger Metalle und Legierungen bei Atmospharendruck. Z. Anorg. Allg. Chem. 1931, 202, 305–324. [Google Scholar] [CrossRef]
- Baker, E.H. Vapor pressures and thermodynamic behavior of liquid zinc–copper alloys at 1150 °C. Trans. Inst. Min. Metall. 1970, 79, C1–C2. [Google Scholar]
- Kleppa, O.J.; Thalmayer, C.E. An EMF Investigation of Binary Liquid Alloys Rich in Zinc. J. Phys. Chem. 1959, 63, 1953–1958. [Google Scholar] [CrossRef]
- Gerling, U.; Predel, B. Thermodynamic properties of liquid copper-zinc alloys. Chem. Inf. 1980, 71, 158–164. [Google Scholar]
- Korber, F.; Oelsen, W. The formation enthalpy of the binary alloys Fe-Sb, Co-Sb, Ni-Sb, Co-Sn, Ni-Sn, Cu-Sn and Cu-Zn in the cast condition. Mitt. Kaiser Wilhelm Inst. Eisenforsch. 1937, 19, 158–164. [Google Scholar]
- Weibke, F. Beiträge zur systematischen Verwandtschaftslehre. 71. Über die Bildungswärmen im System Kupfer-Zink. Z. Anorg. Allg. Chem. 1937, 232, 289–296. [Google Scholar] [CrossRef]
- Kleppa, O.; King, R. Heat of formation of the solid solutions of zinc, gallium and germanium in copper. Acta Metall. 1962, 10, 1183–1186. [Google Scholar] [CrossRef]
- Orr, R.; Argent, B. Heats of formation of the α-brasses. Trans. Faraday Soc. 1965, 61, 2126–2131. [Google Scholar] [CrossRef]
- Blair, G.R.; Downie, D.B. A Calorimetric Study of Silver-Zinc and Copper-Zinc Alloys. Met. Metall. Trus. 1970, 4, 1–5. [Google Scholar] [CrossRef]
- Ölander, A. Eine elektrochemische Untersuchung von Messing. Z. Phys. Chem. 1933, 163, 428–438. [Google Scholar] [CrossRef]
- Seith, W.; Krauss, W. The diffusion and vapour pressure in zinc in brasses. Z. Elektrochem. 1938, 44, 98–102. [Google Scholar]
- Hargreaves, R. The vapour pressure of zinc in brasses. J. Inst. Met. 1939, 64, 115–125. [Google Scholar]
- Argent, B.B.; Wakeman, D.W. Thermodynamic properties of solid solutions. Part 1. Copper-zinc solid solution. Trans. Faraday Soc. 1958, 54, 799–806. [Google Scholar] [CrossRef]
- Pemsler, J.P.; Rapperpo, E.J. Thermodynamic activity measurements using atomic absorption-copper-zinc. Trans. Metall. S. A 1969, 245, 1395. [Google Scholar]
- Masson, D.; Sheu, J. Variations in the composition dependence of the activity coefficient in terminal solid solutions of Ag-Zn, Ag-Cd, and Cu-Zn. Metall. Trans. 1970, 1, 3005–3009. [Google Scholar] [CrossRef]
- Heyding, R.D. The copper/selenium system. Can. J. Chem. 1966, 44, 1233–1236. [Google Scholar] [CrossRef]
- Bernardini, G.P.; Corsini, F.; Trosti, R. Nuove relazioni di fase nel sistema Cu-Se. Period. Mineral. 1972, 41, 565–586. [Google Scholar]
- Murray, R.M.; Heyding, R.D. The copper–selenium system at temperatures to 850 K and pressures to 50 kbar. Can. J. Chem. 1975, 53, 878–887. [Google Scholar] [CrossRef]
- Babitsyna, A.A.; Emel’yanova, T.; Chernitsyna, M.A. Copper-Selenium System. Zh. Neorg. Khim. 1975, 20, 3093–3096. [Google Scholar]
- Glazov, V.M.; Kim, S.G. Acoustic Studies of Liquid Immiscibility in the Cu-Se System. Izv. Akad. Nauk. SSSR Neorg. Mater. 1990, 26, 2488–2490. [Google Scholar]
- Glazov, V.M.; Pavlova, L.M.; Asryan, A.A. Thermal Dissociation of Copper Chalcogenides during Melting. Zh. Fiz. Khim. 1996, 70, 232–236. [Google Scholar]
- Glazov, V.M.; Pashinkin, A.S. Phase equilibria in the Cu-Se system. Inorg. Mater. 2000, 36, 641–652. [Google Scholar] [CrossRef]
- Ogorelec, Z.; Mestnik, B.; Devčič, D. A new contribution to the equilibrium diagram of the Cu-Se system. J. Mater. Sci. 1972, 7, 967–969. [Google Scholar] [CrossRef]
- Chakrabarti, D.; Laughlin, D. The Cu-Se (Copper-Selenium) system. Bull. Alloy. Phase Diagr. 1981, 2, 305–315. [Google Scholar] [CrossRef]
- Muhsin, I. Thermodynamic stability and homogeneity of cuprous selenide by emf and coulometric titration. Solid State Ion. 2019, 329, 140–148. [Google Scholar]
- Gattow, G.; Schneider, A. Die Bildungsenthalpien im System Kupfer-Selen. Z. Anorg. Allg. Chem. 1956, 286, 296–306. [Google Scholar] [CrossRef]
- Askerova, K.A.; Alieva, N.A.; Azizov, T.K.; Abbasov, A.S.; Mustafayev, F.M. Thermodynamic Properties of Copper Selenides. Izv. Akad. Nauk. Azerb. SSR 1976, 6, 137–139. [Google Scholar]
- Rau, H.; Rabenau, A. Vapour Pressure Measurements in the Copper-Selenium System. J. Solid State Chem. 1970, 1, 515–518. [Google Scholar] [CrossRef]
- Mills, K.C. Butterworths; Butterworths Law: London, UK; Boston, MA, USA, 1974. [Google Scholar]
- Stølen, S.; Fjellvag, H.; Grønvold, F.; Sipowska, J.T.; Westrum, J.E.F. Heat capacity, structural and thermodynamic properties of synthetic klockmannite CuSe at temperatures from 5 K to 652.7 K. Enthalpy of decomposition. J. Chem. Thermodyn. 1996, 28, 753–766. [Google Scholar] [CrossRef]
- Kubaschewski, P.; Nölting, J. Spezifische Wärmen und thermische Fehlordnung von Kupferchalkogeniden Teil I: Cu2Se und Cu2Te bei angenähert stöchiometrischer Zusammensetzung. Ber. Der Bunsenges. Für Phys. Chem. 1973, 77, 70–74. [Google Scholar]
- Blachnik, R.; Gunia, P.G. Enthalpien von Kupfer- und Silberchalkogeniden / Enthalpies of Copper and Silver Chalcogenides. Z. Für Nat. A 1978, 33, 190–196. [Google Scholar] [CrossRef]
- Glazov, V.; Mendelevich, A.Y. Entropy of Melting of Silver and Copper Chalcogenides. Elektron. Tekh. Ser. 1968, 1, 114–119. [Google Scholar]
- Du, Z.; Guo, C.; Tao, M.; Li, C. Thermodynamic modeling of the Cu-Se system. Int. J. Mater. Res. 2008, 99, 294–300. [Google Scholar] [CrossRef]
- Sharma, R.C.; Chang, Y.A. The Se-Zn (Selenium-Zinc) System. J. Phase Equilib. 1996, 17, 155–160. [Google Scholar] [CrossRef]
- Blachnik, R.; Bolte, G. Aktivitäten von Se in geschmolzenen Cu-Se und Ag-Se Mischungen. J. Less Common Met. 1978, 57, 21–28. [Google Scholar] [CrossRef]
- Brebrick, R.; Liu, H. Analysis of the Zn-Se System. J. Phase Equilib. 1996, 17, 495–501. [Google Scholar] [CrossRef]
- Okada, H.; Kawanaka, T.; Ohmoto, S. Study on the ZnSe phase diagram by differential thermal analysis. J. Cryst. Growth 1996, 165, 31–36. [Google Scholar] [CrossRef]
- Fischer, A.G. Preparation and Properties of ZnS-Type Crystals from the Melt. J. Electrochem. Soc. 1959, 106, 838. [Google Scholar] [CrossRef]
- Sysoev, L.; Raiskin, E.; Gur’ev, V. Measurement of the Melting Point of Sulfides, Selenides, and Tellurides of Zn and Cd. Izv. Akad. Nauk SSSR Neorg. Mater. 1967, 3, 390–391. [Google Scholar]
- Sharma, R.; Chang, Y. Thermodynamic analysis and phase equilibria calculations for the Zn-Te, Zn-Se and Zn-S systems. J. Cryst. Growth 1988, 88, 193–204. [Google Scholar] [CrossRef]
- Rubenstein, M. Solution growth of some II-VI compounds using tin as a solvent. J. Cryst. Growth 1968, 3, 309–312. [Google Scholar] [CrossRef]
- Ozawa, L.; Hersh, H.N. Resistivity and Photoluminescence of Zn(S, Se):l Annealed in Liquid Zinc. J. Electrochem. Soc. 1973, 120, 935–942. [Google Scholar] [CrossRef]
- Kuzhelev, L.; Mironov, I.; Pavlova, V.; Stroganova, I. Solubility of the selenium and tellurium in zinc in the range 700–1100 °C. J. Phys. Chem 1974, 48, 287. [Google Scholar]
- Kikuma, I.; Furukoshi, M. Solution growth of ZnSe crystals using In-Zn solvents. J. Cryst. Growth 1980, 50, 654–658. [Google Scholar] [CrossRef]
- Nakamura, H.; Sun, L.Y.; Asano, A.; Nakamura, Y.; Washiyama, M.; Aoki, M. Liquid-phase epitaxial growth of ZnSe on ZnTe substrate. Jpn. J. Appl. Phys. 1983, 22, 499–503. [Google Scholar] [CrossRef]
- Unuma, H.; Higuchi, M.; Yamakawa, Y.; Kodaira, K.; Koyama, T. Liquid Encapsulated Flux Growth of ZnSe Single Crystals from Se Solvent. Jpn. J. Appl. Phys. 1992, 31, L383. [Google Scholar] [CrossRef]
- Sharma, R.; Chang, Y. The Te−Zn (Tellurium-Zinc) system. Bull. Alloy. Phase Diagr. 1987, 8, 14–19. [Google Scholar] [CrossRef]
- Korneeva, I.; Sokolov, V.; Novoselova, A. Saturated-vapor pressure of zinc and cadmium selenides in the solid state. Russ. J. Inorg. Chem. 1960, 5, 117–119. [Google Scholar]
- Wosten, W.J.; Geers, M.G. The vapor pressure of zinc selenide. J. Phys. Chem. 1961, 66, 1252–1253. [Google Scholar] [CrossRef]
- Sedgwick, T.O.; Agule, B.J. Bourdon Gauge Determination of Equilibrium in the ZnSe(s)-12(g) System. J. Electrochem. Soc. 1966, 113, 54–57. [Google Scholar] [CrossRef]
- Terpilowski, J.; Ratajczak, E. Thermodynamic Properties of Zinc Selenide. Roczn. Chem. 1967, 41, 429–433. [Google Scholar]
- Flögel, P. Zur Kristallzüchtung von Cadmiumsulfid und anderen II-IV-Verbindungen. III. Zum Gleichgewicht zwischen Selen und Wasserstoff bei 1000 °C. Z. Anorg. Allg. Chem. 1969, 370, 16–30. [Google Scholar] [CrossRef]
- Hassan, M.; Munir, Z.A. Studies on the Sublimation of IIB-VIA Compounds. VI. Thermodynamics of the Dissociation of Zinc Selenide. High Temper. 1973, 5, 34–39. [Google Scholar]
- Kirk, D.; Raven, M. A theory dealing with the vacuum evaporation and deposition of binary semiconducting compounds, with special reference to the thermal evaporation of zinc selenide. J. Phys. D Appl. Phys. 1976, 9, 2015. [Google Scholar] [CrossRef]
- Bardi, G.; Trionfetti, G. Vapour pressure and sublimation enthalpy of zinc selenide and zinc telluride by thermogravimetric knudsen-effusion method. Thermochim. Acta 1990, 157, 287–294. [Google Scholar] [CrossRef]
- Nasar, A.; Shamsuddin, M. Thermodynamic Properties of Zinc Selenide Thermodynamische Eigenschaften von Zinkselenid. Int. J. Mater. Res. 1990, 81, 244–246. [Google Scholar] [CrossRef]
- Schönherr, E.; Freiberg, M.; Siche, D.; Hartmann, H. The vapor composition and vapor pressure of ZnSe from a modified Knudsen technique between 1190 and 1310 K. Ber. Der Bunsenges. Für Phys. Chem. 1996, 100, 1766–1771. [Google Scholar] [CrossRef]
- Yang, C.; Liu, Y.; Chu, M.; Wang, L. Phase diagrams and thermodynamic descriptions for the Bi–Se and Zn–Se binary systems. J. Alloys Compd. 2014, 617, 423–428. [Google Scholar]
- Bale, C.W.; Chartrand, P.; Degterov, S.A.; Eriksson, G.; Hack, K.; Mahfoud, R.B.; Melancon, J.; Pelton, A.D.; Petersen, S. FactSage Thermochemical Software and Databases. Calphad Pergamon Press 2002, 26, 189–228. [Google Scholar] [CrossRef]
- Dinsdale, A.T. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Pelton, A.D.; Degterov, S.A.; Eriksson, G.; Robelin, C.; Dessureault, Y. The modified quasichemical model I—Binary solutions. Metall. Mater. Trans. B 2000, 31, 651–659. [Google Scholar] [CrossRef]
- Pelton, A.D.; Chartrand, P. The modified quasi-chemical model: Part II. Multi-component solutions. Metall. Mater. Trans. A 2001, 32, 1355–1360. [Google Scholar] [CrossRef]
- Kang, Y.B.; Pelton, A.D.; Chartrand, P.; Fuerst, C.D. Critical evaluation and thermodynamic optimization of the Al-Ce, Al-Y, Al-Sc and Mg-Sc binary systems. Calphad 2008, 32, 413–422. [Google Scholar] [CrossRef]
- Dupin, N.; Ansara, I. On the sublattice formalism applied to the B2 phase. Z. Metallk. 1999, 90, 76–85. [Google Scholar]
- Kopp, H.J. Investigations of the specific heat of solid bodies. J. Chem. Soc. 1866, 19, 154–234. [Google Scholar] [CrossRef]
- Goldfinger, P.; Jeunehomme, M. Mass spectrometric and Knudsen-cell vaporization studies of group 2B-6B compounds. Trans. Faraday Soc. 1963, 59, 2851–2867. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z.; Zhang, Y.N.; Han, D.; Medraj, M. Investigation on metallic glass formation in Mg-Zn-Sr ternary system by the CALPHAD method. Mater. Lett. 2019, 256, 126628. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z.; Li, S.; Meng, L.; Rao, W.F. Experimental investigation and thermodynamic modeling of the Mg-Cu-Ca ternary system. Calphad 2021, 75, 102325. [Google Scholar] [CrossRef]
- Wang, J.; Chen, P.; Meng, L.; Jin, L. Investigation on the Mechanical and Corrosion Properties of ZnMnSr Alloys for Biodegradable Orthopedic Implants. Adv. Eng. Mater. 2022, 2101581. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Jin, L.; Zhang, Y.; Sheng, L. Experimental determination of the phase equilibrium in the Mg-Cu-Ca ternary system at 350 °C. J. Alloys Compd. 2019, 818, 152865. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z.; Jung, I.H.; Sheng, L. Experimental investigation and thermodynamic modeling of the Mg-Sn-Sr ternary system-ScienceDirect. Calphad 2021, 72, 102237. [Google Scholar] [CrossRef]
- Wang, J.; Han, D.; Zhang, Z.; Jung, I.H.; Rao, W.F. Experimental measurement and thermodynamic evaluation of the Mg-Cu-Sr ternary system. J. Chem. Thermodyn. 2021, 163, 106582. [Google Scholar] [CrossRef]








| Properties | Experimental Method | Temperature Range (°C) | Composition Range (at% Zn) | Refs. |
| Calorimetry | 1127 | 5–85 | [58] | |
| Adiabatic calorimeter | 1100 | 10–40 | [59] | |
| Calorimetry | 1000 | 0–100 | [60] | |
| Vapor pressure technique | 700–850 | 42.8–79.8 | [61] | |
| Vapor pressure technique | 796–1030 | 32.9–79.2 | [62] | |
| Vapor pressure technique | 927 | 8.1–85.3 | [63] | |
| Vapor pressure technique | 850–1200 | 5–92 | [64] | |
| Vapor pressure technique | 1100 | 1–10 | [65] | |
| Vapor pressure technique | 1100–1150 | 1–8 | [66] | |
| Boiling point method | 915–1500 | 6.5–88.55 | [67] | |
| Boiling point method | 1150 | 18–90 | [68] | |
| EMF | 627 | 80–92 | [69] | |
| EMF | 800–900 | 20–90 | [70] | |
| Calorimetry | 20 | 12–88 | [60] | |
| Calorimetry | 25 | 11.2–87.8 | [71] | |
| Calorimetry | 90 | 39–98 | [72] | |
| Calorimetry | 25 | 7–37 | [73] | |
| Calorimetry | 300 | 10–35 | [74] | |
| Calorimetry | 300–400 | 26–86.5 | [75] | |
| Vapor pressure technique | 850 | 20–60 | [76] | |
| EMF | 400, 500 | 44.4–84.3 | [77] | |
| Vapor pressure technique | 727 | 37.3–45.3 | [78] | |
| Vapor pressure technique | 727 | 2.1–34.1 | [79] | |
| Atomic absorptionmethod | 500 | 5–35 | [80] | |
| Vapor pressure technique | 790 | 1–10 | [81] |
| Phases | (kJ·mol−1) | (J·K−1·mol−1) | (J·K−1·mol−1) | Experimental Method | Temperature (K) | Refs. |
|---|---|---|---|---|---|---|
| A-CuSe | −(39.5 ± 0.5) | calorimetry | [92] | |||
| −(33.5 ± 10.0) | 74.1 | EMF | [93] | |||
| −40.6 | 72.0 | Vapor pressure | [94] | |||
| −41.8 | 78.2 | Evaluation | [95] | |||
| (79.3 ± 0.8) | (50.3 ± 0.6) | adiabatic calorimetry | 5–653 K | [96] | ||
| β-CuSe | heat capacity | adiabatic calorimetry | 5–653 K | [96] | ||
| γ-CuSe | heat capacity | adiabatic calorimetry | 5–653 K | [96] | ||
| α-Cu2Se | −(59.3 ± 0.5) | calorimetry | [92] | |||
| −(65.7 ± 6.5) | 80.2 | EMF | 320 to 420 K | [93] | ||
| −65.3 | 157.3 | Vapor pressure | [94] | |||
| −65.3 | 129.7 | Evaluation | [95] | |||
| heat capacity | 180 to 560 K | [97] | ||||
| 75.23 (300K) | drop calorimetry | 350 to 1500 K | [98] | |||
| β-Cu2Se | −(54.4 ± 0.5) | calorimetry | [92] | |||
| −57.5(Cu1.75Se) | 162.3 | Estimation | [94] | |||
| −54.0(Cu1.75Se) | Evaluation | [95] | ||||
| Evaluation | [84] | |||||
| Evaluation | [99] | |||||
| CuSe2 | −(43.1 ± 4) | calorimetry | [92] | |||
| −(39.3 ± 4) | 98.4 | EMF | [93] | |||
| −48.1 | 120.5 | Vapor pressure | [94] | |||
| −48.1 | 107.5 | Vapor pressure | [95] | |||
| Cu3Se2 | −(98.9 ± 7.1) | calorimetry | [92] | |||
| −(94.6 ± 7.1) | 184.9 | EMF | [93] | |||
| −104.6 | 207.1 | EMF | [94] |
(kJ·mol−1) | (J·K−1·mol−1) | Experimental Method | Temperature (K) | Refs. |
|---|---|---|---|---|
| −(215.9 ± 35.0) | (31.6 ± 20.0) | Knudsen effusion weight loss | 913–1093 | [115] |
| −(198.6 ± 19.0) | (58.9 ± 14.0) | Gas flow method | 1060–1393 | [116] |
| −(185.8 ± 16.0) | (62.2 ± 20.0) | Static method | 900–1200 | [117] |
| −(166.1 ± 6.0) | (69.9 ± 6.0) | Electrochemical cell | 360–420 | [118] |
| −(192.5 ± 23.0) | (54.9 ± 12.0) | Gas flow method | 1173–1413 | [119] |
| −(157.8 ± 13.0) | (88.7 ± 12.0) | Knudsen torsion effusion | 952–1209 | [120] |
| −(164.5 ± 6.0) | (86.2 ± 9.0) | Mass spectrometry and Knudsen effusion weight loss | 923–1123 | [121] |
| −(183.4 ± 14.0) | (66.1 ± 9.0) | Knudsen effusion weight loss | 1025–1288 | [122] |
| −(177.5 ± 6.0) | (59.4 ± 12.0) | Electrochemical cell | 635–693 | [123] |
| −(175.0 ± 6.0) | (63.9 ± 9.0) | Electrochemical cell | 693–825 | [123] |
| −(177.1 ± 8.0) | 707 | [123] | ||
| −(175.4 ± 8.0) | (74.0 ± 6.0) | Optical density | 1260–1410 | [103] |
| −(182.4 ± 14.0) | (68.1 ± 14.0) | Knudsen effusion weight loss | 1190–1310 | [124] |
| −175.9 | 13.2 | Calculated | [125] | |
| −163.85 | 11.8 | Calculated | This work |
| Phase | Pearson Symbol | Strukturbericht Designation | Space Group | Prototype | Refs. | Model |
|---|---|---|---|---|---|---|
| Liquid | MQM | |||||
| α-Cu (fcc_A1) | cF4 | A1 | Fmm | Cu | [43] | CEF |
| β (bcc_A2) | cI2 | A2 | Imm | W | [48] | CEF |
| β’ (bcc_B2) | cP2 | B2 | Pmm | CsCl | [48] | CEF |
| γ (Cu5Zn8) | cI52 | D82 | I3m | Cu5Zn8 | [51] | CEF |
| δ (bcc_A2) | cI2 | A2 | Imm | W | [55] | CEF |
| ε (hcp_A3) | hP6 | A3 | P63/mmc | Mg | [43] | CEF |
| η (hcp_Zn) | hP2 | A3 | P63/mmc | Mg | [43] | CEF |
| hex_A8 | hP3 | A8 | P3121 | hexagonal_A8 | [43] | CEF |
| β-Cu2−xSe | Fmm | fcc | [83] | CEF | ||
| α-Cu2Se | P12₁/c1 | monoclinic | [88] | ST | ||
| Cu3Se2 | P21m | hexagonal | [88] | ST | ||
| α-CuSe | P6₃/mmc | hexagonal | [88] | ST | ||
| β-CuSe | Cmcm | hexagonal | [88] | ST | ||
| γ-CuSe | P63/mmc | orthorhombic | [88] | ST | ||
| CuSe2 | Pnnm | orthorhombic | [88] | ST | ||
| ZnSe | hP4 | B4 | P63mc | ZnS (wurtzite) | [103] | ST |
| Coordination Numbers * | Gibbs Energies of the Pair Exchange Reactions (J/mol-atoms) | |||
|---|---|---|---|---|
| m | n | |||
| Cu | Zn | 6 | 6 | |
| Cu | Se | 7.5 | 4 | |
| Zn | Se | 4 | 4 | |
| Phase, Model and Thermodynamic Parameters (J/mol, or J/(mol·K)) | Refs. |
|---|---|
| Fcc_A1 phase, format (Cu, Zn, Se): | |
| ; | [127] |
| ; | This work |
| ; | This work |
| Bcc_A2 phase, format (Cu, Zn): | |
| ; | [127] |
| ; | This work |
| β’(bcc_B2) phase, format (Cu, Zn)0.5(Cu, Zn)0.5: | |
| ; | This work |
| Hcp_A3 phase, format (Cu, Zn): | |
| ; | [127] |
| ; | This work |
| Hcp_Zn phase, format (Cu, Zn): | |
| ; | [127] |
| ; | This work |
| γ (Cu5Zn8) phase, format (Cu)2(Zn)2(Cu, Zn)3(Cu, Zn)6: | |
| ; | This work |
| ; | This work |
| ; | This work |
| Hex_A8 phase, format (Cu, Se): | |
| ; | [127] |
| β-Cu2Se phase, format (Cu, Va)2(Se): | |
| ; | This work |
| ; | This work |
| α-Cu2Se phase, format (Cu)2(Se): | |
| ; | This work |
| ; | This work |
| ; | This work |
| ; | This work |
| Cu3Se2 phase, format (Cu)3(Se)2: | |
| ; | This work |
| ; | This work |
| ; | This work |
; | This work |
| ; | This work |
| ; ; | This work |
| Reaction | Reaction Type | Temperature (°C) | Composition (Zn at. %) | Refs. | ||
|---|---|---|---|---|---|---|
| Liquid + fcc_A1 ↔ β(bcc_A2) | Peritectic | 903 | 36.8 | 31.9 | 36.1 | [43] |
| 903 | 37.3 | 31.9 | 35.3 | [32] | ||
| 902 | 37.2 | 31.9 | 35.1 | [45] | ||
| 900 | 35.8 | [48] | ||||
| 902 | 36.7 | 31.9 | 36.0 | [50] | ||
| 898 | 39.0 | 33.1 | 36.6 | This work | ||
| Liquid + β(bcc_A2) ↔ γ(Cu5Zn8) | Peritectic | 835 | 59.1 | 55.8 | 59.1 | [43] |
| 835 | 59.2 | 55.8 | 58.6 | [45] | ||
| 837 | 60.6 | 57.2 | 59.9 | [47] | ||
| 834 | 58.7 | [48] | ||||
| 833 | 59.6 | 55.1 | 59.6 | [50] | ||
| 824 | 61.8 | 56.3 | 59.1 | This work | ||
| Liquid + γ(Cu5Zn8) ↔ δ(bcc_A2) | Peritectic | 700 | 80.0 | 69.2 | 72.4 | [43] |
| 700 | 80.2 | 67.8 | 71.9 | [45] | ||
| 700 | 82.0 | 68.9 | 72.5 | [47] | ||
| 703 | 72.0 | [48] | ||||
| 700 | 80.3 | 68.4 | 71.8 | [50] | ||
| 695 | 81.7 | 67.7 | 71.7 | This work | ||
| Liquid + δ(bcc_A2) ↔ hcp_A3 | Peritectic | 598 | 88.0 | 76.0 | 78.1 | [43] |
| 600 | 88.2 | 77.3 | 79.2 | [45] | ||
| 599 | 89.2 | 77.3 | 79.5 | [47] | ||
| 600 | 79.2 | [28] | ||||
| 598 | 87.8 | 76.7 | 79.2 | [50] | ||
| 602 | 89.6 | 77.2 | 79.2 | This work | ||
| δ(bcc_A2) ↔ γ(Cu5Zn8) + hcp_A3 | Eutectoid | 560 | 74.0 | 70.0 | 78.0 | [43] |
| 559 | 74.9 | 69.3 | 77.7 | [45] | ||
| 560 | 74.3 | 69.0 | 77.6 | [47] | ||
| 559 | 74.9 | [48] | ||||
| 560 | 74.6 | 70.0 | 77.6 | [50] | ||
| 557 | 74.6 | 70.4 | 77.5 | This work | ||
| Liquid + hcp_A3 ↔ hcp_Zn | Peritectic | 424 | 98.3 | 87.2 | 97.2 | [43] |
| 422 | 98.3 | 87.5 | 98.1 | [45] | ||
| 419 | 98.4 | 87.4 | 97.6 | [47] | ||
| 421 | 98.3 | [48] | ||||
| 425 | 98.2 | 87.5 | 97.3 | [50] | ||
| 422 | 98.7 | 87.6 | 98.2 | This work | ||
| β(bcc_A2) ↔ β’(bcc_B2) + (Cu5Zn8) | Ordering reaction | 470 | 48.2 | 57.0 | [43] | |
| 469 | 49.1 | 56.1 | [45] | |||
| 466 | 48.4 | 57.5 | [50] | |||
| β(bcc_A2) ↔ β’(bcc_B2) + (Cu5Zn8) | Ordering reaction | 456 | 50.5 | 57.8 | This work | |
| β(bcc_A2) ↔ β’(bcc_B2) + fcc_A1 | Ordering reaction | 453 | 44.8 | 38.3 | 72.4 | [43] |
| 460 | 44.5 | 38.6 | 71.9 | [45] | ||
| 456 | 44.2 | 39.2 | 77.5 | [50] | ||
| 447 | 45.3 | 39.4 | This work | |||
| Reaction | Reaction Type | Temperature (°C) | Composition (Zn at. %) | Refs. | ||
|---|---|---|---|---|---|---|
| Liquid#1 + fcc_A1 ↔ β-Cu2Se | Eutectic | 1063 | 1.8 | 0.0 | 33.3 | [88] |
| 1062 | 2.1 | 0.0 | 33.3 | [100] | ||
| 1060 | 2.3 | 0.0 | 33.3 | This work | ||
| Liquid#2 ↔ liquid#1 + β-Cu2Se | Monotectic | 1107 | 35.8 | [48] | ||
| 1107 | 36.7 | 31.9 | 36.0 | [50] | ||
| 1101 | 39.0 | 33.1 | 36.6 | This work | ||
| Liquid#2 ↔ β-Cu2Se + liquid | Monotectic | 523 | 52.5 | 36.5 | 99.6 | [88] |
| 523 | 51.6 | 36.3 | 99.9 | [100] | ||
| 525 | 50.0 | 35.1 | 99.9 | This work | ||
| β-Cu2Se + liquid ↔ γ-CuSe | Peritectic | 380 | 36.5 | 100.0 | 50.0 | [88] |
| 380 | 36.1 | 100.0 | 50.0 | [100] | ||
| 376 | 35.6 | 100.0 | 50.0 | This work | ||
| β-Cu2Se + β-CuSe ↔ Cu3Se2 | Peritectoid | 112 | 36.3 | 50.0 | 40.0 | [88] |
| 113 | 35.0 | 50.0 | 40.0 | [100] | ||
| 113 | 35.8 | 50.0 | 40.0 | This work | ||
| γ-CuSe + liquid ↔ CuSe2 | Peritectic | 332 | 50.0 | 100.0 | 66.7 | [88] |
| 332 | 50.0 | 100.0 | 66.7 | [100] | ||
| 333 | 50.0 | 100.0 | 66.7 | This work | ||
| Liquid ↔ CuSe2 + hex_A8 | Peritectoid | 221 | ~100 | 66.7 | 100.0 | [88] |
| 221 | ~100 | 66.7 | 100.0 | [100] | ||
| 221 | ~100 | 66.7 | 100.0 | This work | ||
| Fcc_A1 + β-Cu2Se ↔ α-Cu2Se | Eutectoid | 123 | 0.0 | 33.3 | 33.3 | [88] |
| 123 | 0.0 | 33.3 | 33.3 | [100] | ||
| 123 | 0.0 | 33.3 | 33.3 | This work | ||
| Liquid ↔ β-Cu2Se | Congruent melting | 1130 | 33.4 | 33.4 | [88] | |
| 1148 | 33.3 | 33.3 | [100] | |||
| 1130 | 33.3 | 33.3 | This work | |||
| γ-CuSe ↔ β-CuSe | Allotropic | 120 | 50.0 | 50.0 | [88] | |
| 137 | 50.0 | 50.0 | [100] | |||
| 120 | 50.0 | 50.0 | This work | |||
| β(bcc_A2) ↔ β’(bcc_B2) + fcc_A1 | Ordering reaction | 54 | 50.0 | 50.0 | [88] | |
| 54 | 50.0 | 50.0 | [100] | |||
| 51 | 50.0 | 50.0 | This work | |||
| Reaction | Reaction Type | Temperature (°C) | Composition (Zn at. %) | Refs. | ||
|---|---|---|---|---|---|---|
| Liquid#1 + fcc_A1 ↔ β-Cu2Se | Eutectic | 419 | 0.0 | 0.0 | 50.0 | [100] |
| 419 | 0.0 | 0.0 | 50.0 | [123] | ||
| 419 | 0.0 | 0.0 | 50.0 | This work | ||
| Liquid#1 ↔ liquid#2 + ZnSe | Monotectic | 1360 | 10.9 | 42.6 | 50.0 | [100] |
| 1402 | 16.0 | 40.0 | 50.0 | [123] | ||
| 1363 | 9.8 | 41.5 | 50.0 | This work | ||
| Liquid ↔ ZnSe + hex_A8 | Eutectic | 221 | 100.0 | 50.0 | 100.0 | [100] |
| 221 | 100.0 | 50.0 | 100.0 | [123] | ||
| 221 | 100.0 | 50.0 | 100.0 | This work | ||
| Liquid ↔ ZnSe | Congruent | 1526 | 50.0 | 50.0 | [100] | |
| 1526 | 50.0 | 50.0 | [123] | |||
| 1525 | 50.0 | 50.0 | This work | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Ma, J.; Han, D.; Wang, J.; Qi, H.; Jin, L. Critical Evaluation and Thermodynamic Optimization of the Cu-Zn, Cu-Se and Zn-Se Binary Systems. Metals 2022, 12, 1401. https://doi.org/10.3390/met12091401
Tang Y, Ma J, Han D, Wang J, Qi H, Jin L. Critical Evaluation and Thermodynamic Optimization of the Cu-Zn, Cu-Se and Zn-Se Binary Systems. Metals. 2022; 12(9):1401. https://doi.org/10.3390/met12091401
Chicago/Turabian StyleTang, Yu, Jie Ma, Dong Han, Jian Wang, Haiying Qi, and Liling Jin. 2022. "Critical Evaluation and Thermodynamic Optimization of the Cu-Zn, Cu-Se and Zn-Se Binary Systems" Metals 12, no. 9: 1401. https://doi.org/10.3390/met12091401
APA StyleTang, Y., Ma, J., Han, D., Wang, J., Qi, H., & Jin, L. (2022). Critical Evaluation and Thermodynamic Optimization of the Cu-Zn, Cu-Se and Zn-Se Binary Systems. Metals, 12(9), 1401. https://doi.org/10.3390/met12091401






