Abstract
Stephen Wolfram (2002) proposed the concept of computational equivalence, which implies that almost any dynamical system can be considered as a computation, including programmable matter and nonlinear materials such as, so called, quantum matter. Memristors are often used in building and evaluating hardware neural networks. Ukil (2011) demonstrated a theoretical relationship between piezoelectrical materials and memristors. We review that work as a necessary background prior to our work on exploring a piezoelectric material for neural network computation. Our method consisted of using a cubic block of unpoled lead zirconate titanate (PZT) ceramic, to which we have attached wires for programming the PZT as a programmable substrate. We then, by means of pulse trains, constructed on-the-fly internal patterns of regions of aligned polarization and unaligned, or disordered regions. These dynamic patterns come about through constructive and destructive interference and may be exploited as a type of reservoir network. Using MNIST data we demonstrate a learning machine.
1. Introduction and Literature Review
We review the fact that any dynamical system may be considered as a computation and cite some examples. Next, we briefly review reservoir neural networks and quantum reservoir networks. Then, we compare memristors and piezoelectric materials as an introduction to quantum matter and our motivation to use a piezoelectric material for in materio computation.
1.1. Principle of Computational Equivalence and a Brief Review of Novel Computation
Stephen Wolfram [1] pointed out the Principle of Computational Equivalence (PCE), which states that “systems found in the natural world can perform computations up to a maximal (“universal”) level of computational power, and that most systems do in fact attain this maximal level of computational power. Consequently, most systems are computationally equivalent” [2]. This implies that almost any dynamical system can be considered as a computation. For example, Holden et al. [3] suggest that excitable media may be used for computation, Stepney [4,5] points out the potential computational ability of in materio computation, and [5,6] point out that a neural network architecture known as a “reservoir” may be an excellent model for in materio computation. Stepney [5,7] goes even further into the Wolfram principle and points to the fact that black holes, quantum effects, biomolecules and even some simple biological systems, such as slime molds, can be considered as a computational system. Additionally, [7] suggested that when the notion of what is computable is expanded to include interactions of elements, as in the case of programmable matter, the Church-Turing thesis becomes invalid, because we are effectively moving out of the domain of logical operations. Then, process algebras and π-calculus [8] may be applicable to preparing a compiler for programmable matter. Lastly, Calude et al. [9] review a number of unconventional computing methods and Adamatzky [10] describes computing with nonlinear media and automata collectives. While we find these computational methods to be fascinating, the current focus of this paper is on reservoir computing and specifically with an example of “quantum matter.”
1.2. Reservoir Architectures and Quantum Reservoirs: A Brief Review of the Literature
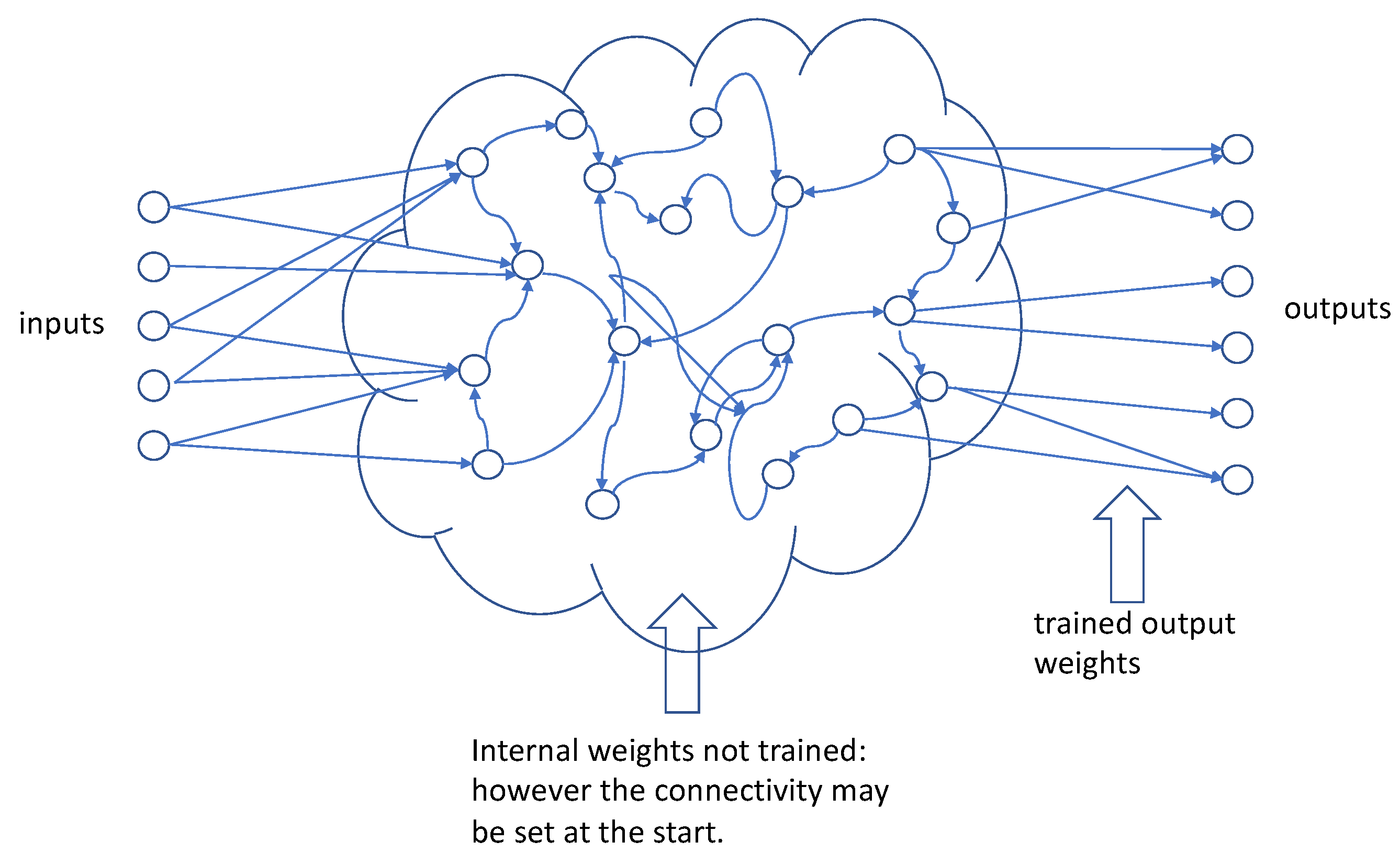
A reservoir network is a generalization of recurrent networks [11] and first developed and described by [12] and is also known as a liquid state machine (see Figure 1). Imagine dropping pebbles into a pond at various locations. By Wolfram’s PCE we realize this is a dynamical computation where the computation consists of constructive and destructive interference of wave fronts. Fernando and Spjakka (2003) [13] actually built a system they called a “liquid brain.” It consists of a transparent water tank positioned on an overhead projector and eight motors to drop “pebbles” at fixed locations. They demonstrated the ability of the system to distinguish spoken digits “zero” and “one” with an accuracy of 0.985. Hughes et al. (2019) [14] simulate, using finite element analysis, a “wave physics” system able to distinguish spoken vowels at an accuracy of 0.863.
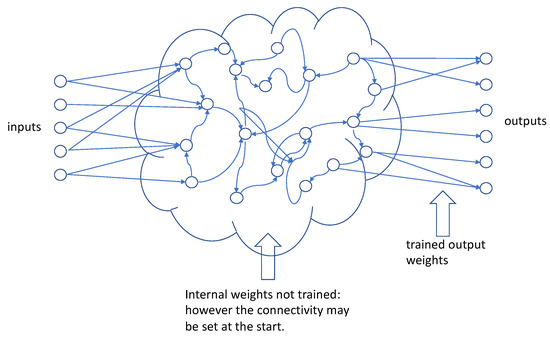
Figure 1.
Schematic of a reservoir neural network. The number of nodes in the reservoir, their connectivity, and their weights are fixed and sometimes called the hyperparameters. The internal weights are not trained. Only the output weights are trained (compare with Figure 2b). Typically, the internal weights are configured at the start (Goodfellow et al. 2016) [11]; however, with a dynamic media like PZT, or other programmable matter, one effectively achieves the same result by submitting the same set of control strings with the input data stream.
Verstraeten et al. (2007) [15] show through a number of rigorous tasks and node complexity (i.e., different types of neurons) the unification of reservoir computing methods. Their first task was spoken digit classification, the second task was an evaluation of memory capacity, and the third task was a regression involving a 10th order polynomial with added random noise. Dale et al. (2019) [16] develop a framework to thoroughly evaluate various substrates that may be applicable to in materio reservoir computing. They develop a 3-D behavior space. This allows one to determine what learning tasks are appropriate to which substrates.
A short review of quantum neuromorphic computing is given by [17] and a small book-length review is given by [18]. More specifically, refs. [19,20,21] review quantum reservoir computing and include an introduction to quantum mechanics and quantum information. They make a good point that quantum reservoir computing can jumpstart us into near-term quantum devices. The advantage of reservoir computing is that unlike Turing machines they do not require sequential transitions between states. This is also true with quantum reservoir computing where gates are not laid out in advance [22]. Lastly, we want to point out [23] proposes using an ensemble of quantum reservoirs. Ensemble machines [11] consist of a number of “identical” machines each receiving the same input data-stream. The average output is often computed as the final answer. Fujii and Nakajima [23] propose an implementation using either an NMR or a photonic quantum reservoir. They show a number of simulations including the Mackey-Glass chaotic system [24]. Their simulation included various time resolutions, as would be expected from an actual system (e.g., NMR or photonic). Negoro et al. [25] demonstrated a physical quantum reservoir with NMR using a single crystal of spin-labeled l-alanine (an amino acid). Then, Tran and Nakajima [26] built a system with three such NMR quantum reservoirs that are connected together using classical electronic circuits.
Lloyd [27] suggested a new kind of quantum computation based on interactions. Later, Lloyd [28] described the proposed system in more detail. It would consist of weakly coupled quantum systems that can be exposed to a series of pulses of well-defined frequency and length. He envisions an optical technique in which, for example, a heteropolymer with side groups that can sustain a “long-lived” excited state (long enough for relevant interaction and readout of the state) can be used for the computation. This system is reminiscent of a cellular automata [29] in which there are variable or, changeable, rules for the interaction. Further, he describes how to load and unload information, do computation, and he describes an error correction technique. The analogy of this, a heteropolymer system behaving like a disordered quantum cellular automata, is an excellent example of exploiting quantum matter.
Quantum matter is a new realization of, or a new understanding of, something that has had technological uses for some decades. This new understanding is the result of research investigating quantum information processing and quantum computing [30,31]. The quantum matter we are exploring, for various applications, are piezoelectric materials, in particular, lead zirconate titanate (PZT), one of the thousands of materials listed at the Open Quantum Materials Database [32].
In this paper we demonstrate a simple learning machine example for MNIST (Modified National Institute of Standards and Technology database) digit recognition using PZT. Since so much of “in materio” computing and programmable matter computation often focus on exploiting memristors, in the next section we draw parallels with memristive materials and piezoelectric materials [33]. We will point out, memristor materials are modified thin films of a piezoelectric, and we demonstrate that ceramic blocks of PZT may be programmed. We describe the architecture for PZT-based reservoir computing; thus, opening up a whole area of materials for programmable matter. Finally, we describe the MNIST digit recognition experiment, results, and discussion.
2. Background
2.1. A Memristance View of Piezoelectricity
Memristors were first proposed by Chua (1971) [34] and with a follow-up publication [35]. One of the first successful materials was TiO2 as described by Strukov et al. [36] They used TiO2, doped or poled. Later investigators experimented with ZnO [37] or silver sulfide nanowires as atomic switches [38]. Except for the Ag2S case, which is a fast ion conductor, in all other cases these materials are also piezoelectric. In this paper we are suggesting using a bulk matrix of piezoelectric material such as PZT as a computational substrate. We are proposing a novel way to exploit the physics of piezoelectric materials for computation. In the following we look at the theoretical connection between piezoelectricity and memristance [33].
2.2. Resistance under Stress
The resistance of a block of dielectric, or any solid matter, is given by , where R is the resistance in ohms, ρ is resistivity in ohm∙m, l and A are the length and area, respectively, of the block. Additionally, those dimensions are in meters. A is the cross-section and given by A = zw. Taking the logarithm of the resistance relation and differentiating we get:
So, we can write, dA/dw = z → dA/A = dw/w. Further, the elastic axial strain in the piezomaterial and the transverse strain are, respectively, defined as: . The Poisson ratio is defined as the negative of the ratio of axial to transverse strains:
If we assume the resistance of the material does not change with strain then . Combining equations, we get:
This equation represents the change in the general resistance due to any induced mechanical stress. Additionally, of course, in a piezoelectric medium, the induced stress could be caused by an external electric field.
2.3. Memristance
Turning now to look at memristance, the well-known charge to flux ratio gives the magnetic flux: , where φ is the magnetic flux, q is the charge, M is the memristance. This can be rewritten as a time derivative:
where v and i are voltage and current. is the average resistance, and depends on the internal state of the device. Now taking the partial derivative of the flux ratio
If the total charge in the system is constant, and then taking the time derivative we get the voltage
Because memristance is an average resistance, , and including Equation (3), we can therefore write:
Using Equation (7) we can write:
The right-hand side of this equation is a product of dynamic action, e.g., mechanical stress, , and average memristance, which results in an electric field . In brief, this equation indicates that the time dynamical stress associated with the memristance is related to piezoelectricity [33].
3. Methods
The PZT Cube
Piezoelectric materials are typically poled. In the case of PZT, poling is done at a temperature above the Curie point, at which point the crystal lattice can easily be distorted by movement of the Ti and Zr atoms. The material is subject to a DC voltage of about 2000 V (Curie point for PZT, 553 K) for a period of time; then it is allowed to cool in the furnace before removing the DC voltage. This poling operation freezes into place the lattice distortions so the crystallites are essentially aligned. This results in resonances at specific frequencies (see Appendix A Figure A3 and Figure A4) and these resonances interfere with program and control signals during attempts to use the PZT as a reservoir architecture. Therefore, we use unpoled PZT for our experiments.
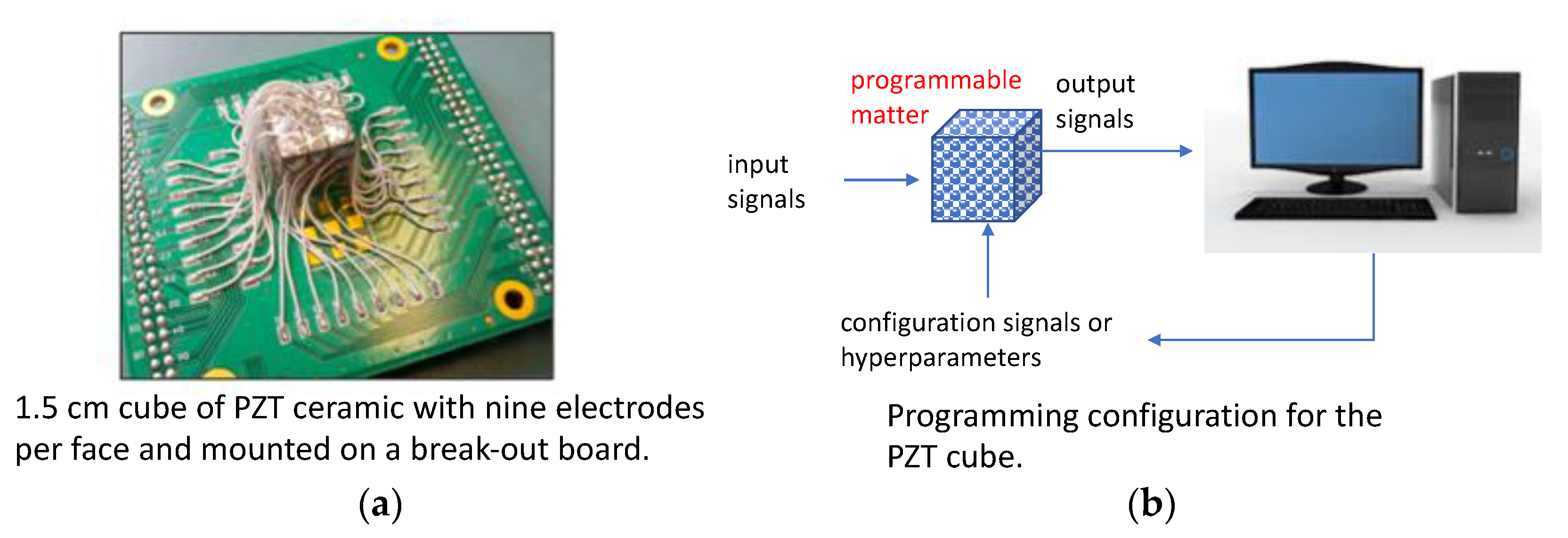
The PZT cube is made from unpoled type 880 material from American Piezo®, Inc. It measures 1.5 cm on an edge and all faces were silvered as received. We used a Dermel® tool to etch nine little squares on etch face, and we further etched along the edges to remove contacts between faces. As seen in Figure 2, wires were then silver soldered to the pads, the entire cube was then coated with 5 min epoxy and attached to the breakout board.
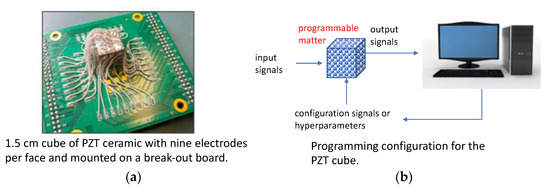
Figure 2.
(a) The unpoled PZT cube mounted on a breakout board. (b) Schematic of the concept for using the cube for computation.
As shown in Figure 1 the reservoir network has inputs that are sent to the reservoir then outputs are read and analyzed by an external computer that trains the output weights using some simple algorithm, such as multilinear regression or gradient descent. Once training is done, one can feed in inputs, read outputs and lookup the results. In the case of the PZT cube (Figure 2a), the configuration signals essentially set up the “internal weights” (Figure 1), which must be streamed in simultaneously with the input signal.
4. Machine Learning Example: MNIST Digit Recognition
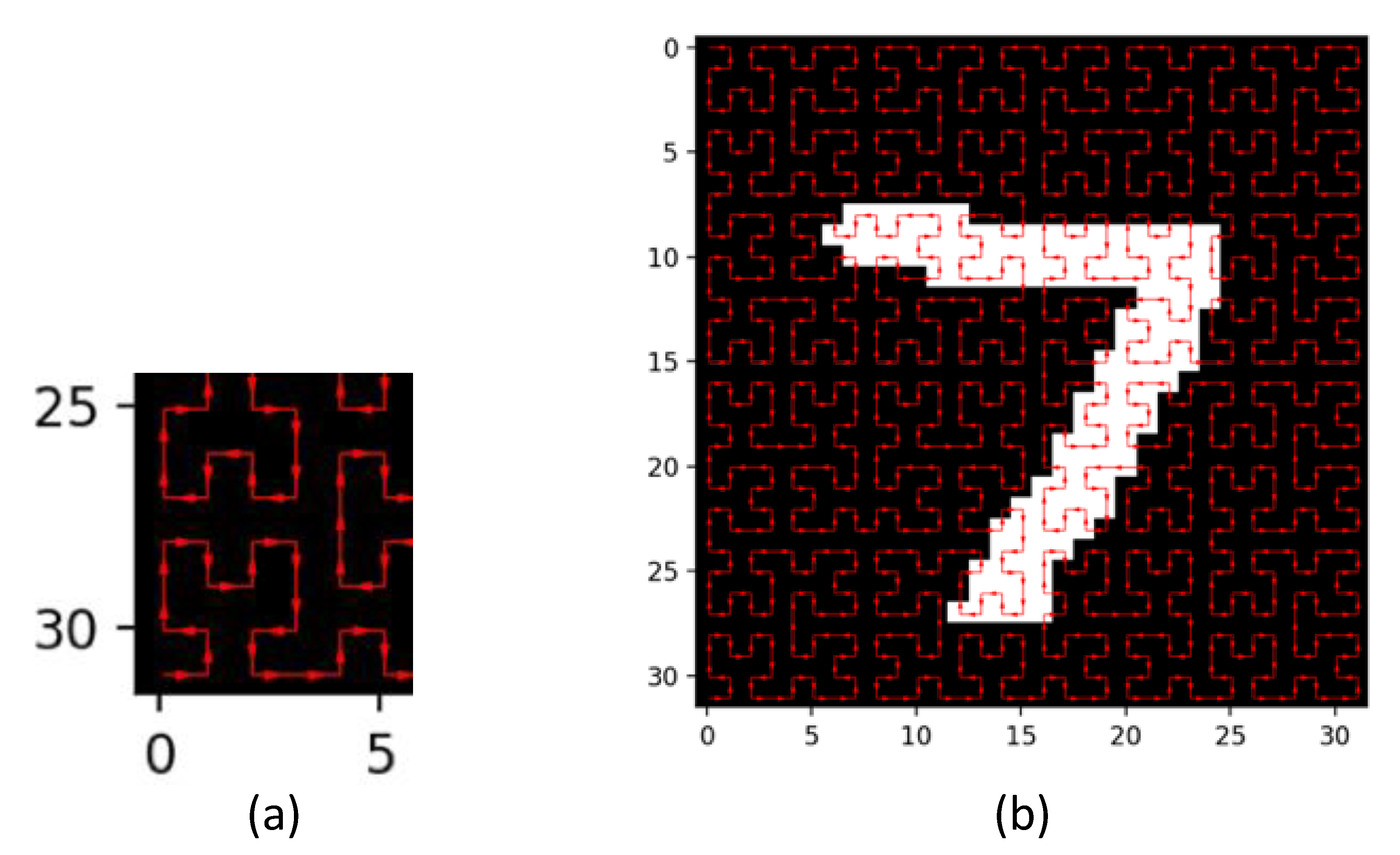
We used the MNIST hand-written digit recognition task to assess the ability of the cube to support machine learning [39]. We downloaded 10,000 cases and used 7500 for training and 2500 for validation. As the cube only provides a limited number of interface-pads it would be impossible to feed the image in parallel, so a sequential scheme was necessary—a simple linear scan of the image would likely hurt the locality of the input since consecutive pixels may be as far away from each other as the full width of the overall image (when wrapping around the image). A 2D Hilbert scan [40] was applied instead since it is known to better preserve locality when transforming 2D images into a linear format. The mapping from 2D to 1D is shown in Figure 3. Hilbert scans require images whose length and width in pixels are powers of 2. Since the original MNIST dataset has 28 × 28-pixel images, these images were rescaled to 32 × 32 pixels (using the numpy image zoom function) to enable the use of Hilbert curves. In addition to converting the original image to 32 × 32, we also converted the image to binary. This avoided the additional complexity of adding an analog conversion at the frontend or amplification of the signal. Thus, making the first demonstration as simple as possible. The input pulse signals and the control signals were generated with an Arduino-Mega and the output signals were sampled with an MCP3008 ADC communicating with an Adafruit Grand Central using SPI.
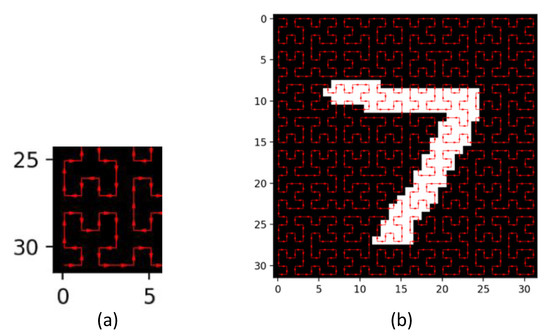
Figure 3.
A Hilbert curve was used to encode the image in a linear sequence which attempts, as much as possible, to preserve locality. The red arrows show the scan sequence. (a) Shows an expanded view the lower left corner of (b) the entire scan sequence.
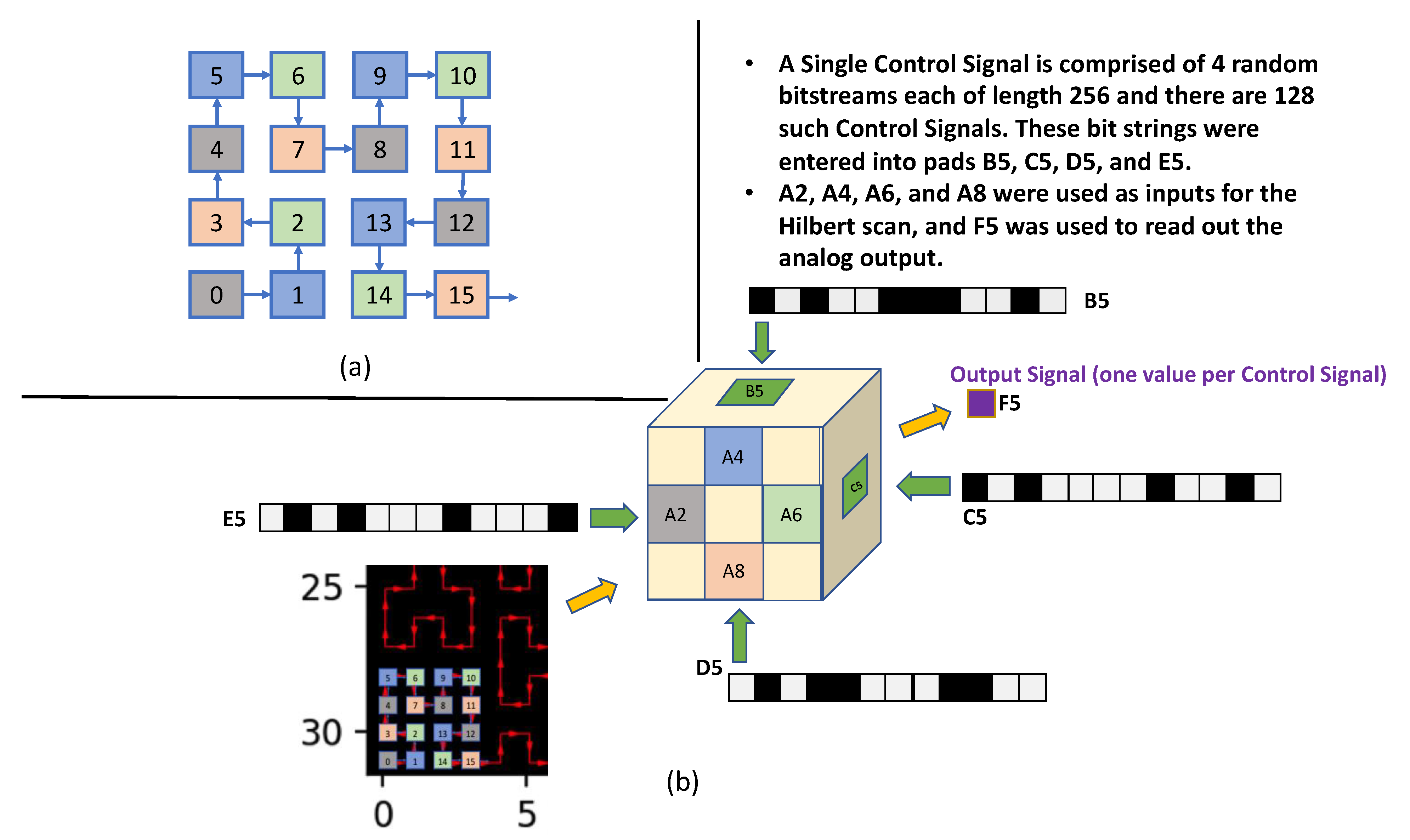
Each set of four image bits was applied to four pads on the A face of the cube (A2, A4, A6, A8 shown in Figure 4). Scanning the Hilbert curve of 1024 pixels was done in 256 time-steps. At each of these steps, along with the image data, four bits of “random control signals” were applied to the pads B5, C5, D5, and E5, respectively, on faces B, C, D, and E (Figure 4); in other words, a total of 4-bits of control signal are used at each time step, and the same bit strings were reused on all images throughout the process (training and validation). This is analogous to configuring the reservoir in a reservoir network architecture. Finally, for every time step (256-time steps/image) the voltage on the center pad, F5, of the output face (face F) is read and summed to yield a single scalar value. The entire procedure is repeated 128 times to produce the final output, which consists of 128 cumulative voltage measurements. These voltages are essentially the output for the reservoir and comprise a set of 10 vectors, one for each digit class, and each vector consisted of 128 scalar voltages.
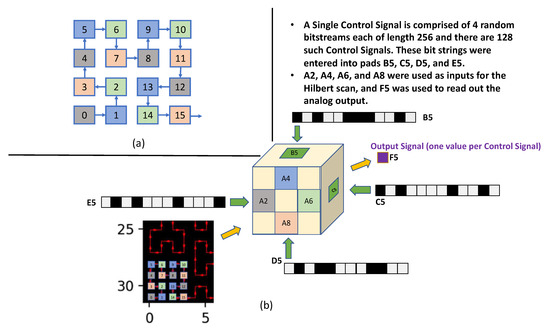
Figure 4.
Panel (a) shows the details of scanning the Hilbert curve into face A of the cube. At time, t = 0, there are four bits of signal representing the scan at positions 0, 1, 2, and 3. Panel (b) shows these bits are entered into the cube at A2, A4, A6, and A8, respectively, following the color code. Additionally, random bit strings, as the control strings, are entered at B5, C5, D5, and E5 all simultaneously with the image bits and reading the output at F5.
Finally, the resulting output for all test images were analyzed by multi-class logistic regression, also known as the softmax. The softmax score sk(y) for a particular digit class, k where k = (0, 1, …, 9) is given by:
where y is a particular instance and θ(k) is a parameter vector, a separate vector for each class. After computing the score for each class, we use the softmax function to get the probability
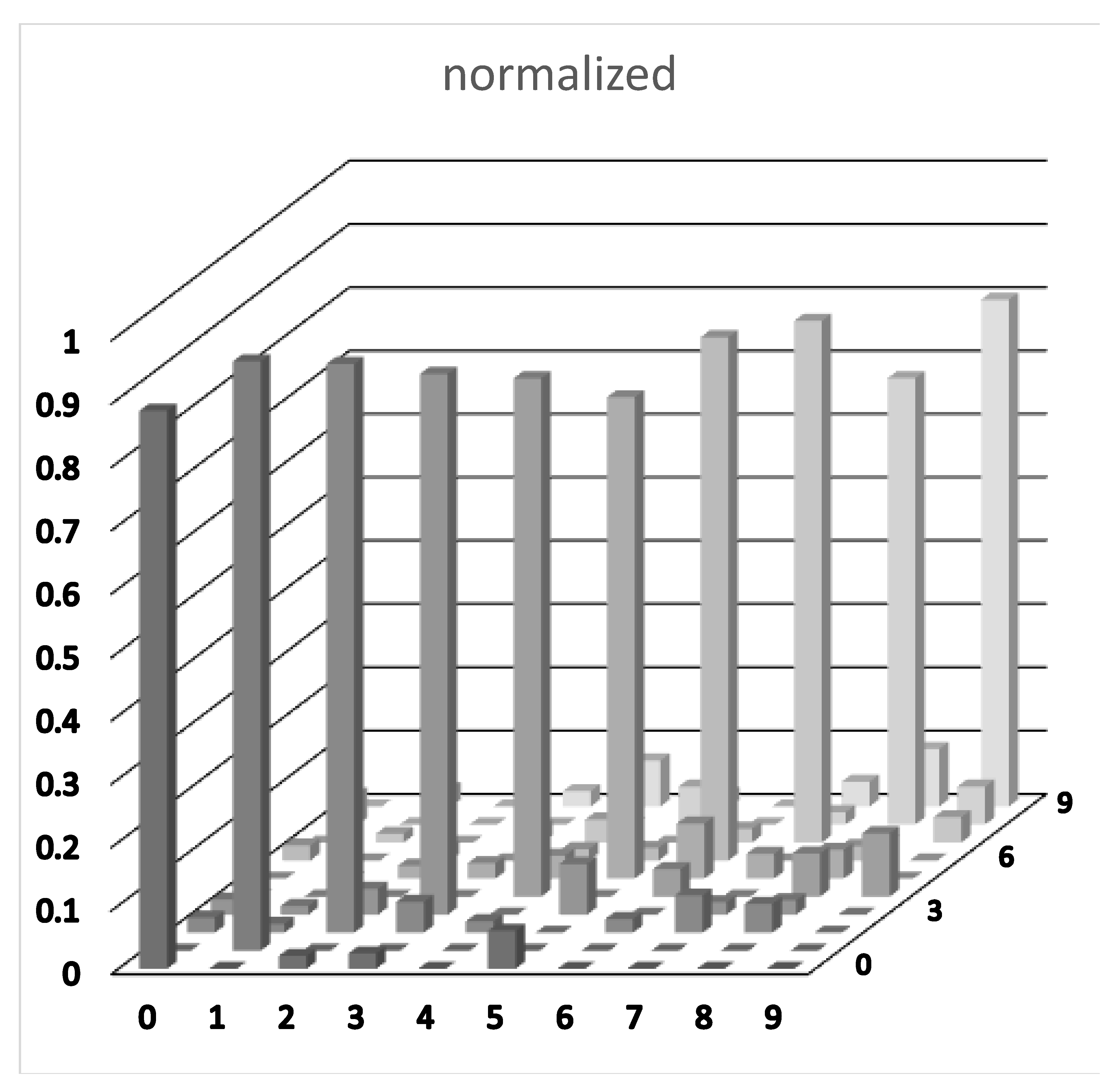
Softmax predicts the highest estimated probability for each class (see Figure 5).
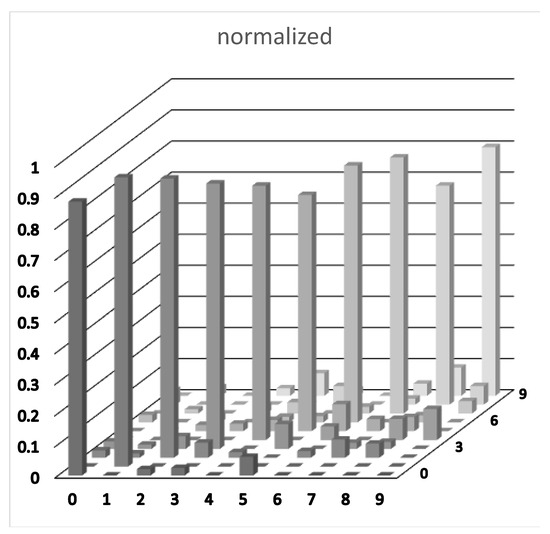
Figure 5.
The x- and y-axis are the input digit-class and output digit-class, respectively. The z-axis is average normalized output response for 2500 test digits.
5. Results and Discussion
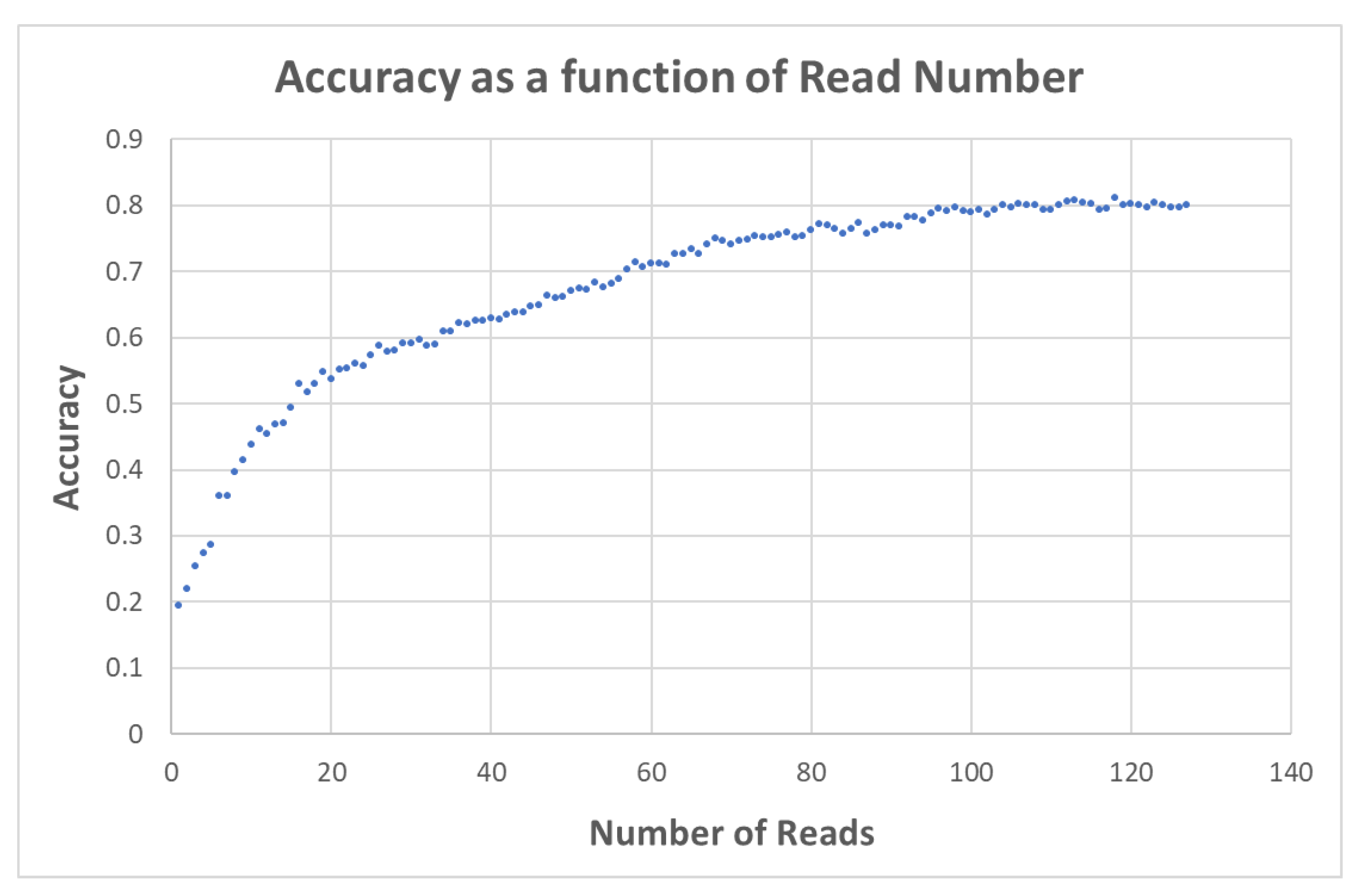
In both training and testing, every image was run 128 times, where in each of these “reads” a different set of control signals was fed into the cube along with the image (as shown in Figure 4). The full set of 128 output features was used in the logistic regression, with the resulting model then being applied to classify the test vectors, yielding the results in Figure 5. In order to assess the incremental value of each additional control signal we ran the logistic regression on an increasingly smaller subset of the output features (i.e., we simulated the outcome of a run where less control signals are used). The resulting data appears to indicate that there is no additional value in having more than about 100 control signals in the case of this dataset, as the accuracy appears to asymptote to about 80% (Figure 6). This approach to analysis of the overall performance is similar to using an ensemble of a machine—a set of similar machines.
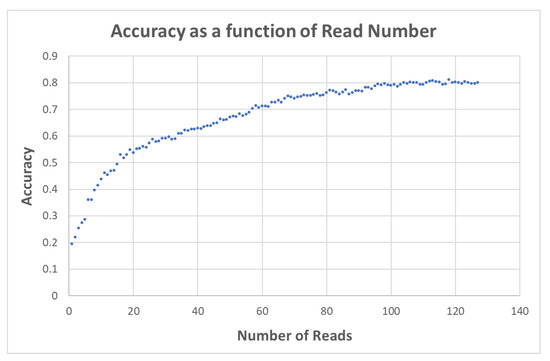
Figure 6.
Testing results increasing the number of reads (where each read of the input image is run along with a set of control signals) appears to increase prediction accuracy until about one hundred reads, beyond which the performance appears to stabilize.
As shown in Figure 5 and Figure 6, the total results are about 80% correct classification for all digits. While 80% is far from the state-of-the-art for a neural network (a simple perceptron with one hidden layer can achieve accuracy of >90%), it is surprisingly good given that the computation was done in a lump of unpoled PZT ceramic. We would argue that the “computation” taking place in the PZT cube is likely due to constructive and destructive interference, similar to a reservoir computer.
To develop an intuition on these results, and the possible dynamics inside the PZT cube, consider Figure 7. Figure 7a is a schematic of the system to describe the dynamics taking place in a PZT cube (see Figure 2 also). We assume the blue connections on the left are input and the blue connections in the right are outputs. The inputs will combine in a linear way and can be monitored on the outputs. However, when control signals are added to any of the control lines, they will act as a “scattering matrix,” U, and linearly combine with the inputs. Thus, effectively making the outputs a non-linear function of the inputs. The resulting output has been changed by the scattering matrix, and is no longer a linear relation of the inputs, but rather it is now a linear superposition of the inputs and the control signals.
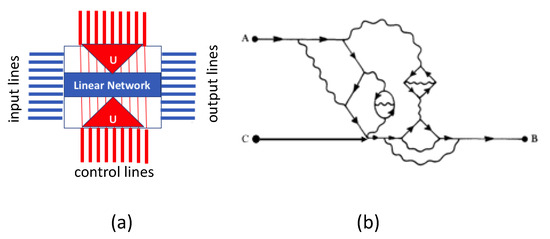
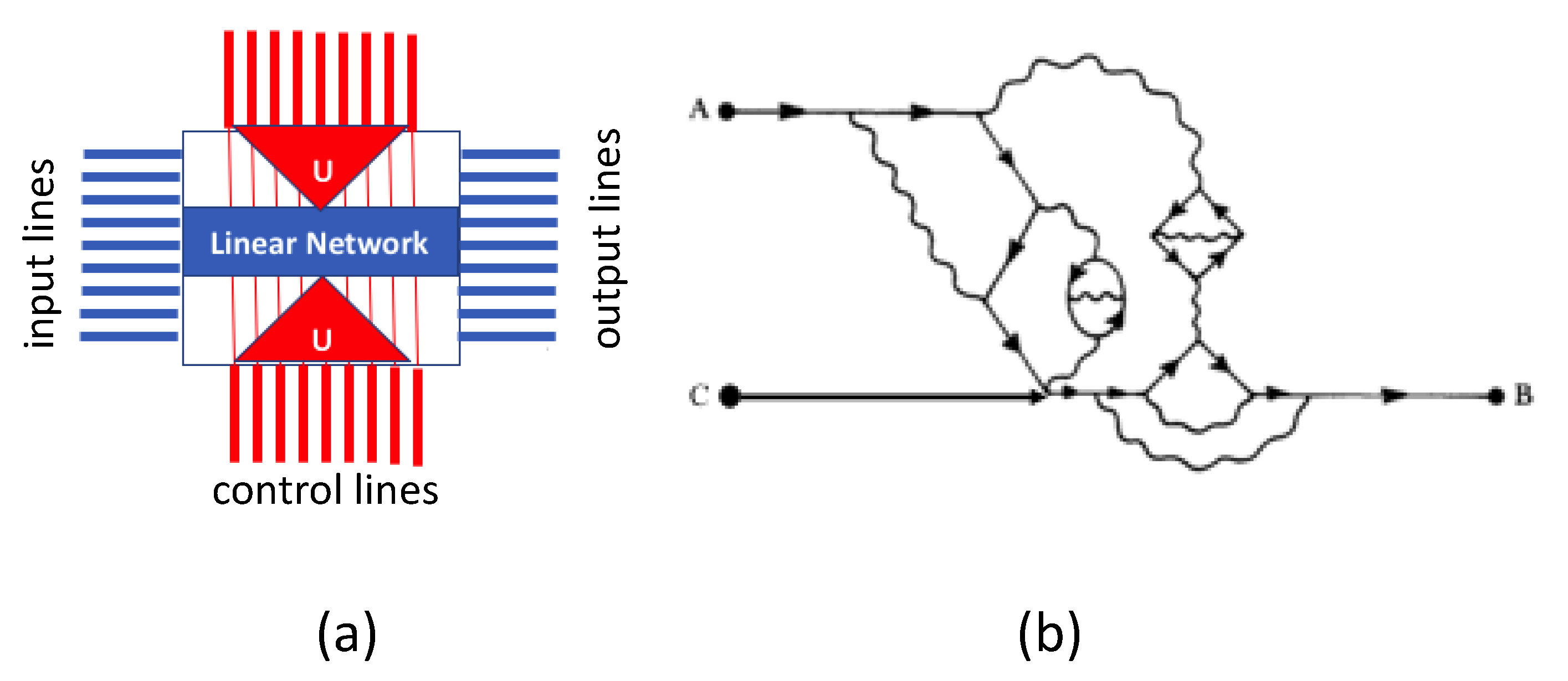
Figure 7.
The figure on the left (a) is schematic diagram to explain the dynamics of the I/O behavior of the PZT cube. Signals on the input lines are read out on the output lines where we observe a linear superposition of the inputs. When signals are applied to the control lines they act as a scattering matrix U, which scrambles the input in a controlled and reproducible way. The figure on the right (b) is an example of a Feynman diagram and simply represents the electron phonon scattering suggesting the type of complex dynamics taking place inside the cube at the nano-scale. Position A represents the input data, Position B represents the output data, and Position C represents the control signals. The figure on the right is modified and based on (Hofstadter 1979) [41].
The schematic of Figure 7b shows a “conjectured” Feynman diagram for the dynamics inside the PZT cube. In the figure, A is an input, B an output, and C is the control. In this case, it represents a complex interaction of electrons and phonons. It would be very difficult, to almost impossible at this time, to do a detailed modeling of the actual dynamics. That being said, we can develop some intuition of the internal dynamics. We first need to examine the crystal structure and the effects of applying an electric field to the crystal.
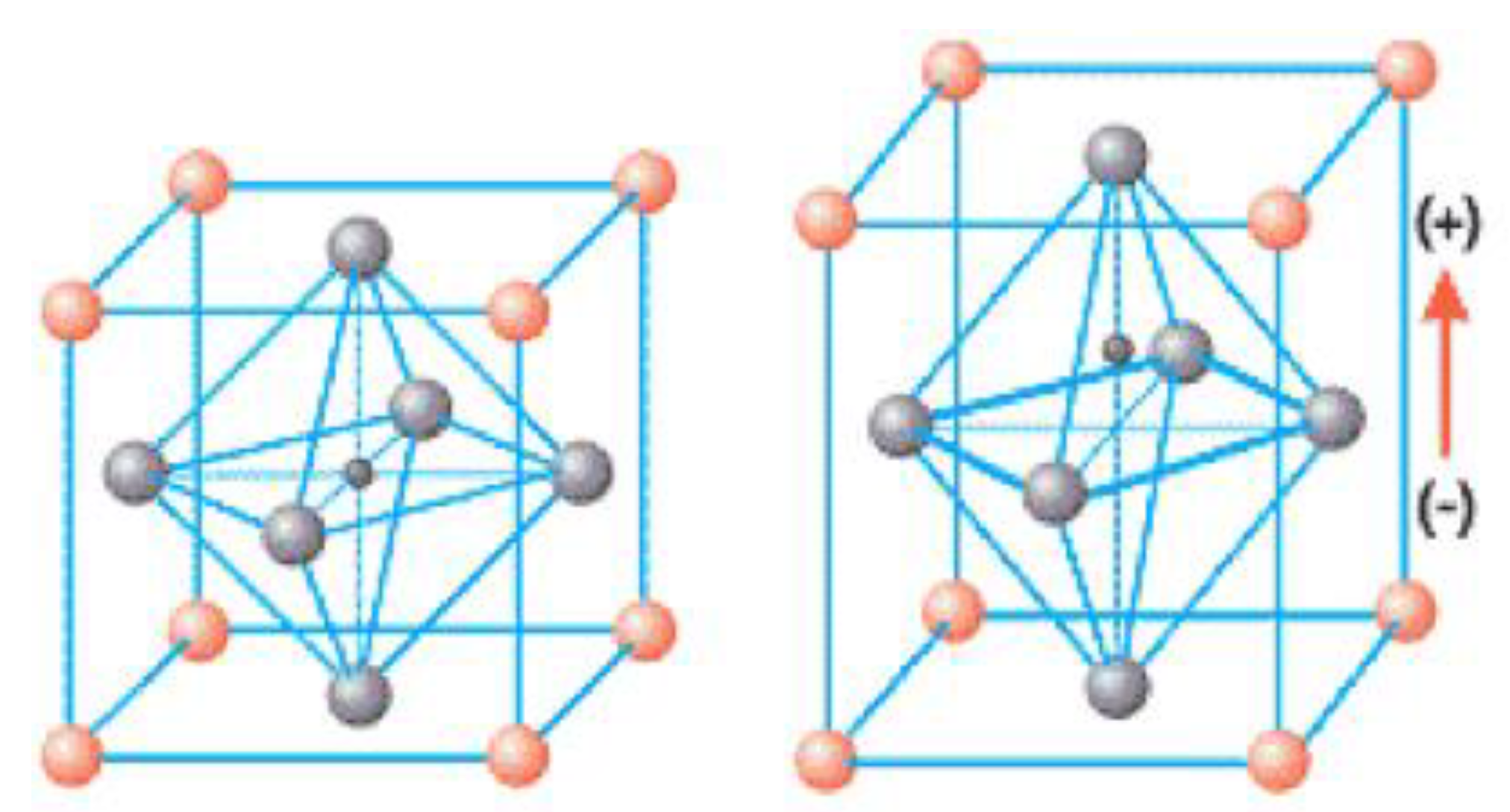
The crystal structure of lead zirconate titanate, a cubic perovskite lattice, is shown in Figure 8. On the left of the figure is seen a “relaxed” crystal of PZT. The lead atoms are on the vertices of a cubic lattice, the oxygen atoms are on the face-centers of the cubic lattice, and zirconium or titanium are in the body-center of the cubic lattice. With an overall stoichiometry for PZT given as: Pb[ZrxTi1-x]O3 with . On the right of the figure is seen a distorted crystal lattice. It is elongated by about 0.1% in the vertical direction when an electric field is applied. These distortions can be very accurately measured in X-ray diffraction (Esteves et al. 2016) [42].
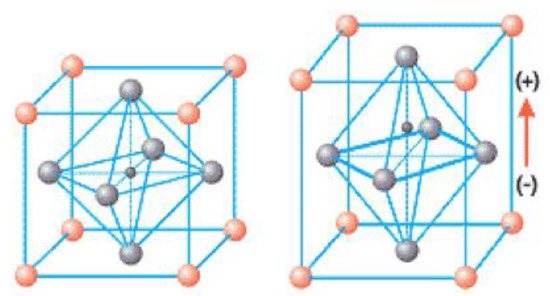
Figure 8.
The crystal structure of PZT. The red spheres are lead (Pb), the gray spheres are oxygen and the small black sphere in the center is titanium (Ti) or zirconium (Zr). When an electric field is applied, the crystal elongates by about 0.1% (shown on the right). The stoichiometry is Pb[ZrxTi1-x]O3 with . Figures used with permission from American Piezo®, Inc. [43].
Since the unpoled ceramic material we are using is comprised of micron-scale crystallites (i.e., single crystals), these crystallites are oriented at random. When an electric field is applied to the bulk unpoled ceramic, the crystallites will align in the field. While an AC signal is propagating through the PZT cube it will naturally form polarized regions of compression and expansion (see Figure 9) of the crystallites, and regions of rarefaction, analogous to a sound wave in a fluid medium. These distortions result in constructive and destructive interference and give rise to an overall linear superposition of the input and control signals at the output, thus enabling us to program the PZT cube as a reservoir network. See the Appendix for basic physics experiments.
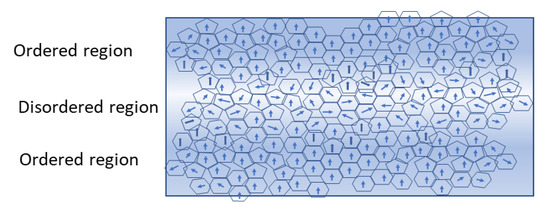
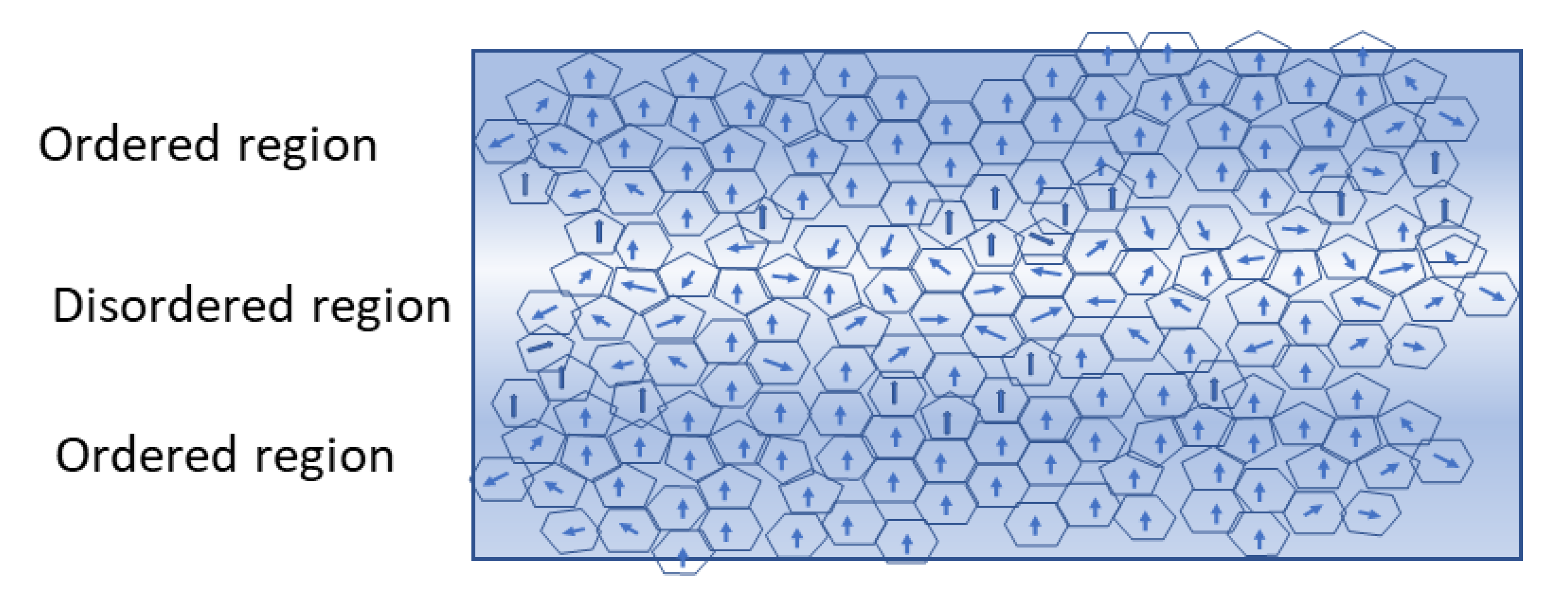
Figure 9.
This cartoon represents the regions of ordered crystallites where many of them are oriented in the same direction because if the lattice stretching shown in Figure 8. This would be analogous to a sound wave passing through a dense medium. The “computation” is thus the result of constructive and destructive interference between the data stream and the control stream. In the diagram we used mixed pentagons and hexagons to represent the ~1micron crystallites, and the gaps between them would represent interstitial regions in the compressed ceramic.
We also found that the results shown in Figure 5 and Figure 6 are reproducible from cube-to-cube. This allows us to exploit the device as a reproducible computation and obtain similar accuracy with the same parameter matrix θ. To be clear, we trained and tested on one PZT cube and tested on two other PZT cubes and obtained comparable results (+/−1%). However, we also found that poled PZT ceramic did not give reproducible accuracy. In effect, each was found to be unique when measuring the impedance spectrum, which suggests that the poled device could act as a physical unclonable function (i.e. a type of security device). This further suggests that poled cubes of PZT may be used as a secure computing component in a larger system. Details are given in the Appendix.
6. Conclusions and Future Work
In summary, we have introduced reservoir architecture as a possible way to exploit new quantum matter for computation. Because much work in programmable matter, or in-materio computation, starts with memristors, we described a similarity between memristors and piezoelectric materials. We have also shown a way to exploit bulk PZT for computation (MNIST digit recognition) and briefly pointed out that the poled PZT may be used for physical unclonable function applications. Lastly, we have described, through some analogies, the possible dynamics taking place inside the PZT cube.
As described above, this initial work was done with Arduino microcontrollers and each digit required about 4 s for processing each image (256-bit strings input and 256-bit strings read and converted from analog to digital). The entire run of the all the training and testing took almost 10 h. We are designing a new system controlled with an FPGA with on board high-speed memory and ADC. With the new system we will be able to process digits at about 100,000× faster. This will enable us to experiment with at-speed speech recognition and experiment with some of the ideas presented in Fujii and Nakajima [23].
Author Contributions
Conceptualization, E.R.; methodology, E.R. and L.S.; software, L.S. and A.S.; validation, M.A.; writing original draft, E.R.; review and editing M.A.; supervision, E.R. and H.S. All authors have read and agreed to the published version of the manuscript.
Funding
All the work described in this manuscript was funded through a DARPA grant W31P4Q-20-0002 managed by U.S. Army Contracting Office, Aviation & Missile Contracting Center. We thank Charlton Lewis, and Oney Soykal, at DARPA, for helpful discussions. The views expressed in this document are not necessarily those of DARPA, the US Army, or any branch of the US Government.
Data Availability Statement
Not applicable.
Acknowledgments
We gratefully thank the Artificial Intelligence Research Group in London, UK, for seed funding and Bill Aronson for asking tough questions. We further thank Peter DelMastro, Thomas Buckley, Qiangfei Xia, and Bart Lipkens for their helpful conversations.
Conflicts of Interest
We declare no conflict of interest.
Correction Statement
This article has been republished with a minor correction to the Acknowledgments. This change does not affect the scientific content of the article.
Appendix A
In this Appendix, we present two experimental results that exhibit some novel dynamical behavior that one cannot get from a simple metal oxide dielectric. The PZT ceramic is not a simple metal oxide. It is quantum matter.
All the data shown in the figures of this Appendix (Figure A1, Figure A2, Figure A3 and Figure A4) were taken with an HP4192A four probe impedance analyzer.
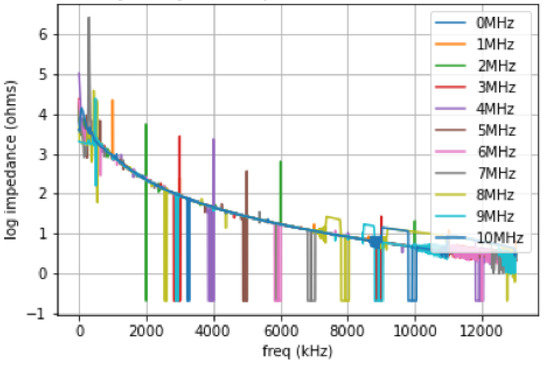
Figure A1.
See text for discussion.
Figure A1.
See text for discussion.
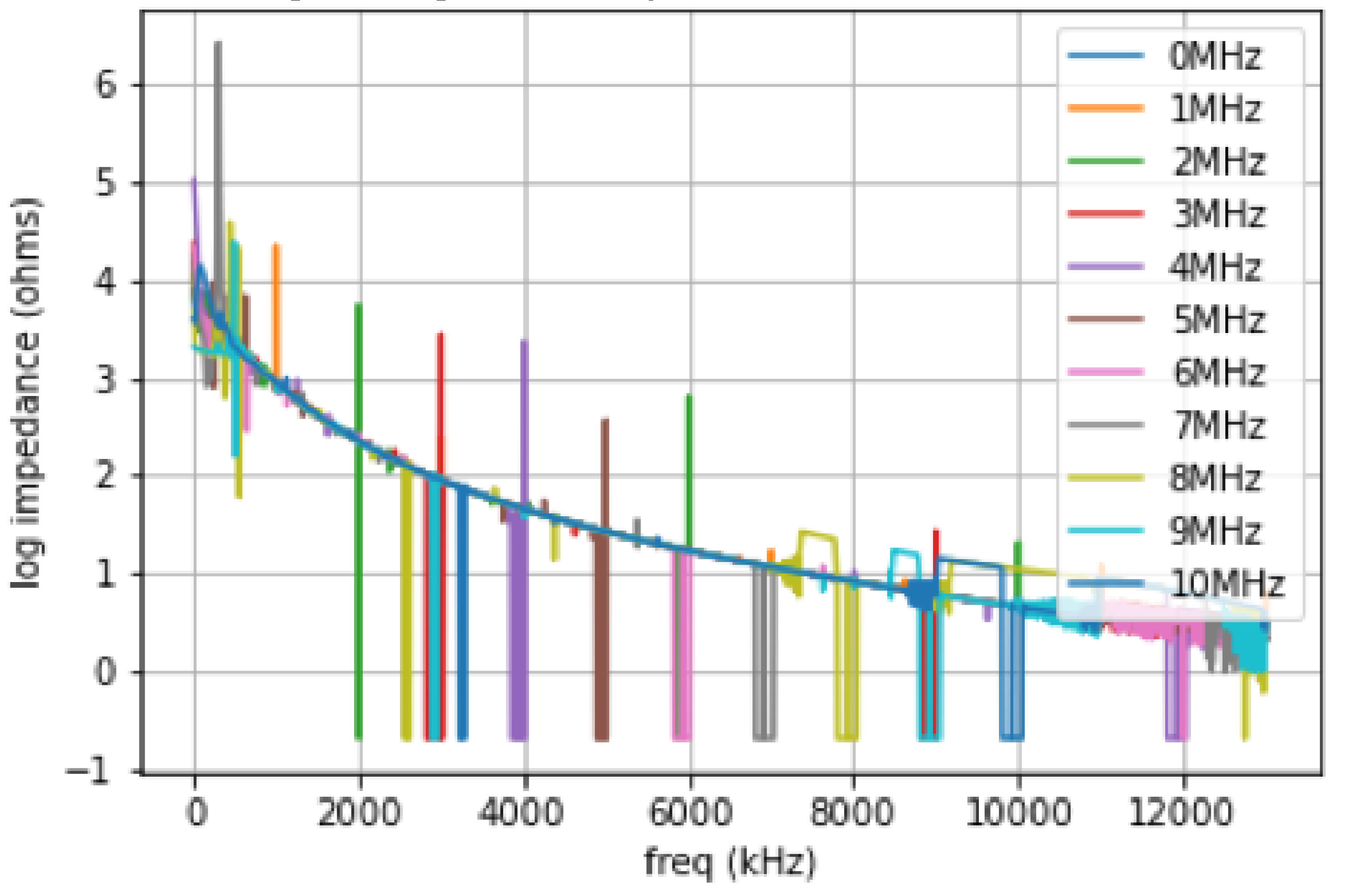
The data for Figure A1 was scanned from 10 kHz to 13 MHz. We attached each of the four probes: low current, low potential, high potential, high current to center pads B5, C5, D5, E5, respectively, on the PZT cube. We also connected pad A5 to a Tektronix AFG1022 function generator, where we could dial in set frequencies between 1 MHz and 10 MHz. square waves at 5 Vpp (volts peak to peak). In this experiment we observe resonances at various test frequencies. The traces are color coded. The 0 MHz trace corresponds to the frequency scan with the AFG1022 not sending a signal to the pad A5 on the cube. This corresponds to the expected results for a metal oxide dielectric—it looks like a capacitor. However, when we conduct the frequency scan from 10 kHz to 13 MHz, while sending a signal from the function generator (AFG1022) things are different! We observe sub- and super-harmonics. Notice that between 1 kHz and 1 MHz there are a bunch of sub-harmonics which are clearly resolved in Figure A2. Naturally one might ask, what about stochastic resonance? We set the AFG1022 to produce white noise but did not observe any differences from the baseline scan.
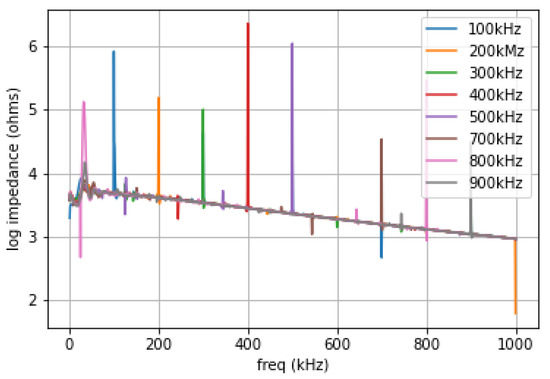
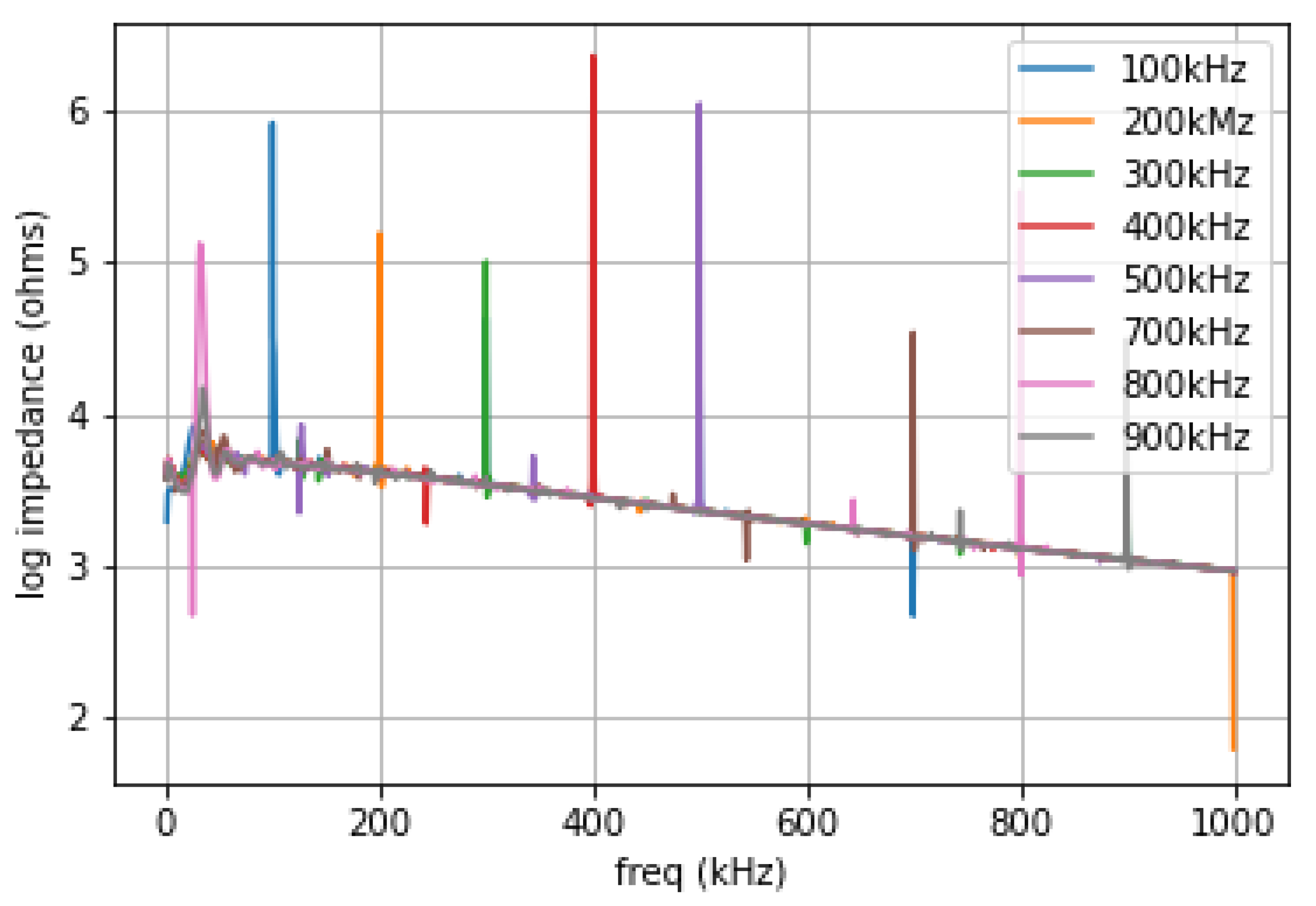
Figure A2.
Resolved sub-harmonics between 1 kHz and 1 MHz. Because this plot includes finer-scale resolution, we did not run the 10 MHz scan.
Figure A2.
Resolved sub-harmonics between 1 kHz and 1 MHz. Because this plot includes finer-scale resolution, we did not run the 10 MHz scan.
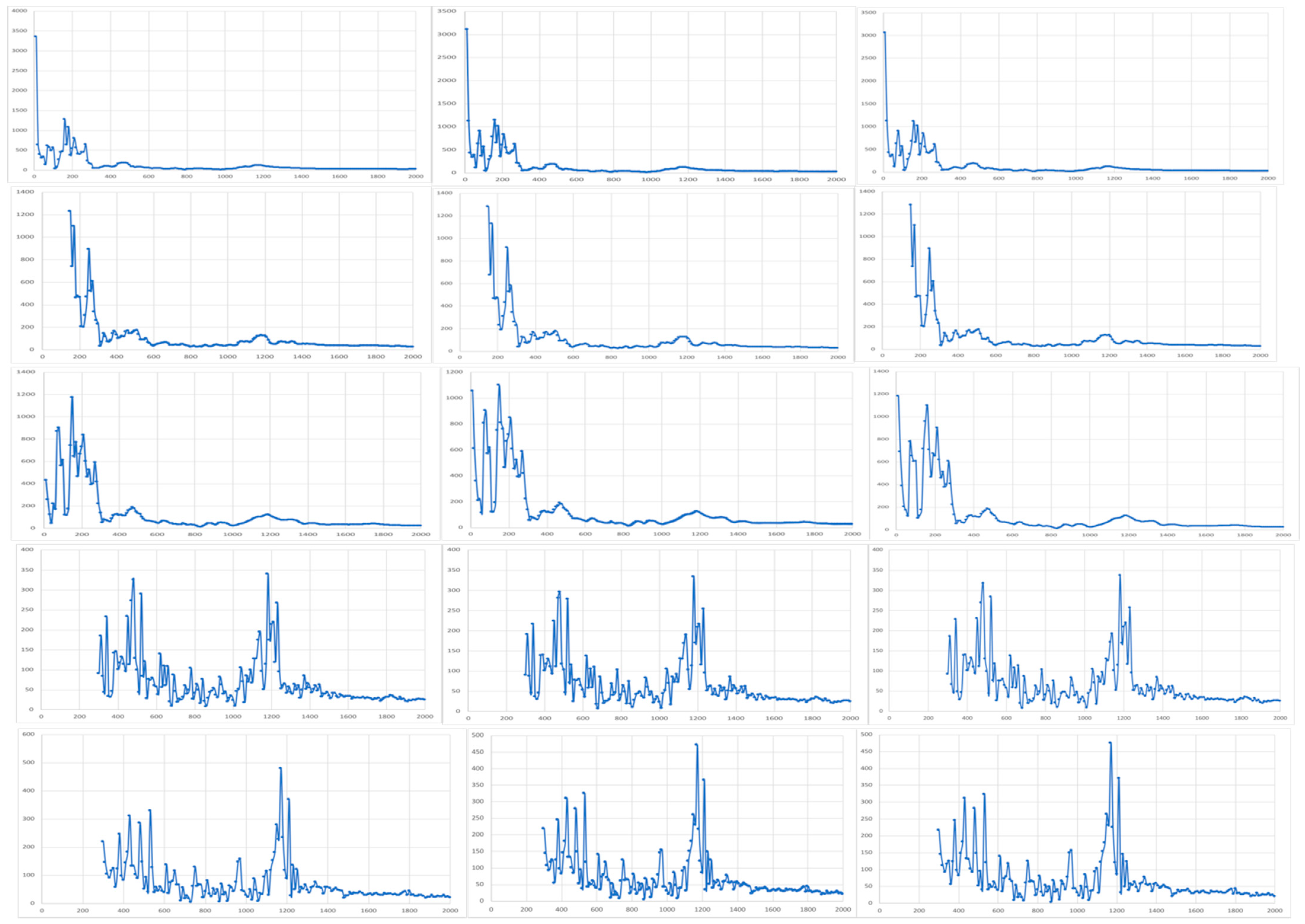
So, Figure A1 and Figure A2 show the impedance scans for unpoled PZT ceramic. Now we will look at poled PZT ceramic, again using the HP4192A but not injecting pulses from the AFG1022. Figure A3 shows the basic scan for a poled PZT sample. These resonance peaks are a result of the poling operation discussed in Section 3, Methods, and are a result of “freezing-in” the alignment of the distortions of the crystal lattice in the individual crystallites. Figure A4 shows five separate samples run in triplicate. These results suggest the poled PZT (or likely any piezoelectric, or even a ferroelectric) may be used as a physical unclonable function for secure computing.
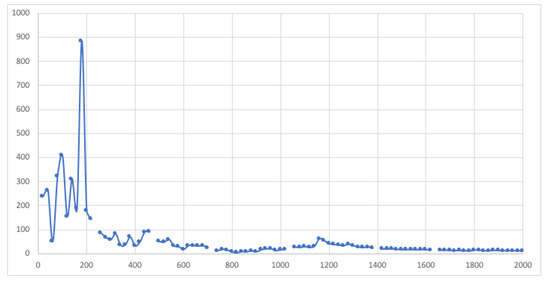
Figure A3.
A single scan enlarged, a fast scan. See text for discussion.
Figure A3.
A single scan enlarged, a fast scan. See text for discussion.
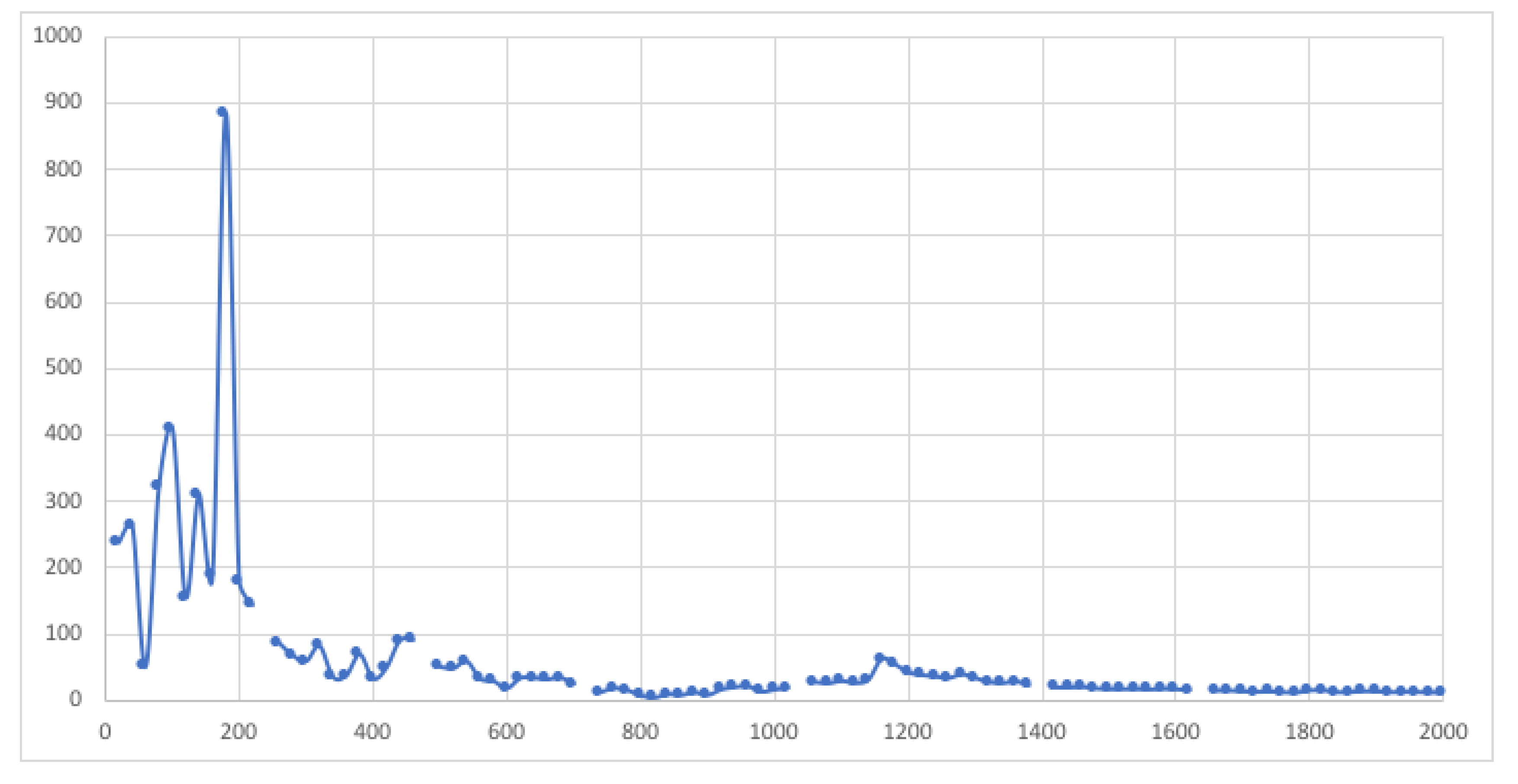
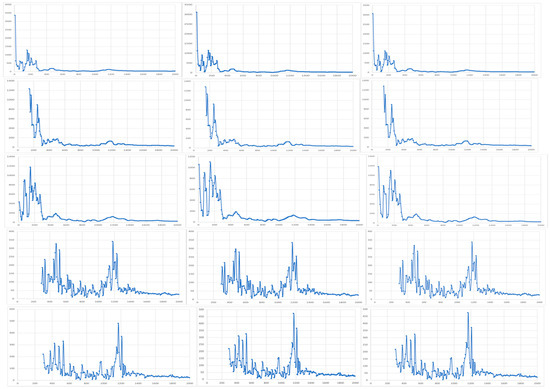
Figure A4.
Poled PZT ceramic may be used as a physical unclonable function for secure computing. Five runs in triplicate are shown above, where each sample was a different piece of ceramic. See text for discussion.
Figure A4.
Poled PZT ceramic may be used as a physical unclonable function for secure computing. Five runs in triplicate are shown above, where each sample was a different piece of ceramic. See text for discussion.
References
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002; pp. 715–846. [Google Scholar]
- Available online: https://mathworld.wolfram.com/PrincipleofComputationalEquivalence.htmlMathWorld (accessed on 14 September 2022).
- Holden, A.V.; Tucker, J.V.; Thompson, B.C. Can excitable media be considered as computational systems? Phys. D 1991, 49, 240–246. [Google Scholar] [CrossRef]
- Stepney, S. The neglected pillar of material computation. Phys. D 2008, 237, 1157–1164. [Google Scholar] [CrossRef]
- Stepney, S. Non-Classical Hypercomputation. Int. J. Unconv. Comput. 2009, 5, 267–276. [Google Scholar]
- Dale, M.; Miller, J.F.; Stepney, S. Reservoir Computing as a model for in-materio computing. In Advances in Unconventional Computing; Adamatzky, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 533–571. [Google Scholar]
- Stepney, S. Programming unconventional computers: Dynamicss, development, self-reference. Entropy 2012, 14, 1939–1952. [Google Scholar] [CrossRef]
- Sangiorgi, D. The Pi-Calculus: A Theory of Mobile Processes; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Calude, C.S.; Casti, J.; Dinneen, M.J. Unconventional Models of Computation; Springer: Singapore, 1998. [Google Scholar]
- Amamatzky, A. Computing in Nonlinear Media and Automata Collectives; Institute of Physics: Bristol, UK, 2001. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; pp. 249–251; 368–384. [Google Scholar]
- Maass, W.; Natschlager, T.; Markram, H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural. Comput. 2002, 14, 2531–2560. [Google Scholar] [CrossRef] [PubMed]
- Fernando, C.; Sojakka, S. Pattern Recogntion in a bucket. European Conference on Artificial Life; Springer: Berlin, Germany, 2003; pp. 588–597. [Google Scholar]
- Hughes, T.W.; Williamson, I.A.D.; Minkov, M.; Fan, S. Wave physics as an analog recurrent neural network. Sci. Adv. 2019, 5, eaay6946. [Google Scholar] [CrossRef]
- Versteaeten, D.; Schrauwen, B.; D’Haene, M.; Stroobandt, D. An experimental unification of reservoir computing methods. Neural Netw. 2007, 20, 391–403. [Google Scholar] [CrossRef]
- Dale, M.; Miller, J.F.; Siepney, S.; Trefzer, M.A. A Substrate-indepenndent framework to characterize reservoir computers. Proc. R. Soc. A 2019, 475, 20180723. [Google Scholar] [CrossRef]
- Markovic, D.; Grollier, J. Quantum neuromorphic computing. App. Phys. Lett. 2020, 117, 150501. [Google Scholar] [CrossRef]
- Wittek, P. Quantum Machine Learning: What Quantum Computing Means to Data Mining; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Ghosh, S.; Opala, A.; Matuszewskim, M.; Paterek, T.; Leiw, T.C.H. Quantum reservoir processing. njp Quant. Inf. 2019, 5, 35. [Google Scholar] [CrossRef]
- Ghosh, S.; Nakajima, K.; Krisnanda, T.; Fujii, K.; Liew, T.C.H. Quantum Neuromorphic with Reservoir Conputing Networks. Adv. Quant. Technol. 2021, 4, 2100053. [Google Scholar] [CrossRef]
- Fujii, K.; Nakajima, K. Quantum Reservoir Computing: A Reservoir Approach Toward Quantum Machine Learning on Nearterm Quantum Devices; Nakajima, K., Fischer, I., Eds.; Reserivor Computing; Natural Computing Series; Springer: Singapore, 2021; pp. 423–450. [Google Scholar]
- Ghosh, S.; Krisnadna, T.; Paterek, T.; Liew, T.C.H. Realising and compressing quantum circuits with quantum reservoir computing. Commun Phys. 2021, 4, 105. [Google Scholar] [CrossRef]
- Fujii, K.; Nakajima, K. Harnessing disidered-ensemble quantum dynamics for machine learning. Phys. Rev. App. 2017, 8, 024030. [Google Scholar] [CrossRef]
- Lichtenberg, A.J.; Liberman, M.A. Regular and Chaotic Dynamics; Springer: New York, NY, USA, 1991; pp. 603–604. [Google Scholar]
- Negoro, M.; Mitarai, K.; Fujii, K.; Nakajima, K.; Kitagawa, M. Machine Learning with controllable quantum dynamics of a nuclear spin ensemble in a solid. arXiv 2018, arXiv:2018.10910. [Google Scholar]
- Tran, Q.H.; Nakajima, K. Higher-order quantum reservoir computing. arXiv 2020, arXiv:2006.08999. [Google Scholar]
- Lloyd, S. A potentially realizable quantum computer. Science 1993, 261, 1569–1571. [Google Scholar] [CrossRef]
- Lloyd, S. Programming pulse driven quantum computers. arXiv 1999, arXiv:quant-ph/9912086v1. [Google Scholar]
- Wolfram, S. Stastical mechanics of cellular automata. Rev. Mod. Phys. 1983, 55, 601–644. [Google Scholar] [CrossRef]
- Carrasquila, J. Machine learning for quantum matter. Adv. Phys. X 2020, 5, 179528. [Google Scholar] [CrossRef]
- Marsden, H. Quantum Information and Algorithms for Correlated Quantum Matter. Chem. Rev. 2021, 121, 3061–3120. [Google Scholar] [CrossRef]
- Available online: https://oqmd.org/materials/composition/PbZrTiO3QuantumMatter (accessed on 15 September 2022).
- Ukil, A. Memristance View of Piezoelectricity. IEEE Sens. J. 2011, 11, 2514–2517. [Google Scholar] [CrossRef]
- Chua, L.O. Memristor—the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Chua, L.O. Resistance switching memories are memristors. Appl. Phys. A 2011, 102, 765–783. [Google Scholar] [CrossRef]
- Strokov, D.B.; Snyder, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Lee, S.; Park, J.-B.; Lee, M.-J.; Boland, J.J. Multilevel resistance in ZnO nanowire memristors enabled by hydrogen annealing treatment. AIP Adv. 2016, 6, 125010. [Google Scholar] [CrossRef]
- Sillin, H.O.; Aguilera, R.; Shieh, H.-H.; Aviziens, A.V.; Aono, M.; Stieg, A.Z.; Gimzewski, J.K. A theoretical and experimental study of neuromorphic atomic switch networks for reservoir computing. Nanotechnology 2013, 24, 3384004. [Google Scholar] [CrossRef]
- Available online: http://www.pymvpa.org/datadb/mnist.html#:~:text=The%20MNIST%20dataset%20of%20handwritten%20digits%2C%20available%20from%20this%20page,in%20a%20fixed%2Dsize%20imageMNISTDatabase (accessed on 17 May 2022).
- Moon, B.; Jagadish, H.V.; Faloutsos, C.; Saltz, J.H. Analysis of the clustering properties of the Hilbert space-filling curve. IEEE Trans. Knowl. Data Eng. 2001, 13, 124–141. [Google Scholar] [CrossRef]
- Hofstadter, D.R. Gödel, Escher, Bach: An Eternal Golden Braid; Basic Books: New York, NY, USA, 1979; p. 145. [Google Scholar]
- Esteves, G.; Fancher, C.M.; Wallace, M.; Johnson-Wilke, R.; Wilke, R.H.; Trolier-McKinstry, S.; Jones, J.L. In situ X-ray Diffraction of Lead Zirconate Titanate PiezoMEMS Cantilever During Actuation. Mater. Des. 2016, 111, 429–434. [Google Scholar] [CrossRef]
- Available online: https://www.americanpiezo.com/blog/ceramic-manufacturing-series-poling-pzt-ceramics/AmericanPiezo (accessed on 10 May 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).