Modelling of a Large Solar PV Facility: England’s Mallard Solar Farm Case Study
Abstract
:1. Introduction
2. System Parameters under Investigation
2.1. Mode of Operation: Fixed versus East–West Tracking and Location Dependence
cos θ = (1 − cos2 δ sin2 ω)0.5
2.2. Near-Horizon Energy Gain with High or Low Reflectance
2.3. Monofacial versus Bifacial Modules
3. Case Study—The Mallard Pass Solar Farm Project
4. Modelling
4.1. Modelling of PV Module Tracking Modes
Modelling the Effect of Location—Tropics versus Higher Latitudes
4.2. Modelling the Near-Horizon Energy Gain with High or Low Reflectance
4.2.1. Energy Exchange from the Ground to PV Modules of Fixed Inclination
4.2.2. Energy Exchange from the Sky to East–West Tracking PV Modules
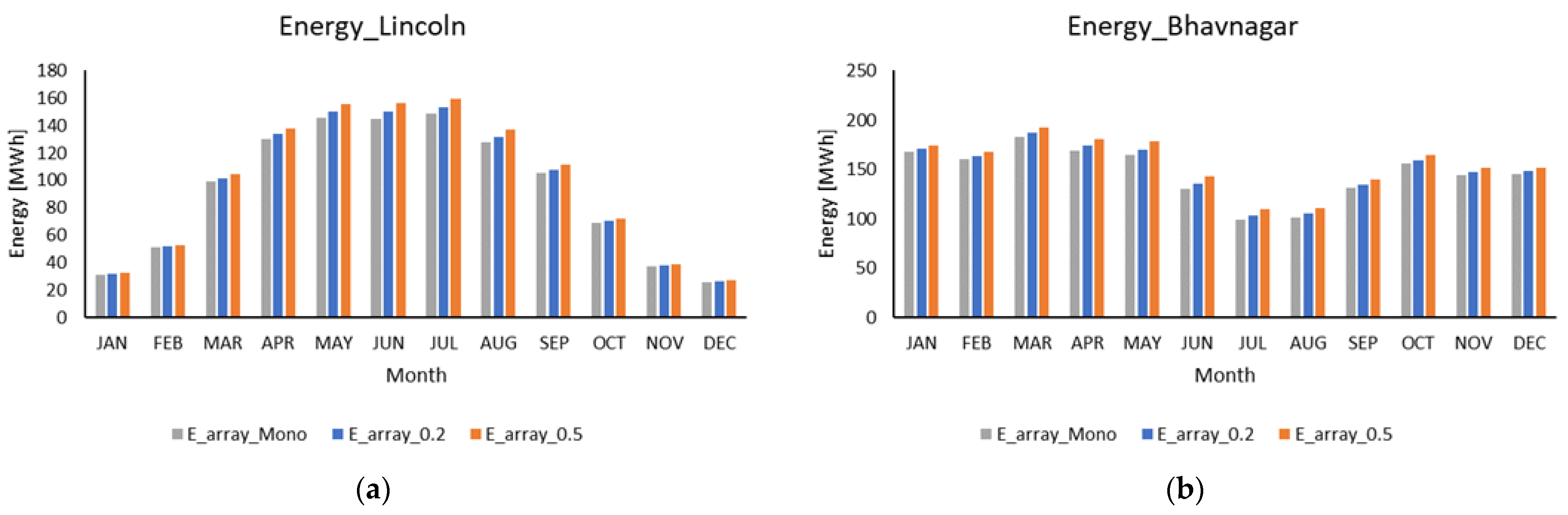
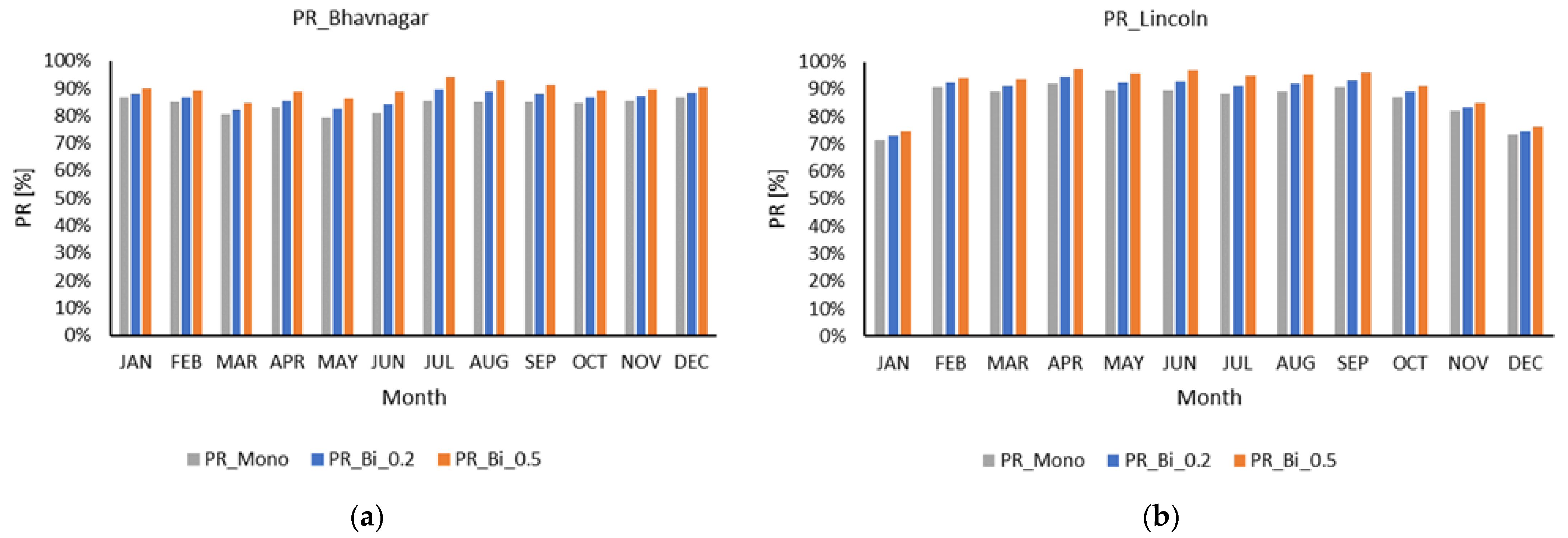
4.3. Modelling and Comparison of Monofacial and Bifacial Modules
4.3.1. Simulation Platform
4.3.2. Assessment of Solar Resource
4.3.3. Simulation Parameters
5. Simulation Output
6. Economic Assessment
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Mallard Pass Solar Farm. Preliminary Environmental Information Report Chapter 1–7; 2022. Available online: https://infrastructure.planninginspectorate.gov.uk/wp-content/ipc/uploads/projects/EN010127/EN010127-000012-Mallard%20Pass%20EIA%20Scoping%20Report%20Appendices.pdf (accessed on 1 September 2022).
- Gov.UK. Policy paper: British Energy Security Strategy. 2022. Available online: https://www.gov.uk/government/publications/british-energy-security-strategy/british-energy-security-strategy (accessed on 2 September 2022).
- Vagiona, D.G. Comparative Multicriteria Analysis Methods for Ranking Sites for Solar Farm Deployment: A Case Study in Greece. Energies 2021, 14, 8371. [Google Scholar] [CrossRef]
- Thabet, A.; Abdelhady, S.; Mobarak, Y. Design modern structure for heterojunction quantum dot solar cells. Int. J. Electr. Comput. Eng. (IJECE) 2020, 10, 2918–2925. [Google Scholar] [CrossRef]
- Thabet, M.A.; Abdelhady, S. Strategy trends of core/multiple shell for quantum dot-based heterojunction thin film solar cells. Aust. J. Electr. Electron. Eng. 2022, 19, 203–218. [Google Scholar] [CrossRef]
- Guerrero-Lemus, R.; Vega, R.; Kim, T.; Kimm, A.; Shephard, L.E. Bifacial solar photovoltaics—A technology review. Renew. Sustain. Energy Rev. 2016, 60, 1533–1549. [Google Scholar] [CrossRef]
- Alam, M.; Gul, M.S.; Muneer, T. Ground view factor computation model for bifacial photovoltaic collector field: Uniform and non-uniform surfaces. Energy Rep. 2021, 7, 9133–9149. [Google Scholar] [CrossRef]
- Roddis, P.; Roelich, K.; Tran, K.; Carver, S.; Dallimer, M.; Ziv, G. What shapes community acceptance of large-scale solar farms? A case study of the UK’s first ‘nationally significant’ solar farm. Solar Energy 2020, 209, 235–244. [Google Scholar] [CrossRef]
- Machlev, R.; Batushansky, Z.; Soni, S.; Chadliev, V.; Belikov, J.; Levron, Y. Verification of Utility-Scale Solar Photovoltaic Plant Models for Dynamic Studies of Transmission Networks. Energies 2020, 13, 3191. [Google Scholar] [CrossRef]
- Gul, M.S.; Puxty, D. Are Bifacial Photovoltaics a Sustainable Alternative to Monofacial Photovoltaics? CESC Res. Bull. 2021, 4. Available online: https://issuu.com/heriot-watt_university_dubai/docs/cesc_bulletin_4_september_2021 (accessed on 25 October 2022).
- VDMA. International Technology Roadmap for Photovoltaic, 11th ed.; ITRPV: Frankfurt am Main, Germany, 2020; p. 76. [Google Scholar]
- Recharge. Spanish renewables giant Iberdrola switches on Europe’s largest solar plant. 2022. Available online: https://www.rechargenews.com/energy-transition/spanish-renewables-giant-iberdrola-switches-on-europes-largest-solar-plant/2-1-1275686/ (accessed on 1 October 2022).
- Krechowicz, M.; Krechowicz, A.; Lichołai, L.; Pawelec, A.; Piotrowski, J.Z.; Stepien, A. Reduction of the Risk of Inaccurate Prediction of ElectricityGeneration from PV Farms Using Machine Learning. Energies 2022, 15, 4006. [Google Scholar] [CrossRef]
- Bazyari, S.; Keypour, R.; Farhangi, S.; Ghaedi, A.; Bazyari, K. A Study on the Effects of Solar Tracking Systems on the Performance of Photovoltaic Power Plants. J. Power Energy Eng. 2014, 2, 718–728. [Google Scholar] [CrossRef]
- Al Ami, A.; Batista, R. Performance Analysis of a Large Scale Photovoltaic Solar Grid Connected System. In Proceedings of the 34th IEEE Photovoltaic Specialists Conference (PVSC), Philadelphia, PA, USA, 7–12 June 2009. [Google Scholar]
- Guo, Y.Z.; Cha, J.Z.; Liu, W.; Tian, Y.B. A System Modeling Method for Optimisation of a Single Axis Solar Tracker. ICCASM 2010, 11, 11–30. [Google Scholar]
- Belt Rán, J.A.; González Rubio, J.L.; García-Beltrán, S.y.C.D. Design, Manufacturing and Performance Test of a Solar Tracker Made by a Embedded Control. In Proceedings of the Electronics, Robotics and Automotive Mechanics Conference (CERMA 2007), Cuernavaca, Mexico, 25–28 September 2007. [Google Scholar]
- Boicea, A.V.; Di Leo, P.; Graditi, G.; Spertino, F. Comparison of Operating Parameters in Grid Connected Photovoltaic Systems with Single/Double Sun-Trackers at Different Latitudes. In Proceedings of the SPEEDAM 2010, Pisa, Italy, 14–16 June 2010; pp. 130–133. [Google Scholar] [CrossRef]
- PV Magazine. Project to build 1.4 GW high-voltage cable linking Germany with the UK moves forward. 2022. Available online: https://www.pv-magazine.com/2022/07/22/project-to-build-1-4-gw-high-voltage-cable-linking-germany-with-the-uk-moves-forward/ (accessed on 1 July 2022).
- Colasante, A.; D’Adamo, I.; Morone, P. What drives the solar energy transition? The effect of policies, incentives and behavior in a cross-country comparison. Energy Res. Soc. Sci. 2022, 85, 102405. [Google Scholar] [CrossRef]
- Sukhatme, S.P. Solar Energy: Principles of Thermal Collection and Storage, 2nd ed.; Tata McGraw-Hill: Delhi, India, 1996. [Google Scholar]
- Liu, B.Y.; Jordan, R.C. The long-term average performance of flat-plate solar-energy collectors: With design data for the U.S., its outlying possessions and Canada. Sol. Energy 1963, 7, 53–74. [Google Scholar] [CrossRef]
- Kotak, Y.; Gul, M.S.; Muneer, T.; Ivanova, S.M. Investigating the Impact of Ground Albedo on the Performance of PV Systems. In Proceedings of the CIBSE Technical Symposium, London, UK, 16–17 April 2015. [Google Scholar]
- Gul, M.; Kotak, Y.; Muneer, T.; Ivanova, S. Enhancement of albedo for solar energy gain with particular emphasis on overcast skies. Energies 2018, 11, 2881. [Google Scholar] [CrossRef] [Green Version]
- Hay, J.E.; McKay, D.C. Estimating Solar Irradiance on Inclined Surfaces, A Review and Assessment of Methodologies. Int. J. Sol. Energy 1985, 3, 203–240. [Google Scholar] [CrossRef]
- Mani, A. Handbook of Solar Radiation Data for India; Allied Publishers Private Limited: Delhi, India, 1981. [Google Scholar]
- Hawas, M.; Muneer, T. Study of diffuse and global radiation characteristics for India. Energy Convers. Manag. 1984, 24, 143. [Google Scholar] [CrossRef]
- Feingold, A. Radiant interchange configuration factors between various selected plane surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. 1966, 292, 51–60. [Google Scholar]
- Mermoud, A.; Wittmer, B. Yield simulation for horizontal axis trackers with bifacial PV module in PVSyst. In Proceedings of the 35th European Photovoltaic Solar Energy Conference, Brussels, Belgium, 24–28 September 2018. [Google Scholar]
- Iqbal, M. An Introduction to Solar Radiation, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Perez, R.; Ineichen, P.; Seals, R.; Michalsky, J.; Stewart, R. Modeling daylight availability and irradiance components from direct and global irradiance. Sol. Energy 1990, 44, 271–289. [Google Scholar] [CrossRef]
- International Energy Agency. Bifacial Photovoltaic Modules and Systems: Experience and Results from International Research and Pilot Applications; Report IEA-PVPS T13-14:2021; International Energy Agency: Paris, France, 2021.
- CEA. 2022. Available online: https://www.cea3.com/cea-blog/lcoe-of-monofacial-vs-bifacial-modules-are-bifacials-worth-the-extra-cost (accessed on 1 November 2022).
- SEforALL. Sustainable Development Goal 7 (SDG7). 2021. Available online: https://www.seforall.org/sustainable-development-goal-7-sdg7#:~:text=SustainableDevelopmentGoal7(SDG7)callsfor“affordable%2C,reliableandmodernenergyservices (accessed on 1 November 2022).


| LINCOLN | M III, Beam | M III, Total | M V, Beam | M V, Total | Fixed Slope | M III/Fixed Slope |
|---|---|---|---|---|---|---|
| January | 449 | 811 | 1071 | 1349 | 1069 | 0.76 |
| March | 1982 | 3219 | 2717 | 3792 | 3295 | 0.98 |
| May | 4070 | 6120 | 4427 | 6385 | 5493 | 1.11 |
| July | 3508 | 5718 | 3765 | 5892 | 5211 | 1.10 |
| September | 2248 | 3692 | 2882 | 4173 | 3731 | 0.99 |
| November | 532 | 962 | 1177 | 1513 | 1245 | 0.77 |
| 2132 | 3420 | 2673 | 3851 | 3341 | 1.02 | |
| BHAVNAGAR | M III, Beam | M III, Tot | M V, Beam | M V, Tot | Fixed Slope | |
| January | 4300 | 5709 | 5426 | 6694 | 5633 | 1.01 |
| March | 6088 | 7740 | 3446 | 8051 | 6824 | 1.13 |
| May | 2067 | 4445 | 2083 | 4457 | 3964 | 1.12 |
| July | 2791 | 5025 | 2880 | 5076 | 4568 | 1.10 |
| September | 3830 | 5364 | 4689 | 6087 | 5265 | 1.02 |
| November | 5847 | 6828 | 7146 | 8047 | 6536 | 1.04 |
| 4154 | 5852 | 4278 | 6402 | 5465 | 1.07 |
| a | |||||
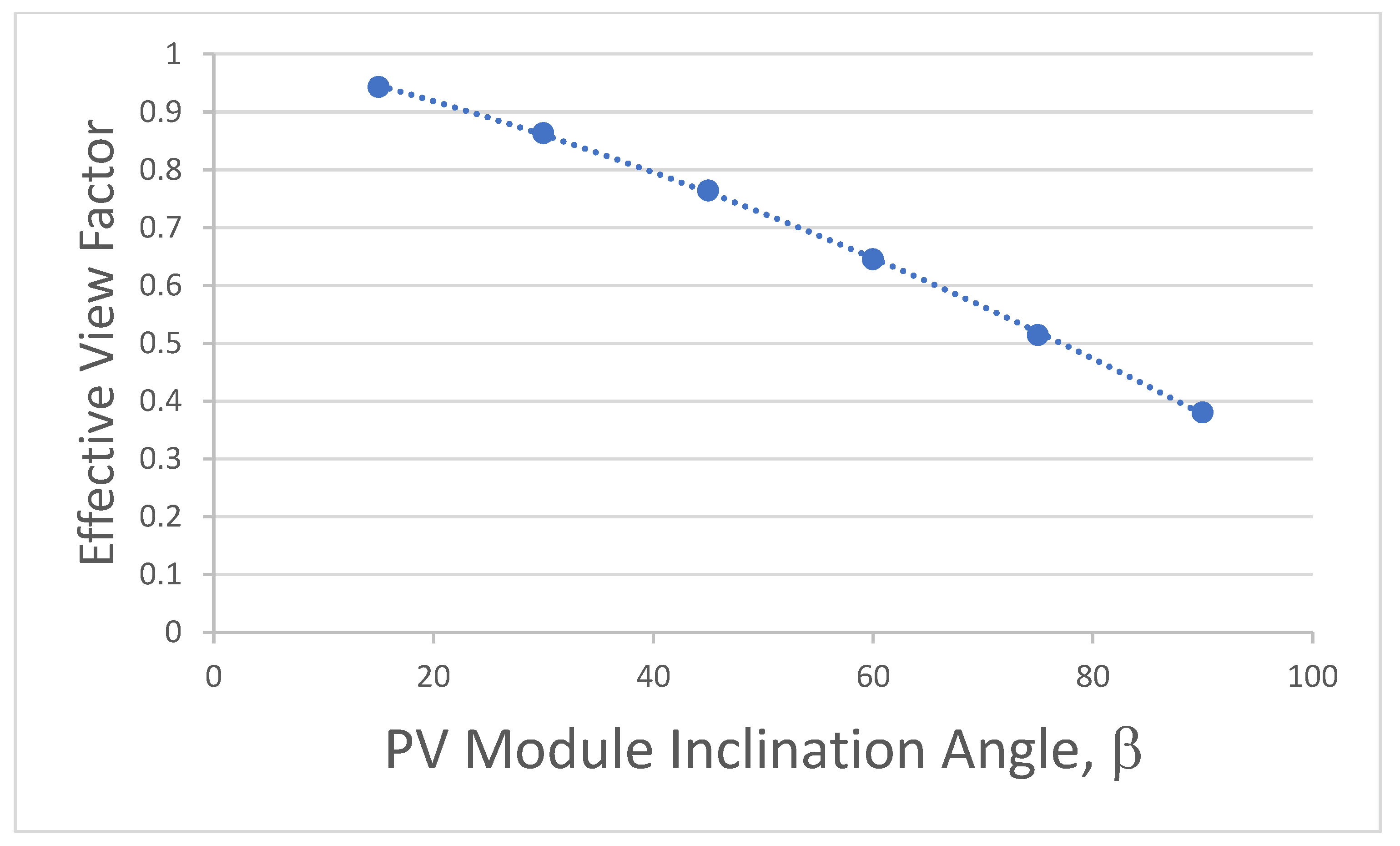
| β, Degrees | View Factor | ||||
| 15 | 0.040 | ||||
| 30 | 0.070 | ||||
| 45 | 0.090 | ||||
| 60 | 0.105 | ||||
| 75 | 0.115 | ||||
| 90 | 0.120 | ||||
| b | |||||
| β | VF1 | Effective VF | |||
| 15 | 0.040 | 0.943 | |||
| 30 | 0.070 | 0.863 | |||
| 45 | 0.090 | 0.764 | |||
| 60 | 0.105 | 0.645 | |||
| 75 | 0.115 | 0.514 | |||
| 90 | 0.120 | 0.380 | |||
| Site Location | Lincoln | Bhavnagar |
|---|---|---|
| Available solar resources | ||
| Global horizontal irradiance (kWh/m2) | 1026 | 1846 |
| Diffuse horizontal irradiance (kWh/m2) | 549 | 878 |
| Global tilted irradiance (kWh/m2) | 1207 | 1991 |
| Ground reflection on the rear side (kWh/m2) | 109 | 200 |
| Average ambient temperature (°C) | 10.13 | 27.33 |
| PV system components | ||
| Module manufacturer | JA Solar | JA Solar |
| Module power (kWp) | 540 | 540 |
| No. of modules | 1856 | 1856 |
| Inverter manufacturer | SMA | SMA |
| Inverter capacity (kWp) | 100 | 100 |
| No. of inverters | 9 | 9 |
| Simulation output | ||
| Total installed capacity (kWp) | 1002 | 1002 |
| Declared net capacity (kWac) | 900 | 900 |
| Specific yield (kWh/kWp/year) | 1132 | 1778 |
| Generation (MWh/year) | 1134 | 1782 |
| Performance ratio (PR) | 93.80% | 89.28% |
| P10 * (MWh) | 1184.1 | 1852.7 |
| P50 (MWh) | 1134 | 1,782 |
| P90 (MWh) | 1084.7 | 1,712 |
| Monofacial | Bifacial | |
|---|---|---|
| Module cost, USD/W | 0.305 | 0.315 |
| Energy index, kWh/kW/year | 1629 | 1650 |
| Generated energy over 25 years, GWh | 191 | 193.4 |
| LCOE, USD/kWh | 0.0224 | 0.0222 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muneer, T.; Gul, M.S.; Alam, M. Modelling of a Large Solar PV Facility: England’s Mallard Solar Farm Case Study. Energies 2022, 15, 8609. https://doi.org/10.3390/en15228609
Muneer T, Gul MS, Alam M. Modelling of a Large Solar PV Facility: England’s Mallard Solar Farm Case Study. Energies. 2022; 15(22):8609. https://doi.org/10.3390/en15228609
Chicago/Turabian StyleMuneer, Tariq, Mehreen Saleem Gul, and Marzia Alam. 2022. "Modelling of a Large Solar PV Facility: England’s Mallard Solar Farm Case Study" Energies 15, no. 22: 8609. https://doi.org/10.3390/en15228609








