Electric Double Layer: The Good, the Bad, and the Beauty
Abstract
:1. Introduction
2. Electrochemical Double Layer—Definition and Classical Models
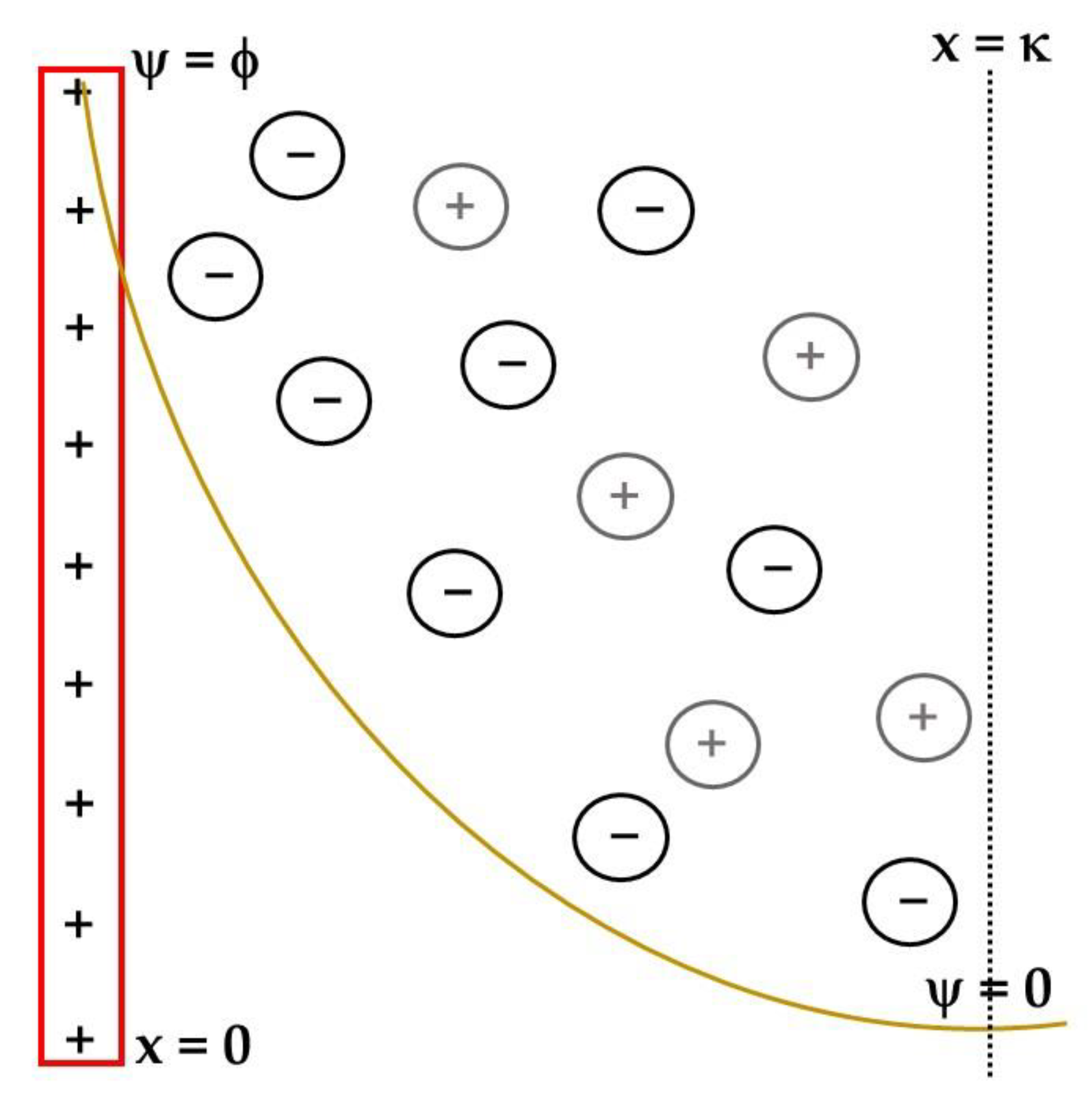
- EDL is a natural phenomenon caused by the interfacial region between the solid electrode and the ionic conducting electrolyte;
- Its most complete modeling considers that the electrode surface charge compensation happens in two layers, a rigid one that can be divided in two sub-layers, IHP (mostly solvent) and OHP (mostly solvated ions compensating the electrode charge) and the diffuse layer;
- The EDL potential drops linearly in the rigid layer and exponentially in the diffuse one.
3. Electrochemistry in the Game
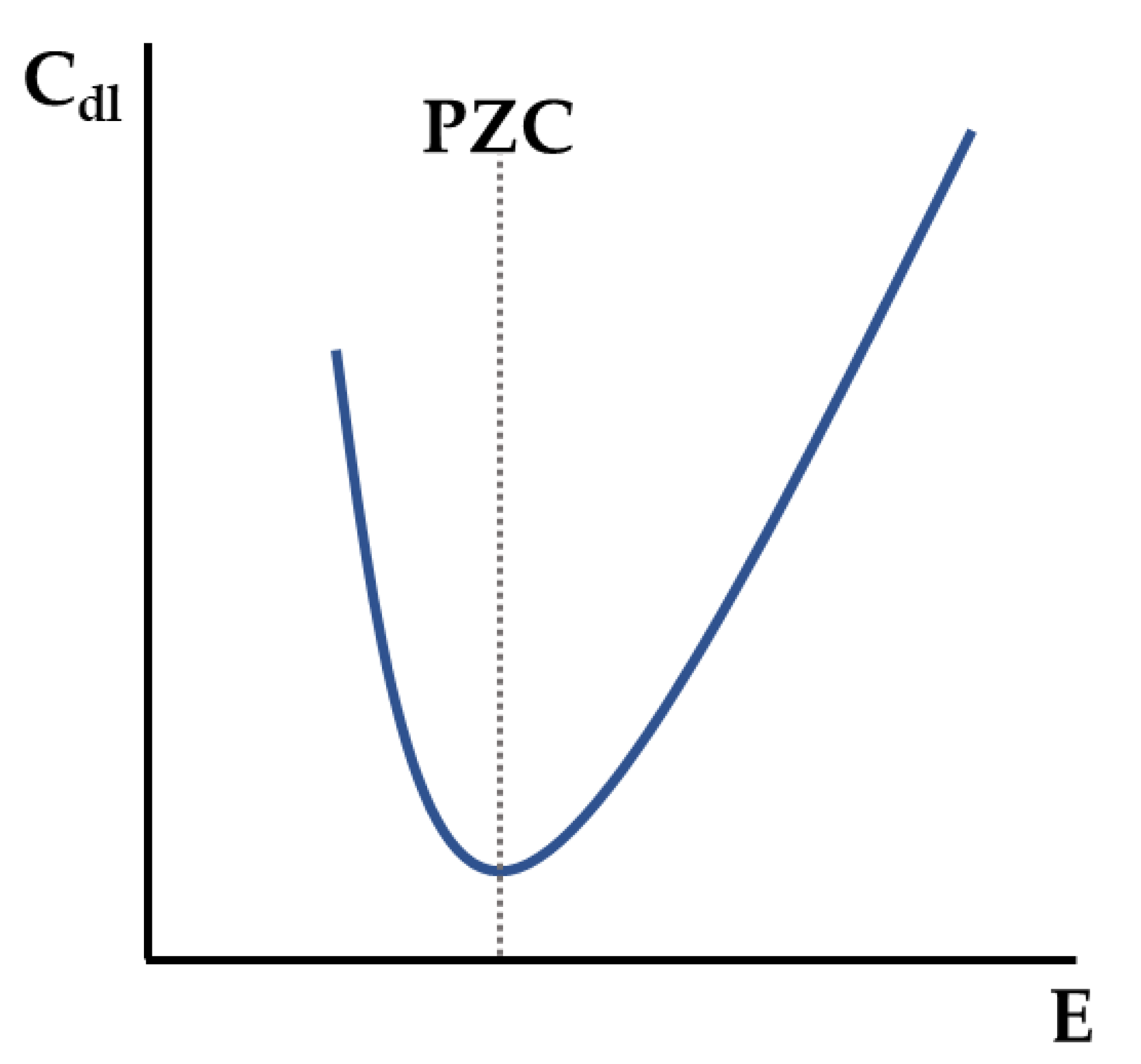
- EDL can be used for charge transfer processes investigation, mainly due to how it is related to W;
- PZC is a quantity that can be easily obtained by EIS measurements and is strongly dependent on the EDL;
- The electrolyte chemical composition affects the EDL, and consequently the PZC and the W. Because of it, the catalysis is strongly affected by the supporting electrolyte.
4. EDL Structure
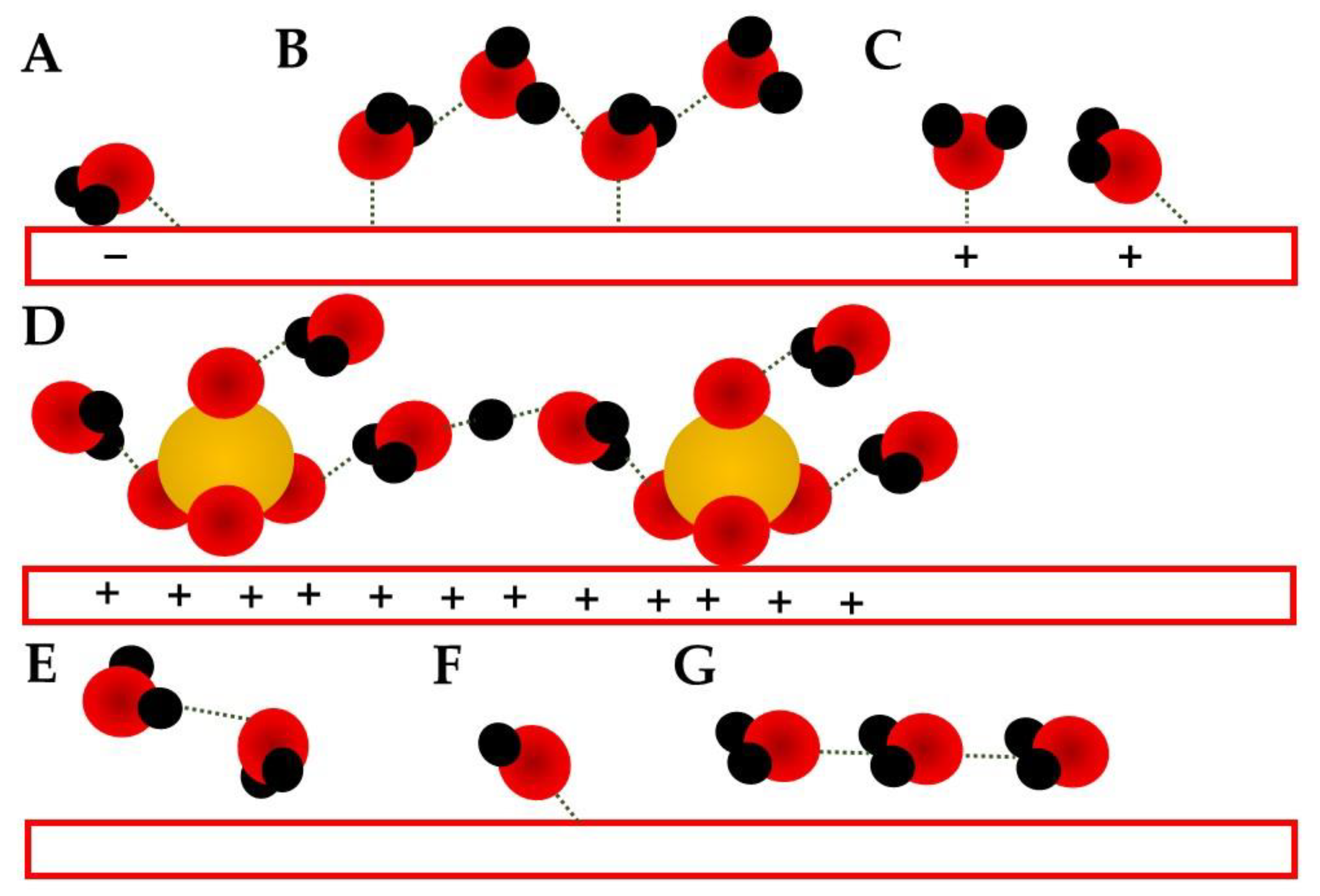
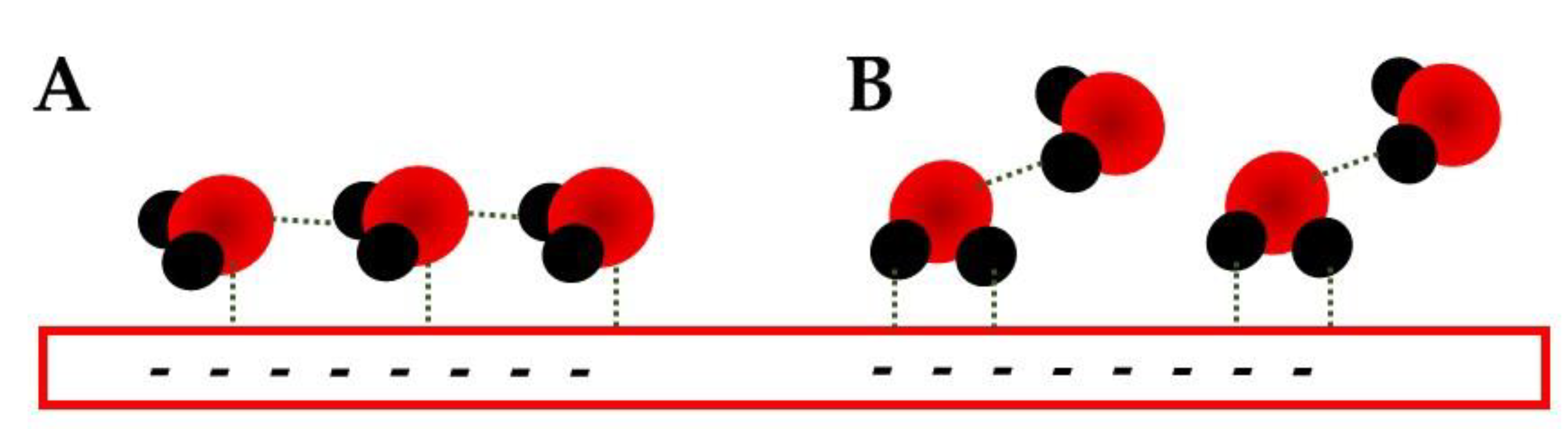
- Spectroelectrochemic techniques can provide the EDL structure evolution during an electrochemical process;
- The water related bands can be deconvoluted and different conformations can be obtained and investigated by them;
- The potential shift of these water bands needs to be taken with care since they can be related to a generation or consumption behavior as well as a Stark shift. Simultaneous consideration of stretching and bending modes is mandatory;
- Anions can also be followed by spectroscopic techniques, and its adsorption can be related to active sites blocking;
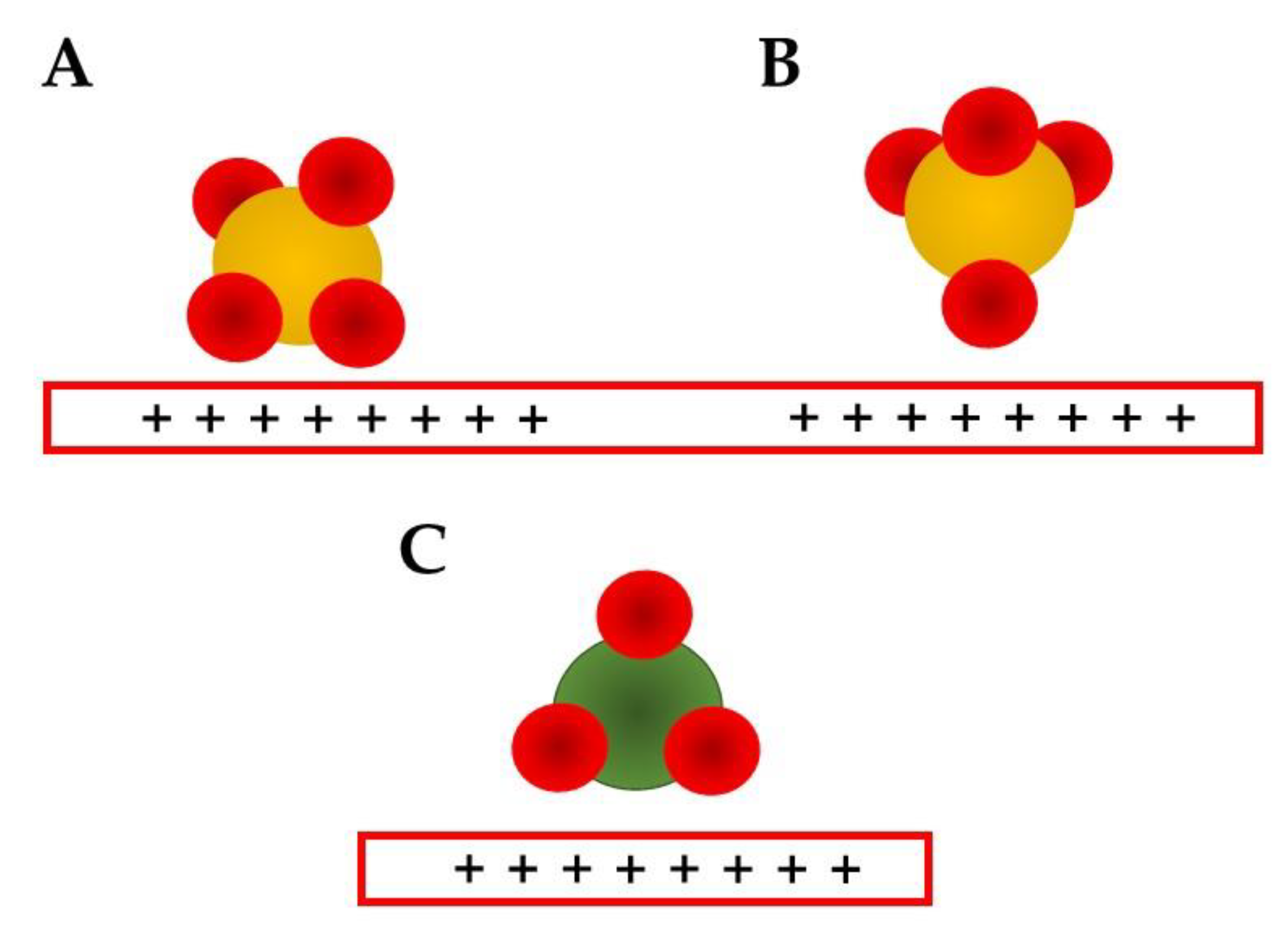
- Cations are considered in alkaline media, but due to the lack of natural bands, the water in the solvation shell is responsible for the probing bands.
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EDL | electric double layer |
| ϕ | electrode surface potential |
| ψ | EDL potential |
| kB | Boltzmann’s constant |
| T | temperature |
| z | ionic charge number |
| e | electron charge |
| N | atomic population |
| x | EDL thickness |
| κ−1 | Debye length |
| I | ionic strength |
| NA | Avogadro’s constant |
| HL | Helmholtz layer |
| ψh | Helmholtz layer potential |
| xh | Helmholtz layer thickens |
| IHP | inner Helmholtz layer |
| OHP | outer Helmholtz layer |
| PZC | potential of zero charge |
| W | work function |
| Xifp | interfacial parameter |
| F | Faraday’s constant |
| μm | electron’s chemical potential |
| Cdl | double layer capacitance |
| EIS | electrochemical impedance spectroscopy |
| CV | cyclic voltammetry |
| C | capacitance |
| Q | charge |
| E | potential |
| CPE | constant phase element |
| RRDE | rotating ring disk electrode |
| SECM | scanning electrochemical microscopy |
| SEIRAS | surface enhanced infrared absorption spectroscopy |
| SERS | surface enhanced Raman spectroscopy |
| SHINERS | shell-isolated nanoparticle-enhanced Raman spectroscopy |
References
- Huang, J.; Chen, Y. Editorial Overview Surface electrochemistry (2022) The double layer: A persisting issue with emerging trends. Curr. Opin. Electrochem. 2022, 35, 101099. [Google Scholar] [CrossRef]
- Schmickler, W. Double Layer Theory. J. Solid State Electrochem. 2020, 24, 2175–2176. [Google Scholar] [CrossRef] [Green Version]
- Fawcett, W.R. Fifty Years of Studies of Double Layer Effects in Electrode Kinetics—A Personal View. J. Solid State Electrochem. 2011, 15, 1347–1358. [Google Scholar] [CrossRef] [Green Version]
- Jacob, T.; Sabo, L. Electrochemical Double Layer Modeling Electrified Interfaces; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Haid, R.W.; Ding, X.; Sarpey, T.K.; Bandarenka, A.S.; Garlyyev, B. Exploration of the Electrical Double-Layer Structure: Influence of Electrolyte Components on the Double-Layer Capacitance and Potential of Maximum Entropy. Curr. Opin. Electrochem. 2022, 32, 100882. [Google Scholar] [CrossRef]
- Stamenkovic, V.R.; Strmcnik, D.; Lopes, P.P.; Markovic, N.M. Energy and Fuels from Electrochemical Interfaces. Nat. Mater. 2016, 16, 57–69. [Google Scholar] [CrossRef] [PubMed]
- Ataka, K.; Yotsuyanagi, T.; Osawa, M. Potential-Dependent Reorientation of Water Molecules at an Electrode/Electrolyte Interface Studied by Surface-Enhanced Infrared Absorption Spectroscopy. J. Phys. Chem. 1996, 100, 10664–10672. [Google Scholar] [CrossRef]
- Garcia-Araez, N.; Rodriguez, P.; Navarro, V.; Bakker, H.J.; Koper, M.T.M. Structural Effects on Water Adsorption on Gold Electrodes. J. Phys. Chem. C 2011, 115, 21249–21257. [Google Scholar] [CrossRef]
- Garcia-Araez, N.; Rodriguez, P.; Bakker, H.J.; Koper, M.T.M. Effect of the Surface Structure of Gold Electrodes on the Coadsorption of Water and Anions. J. Phys. Chem. C 2012, 116, 4786–4792. [Google Scholar] [CrossRef]
- Wandlowski, T.; Ataka, K.; Pronkin, S.; Diesing, D. Surface Enhanced Infrared Spectroscopy—Au(1 1 1–20 Nm)/Sulphuric Acid—New Aspects and Challenges. Electrochim. Acta 2004, 49, 1233–1247. [Google Scholar] [CrossRef]
- Li, C.-Y.; Le, J.-B.; Wang, Y.-H.; Chen, S.; Yang, Z.-L.; Li, J.-F.; Cheng, J.; Tian, Z.-Q. In Situ Probing Electrified Interfacial Water Structures at Atomically Flat Surfaces. Nat. Mater. 2019, 18, 697–701. [Google Scholar] [CrossRef]
- Chen, X.; McCrum, I.T.; Schwarz, K.A.; Janik, M.J.; Koper, M.T.M. Co-Adsorption of Cations as the Cause of the Apparent PH Dependence of Hydrogen Adsorption on a Stepped Platinum Single-Crystal Electrode. Angew. Chem. Int. Ed. 2017, 56, 15025–15029. [Google Scholar] [CrossRef]
- Velasco-Velez, J.J.; Wu, C.H.; Pascal, T.A.; Wan, L.F.; Guo, J.; Prendergast, D.; Salmeron, M. The Structure of Interfacial Water on Gold Electrodes Studied by X-ray Absorption Spectroscopy. Science 2014, 346, 831–834. [Google Scholar] [CrossRef] [PubMed]
- Favaro, M.; Jeong, B.; Ross, P.N.; Yano, J.; Hussain, Z.; Liu, Z.; Crumlin, E.J. Unravelling the Electrochemical Double Layer by Direct Probing of the Solid/Liquid Interface. Nat. Commun. 2016, 7, 12695. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Kim, D.H.; Ringe, S. Electric Double Layer Structure in Aqueous Electrolyte and Its Electrocatalytic Importance. Research Square, 2021; preprint. [Google Scholar] [CrossRef]
- Ledezma-Yanez, I.; Wallace, W.D.Z.; Sebastián-Pascual, P.; Climent, V.; Feliu, J.M.; Koper, M.T.M. Interfacial Water Reorganization as a PH-Dependent Descriptor of the Hydrogen Evolution Rate on Platinum Electrodes. Nat. Energy 2017, 2, 17031. [Google Scholar] [CrossRef] [Green Version]
- Nesselberger, M.; Arenz, M. In Situ FTIR Spectroscopy: Probing the Electrochemical Interface during the Oxygen Reduction Reaction on a Commercial Platinum High-Surface-Area Catalyst. ChemCatChem 2016, 8, 1125–1131. [Google Scholar] [CrossRef] [Green Version]
- Moraes, I.R.; da Cunha, M.C.P.M.; Nart, F.C. Vibrational Spectroscopy of Adsorbed Sulfate and Nitrate Ions on Au(100) Electrodes. J. Braz. Chem. Soc. 1996, 7, 453–460. [Google Scholar] [CrossRef]
- Martins, V.L.; Neves, H.R.; Monje, I.E.; Leite, M.M.; de Oliveira, P.F.M.; Antoniassi, R.M.; Chauque, S.; Morais, W.G.; Melo, E.C.; Obana, T.T.; et al. An Overview on the Development of Electrochemical Capacitors and Batteries—Part I. An. Acad. Bras. Cienc. 2020, 92, 1–28. [Google Scholar] [CrossRef]
- Sagadevan, S.; Marlinda, A.R.; Chowdhury, Z.Z.; Wahab, Y.B.A.; Hamizi, N.A.; Shahid, M.M.; Mohammad, F.; Podder, J.; Johan, M.R. Fundamental Electrochemical Energy Storage Systems. In Advances in Supercapacitor and Supercapattery: Innovations in Energy Storage Devices; Elsevier: Amsterdam, The Netherlands, 2020; pp. 27–43. ISBN 9780128198971. [Google Scholar]
- Sagadevan, S.; Johan, M.R.; Marlinda, A.R.; Akbarzadeh, O.; Pandian, K.; Shahid, M.M.; Mohammad, F.; Podder, J. Background of Energy Storage. In Advances in Supercapacitor and Supercapattery: Innovations in Energy Storage Devices; Elsevier: Amsterdam, The Netherlands, 2020; pp. 1–26. ISBN 9780128198971. [Google Scholar]
- Bashir, S.; Chong, M.Y.; Hina, M.; Kamran, K.; Ramesh, S.; Ramesh, K. Aqueous Solid and Gel Electrolytes for Supercapattery. In Advances in Supercapacitor and Supercapattery: Innovations in Energy Storage Devices; Elsevier: Amsterdam, The Netherlands, 2020; pp. 271–310. ISBN 9780128198971. [Google Scholar]
- Wu, J. Understanding the Electric Double-Layer Structure, Capacitance, and Charging Dynamics. Chem. Rev. 2022, 122, 10821–10859. [Google Scholar] [CrossRef]
- Drab, M.; Kralj-Iglič, V. Electric Double Layer of Electrons: Attraction between Two like-Charged Surfaces Induced by Fermi–Dirac Statistics. Phys. Lett. A 2019, 383, 358–365. [Google Scholar] [CrossRef]
- Drab, M.; Kralj-Iglič, V. Diffuse Electric Double Layer in Planar Nanostructures Due to Fermi-Dirac Statistics. Electrochim. Acta 2016, 204, 154–159. [Google Scholar] [CrossRef]
- Du, H.; Lin, X.; Xu, Z.; Chu, D. Electric Double-Layer Transistors: A Review of Recent Progress. J. Mater. Sci. 2015, 50, 5641–5673. [Google Scholar] [CrossRef]
- De Rodrigues, M.P.S.; Dourado, A.H.B.; de Cutolo, L.O.; Parreira, L.S.; Alves, T.V.; Slater, T.J.A.; Haigh, S.J.; Camargo, P.H.C.; Cordoba de Torresi, S.I. Gold–Rhodium Nanoflowers for the Plasmon-Enhanced Hydrogen Evolution Reaction under Visible Light. ACS Catal. 2021, 11, 13543–13555. [Google Scholar] [CrossRef]
- Dourado, A.H.B.; Silva, N.A.; Munhos, R.L.; del Colle, V.; Arenz, M.; Varela, H.; Córdoba de Torresi, S.I. Influence of Anion Chaotropicity on the SO2 Oxidation Reaction: When Spectator Species Determine the Reaction Pathway. ChemElectroChem 2020, 7, 1843–1850. [Google Scholar] [CrossRef]
- Dourado, A.H.B.; Munhos, R.L.; Silva, N.A.; del Colle, V.; Carvalho, G.G.A.; Oliveira, P.V.; Arenz, M.; Varela, H.; Córdoba de Torresi, S.I. Opportunities and Knowledge Gaps of SO2 Electrocatalytic Oxidation for H2 Electrochemical Generation. ACS Catal. 2019, 9, 8136–8143. [Google Scholar] [CrossRef]
- Lamoureux, P.S.; Singh, A.R.; Chan, K. PH Effects on Hydrogen Evolution and Oxidation over Pt(111): Insights from First-Principles. ACS Catal. 2019, 9, 6194–6201. [Google Scholar] [CrossRef]
- Zheng, Y.; Jiao, Y.; Vasileff, A.; Qiao, S.Z. The Hydrogen Evolution Reaction in Alkaline Solution: From Theory, Single Crystal Models, to Practical Electrocatalysts. Angew. Chem. Int. Ed. 2018, 57, 7568–7579. [Google Scholar] [CrossRef] [PubMed]
- Barnes, C.T.; Gentle, I.R. Interfacial Science: An Introduction, 2nd ed.; Oxford Press: New York, NY, USA, 2010. [Google Scholar]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Damaskin, B.; Petri, O. Fundamentos de Eletroquímica Teórica, 1st ed.; Mir: Moscow, Russia, 1985. [Google Scholar]
- Bockris, J.O.; Reddy, A.K.N. Modern Electrochemistry 1, 2nd ed.; Kluwer Academic Publishers: Boston, MA, USA, 2002; ISBN 0-306-45554-4. [Google Scholar]
- Grahame, D.C. The Electrical Double Layer and the Theory of Electrocapillarity. Chem. Rev. 1947, 41, 441–501. [Google Scholar] [CrossRef] [PubMed]
- Petrii, O.A. Zero Charge Potentials of Platinum Metals and Electron Work Functions (Review). Russ. J. Electrochem. 2013, 49, 401–422. [Google Scholar] [CrossRef]
- Trasatti, S. Work Function, Electronegativity, and Electrochemical Behaviour of Metals. II. Potentials of Zero Charge and “Electrochemical” Work Functions. J. Electroanal. Chem. 1971, 33, 351–378. [Google Scholar] [CrossRef]
- Nitopi, S.; Bertheussen, E.; Scott, S.B.; Liu, X.; Engstfeld, A.K.; Horch, S.; Seger, B.; Stephens, I.E.L.; Chan, K.; Hahn, C.; et al. Progress and Perspectives of Electrochemical CO2 Reduction on Copper in Aqueous Electrolyte. Chem. Rev. 2019, 119, 7610–7672. [Google Scholar] [CrossRef] [Green Version]
- Verdaguer-Casadevall, A.; Li, C.W.; Johansson, T.P.; Scott, S.B.; McKeown, J.T.; Kumar, M.; Stephens, I.E.L.; Kanan, M.W.; Chorkendorff, I. Probing the Active Surface Sites for CO Reduction on Oxide-Derived Copper Electrocatalysts. J. Am. Chem. Soc. 2015, 137, 9808–9811. [Google Scholar] [CrossRef] [PubMed]
- Li, C.W.; Kanan, M.W. CO2 Reduction at Low Overpotential on Cu Electrodes Resulting from the Reduction of Thick Cu2O Films. J. Am. Chem. Soc. 2012, 134, 7231–7234. [Google Scholar] [CrossRef] [PubMed]
- Schalenbach, M.; Durmus, Y.E.; Tempel, H.; Kungl, H.; Eichel, R.A. Double Layer Capacitances Analysed with Impedance Spectroscopy and Cyclic Voltammetry: Validity and Limits of the Constant Phase Element Parameterization. Phys. Chem. Chem. Phys. 2021, 23, 21097–21105. [Google Scholar] [CrossRef]
- Schalenbach, M.; Durmus, Y.E.; Robinson, S.A.; Tempel, H.; Kungl, H.; Eichel, R.A. Physicochemical Mechanisms of the Double-Layer Capacitance Dispersion and Dynamics: An Impedance Analysis. J. Phys. Chem. C 2021, 125, 5870–5879. [Google Scholar] [CrossRef]
- Schalenbach, M.; Durmus, Y.E.; Tempel, H.; Kungl, H.; Eichel, R.A. The Role of the Double Layer for the Pseudocapacitance of the Hydrogen Adsorption on Platinum. Sci. Rep. 2022, 12, 3375. [Google Scholar] [CrossRef] [PubMed]
- Morales, D.M.; Risch, M. Seven Steps to Reliable Cyclic Voltammetry Measurements for the Determination of Double Layer Capacitance. J. Phys. Energy 2021, 3, 034013. [Google Scholar] [CrossRef]
- Gharbi, O.; Tran, M.T.T.; Tribollet, B.; Turmine, M.; Vivier, V. Revisiting Cyclic Voltammetry and Electrochemical Impedance Spectroscopy Analysis for Capacitance Measurements. Electrochim. Acta 2020, 343, 136109. [Google Scholar] [CrossRef]
- Alexander, C.L.; Tribollet, B.; Orazem, M.E.; Vivier, V.; Orazem, M.E. Contribution of Surface Distributions to Constant-Phase-Element (CPE) Behavior: 1. Influence of Roughness. Electrochim. Acta 2015, 173, 99–108. [Google Scholar] [CrossRef]
- Córdoba-Torres, P. A Generalized Expression for the Resistivity Distribution in Films: From the Young Model to Constant-Phase Element (CPE) Behavior. Electrochim. Acta 2017, 241, 535–543. [Google Scholar] [CrossRef]
- Córdoba-Torres, P. Relationship between Constant-Phase Element (CPE) Parameters and Physical Properties of Films with a Distributed Resistivity. Electrochim. Acta 2017, 225, 592–604. [Google Scholar] [CrossRef]
- Du, H.; Lin, X.; Xu, Z.; Chu, D. A Review of Molecular Modelling of Electric Double Layer Capacitors. Phys. Chem. Chem. Phys. 2014, 16, 6519–6538. [Google Scholar]
- Brug, G.J.; van den Eeden, A.L.G.; Sluyters-Rehbach, M.; Sluyters, J.H. The Analysis of Electrode Impedances Complicated by the Presence of a Constant Phase Element. J. Electroanal. Chem. Interfacial Electrochem. 1984, 176, 275–295. [Google Scholar] [CrossRef]
- Xue, S.; Garlyyev, B.; Auer, A.; Kunze-Liebhäuser, J.; Bandarenka, A.S. How the Nature of the Alkali Metal Cations Influences the Double-Layer Capacitance of Cu, Au, and Pt Single-Crystal Electrodes. J. Phys. Chem. C 2020, 124, 12442–12447. [Google Scholar] [CrossRef]
- Ninham, B.W.; Duignan, T.T.; Parsons, D.F. Approaches to Hydration, Old and New: Insights through Hofmeister Effects. Curr. Opin. Colloid Interface Sci. 2011, 16, 612–617. [Google Scholar] [CrossRef]
- Schwierz, N.; Horinek, D.; Sivan, U.; Netz, R.R. Reversed Hofmeister Series—The Rule Rather than the Exception. Curr. Opin. Colloid Interface Sci. 2016, 23, 10–18. [Google Scholar] [CrossRef]
- Gibb, B.C. Hofmeister’s Curse. Nat. Chem. 2019, 11, 963–965. [Google Scholar] [CrossRef]
- Kunz, W.; Henle, J.; Ninham, B.W. “Zur Lehre von Der Wirkung Der Salze” (about the Science of the Effect of Salts): Franz Hofmeister’s Historical Papers. Curr. Opin. Colloid Interface Sci. 2004, 9, 19–37. [Google Scholar] [CrossRef]
- Zhao, L.; Damodaran, S. Hofmeister Order of Anions on Protein Stability Originates from Lifshitz-van Der Waals Dispersion Interaction with the Protein Phase. Langmuir 2019, 35, 12993–13002. [Google Scholar] [CrossRef]
- Iamprasertkun, P.; Hirunpinyopas, W.; Keerthi, A.; Wang, B.; Radha, B.; Bissett, M.A.; Dryfe, R.A.W. Capacitance of Basal Plane and Edge-Oriented Highly Ordered Pyrolytic Graphite: Specific Ion Effects. J. Phys. Chem. Lett. 2019, 10, 617–623. [Google Scholar] [CrossRef]
- Pajkossy, T.; Kolb, D.M. Anion-Adsorption-Related Frequency-Dependent Double Layer Capacitance of the Platinum-Group Metals in the Double Layer Region. Electrochim. Acta 2008, 53, 7403–7409. [Google Scholar] [CrossRef]
- Zhu, J.; Le, J.; Koper, M.T.M.; Doblhoff-Dier, K.; Cheng, J. Effects of Adsorbed OH on Pt(100)/Water Interfacial Structures and Potential. J. Phys. Chem. C 2021, 125, 21571–21579. [Google Scholar] [CrossRef]
- Climent, V.; Feliu, J.M. Surface Electrochemistry with Pt Single-Crystal Electrodes. In Advances in Electrochemical Science and Engineering: Nanopatterned and Nanoparticle-Modified Electrodes; Elsevier: Amsterdam, The Netherlands, 2017; pp. 1–57. ISBN 9783527340934. [Google Scholar]
- Marković, N.M.; Adžić, R.R.; Cahan, B.D.; Yeager, E.B. Structural Effects in Electrocatalysis: Oxygen Reduction on Platinum Low Index Single-Crystal Surfaces in Perchloric Acid Solutions. J. Electroanal. Chem. 1994, 377, 249–259. [Google Scholar] [CrossRef]
- Attard, G.A.; Brew, A.; Hunter, K.; Sharman, J.; Wright, E. Specific Adsorption of Perchlorate Anions on Pt{hkl} Single Crystal Electrodes. Phys. Chem. Chem. Phys. 2014, 16, 13689–13698. [Google Scholar] [CrossRef] [Green Version]
- Perry, S.C.; Denuault, G. The Oxygen Reduction Reaction (ORR) on Reduced Metals: Evidence for a Unique Relationship between the Coverage of Adsorbed Oxygen Species and Adsorption Energy. Phys. Chem. Chem. Phys. 2016, 18, 10218–10223. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gubanova, E.; Schmidt, T.O.; Watzele, S.; Alexandrov, V.; Bandarenka, A.S. Structure-Dependent Electrical Double-Layer Capacitances of the Basal Plane Pd(Hkl) Electrodes in HClO4. J. Phys. Chem. C 2022, 126, 11414–11420. [Google Scholar] [CrossRef]
- Watzele, S.A.; Katzenmeier, L.; Sabawa, J.P.; Garlyyev, B.; Bandarenka, A.S. Temperature Dependences of the Double Layer Capacitance of Some Solid/Liquid and Solid/Solid Electrified Interfaces. An Experimental Study. Electrochim. Acta 2021, 391, 138969. [Google Scholar] [CrossRef]
- Wu, J.; Zheng, W.; Chen, Y. Factors Affecting the Cathode/Electrolyte Interfacial PH Change during Water Reduction: A Simulation Study. Int. J. Hydrogen Energy 2022, 47, 18597–18605. [Google Scholar] [CrossRef]
- Monteiro, M.C.O.; Koper, M.T.M. Measuring Local PH in Electrochemistry. Curr. Opin. Electrochem. 2021, 25, 100649. [Google Scholar] [CrossRef]
- Henckel, D.A.; Counihan, M.J.; Holmes, H.E.; Chen, X.; Nwabara, U.O.; Verma, S.; Rodríguez-López, J.; Kenis, P.J.A.; Gewirth, A.A. Potential Dependence of the Local PH in a CO2 Reduction Electrolyzer. ACS Catal. 2021, 11, 255–263. [Google Scholar] [CrossRef]
- Jong, M.; Sleegers, N.; Schram, J.; Daems, D.; Florea, A.; de Wael, K. A Benzocaine-Induced Local Near-Surface PH Effect: Influence on the Accuracy of Voltammetric Cocaine Detection. Anal. Sens. 2021, 1, 54–62. [Google Scholar] [CrossRef]
- Varela, A.S.; Kroschel, M.; Reier, T.; Strasser, P. Controlling the Selectivity of CO2 electroreduction on Copper: The Effect of the Electrolyte Concentration and the Importance of the Local PH. Catal. Today 2016, 260, 8–13. [Google Scholar] [CrossRef]
- Wang, X.; Xu, C.; Jaroniec, M.; Zheng, Y.; Qiao, S.Z. Anomalous Hydrogen Evolution Behavior in High-PH Environment Induced by Locally Generated Hydronium Ions. Nat. Commun. 2019, 10, 4876. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zülke, A.; Perroni, P.; Machado, E.G.; Varela, H. Rrde Studies of Glycerol Electro-Oxidation: Local PH Variation and Oscillatory Dynamics. ECS Trans. 2017, 77, 1643–1650. [Google Scholar] [CrossRef]
- Ayemoba, O.; Cuesta, A. Spectroscopic Evidence of Size-Dependent Buffering of Interfacial PH by Cation Hydrolysis during CO2 Electroreduction. ACS Appl. Mater. Interfaces 2017, 9, 27377–27382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barrozo, A.V.; Benedetti, S. Compreensão Matemática Da Difusão No Contexto Eletroquímico. Quim. Nova 2016, 39, 356–370. [Google Scholar] [CrossRef]
- Southampton Electrochemistry Group. Convective Diffusion Systems—The Rotating Disc and Ring-Disc Electrodes. In Instrumental Methods in Electrochemistry; Ellis Horwood Limired: West Sussex, UK, 1990; pp. 113–148. [Google Scholar]
- Albery, W.J.; Hitchman, M.L. Ring-Disc Electrodes, 1st ed.; Oxford University Press: London, UK, 1971. [Google Scholar]
- Miller, B.; Bruckenstein, S. Hydrodynamic Potentiometry and Amperometry at Ring-Disk Electrodes. J. Electrochem. Soc. 1970, 117, 1032–1039. [Google Scholar] [CrossRef]
- Popović, N.D.; Johnson, D.C. A Ring−Disk Study of the Competition between Anodic Oxygen-Transfer and Dioxygen-Evolution Reactions. Anal. Chem. 1998, 70, 468–472. [Google Scholar] [CrossRef]
- Albery, W.J.; Calvo, E.J. Ring–Disc Electrodes. Part 21—PH Measurement with the Ring. J. Chem. Soc. Faraday Trans. 1 1983, 79, 2583. [Google Scholar] [CrossRef]
- Hessami, S.; Tobias, C.W. In-situ Measurement of Interfacial PH Using a Rotating Ring-disk Electrode. AIChE J. 1993, 39, 149–162. [Google Scholar] [CrossRef]
- Zimer, A.M.; Medina da Silva, M.; Machado, E.G.; Varela, H.; Mascaro, L.H.; Pereira, E.C. Development of a Versatile Rotating Ring-Disc Electrode for in Situ PH Measurements. Anal. Chim. Acta 2015, 897, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Steegstra, P.; Ahlberg, E. In Situ PH Measurements with Hydrous Iridium Oxide in a Rotating Ring Disc Configuration. J. Electroanal. Chem. 2012, 685, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Vos, J.G.; Koper, M.T.M. Examination and Prevention of Ring Collection Failure during Gas-Evolving Reactions on a Rotating Ring-Disk Electrode. J. Electroanal. Chem. 2019, 850, 113363. [Google Scholar] [CrossRef]
- Bard, A.J.; Fan, F.F.; Kwak, J.; Lev, O. Scanning Electrochemical Microscopy. Introduction and Principles. Anal. Chem. 1989, 61, 132–138. [Google Scholar] [CrossRef]
- Davis, J.M.; Fan, F.-R.F.; Bard, A.J. Currents in thin layer electrochemical cells with spherical and conical electrodes. J. Electroanal. Chem. 1987, 238, 9–31. [Google Scholar] [CrossRef]
- Kwak, J.; Bard, A.J. Scanning Electrochemical Microscopy. Theory of the Feedback Mode. Anal. Chem. 1989, 61, 1221–1227. [Google Scholar] [CrossRef]
- Zoski, C.G. Scanning Electrochemical Microscopy. In Encyclopedia of Analytical Chemistry; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Zhi, F.; Lu, X.; Yang, J.; Wang, X.; Shang, H.; Zhang, S.; Xue, Z. Selective Anion Sensing through a Self-Assembled Monolayer of Thiol-End-Functionalized Porphyrin. J. Phys. Chem. C 2009, 113, 13166–13172. [Google Scholar] [CrossRef]
- Kwak, J.; Bard, A.J. Scanning Electrochemical Microscopy. Apparatus and Two-Dimensional Scans of Conductive and Insulating Substrates. Anal. Chem. 1989, 61, 1794–1799. [Google Scholar] [CrossRef]
- Huang, V.M.; Wu, S.L.; Orazem, M.E.; Pébre, N.; Tribollet, B.; Vivier, V. Local Electrochemical Impedance Spectroscopy: A Review and Some Recent Developments. Electrochim. Acta 2011, 56, 8048–8057. [Google Scholar] [CrossRef] [Green Version]
- Ochoa, N.; Moran, F.; Pébère, N.; Tribollet, B. Influence of Flow on the Corrosion Inhibition of Carbon Steel by Fatty Amines in Association with Phosphonocarboxylic Acid Salts. Corros. Sci. 2005, 47, 593–604. [Google Scholar] [CrossRef]
- Noël, J.-M.; Kanoufi, F. Probing the Reactive Intermediate Species Generated during Electrocatalysis by Scanning Electrochemical Microscopy. Curr. Opin. Electrochem. 2022, 35, 101071. [Google Scholar] [CrossRef]
- Trinh, D.; Keddam, M.; Novoa, X.R.; Vivier, V. Alternating Current Measurements in Scanning Electrochemical Microscopy, Part 2: Detection of Adsorbates. ChemPhysChem 2011, 12, 2177–2183. [Google Scholar] [CrossRef] [PubMed]
- Wittstock, G.; Burchardt, M.; Pust, S.E.; Shen, Y.; Zhao, C. Scanning Electrochemical Microscopy for Direct Imaging of Reaction Rates. Angew. Chem. Int. Ed. Engl. 2007, 46, 1584–1617. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Li, X.; Wang, X.; Shang, H.; Liu, X.; Lu, X. Comparative Electrochemical Behaviors of a Series of SH-Terminated-Functionalized Porphyrins Assembled on a Gold Electrode by Scanning Electrochemical Microscopy (SECM). J. Phys. Chem. B 2010, 114, 10436–10441. [Google Scholar] [CrossRef]
- Trinh, D.; Keddam, M.; Novoa, X.R.; Vivier, V. Alternating-Current Measurements in Scanning Electrochemical Microscopy, Part 1: Principle and Theory. ChemPhysChem 2011, 12, 2169–2176. [Google Scholar] [CrossRef] [PubMed]
- Brolo, A.G.; Germain, P.; Hager, G. Investigation of the Adsorption of L-Cysteine on a Polycrystalline Silver Electrode by Surface-Enhanced Raman Scattering (SERS) and Surface-Enhanced Second Harmonic Generation (SESHG). J. Phys. Chem. B 2002, 106, 5982–5987. [Google Scholar] [CrossRef]
- Mendes, R.K.; Freire, R.S.; Fonseca, C.P.; Neves, S.; Kubota, L.T. Characterization of Self-Assembled Thiols Monolayers on Gold Surface by Electrochemical Impedance Spectroscopy. J. Braz. Chem. Soc. 2004, 15, 849–855. [Google Scholar] [CrossRef] [Green Version]
- Björneholm, O.; Hansen, M.H.; Hodgson, A.; Liu, L.M.; Limmer, D.T.; Michaelides, A.; Pedevilla, P.; Rossmeisl, J.; Shen, H.; Tocci, G.; et al. Water at Interfaces. Chem. Rev. 2016, 116, 7698–7726. [Google Scholar] [CrossRef]
- Jensen, K.D.; Tymoczko, J.; Rossmeisl, J.; Bandarenka, A.; Chorkendorff, I.; Escudero-Escribano, M.; Stephens, I.E.L. Elucidation of the Oxygen Reduction Volcano in Alkaline Media Using a Copper-Platinum(111) Alloy. Angew. Chem. Int. Ed. 2018, 57, 2800–2805. [Google Scholar] [CrossRef]
- Zana, A.; Wiberg, G.K.H.; Deng, Y.; Østergaard, T.; Rossmeisl, J.; Arenz, M. Accessing the Inaccessible: Analyzing the Oxygen Reduction Reaction in the Diffusion Limit. ACS Appl. Mater. Interfaces 2017, 9, 38176–38180. [Google Scholar] [CrossRef]
- Sebastián-Pascual, P.; Petersen, A.S.; Bagger, A.; Rossmeisl, J.; Escudero-Escribano, M. PH and Anion Effects on Cu–Phosphate Interfaces for CO Electroreduction. ACS Catal. 2021, 1128–1135. [Google Scholar] [CrossRef]
- Rossmeisl, J.; Chan, K.; Skúlason, E.; Björketun, M.E.; Tripkovic, V. On the PH Dependence of Electrochemical Proton Transfer Barriers. Catal. Today 2016, 262, 36–40. [Google Scholar] [CrossRef]
- Tripkovic, V.; Björketun, M.E.; Skúlason, E.; Rossmeisl, J. Standard Hydrogen Electrode and Potential of Zero Charge in Density Functional Calculations. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 115452. [Google Scholar] [CrossRef] [Green Version]
- Timoshenko, J.; Roldan Cuenya, B. In Situ/Operando Electrocatalyst Characterization by X-ray Absorption Spectroscopy. Chem. Rev. 2021, 121, 882–961. [Google Scholar] [CrossRef]
- Mesa, C.A.; Pastor, E.; Francàs, L. UV-Vis Operando Spectroelectrochemistry for (Photo)Electrocatalysis: Principles and Guidelines. Curr. Opin. Electrochem. 2022, 35, 101098. [Google Scholar] [CrossRef]
- Cuesta, A. ATR-SEIRAS for Time-Resolved Studies of Electrode–Electrolyte Interfaces. Curr. Opin. Electrochem. 2022, 35, 101041. [Google Scholar] [CrossRef]
- Yu, A.; Chen, W.; Chen, Y.-X.; Zhu, B.-Q.; Sun, Z.-J.; Cai, J. Probing Complex Electrocatalytic Reactions Using Electrochemical in Situ Infrared Spectroscopy. Curr. Opin. Electrochem. 2019, 14, 113–123. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, Y.-W.; Cai, W.-B. Recent Applications of in Situ ATR-IR Spectroscopy in Interfacial Electrochemistry. Curr. Opin. Electrochem. 2017, 1, 73–79. [Google Scholar] [CrossRef]
- Sanghapi, A.; Ramakrishan, S.; Fan, S.; Shannon, C. InSitu Characterization of Bipolar Electrodes by Using Vibrational Stark Spectroscopy and Surface-Enhanced Raman Spectroelectrochemistry. ChemElectroChem 2016, 3, 436–440. [Google Scholar] [CrossRef]
- Kaim, W.; Fiedler, J. Spectroelectrochemistry: The Best of Two Worlds. Chem. Soc. Rev. 2009, 38, 3373–3382. [Google Scholar] [CrossRef] [PubMed]
- Scherson, D.A.; Tolmachev, Y.V.; Stefan, I.C. Ultraviolet/Visible Spectroelectrochemistry; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; pp. 10172–10225. [Google Scholar]
- Dourado, A.H.B.; Arenz, M.; Córdoba de Torresi, S.I. Mechanism of Electrochemical L-Cysteine Oxidation on Pt. ChemElectroChem 2019, 6, 1009–1013. [Google Scholar] [CrossRef]
- Blizanac, B.B.; Lucas, C.A.; Gallagher, M.E.; Arenz, M.; Ross, P.N.; Marković, N.M. Anion Adsorption, CO Oxidation, and Oxygen Reduction Reaction on a Au(100) Surface: The PH Effect. J. Phys. Chem. B 2004, 108, 625–634. [Google Scholar] [CrossRef]
- Dourado, A.H.B.; del Colle, V.; Munhos, R.L.; Feliu, J.M.; Varela, H.; de Torresi, S.I.C. SO2 Electrooxidation Reaction on Pt Single Crystal Surfaces in Acidic Media: Electrochemical and in Situ FTIR Studies. Electrochim. Acta 2022, 403, 139601. [Google Scholar] [CrossRef]
- Dourado, A.H.B.; da Silva, A.G.M.; Pastrián, F.A.C.; Munhos, R.L.; de Lima Batista, A.P.; de Oliveira-Filho, A.G.S.; Quiroz, J.; de Oliveira, D.C.; Camargo, P.H.C.; Córdoba de Torresi, S.I. In Situ FTIR Insights into the Electrooxidation Mechanism of Glucose as a Function of the Surface Facets of Cu2O-Based Electrocatalytic Sensors. J. Catal. 2019, 375, 95–103. [Google Scholar] [CrossRef]
- Pastrián, F.A.C.; da Silva, A.G.M.; Dourado, A.H.B.; de Lima Batista, A.P.; de Oliveira-Filho, A.G.S.; Quiroz, J.; de Oliveira, D.C.; Camargo, P.H.C.; Córdoba de Torresi, S.I. Why Could the Nature of Surface Facets Lead to Differences in the Activity and Stability of Cu2O-Based Electrocatalytic Sensors? ACS Catal. 2018, 8, 6265–6272. [Google Scholar] [CrossRef]
- Dourado, A.H.B.; de Lima Batista, A.P.; Oliveira-Filho, A.G.S.; Sumodjo, P.T.A.; Cordoba de Torresi, S.I. L-Cysteine Electrooxidation in Alkaline and Acidic Media: A Combined Spectroelectrochemical and Computational Study. RSC Adv. 2017, 7, 7492–7501. [Google Scholar] [CrossRef] [Green Version]
- Osawa, M.; Ataka, K.; Yoshii, K.; Yotsuyanagi, T. Surface-Enhanced Infrared ATR Spectroscopy for in Situ Studies of Electrode/Electrolyte Interfaces. J. Electron. Spectros Relat. Phenomena 1993, 64–65, 371–379. [Google Scholar] [CrossRef]
- Hoffmann, F. Infrared Reflection-Absorption Spectroscopy of Adsorbed Molecules. Surf. Sci. Rep. 1983, 3, 107. [Google Scholar] [CrossRef]
- Chabal, Y.J. Surface Infrared Spectroscopy. Surf. Sci. Rep. 1988, 8, 211–357. [Google Scholar] [CrossRef]
- Osawa, M.; Ataka, K.I.; Yoshii, K.; Nishikawa, Y. Surface-Enhanced Infrared Spectroscopy: The Origin of the Absorption Enhancement and Band Selection Rule in the Infrared Spectra of Molecules Adsorbed on Fine Metal Particles. Appl. Spectrosc. 1993, 47, 1497–1502. [Google Scholar] [CrossRef]
- Ras, R.H.A.; Schoonheydt, R.A.; Johnston, C.T. Relation between S-Polarized and p-Polarized Internal Reflection Spectra: Application for the Spectral Resolution of Perpendicular Vibrational Modes. J. Phys. Chem. A 2007, 111, 8787–8791. [Google Scholar] [CrossRef]
- Cai, W.-B.; Ren, B.; Li, X.Q.; She, C.X.; Liu, F.M.; Cai, X.W.; Tian, Z.-Q. Investigation of Surface-Enhanced Raman Scattering from Platinum Electrodes Using a Confocal Raman Microscope: Dependence of Surface Roughening Pretreatment. Surf. Sci. 1998, 406, 9–22. [Google Scholar] [CrossRef]
- Tian, Z.; Ren, B. Infrared and Raman Spectroscopy in Analysis of Surfaces. In Encyclopedia of Analytical Chemistry; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; pp. 1–40. ISBN 9780470027318. [Google Scholar]
- Xie, W.; Schlücker, S. Rationally Designed Multifunctional Plasmonic Nanostructures for Surface-Enhanced Raman Spectroscopy: A Review. Rep. Prog. Phys. 2014, 77, 116502. [Google Scholar] [CrossRef]
- Tian, Z.-Q.; Ren, B.; Li, J.-F.; Yang, Z.-L. Expanding Generality of Surface-Enhanced Raman Spectroscopy with Borrowing SERS Activity Strategy. Chem. Commun. 2007, 34, 3514–3534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nakamura, M.; Kato, H.; Hoshi, N. Infrared Spectroscopy of Water Adsorbed on M(111) (M = Pt, Pd, Rh, Au, Cu) Electrodes in Sulfuric Acid Solution. J. Phys. Chem. C 2008, 112, 9458–9463. [Google Scholar] [CrossRef]
- Osawa, M.; Tsushima, M.; Mogami, H.; Samjeské, G.; Yamakata, A. Structure of Water at the Electrified Platinum-Water Interface: A Study by Surface-Enhanced Infrared Absorption Spectroscopy. J. Phys. Chem. C 2008, 112, 4248–4256. [Google Scholar] [CrossRef]
- Shen, A.; Pemberton, J.E. Investigation of Trace Interfacial Water at Silver Electrodes in a Series of Normal Alcohols Using Surface Enhanced Raman Scattering. Phys. Chem. Chem. Phys. 1999, 1, 5677–5684. [Google Scholar] [CrossRef]
- Dourado, A.H.B.; Silva, R.A.; Torresi, R.M.; Sumodjo, P.T.A.; Arenz, M.; Cordoba de Torresi, S.I. Kinetics, Assembling, and Conformation Control of L-Cysteine Adsorption on Pt Investigated by in Situ FTIR Spectroscopy and QCM-D. ChemPhysChem 2018, 19, 2340–2348. [Google Scholar] [CrossRef]
- Brooker, J.; Christensen, P.A.; Hamnett, A.; He, R.; Paliteiro, C.A. Combined Scanning Tunnelling Microscopy and in Situ Fourier Transform Infrared Study of Dioxygen Reduction on Gold. Faraday Discuss. 1992, 94, 339. [Google Scholar] [CrossRef]
- Doneux, T.; Buess-Herman, C.; Lipkowski, J. Electrochemical and FTIR Characterization of the Self-Assembled Monolayer of 2-Mercaptobenzimidazole on Au(111). J. Electroanal. Chem. 2004, 564, 65–75. [Google Scholar] [CrossRef]
- Zinola, C.F.; Rodríguez, J.L.; Arévalo, M.C.; Pastor, E. FTIR Studies of Tyrosine Oxidation at Polycrystalline Pt and Pt(111) Electrodes. J. Electroanal. Chem. 2005, 585, 230–239. [Google Scholar] [CrossRef]
- Ogura, K.; Kobayashi, M.; Nakayama, M.; Miho, Y. In-Situ FTIR Studies on the Electrochemical Oxidation of Histidine and Tyrosine. J. Electroanal. Chem. 1999, 463, 218–223. [Google Scholar] [CrossRef]
- Gómez-Marín, A.M.; Feliu, J.M. Pt(111) Surface Disorder Kinetics in Perchloric Acid Solutions and the Influence of Specific Anion Adsorption. Electrochim. Acta 2012, 82, 558–569. [Google Scholar] [CrossRef]
- Agmon, N. Infrared Spectroscopy: The Acid Test for Water Structure. Nat. Chem. 2016, 8, 206–207. [Google Scholar] [CrossRef] [PubMed]
- Max, J.-J.; Trudel, M.; Chapados, C. Substraction of the Water Spectra from the Infrared Spectrum of Acidic and Alkaline Solutions. Appl. Spectrosc. 1998, 52, 963–969. [Google Scholar] [CrossRef]
- Thamer, M.; de Marco, L.; Ramasesha, K.; Mandal, A.; Tokmakoff, A. Ultrafast 2D IR Spectroscopy of the Excess Proton in Liquid Water. Science 2015, 350, 78–82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Max, J.J.; Trudel, M.; Chapados, C. Infrared Titration of Aqueous Glycine. Appl. Spectrosc. 1998, 52, 226–233. [Google Scholar] [CrossRef]
- Max, J.-J.; Ménichelli, C.; Chapados, C. Infrared Titration of Aqueous Sulfuric Acid. J. Phys. Chem. A 2000, 104, 2845–2858. [Google Scholar] [CrossRef]
- Max, J.-J.; Chapados, C. Infrared Titration of Aqueous NaOH by Aqueous HCl. Can. J. Chem. 2000, 78, 64–72. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dourado, A.H.B. Electric Double Layer: The Good, the Bad, and the Beauty. Electrochem 2022, 3, 789-808. https://doi.org/10.3390/electrochem3040052
Dourado AHB. Electric Double Layer: The Good, the Bad, and the Beauty. Electrochem. 2022; 3(4):789-808. https://doi.org/10.3390/electrochem3040052
Chicago/Turabian StyleDourado, André H. B. 2022. "Electric Double Layer: The Good, the Bad, and the Beauty" Electrochem 3, no. 4: 789-808. https://doi.org/10.3390/electrochem3040052
APA StyleDourado, A. H. B. (2022). Electric Double Layer: The Good, the Bad, and the Beauty. Electrochem, 3(4), 789-808. https://doi.org/10.3390/electrochem3040052





