A New Cure Rate Model Based on Flory–Schulz Distribution: Application to the Cancer Data
Abstract
:1. Introduction
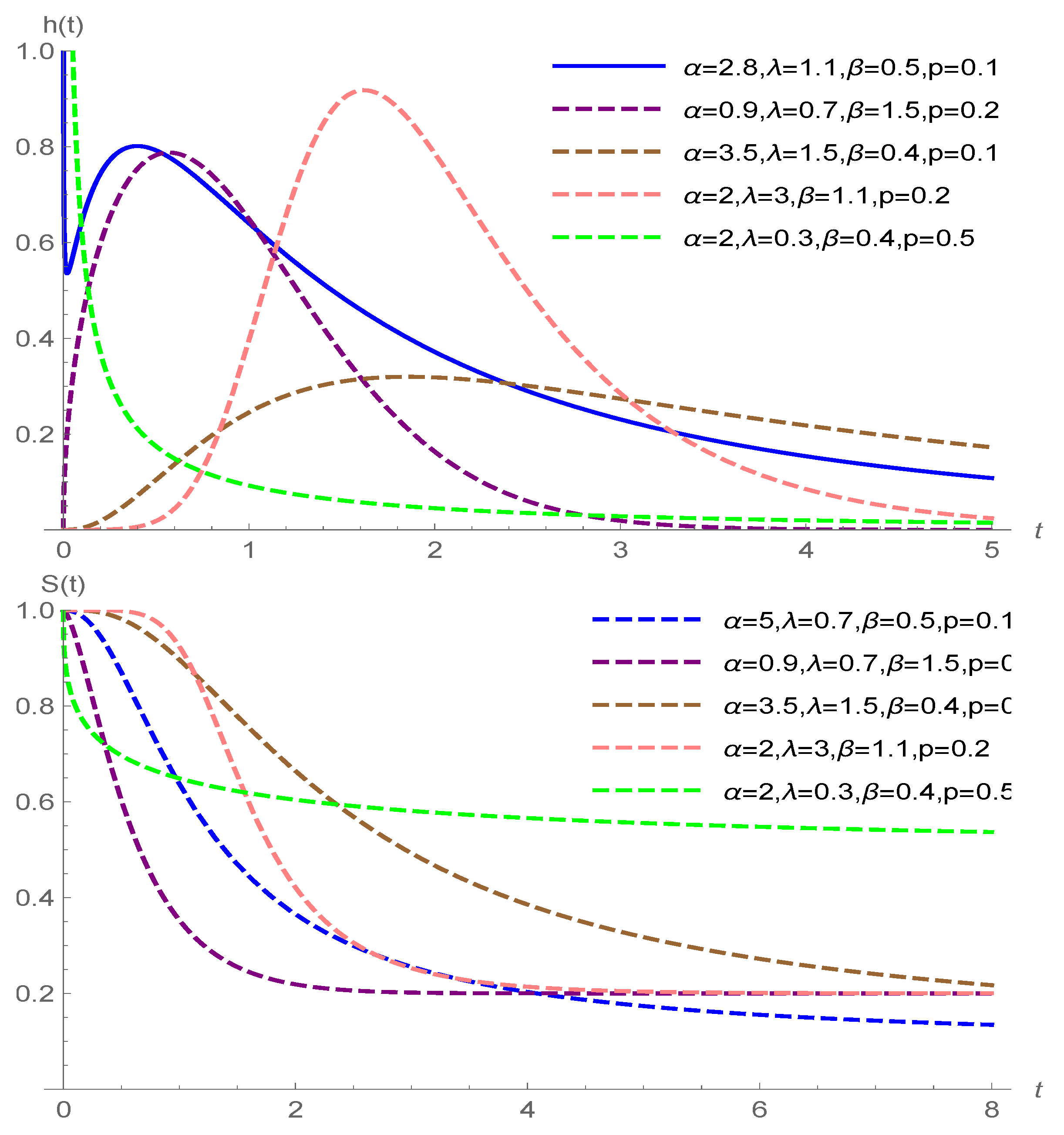
2. Modeling
3. Inference
4. Applications: Data Analysis
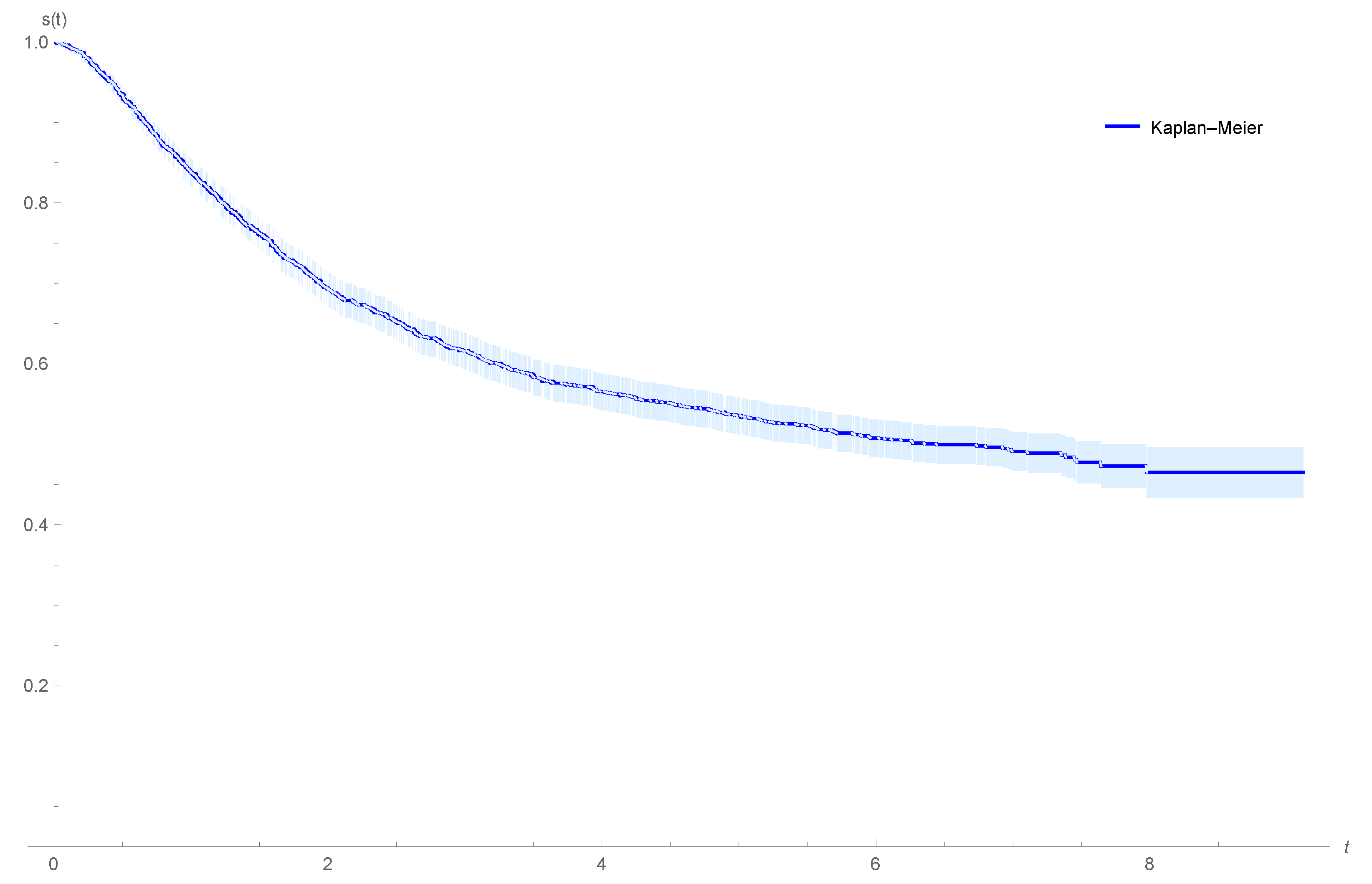
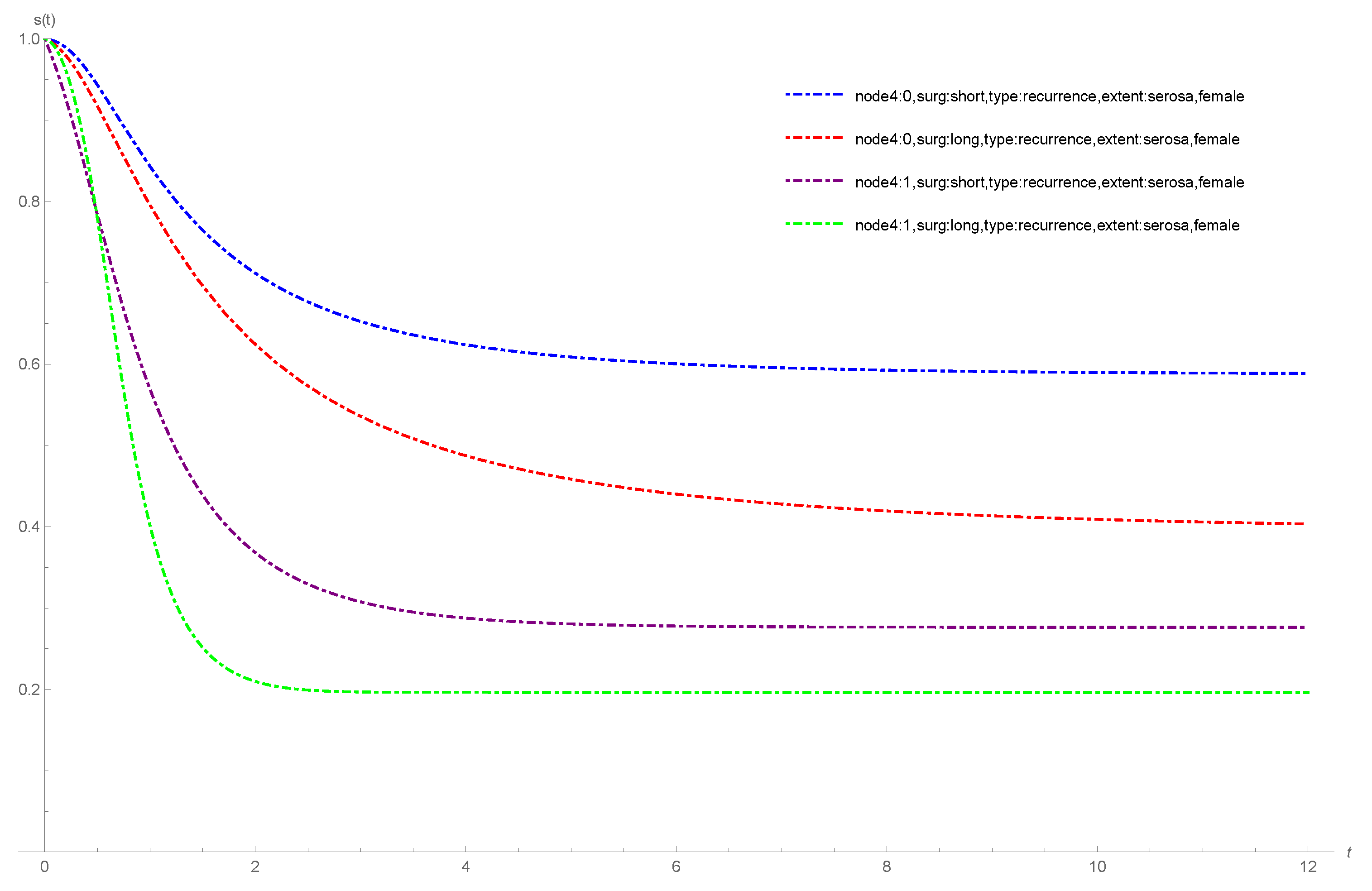
4.1. Colon Cancer Data
- node4: , more than four positive lymph nodes (0 = no, 1 = yes),
- sex: (1 = male, 0 = female),
- etype: (1 = recurrence, 2 = death),
- surg: , time from surgery to registration (0 = short, 1 = long),
- extent: , extent of local spread (1 = submucosa, 2 = muscle, 3 = serosa, 4 = contiguous structures).
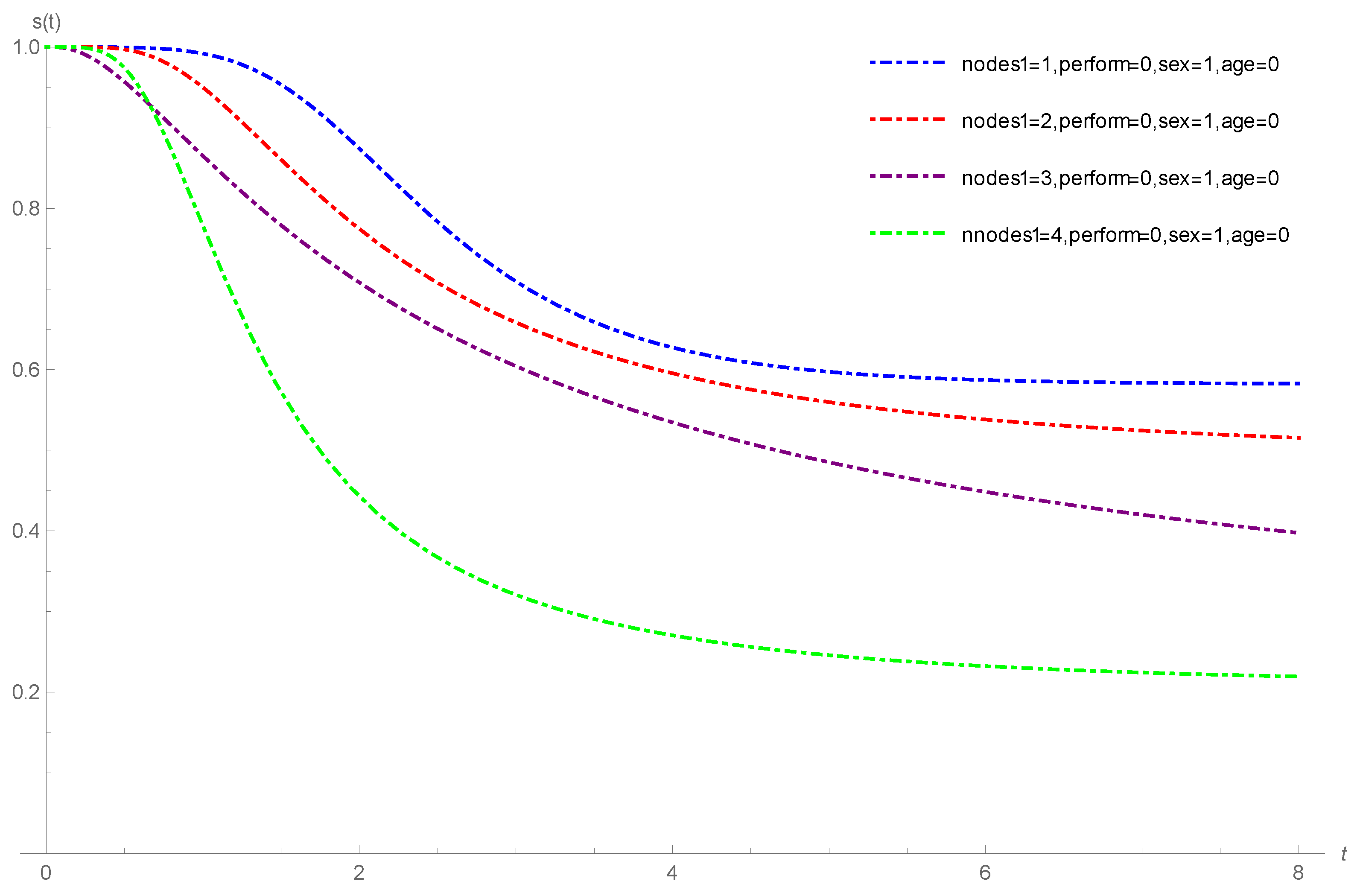
4.2. Melanoma Cancer Data
- age: , classified as zero when the age was below the third quartile (57.56 years) and as one otherwise;
- nodes1: , nodule category 1 to 4, with 4 being the most severe category of cancer;
- perform: , performance status. This means a patient’s functional capacity scale as regards his or her daily activities (0: fully active, 1: other);
- sex: , (0: male; 1: female).
4.3. Oropharynx Cancer Data
- age: (0: less than 60 years; 1: greater or equal to 60 years);
- T stage: ; 1: primary tumour measuring 2 cm or less in largest diameter; 2: primary tumour measuring 2 cm to 4 cm in the largest diameter with minimal infiltration in depth; 3: primary tumour measuring more than 4 cm; 4: massive invasive tumour,
- N stage: ; 0: no clinical evidence of node metastases; 1: single positive node 3 cm or less in diameter, not fixed; 2: single positive node more than 3 cm in diameter, not fixed; 3: multiple positive nodes or fixed positive nodes;
- sex: (1: male; 2: female).
5. Simulation Study
- Step 1:
- Fix the parameter values, , and , as well as the value of the cure fraction .
- Step 2:
- Generate n random samples from
- Step 3:
- The random survival time can be calculated from the equationif ; otherwise, is infinity.
- Step 4:
- Generate the simple sample of the censoring times from a GeTNH distribution and adjust the parameters of the GeTNH distribution to obtain the desired censoring rates.
- Step 5:
- Calculate . Pairs of simulated values , are thus obtained, where if and if . In the simulation study, we pick the F-SCR model with three covariates and , where , and . In the case of high cure rate the initial values of parameters are and in the case of low cure rate they are . The initial value of and is computed from four combinations of values of and cure rates . For , we choose (0, 0, 0), (1, 0, 0), (0, 1, 2) and (1, 2, 1). In the studies, we also consider two levels of the cure rate, say high cure rate (0.8, 0.7, 0.6, 0.5) and low cure rate (0.25, 0.2, 0.15, 0.10). Solving the four equations resulting from Equation (7), for high cure rate we obtain and , and for low cure rate we obtain and .
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Regularity Conditions
Appendix B. The Survival Function for Cure Rate Models Parameterized in Terms of the Cure Rate
References
- De Castro, M.; Gomez, Y.M. A Bayesian Cure Rate Model Based on the Power Piecewise Exponential Distribution. Methodol. Comput. Appl. Probab. 2020, 22, 677–692. [Google Scholar] [CrossRef]
- Cancho, V.G.; Rodrigues, J.; de Castro, M. A flexible model for survival data with a cure rate: A Bayesian approach. J. Appl. Stat. 2011, 38, 57–70. [Google Scholar] [CrossRef]
- Yiqi, B.; Russo, C.M.; Cancho, V.G.; Louzada, F. Influence diagnostics for the Weibull-Negative-Binomial regression model with cure rate under latent failure causes. J. Appl. Stat. 2015, 43, 1027–1060. [Google Scholar] [CrossRef]
- Ortega, E.M.M.; Cordeiro, G.M.; Kattan, M.W. The negative binomial–beta Weibull regression model to predict the cure of prostate cancer. J. Appl. Stat. 2012, 39, 1191–1210. [Google Scholar] [CrossRef]
- D’Andrea, A.; Rocha, R.; Tomazella, V.; Louzada, F. Negative Binomial Kumaraswamy-G Cure Rate Regression Model. J. Risk Financ. Manag. 2018, 11, 6. [Google Scholar] [CrossRef] [Green Version]
- Leão, J.; Bourguignon, M.; Gallardo, D.I.; Rocha, R.; Tomazella, V. A new cure rate model with flexible competing causes with applications to melanoma and transplantation data. Stat. Med. 2020, 39, 1–13. [Google Scholar] [CrossRef]
- Gallardo, D.I.; Gómez, H.W.; Bolfarine, H. A new cure rate model based on the Yule-Simon distribution with application to a melanoma data set. J. Appl. Stat. 2017, 44, 1153–1164. [Google Scholar] [CrossRef]
- Gallardo, D.I.; Gómez, Y.M.; Castro, M.D. A flexible cure rate model based on the polylogarithm distribution. J. Stat. Comput. Simul. 2018, 88, 2137–2149. [Google Scholar] [CrossRef]
- Gallardo, D.I.; Gómez, Y.M.; Gómez, H.W.; de Castro, M. On the use of the modified power series family of distributions in a cure rate model context. Stat. Methods Med. Res. 2019, 29, 1831–1845. [Google Scholar] [CrossRef]
- Cancho, V.G.; Louzada-Neto, F.; Ortega, E.M.M. Ortega. The Power Series Cure Rate Model: An Application to a Cutaneous Melanoma Data. Commun.-Stat.-Simul. Comput. 2013, 42, 586–602. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Koutras, M.V.; Milienos, F. A weighted Poisson distribution and its application to cure rate models. Commun.-Stat.-Theory Methods 2018, 47, 4297–4310. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Pal, S. Expectation maximization-based likelihood inference for flexible cure rate models with Weibull lifetimes. Stat. Methods Med. Res. 2016, 25, 1535–1563. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.H.; Ibrahim, J.G.; Sinha, D. A New Bayesian Model for Survival Data with a Surviving Fraction. J. Am. Stat. Assoc. 1999, 94, 909–919. [Google Scholar] [CrossRef]
- Azimi, R.; Esmailian, M. A New Generalization of Nadarajah–Haghighi Distribution with Application to Cancer and COVID-19 Deaths Data. Math. Slovaca 2022. (accepted). [Google Scholar]
- Tsodikov, A.D.; Ibrahim, J.G.; Yakovlev, A.Y. Estimating Cure Rates from Survival Data: An Alternative to Two-Component Mixture Models. J. Am. Stat. Assoc. 2003, 98, 1063–1078. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodrigues, J.; Cancho, V.G.; de Castro, M.; Louzada-Neto, F. On the Unification of the Long-term Survival Models. Stat. Probab. Lett. 2009, 79, 753–759. [Google Scholar] [CrossRef]
- Flory, P.J. Molecular Size Distribution in Linear Condensation Polymers. J. Am. Chem. Soc. 1936, 58, 1877–1885. [Google Scholar] [CrossRef]
- Li, C.S.; Taylor, J.M.; Sy, J.P. Identifiability of cure models. Stat. Probab. Lett. 2001, 54, 389–395. [Google Scholar] [CrossRef]
- Hanin, L.; Huang, L. Identifiability of cure models revisited. J. Multivar. Anal. 2014, 130, 261–274. [Google Scholar] [CrossRef]
- Williams, J.S.; Lagakos, S.W. Models for Censored Survival Analysis: Constant-Sum and Variable-Sum Models. Biometrika 1997, 64, 215–224. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G.E. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Hannan, E.J.; Quinn, B.G. The Determination of the order of an autoregression. J. R. Stat. Soc. Ser. B 1979, 41, 190–195. [Google Scholar] [CrossRef]
- R Core Team R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014; Available online: http://www.R-project.org/ (accessed on 1 November 2022).
- Therneau, T.M.; A Package for Survival Analysis in R. R Package Version 3.2-13. 2021. Available online: https://CRAN.R-project.org/package=survival (accessed on 1 November 2022).
- Laurie, J.A.; Moertel, C.G.; Fleming, T.R.; Wieand, H.S.; Leigh, J.E.; Rubin, J.; McCormack, G.W.; Gerstner, J.B.; Krook, J.E.; Malliard, J. Surgical adjuvant therapy of large-bowel carcinoma: An evaluation of levamisole and the combination of levamisole and fluorouracil. the north central cancer treatment group and the Mayo. J. Clin. Oncol. Off. J. Am. Soc. Clin. Oncol. 1989, 7, 1447–1456. [Google Scholar] [CrossRef]
- Ibrahim, J.G.; Chen, M.H.; Sinha, D. Bayesian semiparametric models for survival data with a cure fraction. Biometrics 2001, 57, 383–388. [Google Scholar] [CrossRef]
- Kalbfleisch, J.D.; Prentice, R.L. The Statistical Analysis of Failure Time Data; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 360. [Google Scholar]
- Kutal, D.H.; Qian, L. A Non-Mixture Cure Model for Right-Censored Data with Fréchet Distribution. Stats 2018, 1, 176–188. [Google Scholar] [CrossRef]
- Sen, P.K.; Singer, J.M.; Pedroso-de-Lima, A.C. From Finite Sample to Asymptotic Methods in Statistics; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]


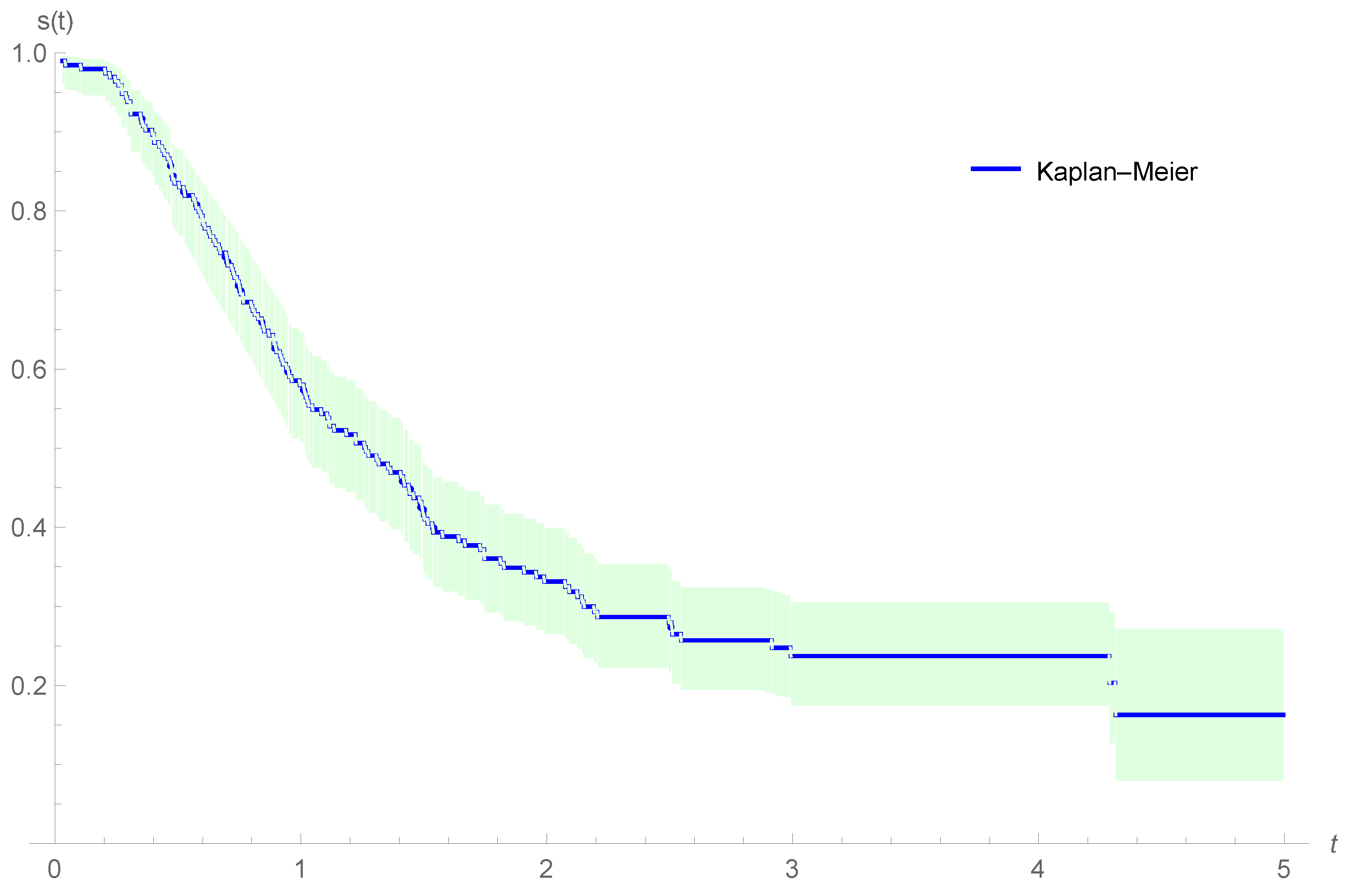
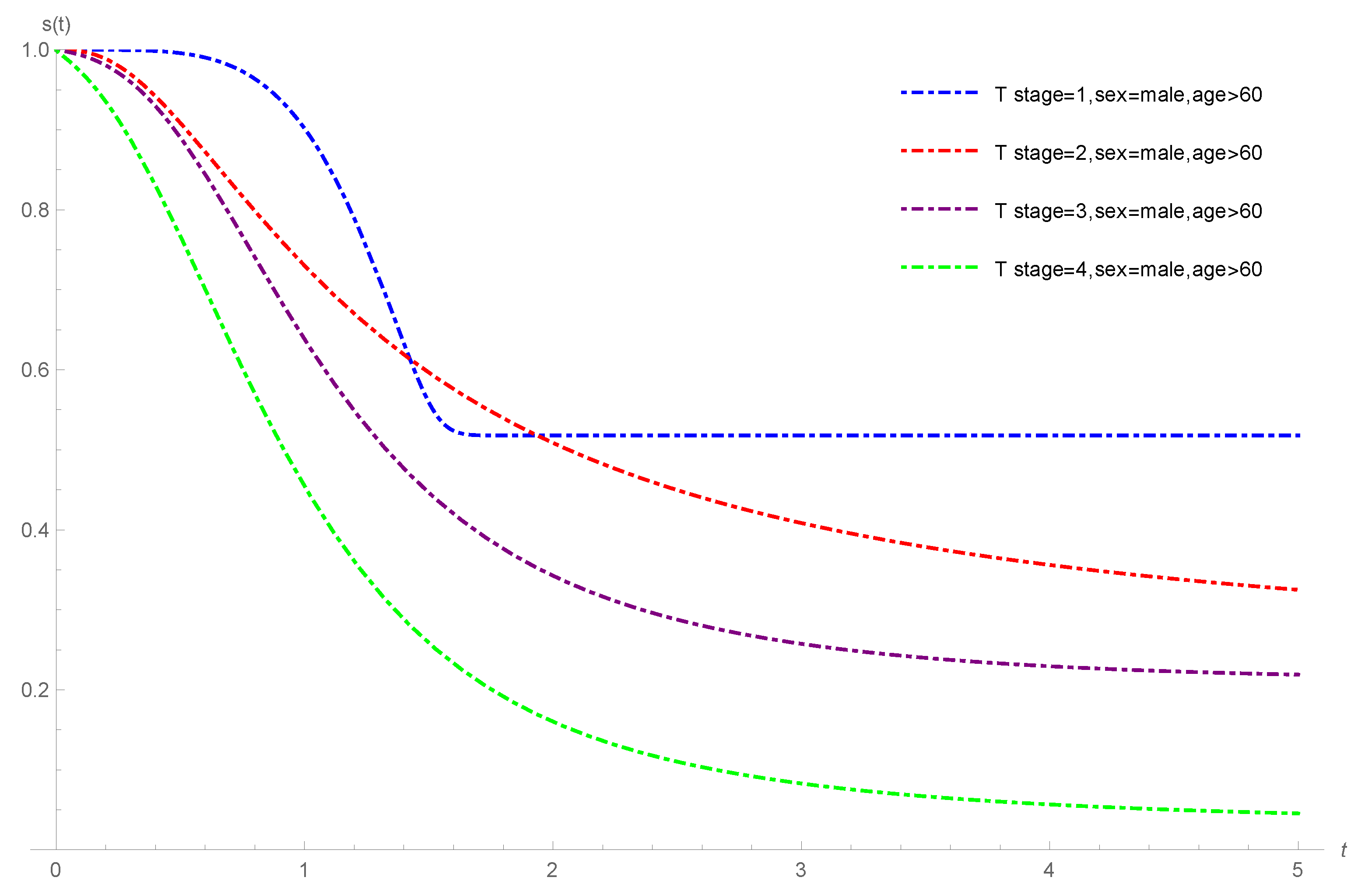
| Parameter | F-SCR | BeCR | PCR | BCR (n = 3) | NBCR |
|---|---|---|---|---|---|
| 4.3951 (0.6745, 8.1158) | 254916 (0, 61.6073) | 8.3250 (1.8283, 14.8216) | 11.8014 (4.2472, 19.3556) | 5.5195 (0, 11.2536) | |
| 0.7715 (0.0477, 1.4953) | 0.0898 (0, 0.2192) | 0.3467 (0.0614, 0.6321) | 0.2240 (0.0750, 0.3729) | 0.5748 (0, 1.2229) | |
| 0.4607 (0.3577, 0.5643) | 0.5872 (0.5220, 0.6535) | 0.4845 (0.4060, 0.5629) | 0.5179 (0.4476, 0.5882) | 0.4679 (0.3671, 0.5688) | |
| −1.7108 (−2.3432, −1.0783) | −1.0427 (−1.8952, −0.1901) | −1.5487 (−2.2566, −0.8408) | −1.3594 (−2.1085, −0.6104) | −1.6609 (−2.3275, −0.9944) | |
| −1.4150 (−1.6399, −1.1900) | −1.5918 (−1.9791, −1.2045) | −1.5324 (−1.8078, −1.2570) | −1.5733 (−1.8830, −1.2636) | −1.4652 (−1.7089, −1.2215) | |
| 0.0234 (−0.1680, 0.2148) | −0.0494 (−0.2795, 0.1805) | 0.0044 (−0.2044, 0.2134) | −0.0136 (−0.2312, 0.2039) | 0.0161 (−0.1825, 0.2149) | |
| 0.4773 (0.2853, 0.6693) | 0.1442 (−0.0848, 0.3733) | 0.3816 (0.1725, 0.5908) | 0.3030 (0.0856, 0.5203) | 0.4436 (0.2444, 0.6428) | |
| −0.3559 (−0.6270, −0.0847) | −0.5282 (−0.8868, −0.1704) | −0.4197 (−0.7248, −0.1147) | −0.4568 (−0.7830, −0.1323) | −0.3813 (−0.6659, −0.0966) | |
| 1.9283 (1.0315, 2.8253) | 2.0967 (1.0200, 3.1734) | 2.0359 (1.0741, 2.9978) | 2.0438 (1.0475, 3.0401) | 1.9774 (1.0546, 2.9001) | |
| −0.3559 (−0.9082, 0.1964) | 1.7761 (0.9681, 2.5841) | 1.7596 (1.1200, 2.3992) | 1.7698 (1.0779, 2.4617) | 1.7146 (1.1280, 2.3012) | |
| 1.9283 (1.4568, 2.3999) | 0.9470 (0.2103, 1.6837) | 0.9172 (0.3552, 1.4791) | 0.9171 (0.3007, 1.5335) | 0.8881 (0.3810, 1.3952) | |
| AIC | 5273.42 | 5342.46 | 5293.82 | 5309.27 | 5281.06 |
| BIC | 5334.22 | 5403.26 | 5354.62 | 5370.07 | 5341.86 |
| HQIC | 5295.83 | 5364.86 | 5316.22 | 5331.68 | 5303.47 |
| Parameter | F-SCR | BeCR | PCR | BCR (n = 3) | NBCR |
|---|---|---|---|---|---|
| 8.0827 (0, 40.8266) | 1.3739 (0.8832, 1.8647) | 3.3845 (0.4263, 6.3427) | 2.1514 (0.9370, 3.3658) | 1.3408 (0, 2.8064) | |
| 0.0241 (0, 0.1234) | 0.2609 (0.1497, 0.3722) | 0.0702 (0.0055, 0.1349) | 0.1275 (0.0487, 0.2062) | 0.1547 (0.0105, 0.2990) | |
| −1.2567 (−1.8094, −0.7041) | −0.7394 (−1.4285, −0.0503) | −1.1281 (−1.7334, −0.5228) | −1.0044 (−1.6390, −0.3699) | 0.0590 (−0.5741, 0.6922) | |
| −1.3012 (−1.5103, −1.0921) | −1.3790 (−1.6593, −1.0986) | −1.3887 (−1.6206, −1.1568) | −1.4059 (−1.6533, −1.1586) | −1.3500 (−1.5930, −1.1076) | |
| 0.0180 (−0.1658, 0.2018 ) | −0.0399 (−0.2496, 0.1697) | 0.0016 (−0.1931, 0.1964) | −0.0155 (−0.2122, 0.1891) | 0.0102 (−0.1822, 0.2027) | |
| 0.4169 (0.2329, 0.6009) | 0.1324 (−0.0764, 0.3414) | 0.3406 (0.1460, 0.5351) | 0.2722 (0.0720, 0.4724) | 0.2969 (0.1046, 0.4892) | |
| −0.3422 (−0.5262, −0.1581) | −0.4609 (−0.7752, −0.1466) | −0.3888 (−0.6694, −0.1083) | −0.4161 (−0.7089, −0.1232) | −0.5492 (−0.8309, −0.2675) | |
| 1.8593 (0.9833, 2.7354) | 1.8636 (0.9021, 2.8250) | 1.8709 (0.9649, 2.7768) | 1.8763 (0.9505, 2.8021) | 0.3137 (−0.5514, 1.1788) | |
| 1.5598 (1.0356, 2.0841) | 1.5378 (0.8796, 2.1959) | 1.6046 (1.0276, 2.1816) | 1.5947 (0.9897, 2.1998) | 0.1146 (−0.4464, 0.6758) | |
| 0.7879 (0.3430, 1.2328) | 0.7667 (0.1790, 1.3544) | 0.8143 (0.3111, 1.3175) | 0.8054 (0.2724, 1.3385) | −0.5144 (−1.0106, −0.0182) | |
| AIC | 5351.46 | 5400.35 | 5360.52 | 5372.07 | 5397.35 |
| BIC | 5406.73 | 5455.63 | 5415.79 | 5427.34 | 5452.62 |
| HQIC | 5371.83 | 5420.72 | 5380.89 | 5392.44 | 5417.22 |
| Parameter | F-SCR | BeCR | PCR | BCR (n = 3) | NBCR |
|---|---|---|---|---|---|
| 1.3870 (1.3033, 1.4706) | 1.2638 (1.1873, 1.3404) | 1.3110 (1.2315, 1.3905) | 1.2678 (1.1906, 1.3451) | 1.3552 (1.2733, 1.4371) | |
| 3.4296 (3.0848, 3.7743) | 2.4872 (2.3097, 2.6647) | 3.0634 (2.7882, 3.3386) | 2.8324 (2.5963, 3.0685) | 3.2821 (2.9663, 3.5980) | |
| −1.3696 (−1.9265, −0.8130) | 0.4224 (−0.1586, 1.0036) | −1.1840 (−1.7891, −0.5789) | −1.0136 (−1.6389, −0.3883) | −1.3097 (−1.8882, −0.7311) | |
| −1.3721 (−1.9289, −0.8154) | −1.2403 (−1.4862, −0.9944) | −1.4100 (−1.6414, −1.1786) | −1.4032 (−1.6448, −1.1617) | −1.3944 (−1.6147, −1.1741) | |
| 0.0236 (−0.1884, 0.2358) | −0.0894 (−0.2908, 0.1119) | 0.0052 (−0.1894, 0.2000) | −0.0089 (−0.2082, 0.1903) | 0.0169 (−0.1725, 0.2064) | |
| 0.4622 (0.2769, 0.6476) | 0.1135 (−0.0868, 0.3139) | 0.3592 (0.1646, 0.5539) | 0.2802 (0.0814, 0.4790) | 0.4246 (0.2350, 0.6143) | |
| −0.3460 (−0.6077, −0.0843) | −0.1777 (−0.4685, 0.1130) | −0.3880 (−0.6684, −0.1077) | −0.4112 (−0.7013, −0.1211) | −0.3637 (−0.6334, −0.0940) | |
| 1.8766 (1.0021, 2.7511) | −0.3295 (−1.1358, 0.4766) | 1.9038 (0.9965, 2.8110) | 1.8838 (0.9623, 2.8053) | 1.8976 (1.0087, 2.7866) | |
| 1.6349 (1.1025, 2.1674) | 0.4546 (−0.1042, 1.0136) | 1.6456 (1.0660, 2.2252) | 1.6076 (1.0074, 2.2079) | 1.6509 (1.0975, 2.2042) | |
| 0.8398 (0.3858, 1.2938) | −0.4032 (−0.8844, 0.0778) | 0.8491 (0.3427, 1.3555) | 0.8191 (0.2903, 1.3479) | 0.8531 (0.3757, 1.3304) | |
| AIC | 5289.16 | 5414.95 | 5315.32 | 5335.08 | 5298.92 |
| BIC | 5344.43 | 5470.22 | 5370.59 | 5390.35 | 5354.19 |
| HQIC | 5309.53 | 5435.32 | 5335.69 | 5355.45 | 5319.29 |
| Parameter | F-SCR | BeCR | PCR | BCR (n = 3) | NBCR |
|---|---|---|---|---|---|
| 2.7341 (0, 6.7091) | 11.8753 (0, 33.3400) | 3.7032 (0, 10.5647) | 4.813 (0, 15.0957) | 3.706 (0, 7.4403) | |
| 1.3627 (0, 3.7506) | 0.2138 (0, 0.6180) | 0.8785 (0, 2.7420) | 0.62 (0, 2.0907) | 0.8774 (0, 1.8854) | |
| 0.6855 (0.4123, 0.9587) | 0.7691 (0.6189, 0.9193) | 0.7085 (0.4566, 0.9603) | 0.7276 (0.5039, 0.9512) | 0.7087 (0.5103, 0.9070) | |
| 0.8855 (0.0811, 1.6899) | 0.9445 (0.0160, 1.8731) | 0.9269 (0.1007, 1.7530) | 0.9456 (0.1106, 1.7805) | 0.9356 (0.1031, 1.7680) | |
| −0.1819 (−0.5895, 0.2111) | −0.2928 (−0.7564, 0.1706) | −0.2287 (−0.6546, 0.1972) | −0.2535 (−0.6933, 0.1863) | −0.229 (−0.6558, 0.1978) | |
| −0.5181 (−0.7080, −0.3283) | −0.5023 (−0.7312, −0.2734) | −0.5270 (−0.7318, −0.3221) | −0.5427 (−0.7557, −0.3296) | −0.5277 (−0.7329, −0.3224) | |
| −0.2377 (−0.8353, 0.3599) | −0.1915 (−0.8935, −0.5105) | −0.2412 (−0.8854, 0.4030) | −0.2323 (−0.9000, 0.4354) | −0.2405 (−0.8810, 0.4000) | |
| 0.2313 (−0.1871, 0.6498) | 0.2416 (−0.2601, 0.7524) | 0.2457 (−0.1951, 0.6865) | 0.2487 (−0.2042, 0.7016) | 0.2466 (−0.1891, 0.6823) | |
| AIC | 1031.99 | 1040.92 | 1034.46 | 1036.45 | 1035.90 |
| BIC | 1064.25 | 1073.19 | 1066.72 | 1068.71 | 1068.17 |
| HQIC | 1044.74 | 1053.68 | 1047.21 | 1049.21 | 1048.66 |
| Parameter | F-SCR | BeCR | PCR | BCR (n = 3) | NBCR |
|---|---|---|---|---|---|
| 2.8366 (0, 5.9192) | 92.1391 (82.3222, 101.9559) | 7.8794 (0, 17.7203) | 69.1816 (51.0566, 87.3065) | 9.3282 (0, 18.8265) | |
| 1.0798 (0, 2.5329) | 0.0156 (0.0120, 0.0191) | 0.2585 (0, 0.6475) | 0.0276 (0.0189, 0.0362) | 0.2405 (0, 0.5015) | |
| 0.7931 (0.4626, 1.1235) | 1.1181 (0.9013, 1.3348) | 0.8437 (0.5528, 1.1345) | 0.9086 (0.64106, 1.1761) | 0.8402 (0.5512, 1.1291) | |
| 0.5378 (−1.2467, 2.3223) | 0.5604 (−1.9027, 3.0235) | 0.6971 (−1.3454, 2.7396) | 0.729 (−1.5204, 2.9784) | 0.6657 (−1.4416, 2.7730) | |
| 0.1405 (−0.4627, 0.7437) | 0.1198 (−0.7535, 0.9931) | 0.1401 (−0.5776, 0.8578) | 0.1293 (−0.6633, 0.9219) | 0.1354 (−0.5807, 0.8515) | |
| −0.627 (−1.0150, −0.2389) | −0.615 (−1.1624, −0.0675) | −0.6796 (−1.1413, −0.2178) | −0.6904 (−1.2021, −0.1786) | −0.6674 (−1.1329, −0.2019) | |
| −0.294 (−0.5495, −0.0384) | −0.2668 (−0.6454, 0.1118) | −0.3114 (−0.6212, −0.0015) | −0.311 (−0.6581, 0.0361) | −0.3071 (−0.6257, 0.0115) | |
| 0.2054 (−0.4931, 0.9039) | 0.2395 (−0.7212, 1.2002) | 0.2455 (−0.5669, 1.0579) | 0.2661 (−0.6190, 1.1512) | 0.2453 (−0.5845, 1.0751) | |
| AIC | 463.49 | 475.45 | 466.15 | 468.37 | 465.86 |
| BIC | 489.67 | 501.63 | 492.33 | 494.55 | 492.04 |
| HQIC | 474.09 | 486.05 | 476.75 | 478.97 | 476.46 |
| Levels of the Cure Rate | High Cure Rate | Low Cure Rate | |||
|---|---|---|---|---|---|
| Parameters | Bias | MSE | Bias | MSE | |
| 400 | −0.1519 | 0.8403 | −0.3038 | 0.8452 | |
| −0.4009 | 0.3222 | −0.1507 | 0.1749 | ||
| −0.029 | 0.0025 | 0.0542 | 0.0007 | ||
| −1.2507 | 1.6593 | −0.0972 | 0.1422 | ||
| −0.5083 | 0.3248 | 0.1013 | 0.1063 | ||
| 0.1876 | 0.0581 | 0.0690 | 0.0337 | ||
| 0.3795 | 0.1629 | 0.2939 | 0.1121 | ||
| 600 | −0.1532 | 0.6861 | −0.3627 | 0.2544 | |
| −0.466 | 0.3219 | −0.1664 | 0.1583 | ||
| −0.0269 | 0.0019 | 0.0531 | 0.0006 | ||
| −1.1943 | 1.529 | −0.1203 | 0.1246 | ||
| 0.4993 | 0.3103 | 0.1350 | 0.0887 | ||
| 0.2118 | 0.0508 | 0.0811 | 0.0301 | ||
| 0.3592 | 0.1377 | 0.2874 | 0.1037 | ||
| 800 | −0.1972 | 0.6233 | −0.3706 | 0.2499 | |
| −0.4748 | 0.3276 | −0.1422 | 0.1482 | ||
| −0.0255 | 0.0017 | 0.0516 | 0.0004 | ||
| −1.1959 | 1.5223 | −0.1093 | 0.1217 | ||
| 0.5070 | 0.3037 | 0.1267 | 0.0856 | ||
| 0.2089 | 0.0488 | 0.0773 | 0.0275 | ||
| 0.3615 | 0.1373 | 0.2858 | 0.1003 | ||
| 1000 | −0.1896 | 0.5862 | −0.4117 | 0.2341 | |
| −0.4799 | 0.3260 | −0.1252 | 0.1651 | ||
| −0.0261 | 0.0016 | 0.0518 | 0.0004 | ||
| −1.1898 | 1.5023 | −0.1292 | 0.1204 | ||
| 0.5040 | 0.2956 | 0.1281 | 0.0810 | ||
| 0.2081 | 0.0481 | 0.0807 | 0.0253 | ||
| 0.3598 | 0.1354 | 0.2853 | 0.0978 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azimi, R.; Esmailian, M.; Gallardo, D.I.; Gómez, H.J. A New Cure Rate Model Based on Flory–Schulz Distribution: Application to the Cancer Data. Mathematics 2022, 10, 4643. https://doi.org/10.3390/math10244643
Azimi R, Esmailian M, Gallardo DI, Gómez HJ. A New Cure Rate Model Based on Flory–Schulz Distribution: Application to the Cancer Data. Mathematics. 2022; 10(24):4643. https://doi.org/10.3390/math10244643
Chicago/Turabian StyleAzimi, Reza, Mahdy Esmailian, Diego I. Gallardo, and Héctor J. Gómez. 2022. "A New Cure Rate Model Based on Flory–Schulz Distribution: Application to the Cancer Data" Mathematics 10, no. 24: 4643. https://doi.org/10.3390/math10244643
APA StyleAzimi, R., Esmailian, M., Gallardo, D. I., & Gómez, H. J. (2022). A New Cure Rate Model Based on Flory–Schulz Distribution: Application to the Cancer Data. Mathematics, 10(24), 4643. https://doi.org/10.3390/math10244643






