About the Global Effect and the Critical Role of Retinal Eccentricity: Implications for Eye Movements in Reading
Abstract
:The global effect: A universal phenomenon
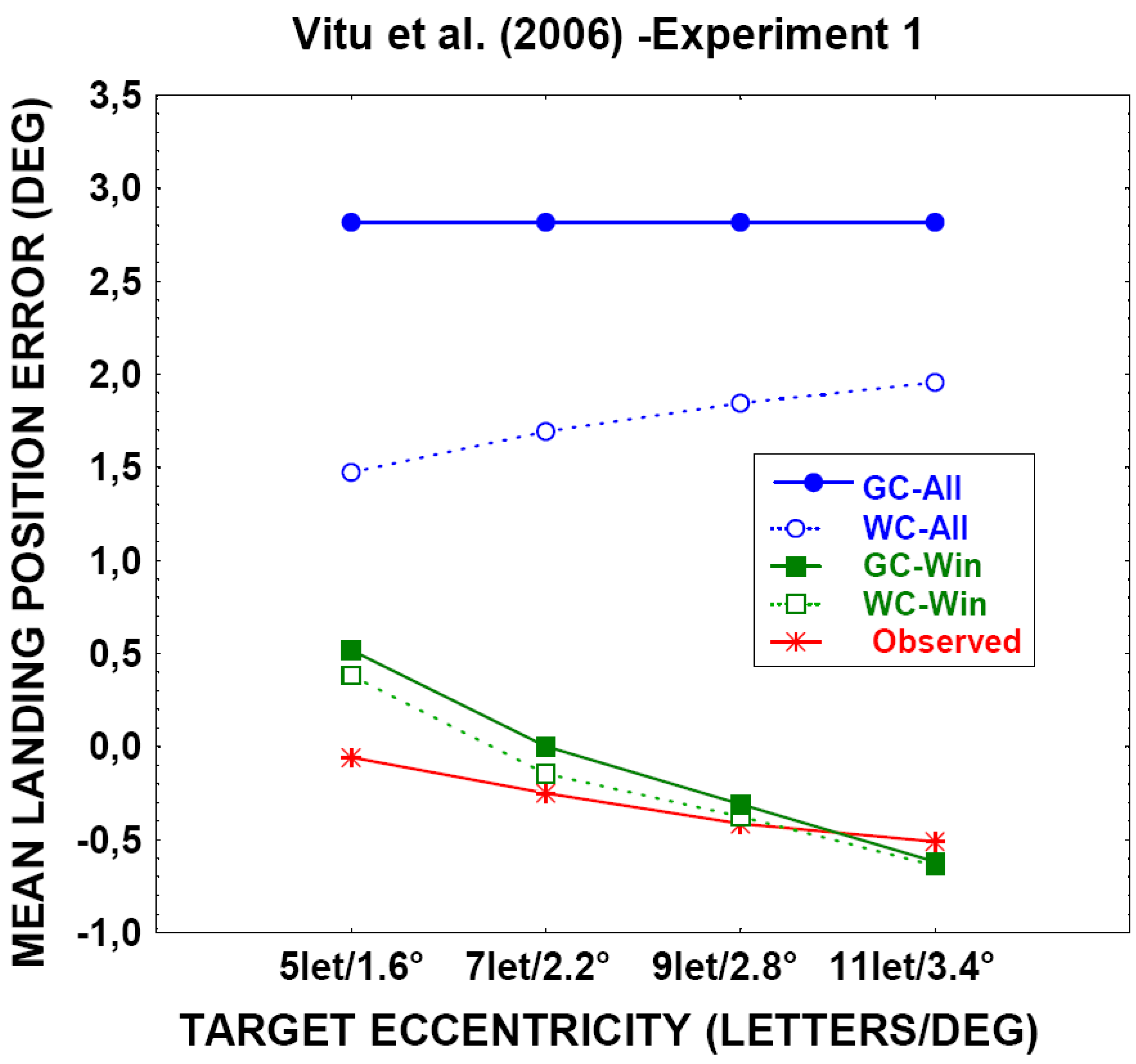
The critical role of retinal eccentricity
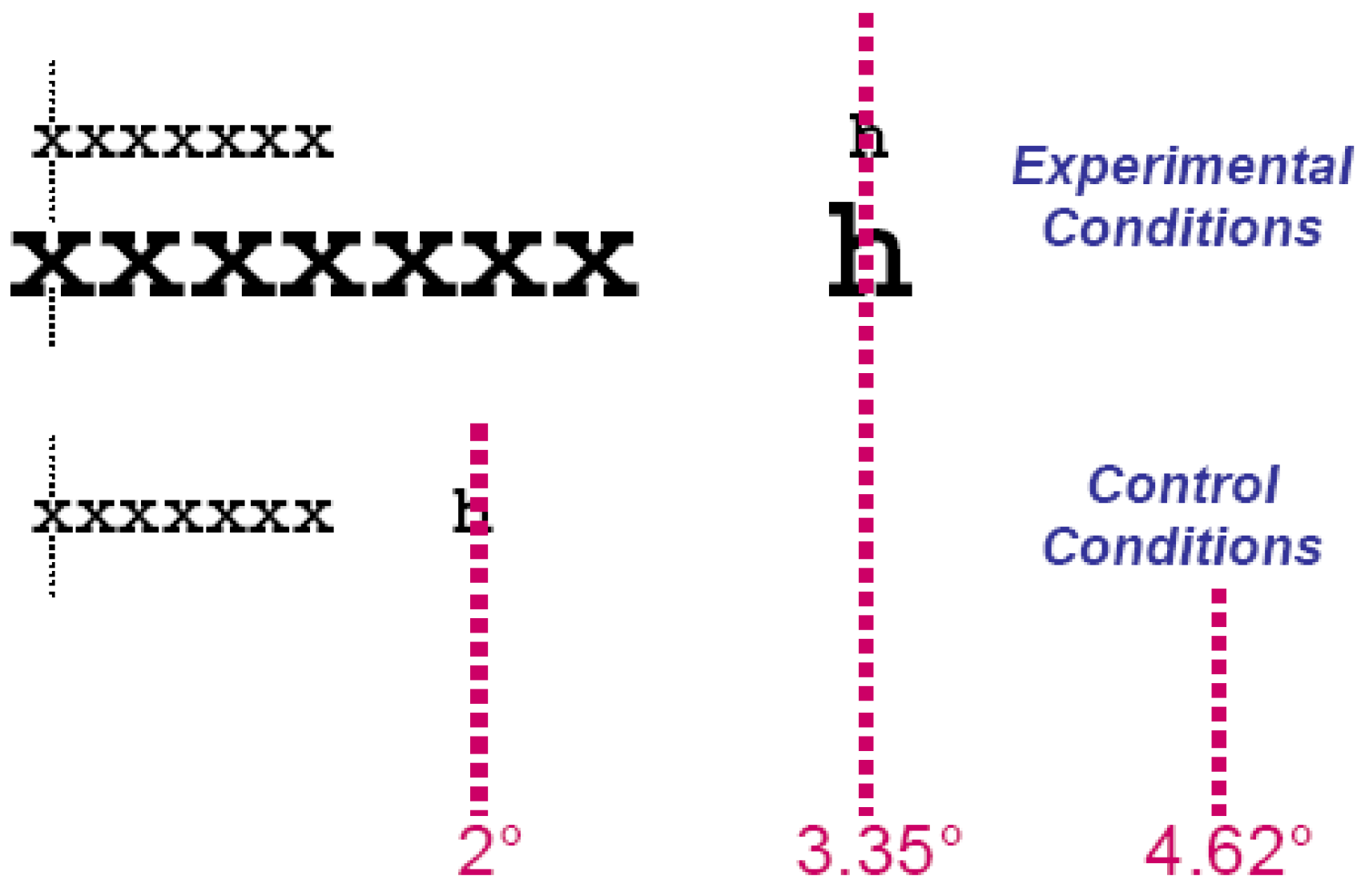
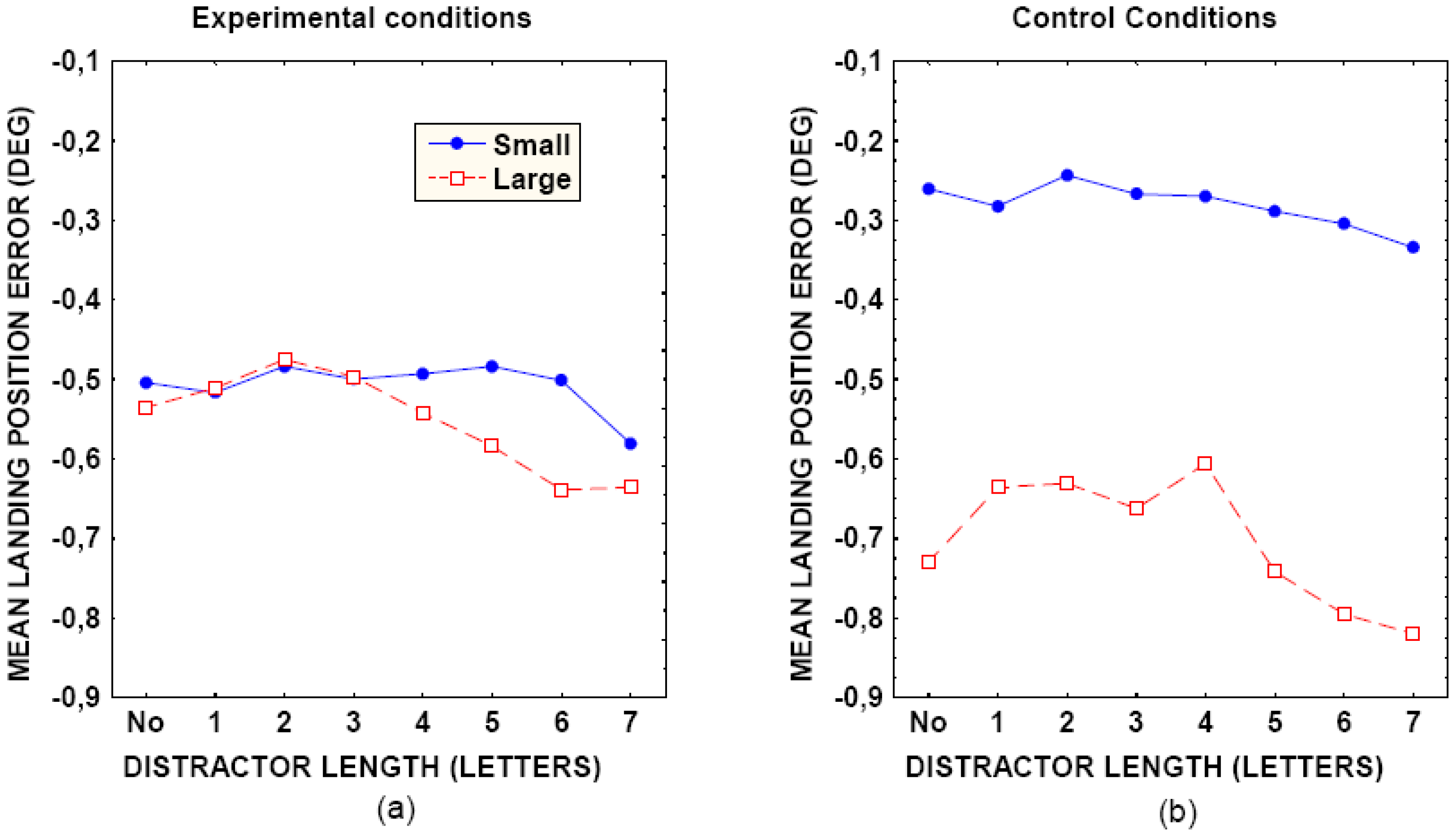
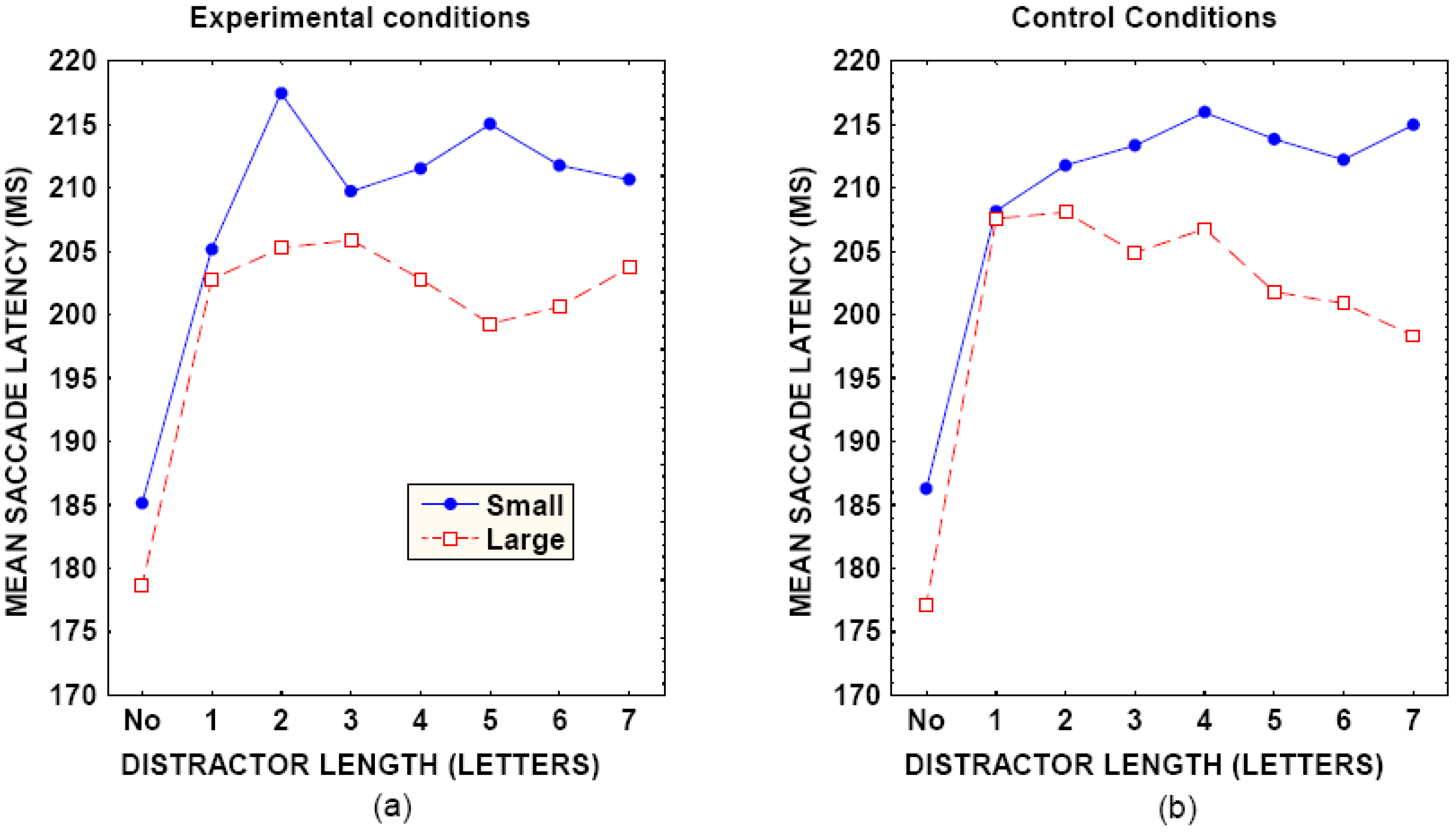
A foveal dead zone for the global effect
The global effect within a limited peripheral window
Accounting for eye movements in reading
Acknowledgments
References
- Arai, K., R. M. McPeek, and E. L. Keller. 2004. Properties of saccadic responses in monkey when multiple competing visual stimuli are present. Journal of Neurophysiology 91: 890–900. [Google Scholar] [PubMed]
- Brysbaert, M., D. Drieghe, and F. Vitu. 2005. Edited by G. Underwood. Word skipping: Implications for theories of eye movement control in reading. In Cognitive processes in eye guidance. Oxford, NY: Oxford University Press, pp. 53–77. [Google Scholar]
- Brysbaert, M., and F. Vitu. 1998. Edited by G. Underwood. Word skipping: Implications for theories of eye movement control in reading. In Eye guidance in reading and scene perception. Oxford: Elsevier, pp. 125–147. [Google Scholar]
- Chou, I. H., M. A. Sommer, and P. H. Schiller. 1999. Express averaging saccades in monkeys. Vision Research 39, 25: 4200–4216. [Google Scholar] [PubMed]
- Coëffé, C., and J. K. O’Regan. 1987. Reducing the influence of non-target stimuli on saccade accuracy: Predictability and latency effects. Vision Research 27: 227–240. [Google Scholar] [PubMed]
- Cohen, M. E., and L. E. Ross. 1978. Latency and accuracy characteristics of saccades and corrective saccades in children and adults. Journal of Experimental Child Psychology 26: 517–527. [Google Scholar]
- Coren, S., and P. Hoenig. 1972. Effects of non-target stimuli upon length of volontary saccades. Perceptual and Motor Skills 34: 499–508. [Google Scholar]
- Deubel, H., J. M. Findlay, A. Jacobs, and Brogan. 1988. Edited by G. Lüer, U. Lass and J. ShalloHoffmann. Saccadic eye movements to targets defined by structure differences. In Eye movement research: Physiological and psychological aspects. Toronto: Hogrefe, pp. 107–145. [Google Scholar]
- Deubel, H., W. Wolf, and G. Hauske. 1984. Edited by A. G. Gale and F. Johnson. The evaluation of the oculomotor error signal. In Theoretical and applied aspects of eye movement research. Elsevier Science Publishers B.V. (North Holland): pp. 55–62. [Google Scholar]
- Edelman, J. A., and E. L. Keller. 1998. Dependence on target configuration of express saccade-related activity in the primate superior colliculus. Journal of Neurophysiology 80, 3: 1407–1426. [Google Scholar] [CrossRef]
- Eggert, T., U. Sailer, J. Ditterich, and A. Straube. 2002. Differential effect of a distractor on primary saccades and perceptual localization. Vision Research 42: 2969–2984. [Google Scholar]
- Engbert, R., A. Nuthmann, E. Richter, and R. Kliegl. 2005. Swift: A dynamical model of saccade generation during reading. Psychological Review 112, 4: 777–813. [Google Scholar]
- Findlay, J. M. 1982. Global visual processing for saccadic eye movements. Vision Research 22: 10331045. [Google Scholar]
- Findlay, J. M. 1997. Saccade target selection during visual search. Vision Research 37, 5: 617–631. [Google Scholar]
- Findlay, J. M. 2004. Edited by F. Ferreira and J. Henderson. Eye scanning and visual search. In Interface of language, vision, and action: Eye movements and the visual world. New York: Psychology Press, pp. 135–159. [Google Scholar]
- Findlay, J. M., and H. I. Blythe. in press. Saccade target selection: Do distractors affect saccade accuracy? Vision Research. [Google Scholar]
- Findlay, J. M., D. Brogan, and M. G. Wenban-Smith. 1993. The spatial signal for saccadic eye movements emphasizes visual boundaries. Perception & Psychophysics 53, 6: 633–641. [Google Scholar]
- Findlay, J. M., and V. Brown. 2006. Eye scanning of multi-element displays: Ii. Saccade planning. Vision Research 46, 1-2: 216–227. [Google Scholar] [CrossRef]
- Findlay, J. M., V. Brown, and I. D. Glichrist. 2001. Saccade target selection in visual search: The effect of information from the previous fixation. Vision Research 41, 1: 87–95. [Google Scholar]
- Findlay, J. M., and I. D. Gilchrist. 1997. Spatial scale and saccade programming. Perception 26: 1159–1167. [Google Scholar] [CrossRef]
- Findlay, J. M., and Z. Kapoula. 1992. Scrutinization, spatial attention, and the spatial programming of saccadic eye movements. The Quarterly Journal of Experimental Psychology 45A, 4: 633–647. [Google Scholar]
- Findlay, J. M., and R. Walker. 1999. A model of saccade generation based on parallel processing and competitive inhibition. Behavioral and Brain Sciences 22, 4: 661–720. [Google Scholar]
- Gandhi, N. J., and E. L. Keller. 1999. Comparison of saccades perturbed by stimulation of the rostral superior colliculus, the caudal superior colliculus, and the omnipause neuron region. Journal of Neurophysiology 82, 6: 3236–3253. [Google Scholar] [PubMed]
- Godjin, R., and J. Theeuwes. 2002. Programming of endogenous and exogenous saccades: Evidence for a competitive integration model. Journal of Experimental Psychology:Human Perception and Performance 28, 5: 1039–1054. [Google Scholar]
- Goffart, L., Z. M. Hafed, N. Dill, and R. J. Krauzlis. 2006. Changes in eye position during fixation caused by inactivation of the rostral superior colliculus. Neuroscience. [Google Scholar]
- Guez, J. E., P. Marchal, J. F. Le Gargasson, Y. Grall, and J. K. O’Regan. 1994. Eye fixations near corners: Evidence for a centre of gravity calculation based on contrast, rather than luminance or curvature. Vision Research 34, 12: 1625–1635. [Google Scholar]
- He, P. Y., and E. Kowler. 1989. The role of location probability in the programming of saccades: Implications for “center-of-gravity” tendencies. Vision Research 29, 9: 1165–1181. [Google Scholar] [CrossRef] [PubMed]
- He, P. Y., and E. Kowler. 1991. Saccadic localization of eccentric forms. Journal of the Optical Society of America 8, 2: 440–449. [Google Scholar] [CrossRef]
- Jacobs, A. 1987. On localization and saccade programming. Vision Research 27, 11: 1953–1966. [Google Scholar] [CrossRef] [PubMed]
- Just, M. A., and P. A. Carpenter. 1980. A theory of reading: From eye fixations to comprehension. Psychological Review 87: 329–354. [Google Scholar] [CrossRef]
- Kapoula, Z. 1985. Evidence for a range effect in the saccadic system. Vision Research 25, 8: 1155–1157. [Google Scholar] [CrossRef]
- Lee, C., W. H. Rohrer, and D. L. Sparks. 1988. Population coding of saccadic eye movements by neurons in the superior colliculus. Nature 332, 6162: 357–360. [Google Scholar] [CrossRef]
- McConkie, G. W., P. W. Kerr, M. D. Reddix, and D. Zola. 1988. Eye movement control during reading: I. The location of initial eye fixations on words. Vision Research 28, 10: 1107–1118. [Google Scholar] [CrossRef]
- McDonald, S. A., R. H. S. Carpenter, and R. C. Shillcock. 2005. An anatomically constrained, stochastic model of eye movement control in reading. Psychological Review 112: 814–840. [Google Scholar] [CrossRef] [PubMed]
- McGowan, J. W., E. Kowler, A. Sharma, and C. Chubb. 1998. Saccadic localization of random dot targets. Vision Research 38, 6: 895–909. [Google Scholar] [CrossRef]
- McIlwain, J. T. 1976. Edited by R. Porter. Large receptive fields and spatial transformations in the visual system. In International review of physiology, vol 10, neurophysiology ii. pp. 223–247. [Google Scholar]
- McIlwain, J. T. 1991. Distributed spatial coding in the superior colliculus. Visual Neuroscience 6: 3–13. [Google Scholar] [CrossRef]
- McSorley, E., and J. M. Findlay. 2003. Saccade target selection in visual search: Accuracy improves when more distractors are present. Journal of Vision 3: 877–892. [Google Scholar] [PubMed]
- Melcher, D., and E. Kowler. 2001. Visual scene memory and the guidance of saccadic eye movements. Vision Research 41: 3597–3611. [Google Scholar] [CrossRef] [PubMed]
- Menz, C., and R. Gröner. 1987. Edited by J. K. O’Regan and A. Lévy-Schoen. Saccadic programming with multiple targets under different task conditions. In Eye movements: From physiology to cognition. Amsterdam: North-Holland. [Google Scholar]
- Munoz, D. P., and J. H. Fecteau. 2002. Edited by J. Hyönä, D. P. Munoz, W. Heide and R. Radach. Vying for dominance: Dynamic interactions control visual fixation and saccadic initiation in the superior colliculus. In Progress in brain research. Elsevier Science B.V.: Vol. 140, pp. 3–19. [Google Scholar]
- Munoz, D. P., and R. H. Wurtz. 1993a. Fixation cells in monkey superior colliculus. I. Characteristics of cell discharge. Journal of Neurophysiology 70, 2: 559575. [Google Scholar] [CrossRef]
- Munoz, D. P., and R. H. Wurtz. 1993b. Fixation cells in monkey superior colliculus. Ii. Reversible activation and deactivation. Journal of Neurophysiology 70, 2: 576–589. [Google Scholar] [PubMed]
- Nazir, T. 1991. On the role of refixations in letter strings: The influence of oculomotor factors. Perception and Psychophysics 49, 4: 373–389. [Google Scholar]
- Nuthmann, A., R. Engbert, and R. Kliegl. 2007. The iovp effect in mindless reading: Experiment and modeling. Vision Research 47: 990–1002. [Google Scholar] [CrossRef]
- Nuthmann, A., F. Vitu, R. Kliegl, and R. Engbert. in preparation. Failure to replicate the range effect in a simple oculomotor task - implications for eye-movement control in reading. [Google Scholar]
- O’Regan, J. K. 1989. Edited by B. Elsendoorn and H. Bouma. Visual acuity, lexical structure and eye movements in word recognition. In Working models of human perception. Academic Press: London: pp. 261–292. [Google Scholar]
- O’Regan, J. K. 1990. Edited by E. Kowler. Eye movements and reading. In Eye movements and their role in visual and cognitive processes. Elsevier: pp. 395–453. [Google Scholar]
- O’Regan, J. K. 1992. Edited by K. Rayner. Optimal viewing position in words and the strategy-tactics theory of eye movements in reading. In Eye movements and visual cognition: Scene perception and reading. New York: Springer-Verlag. [Google Scholar]
- O’Regan, J. K., and A. Lévy-Schoen. 1987. Edited by M. Coltheart. Eye movement strategy and tactics in word recognition and reading. In Attention and performance xii: The psychology of reading. Hillsdale, NJ: Erlbaum, p. 363383. [Google Scholar]
- Ottes, F. P., J. A. M. Van Gisbergen, and J. J. Eggermont. 1984. Metrics of saccade responses to visual double stimuli-2 different modes. Vision Research 25: 849862. [Google Scholar]
- Ottes, F. P., J. A. M. Van Gisbergen, and J. J. Eggermont. 1985. Latency dependence of colour-based target vs. Nontarget discrimination by the saccadic system. Vision Research 25, 6: 849–862. [Google Scholar]
- Rayner, K. 1979. Eye guidance in reading: Fixation location within words. Perception 8: 21–30. [Google Scholar]
- Rayner, K., and M. H. Fischer. 1996. Mindless reading revisited: Eye movements during reading and scanning are different. Perception & Psychophysics 58, 5: 734–747. [Google Scholar]
- Reichle, E. D., K. Rayner, and A. Pollatsek. 2003. The ez reader model of eye movement control in reading: Comparisons to other models. Behavioral and Brain Sciences 26: 445–526. [Google Scholar] [CrossRef] [PubMed]
- Reilly, R., and J. K. O’Regan. 1998. Eye movement control during reading: A simulation of some wordtargeting strategies. Vision Res 38, 2: 303–317. [Google Scholar] [CrossRef] [PubMed]
- Reilly, R., and R. Radach. 2003. Edited by J. Hyönä, R. Radach and H. H. Deubel. Foundations of an interactive model of eye movement control in reading. In Cognitive and applied aspects of eye movement research. Amsterdam: Elsevier, pp. 429–455. [Google Scholar]
- Reilly, R., and R. Radach. 2006. Some empirical tests of an interactive activation model of eye movement control in reading. Cognitive Systems Research 7: 34–55. [Google Scholar] [CrossRef]
- Rovamo, J., V. Virsu, and R. Nasanen. 1978. Cortical magnification factor predicts photopic contrast sensitivity of peripheral vision. Nature 271, 5640: 54–56. [Google Scholar]
- Van Rensbergen, J., and A. de Troy. 1993. A reference guide for the leuven dual-pc controlled purkinje eyetracking system. Technical Report. Laboratory of Experimental Psychology, Catholic University of Leuven. [Google Scholar]
- Vitu, F. 1991a. The existence of a center of gravity effect during reading. Vision Research 31, 7/8: 12891313. [Google Scholar] [CrossRef]
- Vitu, F. 1991b. Research note: Against the existence of a range effect during reading. Vision Research 31, 11: 2009–2015. [Google Scholar] [CrossRef]
- Vitu, F. 2003. The basic assumptions of e-z reader are not well-founded. Behavioral and Brain Sciences 26, 4: 506–507. [Google Scholar] [CrossRef]
- Vitu, F. 2005. Edited by G. Underwood. Visual extraction processes and regressive saccades in reading. In Cognitive processes in eye guidance. Oxford, NY: Oxford University Press, pp. 1–32. [Google Scholar]
- Vitu, F., and S. Casteau. 2008. Saccadic eye movements in two-stimulus visual displays: Foveal and peripheral distractor stimuli are not equal. Perception 35. ECVP Abstract Supplement. [Google Scholar]
- Vitu, F., D. Lancelin, A. Jean, and F. Farioli. 2006. Influence of foveal distractors on saccadic eye movements: A dead zone for the global effect. Vision Research 46: 4684–4708. [Google Scholar] [CrossRef]
- Vitu, F., D. Lancelin, and V. Marrier d’Unienville. 2007. A perceptual-economy account for the Inverted-Optimal Viewing Position effect. Journal of Experimental Psychology: Human Perception and Performance 33, 5: 1220–1249. [Google Scholar]
- Vitu, F., J. K. O’Regan, A. W. Inhoff, and R. Topolski. 1995. Mindless reading: Eye-movement characteristics are similar in scanning letter strings and reading texts. Perception and Psychophysics 57: 352–364. [Google Scholar] [CrossRef] [PubMed]
- Viviani, P., and R. G. Swensson. 1982. Saccadic eye movements to peripherally discriminated visual targets. Journal of Experimental Psychology: Human Perception and Performance 8, 1: 113–126. [Google Scholar] [CrossRef] [PubMed]
- Walker, R., H. Deubel, W. X. Schneider, and J. M. Findlay. 1997. Effect of remote distractors on saccade programming: Evidence for an extended fixation zone. Journal of Neurophysiology 78, 2: 1108–1119. [Google Scholar] [CrossRef]
- Weber, H., A. Latanov, and B. Fischer. 1993. Context dependent modulations of express and regular saccades in man and monkey. Experimental Brain Research 93: 335–344. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.-N. 2006. An oculomotor-based model of eye movements in reading: The competition-interaction model. Cognitive Systems Research 7: 56–69. [Google Scholar] [CrossRef]
- Yang, S.-N., and G. W. McConkie. 2001. Eye movements during reading: A theory of saccade initiation times. Vision Research 41: 3567–3585. [Google Scholar] [CrossRef]
- Yang, S.-N., and G. W. McConkie. 2004. Saccade generation during reading: Are words necessary? The European Journal of Cognitive Psychology 16, 1/2. [Google Scholar] [CrossRef]
- Zelinsky, G. J., R. P. N. Rao, M. M. Hayhoe, and D. H. Ballard. 1997. Eye movements reveal the spatiotemporal dynamics of visual search. Psychological Science 8: 448–453. [Google Scholar] [CrossRef]



Copyright © 2008. This article is licensed under a Creative Commons Attribution 4.0 International License.
Share and Cite
Vitu, F. About the Global Effect and the Critical Role of Retinal Eccentricity: Implications for Eye Movements in Reading. J. Eye Mov. Res. 2008, 2, 1-18. https://doi.org/10.16910/jemr.2.3.6
Vitu F. About the Global Effect and the Critical Role of Retinal Eccentricity: Implications for Eye Movements in Reading. Journal of Eye Movement Research. 2008; 2(3):1-18. https://doi.org/10.16910/jemr.2.3.6
Chicago/Turabian StyleVitu, Françoise. 2008. "About the Global Effect and the Critical Role of Retinal Eccentricity: Implications for Eye Movements in Reading" Journal of Eye Movement Research 2, no. 3: 1-18. https://doi.org/10.16910/jemr.2.3.6
APA StyleVitu, F. (2008). About the Global Effect and the Critical Role of Retinal Eccentricity: Implications for Eye Movements in Reading. Journal of Eye Movement Research, 2(3), 1-18. https://doi.org/10.16910/jemr.2.3.6


