Lobatto-Milstein Numerical Method in Application of Uncertainty Investment of Solar Power Projects
Abstract
:1. Introduction
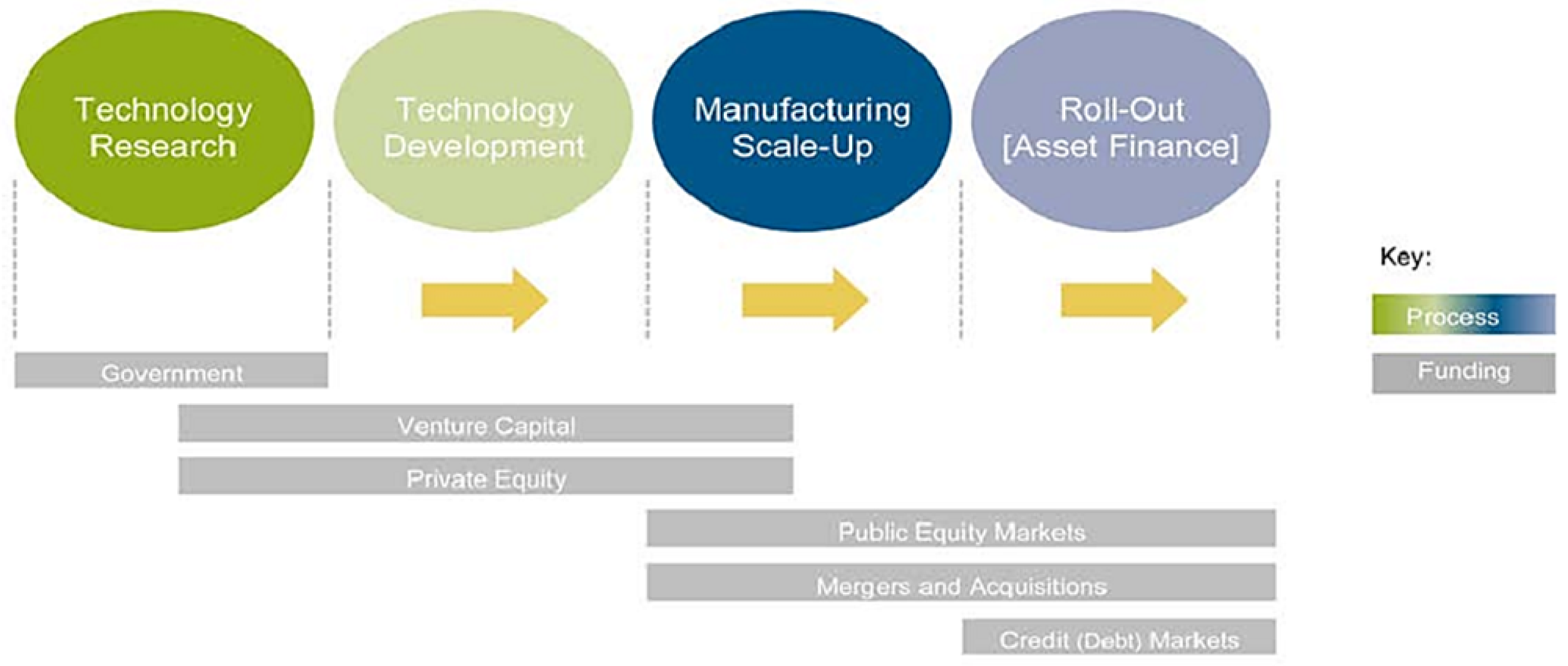
2. Renewable Energy Investment
- Regulatory price-based mechanisms (a payment for kWh of energy produced)
- Regulatory quantity-based mechanisms (the government sets a desired level of RES, and “green” generators receive tradable certificates according to their production)
- The type of instrument (e.g., feed-in tariffs, tradable green certificates)
- Constantly changing support schemes
- The design details of the particular instrument
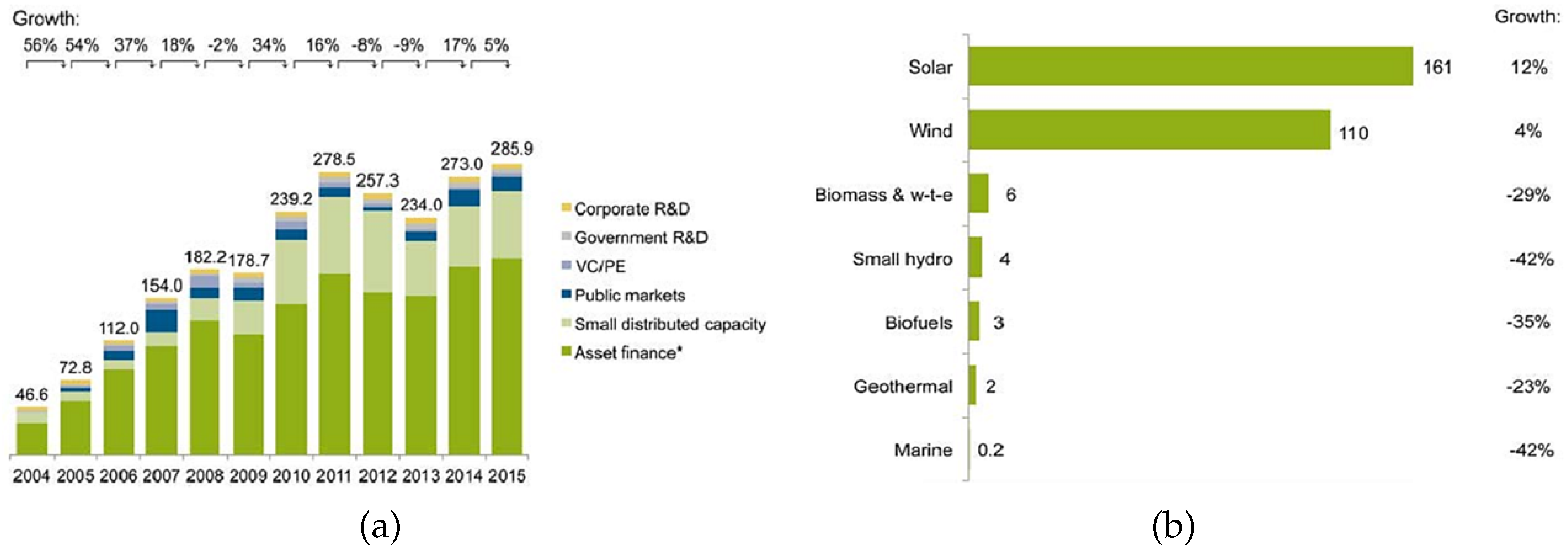
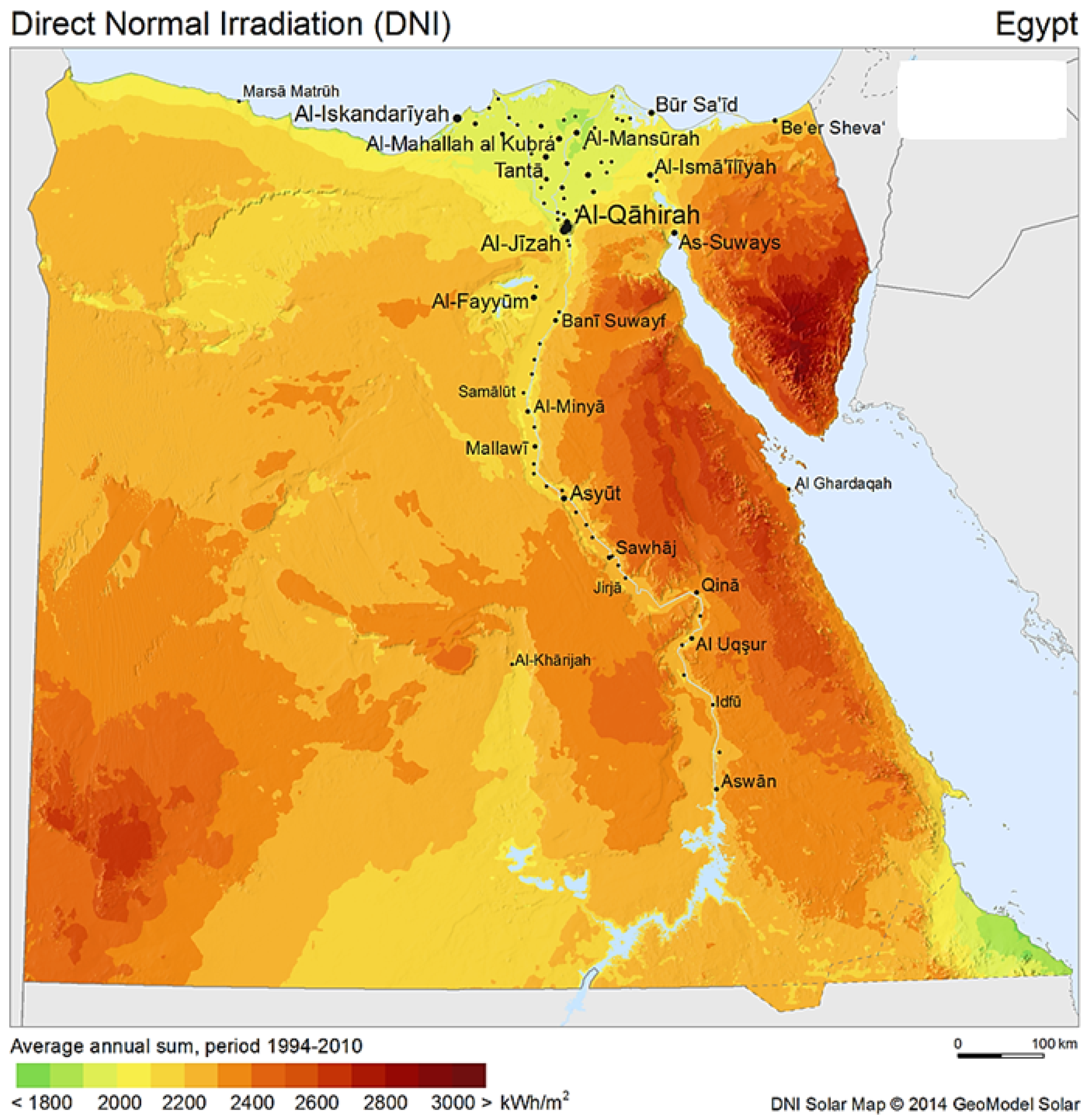
3. Renewable Energy Sector in Egypt
- Public competitive bidding:Issuing tenders internationally requesting the private sector to supply power from RE projects.
- Third party access (TPA):Investors are allowed to build and operate RE power plants to satisfy their electricity needs or to sell electricity to other consumers though the national grid.
- Feed-in tariff (FIT):In September 2014, the government passed the key Feed-In Tariff Law (the feed-in tariff enacted by decree 1947/2014 [43,44]), triggering wide interest from international developers and investors. The main parameters of the feed-in tariffs are:
- Solar power stations: The value of the tariff is divided into five scales according to the production capacity of the station, and the value of the tariff will be fixed during the contract period, which reaches 25 years.
- Land allocation: Through the use of the craft scheme for a period of time equal to the contract period. Furthermore, the land will be given just 2% of the total power generated revenue from the plant. In addition, the customs will be 2% of the total items cost.
- Electricity: That produced through renewable energy stations has priority access to the electricity grid.
- Government support and guarantee: For power stations that exceed 500 kW, include low-interest credit facilities.
- Net metering:In January 2013, EgyptERAadopted a net-metering policy that allows small-scale renewable energy projects to feed electricity to the grid. Generated surplus electricity will be discounted from the balance through the net-metering process.
- Quota system:Heavy industries will be obliged to use a percentage of their electricity consumption from RE sources.
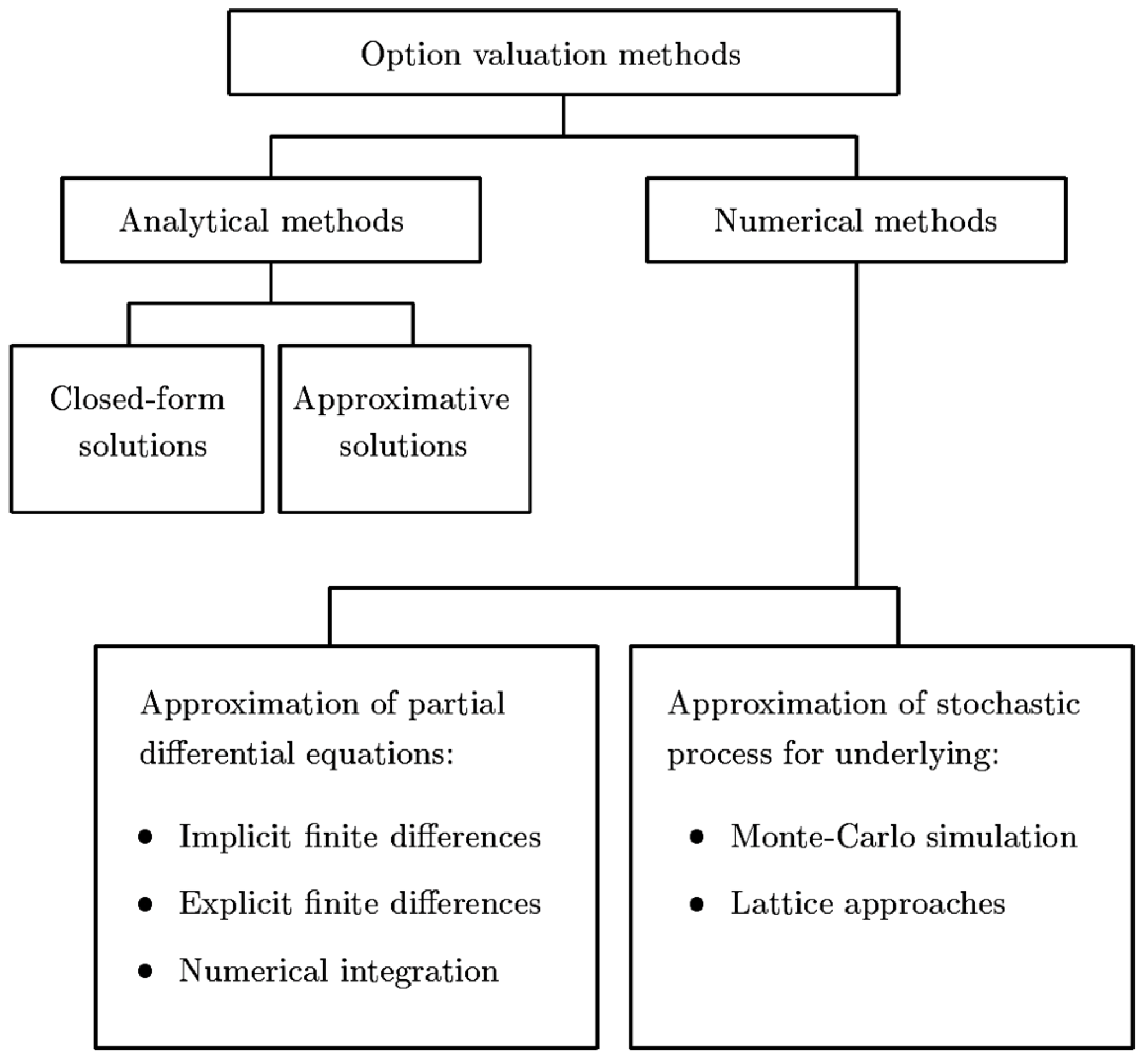
4. The Lobatto3C-Milstein Method for SDEs
5. The Real Option Framework
- Finding uncertainty investment opportunity.
- The probability distribution of the uncertainties is approximated.
- Know and analyze available real options.
- Real option valuation.
- Develop real options mind-set: by comparing the value of the options and the cost to obtain options, a set of strategies and decisions can be reached. Meanwhile, the mind-set regarding flexibility that is available and different is established.
5.1. Framework Application
- Availability of the solar energy source:At the outset, since this is not known with certainty, the availability of renewables has to be estimated. The investor can estimate the installed capacity (MW) of the solar energy plant and produced energy (kWh) by environmental assessment studies.
- Estimated cost of establishing the solar energy plant:The estimated development cost is the exercise price of the option. The cost of establishing the solar energy plant can be estimated by feasibility studies for the projects.
- Time to expiration of the option:The life of an RE option can be defined as a contract period; that period will be the lifetime of the option. For example, the contract in the sector of RE is a long-term contract of approximately 20 to 25 years.
- Variance in the value of the cash flows:The variance in the value of the cash flows is determined by two factors, variability in the pricing system of the RE and variability in the estimate of the availability of the RE. In the more realistic case where the average of the RE resources and the RE price can change over time, the option becomes more difficult to value.
- Cost of delay:Since the net production revenue cannot be started instantaneously, a time lag has to be allowed between the decision to establish the solar energy plant, and the actual production is the cost of delay (If the cash flows are evenly distributed over time and the exclusive rights last n years (20 years), the annual cost of delay can be written as: a year. Though, this cost of delay rises each year, to in Year 2, in Year 3, and so on, making the cost of delaying the exercise larger over time.).
5.2. Stochastic Model
The Deferred Option
6. A Case Study: 140-MW Solar Power Plant in Kuraymat, Egypt
- The installed capacity is MW, including the solar share of 20 MW (think of the total area of the integrated solar field being about 644,000 m and the total solar collectors is about 1920 solar collectors containing 53,760 mirrors) (NREA annual report 2012/2013 [42]).
- The total cost is about $ million, and the development lag is four years (NREA annual report 2012/2013 [42]).
- The risk-free interest rate considered is %, which corresponds to the 10-year Egypt government debt in September 2014 (source: Egypt Central Bank [49]).
6.1. Estimate Discount Cash Flows
- 500 kW up to 20 MW: $0.136
- 20 MW up to 50 MW: $0.1434
6.2. Estimate the Volatility
6.3. Valuation of the Deferred Option
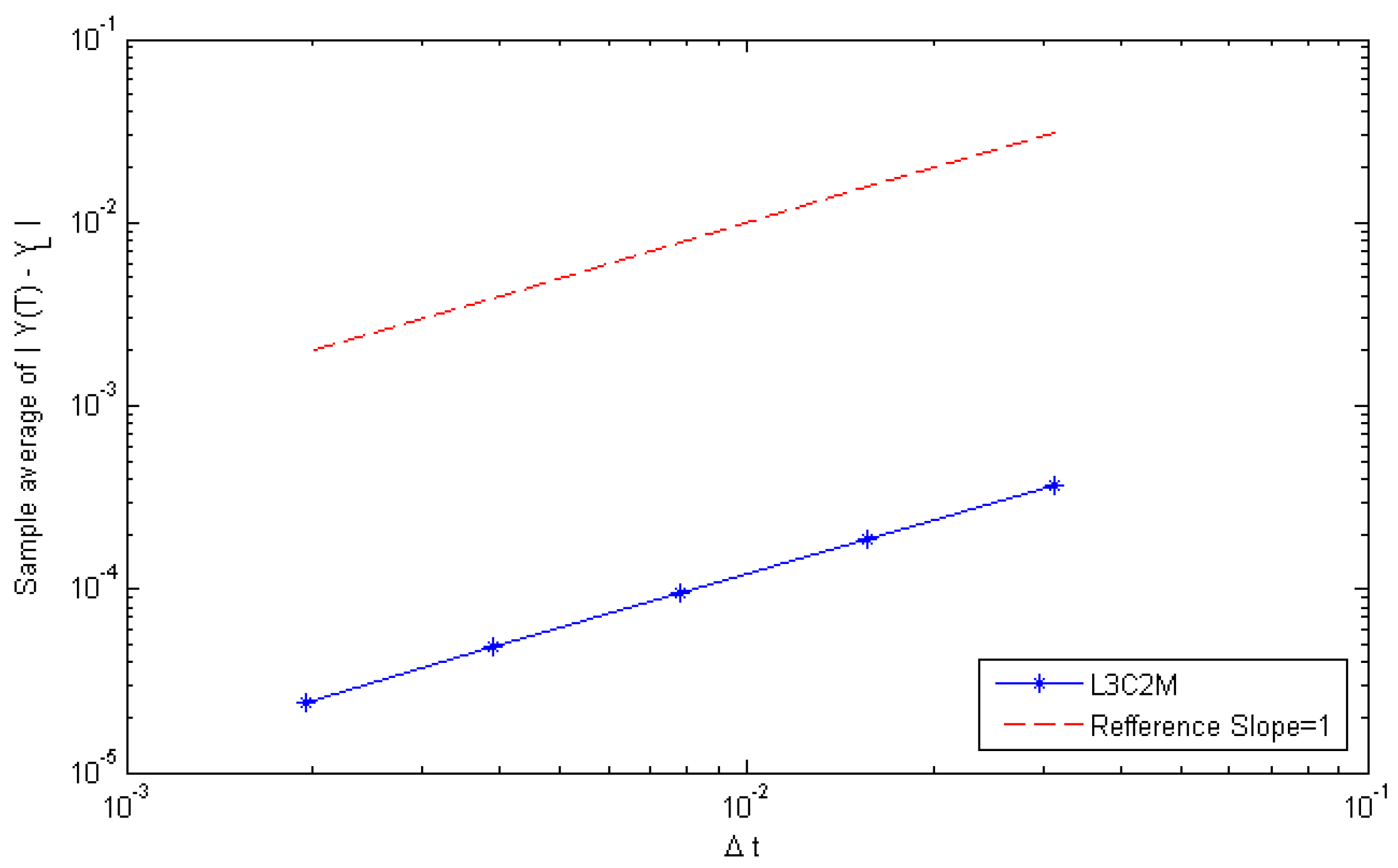
6.3.1. L3C2M Method
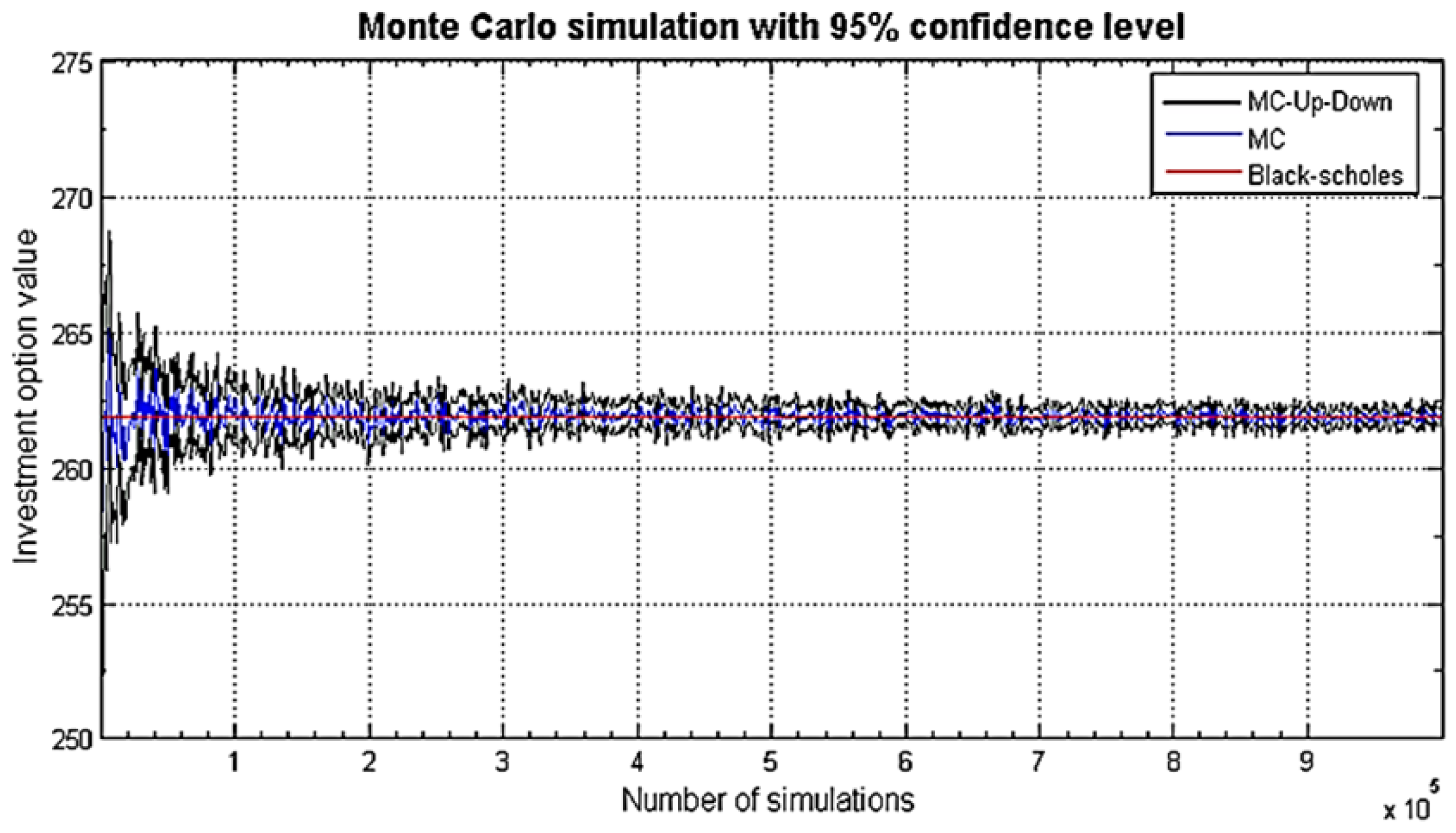
6.3.2. Monte Carlo Simulation
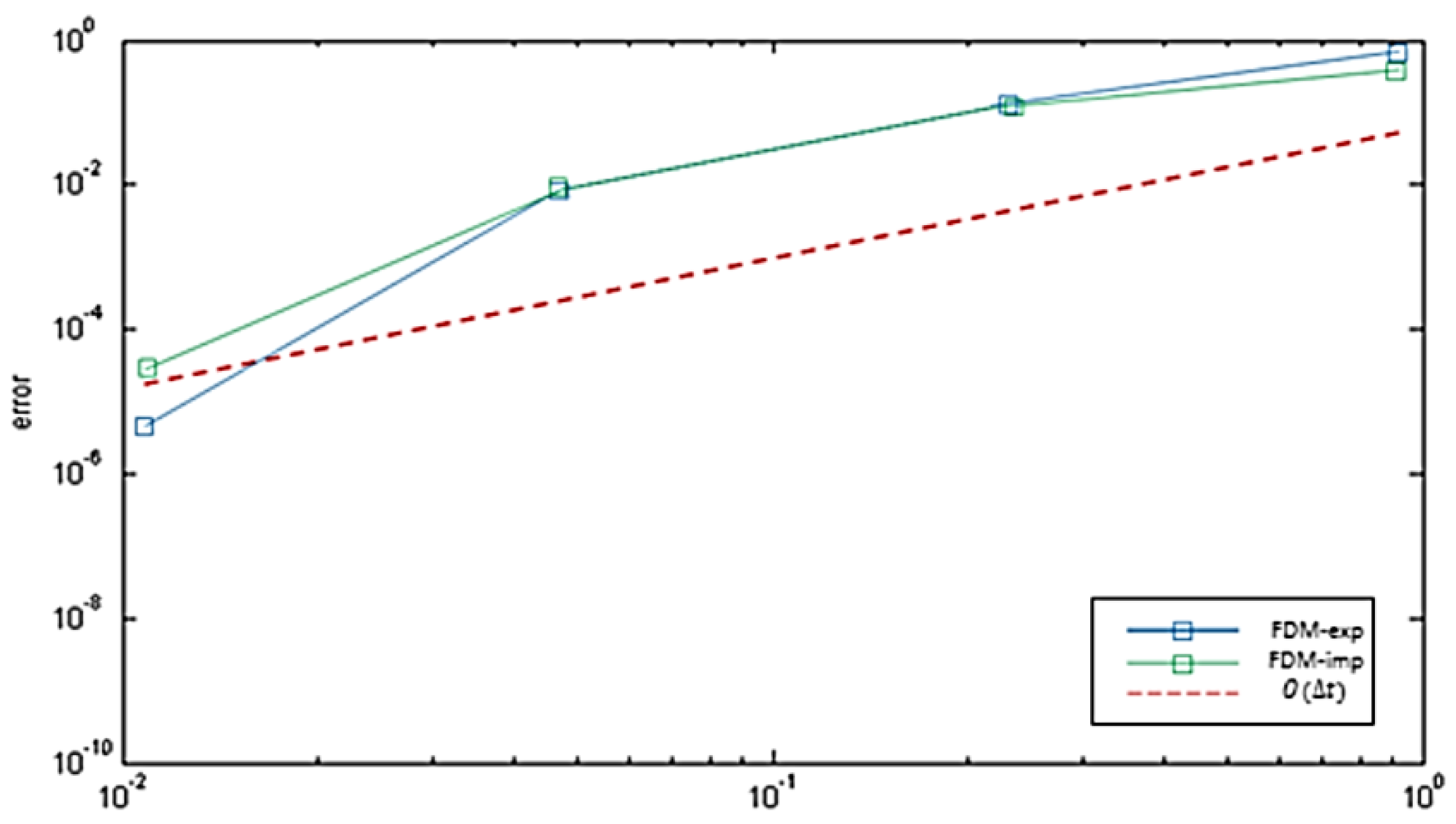
6.3.3. Finite Difference Method
6.4. Discussion of the Results
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
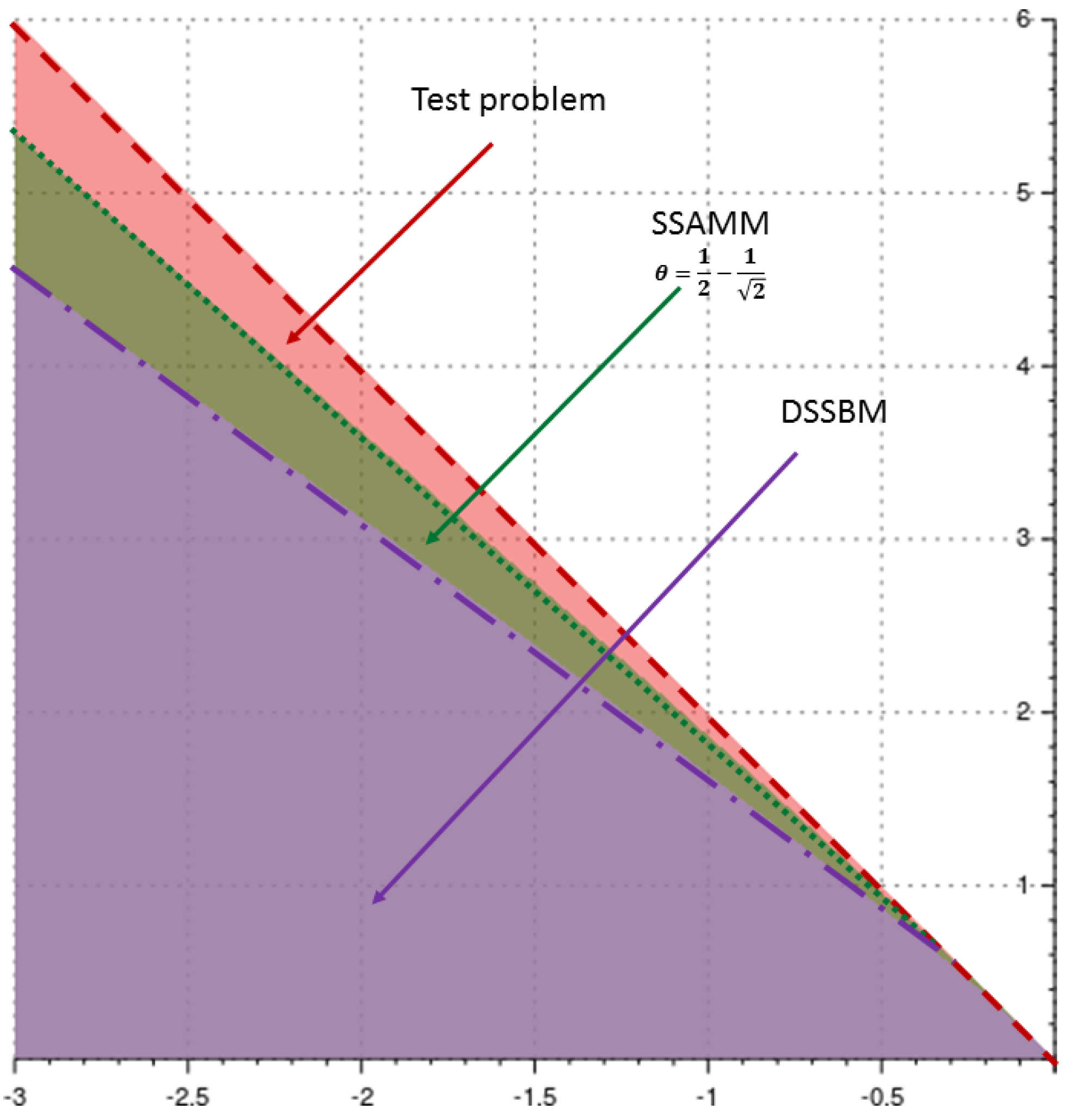
Appendix A. Background of Lobatto3C Methods
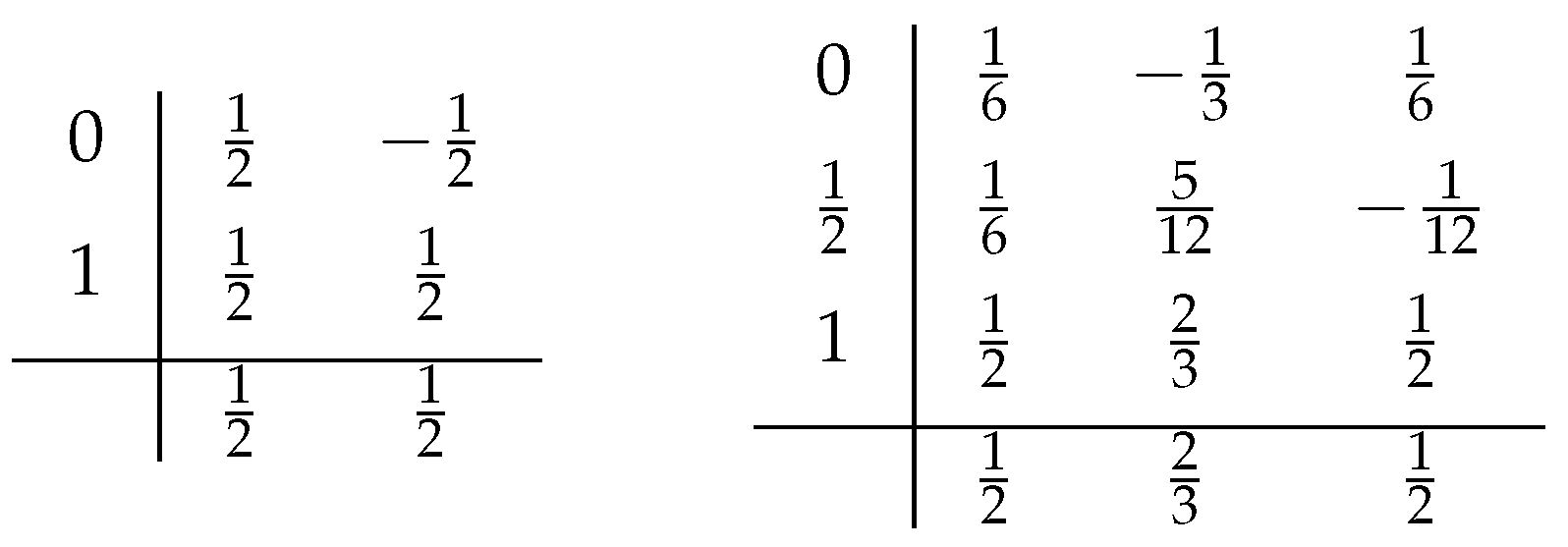
References
- World Wildlife Fund (WWF). The Energy Report—100% Renewable Energy by 2050; WWF: Gland, Switzerland, 2011. [Google Scholar]
- International Energy Outlook (IEO). 2016. Available online: http://www.eia.gov/forecasts/ieo/ (accessed on 5 August 2016).
- Andersson, B.A.; Azar, C.; Holmberg, J.; Karlsson, S. Material constraints for thin-film solar cells. Energy 1998, 23, 407–411. [Google Scholar] [CrossRef]
- Parida, B.; Iniyan, S.; Goic, R. A review of solar photovoltaic technologies. Renew. Sustain. Energy Rev. 2011, 15, 1625–1636. [Google Scholar] [CrossRef]
- EIA (2016) Updated Capital Cost Estimates for Electricity Generation Plants. Available online: www.eia.gov/forecasts/ieo/pdf/0484(2016).pdf (accessed on 5 August 2016).
- Wiser, R.; Bolinger, M.; Barbose, G. Using the federal production tax credit to build a durable market for wind power in the United States. Electr. J. 2007, 20, 77–88. [Google Scholar] [CrossRef]
- Fagiani, R.; Barquín, J.; Hakvoort, R. Risk-based assessment of the cost-efficiency and the effectivity of renewable energy support schemes: Certificate markets versus feed-in tariffs. Energy Policy 2013, 55, 648–661. [Google Scholar] [CrossRef]
- Daim, T.U.; Amer, M.; Brenden, R. Technology roadmapping for wind energy: Case of the Pacific Northwest. J. Clean. Prod. 2012, 20, 27–37. [Google Scholar] [CrossRef]
- Sorsimo, A. Numerical Methods in Real Option Analysis. Master’s Thesis, Aalto University, Helsinki, Finland, 2015. [Google Scholar]
- Toke, D. Renewable financial support systems and cost-effectiveness. J. Clean. Prod. 2007, 15, 280–287. [Google Scholar] [CrossRef]
- Dixit, A.K.; Pindyck, R.S. Investment under Uncertainty; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Graham, J.R.; Harvey, C.R. The theory and practice of corporate finance: Evidence from the field. J. Financ. Econ. 2001, 60, 187–243. [Google Scholar] [CrossRef]
- Graham, J.; Harvey, C. How do CFOs make capital budgeting and capital structure decisions? J. Appl. Corp. Financ. 2002, 15, 8–23. [Google Scholar] [CrossRef]
- Fernandes, B.; Cunha, J.; Ferreira, P. The use of real options approach in energy sector investments. Renew. Sustain. Energy Rev. 2011, 15, 4491–4497. [Google Scholar] [CrossRef] [Green Version]
- Abadie, L.M.; Chamorro, J.M. Valuation of wind energy projects: A real options approach. Energies 2014, 7, 3218–3255. [Google Scholar] [CrossRef]
- Gazheli, A.; Di Corato, L. Land-use change and solar energy production: A real option approach. Agric. Financ. Rev. 2013, 73, 507–525. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: Berlin, Germany, 1999. [Google Scholar]
- Kloeden, P.E.; Platen, E. Higher-order implicit strong numerical schemes for stochastic differential equations. J. Stat. Phys. 1992, 66, 283–314. [Google Scholar] [CrossRef]
- Higham, D.J.; Mao, X.; Stuart, A.M. Strong convergence of Euler-type methods for nonlinear stochastic differential equations. SIAM J. Numer. Anal. 2002, 40, 1041–1063. [Google Scholar] [CrossRef]
- Ding, X.; Ma, Q.; Zhang, L. Convergence and stability of the split-step θ-method for stochastic differential equations. Comput. Math. Appl. 2010, 60, 1310–1321. [Google Scholar] [CrossRef]
- Huang, C. Exponential mean square stability of numerical methods for systems of stochastic differential equations. J. Comput. Appl. Math. 2012, 236, 4016–4026. [Google Scholar] [CrossRef]
- Wang, P.; Liu, Z. Split-step backward balanced Milstein methods for stiff stochastic systems. Appl. Numer. Math. 2009, 59, 1198–1213. [Google Scholar] [CrossRef]
- Guo, Q.; Li, H.; Zhu, Y. The improved split-step θ methods for stochastic differential equation. Math. Methods Appl. Sci. 2014, 37, 2245–2256. [Google Scholar] [CrossRef]
- Voss, D.A.; Khaliq, A.Q. Split-step Adams-Moulton Milstein methods for systems of stiff stochastic differential equations. Int. J. Comput. Math. 2015, 92, 995–1011. [Google Scholar] [CrossRef]
- Tian, B.; Eissa, M.A.; Zhang, S. Two families of theta milstein methods in a real options framework. In Proceedings of the 5th Annual International Conference on Computational Mathematics, Computational Geometry and Statistics (CMCGS 2016), Singapore, 18–19 January 2016.
- Copeland, T.E.; Weston, J.F.; Shastri, K. Financial Theory and Corporate Policy, 4th ed.; Pearson Addison Wesley: New York, NY, USA, 2005. [Google Scholar]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Merton, R.C. Theory of rational option pricing. Bell J. Econ. Manag. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef]
- Brennan, M.J.; Schwartz, E.S. Finite difference methods and jump processes arising in the pricing of contingent claims: A synthesis. J. Financ. Quant. Anal. 1978, 13, 461–474. [Google Scholar] [CrossRef]
- Boyle, P.P. Options: A monte carlo approach. J. Financ. Econ. 1977, 4, 323–338. [Google Scholar] [CrossRef]
- Fadugba, S.; Nwozo, C.; Babalola, T. The comparative study of finite difference method and Monte Carlo method for pricing European option. Math. Theory Model. 2012, 2, 60–66. [Google Scholar]
- Pringles, R.; Olsina, F.; Garcés, F. Real option valuation of power transmission investments by stochastic simulation. Energy Econ. 2015, 47, 215–226. [Google Scholar] [CrossRef]
- Thompson, M.; Barr, D. Cut-off grade: A real options analysis. Resour. Policy 2014, 42, 83–92. [Google Scholar] [CrossRef]
- Sauer, T. Numerical Analysis; Pearson: Boston, MA, USA, 2005. [Google Scholar]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems; Springer: Berlin, Germany, 1996. [Google Scholar]
- Global Trends in Renewable Energy Investment 2016, Frankfurt School UNEP Collaborating Centre for Climate and Sustainable Energy Finance. 2016. Available online: http://fs-unep-centre.org/publications/global-trends-renewable-energy-investment-2016 (accessed on 5 August 2016).
- Hirth, L. The market value of variable renewables: The effect of solar wind power variability on their relative price. Energy Econ. 2013, 38, 218–236. [Google Scholar] [CrossRef]
- Scorah, H.; Sopinka, A.; van Kooten, G.C. The economics of storage, transmission and drought: Integrating variable wind power into spatially separated electricity grids. Energy Econ. 2012, 34, 536–541. [Google Scholar] [CrossRef]
- Gross, R.; Blyth, W.; Heptonstall, P. Risks, revenues and investment in electricity generation: Why policy needs to look beyond costs. Energy Econ. 2010, 32, 796–804. [Google Scholar] [CrossRef]
- Egypt in Transition: Infrastructure and Development, British Expertise. Available online: http://www.britishexpertise.org/bx/upload/Events/Egyptintransition_Spring2015_LR.pdf (accessed on 5 August 2016).
- Egyptian Electricity Holding Company (EEHC). Annual Report for FY 2012/2013; EEHC: Cairo, Egypt, 2013. [Google Scholar]
- New and Renewable Energy Authority (NREA). Annual Report 2012/2013. Available online: http://nrea.gov.eg/annual%20report/Annual_Report_2012_2013_eng.pdf (accessed on 5 August 2016).
- Amereller, Investing in Renewable Energy in Egypt. January 2015. Available online: http://amereller.de/fileadmin/PDFs/ALC_Investing-in-Renewable-Energies-Jan-2015.pdf (accessed on 5 August 2016).
- New and Renewable Energy Authority (NREA). Available online: http://nrea.gov.eg/beta/Investors/Legislation (accessed on 5 August 2016).
- Min, K.J.; Lou, C.; Wang, C.H. An exit and entry study of renewable power producers: A real options approach. Eng. Econ. 2012, 57, 55–75. [Google Scholar] [CrossRef]
- Eissa, M.A.; Xiao, Y.; Yang, Z.Y. Lobatto3C-Milstein methods for stiff stochastic differential equations. Appl. Numer. Math. 2016. under review. [Google Scholar]
- Schulmerich, M. Real Options Valuation: The Importance of Interest Rate Modelling in Theory and Practice; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Wang, T. Analysis of Real Options in Hydropower Construction Projects—A Case Study in China. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2003. [Google Scholar]
- The Central Bank of Egypt. Available online: http://www.tradingeconomics.com/egypt/interest-rate (accessed on 5 August 2016).
- New and Renewable Energy Authority (NREA), Annual Report 2009/2010. Available online: http://nrea.gov.eg/annual%20report/annual2010En.pdf (accessed on 5 August 2016).
- Stern, N. Real Option; New York University: New York, NY, USA, 2007. [Google Scholar]
- Egypt’s Information Portal. Available online: http://www.eip.gov.eg/Documents/StudiesDetails.aspx?id=2142 (accessed on 5 August 2016).
- Hairer, E.; Nrsett, S.P.; Wanner, G. Solving Ordinary Differential Equations I: Nonstiff Problems; Springer: Berlin, Germany, 1993. [Google Scholar]
- Ramadan, M.; ElDanaf, T.S.; Eissa, M.A. System of ordinary differential equations solving using cellular neural networks. J. Adv. Math. Appl. 2014, 3, 182–194. [Google Scholar] [CrossRef]
- Ramadan, M.; ElDanaf, T.S.; Eissa, M.A. Approximate solutions of partial differential equations using cellular neural networks. Int. J. Sci. Eng. Investig. 2015, 4, 14–21. [Google Scholar]
- Ehle, B.L. On Pade Approximations to the Exponential Function and a-Stable Methods for the Numerical Solution of Initial Value Problems. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 1969. [Google Scholar]
- Axelsson, O. A note on a class of strongly A-stable methods. BIT Numer. Math. 1972, 12, 1–4. [Google Scholar] [CrossRef]
- Chipman, F. A-stable Runge-Kutta processes. BIT Numer. Math. 1971, 11, 384–388. [Google Scholar] [CrossRef]

| 2010/2011 | 2011/2012 | 2012/2013 | Average |
|---|---|---|---|
| 206 | 479 | 230 | 305 |
| Parameter | Symbol | Value | Unit | Source |
|---|---|---|---|---|
| Current CFfrom investment | 302.8878 | $US million | Section 6.1 | |
| Fixed investment cost | I | 340 | $US million | NREA annual report 2012/2013 [42] |
| Time to invest | T | 25 | Years | Feed-in tariff decree 1947/2014 [43,44] |
| S.d. of cash flows | σ | 0.1045 | Section 6.2 | |
| Risk-free discount rate | r | 0.0875 | Egypt Central Bank [49] |
| MC | FDM-Exp | FDM-Imp | L3C2M | |
|---|---|---|---|---|
| Inputs | (80, 9000) | (80, 9000) | (5000, 172) | |
| Value (V) | 264.8050 | 264.7458 | 264.7362 | 264.7611 |
| Clock time | 48.2573 | 0.7747 | 0.6002 | 0.0695 |
| Error | 0.00024165 | 0.00001804 | 0.00001804 | 0.0000132 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eissa, M.A.; Tian, B. Lobatto-Milstein Numerical Method in Application of Uncertainty Investment of Solar Power Projects. Energies 2017, 10, 43. https://doi.org/10.3390/en10010043
Eissa MA, Tian B. Lobatto-Milstein Numerical Method in Application of Uncertainty Investment of Solar Power Projects. Energies. 2017; 10(1):43. https://doi.org/10.3390/en10010043
Chicago/Turabian StyleEissa, Mahmoud A., and Boping Tian. 2017. "Lobatto-Milstein Numerical Method in Application of Uncertainty Investment of Solar Power Projects" Energies 10, no. 1: 43. https://doi.org/10.3390/en10010043
APA StyleEissa, M. A., & Tian, B. (2017). Lobatto-Milstein Numerical Method in Application of Uncertainty Investment of Solar Power Projects. Energies, 10(1), 43. https://doi.org/10.3390/en10010043





