Partial Stray Inductance Modeling and Measuring of Asymmetrical Parallel Branches on the Bus-Bar of Electric Vehicles
Abstract
:1. Introduction
2. Inverter Layout and Equivalent Circuit of the Bus-Bar
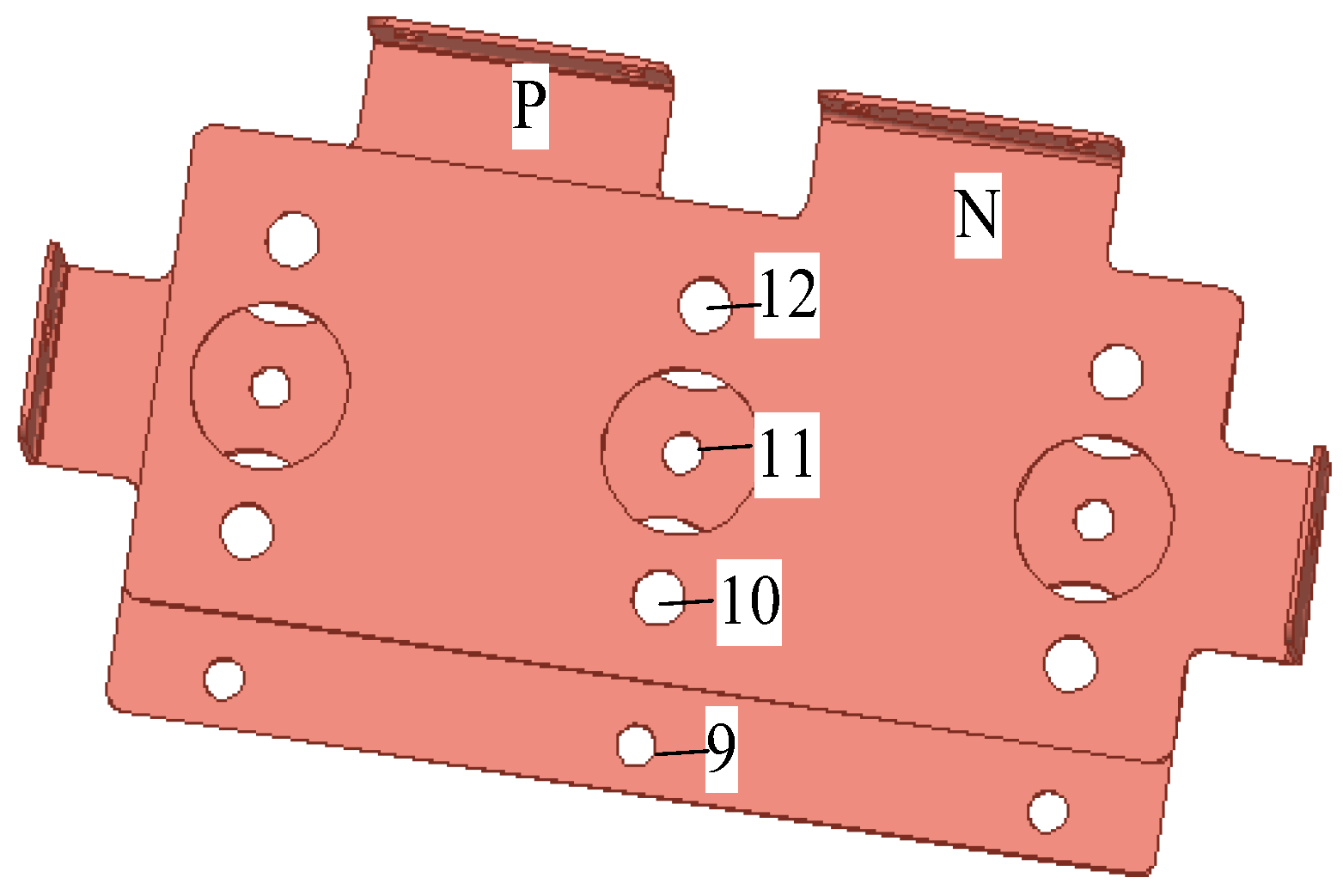
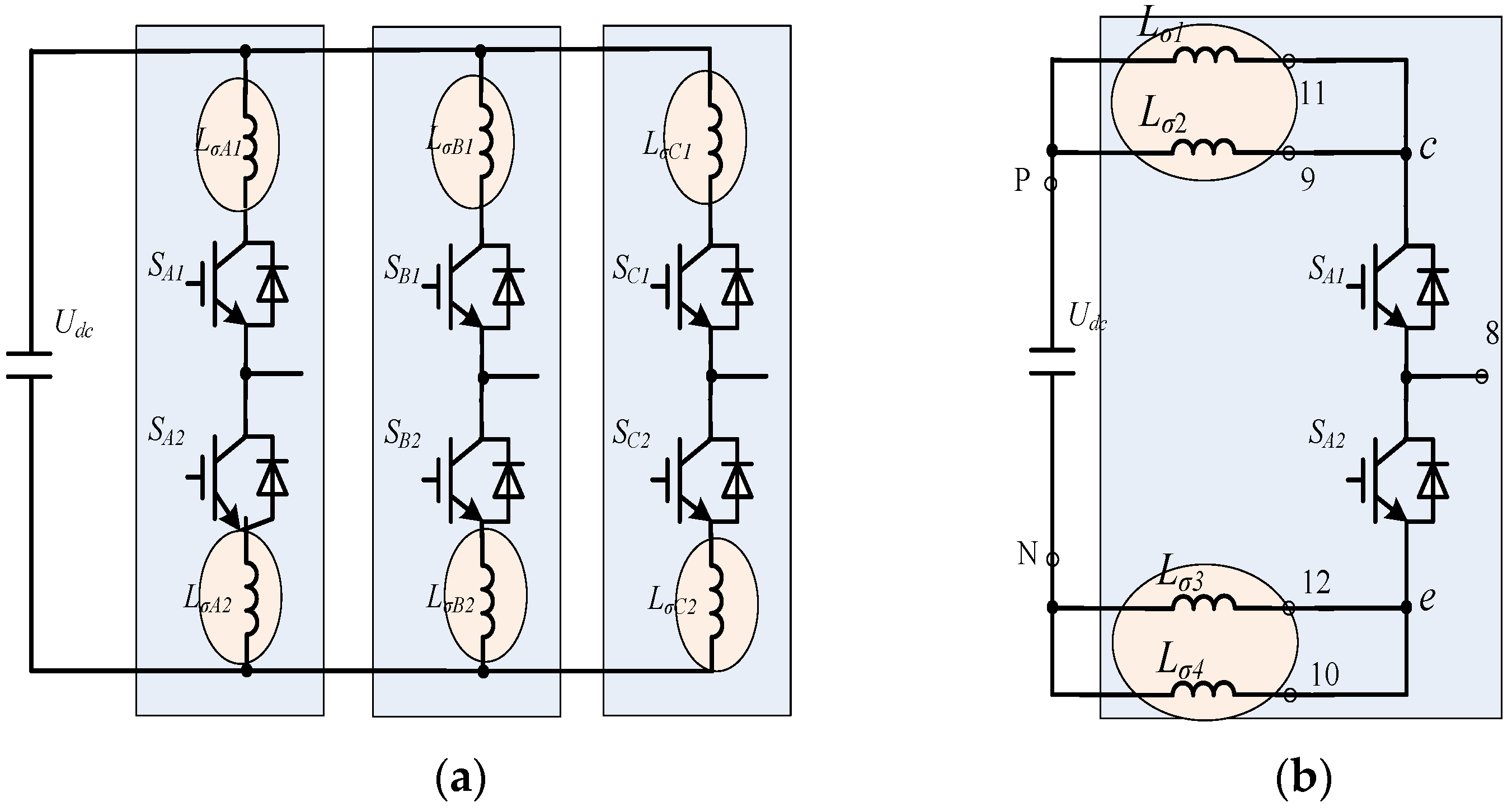
2.1. Inverter Layout Consideration
2.2. Equivalent Circuit of Bus-bar Considering Stray Inductance
3. Transient Analysis and Modeling of Asymmetrical Branches
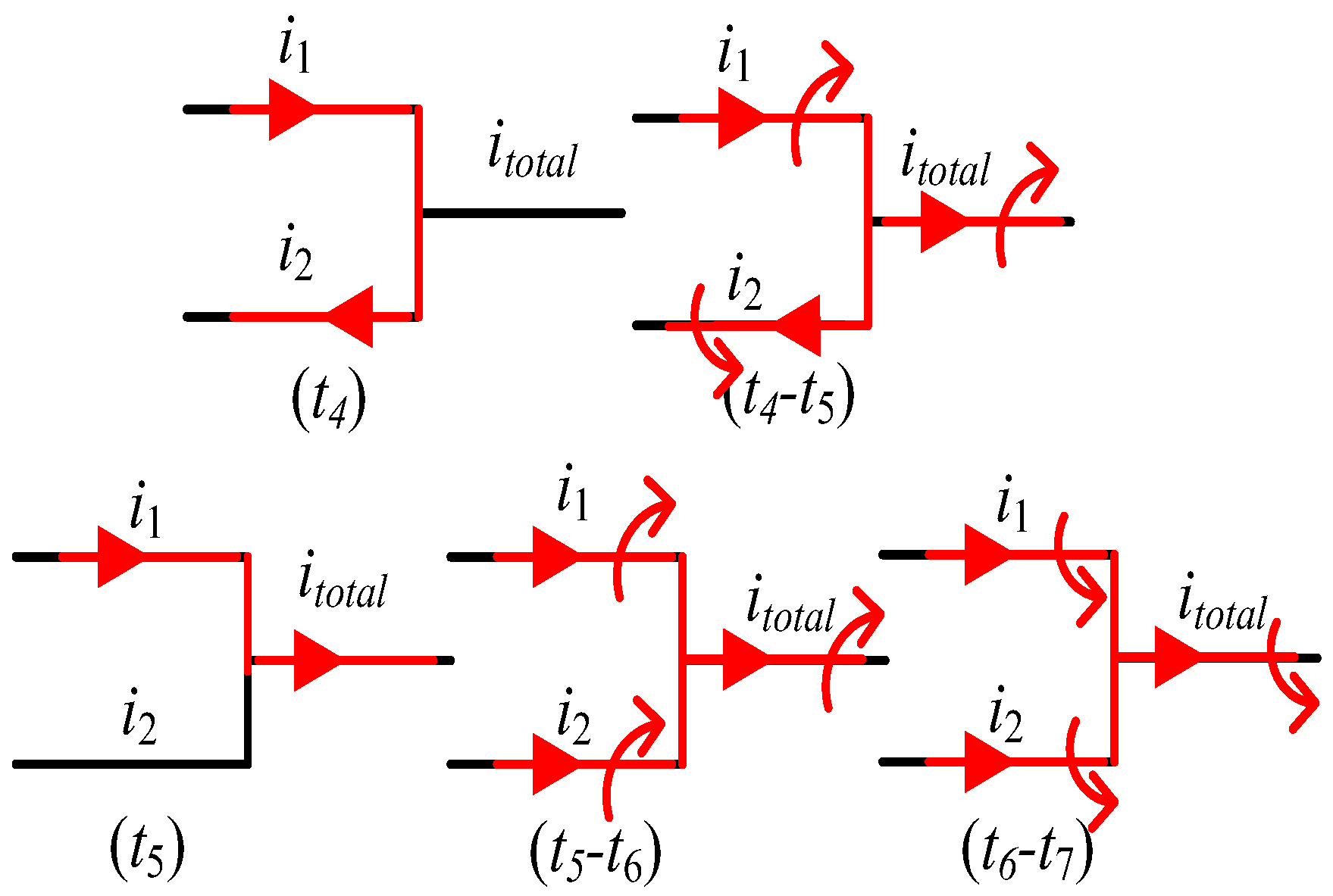
3.1. Transient Analysis
3.1.1. Turn-Off Transient
3.1.2. Turn-On Transient
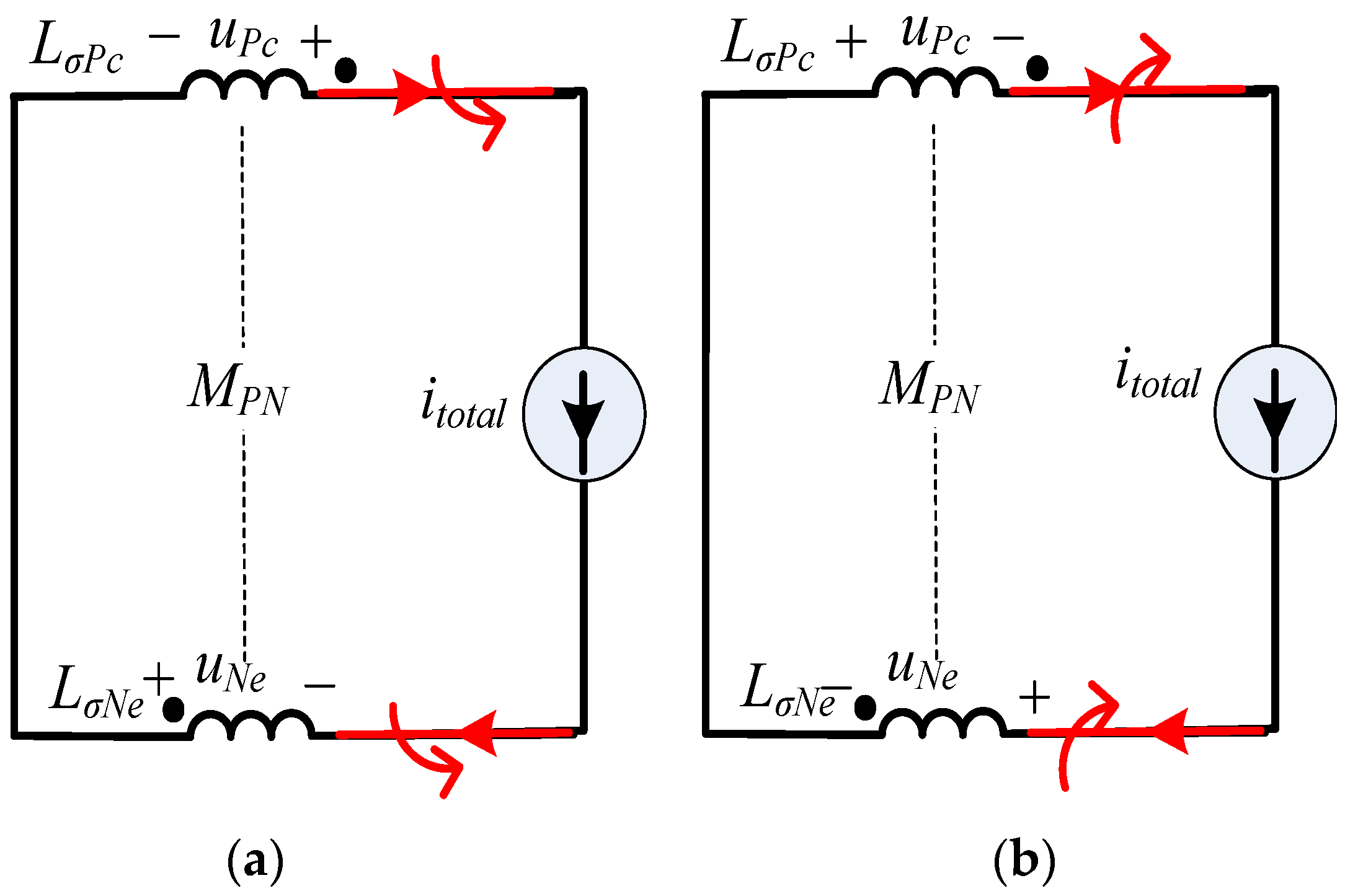
3.2. Model of Stray Inductance
4. Measuring Method for Partial Stray Inductance
4.1. Basic Principle
4.2. Measurement Error Analysis
5. Simulation and Experimental Results
5.1. Parameter Extraction
5.2. Experimental Measurement
5.3. Indirect Measurement
5.4. Direct Measurement
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Mollah, M.N.; Hossain, E. A Comprehensive Study of Key Electric Vehicle (EV) Components, Technologies, Challenges, Impacts, and Future Direction of Development. Energies 2017, 10, 1217. [Google Scholar] [CrossRef]
- Bucher, A.; Schmidt, R.; Werner, R.; Leipenat, M.; Hasenohr, C.; Werner, T.; Schmitz, S.; Heitmann, A. Design of a Full SiC Voltage Source Inverter for Electric Vehicle Applications. In Proceedings of the 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; pp. 1–10. [Google Scholar]
- Liu, J.; Sun, W.; Su, W.; Tai, X.; Wen, X. Inverter Output Power Density Increasing Technologies for EV/HEV Applications. In Proceedings of the 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–4. [Google Scholar]
- Mühlfeld, O.; Paulsen, L.; Olesen, K.; Ströbel-Maier, H. Automotive Traction Inverter for Highest Power Density. In Proceedings of the International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 19–20 May 2015; pp. 871–878. [Google Scholar]
- Caponet, C.; Profumo, D.; Doncker, W. Low stray inductance bus bar design and construction for good EMC performance in power electronic circuit. IEEE Trans. Power Electron. 2002, 17, 225–231. [Google Scholar] [CrossRef]
- Chen, C.; Pei, X.; Chen, Y.; Kang, Y. Investigation, Evaluation, and Optimization of Stray Inductance in Laminated Busbar. IEEE Trans. Power Electron. 2014, 29, 3679–3693. [Google Scholar] [CrossRef]
- Wang, J.; Yang, B.-J.; Xu, Z.-X.; Deng, Y.; Zhao, R.-X.; He, X.-N. Configuration of Low Inductive Laminated Bus Bar in 750 kVA NPC Three-level Universal Converter Module of High Power Density. Proc. CSEE 2010, 30, 47–54. [Google Scholar]
- Callegaro, A.D.; Guo, J.; Eull, M.; Gibson, J.; Preindl, M.; Bilgin, B. Bus Bar Design for High-Power Inverters. IEEE Trans. Power Electron. 2017. [Google Scholar] [CrossRef]
- Xuesong, W.; Zhengming, Z.; Liqiang, Y. Conducted EMI Reduction in IGBT Based Converters. In Proceedings of the Asia-Pacific International Conference on Electromagnetic Compatibility (APEC), Beijing, China, 12–16 April 2010. [Google Scholar]
- Khan, M.; Magne, P.; Bilgin, B.; Wirasingha, S.; Emadi, A. Laminated Busbar Design Criteria in Power Converters for Electrified Powertrain Applications. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 15–18 June 2014; pp. 1–6. [Google Scholar]
- Dong, Y.F.; Luo, H.Z.; Yang, H.Y.; He, Y.M.; Li, W.H.; He, X.G. Engineering Design for Structure and Bus Bar of 1.2MV·A Hybrid Clamped Five-Level Converter Module. Trans. China Electrotech. Soc. 2016, 31, 11–18. [Google Scholar]
- Schanen, J.L.; Clavel, E.; Roudet, J. Modeling of Low Inductive Bus bar Connection. IEEE Ind. Appl. Mag. 1996, 2, 39–43. [Google Scholar] [CrossRef]
- Ruehli, A.E. Inductance Calculations in a Complex Integrated Circuit Environment. IBM J. Res. Dev. 1972, 16, 470–481. [Google Scholar] [CrossRef]
- Paul, C.R. Inductance, Loop and Partial; Willey & Sons: New York, NY, USA, 2010; pp. 246–254. [Google Scholar]
- Bryant, A.T.; Vadlapati, K.K.; Starkey, J.P.; Goldney, A.P.; Kandi-lidis, S.Y.; Hinchley, D.A. Current distribution in high power laminated busbars. In Proceedings of the 14th European Conference on Power Electronics and Application, Birmingham, UK, 30 August–1 September 2011; pp. 1–10. [Google Scholar]
- Pasterczyk, R.J.; Martin, C.; Guichon, J.-M.; Schanen, J.-L. Planar Busbar Optimization Regarding Current Sharing and Stray Inductance Minimization. In Proceedings of the European Conference on Power electronics and applications, Dresden, Germany, 11–14 September 2005; pp. 1–9. [Google Scholar]
- Zhang, N.; Wang, S.; Zhao, H. Develop Parasitic Inductance Model for the Planar Busbar of an IGBT H Bridge in a Power Inverter. IEEE Trans. Power Electron. 2015, 30, 6924–6933. [Google Scholar] [CrossRef]
- Eupec marketing department; European Power Semiconductor; Electronics Company. Measurement of the Circuit Stray Inductance Lσ; Application Note; European Power Semiconductor and Electronics Company: Warstein, Germany, 1999. [Google Scholar]
- Zhu, H.; Hefner, R.; Allen, R.; Lai, J.-S. Characterization of power electronics system interconnect parasitics using time domain reflectometry. IEEE Trans. Power Electron. 1999, 14, 622–628. [Google Scholar]
- Feng, G.; Yuan, L.; Zhao, Z.; Zhao, J.; Lu, T. A Novel Stray Inductance Extraction Method for Bus Bars Based on Turn-on/off Transient Process. Proc. CSEE 2014, 34, 6442–6449. [Google Scholar]
- Wen, H.; Liu, J.; Zhang, X.; Wen, X. Electric Vehicle Drive Inverters Simulation Considering Parasitic Parameters. In Proceedings of the 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008; pp. 417–421. [Google Scholar]














| nH | Lσ1 | Lσ2 | Lσ3 | Lσ4 |
|---|---|---|---|---|
| Lσ1 | 22.72 | 23.95 | −1.56 | −7.56 |
| Lσ2 | 23.95 | 37.42 | −2.18 | −14.5 |
| Lσ3 | −1.56 | −2.18 | 17.18 | 17.48 |
| Lσ4 | −7.56 | −14.5 | 17.48 | 29.37 |
| nH | LσPc | LσNe |
|---|---|---|
| LσPc | 17.81 | −1.44 |
| LσNe | −1.44 | 16.46 |
| nH | LσPc | LσNe |
|---|---|---|
| LσPc | 19.14 | −1.51 |
| LσNe | −1.51 | 17.15 |
| Equipment | Parameter |
|---|---|
| IGBT module | FF1400R12IP4 |
| IGBT driver | 2SP0320V2A0 |
| Rogowski coil | CWT30B |
| Voltage probe | Agilent-10073C |
| Oscilloscope | Agilent-MSO8064A |
| Inductive load | About 7uH |
| Δi(A) | Δi1 | Δi2 | Δi3 | Δi4 |
|---|---|---|---|---|
| S1 | 104.57 | 76.71 | 66.36 | 108.46 |
| S2 | 106.25 | 75.21 | 70.35 | 110.36 |
| nH | Lσ1 | Lσ2 | Lσ3 | Lσ4 |
|---|---|---|---|---|
| Turn on transient of S1 | 31.45 | 47 | 40.68 | 28.11 |
| Turn on transient of S2 | 30.69 | 47.9 | 39.8 | 24 |
| Difference | 0.76 | 0.9 | 0.88 | 4.11 |
| nH | Lσ1 | Lσ2 | Lσ3 | Lσ4 |
|---|---|---|---|---|
| Turn-on transient | 30.56 | 45.6 | 39.56 | 26.6 |
| Turn-off transient | 31.37 | 42.77 | 41.37 | 27.57 |
| Difference | 0.81 | 2.83 | 1.81 | 0.97 |
| nH | Lσ1 | Lσ2 | Lσ3 | Lσ4 |
|---|---|---|---|---|
| Indirect measurement | 31.56 | 47.4 | 40.24 | 26.01 |
| Direct measurement | 30.9 | 44.19 | 40.46 | 27.1 |
| Difference | 0.66 | 3.21 | 0.22 | 1.01 |
| Method | LσPc | LσNe |
|---|---|---|
| simulation | 16.37 | 15.02 |
| calculation | 17.6 | 15.6 |
| measurement | 17.2 | 16.1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, C.; He, F.; Zhang, J.; Hu, H. Partial Stray Inductance Modeling and Measuring of Asymmetrical Parallel Branches on the Bus-Bar of Electric Vehicles. Energies 2017, 10, 1519. https://doi.org/10.3390/en10101519
Geng C, He F, Zhang J, Hu H. Partial Stray Inductance Modeling and Measuring of Asymmetrical Parallel Branches on the Bus-Bar of Electric Vehicles. Energies. 2017; 10(10):1519. https://doi.org/10.3390/en10101519
Chicago/Turabian StyleGeng, Chengfei, Fengyou He, Jingwei Zhang, and Hongsheng Hu. 2017. "Partial Stray Inductance Modeling and Measuring of Asymmetrical Parallel Branches on the Bus-Bar of Electric Vehicles" Energies 10, no. 10: 1519. https://doi.org/10.3390/en10101519
APA StyleGeng, C., He, F., Zhang, J., & Hu, H. (2017). Partial Stray Inductance Modeling and Measuring of Asymmetrical Parallel Branches on the Bus-Bar of Electric Vehicles. Energies, 10(10), 1519. https://doi.org/10.3390/en10101519






