Evaluation of Comfort Level and Harvested Energy in the Vehicle Using Controlled Damping
Abstract
1. Introduction
2. Materials and Methods
3. Mathematical Model
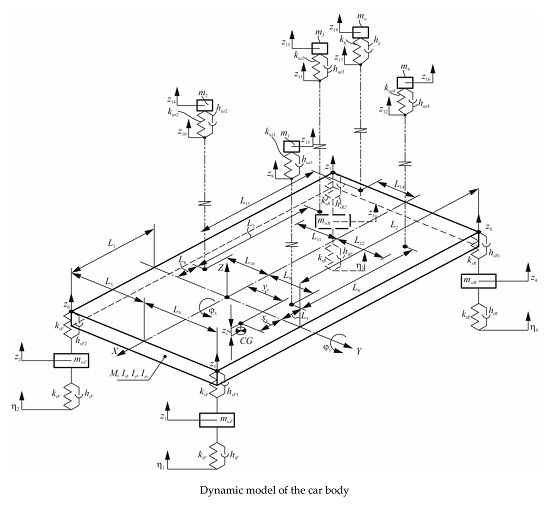
3.1. Dynamic Model of the Vehicle
3.2. Damping Law Optimization
4. Results and Discussion
4.1. Experimental Results
4.2. Theoretical Results
5. Conclusions
Acknowledgments

Author Contributions
Conflicts of Interest
References
- Cassidy, I.L.; Scruggs, J.T.; Behrens, S.; Gavin, H.P. Design and experimental characterization of an electromagnetic transducer for large-scale vibratory energy harvesting applications. J. Intell. Mater. Syst. Struct. 2011, 22, 2009–2024. [Google Scholar] [CrossRef]
- Zhu, S.; Shen, W.-A.; Xu, Y.-L. Linear electromagnetic devices for vibration damping and energy harvesting: Modeling and testing. Eng. Struct. 2012, 34, 198–212. [Google Scholar] [CrossRef]
- Tang, X.; Zuo, L. Simultaneous energy harvesting and vibration control of structures with tuned mass dampers. J. Intell. Mater. Syst. Struct. 2012, 23, 2117–2127. [Google Scholar] [CrossRef]
- Ali, S.F.; Adhikari, S. Energy harvesting dynamic vibration absorbers. J. Appl. Mech. 2013, 80, 41004. [Google Scholar] [CrossRef]
- Gonzalez-Buelga, A.; Clare, L.; Cammarano, A.; Neild, S.; Burrow, S.; Inman, D. An optimised tuned mass damper/harvester device. Struct. Control Health Monit. 2014, 21, 1154–1169. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, W. Coupled analysis of multi-impact energy harvesting from low-frequency wind induced vibrations. Smart Mater. Struct. 2015, 24, 45007. [Google Scholar] [CrossRef]
- Madhav, C.; Ali, S.F. Harvesting Energy from Vibration Absorber under Random Excitations. IFAC-Pap. 2016, 49, 807–812. [Google Scholar] [CrossRef]
- Salvi, J.; Giaralis, A. Concept Study of A Novel Energy Harvesting-Enabled Tuned Mass-Damper-Inerter (EH-TMDI) Device for Vibration Control of Harmonically-Excited Structures. J. Phys. Conf. Ser. 2016, 744, 012082. [Google Scholar] [CrossRef]
- Luo, Y.; Sun, H.; Wang, X.; Zuo, L.; Chen, N. Wind Induced Vibration Control and Energy Harvesting of Electromagnetic Resonant Shunt Tuned Mass-Damper-Inerter for Building Structures. Shock Vib. 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Takeya, K.; Sasaki, E.; Kobayashi, Y. Design and parametric study on energy harvesting from bridge vibration using tuned dual-mass damper systems. J. Sound Vib. 2016, 361, 50–65. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Olejnik, P. Active control of two degrees-of-freedom building-ground system. Arch. Control Sci. 2007, 17, 393–408. [Google Scholar]
- Liao, Y.; Sodano, H.A. Model of a single mode energy harvester and properties for optimal power generation. Smart Mater. Struct. 2008, 17, 65026. [Google Scholar] [CrossRef]
- Simon, P.; Yves, S.-A. Improving the performance of a piezoelectric energy harvester using a variable thickness beam. Smart Mater. Struct. 2010, 19, 105020. [Google Scholar]
- Bucinskas, V. Energy Harvesting Shock Absorber and Method for Controlling Same. U.S. Patent 20140027217 A1, 30 January 2014. [Google Scholar]
- Bucinskas, V.; Klevinskis, A.; Sesok, N.; Iljin, I.; Warsza, Z.L. Evaluation of damping characteristics of a damper with magneto-rheological fluid. In Advanced Mechatronics Solutions; Jablonski, R., Brezina, T., Eds.; Springer: Cham, Switzerland, 2016; pp. 411–420. [Google Scholar]
- Mitrouchev, P.; Klevinskis, A.; Bucinskas, V.; Dragasius, E.; Udris, D.; Morkvenaite-Vilkonciene, I. Analytical research of damping efficiency and heat generation of magnetorheological damper. Smart Mater. Struct. 2017, 26, 65026. [Google Scholar] [CrossRef]
- Lei, Z.; Brian, S.; Jurgen, S.; Yu, Z. Design and characterization of an electromagnetic energy harvester for vehicle suspensions. Smart Mater. Struct. 2010, 19, 45003. [Google Scholar]
- Abed, I.; Kacem, N.; Bouhaddi, N.; Bouazizi, M.L. Multi-modal vibration energy harvesting approach based on nonlinear oscillator arrays under magnetic levitation. Smart Mater. Struct. 2016, 25, 25018. [Google Scholar] [CrossRef]
- Kacem, N.; Baguet, S.; Hentz, S.; Dufour, R. Nonlinear phenomena in nanomechanical resonators: Mechanical behaviors and physical limitations. Mech. Ind. 2010, 11, 521–529. [Google Scholar] [CrossRef]
- Czop, P.; Sławik, D. A high-frequency first-principle model of a shock absorber and servo-hydraulic tester. Mech. Syst. Signal Process. 2011, 25, 1937–1955. [Google Scholar] [CrossRef]
- Lam, A.H.-F.; Liao, W.-H. Semi-active control of automotive suspension systems with magneto-rheological dampers. Int. J. Veh. Des. 2003, 33, 50–75. [Google Scholar] [CrossRef]
- Lee, H.-S.; Choi, S.-B. Control and response characteristics of a magneto-rheological fluid damper for passenger vehicles. J. Intell. Mater. Syst. Struct. 2000, 11, 80–87. [Google Scholar] [CrossRef]
- Li, S.; Lu, Y.; Li, L. Dynamical test and modeling for hydraulic shock absorber on heavy vehicle under harmonic and random loadings. Res. J. Appl. Sci. Eng. Technol. 2012, 4, 1903–1910. [Google Scholar]
- Worden, K.; Hickey, D.; Haroon, M.; Adams, D.E. Nonlinear system identification of automotive dampers: A time and frequency-domain analysis. Mech. Syst. Signal Process. 2009, 23, 104–126. [Google Scholar] [CrossRef]
- Zubieta, M.; Elejabarrieta, M.J.; Bou-Ali, M.M. Characterization and modeling of the static and dynamic friction in a damper. Mech. Mach. Theory 2009, 44, 1560–1569. [Google Scholar] [CrossRef]
- Lajqi, S.; Pehan, S. Designs and optimizations of active and semi-active non-linear suspension systems for a terrain vehicle. Stroj. Vestnik J. Mech. Eng. 2012, 58, 732–743. [Google Scholar] [CrossRef]
- Mangal, S.K.; Kumar, A. Geometric parameter optimization of magneto-rheological damper using design of experiment technique. Int. J. Mech. Mater. Eng. 2015, 10, 4. [Google Scholar] [CrossRef]
- Hudha, K.; Jamaluddin, H.; Samin, P.M.; Rahman, R.A. Non-parametric linearised data driven modelling and force tracking control of a magnetorheological damper. Int. J. Veh. Des. 2008, 46, 250–269. [Google Scholar] [CrossRef]
- Muhammad, A.; Yao, X.-L.; Deng, Z.-C. Review of magnetorheological (MR) fluids and its applications in vibration control. J. Mar. Sci. Appl. 2006, 5, 17–29. [Google Scholar] [CrossRef]
- Sapiński, B.; Rosół, M.; Węgrzynowski, M. Investigation of an energy harvesting MR damper in a vibration control system. Smart Mater. Struct. 2016, 25, 125017. [Google Scholar] [CrossRef]
- Jastrzębski, Ł.; Sapiński, B. Electrical interface for an MR damper-based vibration reduction system with energy harvesting capability. In Proceedings of the IEEE 18th International Carpathian Control Conference (ICCC), Sinaia, Romania, 28–31 May 2017; pp. 189–192. [Google Scholar]
- Hu, G.; Tang, L.; Banerjee, A.; Das, R. Metastructure With Piezoelectric Element for Simultaneous Vibration Suppression and Energy Harvesting. J. Vib. Acoust. 2017, 139, 11012. [Google Scholar] [CrossRef]
- Hu, G.; Tang, L.; Das, R. Metamaterial-inspired piezoelectric system with dual functionalities: Energy harvesting and vibration suppression, Active and Passive Smart Structures and Integrated Systems. In Proceedings of the International Society for Optics and Photonics, Portland, OR, USA, 11–16 April 2017; p. 101641X. [Google Scholar]
- Bowden, J.A.; Burrow, S.G.; Cammarano, A.; Clare, L.R.; Mitcheson, P.D. Switched-mode load impedance synthesis to parametrically tune electromagnetic vibration energy harvesters. IEEE/ASME Trans. Mechatron. 2015, 20, 603–610. [Google Scholar] [CrossRef]
- Mitcheson, P.D.; Toh, T.T.; Wong, K.H.; Burrow, S.G.; Holmes, A.S. Tuning the resonant frequency and damping of an electromagnetic energy harvester using power electronics. IEEE Trans. Circuits Syst. II 2011, 58, 792–796. [Google Scholar] [CrossRef]
- Balato, M.; Costanzo, L.; Vitelli, M. Resonant electromagnetic vibration harvesters: Determination of the equivalent electric circuit parameters and simplified closed-form analysis for the identification of the optimal diode bridge rectifier DC load. Int. J. Electr. Power Energy Syst. 2017, 84, 111–123. [Google Scholar] [CrossRef]
- Balato, M.; Costanzo, L.; Vitelli, M. Maximization of the extracted power in resonant electromagnetic vibration harvesters applications employing bridge rectifiers. Sens. Actuators A 2017, 263, 63–75. [Google Scholar] [CrossRef]
- Bakar, S.A.A.; Jamaluddin, H.; Rahman, R.A.; Samin, P.M.; Masuda, R.; Hashimoto, H.; Inaba, T. Modelling of magnetorheological semi-active suspension system controlled by semi-active damping force estimator. Int. J. Comput. Appl. Technol. 2011, 42, 49–64. [Google Scholar] [CrossRef]
- Goncalves, F.D.; Ahmadian, M. A hybrid control policy for semi-active vehicle suspensions. Shock Vib. 2003, 10, 59–69. [Google Scholar] [CrossRef]
- Ahmadian, M.; Vahdati, N. Transient dynamics of semiactive suspensions with hybrid control. J. Intell. Mater. Syst. Struct. 2006, 17, 145–153. [Google Scholar] [CrossRef]
- Wang, W.L.; Yang, X.J.; Xu, G.X.; Huang, Y. Multi-objective design optimization of the complete valve system in an adjustable linear hydraulic damper. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 679–699. [Google Scholar] [CrossRef]
- Li, Z.; Zuo, L.; Luhrs, G.; Lin, L.; Qin, Y.-X. Electromagnetic energy-harvesting shock absorbers: Design, modeling, and road tests. IEEE Trans. Veh. Technol. 2013, 62, 1065–1074. [Google Scholar] [CrossRef]
- Tang, X.; Lin, T.; Zuo, L. Design and optimization of a tubular linear electromagnetic vibration energy harvester. IEEE/ASME Trans. Mechatron. 2014, 19, 615–622. [Google Scholar] [CrossRef]
- Li, Z.; Zuo, L.; Kuang, J.; Luhrs, G. Energy-harvesting shock absorber with a mechanical motion rectifier. Smart Mater. Struct. 2012, 22, 25008. [Google Scholar] [CrossRef]
- Cassidy, I.L.; Scruggs, J.T.; Behrens, S. Design of electromagnetic energy harvesters for large-scale structural vibration applications. In Proceedings of the Society of Photo-Optical Instrumentation Engineers 7977, Active and Passive Smart Structures and Integrated Systems, San Diego, CA, USA, 27 April 2011; p. 79770P. [Google Scholar]
- Chen, C.; Liao, W.-H. A self-sensing magnetorheological damper with power generation. Smart Mater. Struct. 2012, 21, 25014. [Google Scholar] [CrossRef]










| Definition, Units | Value | Comments |
|---|---|---|
| hg, Ns/m | 2064 | coefficient of damping of the load in the baggage box |
| hSF1, Ns/m | 7500 | constant or calculated by Equation (7). |
| hSF2, Ns/m | 7500 | constant or calculated by Equation (7). |
| hSR1, Ns/m | 7500 | constant or calculated by Equation (7). |
| hSR2, Ns/m | 7500 | constant or calculated by Equation (7). |
| htF, Ns/m | 300 | coefficient of damping of front tire |
| htR, Ns/m | 300 | coefficient of damping of rear tire |
| huz1, Ns/m | 2064 | coefficient of damping of human body (driver) |
| huz2, Ns/m | 2064 | coefficient of damping of front right passenger |
| huz3, Ns/m | 2064 | coefficient of damping of rear right passenger |
| huz4, Ns/m | 2064 | coefficient of damping of rear left passenger |
| Jx, kg·m2 | 670 | moment of inertia of the vehicle around X axis |
| Jxy, kg·m2 | 0 | mixed moment of inertia |
| Jy, kg·m2 | 2900 | moment of inertia of the vehicle around Y axis |
| kg, N/m | 90,000 | coefficient of stiffness of the load in baggage box |
| ksF, N/m | 49,976 | stiffness of front wheel suspension (single side) |
| ksR, N/m | 87,898.5 | stiffness of rear wheel suspension (single side) |
| ktF, N/m | 270,000 | stiffness of front tire |
| ktR, N/m | 270,000 | stiffness of rear tire |
| kuz1, N/m | 90,000 | coefficient of stiffness of driver body |
| kuz2, N/m | 90,000 | coefficient of stiffness of front right passenger body |
| kuz3, N/m | 90,000 | coefficient of stiffness of rear right passenger body |
| kuz4, N/m | 90,000 | coefficient of stiffness of rear left passenger body |
| L1, m | 1.7867 | distance, represented in dynamical model |
| L10, m | 0.422625 | distance, represented in dynamical model |
| L11, m | 0.422625 | distance, represented in dynamical model |
| L12, m | 0.422625 | distance, represented in dynamical model |
| L13, m | 1.4286 | distance, represented in dynamical model |
| L14, m | 0.1 | distance, represented in dynamical model |
| L2, m | 1.1363 | distance, represented in dynamical model |
| L3, m | 0.84525 | distance, represented in dynamical model |
| L4, m | 0.84525 | distance, represented in dynamical model |
| L5, m | 0.47135 | distance, represented in dynamical model |
| L6, m | 0.47135 | distance, represented in dynamical model |
| L7, m | 0.99015 | distance, represented in dynamical model |
| L8, m | 0.99015 | distance, represented in dynamical model |
| L9, m | 0.422625 | distance, represented in dynamical model |
| M, kg | 2613 | mass of the vehicle |
| m1, kg | 80 | mass of driver |
| m2, kg | 0.01 | front right passenger mass |
| m3, kg | 0.01 | rear right passenger mass |
| m4, kg | 0.01 | rear left passenger mass |
| mw, kg | 0.01 | mass of the load in baggage box |
| mwf, kg | 94 | mass of the front wheel with belonging parts |
| mwr, kg | 80.9 | mass of the rear wheel with belonging parts |
| xc, m | 0.3617 | coordinate of center of gravity on X axis |
| yc, m | 0 | coordinate of center of gravity on Y axis |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bucinskas, V.; Mitrouchev, P.; Sutinys, E.; Sesok, N.; Iljin, I.; Morkvenaite-Vilkonciene, I. Evaluation of Comfort Level and Harvested Energy in the Vehicle Using Controlled Damping. Energies 2017, 10, 1742. https://doi.org/10.3390/en10111742
Bucinskas V, Mitrouchev P, Sutinys E, Sesok N, Iljin I, Morkvenaite-Vilkonciene I. Evaluation of Comfort Level and Harvested Energy in the Vehicle Using Controlled Damping. Energies. 2017; 10(11):1742. https://doi.org/10.3390/en10111742
Chicago/Turabian StyleBucinskas, Vytautas, Peter Mitrouchev, Ernestas Sutinys, Nikolaj Sesok, Igor Iljin, and Inga Morkvenaite-Vilkonciene. 2017. "Evaluation of Comfort Level and Harvested Energy in the Vehicle Using Controlled Damping" Energies 10, no. 11: 1742. https://doi.org/10.3390/en10111742
APA StyleBucinskas, V., Mitrouchev, P., Sutinys, E., Sesok, N., Iljin, I., & Morkvenaite-Vilkonciene, I. (2017). Evaluation of Comfort Level and Harvested Energy in the Vehicle Using Controlled Damping. Energies, 10(11), 1742. https://doi.org/10.3390/en10111742