Freeway Driving Cycle Construction Based on Real-Time Traffic Information and Global Optimal Energy Management for Plug-In Hybrid Electric Vehicles
Abstract
:1. Introduction
2. Local Database Construction Method
2.1. Velocity Segments Database Construction
2.1.1. Driving Cycle Data Acquisition
2.1.2. Driving Cycle Data Classification Rule
2.2. Real-Time Traffic Information Model Construction
2.2.1. Tensor Introduction
2.2.2. Traffic Information Analysis
3. Freeway Driving Cycle Construction
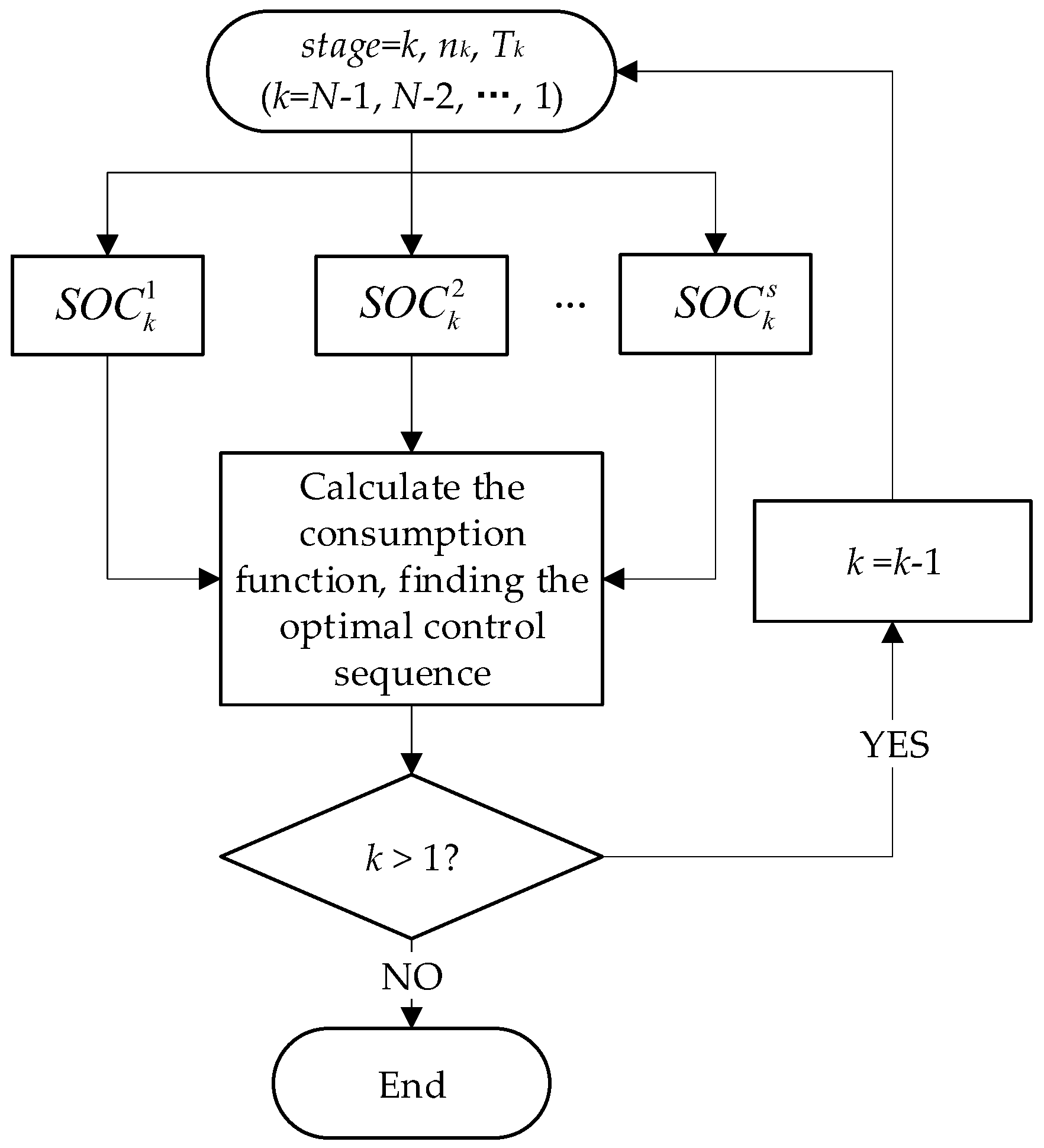
4. Global Optimal Energy Management Control Strategy
4.1. Economic Driving System
4.2. PHEV Transection Structure and Parameters
4.3. Optiamal Problem Construction
5. Results and Discussion
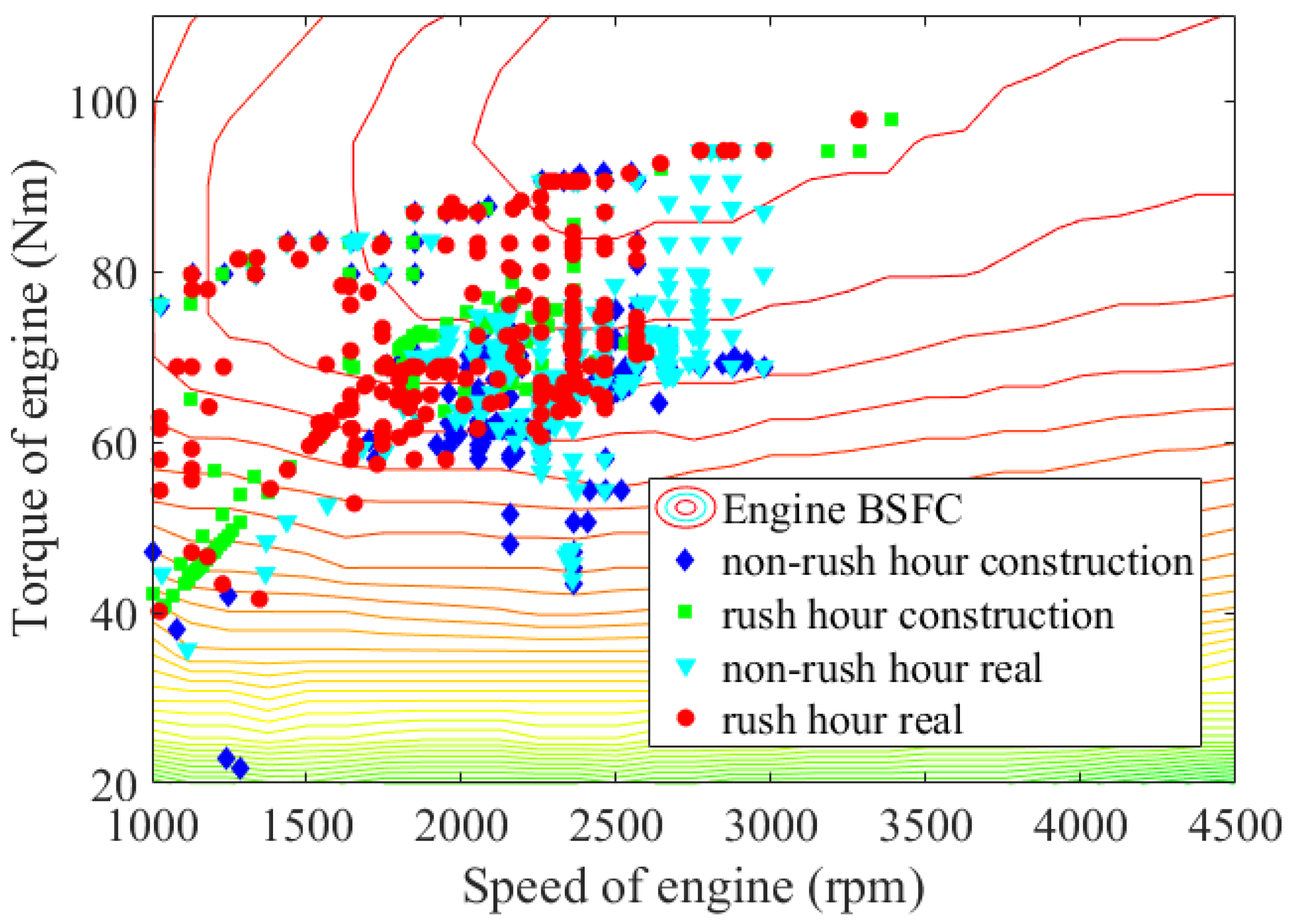
5.1. Analysis of the Freeway Driving Cycles
5.2. Update Construction Freeway Driving Cycle Error Analysis
5.3. Global Optimal Energy Management
6. Conclusions
- The history and real-time traffic information tensor model are constructed and the correlation between real-time traffic information from the perspective of time domain and spatial domain are deeply explored.
- The variation law of road velocity and the change rule of working day and weekend are clarified. The validity of the FDC construction method is proved by comparing the CFDC and RFDC.
- The FDC uses real-time traffic information, which is applied for the first time in the driving cycle construction method, and the parameter between CFDC and RFDC are in the reasonable error horizon.
- The driving cycles are applied in PHEVs to achieve real-time optimal control strategy based on the DP algorithm. There are fuel economy rates of up to 14.37% compared with rule-based control strategy.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Armas, O.; García-Contreras, R.; Ramos, Á. Impact of alternative fuels on performance and pollutant emissions of a light duty engine tested under the new European driving cycle. Appl. Energy 2013, 107, 183–190. [Google Scholar] [CrossRef]
- Fontaras, G.; Franco, V.; Dilara, P.; Martini, G.; Manfredi, U. Development and review of Euro 5 passenger car emission factors based on experimental results over various driving cycles. Sci. Total Environ. 2014, 469, 1034–1042. [Google Scholar] [CrossRef] [PubMed]
- Damiano, A.; Musio, C.; Marongiu, I. Experimental validation of a dynamic energy model of a battery electric vehicle. In Proceedings of the International Conference on Renewable Energy Research and Applications, Palermo, Italy, 22–25 November 2015; pp. 803–808. [Google Scholar]
- Zhang, S.; Xiong, R. Adaptive energy management of a plug-in hybrid electric vehicle based on driving pattern recognition and dynamic programming. Appl. Energy 2015, 155, 68–78. [Google Scholar] [CrossRef]
- Galgamuwa, U.; Perera, L.; Bandara, S. Developing a General Methodology for Driving Cycle Construction: Comparison of Various Established Driving Cycles in the World to Propose a General Approach. J. Transp. Technol. 2015, 5, 191–203. [Google Scholar] [CrossRef]
- Li, M.; Zhu, X.; Zhang, J. A Study on the Construction of Driving Cycle for Typical Cities in China. Automot. Eng. 2005, 27, 557–560. [Google Scholar]
- Jian, P. Study on the Construction of Urban Mixed Road Driving Condition; Hefei University of Technology: Hefei, China, 2011. [Google Scholar]
- Jiang, P.; Shi, Q.; Chen, W.; Huang, Z. A Research on the Construction of City Road Driving Cycle Based on Wavelet Analysis. Automot. Eng. 2011, 33, 70–73. [Google Scholar]
- Hung, W.T.; Tong, H.Y.; Lee, C.P.; Ha, K.; Pao, L.Y. Development of a practical driving cycle construction methodology: A case study in Hong Kong. Transp. Res. Part D Transp. Environ. 2007, 12, 115–128. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Wang, C.; Cao, J. An on-line predictive energy management strategy for plug-in hybrid electric vehicles to counter the uncertain prediction of the driving cycle. Appl. Energy 2017, 185, 1663–1672. [Google Scholar] [CrossRef]
- Li, L.; Yang, C.; Zhang, Y.; Zhang, L.; Song, J. Correctional DP-Based Energy Management Strategy of Plug-In Hybrid Electric Bus for City-Bus Route. IEEE Trans. Veh. Technol. 2015, 64, 2792–2803. [Google Scholar] [CrossRef]
- Banvait, H.; Anwar, S.; Chen, Y. A rule-based energy management strategy for plug-in hybrid electric vehicle (PHEV). In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3938–3943. [Google Scholar]
- Padmarajan, B.; Mcgordon, A.; Jennings, P. Blended rule based energy management for PHEV: System Structure and Strategy. IEEE Trans. Veh. Technol. 2016, 66, 8757–8762. [Google Scholar] [CrossRef]
- Zhang, J.; Shen, T. Real-Time Fuel Economy Optimization with Nonlinear MPC for PHEVs. IEEE Trans. Control Syst. Technol. 2016, 24, 2167–2175. [Google Scholar] [CrossRef]
- Pahasa, J.; Ngamroo, I. PHEVs Bidirectional Charging/Discharging and SoC Control for Microgrid Frequency Stabilization Using Multiple MPC. IEEE Trans. Smart Grid 2015, 6, 526–533. [Google Scholar] [CrossRef]
- Son, H.; Kim, H. Development of Near Optimal Rule-Based Control for Plug-In Hybrid Electric Vehicles Taking into Account Drivetrain Component Losses. Energies 2016, 9, 420. [Google Scholar] [CrossRef]
- Chen, C. Freeway Performance Measurement System (PeMS); University of California, Berkeley: Berkeley, CA, USA, 1 July 2003. [Google Scholar]
- Varaiya, P.P. The Freeway Performance Measurement System (PeMS), PeMS 9.0: Final Report; Path Research Report; University of California, Berkeley: Berkeley, CA, USA, 30 November 2008. [Google Scholar]
- Jia, Z.; Chen, C.; Coifman, B.; Varaiya, P. The PeMS algorithms for accurate, real-time estimates of g-factors and speeds from single-loop detectors. In Proceedings of the 2001 IEEE Intelligent Transportation Systems, Oakland, CA, USA, 25–29 August 2001; pp. 536–541. [Google Scholar]
- Tong, H.Y.; Hung, W.T.; Cheung, C.S. Development of a driving cycle for Hong Kong. Atmos. Environ. 1999, 33, 2323–2335. [Google Scholar] [CrossRef]
- Shi, Q.; Zheng, Y.; Jiang, P. A Research on Driving Cycle of City Roads Based on Microtrips. Automot. Eng. 2011, 33, 256–261. (In Chinese) [Google Scholar]
- Kolda, T.G.; Bader, B.W. Tensor Decompositions and Applications. Siam Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Ali, M.; Foroosh, H. Character recognition in natural scene images using rank-1 tensor decomposition. In Proceedings of the IEEE International Conference on Image Processing, Phoenix, AZ, USA, 25–28 September 2016; pp. 2891–2895. [Google Scholar]
- Sidiropoulos, N.D.; Lathauwer, L.D.; Fu, X.; Huang, K.; Papalexakis, E.E.; Faloutsos, C. Tensor Decomposition for Signal Processing and Machine Learning. IEEE Trans. Signal Process. 2017, 65, 3551–3582. [Google Scholar] [CrossRef]
- Huang, K.; Sidiropoulos, N.D.; Liavas, A.P. A Flexible and Efficient Algorithmic Framework for Constrained Matrix and Tensor Factorization; IEEE Press: Piscatway, NJ, USA, 2016. [Google Scholar]
- Zhou, Y.; Han, C.; Wang, X.; Yu, T. Research on power train source matching for single-axle PHEV. In Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference (VPPC’08), Harbin, China, 3–5 September 2008; pp. 1–4. [Google Scholar]
- Pourabdollah, M.; Murgovski, N.; Grauers, A.; Egardt, B. Optimal Sizing of a Parallel PHEV Powertrain. IEEE Trans. Veh. Technol. 2013, 62, 2469–2480. [Google Scholar] [CrossRef]
- Domingues, G.; Reinap, A.; Alaküla, M. Design and cost optimization of electrified automotive powertrain. In Proceedings of the International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference, Toulouse, France, 2–4 November 2016; pp. 1–6. [Google Scholar]
- Howard, R.A. Dynamic Programming and Markov Processes; The Technology Press of the Massachusetts Institute of Technology and John Wiley & Sons, Inc.: Providence, RI, USA, April 1961. [Google Scholar]
- Bellman, R. Dynamic Programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef] [PubMed]
- Wang, X. Optimization Study on Powertrain Matching and System Control for Plug-In Hybrid Electric Urban Bus; Beijing Institute of Technology: Beijing, China, 2015. [Google Scholar]
- Cai, Y.; Ouyang, M.; Yang, F. Energy management and design optimization for a series-parallel PHEV city bus. Int. J. Automot. Technol. 2017, 18, 473–487. [Google Scholar] [CrossRef]
- Huang, Y.J.; Yin, C.L.; Zhang, J.W. Design of an energy management strategy for parallel hybrid electric vehicles using a logic threshold and instantaneous optimization method. Int. J. Automot. Technol. 2009, 10, 513–521. [Google Scholar] [CrossRef]


















| Classification Items | 1 | 2 | … | 12 |
|---|---|---|---|---|
| Velocity interval (km/h) | [0,0] | [10,10] | … | [110,110] |
| Classification Items | 1 | 2 | … | 11 |
|---|---|---|---|---|
| Average velocity (km/h) | [0,10) | [10,20) | … | [100,+∞) |
| Time | 8:00 | 8:05 | 8:10 | 8:15 | 8:20 | 8:25 | 8:30 | 8:35 | 8:40 |
|---|---|---|---|---|---|---|---|---|---|
| 8:00 | 1.000 | 0.996 | 0.990 | 0.986 | 0.964 | 0.949 | 0.818 | 0.700 | 0.793 |
| 8:05 | 0.996 | 1.000 | 0.998 | 0.997 | 0.982 | 0.975 | 0.867 | 0.765 | 0.846 |
| 8:10 | 0.990 | 0.998 | 1.000 | 1.000 | 0.991 | 0.982 | 0.877 | 0.786 | 0.860 |
| 8:15 | 0.986 | 0.997 | 1.000 | 1.000 | 0.994 | 0.986 | 0.887 | 0.802 | 0.871 |
| 8:20 | 0.964 | 0.982 | 0.991 | 0.994 | 1.000 | 0.991 | 0.908 | 0.846 | 0.898 |
| 8:25 | 0.949 | 0.975 | 0.982 | 0.986 | 0.991 | 1.000 | 0.952 | 0.889 | 0.941 |
| 8:30 | 0.818 | 0.867 | 0.877 | 0.887 | 0.908 | 0.952 | 1.000 | 0.974 | 0.998 |
| 8:35 | 0.700 | 0.765 | 0.786 | 0.802 | 0.846 | 0.889 | 0.974 | 1.000 | 0.985 |
| 8:40 | 0.793 | 0.846 | 0.860 | 0.871 | 0.898 | 0.941 | 0.998 | 0.985 | 1.000 |
| Component | Parameters | Quantity |
|---|---|---|
| Engine | Displacement | 1.8 L |
| Max Power | 57 kw | |
| Max Torque | 110 Nm | |
| Motor/Generator | M/G1 Max power | 30 kW |
| M/G2 Max power | 35 kW | |
| Battery | C-LiFePO4 | 6.5 Ah |
| Transmission | E-CVT | |
| Vehicle | Curb weight | 1400 kg |
| Frontal area | 2.23 m2 | |
| Drag coefficient | 0.26 | |
| Drive wheel radius | 0.287 m |
| Items | CFDC | RFDC |
|---|---|---|
| Avg. velocity (km/h) | 70.85 | 70.75 |
| Max. velocity (km/h) | 99.87 | 100.51 |
| Max. acceleration (m/s2) | 4.06 | 3.21 |
| Max. deceleration (m/s2) | −4.05 | −3.77 |
| Acceleration time proportion | 52.25% | 49.58% |
| Deceleration time proportion | 47.75% | 50.08% |
| Items | CFDC | RFDC |
|---|---|---|
| Avg. velocity (km/h) | 92.57 | 92.81 |
| Max. velocity (km/h) | 115.39 | 115.51 |
| Max. acceleration (m/s2) | 2.8 | 3.05 |
| Max. deceleration (m/s2) | −2.5 | −2.77 |
| Acceleration time proportion | 52.79% | 50.63% |
| Deceleration time proportion | 47.21% | 49.19% |
| Item | DP | Rule Based | ||
|---|---|---|---|---|
| Driving cycle | RFDC | CFDC | RFDC | CFDC |
| Fuel cost (L/100 km) | 4.15 | 4.29 | 4.63 | 4.75 |
| SOC cost | 0.1 | 0.1 | 0.1 | 0.1 |
| Ratio of fuel cost | 100.00% | 103.37% | 111.57% | 114.46% |
| Item | DP | Rule Based | ||
|---|---|---|---|---|
| Driving cycle | RFDC | CFDC | RFDC | CFDC |
| Fuel cost (L/100 km) | 3.34 | 3.51 | 3.82 | 3.95 |
| SOC cost | 0.07 | 0.07 | 0.07 | 0.07 |
| Ratio of fuel cost | 100.00% | 105.09% | 114.37% | 118.26% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, H.; Guo, J.; Zhou, N.; Sun, C.; Peng, J. Freeway Driving Cycle Construction Based on Real-Time Traffic Information and Global Optimal Energy Management for Plug-In Hybrid Electric Vehicles. Energies 2017, 10, 1796. https://doi.org/10.3390/en10111796
He H, Guo J, Zhou N, Sun C, Peng J. Freeway Driving Cycle Construction Based on Real-Time Traffic Information and Global Optimal Energy Management for Plug-In Hybrid Electric Vehicles. Energies. 2017; 10(11):1796. https://doi.org/10.3390/en10111796
Chicago/Turabian StyleHe, Hongwen, Jinquan Guo, Nana Zhou, Chao Sun, and Jiankun Peng. 2017. "Freeway Driving Cycle Construction Based on Real-Time Traffic Information and Global Optimal Energy Management for Plug-In Hybrid Electric Vehicles" Energies 10, no. 11: 1796. https://doi.org/10.3390/en10111796
APA StyleHe, H., Guo, J., Zhou, N., Sun, C., & Peng, J. (2017). Freeway Driving Cycle Construction Based on Real-Time Traffic Information and Global Optimal Energy Management for Plug-In Hybrid Electric Vehicles. Energies, 10(11), 1796. https://doi.org/10.3390/en10111796






