Ground-Fault Characteristic Analysis of Grid-Connected Photovoltaic Stations with Neutral Grounding Resistance
Abstract
:1. Introduction
2. Fault-Calculation Model of Grid-Connected PV Station with Neutral Grounding Resistance
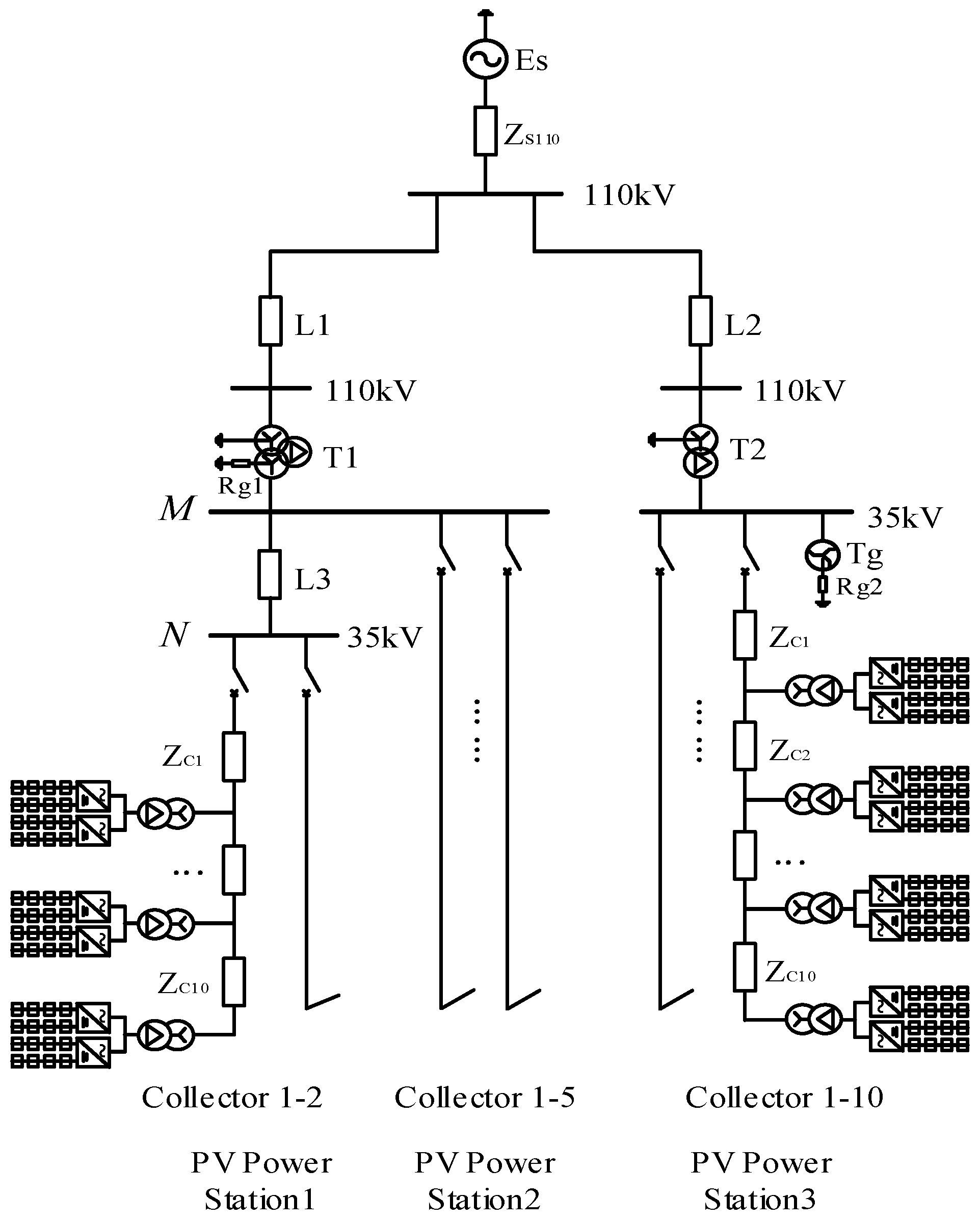
2.1. Structure of Grid-Connected PV Power Station with Neutral Grounding Resistance
2.2. Fault-Calculation Model of Tie-Line
2.3. Fault-Calculation Model of PV-Collector Lines
2.4. General Nature of the Fault Model
- (1)
- The maximum capacity of a PV power-supply model with a fault on the tie-line must be n × PMW.
- (2)
- The capacity of three power supplies in the collector-line model are the following: the collector line power supply without a fault is (n − 1) × PMW, and the two collector line power supplies with a fault are mMW and nMW (m + n = P).
3. Analysis of the Ground Fault
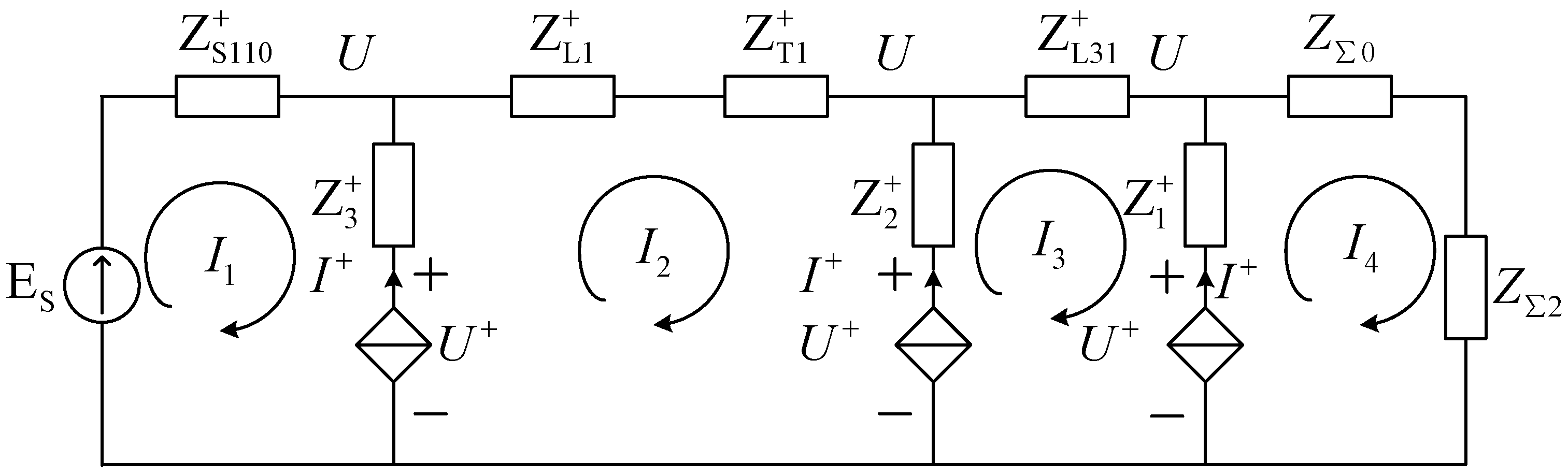
3.1. Short-Circuit Calculation Principle
3.2. Analysis of Tie-Line Ground Fault
3.3. Analysis of Collector-Line Ground Fault
4. Analysis of the Fault Characteristic and Impact on Protection
4.1. Fault Characteristic of the PV Power Supply
4.2. Fault Characteristics of Zero-Sequence Current
4.3. Fault Characteristics of the Phase Current
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A.
- (1)
- The short-circuit capacity of a 110-kV system is 3000 MVA.
- (2)
- The parameters of the transformers are as follows:
- (a)
- The capacity of the transformers varies with the PV source.
- (b)
- T1 parameters: VI/VII/VIII (Yg/yn/d) = 110/35/10 kV; UKI = 10.75%, UKII = 0, and UKIII = 6.75%.
- (c)
- T2 parameters: VI/VII (Yg/d) = 110/35 kV; UK = 10.75%.
- (d)
- All the box-type transformers have the same parameters: Sn = 1 MVA, VI/VII (Y/d) = 35/0.27 kV, and UK = 6%.
- (3)
- The line lengths and impedance (per kilometer) are as follows:
- (a)
- All the pre-unit parameters of the positive and negative sequences are the same, and the pre-unit parameters of the zero sequence are 3 times those of the positive and negative sequences.
- (b)
- L1 = 9 km and L2 = 6 km, which uses LGJ-2 × 400, and the positive sequence impedance is 0.08 + j0.414 Ω/km.
- (c)
- L3 = 10 km, which uses LGJ-240, and the positive sequence impedance is 0.132 + j0.386 Ω/km.
- (4)
- The cable length of each collector line is 3 km, which uses YJV22-3 × 95 mm, and the positive sequence impedance is 0.196 + j0.129 Ω/km.
References
- Guerrero, J.M.; Blaabjerg, F.; Zhelev, T.; Hemmes, K.; Monmasson, E.; Jemei, S.; Comech, M.P.; Granadino, R.; Frau, J.I. Distributed generation: Toward a new energy paradigm. IEEE Ind. Electron. Mag. 2010, 4, 52–64. [Google Scholar] [CrossRef]
- Castilla, M.; Miret, J.; Sosa, J.L.; Matas, J.; de Vicuña, L.G. Grid-fault control scheme for three-phase photovoltaic inverters with adjustable power quality characteristics. IEEE Trans. Power Electron. 2010, 25, 2930–2940. [Google Scholar] [CrossRef]
- Miret, J.; Castilla, M.; Camacho, A.; de Vicuña, L.G.; Matas, J. Control scheme for photovoltaic three-phase inverters to minimize peak currents during unbalanced grid-voltage sags. IEEE Trans. Power Electron. 2012, 27, 4262–4271. [Google Scholar] [CrossRef]
- Hooshyar, H.; Baran, M.E. Fault analysis on distribution feeders with high penetration of PV systems. IEEE Trans. Power Syst. 2013, 28, 2890–2896. [Google Scholar] [CrossRef]
- State Grid Corporation of China (SGCC). Q/GDW 1617-2015 Technical Rule for Connecting Photovoltaic Power Station to Power Grid; State Grid Corporation of China: Beijing, China, 2015. [Google Scholar]
- Nimpitiwan, N.; Heydt, G.T.; Ayyanar, R.; Suryanarayanan, S. Fault current contribution from synchronous machine and inverter based distributed generators. IEEE Trans. Power Deliv. 2007, 22, 634–641. [Google Scholar] [CrossRef]
- Nuutinen, P.; Peltoniemi, P.; Silventoinen, P. Short-circuit protection in a converter-fed low-voltage distribution network. IEEE Trans. Power Electron. 2013, 28, 1587–1597. [Google Scholar] [CrossRef]
- Ustun, T.S.; Ozansoy, C.; Ustun, A. Fault current coefficient and time delay assignment for microgrid protection system with central protection unit. IEEE Trans. Power Syst. 2013, 28, 598–606. [Google Scholar] [CrossRef]
- Haj-ahmed, M.A.; Illindala, M.S. The influence of inverter-based DGs and their controllers on distribution network protection. IEEE Trans. Ind. Appl. 2014, 50, 2928–2937. [Google Scholar] [CrossRef]
- Pan, G.; Zeng, D.; Wang, G.; Zhu, G.L.; Li, H.F. Fault analysis on distribution network with inverter interfaced distributed generations based on PQ control strategy. Proc. CSEE 2014, 34, 555–561. [Google Scholar]
- Baran, M.E.; El-Markaby, I. Fault analysis on distribution feeders with distributed generators. IEEE Trans. Power Syst. 2005, 20, 1757–1764. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, G.; Li, H.; Pan, G.; Gao, X. Analysis on the distribution network with distributed generators under phase-to-phase short-circuit faults. Proc. CSEE 2013, 33, 130–136. [Google Scholar] [CrossRef]
- Camacho, A.; Castilla, M.; Miret, J.; Vasquez, J.C.; Alarcón-Gallo, E. Flexible voltage support control for three-phase distributed generation inverters under grid fault. IEEE Trans. Ind. Electron. 2013, 60, 1429–1441. [Google Scholar] [CrossRef]
- Guo, W.M.; Mu, L.H.; Zhang, X. Fault Models of Inverter-Interfaced Distributed Generators within a Low-Voltage Microgrid. IEEE Trans. Power Deliv. 2017, 32, 453–461. [Google Scholar] [CrossRef]
- Camacho, A.; Castilla, M.; Miret, J.; Borrell, A.; de Vicuña, L.G. Active and reactive power strategies with peak current limitation for distributed generation inverters during unbalanced grid faults. IEEE Trans. Ind. Electron. 2015, 62, 1515–1525. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, X.; Wang, B.; Wu, W.; Guerrero, J.M. Asymmetrical grid fault ride-through strategy of three-phase grid-connected inverter considering network impedance impact in low-voltage grid. IEEE Trans. Power Electron. 2014, 29, 1064–1068. [Google Scholar] [CrossRef]
- Shuai, Z.; Shen, C.; Yin, X.; Liu, X.; Shen, J. Fault analysis of inverter-interfaced distributed generators with different control schemes. IEEE Trans. Power Deliv. 2017, 10, 1–13. [Google Scholar] [CrossRef]
- Bayrak, F.; Erturk, G.; Oztop, H.F. Effects of partial shading on energy and exergy efficiencies for photovoltaic panels. J. Clean. Prod. 2017, 164, 58–69. [Google Scholar] [CrossRef]
- Das, S.K.; Verma, D.; Nema, S.; Nema, R.K. Shading mitigation techniques: State-of-the-art in photovoltaic applications. Renew. Sustain. Energy Rev. 2017, 78, 369–390. [Google Scholar] [CrossRef]
- Bana, S.; Saini, R.P. Experimental investigation on power output of different photovoltaic array configurations under uniform and partial shading scenarios. Energy 2017, 127, 438–453. [Google Scholar] [CrossRef]
- Bastidas-Rodríguez, J.D.; Trejos-Grisales, L.A.; González-Montoya, D.; Ramos-Paja, C.A.; Petrone, G.; Spagnuolo, G. General modeling procedure for photovoltaic arrays. Electr. Power Syst. Res. 2018, 155, 67–79. [Google Scholar] [CrossRef]
- Wang, F.; Duarte, J.L.; Hendrix, M.A. Pliant active and reactive power control for grid-interactive converters under unbalanced voltage dips. IEEE Trans. Power Electron. 2011, 26, 1511–1521. [Google Scholar] [CrossRef]
- Peng, F.Z.; Lai, J.S. Generalized instantaneous reactive power theory for three-phase power systems. IEEE Trans. Instrum. Meas. 1996, 45, 293–297. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, N.; Ye, L. Fault analysis for distribution networks with current-controlled three-phase inverter-interfaced distributed generators. IEEE Trans. Power Deliv. 2015, 30, 1532–1542. [Google Scholar] [CrossRef]
- Bae, Y.; Vu, T.K.; Kim, R.Y. Implemental control strategy for grid stabilization of grid-connected PV system based on German grid code in symmetrical low-to-medium voltage network. IEEE Trans. Energy Convers. 2013, 28, 619–631. [Google Scholar] [CrossRef]
- State Grid Corporation of China (SGCC). GB/T 32826-2016 Guide for Modeling Photovoltaic Power System; Standardization Administration of China: Beijing, China, 2016.
- Grainger, J.; Stevenson, W. Power System Analysis; McGraw-Hill: New York, NY, USA, 1994; pp. 470–527. [Google Scholar]














| SR (Shading Ratio) | Power Loss Coefficient (%) | ||
|---|---|---|---|
| Single-Cell | Horizontal | Vertical | |
| 0.00 | 0.00 | 0.00 | 0.00 |
| 0.25 | 9.06 | 34.53 | 16.99 |
| 0.50 | 65.88 | 75.97 | 18.85 |
| 0.75 | 66.38 | 92.96 | 61.88 |
| 1.00 | 69.22 | 99.98 | 66.93 |
| Fault Type | SR (Shading Ratio) | PV1 Output Current Values |IPV1| (A) | ||
|---|---|---|---|---|
| Single-Cell | Horizontal | Vertical | ||
| Single phase to ground | 0.00 | 503.11 | 503.11 | 503.11 |
| 0.25 | 455.75 | 334.72 | 423.85 | |
| 0.50 | 176.16 | 123.81 | 415.83 | |
| 0.75 | 175.62 | 35.83 | 201.16 | |
| 1.00 | 158.40 | 9.02 | 175.32 | |
| Double phase to ground | 0.00 | 700.07 | 700.07 | 700.07 |
| 0.25 | 632.46 | 461.17 | 587.10 | |
| 0.50 | 243.68 | 168.26 | 575.72 | |
| 0.75 | 241.53 | 48.39 | 274.80 | |
| 1.00 | 215.76 | 12.41 | 239.32 | |
| Fault Type | SR (Shading Ratio) | Zero-Sequence Current Values |I0| (A) | ||
|---|---|---|---|---|
| Single-Cell | Horizontal | Vertical | ||
| Single phase to ground | 0.00 | 353.37 | 353.37 | 353.37 |
| 0.25 | 350.17 | 341.89 | 348.00 | |
| 0.50 | 331.02 | 327.05 | 347.45 | |
| 0.75 | 330.83 | 320.64 | 332.57 | |
| 1.00 | 329.53 | 318.64 | 330.66 | |
| Double phase to ground | 0.00 | 198.62 | 198.62 | 198.62 |
| 0.25 | 196.36 | 190.59 | 194.83 | |
| 0.50 | 183.32 | 180.61 | 194.45 | |
| 0.75 | 183.10 | 176.46 | 184.26 | |
| 1.00 | 182.24 | 175.20 | 183.03 | |
| Fault Type | Rg1 (Ω) | Zero Sequence Current with Different Fault Locations |I0| (A) | ||
|---|---|---|---|---|
| Start | Middle | End | ||
| Single phase to ground | 10 | 739.81 | 641.14 | 550.60 |
| 30 | 254.61 | 250.24 | 244.33 | |
| 50 | 153.93 | 153.94 | 153.95 | |
| 100 | 77.02 | 78.30 | 79.49 | |
| 200 | 38.57 | 39.45 | 40.32 | |
| Double phase to ground | 10 | 395.13 | 365.69 | 334.46 |
| 30 | 132.51 | 132.37 | 132.23 | |
| 50 | 79.58 | 80.51 | 81.71 | |
| 100 | 39.82 | 40.63 | 41.64 | |
| 200 | 19.91 | 20.41 | 21.00 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Lu, J.; Zhu, Y.; Jiang, W. Ground-Fault Characteristic Analysis of Grid-Connected Photovoltaic Stations with Neutral Grounding Resistance. Energies 2017, 10, 1910. https://doi.org/10.3390/en10111910
Li Z, Lu J, Zhu Y, Jiang W. Ground-Fault Characteristic Analysis of Grid-Connected Photovoltaic Stations with Neutral Grounding Resistance. Energies. 2017; 10(11):1910. https://doi.org/10.3390/en10111910
Chicago/Turabian StyleLi, Zheng, Jiping Lu, Ya Zhu, and Wang Jiang. 2017. "Ground-Fault Characteristic Analysis of Grid-Connected Photovoltaic Stations with Neutral Grounding Resistance" Energies 10, no. 11: 1910. https://doi.org/10.3390/en10111910
APA StyleLi, Z., Lu, J., Zhu, Y., & Jiang, W. (2017). Ground-Fault Characteristic Analysis of Grid-Connected Photovoltaic Stations with Neutral Grounding Resistance. Energies, 10(11), 1910. https://doi.org/10.3390/en10111910




