Insertion of Mono- vs. Bi- vs. Trivalent Atoms in Prospective Active Electrode Materials for Electrochemical Batteries: An ab Initio Perspective

Abstract

Rational design of active electrode materials is important for the development of advanced lithium and post-lithium batteries. Ab initio modeling can provide mechanistic understanding of the performance of prospective materials and guide design. We review our recent comparative ab initio studies of lithium, sodium, potassium, magnesium, and aluminum interactions with different phases of several actively experimentally studied electrode materials, including monoelemental materials carbon, silicon, tin, and germanium, oxides TiO₂ and V_xO_y as well as sulphur-based spinels MS₂ (M = transition metal). These studies are unique in that they provided reliable comparisons, i.e., at the same level of theory and using the same computational parameters, among different materials and among Li, Na, K, Mg, and Al. Specifically, insertion energetics (related to the electrode voltage) and diffusion barriers (related to rate capability), as well as phononic effects, are compared. These studies facilitate identification of phases most suitable as anode or cathode for different types of batteries. We highlight the possibility of increasing the voltage, or enabling electrochemical activity, by amorphization and p-doping, of rational choice of phases of oxides to maximize the insertion potential of Li, Na, K, Mg, Al, as well as of rational choice of the optimum sulfur-based spinel for Mg and Al insertion, based on ab initio calculations. Some methodological issues are also addressed, including construction of effective localized basis sets, applications of Hubbard correction, generation of amorphous structures, and the use of a posteriori dispersion corrections.

1. Introduction

1.1. Ab Initio Modeling Assists in Rational Design of Active Electrode Materials for Advanced Electrochemical Batteries

In 2016, fossil fuels (oil, natural gas and coal) accounted for about 85% of the world’s primary energy consumption [1], an amount which is inevitably increasing, with no end to this development yet in sight. Although fossil fuels, especially in combination with nuclear energy, bear the potential to shoulder the increasing global energy demand burden for centuries, major concerns with regard to their ecological impact, as well as the uneven distribution of these resources leading to sensible dependencies on fuel trade, caused a steadily growing interest in the development of sustainable energy conversion technologies. Nuclear energy faces public mistrust, with its long-standing final deposition issues still not resolved. Renewable energy sources exhibit consequently the largest annual growth rate of all energy conversion technologies [1]. Nevertheless, an extensive, global use of renewable energy sources is still disadvantaged by several obstacles. Besides the current technical limitations of the energy conversion technologies themselves, their intermittency in many places is one of the most important difficulties for the expansion of renewables to a major component of the energy mix. Furthermore, automobility is still heavily dependent on fuel combustion engines, accounting for roughly 20% of the global liquid fuel demand [1]. The improvement of energy storage technologies is a central building block for the future success of sustainable energy conversion, on a large as well as on a small application scale. The requirements for a successful storage technology depend on its application, but in general a fast storage/release rate, high energy density, and high capacity are desirable features. A promising and already widely implemented technology (especially in portable electronics and automobile applications) is electrochemical energy storage in the form of batteries. Although ‘older’ battery types (lead acid, Ni–Cd) still dominate in terms of installed capacity, Li-ion batteries recently gained sharply increasing market share and are especially dominant in consumer electronics due to their relatively large energy density. Although crucial parameters like capacity, price, and cycle life have improved significantly in the past years, their intrinsic limitations and especially material availability constraints make the development of alternative electrochemical storage technologies desirable. The demand for lithium for application in batteries recently became the dominant Li sink, and although the global reserves-to-production ratio is currently still at around 430 years [2], the breakthrough of electric vehicles into the mass market might drastically decrease this number. Also, further competition for Li resources might eventually arise in the future by the deployment of novel technologies, e.g., in the form of nuclear fusion reactors likely depending on ⁶Li (and potentially ⁷Li) as a tritium precursor nuclide. A replacement of lithium in future high-performance electrochemical energy storage applications is therefore desirable. Naturally, the chemically similar heavier alkaline metal elements like Na or K come first to mind. Indeed, these elements have some of the highest concentrations in the Earth’s continental crust (Na: 2.36%, K: 2.14%) [3] so that scarcity is not expected to be an issue. Also, these elements’ standard electrode potentials are comparable (Li⁺/Li: −3.040 V, Na⁺/Na: −2.714 V, K⁺/K: −2.936 V against the standard hydrogen electrode) [4], so that expected battery voltages could in principle reach similar values, and their Stokes radii generally decrease with increasing mass, which leads to faster diffusion in liquid electrolytes [5]. On the other hand, the increasing mass-to-carried-charge ratio leads to a decrease of the energy density from Li to K and the increasing ionic radii complicate the accommodation of the metal ions in an electrode host structure. Further, safety concerns typical of the use of alkali metals due to the high reactivity of the pure elements and dendrite formation upon metal plating or when using pure metal electrodes also make other alternatives desirable. To counter the decrease in energy density, the use of multivalent metal ions could help due to a larger number of valence electrons. Other abundant metals with comparatively low mass like Mg and Al (Mg: 2.20%, Al: 7.96% concentration in continental earth crust) [3] are therefore of interest for the use in metal ion batteries as well, although their standard potential is somewhat higher (Mg²⁺/Mg: −2.38 V, Al³⁺/Al: −1.66 V against the standard hydrogen electrode) [6].

The number of possible ions is by far exceeded by the variety of host structures that can be used as electrode materials in electrochemical battery storage. It is beyond the scope of this work to give an overview of all currently investigated electrode materials, but rather to outline the process of rational materials selection and prediction of crucial properties by modeling. Various modeling techniques can be applied to help understand the performance of and to help design batteries and specifically active electrode materials. These include continuous modeling methods, molecular dynamics, and ab initio methods. Among these, ab initio methods play a critical role, because the phenomena providing the functionality of an active electrode material involve changes in electronic level occupancies and energies, and changes in charge states. This is conspicuous in materials with redox centers, such as oxides, in which changes in the oxidation and charge state are the origin of capacity, but also in materials without such redox centers, such as monoelemental semiconductors like Si where electronic interactions and bandstructure play a critical role [7]. Methods that in principle do not provide electronic properties, such as force field molecular dynamics, therefore, cannot in principle model the mechanism of charge-discharge, although they can assist in finding structures and in modeling ionic transport related to the cycling rate. The workhorse ab initio method for modeling of solid electrode materials is density functional theory (DFT) [8,9]. A by now significant body of ab initio literature on modeling of electrode materials exists, mostly considering lithiation, to a smaller degree sodiation, and to a much smaller degree material interactions with prospective electrode materials for other types of batteries. This body of work and respective reviews [8,9] establish that DFT can provide semi-quantitative, and sometimes quantitative, accuracy of estimates of voltage-capacity curves and ion diffusion barriers observed in experiments (with achievable accuracies on the order of a fraction of 1 V or 0.1 eV, respectively), even when modeling idealized bulk systems abstracting from microstructural or even interfacial effects.

DFT modeling is, therefore, of much help in understanding the mechanism and limits of performance of known materials for different types of electrochemical batteries as well as for design (by computational pre-screening) of novel and better (for specific properties) materials. In this logic, comparison of DFT-computed properties across multiple materials and types of ions (Li, Na, K, Mg, and Al) is important. Such comparisons among numbers produced by disparate groups may not, however, be reliable, due to the semi-quantitative accuracy of DFT and the use by different groups of different codes, exchange-correlation functionals, types of basis sets and pseudopotentials. We note here that the error bars on electronic properties which are important in this application are much wider than on e.g., structural parameters, so that the somewhat self-congratulatory statements in Ref. [10] about excellent agreement of various DFT codes and setups are not fully applicable. As a result, different DFT setups may result in differences in e.g., voltage estimates comparable to those caused by the use of a different phase of a material. Clearly, it is advantageous to have estimates of key electrode material properties for different materials and different ions made with the same approximations and the same computational setup.

1.2. This Review

Over the last several years, our group has performed a series of comparative ab initio studies of the Li, Na, K, Mg, and Al interactions with several phases of several potential electrode materials which have been extensively studied in experimental labs, and some also computationally [7,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37], including amorphous phases. These studies were the first truly comparative, i.e., using the same approximations and computational parameters, studies permitting comparisons among different phases and types of ions. They therefore permitted identifying trends with ionic radius as well as with valence, and they allowed identifying phases most suited in terms of predicted voltage and/or kinetic properties for specific types of batteries. We studied monoelemental materials as well as oxides and sulfides with different redox centers. Not all five types of ions and properties were considered in all these studies, but all of them considered more than one ion type substantially different in size or valence and all of them considered interactions with more than one phase of a prospective electrode material. Some of these studies considered for the first time phononic effects on lithiation, sodiation, and magnesiation, and effects on voltage of doping. While most of these studies helped explain the mechanism and parameters of performance which had already been observed experimentally, some of them predicted electrochemical activity before it was confirmed experimentally, for example, the recently confirmed sodiation of amorphous silicon [20,38] or voltages achieved with magnesiated TiO₂ [22,39]. Some of the calculations we performed and review below still await experimental confirmation such as our prediction of significantly enhanced insertion energetics by p-doping. We therefore hope that this review will help spur such studies.

Some of the studies reviewed below also addressed methodological issues such as the construction of a localized basis set, the use of dispersion corrections to DFT, the use of Hubbard corrections including those on s and p states, the relation between charge and oxidation states as well as phononic effects. It is useful to bring the key results and conclusions of these studies under one roof to highlight similar effects at play in different kinds of materials, such as the influence of strain on thermodynamics of storage or effects of amorphization on binding energy (voltage), and to summarize methodological issues, which could be of use for future modeling works. This review attempts to achieve exactly this. In it, we list key findings of our studies of phases of silicon, carbon, tin, germanium, titania, vanadium oxides, and sulfides as potential hosts for Li, Na, K, Mg, and Al in Section 2, and then summarize common trends in Section 3.

1.3. Key Computed Quantities

All results reviewed here were computed using density functional theory (DFT) [40,41]. Different functionals, basis sets, and software were used which were deemed most suitable for a specific system. The reader is referred to the original papers for details of calculation setups [7,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. Here, we only introduce key computed quantities which are important for a material’s performance as an active electrode material and which are discussed in Section 2 and Section 3. To analyze the thermodynamics of interaction of a potential electrode material with Li, Na, K, Mg, or Al, we use the binding energy E_b(n) of n of these atoms to the active material, which is effectively the defect formation energy (E_f, which is the term used in many studies [11,12,13,15,16,19,20,21,22,23,24,25]). It is computed as:

$$E_b\left(n\right)=\frac{1}{n}\left[E\left(nX-\mathrm{material}\right)-E\left(\mathrm{material}\right)-nE\left(X\right)\right]$$

(1)

where X is one of Li, Na, K, Mg or Al, and n is the number of atoms of type X. E(nX − material) is the energy of the active material (a supercell of a periodic solid) with n atoms of type X, E(material) is the energy of the supercell before the insertion of X, and E(X) is the energy of one atom of X in its chosen reference state (typically bcc Li, bcc Na, bcc K, hcp Mg, and fcc Al when E_b is used to estimate voltages, although in some studies we used single atom reference also called “vacuum”, where indicated). Here, the binding energy is defined per one atom of type X. In the case of substitutional defects, E(material) is corrected for the changes in the number of atoms in the host material. A negative binding energy implies favorable X insertion (electrochemical activity) and vice versa. The binding energy is related to the average voltage for insertion up to a concentration of X corresponding to n atoms per simulation cell via the equation [42]:

$$V=-\frac{E_b\left(n\right)}{eq}$$

(2)

where e is the elementary charge and q is valence charge, q = 1 for Li, Na and K, q = 2 for Mg, and q = 3 for Al. In some cases, we also estimated the shapes of voltage-capacity curves, with which active electrode materials are typically characterized, using [9]:

$$V=-\frac{E\left(n_{2}X-\mathrm{material}\right)-E\left(n_{1}X-\mathrm{material}\right)-\left(n_2-n_1\right)E\left(X\right)}{q\left(n_2-n_1\right)}$$

(3)

The voltage curve is thus computed as a series of piecewise average voltages between concentrations corresponding to n₁ and n₂. These concentrations are chosen as points on the convex hull built on the formation energy—concentration curve:

$$E_{\mathrm{form}}\left(n\right)=\frac{1}{\left(N+n\right)}\left[E\left(nX-\mathrm{material}\right)-E\left(\mathrm{material}\right)-nE\left(X\right)\right]$$

(4)

where N is the number of formula units of the host material (e.g., number of Si atoms or number of TiO₂ units).

In some of the materials analyzed below, we analyzed kinetic properties which inform on the rate capability of the material by computing the diffusion barriers E_a that determine the diffusion rate D of atoms M in the host material:

$$D=a_0^2\mathsf{\Gamma }{e}^{-\frac{E_a}{k_{B}T}}$$

(5)

where a₀ is the hopping distance in diffusion events, $\mathsf{\Gamma }$ the attempt frequency, k_B the Boltzmann constant, and T is the temperature [9,43]. While it is possible to use E_a and vibrational frequencies computed ab initio (using the transition state theory) [43,44] to estimate D, this comes at a cost of further approximations which typically result in D values up to orders of magnitude different from experimental estimates [45], i.e., D is often not quantitatively accurate. We therefore limited ourselves to the calculations of the barriers, which are expected to be quantitatively accurate with the level of theory we used [46].

The energies in the above are Gibbs free energies; however, they are typically well approximated by the electronic (internal) energies computed with DFT, as is done in nearly all ab initio studies of battery materials [9,47] with rare exceptions [14,23]. In our work, we also considered vibrational contributions to E_b and E_a in some of the considered systems, where such contributions were computed using the harmonic approximation as:

$$E_{vib}-\mathrm{T}{S}_{vib}={\displaystyle \int }d\mathit{k}{\displaystyle \sum }_{i=1}^N\{\frac{1}{2}{\nu }_i+k_B\mathrm{Tln}\left(1-e^{-{\nu }_i/k_B\mathrm{T}}\right)\}$$

(6)

where ν_i is the energy of one quantum in the ith normal mode, k is the wave vector in the Brillouin zone, and S_vib is the vibrational entropy. These calculations were also necessarily considered where phase stability was studied [23,28].

2. Results

In this section, we review key results of modeling of Li, Na, K, Mg, and Al interaction with different phases of carbon, silicon, tin, germanium, titania, vanadium oxides of different stoichiometries, and sulfur-based spinels MS₂, where M is a transition metal.

2.1. Interactions of Li, Na, K, and Mg with Monoelemental Group IV Materials

Monoelemental group IV materials carbon, silicon, germanium, and tin have all been successfully used as anode materials in Li and post-Li batteries. They attract attention because of their high specific capacity. The most famous of these materials is silicon, which achieves up to 4200 mAh g⁻¹ during lithiation at a good anodic voltage of about 0.1 V vs. Li/Li⁺ [48,49]. Silicon is, however, electrochemically inactive for Na and Mg, despite the favorable formation energy of Mg₂Si which corresponds to a voltage of about 0.2 V. Further down the periodic table, Ge was also found to be effective for Li, with a specific capacity of about 1568 mAh g⁻¹ (based on Li₁₇Ge₄) [49] and faster diffusion for both Li and Na, but sodiation and magnesiation of Ge are inefficient, although sodiation has been observed after prior pre-lithiation [50]. Tin, on the other hand, was successfully tested for Li, Na, and Mg insertion, providing the following specific capacities: for Li, 959.5 mAh g⁻¹ (Li₁₇Sn₄), 847 mAh g⁻¹ for Na (Na₁₅Sn₄), and 911 mAh g⁻¹ for Mg (Mg₂Sn) [49,51,52]. While Si and Ge have a stable diamond crystal structure at 0 K as well as at normal conditions (which is maintained at low concentrations of ions even though higher states of charge induce phase changes) [53,54], this is not the case in Sn, where the diamond phase (stable at 0 K) converts to the beta tin phase at 13 °C. This phase competition had to be considered. The remaining group IV material considered here, carbon, is not used in its diamond form but in graphite form in Li ion batteries. Graphite is, however, electrochemically inactive for Na and Mg [55]. On the other hand, amorphous carbons were reported as effective Na ion battery anode materials [56,57]. Layers of graphite–graphene—also find use in Li and Na ion batteries. Here again, one needs to consider different phases and also ask the question “can amorphization improve electrochemical performance of other group IV materials, too?” It is therefore instructive to compare the mechanism across the group IV elements and among Li, Na, and Mg. While a multitude of good ab initio studies have been produced studying interactions of particular materials with particular ions [58,59,60,61,62,63,64,65,66], truly comparative studies were lacking. We produced several such studies and they are surveyed next.

2.1.1. Interaction of Li, Na, and Mg with Silicon: Effects Due to Ion Size and Valence, of Host Amorphization, and of Phonons, and How to Build Effective Localized Basis Sets

In references [11,12,14,15,16,20,24], we produced comparative studies of Li, Na, and Mg insertion in crystalline and amorphous silicon. While lithiation of Si is an alloying reaction, we will further, for the sake of consistency, use the word “insertion”, since for small concentrations and only interstitial sites occupied, the two mechanisms do not differ. Some of these studies used plane wave bases [12] and some used localized basis sets [14,20]. Specifically, when using the localized basis sets, which are more computationally efficient for many kinds of calculations, the issue of basis size and shape selection arises. This is in contrast to plane wave bases, where a single parameter, the cutoff energy, controls the basis quality. We found that it is useful to choose the width of localized basis functions (of a given basis size such as double-Ϛ polarized (DZP) that we used) to reproduce the cohesive energy of each component individually (e.g., of bcc Li and diamond Si). In this way, the interaction energies can be accurately (i.e., matching plane wave and/or experimental results) obtained with a modest basis size such as DZP. This can be seen by comparing the insertion energies of Refs. [20,67], where default basis sets of the Spanish Initiative for Electronic Simulations with Thousands of Atoms (SIESTA) program were used, with those of Ref. [14], where bases tuned in this way were used, as well as with available plane wave results [12,59,60]. This strategy was then used by us to build the basis sets for studies of Sn and TiO₂ where we also achieved good agreement between our results obtained with DZP bases and our, or others’, plane wave calculations [21,22,23,28].

We studied early stages of lithiation, sodiation, and magnesiation. While thermodynamics and kinetics change along the charge-discharge curve, studies of dilute concentrations permit understanding the basic mechanism of interaction between the ions and the host. It is often possible to make informative statements based on dilute concentration studies. For example, Mg₂Si has a formation energy which would correspond to an average voltage of about 0.2 V. Yet spontaneous magnesiation is not observed, in part because Mg atoms do not insert into Si due to high E_b and high diffusion barriers as explained below. This can be understood from dilute concentration studies.

We first considered insertion of one or two interacting Li, Na, Mg atoms in the Si crystal (c-Si). The insertion sites are known to be tetrahedral (Td) sites, and the hexahedral (Hex) sites serve as transition states for diffusion between Td sites [12,14,59,60]. While Li and Na strongly prefer interstitial Td sites, Mg insertion energy at the substitutional (S) site is competitive with that at the Td site. We found that Li insertion energies (Figure 1) were about 0.3 eV weaker than Li cohesive energy, in agreement with other studies [59,60]; the diffusion barrier in Si of about 0.6 eV is also in agreement with other studies [59,60]. Rather than being a fluke of the DFT modeling which is in contradiction with the observed lithiation of Si, the fact that E_b is weaker than the cohesive energy of Li indicates that single atom insertion and diffusion mechanism of lithiation is unlikely. Indeed, it was eventually (and after first DFT models of Li insertion were published) understood that lithiation proceeds with a front and not by way of single atom insertion and diffusion [68,69]. The insertion energies of Na and Mg were very high and positive, implying, consistent with experimental observations, that c-Si cannot serve as electrode material for Na and Mg ion batteries. Diffusion barriers of Na and Mg were also high on the order of 1 eV [14]. We found that when two Li, Na, or Mg are inserted in neighboring sites, their E_b is destabilized by about, respectively, 0.2, 0.3, or 0.4 eV (vs. well-separated defects); as a result, the diffusion barrier towards further sites is lowered by a similar amount. In general, E_b decays with inter-dopant distance with some metastable minima at certain distances [12,13,15].

Our calculations on Si showed that the high insertion energy of Na and Mg (as well as of other ions and in other materials some of which are considered below) is largely due to the so-called strain energy, which is the energy cost to distort the Si lattice to the positions that Si atoms occupy upon Li, Na, or Mg insertion. Indeed, R² correlation coefficients between the diffusion barriers and Si lattice strain energy and between the change in the barrier due to the presence of a second neighboring Li, Na, or Mg atom and the change in the Si lattice strain energy are about 0.8–0.9 [14]. The large strain energies induced by Na and Mg are due to the larger ionic size of Na and larger polarization caused by the Mg ion due to its bivalency.

The electronic mechanism of Li, Na, and Mg accommodation is donation of Li, Na, or Mg valence electrons to the conduction band of Si, as evidenced by the shift of the Fermi level to the conduction band [24,60]. Li and Na donate their only valence electron, as reflected in their Bader charges of about 0.9 |e|. The Mg charge is on the order of 1.5 |e|, which can be attributed to donation of both valence electrons to the conduction band (see Section 2.1.5). In Section 2.1.5, we will show how this mechanism can be used to strengthen E_b with p-doping.

In Ref. [17] we studied for the first time the effect of an electrolyte molecule, ethylene carbonate (EC), on Li insertion into Si. We considered (100) and (111) reconstructed surfaces. We found that Li insertion barriers into (100) and (111) bare surfaces are about 1 and 1.1 eV, respectively. These are much larger barriers than the well-studied diffusion barriers of Li in bulk Si, which are on the order of 0.5 eV, and could be the kinetic bottleneck in initial stages of lithiation. One reason for such high barriers is that while the transition state is at a Hex site similar to bulk Si, the initial state in the diffusion event is a surface site which is more stable than inner sites. This is typical of many of the materials we considered. These barriers can be significantly changed by the presence of EC: the EC molecule can adsorb on these surfaces in a molecular, semi-dissociated (SD) configuration or a ketone-like configuration, with a preference for SD. The SD configuration, whose formation is very exothermic, lowers the insertion barrier of a neighboring Li atom by about 0.2 eV on the (100) surface but raises it by a similar amount on (111). The ketone-like configuration, however, which is only by about 0.2 eV less stable on the (111) surface, raises the barrier by 0.4 eV. Focusing on the (111) surface, in Ref. [11], we compared insertion barriers of Li, Na, and Mg. The (defect formation) energies of surface and subsurface sites on an (111) passivated eight-layer nanosheet and the insertion barriers are shown in Figure 2. They vary significantly and in the case of Na and Mg, prohibitively high barriers demonstrate the key role of the active material’s interface in the charge-discharge kinetics. Note a slight difference in barriers computed with a reconstructed surface model in Ref. [17] and a passivated nanosheet model in [11].

In [14] we studied for the first time the effect of phononic contributions to the Gibbs free energy on Li, Na, and Mg insertion energies and diffusion barriers. We found that at room temperature, those are on the order of 0.1, 0.1, and 0.2 eV for Li, Na, and Mg insertion, respectively, and can be double this amount (per dopant) for nearest-neighbor dopants. The effects on the diffusion barriers were on the order of 0.1 eV (making them lower). That is to say, the combined effects of dopant–dopant interactions and vibrations could change the diffusion rate by orders of magnitude. These calculations imply an effect on voltage on the order of 0.1 eV (which is also similar in magnitude to those observed in Sn discussed below), which may or may not be negligible. Most ab initio studies of potential electrode materials do not include phonons due to increased CPU cost; our calculations showed that this is acceptable if one is comfortable with errors of this magnitude.

Having understood the impossibility of using c-Si as electrode material for Na or Mg ion batteries but enticed by its potentially high specific capacity, we considered possibilities to facilitate sodiation and magnesiation of Si. We came up with two effective strategies: p-doping, considered in Section 2.1.5 below, and amorphization, considered here [15,20]. The rationale behind using an amorphous structure is two-fold: firstly, an amorphous structure may have larger-volume insertion sites, which would lead to lower strain energy; secondly, a metastable amorphous structure is expected to be more reactive towards Li, leading to a lower (stronger) E_b. We used a previously published [67] amorphous Si (a-Si) structure. An amorphous structure has multiple insertion sites with different E_b, and we found that many of those sites had E_b much lower than that of c-Si; this is shown in Figure 1. For Li, a number of sites with E_b < 0 imply that single-atom insertion mechanism is made thermodynamically more favorable than in c-Si. A number of insertion sites had E_b of Mg by up to 1.5 eV lower than in c-Si. It is conceivable that amorphous Si structures can be made that will favor magnesiation (we note that while metallic Mg is easier to use as anode than Li or Na, Mg does show dendrite formation in some electrolytes [70,71] so that a Mg ion battery anode material is still desirable). More importantly, a number of insertion sites had E_b < 0 for Na, implying that a-Si should be electrochemically active for Na (while c-Si is not). In 2016, exactly this was confirmed in an experimental study of Lim et al. [38]. This is an example of theory leading the experiment in the design of new electrode materials for post-Li batteries. A computational work by Jung et al. [64] which was submitted soon after ours [15,20] also predicted sodiation of a-Si.

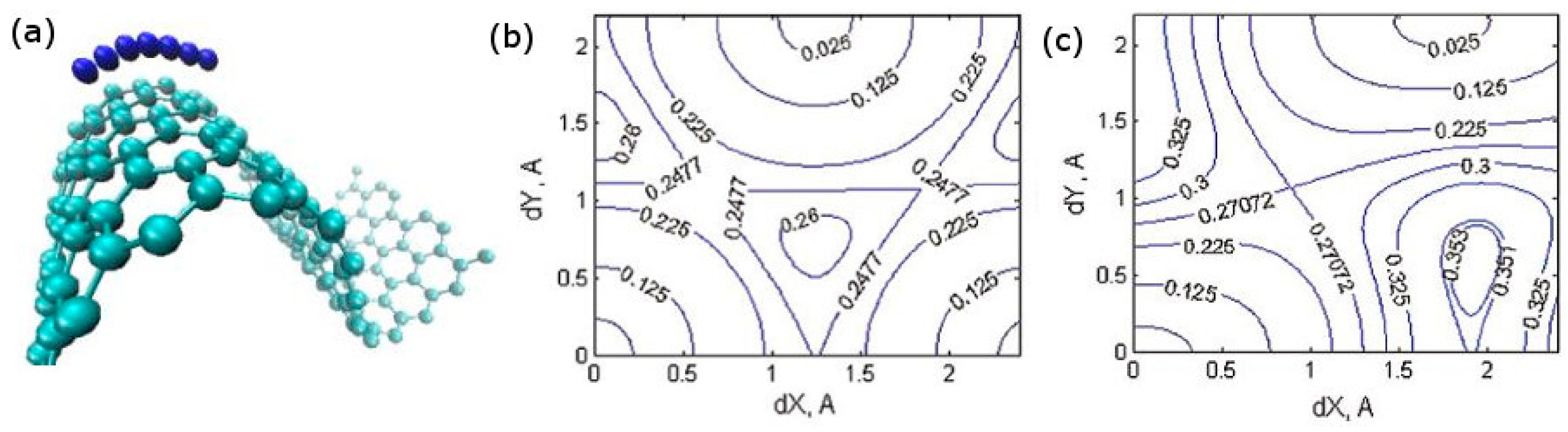
2.1.2. Insertion of Li, Na, K, and Mg in Carbon: Effects Due to Ion Size and of Host Amorphization

A somewhat similar situation as with Si exists with carbon: a thermodynamically stable crystalline phase, graphite, is a very effective anode for Li ion batteries, but graphite is not electrochemically sodiated (or magnesiated) [62,72]. It was quickly understood that “amorphous” carbon can be an effective Na ion battery anode [73]. We note that what is often called “amorphous carbon” in experimental literature is in fact nanoparticular graphite, as opposed to the so-called glassy amorphous structures [74]. Nevertheless, this means that loss of long-range order and availability of larger insertion sites are responsible for sodiation. We compared Li, Na, K as well as Mg insertion in graphite and amorphous (glassy) carbon (a-C). We found a similar effect of amorphization as in Si: multiple insertion sites were identified in a-C where E_b was lowered by up to 1.5/2/2/3.5 V for Li/Na/K/Mg vs. graphite, as shown in Figure 3. Specifically multiple insertion sites had E_b < 0 of Na, implying the possibility of sodiation. For Li, this meant increased voltages. Computed voltage-capacity curves for lithiation and sodiation agreed well with experimentally measured curves using thoroughly amorphized carbon [25]. Our calculations also showed a significant magnitude of strengthening of insertion energy of Mg and K by amorphization [27], as is also shown in Figure 3, implying the possibility of electrochemical activity after amorphization. Graphite has been shown experimentally to work as an anode in K ion batteries [75]. The positive computed E_b for single-atom insertion might mean that higher states of charge are formed during potassiation, i.e., there is phase segregation. The same work found that amorphization significantly improves electrochemical performance, consistent with the calculation [75]. Specifically, the initial part of the voltage capacity curve was at about 1 V, consistent with Figure 3. Our calculations also suggest that a-C might work for Mg with initial voltages on the order of 0.7 V (−E_b/2).

To generate the amorphous structures used in [25,27], we developed an approach in which we made structures directly reproducing the density and the radial distribution function (RDF) known experimentally. To this end, a cubic simulation cell was set up into which a number of C atoms were placed corresponding to the desired density. The atoms were placed on regular grid points with the only restriction that atoms should not be too close. All or a very large number of such placements were scanned and those providing the closest match to the experimental RDF were selected for further optimization with DFT. The DFT optimization of such structures (atomic positions and cell vectors) did not show significant changes in density or RDF, and the structures were also stable under insertion of Li, Na, K, Mg. This is in contrast to some quenched MD derived a-C structures from the literature which we tried and which fell apart under cell vector optimization. We believe this to be a useful approach for other materials as well.

Single layers of graphite, graphene, also attracted attention as electronic and ionic conductors providing connectivity between e.g., nanoparticles of the active material [76,77,78]. Multilayer or functionalized graphene can also have reversible capacity, although ideal graphene does not [79]. There are multiple ab initio models of alkali atom interaction with ideal planar graphene or planar defected graphene and other 2D carbons [80,81,82,83,84,85]. In reality, however, graphene has a crumpled morphology, with areas of significant curvature. In [18], we studied for the first time the effect of curvature on attachment energy and diffusion barriers of Li and Na. We considered curvature induced by contraction of one of the axis by up to 1/3 (Figure 4). We found that the change in diffusion barriers due to curvature is similar for Li and Na, on the order of ±0.1 eV on the convex and concave sides. The difference in the barrier for the alkali metal atoms adsorbed on the concave and convex sides can reach 0.2 eV. This modulation of the diffusion barrier by curvature by multiples of k_BT at room temperature is therefore expected to affect significantly the rate capability of graphene-based electrodes. Changes in E_b were up to about 0.2 eV.

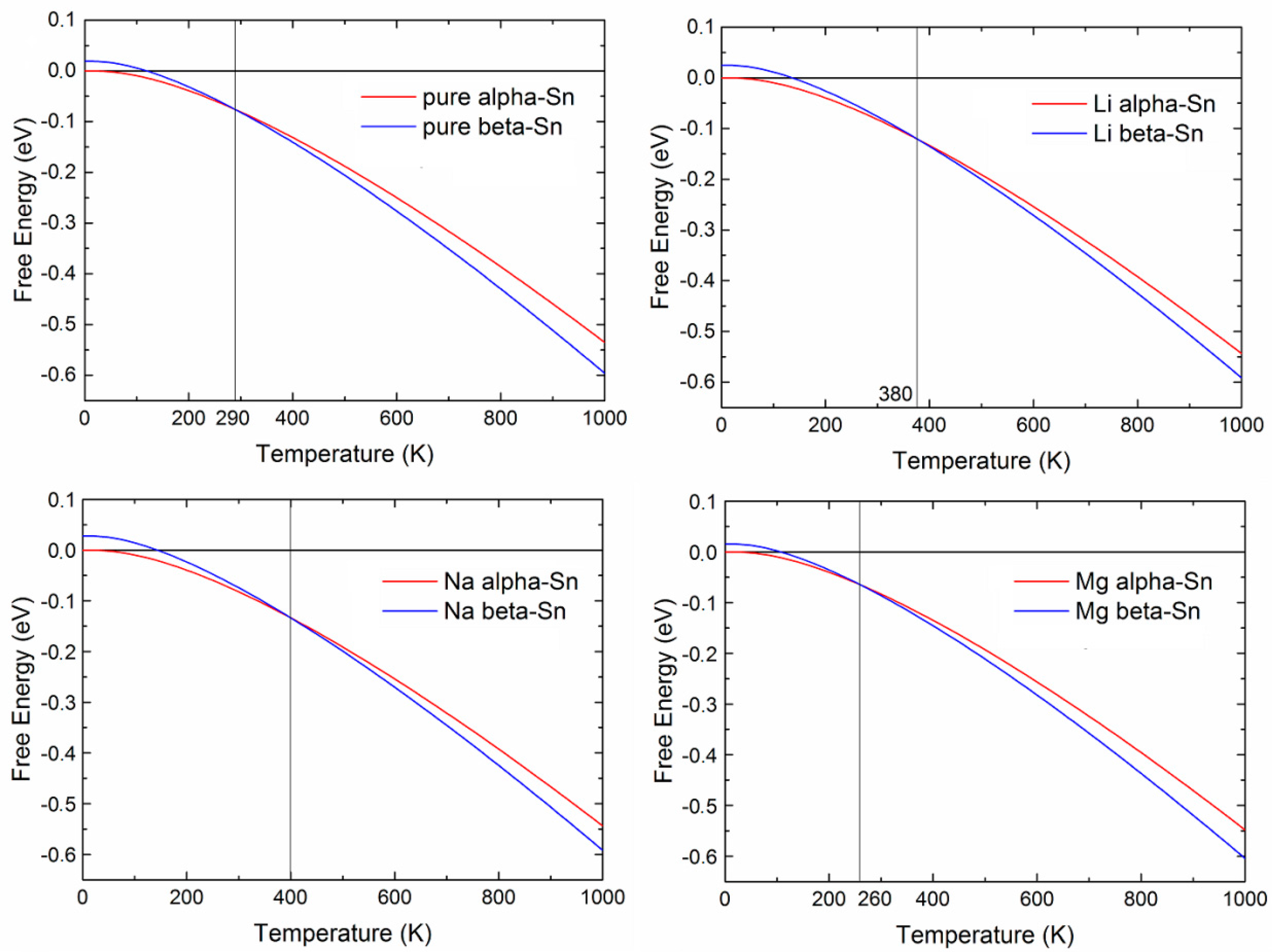
2.1.3. Insertion of Li, Na, and Mg in Tin: Effects Due to Ion Size and Valence, and Phase Competition

In [13], we compared with the same computational setup the insertion of Mg in Ge, Si, and α-Sn. With all these hosts, Mg forms Mg₂X compounds. Based on its formation energy, one expects voltages of 0.24, 0.15, and 0.18 for Ge, Si, and Sn, respectively, and specific capacities of 1476, 3817, and 911 mAh g⁻¹, respectively. However, as described above, Si is not electrochemically active for Mg, while use of Sn as a Mg ion battery anode was reported [86]. This highlights the importance of studying intermediate states of charge and specifically low states of charge down to the dilute limit.

In Refs. [21,23], we modeled insertion of Li, Na, and Mg atoms in α and β Sn (one atom of Li, Na, or Mg in a 64-atom simulation cell of Sn). The E_b values (before vibrational contributions, i.e., electronic energy alone) for Li insertion in α/β tin were −0.32/0.02 eV, for Na insertion −0.09/0.50 eV, and for Mg insertion, 0.79/0.55 eV [23]. That is to say, lithiation and sodiation of the alpha phase is strongly favored at dilute concentration. While E_b for Li in beta Sn is near 0, i.e., lithiation is possible, sodiation of beta tin is strongly disfavored. Magnesiation of both phases is strongly disfavored. The conclusions one can draw from these data are: while lithiation and sodiation can proceed in alpha Sn by the mechanism of single atom insertion and diffusion, in the cases where E_b > 0, charge-discharge must involve a phase front e.g., of Mg₂Sn. This is expected to be kinetically inefficient. Indeed, while magnesiation of Sn was reported by Toyota research labs [86], the rate performance was very poor. This is in spite of the fact that diffusion barriers of Mg were below 0.5 eV in alpha tin, and the lowest diffusion barriers of all Li, Na, Mg in beta tin were computed to be low, on the order of 0.1 eV and therefore consistent with high rate operation [23].

The vibrational contributions (Equation (6)) at room temperature were computed to be for Li insertion in α/β tin −0.05/0.04 eV, for Na insertion 0.01/−0.01 eV, and for Mg insertion, −0.13/−0.02 eV [23]. These are small compared to the electronic contributions (i.e., would have a minor effect on voltages), however, they substantially affect the alpha-beta phase transition temperature. Figure 5 shows free energy—temperature curves for pure tin as well as those following Li, Na, Mg insertion. Li and Na stabilize the alpha phase, while Mg insertion stabilizes the beta phase. This is in agreement with E_b values which are lower for the alpha phase for Li, Na and the beta phase for Mg. This is also in agreement with experimentally observed formation of α Sn upon lithiation [87,88].

Our work on Li, Na, and Mg insertion in Sn also highlighted a couple methodological issues. One is the level of sensitivity of the results to the computational setup. We modeled the Li, Na, Mg-Sn system using two codes with very different basis sets and pseudopotentials. We used SIESTA [89] with a DZP basis built in a way described in Section 2.1.1 and with norm-conserving pseudopotentials (where the pseudopotential of Sn was regenerated to reproduce well the cohesive energy) as well as the Vienna Ab initio Simulation Package (VASP) [90] with a plane wave basis and the Projector-Augmented Wave (PAW) [91] scheme. The results we reported in [23] were obtained with VASP; we reported α-Sn results computed in SIESTA in [28], and we also computed in SIESTA other properties that were reported in Ref. [23]. There was a fair agreement between the two calculation setups with differences in E_b on the order of 0.1 eV and similar phononic contributions. We also performed a subset of the calculations (E_b of Li in alpha and beta Sn) in Quantum Open-Source Package for Research in Electronic Structure, Simulation, and Optimization (ESPRESSO) [92] with PAW and ultrasoft pseudopotentials (USPP): while the PAW results agreed with VASP and SIESTA calculations to within about 0.1 eV, the USPP results differed from them by about 0.5 eV! One therefore needs to be careful when selecting pseudopotentials.

The second and critical methodological issue is that both SIESTA and VASP calculations overestimated the difference in cohesive energies between α and β Sn, ΔE_coh. Experimental estimates put ΔE_coh at about 0.02 eV [93] while the computed values were about 0.04 eV. This seemingly small difference which is on the edge of DFT accuracy is nevertheless sufficient to throw off the phase transition temperature by hundreds degrees, so much so that in [23] we had to offset the enthalpy-temperature curves for pure Sn to match the experimental transition temperature. The values of ΔE_coh that we then computed in other codes using localized or plane wave bases, different types of pseudopotentials as well as full-potential calculations in the Fritz Haber Institute Ab Initio Molecular Simulations (FHI-AIMS) package [94,95] and the Elk all-electron full-potential linearised augmented-planewave (Elk FP-LAPW) code [96] were also about 0.04 eV. Using a hybrid functional did not help. In Ref. [28], we analyzed the origin of this discrepancy, considering the possibility that both the vibrational contributions (Equation (6)) were in error or the electronic contributions (i.e., DFT). We modeled effects of anharmonicity on the vibrational contributions and concluded that they were negligible. We then analyzed the electronic contributions to the cohesive energy and concluded that the error in ΔE_coh results from differences in the valence bandstructure and specifically s and p band occupancy between alpha and beta tin combined with different DFT errors in band energies of different bands. We were able to fix this by applying a small Hubbard U correction on s-like states. Figure 6 shows the partial densities of states of alpha and beta tin. The valence band of both phases is dominated by p and s bands with negligible contribution from d-like states. Application of a Hubbard correction on s-like states stabilized the s band and with a correction on the order of 1 eV we obtained ΔE_coh ≈ 0.02 eV [28]. As a result, one can produce a computational setup with which both phases can be modeled correctly simultaneously, which is necessary when modeling phenomena involving phase transitions, such as lithiation of tin. In [29], we further demonstrated the utility of applying U corrections on s, p states to get a correct electronic structure of molecules. The Hubbard corrections are traditionally used to improve the modeling of d and f states. We showed that they can be very useful also to correctly model s and p states. The idea of applying U correction to s, p states has since been gaining some traction [97].

2.1.4. Interaction of Li, Na, and Mg with Germanium: Effects Due to Ion Size and Valence and Competition between Interstitial and Substitutional Sites

Germanium has an important advantage over its group IV neighbor silicon as a potential battery electrode material: compared to Si, Ge provides higher ionic diffusivities and more stable insertion sites for Li/Na/Mg (i.e., the intercalation of Na and Mg can be easier in Ge compared to Si) [98], and its isotropic expansion (reported for Li) can reduce the mechanical stresses generated during intercalation, compared to the anisotropic swelling of Si [68]. In [37], we performed a comparative ab initio study of lithiation, sodiation, and magnesiation of Ge, in which we showed that there exists competition between interstitial and substitutional sites for Li/Na/Mg insertion, with preferred sites dependent on the type of inserted atom type and concentration. Figure 7 shows defect formation energies associated with different Li/Na/Mg distributions among substitutional and interstitial sites, which illustrates this point. This is an important finding, as most previous ab initio studies of alkali atom interactions with alloying-type electrode materials Si and Ge ignored substitutional sites [58,59,60,61]. Indeed, it is well known that in the dilute regime Li and Na occupy tetrahedral interstitial sites in Si and Ge, while Mg may occupy substitutional sites. Our study in a way bridged the many single-atom insertion studies [59,60,61] and a handful of studies modeling higher charge states and thereby shed light on initial stages of lithiation, sodiation, and magnesiation [64,98]. It follows from Figure 7 that lithiation of Ge is slightly favored (E_b = −0.04 eV for single Li insertion) while sodiation and magnesiation are strongly disfavored (E_b > 0). That is, similarly to Si, ideal germanium cannot be used as electrode for Na and Mg ion batteries. This agrees with available experimental data [50]. Similarly to Si, the high E_b with Na correlates with a significant strain energy; however, while interstitial Mg causes significant strain, the strain caused by substitutional Mg (which is a strongly preferred Mg site in Ge) is similar to the strain caused by interstitial Li (which is a strongly preferred Li site in Ge). The computed diffusion barriers of Li/Na/Mg between interstitial sites were 0.385/0.79/0.66 eV, and between substitutional sites, 0.77/0.93/1.83 eV; these barriers are significantly lowered by the presence of other Li/Na/Mg atoms at neighboring sites [37].

The optimal balance between substitutional and interstitial sites is explained by the electronic structure changes caused by Li, Na, or Mg insertion: interstitial atoms donate their valence electrons (Li and Na, one, Mg, two) to the conduction band and are therefore n-dopants, while substitutional atoms create equivalent holes in the valence band (Li and Na, three, Mg, two) and are therefore p-dopants. The lowest energy state is achieved when the number of electrons donated by the interstitial dopants equals the number of hole states created by substitutional dopants, allowing all electrons donated by the interstitials to occupy lower-lying states in the valence band rather than higher-energy states in the conduction band. We dubbed this effect “self-doping” [7].

2.1.5. p-Doping of Si and Ge as a Way to Enhance Li, Na, and Mg Insertion Energetics

The previous section illustrated that available empty states in the valence band can accept electrons from interstitial Li, Na, or Mg and thereby stabilize E_b via the bandstructure component of the total energy. In Section 2.1.4, this effect was achieved by “self-doping” where the inserted Li, Na or Mg themselves provide hole states when they occupy substitutional sites. Naturally, one could use explicit p-doping to achieve the same effect of stabilization of E_b. This was confirmed by our studies on p-doped Si (doped with Al) and Ge (doped with Ga) [24,37]. Figure 8 shows that p-doping leads to a substantial strengthening of binding of all Li, Na or Mg. At concentrations of p-dopants which have been shown to be feasible [99], it is possible to make Na and Mg insertion favorable (E_b becomes negative). For Li in Si, single atom insertion also becomes thermodynamically favored (cf. Section 2.1.1). p-Doping is therefore a powerful strategy to enhance the voltage or to enable electrochemical activity. The reader is also referred to a recent review on doping strategies for electrode materials [7]. Achieving electrochemical sodiation and magnesiation of Si and Ge with the help of p-doping still awaits experimental verification, and we hope that our computational results will inspire such experiments.

2.2. Interactions of Li, Na, and Mg with Different Phases of Titania

2.2.1. Mapping Li, Na, and Mg Insertion Energies among Different Phases Including Amorphous

We have produced the first comparative computational study [22] of Li, Na, and Mg interaction with four phases of titania which are intensely studied by experimentalists as potential electrode materials: anatase, rutile, (B), and amorphous TiO₂ [39,100,101,102,103,104,105,106,107,108,109,110,111,112]. Interaction energies were mapped for the first time among the three types of inserted metal atoms and four phases. These are shown in Figure 9. These energies were in agreement with observed voltages at the specific capacity corresponding to one Li, Na, or Mg atom per simulation cell (on the order of 5–10 mAh g⁻¹ depending on the phase). For example, about 1.8/0.3 V for Li/Na in anatase [107,110] and about 2 V for Li and Na in the (B) phase [100,101]. Our estimated voltage for magnesiation of the anatase phase (about 0.9 V, note that the numbers in Figure 9 are for defect formation energies and expected voltage is −E_f/q) was shortly after confirmed experimentally [113]. For cases where there were no measurements or where the experimental results in different publications are contradictory (e.g., Na in rutile where both activity and lack of activity were reported [108,109,111]), our calculations provided practically useful information on the contribution to voltage due to the properties of the material itself, which is not directly accessible in experiments which compound contributions from interfaces, nanosizing, binders etc. An important finding is that amorphization of TiO₂ strengthens binding of Li, Na, and Mg vs any crystalline phase and can be used to control voltage. This was the first time amorphous TiO₂ was computationally studied for potential use in Li and post-Li batteries and compared to crystalline phases. The finding of lower E_b due to amorphization, and the magnitude of stabilization, are similar to those we computed in silicon and carbon (Section 2.1.1 and Section 2.1.2 above). Amorphization therefore appears to be a universal strategy to enhance voltage or to enable electrochemical activity. We have also studied the interaction of molecules with the surfaces of the four phases [26] and observed a similar tendency of the amorphous phase to stronger binding.

2.2.2. Electronic Structure of Doped Titania

Our study [22] of Li, Na, and Mg insertion in TiO₂ also resulted in an interesting methodological finding: we found that, contrary to the common view, it is possible to reproduce the correct electronic structure of doped TiO₂ at the generalized gradient approximation (GGA) level without requiring the Hubbard correction (the so-called +U). Our study used a localized basis set which was tuned to reproduce the cohesive energies of the components (i.e., of TiO₂, Li, Na, and Mg) as described in Section 2.1.1. This resulted in good agreement with previous plane wave calculations of the Li-TiO₂ system [114,115]. It also resulted in the formation of gap states which were Ti d states, as expected, see Figure 9 (this is what is often referred to as the Ti³⁺, see below about charge and oxidation states). Previously it had been shown (in plane wave calculations) that either a hybrid functional or a Hubbard U correction was needed to reproduce such states, or else the electron donated by Li would occupy a state in the conduction band [114,115]. That we were able to obtain the correct electronic structure at the GGA level at the least shows that it can be done effectively; it also poses a question of whether the previously reported inability of the GGA approximation to model the gap states has to do not only with the limitation of the GGA approximation itself but also with the use of specific computational setups.

2.2.3. On the Charge and Oxidation State of Titanium in TiO₂

In [32,33], we analyzed the charge state (and from there oxidation state) of Ti in TiO₂. Titanium dioxide is by far the most prominent oxide that found use in multiple electrochemical power generation and storage technologies such as solar cells (dye-sensitized and sensitized-type perovskite) and batteries (including post-lithium batteries considered here) as well as in photocatalysis for environmental remediation and water splitting [39,101,102,103,104,105,106,107,110,112]. The understanding of the mechanism of operation of all these technologies critically depends on the understanding of the electronic structure of TiO₂. It has been commonly assumed for decades that the oxidation state of Ti in TiO₂ is +4 and from there, mechanisms in various technologies were rationalized (e.g., via formation of Ti³⁺ due to Li or Na insertion or doping, as considered above). The assumption of +4 has wide-ranging consequences, e.g., it implies no further oxidation of Ti and no further reduction of O.

We had a critical look at this concept and directly analyzed the valence electron density around Ti in Ti ions, Ti containing molecules, and solid TiO₂. We found that valence electron density amounting to one electron charge resides on Ti in TiO₂ within less than half of the Ti-O bond length, independently of definitions of common charge assignment schemes such as Mulliken or Bader charges. This means that Ti could possibly be further oxidized, and, importantly for applications, O could be further reduced. We also found that Bader charges, which have been known to be about +2.5 |e| on Ti in TiO₂ are reasonable and consistent with conclusions derived from direct analysis of the valence density.

Our work, together with previous works that established that the charge on a transition metal atom in a compound is very stable with respect to changes of the formal oxidation state [116,117] shed a new light on the electronic structure of titania and questioned the utility of the concept of formal oxidation states in this case (which dates back to 1930s, i.e., before the development of modern quantum and computational chemistry). Specifically, it implies that oxygen could in fact be further reduced, which is in agreement with the recently accepted notion that oxygen redox contributes to reversible capacity in electrochemical batteries, which is also easily seen in DFT calculations even in non-defected systems [22,34].

2.3. Interactions of Li, Na, Na, Mg, and Al with Different Phases and Stoichiometries of Vanadium Oxides: Effects Due to Ion Size and Valency

Vanadium oxides have been known for a long time to be promising electrode materials for Li-ion batteries due to their high energy densities [118,119,120]. Although investigations on their use in LIBs are still predominant, increasing attention is paid to the incorporation of other metal ions, such as Na, Mg and Al. Appreciable voltages and capacities could be reached with these elements with different vanadium oxide phases and stoichiometries [121,122,123,124,125,126,127,128,129,130]. A systematic experimental rationalization and conclusive statement about the performance of vanadium oxides as electrode materials with regard to capacity, potential or rate is, however, complicated by the large number of stoichiometric and non-stoichiometric phases at different conditions and their close proximity in the phase space. Electronic structure investigations bear the potential to provide the necessary insight into rational material selection.

DFT investigations have been previously conducted to predict relative stabilities of vanadium oxide phases and construct phase diagrams which can help with a preliminary phase selection for electrode applications. Stable stoichiometries on the convex hull in a binary VO₂ phase diagram are calculated to be V₂O₃, V₃O₅, VO₂, V₃O₇, V₂O₅ and VO₃ [131]. Between V₂O₃ and VO₂ the Magnéli series includes metastable phases of the general composition V_nO_2n-1, while between VO₂ and V₂O₅ compounds with general formula V_nO_2n+1 of the Wadsley series represent possible intermediate structures. Many stoichiometric vanadium oxides further exhibit a pronounced polymorphism. The most stable vanadium dioxide modification at room temperature is a semiconductor distorted rutile-type P21/c structure transforming into a metallic pure rutile-VO₂ P42/mnm polymorph above 340 K [132], a practically relevant temperature regime for many battery applications. The rutile phase is however predicted by DFT to be the most stable phase; more importantly, it is stabilized by Li insertion which makes it more stable than the semiconductor phase [34]. Stabilization of rutile VO₂ was also reported in experimental studies on hydrogen and boron doping in VO₂ nanowires [133,134]. Moreover, the X-ray diffraction (XRD) measurements identified the presence of VO₂(R) phase during Li-ion battery cycling, consistent with our calculations [124]. Another VO₂ phase is bronze-type C2/m vanadium(IV) oxide; predicted to lie 20 meV/atom above the convex hull [131], it is an experimentally accessible, regularly investigated vanadium dioxide electrode material [122,123,128]. Both, bronze- and rutile-type vanadium dioxides (further referenced as VO₂(B) and VO₂(R)) exhibit linear arrangements of interstitial sites throughout the crystal leading to channel-like structures which enable easy metal-ion incorporation as well as low diffusion barriers along the less hindered channel directions.

In contrast to these channeled structures, many vanadium pentoxide and Wadsley series phases are layered compounds held together by relatively weak van-der-Waals interactions between the internally strongly bound sheets. This structural feature enables an easy metal ion insertion and may lead to low diffusion barriers due to the relatively large interstitial sites, which is why vanadium pentoxides are another class of frequently investigated electrode materials leading to often observed relatively high voltages, capacities and cycle rates [127,129,135]. The thermodynamically most stable V₂O₅ polymorph at ambient temperatures is the orthorhombic Pmmn vanadium pentoxide, further referred to as α-V₂O₅ [130]. It is intuitively understandable and can be supported by experimental, as well as theoretical, evidence that an increase in interlayer spacing in vanadium oxides has a potentially beneficial effect on cycling rate (lowering of diffusion barriers), as well as on capacity (increasing the amount of sites which can be preferentially occupied) and also voltage (reduction of lattice strains upon metal ion insertion) [136].

Ways to increase the interlayer spacing in vanadium oxides include the preparation of pure vanadium oxide phases with the desired structural features at non-ambient or under stabilizing conditions, as for example the high-pressure P2₁/m V₂O₅, or by phase transformation upon metal insertion. Structural changes in α-V₂O₅ upon Li intercalation have been previously investigated and are also predicted for other metals like Mg. For LiV₂O₅, an interlayer shear distortion leads to a phase with significantly larger interlayer spacing. The underlying Cmcm V₂O₅ will be referred to as β-V₂O₅ in the following and was used in our investigations as an example of metastable vanadium oxide structures with widened interlayer distance [137,138]. Besides β-V₂O₅, VO₂(R), and α-V₂O₅ as thermodynamically most stable layered and non-layered phases at typical application conditions, VO₂(B) as a frequently experimentally investigated vanadium dioxide phase was chosen [122,123].

2.3.1. Li, Na, K, Mg and Al Insertion Properties

In [31,34,36], we compared insertion of Li, Na, K, Mg, and Al into the four VO compounds, α-V₂O₅, β-V₂O₅, VO₂(R), and VO₂(B). We found that there is a clear dependence of insertion behavior on the type of inserted cation, as well as stoichiometry and crystal symmetry of the VO host. It appears that the lattice strain factor is dominant for differences in E_b among monovalent Li, Na, and K atoms. Take VO₂(B) host as an example. Here, Li, Na, and K all prefer the C site inside the open channel of VO₂(B), which provides the largest void space [31]. In contrast, insertion of multivalent Mg and Al atoms is energetically more favorable at the sites with a large oxygen coordination, such as the five-coordinated A1 site in VO₂(B). In this case, oxygen can effectively screen the strong electrostatic M–M and M–V ion interactions.

The calculated insertion energies in [31,36] and demonstrate several important differences between V₂O₅ and VO₂ phases. Single Li insertion occurs at the predicted voltages of similar order in all VO phases (3.13–3.65 V), in good agreement with the experimental measurements [125,139,140]. Single-atom insertion of Na and K is much less favorable in VO₂ versus V₂O₅, as evidenced by the significant drop-off in respective voltages. The estimated voltage for single Al insertion is improved in vanadium dioxides as compared to pentoxide: namely, from 1.70 V in α-V₂O5 to 1.99 V in VO₂(R). The calculated voltages correlate well with the differences in M–O bond lengths in the VO host and equilibrium M-oxide phase. For example, the optimized Na–O bond lengths in VO₂(R) and Na₂O are 1.96 and 2.42 Å, respectively. On the contrary, the optimized Al–O bond lengths in VO₂(R) and Al₂O₃ are much closer at 1.78 and 1.87 Å, respectively, suggesting energetically easier Al insertion.

Due to their low ionization energies, the inserted Li, Na, K, Mg and Al atoms transfer their valence electrons to the unoccupied V-d states, causing a Fermi level shift towards the conduction band (Figure 10), as also observed experimentally during Na insertion in V₂O₅ [141]. The newly-occupied V-d states appear as the spin-polarized defect peaks in the middle of V₂O₅ gap. Contrary to the Li, Na, and Mg insertion in TiO₂ (where the occupied Ti-d states are localized on a single Ti atom), the transferred electrons in V₂O₅ are delocalized over a V–O–V bond (Figure 10). As shown on the example of K insertion, each of the V atoms carries a magnetic moment of 0.5 μ_B and has an opposite spin to the bridging O atom. Similar observations have been reported for sodiated α-V₂O₅ by Smolinski [142]. Aside from the V reduction, we have also found a sizeable electron transfer from the inserted cations to the surrounding O atoms. DFT calculations therefore suggest here (as in TiO₂ considered above) that oxygen redox phenomena are present even in non-defected materials. Defects were previously proposed as the explanation of oxygen redox [143].

The observed oxygen redox is particularly important for the multivalent battery application of vanadium oxides, as it allows larger capacities and positive voltages beyond the traditional one-electron vanadium reduction chemistry. This was confirmed in [34], where we explored effects of Li, Mg and Al concentration on insertion energetics in VO₂(R). The available experimental voltage for the full lithiation of VO₂ to LiVO₂ (~2.0 V [124]) was reasonably well matched by our computational model. The predicted convex hulls and voltage-composition curves for Mg and Al insertions (Figure 11) demonstrate that positive voltages can be maintained up to the concentrations of MgVO₂ and Al_0.5VO₂ (beyond the expected Mg_0.5VO₂ and Al_0.33VO₂, respectively, based on vanadium redox), resulting in specific capacities among the highest for existing Mg [144,145,146] and Al [126,147,148] cathode materials.

2.3.2. On the Treatment of Dispersion Interactions

The above mentioned studies included layered as well as non-layered phases. The layered phases are typically modelled included dispersion corrections to DFT, to palliate the latter’s deficiency in modeling such interactions. On the other hand, the rutile and B phases do not require such corrections. To compare reliably the ion insertion properties among these phases, however, a single computational setup should be used for all these phases. We were able to model the two non-layers and two layered pure (i.e., before insertion) phases considered above accurately by using the revised Perdew-Burke-Ernzerhof functional for densely-packed solids (PBEsol) without dispersion corrections [149]. When modeling potassium insertion, however, we saw substantial expansion of the interlayer spacing of V₂O₅ which might be due to the failure of the GGA approximation [31]. We therefore also computed potassium insertion when applying Grimme D2 corrections [150] on oxygen atoms. The insertion energies and diffusion barriers were in good agreement with those obtained without the correction, with differences within 0.1 eV for phases with E_b < 0.

We note here that we did not apply the corrections on the ionized atoms (K in this case). This is because when an atom’s valence shell is fully ionized, the correction is simply undefined. That dispersion corrections (at least as far as the Grimme scheme is concerned) should not be used on ionized atoms is also corroborated by other studies. Ref. [30] compared experimental and simulated voltage curves of disodium terephthalate. It used DFT, DFT + D with Grimme corrections applied to all atoms or atoms excluding Na, as well as van der Waals (vdW) functionals. It showed that DFT provides the best match, followed by DFT + D without corrections on Na (i.e., with corrections on the organic part only), while DFT + D with Grimme corrections on all atoms was completely off (see SI of that paper) [30]. For Li and K terephthalates, Zhang et al. [151] compared voltages with and without dispersion corrections (on all atoms) and also concluded that DFT without the correction results in more accurate voltages. We therefore stress that application of Grimme correction on ionized atoms is not warranted and would lead to artificially higher voltages.

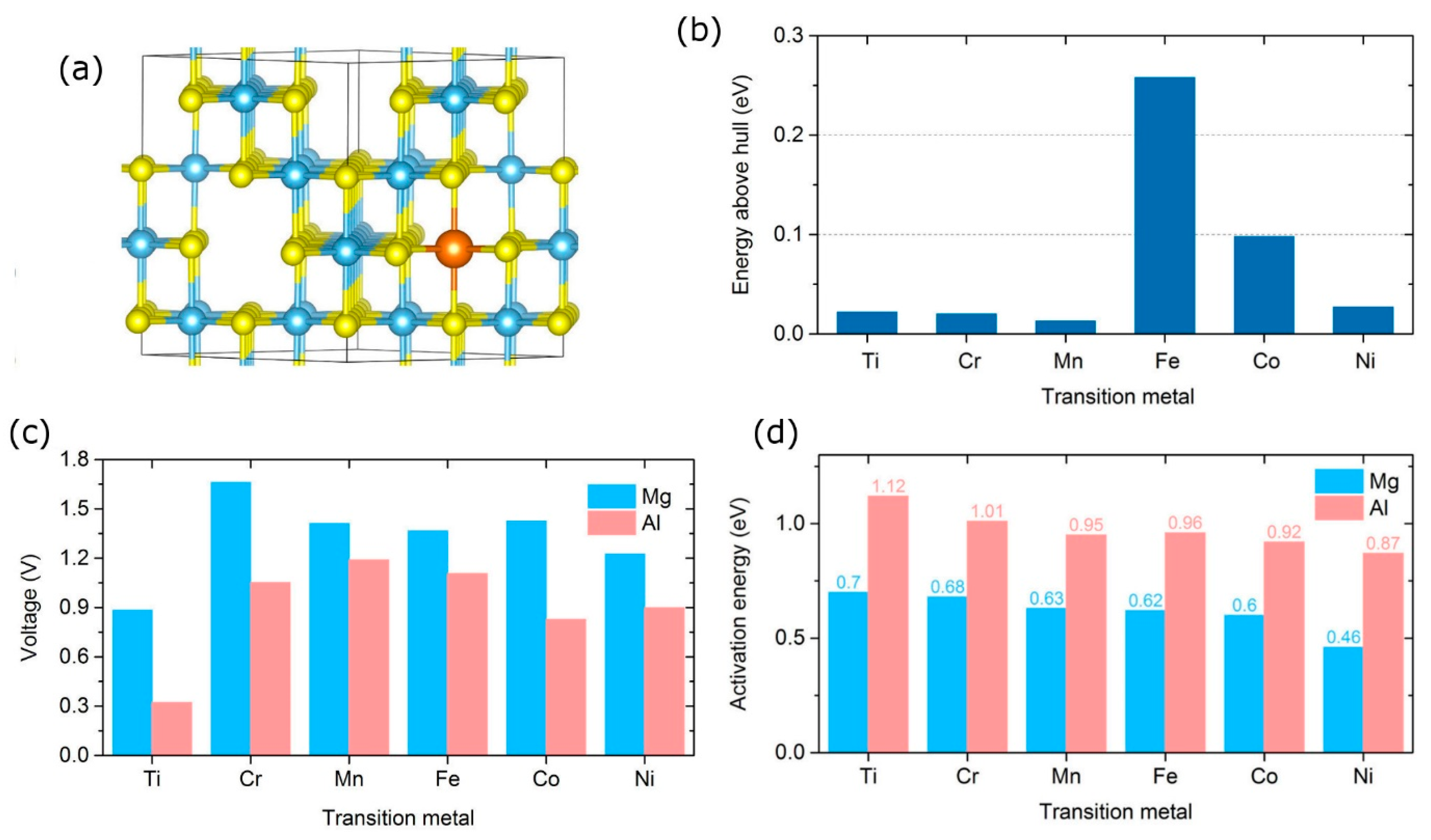
2.4. From Oxides to Sulfides: A Promising Direction for Multivalent Batteries

Although oxide materials have shown an excellent cycling capability in Li-ion batteries, their performance tends to be lower in multivalent batteries. One of the major reasons is that transition metal oxides have a high degree of ionicity, which makes the host structure prone to polarization, disorder and additional conversion reactions. Consequently, the ionic mobility of inserted multivalent cations is greatly affected. The electronic structure of transition metal oxides is also quite complex, often exhibiting localized states that can be affected by the local structural distortions. Therefore, utilizing sulfide lattices instead of oxides has been suggested as a promising strategy for multivalention batteries (Mg, Al, or Zn-ion) [152]. Layered LiTiS₂ and LiSnS₂ have been identified as suitable prototypes for studying sulphide electrodes because they are not complicated by the strong charge localization and Jahn-Teller effects (in contrast to, for example, layered nickel oxides). Very recently, sulfide materials with spinel-type crystal structure (called thiospinels) have been introduced as high-performance Mg insertion hosts [144]. Thiospinel compounds have the general formula AM₂X₄ and belong to the space group Fd-3m. Here, A is Li, Na, Mg, or Al; M is a transition metal (TM), and X is either S or Se. The structure is shown in Figure 12. The prototypical spinel compound, MgTi₂S₄, exhibited a satisfactory specific capacity of 200 mAh g⁻¹ and fast charge/discharge rates, but the average insertion voltage was rather low (1.2 V) [144,153]. It would be desirable to investigate whether low voltage in Ti₂S₄ can be improved by any chemical means.

In [35], we investigated the possibility of going beyond the prototypical TiS₂ electrode. We systematically analyzed insertion of Al and Mg atoms and compared possible sulfur-based spinel candidates. Although many spinel phases can be constructed, there is currently limited understanding about their energetic stability. We compared the total energy of each spinel structure with the convex energy hull in the phase diagram. We found that the majority of the spinel phases are relatively stable, possessing the energy above hull less than 0.05 eV per atom. Such a small energy value falls within the accuracy of our calculations and within typical energy differences due to vibrational and temperature effects. However, there are some spinel phases which are thermodynamically much less stable. In particular, the high energy above hull for FeS₂ suggests possible difficulty in synthesis and/or use. This is expected since Fe⁴⁺ is only known to exist in ternary and higher component number compounds. On the other hand, MnS₂, CrS₂, and NiS₂ are the most promising from the stability perspective.

We found that substitution of the transition metal can drastically affect both insertion voltages and diffusion barriers in sulfides. Based on the experimentally achieved MgTi₂S₄ composition, we calculated the average intercalation voltage for the full reaction Mg + M₂S₄→MgM₂S₄ [144]. Even though it is not certain that MgM₂S₄ would be the final state of charge with each of these materials, we confirmed that at MgM₂S₄ the voltages are still positive; it is also instructive to compare different M at the same state of charge. As shown in Figure 12, the voltage for Mg and Al intercalation follows a volcano shape curve with the peak in the middle of TM series. The calculated average insertion voltage for the Mg_xTi₂S₄ system is the lowest among the considered systems (0.88 V from the experimental data and theoretical calculations) [144]. In contrast, the Mg_xCr₂S₄ host provides the highest voltage. The same trend holds for Al intercalation and can be directly related to the electronic configurations of TM atoms. For example, Cr in the magnesiated compound, MgCr₂S₄, has a (formal) oxidation state of Cr³⁺. Compounds with Cr³⁺ (for example, Cr₂O₃, Cr₂S₃, and Cr₂Se₃) are quite abundant in nature. In contrast, compounds with Cr⁴⁺ as in CrS₂ are less stable, explaining the large energy difference (hence, large voltage) between charged and discharged states. Similar trends were also observed during Li intercalation in oxide spinels [154]. The activation barrier for Mg diffusion in the benchmark TiS₂ electrode material is estimated to be 0.70 eV. The diffusion barrier can be conveniently tailored by TM-substitution. For instance, the barrier decreases in the Cr-based (0.68 eV), Mn-based (0.63 eV) and Ni-based (0.46 eV) spinels. The Mg and Al diffusion in NiS₂ is expected to be particularly facile. The activation energy for Mg diffusion in NiS₂ (0.46 eV) is comparable to Li diffusion barriers in the state-of-the-art electrode materials, such as LiTi₂O₄ (0.56 eV) [155] and bulk silicon (0.61 eV) [19].

There is some drop-off in voltage when going from mono- to bi- to trivalent atoms insertion. The calculated voltages for Al insertion in sulfides are about 0.2–0.6 V lower than those for Mg insertion (Figure 12). However, considering the additional charge carried by multivalent cations, a multivalent spinel cathode can still exhibit a significantly higher energy density than the corresponding Li analogue. Due to the larger ionic charge, the insertion of Mg and Al atoms is accompanied by strong Coulombic repulsion induced by the two/three electrons carried by the Mg/Al. Due to stronger polarization, the calculated energy barriers for Al diffusion are ~0.3–0.4 eV larger than those for Mg diffusion in spinels (Figure 12).

One of the biggest advantages of sulfides over oxides is a faster charge/discharge rate. The ionic diffusion rates, as shown in Figure 12, represent a considerable improvement over the energy barriers in oxides (e.g., 1.25–1.75 eV in spinel-type MnO₂) [154,156]. Furthermore, the diffusion barriers in spinels can be lowered by doping, defect engineering or surface engineering. For instance, it has been shown that a particle morphology consisting of (110) surfaces can promote the rate performance in spinel LiTi₂O₄, because this kind of shape will greatly reduce the mean diffusion distance of lithium ions [155]. It should be noted that the diffusion pathways in the spinel structure are arranged along six equivalent directions due to the crystal symmetry, and they are interconnected, forming a three-dimensional fast diffusion network within the crystal. Volume expansion during multivalent atom insertion is another critical indicator of electrode performance. The maximum volume expansion after magnesiation of Co-based sulfide is about 23%. For comparison, this value is smaller than the volume change of 33% in the β-MnO₂ electrode for Li-ion battery [63]. The above results indicate good structural stability of sulfide electrodes which can potentially lead to long cycle life in the practical batteries.

3. Discussion and Conclusions

We have reviewed herein our recent studies on Li, Na, K, Mg, and Al insertion in several structures which attracted significant research interest and have been extensively studied experimentally, including monoelemental materials, binary oxides, and sulfides. The studies consider several types of ions covering a wide range of ionic radii and valences. The generated knowledge can be directly applied for rational selection of novel electrodes for post-Li batteries. The studies show that among the factors affecting electrode performance, strain and lattice deformations appear to be particularly critical. The strain effects become particularly pronounced in the Li-Na-K series, as the ionic radius increases from 0.76 (Li) to 1.02 (Na) to 1.38 Å (K). Although insertion of Li atoms is energetically possible in many host materials including all materials considered above, lattice deformations become significant at higher stages of charge (even though not considered here) and can lead to mechanical degradation (the most prominent example being pulverization and cracking of bulk Si and Si nanowires [68]). In contrast, the insertion of Na, Mg and K ions is typically thermodynamically less favored than that of Li even at the single-atom level. Our calculations have shown that Na and Mg atoms have unfavorable insertion energies in a number of prominent battery electrodes, such as graphite, silicon, and β tin. Overall, with the increase in ionic size or polarization caused by multivalency, it becomes progressively more challenging to find suitable electrode materials for non-Li batteries. Our studies show that the strain energy (i.e., energy cost to distort the host lattice to accommodate inserted atoms) can be a very strong indicator to use in the pre-screening of electrode candidates. For example, the R² correlation coefficients between the diffusion barriers and Si lattice strain energy and between the change in the barrier due to the presence of a second neighboring Li, Na, or Mg atom and the change in the Si lattice strain energy are about 0.8–0.9. There is also a noticeable connection between decreasing binding energies and increasing steric hindrance by narrowing of the channel sizes in vanadium oxide compounds. As the (favored) channels can be approximated as cylindrical tubes, the radii of those imaginary cylindrical cross sections in α-V₂O₅, β-V₂O₅, VO₂(B) and VO₂(R) correlate with the potassium binding energies in those compounds.

There are several ways to overcome the negative effects of lattice strain caused by ion insertion. It is known that fast kinetics and high capacity can be achieved in battery materials by introducing porosity and large void spaces, as demonstrated in nanotubes and porous nanostructures [19,157,158,159,160,161,162,163]. Improvements in charge-discharge rates can be achieved in layered materials and ultra-thin nanosheets, where Li/Na/K/Mg/Al storage mainly takes place on the surfaces (in a pseudocapacitive manner), maintaining rapid surface diffusion [11,164,165,166,167]. Increase in interlayer spacing in vanadium oxides has a potentially beneficial effect on cycling rate (lowering of diffusion barriers), as well as on capacity (increasing the amount of sites which can be preferentially occupied) and also voltage (reduction of lattice strains upon metal ion insertion). One example is Cmcm V₂O₅, also referred to as β-V₂O₅, which was used in our studies as a metastable vanadium oxide structure with widened interlayer distance.

Another successful strategy is amorphization of the active electrode material. There are several important benefits of amorphous structures for battery application: firstly, an amorphous structure may have larger-volume insertion sites, lowering the strain energy; secondly, a metastable amorphous structure is expected to be more reactive towards Li/Na/K/Mg/Al. The increase of average voltage by amorphization was shown by us on the examples of silicon, carbon, and TiO₂. We showed that defect formation energies of Li, Na, and Mg defects in a-Si are respectively 0.71, 1.72, and 1.82 eV lower compared to those in c-Si. The defect formation energies of Na, and Mg defects (vs. vacuum reference states) in a-Si and a-C are comparable with the respective metal cohesive energies, meaning that insertion of Na and Mg atoms could be feasible. Sodiation of a-Si has now been confirmed experimentally [38]. This is in contrast to c-Si and graphite, where the storage of Na and Mg atoms is limited due to high energy cost of Na and Mg insertion into c-Si. We have also shown that insertion of Li, Na, and Mg in a-TiO₂ can occur at multiple insertion sites with well-dispersed insertion energies, with a lowest energy site more thermodynamically favorable than insertion sites in the crystalline phases.

One of the most critical steps in the computational studies of amorphous electrode materials is generation of amorphous structures. The crystalline structures are well defined and well documented in multiple materials databases, such as materialsproject.org. In contrast, theirs amorphous counterparts are structurally much more diverse and not as well described. Despite the lack of long-range translational symmetry, the properties of amorphous materials depend crucially on structural order on the local and intermediate length scales. For reliable generation of amorphous structures, one typically requires large unit cells and long simulation times, which makes it very difficult for DFT simulations.

The most common computational approach for generating amorphous structures (called “melt-and-quench”) aims to replicate the experimental amorphization procedures. In the melt-and-quench simulation, the atomic lattice is first generated at the appropriate density and then melted at a very high constant temperature. The simulation cell is then quenched with a (often) linearly decreasing temperature profile, and finally annealed. While the melt-and-quench protocol is quite straightforward, the important challenge has been producing accurate interatomic potentials (force-field) for a material of interest. Traditional interatomic potentials, such as Tersoff and Brenner force-fields, reactive bond-order (REBO) potentials, and reactive force field (ReaxFF) are used in fast, large-scale molecular-dynamics (MD) simulations; however, they lack the accuracy of DFT methods. On the other hand, direct DFT-based MD is much more accurate but restricted to very small system sizes. We note that although the idea of the melt-and-quench method derives from the way amorphous structures are experimentally generated, in practice the simulation does not nearly model the experimental conditions due to time scales which are shorter by orders of magnitude even with the force field-based simulations.

We introduced a novel approach for amorphous structure generation. The proposed method belongs to the class of geometry-based approaches and relies on the exhaustive sampling of the configuration space. A large number (>10⁶) of distributions are then sampled, for which the radial distribution functions (RDF) are compared to the experimental RDF. The structures giving a good fit of the RDF to the experimental RDF is then optimized ab initio including optimization of lattice vectors. A significant improvement of our method is that we fit to the experimental RDF and ensure that the structure is stable under cell vector optimization to target pressure.

One of the challenges specific to multivalent batteries is achieving voltages suitable for cathodes. In this case, the insertion energy has to be very low (strong) due to the relation between V and E_f of Equation (2). This can be seen on the examples of Li/Na and Mg insertion in titania considered in Section 2.2.1 and Li/Na/K, Mg, and Al insertion in vanadium oxides considered in Section 2.3.1. In Figure 9a, the insertion energy of Mg for example in TiO₂(B) is of similar magnitude to that of Li and Na, at about 2.1 eV. This implies voltages at early stages of lithiation and sodiation of about 2 V but magnesiation would only result in a voltage of about 1 V with this phase. This situation becomes even direr for trivalent ion insertion. In Figure 13, we show in panel (a) the single atom insertion energies of Li/Na/K, Mg, and Al, and in panel (b) the corresponding voltages. Even though significant insertion energies on the order of −6 eV are achieved for Al, this translates in rather low voltage estimates not exceeding about 2 V. Besides the challenges in the active electrode materials design, there are still important methodological issues in the computational modeling of battery materials. Typically, theoretical studies on battery materials only consider electronic energies, while ignoring the vibrational contributions. While this approach is suitable for many materials, it is insufficient for materials with phase transitions. An example is alpha-beta tin phase transition occurring for pure tin at around 13°C and affected by ion insertion. We showed that the vibrational contributions at room temperature substantially affect the phase transition temperature. We found that Li and Na stabilize the alpha phase, while Mg insertion stabilizes the beta phase of tin. The magnitude of vibrational contributions to insertion energies and diffusion barriers can reach 0.1 eV [14,23], which may or may not be negligible. In order to accurately describe the relative phase stability, the accuracy of DFT calculations should be on the order of 0.01 eV [23,28], which is beyond the accuracy of typical DFT setups. Specifically in the case of Sn, we found that the difference in cohesive energies between alpha and beta Sn is overestimated with many standard DFT setups (using different basis types, pseudopotentials, and codes). This leads to a significant error in transition temperature. We analyzed the electronic contributions to the cohesive energy and concluded that the overestimation results from differences in the valence bandstructure and specifically s and p band occupancy between alpha and beta tin combined with different DFT errors in band energies between alpha and beta tin. This can be fixed by applying a small Hubbard U correction on s-like states. For alpha and beta tin, the valence band of both phases is dominated by p and s bands with negligible contribution from d-like states. Application of a Hubbard correction on s-like states stabilized the s band, allowing one to achieve the correct cohesive energies of both phases with the same GGA based computational setup.

In our work, we used both plane wave and localized basis sets. We were able to achieve good agreement between them when tuning localized basis sets of small size (DZP) to reproduce cohesive energies of components (such as bcc Li, diamond Si etc.). We expect this to be useful to perform accurate simulations with lower CPU cost.

When treating layered phases computationally, the inclusion of vdW corrections can help correctly model the interlayer binding for which dispersive interactions are expected to play a major role and that common DFT functionals often fail to properly take into account. We have shown for layered vanadium oxides as well as other compounds (e.g., disodium terephtalate) [30] that the a posteriori Grimme-D2 correction should not be applied on the ions of the inserted metal species due to their high degrees of ionization. This is intuitively understandable on the conceptual level, since the absence of valence density nullifies any contributions from it to the interaction energy. We further found that the influence of the D2 correction (excluding that on ions) for layered vanadium oxides on insertion energies and diffusion barriers is rather small.

It is also crucial for the rationalization of redox processes as they happen in electrode materials (but also in the general context) to understand the electron fluxes accompanying them. The conventional way to determine whether and where reduction and oxidation take place, namely formal oxidation states, is often misaligned with the observations one can make from an analysis of the charge density, e.g., upon metal intercalation into a host crystal. While formal oxidation states are derived from orbital occupancies, the electron density is a physical observable and its local change can be directly related to electron fluxes into and out of a certain volume element and can therefore help rationalize the direction of electron transfers, which formal oxidation states often fail to represent. We showed this mismatch by a detailed charge density analysis in TiO₂ molecules and crystals from which we concluded that there is still a substantial charge remainder on Ti in titanium dioxide [32,33], which is, although not formally conflicting with a +4 oxidation state, a rather counter-intuitive observation and in principle allows for electron density transfers away from Ti or to O. Similar observations can be made for a variety of other materials and were previously described in the literature [117]. The contribution from oxygen redox can be quite important for battery applications as it allows maintaining positive voltages e.g., in the case of Al up to Al_0.5VO₂ and not up to Al_0.33VO₂ which would follow from only one-electron vanadium reduction.