An Isolated Three-Port Bidirectional DC-DC Converter with Enlarged ZVS Region for HESS Applications in DC Microgrids
Abstract
:1. Introduction
- (1)
- A new two-stage three-port isolated BDC topology is proposed to integrate SC and BA.
- (2)
- Methods to enlarge ZVS region and to reduce power circulation loss for three-port SR BDC under varying port voltages are first investigated.
- (3)
- A front-end converter in SC channel is introduced to keep input of full bridge constant. For BA channel, PWM-PHS control method is developed to improve the characteristics of the proposed three-port BDC.
- (4)
- By adopting the two-stage structure, all switches of SC and DC bus ports have realized ZVS with variable VSC. By applying the proposed PWM-PHS control method, two more switches of BA port realize ZVS even under the worst input voltage condition of MBA = 1.15.
2. Proposed System
2.1. Three-Port SR BDC
- (1)
- Three-port structure with transformer coupling reduces amount of power switches, increases power density.
- (2)
- Power flow between BA port and DC bus port, SC port and DC bus port are bidirectional.
- (3)
- Centralized control method of power flow by changing the direction and magnitude of the phase shift angles between three ports is applied.
- (4)
- Three-phase interleaved BDC is introduced in the SC channel to keep voltage gain MSC = 1, which guarantee best operating characteristics of SC channel of SR BDC.
- (5)
- PWM-PHS hybrid control strategy is proposed for the BA channel to increase the number of switches, which can achieve ZVS, under a variation voltage VBA.
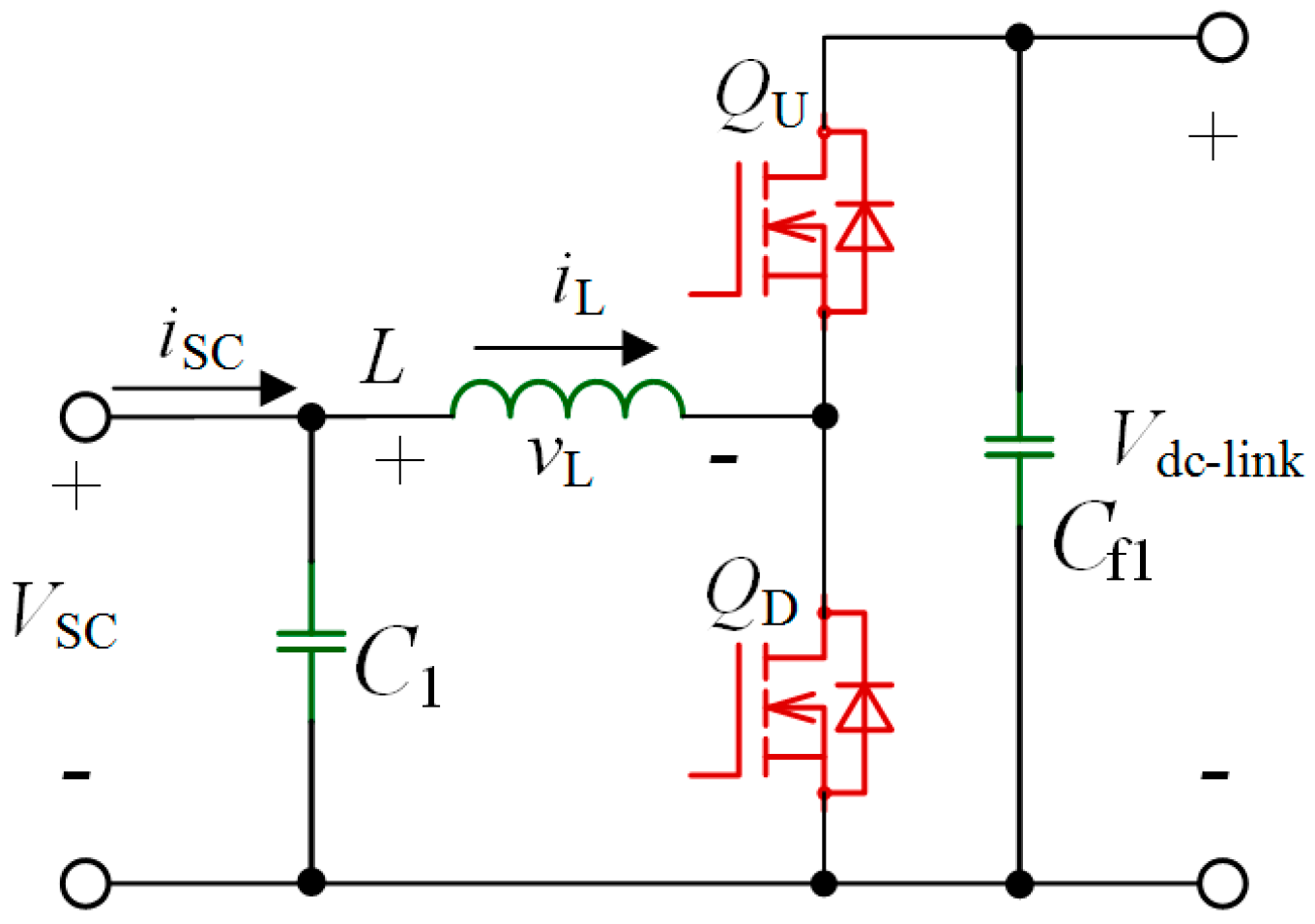
2.2. Three-Phase Interleaved BDC
- (1)
- The structure is simple, and it combines a boost converter together with a buck converter connected in antiparallel.
- (2)
- Three-phase interleaved structure is adopted to reduce current ripple, improve power level and reduce current stress of the converter.
- (3)
- It works under DCM, which can reduce the inductance value.
- (4)
- Two MOSFETs of one phase-leg conduct complementarily, and the inductor operates under DCM condition, and thus ZVS of MOSFETs is achieved.
3. Operating Analysis
3.1. Operating Principle of Three-Port SR BDC
3.1.1. Operating Mode Analysis
3.1.2. Analysis for Voltage Source Load
3.1.3. Analysis for Resistive Load
3.2. Operating Principle of Three-Phase Interleaved BDC
4. ZVS Region Analysis and Proposed Method for Expanding ZVS Realization Range
4.1. ZVS Region and Current Stress Analysis of Single Channel SR BDC
- (1)
- For the SC channel, the voltage has a large variation range, and can’t get an ideal operating state only by reasonable parameters design. Therefore, a three-phase interleaved BDC is introduced between SC and port 1 of the three-phase SR BDC. The interleaved BDC is used to convert the widely fluctuating VSC to a fixed Vdc-link, and thus ensuring MSC = 1.
- (2)
- Since voltage variation scale is relatively small for the BA channel, it is not essential to add BDC converter as SC channel does. A new PWM-PHS control strategy is proposed for the BA channel. The newly proposed control method has two phase shift angles for modulation, and can increase number of MOSFETs which can realize ZVS.
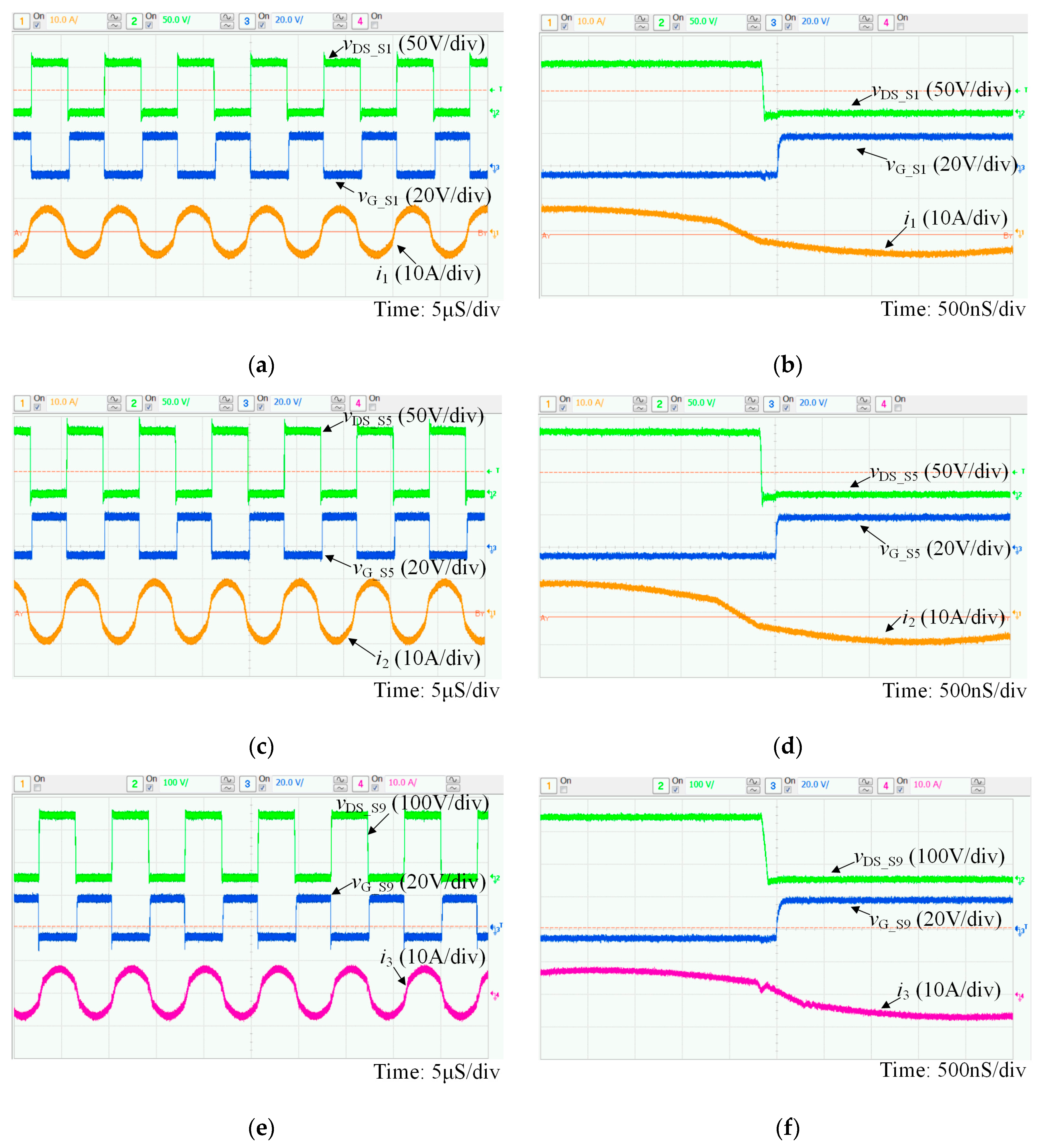
4.2. Proposed PWM and Phase Shift Hybrid Control Strategy
4.3. Control Strategy of the Proposed Two-Stage Three-Port BDC
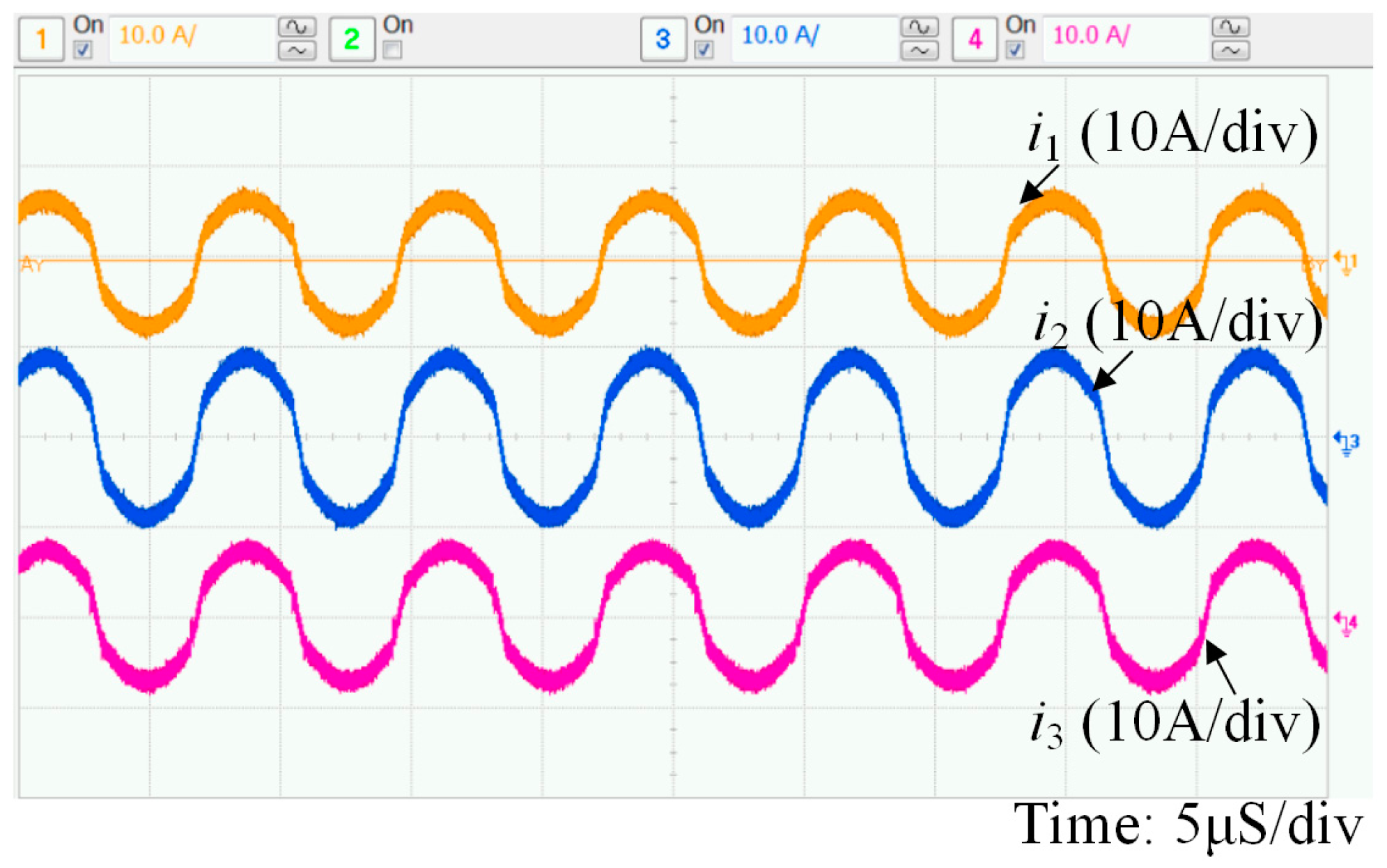
5. Experimental Results
5.1. SC and BA Charging Mode
5.2. SC and BA Discharging Mode
5.3. Proposed PWM-PHS Control Method
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Marzband, M.; Ardeshiri, R.R.; Moafi, M.; Uppal, H. Distributed generation for economic benefit maximization through coalition formation based on Game Theory. Int. Trans. Electr. Energy Syst. 2017, 1–16. [Google Scholar] [CrossRef]
- Han, Y.; Chen, W.; Li, Q. Energy Management Strategy Based on Multiple Operating States for a Photovoltaic/Full Cell/Energy Storage DC Microgrid. Energies 2017, 10, 136. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, L. Strategy Design of Hybrid Energy Storage System for Smoothing Wind Power Fluctuations. Energies 2016, 9, 991. [Google Scholar] [CrossRef]
- Marzband, M.; Ghazimirsaeid, S.S.; Uppal, H.; Fernando, T. A real-time evaluation of energy management systems for smart hybrid home Microgrids. Electr. Power Syst. Res. 2017, 143, 624–633. [Google Scholar] [CrossRef]
- Marzband, M.; Moghaddam, M.M.; Akorede, M.F.; Khomeyrani, G. Adaptive load shedding scheme for frequency stability enhancement in microgrids. Electr. Power Syst. Res. 2016, 140, 78–86. [Google Scholar] [CrossRef]
- Xu, Q.; Hu, X.; Wang, P.; Xiao, J.; Tu, P.; Wen, C.; Lee, M.Y. A Decentralized Dynamic Power Sharing Strategy for Hybrid Energy Storage System in Autonomous DC Microgrid. IEEE Trans. Ind. Electr. 2016. [Google Scholar] [CrossRef]
- Kollimalla, S.K.; Mishra, M.K.; Ukil, A.; Gooi, H.B. DC Grid Voltage Regulation Using New HESS Control Strategy. IEEE Trans. Sustain. Energy 2016, 8, 772–781. [Google Scholar] [CrossRef]
- Jin, Z.; Hou, M.; Dong, F.; Li, Y. A New Control Strategy of DC Microgrid with Photovoltaic Generation and Hybrid Energy Storage. In Proceedings of the IEEE PES Asia-Pacific Power and Energy Conference, Xi’an, China, 25–28 October 2016; pp. 434–438. [Google Scholar]
- Marzband, M.; Alavi, H.; Ghazimirsaeid, S.S.; Uppal, H.; Fernando, T. Optimal Energy Management System Based on Stochastic Approach for a Home Microgrid with Integrated Responsive Load Demand and Energy Storage. Sustain. Cities Soc. 2017, 28, 256–264. [Google Scholar] [CrossRef]
- Marzband, M.; Parhizi, N.; Savaghebi, M.; Guerrero, J.M. Distributed Smart Decision-Making for a Multi-microgrid System Based on a Hierarchical Interactive Architecture. IEEE Trans. Energy Convers. 2016, 31, 637–648. [Google Scholar] [CrossRef]
- Marzband, M.; Azarinejadian, F.; Savaghebi, M.; Guerrero, M. An Optimal Energy Management System for Islanded Microgrids Based on Multiperiod Artificial Bee Colony Combined With Markov Chain. IEEE Syst. J. 2015, 100, 1–11. [Google Scholar] [CrossRef]
- Marzband, M.; Yousefnejad, E.; Sumper, A.; Domínguez-García, J.L. Real Time Experimental Implementation of Optimum Energy Management System in Standalone Microgrid by Using Multi-layer Ant Colony Optimization. Int. Trans. Electr. Energy Syst. 2016, 75, 265–274. [Google Scholar] [CrossRef]
- Marzband, M.; Ghadimi, M.; Sumper, A.; Domínguez-García, J.L. Experimental validation of a real-time energy management system using multi-period gravitational search algorithm for microgrids in islanded mode. Appl. Energy 2014, 128, 164–174. [Google Scholar] [CrossRef]
- Marzband, M.; Parhizi, N.; Adabi, J. Optimal energy management for stand-alone microgrids based on multi-period imperialist competition algorithm considering uncertainties: Experimental validation. Int. Trans. Electr. Energy Syst. 2016, 26, 1358–1372. [Google Scholar] [CrossRef]
- Marzband, M.; Sumper, A.; Ruiz-Álvarez, A.; Domínguez-García, J.L. Experimental evaluation of a real time energy management system for stand-alone microgrids in dayahead markets. Appl. Energy 2013, 106, 365–376. [Google Scholar] [CrossRef]
- Marzband, M.; Sumper, A.; Domínguez-García, J.L.; Gumara-Ferret, R. Experimental Validation of a Real Time Energy Management System for Microgrids in Islanded Mode Using a Local Day-Ahead Electricity Market and MINLP. Energy Convers. Manag. 2013, 76, 314–322. [Google Scholar] [CrossRef]
- Zhang, N.; Sutanto, D.; Muttaqi, K.M. A review of topologies of three-port DC–DC converters for the integration of renewable energy and energy storage system. Renew. Sustain. Energy Rev. 2016, 56, 388–401. [Google Scholar] [CrossRef]
- Chien, L.J.; Chen, C.C.; Chen, J.F.; Hsieh, Y.P. Novel Three-Port Converter with High-Voltage Gain. IEEE Trans. Power Electron. 2014, 29, 4693–4703. [Google Scholar] [CrossRef]
- Lai, C.M.; Yang, M.J. A High-Gain Three-Port Power Converter with Fuel Cell, Battery Sources and Stacked Output for Hybrid Electric Vehicles and DC-Microgrids. Energies 2016, 9, 180. [Google Scholar] [CrossRef]
- Hu, Y.; Xiao, W.; Cao, W.; Ji, B. Three-Port DC–DC Converter for Stand-Alone Photovoltaic Systems. IEEE Trans. Power Electron. 2015, 30, 3068–3076. [Google Scholar] [CrossRef]
- Wang, Z.; Li, H. An Integrated Three-Port Bidirectional DC-DC Converter for PV Application on a DC Distribution System. IEEE Trans. Power Electron. 2013, 28, 4612–4624. [Google Scholar] [CrossRef]
- Sun, X.; Shen, Y.; Li, W. A Novel LLC Integrated Three-port DC-DC Converter for Stand-alone PV/Battery System. In Proceedings of the IEEE Transportation Electrification Conference and Expo, Asia-Pacific, Beijing, China, 31 August–3 September 2014; pp. 1–6. [Google Scholar]
- Duarte, J.L.; Hendrix, M.; Simões, M.G. Three-Port Bidirectional Converter for Hybrid Fuel Cell Systems. IEEE Trans. Power Electron. 2007, 22, 480–487. [Google Scholar] [CrossRef]
- Phattanasak, M.; Gavagsaz-Ghoachani, R.; Martin, J.P.; Pierfederici, S. Flatness Based control of an Isolated Three-port Bidirectional DC-DC converter for a Fuel cell hybrid source. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 977–984. [Google Scholar]
- Fontana, C.; Buja, G.; Bertoluzzo, M.; Kumar, K. Power and control characteristics of an isolated three-port DC-DC converter under DCM operations. In Proceedings of the Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–27 October 2016; pp. 4211–4216. [Google Scholar]
- Phattanasak, M.; Gavagsaz-Ghoachani, R.; Martin, J.P.; Nahid-Mobarakeh, B. Control of a Hybrid Energy Source Comprising a Fuel Cell and Two Storage Devices Using Isolated Three-Port Bidirectional DC–DC Converters. IEEE Trans. Ind. Appl. 2015, 51, 491–497. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Li, H. Asymmetrical Duty Cycle Control and Decoupled Power Flow Design of a Three-port Bidirectional DC-DC Converter for Fuel Cell Vehicle Application. IEEE Trans. Power Electron. 2012, 27, 891–904. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, B.; Zhang, Y.; Cheng, M.; Chu, K.; Xu, L. The Chaotic-Based Control of Three-Port Isolated Bidirectional DC/DC Converters for Electric and Hybrid Vehicles. Energies 2016, 9, 83. [Google Scholar] [CrossRef]
- Ling, Z.; Wang, H.; Yan, K.; Gan, J. Optimal Isolation Control of Three-Port Active Converters as a Combined Charger for Electric Vehicles. Energies 2016, 9, 715. [Google Scholar] [CrossRef]
- Li, X.; Bhat, A.K.S. Analysis and Design of High-Frequency Isolated Duan-Bridge Series Resonant DC/DC Converter. IEEE Trans. Power Electron. 2010, 25, 850–862. [Google Scholar]
- Krishnaswami, H.; Mohan, N. Three-Port Series-Resonant DC-DC Converter to Interface Renewable Energy Sources with Bidirectional Load and Energy Storage Ports. IEEE Trans. Power Electron. 2009, 24, 2289–2297. [Google Scholar] [CrossRef]
- Shreelekha, K.; Arulmozhi, S. Multiport isolated bidirectional DC-DC converter interfacing battery and supercapacitor for hybrid energy storage application. In Proceedings of the International Conference on Electrical, Electronics, and Optimization Techiniques, Chennai, India, 3–5 March 2016; pp. 2763–2768. [Google Scholar]
- Tao, H.; Kotsopoulos, A.; Duarte, J.L.; Hendrix, M.A.M. Transformer-Coupled Multiport ZVS Bidirectional DC–DC Converter with Wide Input Range. IEEE Trans. Power Electron. 2008, 23, 771–781. [Google Scholar] [CrossRef]
- Oggier, G.; Garcia, G.O.; Oliva, A. Switching Control Strategy to Minimize Dual Active Bridge Converter Losses. IEEE Trans. Power Electron. 2009, 24, 1826–1838. [Google Scholar] [CrossRef]
- Xu, D.; Zhao, C.; Fan, H. A PWM Plus Phase-Shift Control Bidirectional DC-DC Converter. IEEE Trans. Power Electron. 2004, 19, 666–675. [Google Scholar] [CrossRef]
- Tao, H.; Duarte, J.L.; Hendrix, M.A.M. Three-Port Triple-Half-Bridge Bidirectional Converter with Zero-Voltage Switching. IEEE Trans. Power Electron. 2008, 23, 782–792. [Google Scholar]
- Baek, J.-B.; Choi, W.-I.; Cho, B.-H. Digital Adaptive Frequency Modulation for Bidirectional DC-DC Converter. IEEE Trans. Power Electron. 2013, 60, 5167–5176. [Google Scholar] [CrossRef]
- Nandankar, P.V.; Rothe, J. Hihgly efficient discontinuous mode interleaved DC-DC converter. In Proceedings of the International Conference on Electrical, Electronics, and Optimization Techiniques, Chennai, India, 3–5 March 2016; pp. 476–481. [Google Scholar]




















| Converter Parameter | Value |
|---|---|
| Resonant Inductor Lr1 and Lr2 | 15 μH |
| Resonant Capacitors Cr1 and Cr2 | 141 nF |
| Transformer turns ratio n13:n23:1 | 0.425:0.51:1 |
| Port 1 voltage Vdc-link | 85 V |
| Port 2 voltage VBA | 90 V–102 V |
| Port 3 voltage Vbus | 200 V |
| Voltage Gain MSC | 1 |
| Voltage Gain MBA | 1–1.15 |
| Super Capacitor Voltage VSC | 30 V–75 V |
| Buck/Boost Inductor of BDC L | 15 μH |
| Method | φ1 | φ2 |
|---|---|---|
| Theoretical Calculation | −19.1° | −19.1° |
| Experiment | −18.5° | −20° |
| Method | φ1 | φ2 |
|---|---|---|
| Theoretical Calculation | 19.8° | 13.6° |
| Experiment | 18.2° | 13.4° |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-S.; Li, W.; Wang, Y.-F.; Han, F.-Q.; Meng, Z.; Li, G.-D. An Isolated Three-Port Bidirectional DC-DC Converter with Enlarged ZVS Region for HESS Applications in DC Microgrids. Energies 2017, 10, 446. https://doi.org/10.3390/en10040446
Wang C-S, Li W, Wang Y-F, Han F-Q, Meng Z, Li G-D. An Isolated Three-Port Bidirectional DC-DC Converter with Enlarged ZVS Region for HESS Applications in DC Microgrids. Energies. 2017; 10(4):446. https://doi.org/10.3390/en10040446
Chicago/Turabian StyleWang, Cheng-Shan, Wei Li, Yi-Feng Wang, Fu-Qiang Han, Zhun Meng, and Guo-Dong Li. 2017. "An Isolated Three-Port Bidirectional DC-DC Converter with Enlarged ZVS Region for HESS Applications in DC Microgrids" Energies 10, no. 4: 446. https://doi.org/10.3390/en10040446
APA StyleWang, C. -S., Li, W., Wang, Y. -F., Han, F. -Q., Meng, Z., & Li, G. -D. (2017). An Isolated Three-Port Bidirectional DC-DC Converter with Enlarged ZVS Region for HESS Applications in DC Microgrids. Energies, 10(4), 446. https://doi.org/10.3390/en10040446






