Analytical Calculation of the Magnetic Field Distribution in a Linear and Rotary Machine with an Orthogonally Arrayed Permanent Magnet
Abstract
:1. Introduction
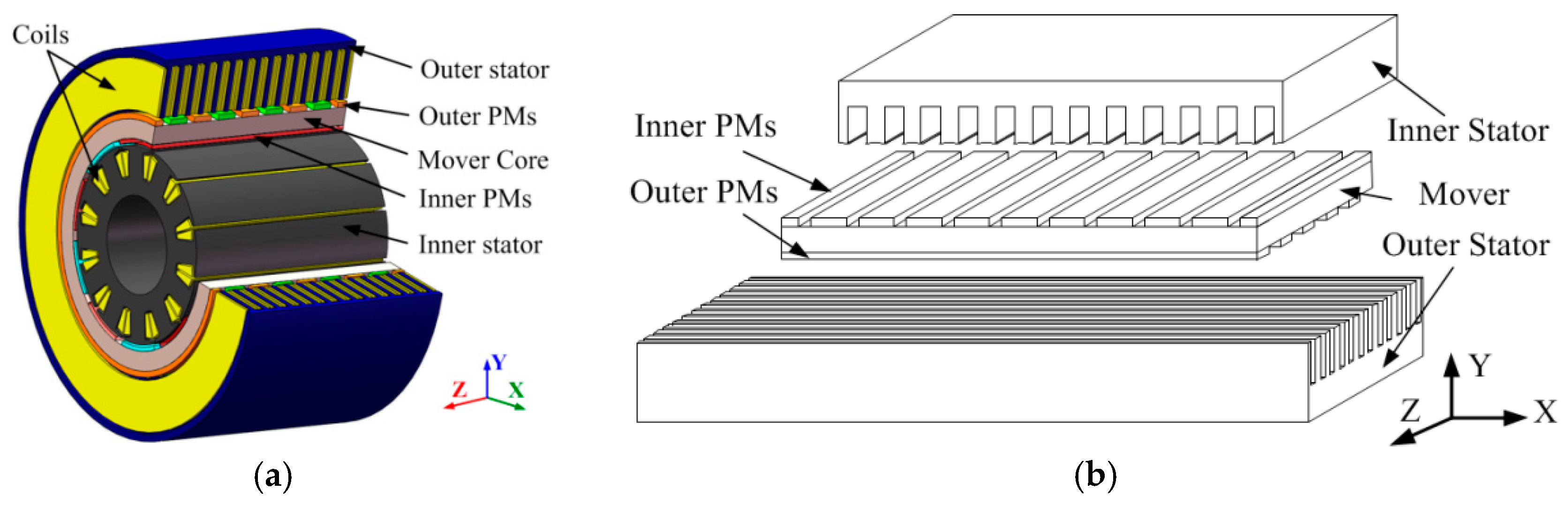
2. Description of the DSLRPMM
- (1)
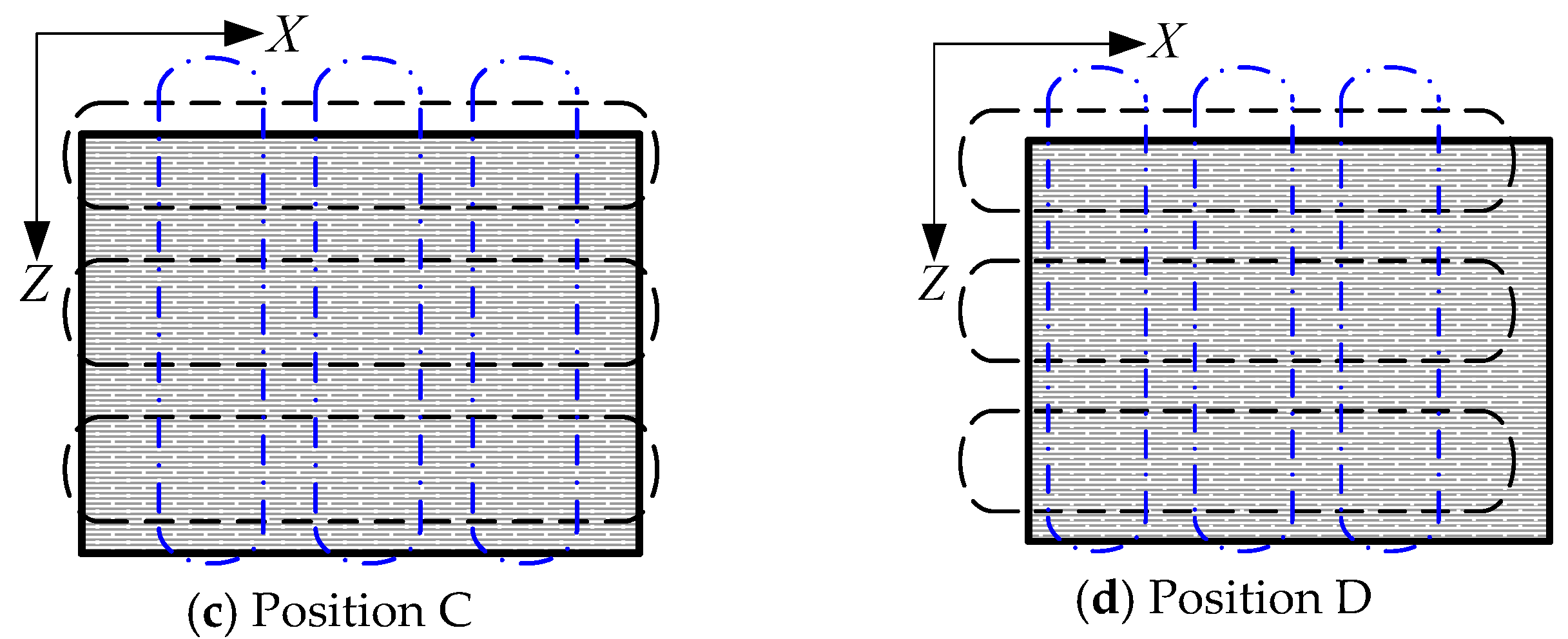
- When the windings of the rotary motion unit are excited by three phase AC currents, the inner armature and PMs will produce the rotating magnetic field, and the mover will move along the x direction (such as from Figure 2a to Figure 2b or Figure 2c to Figure 2d). At the same time the outer PM remains relatively static. Therefore, the rotary motion unit is a standard PMSM.
- (2)
- When the windings of the linear unit are excited by three phase AC currents, the outer armature and PMs will produce the traveling magnetic field, and the mover will move along the z direction (such as from Figure 2a to Figure 2c or Figure 2b to Figure 2d). In this case the linear motion unit is a normal PMLSM.
- (3)
- When the windings of the rotary and linear unit are all excited by three phase AC currents, the rotating and traveling magnetic field will be established in the two air-gaps synchronously. The mover will move along a slant (such as from Figure 2a to Figure 2d or Figure 2b to Figure 2c), which can be called the helical motion.
3. Magnetic Field Calculation and Performances Prediction in Open Circuit
- (1)
- The magnetic material has a uniform magnetization and the relative recoil permeability μr is constant and has a value close to unity such as in NdFeB materials.
- (2)
- For the computation of armature reaction field, the magnet regions are regarded as free space.
- (3)
- Magnetic saturation is absent and the rotor iron cores have infinite magnetic permeability.
- (4)
- Eddy current effects are neglected, which avoids the need for the complex eddy current field formulation.
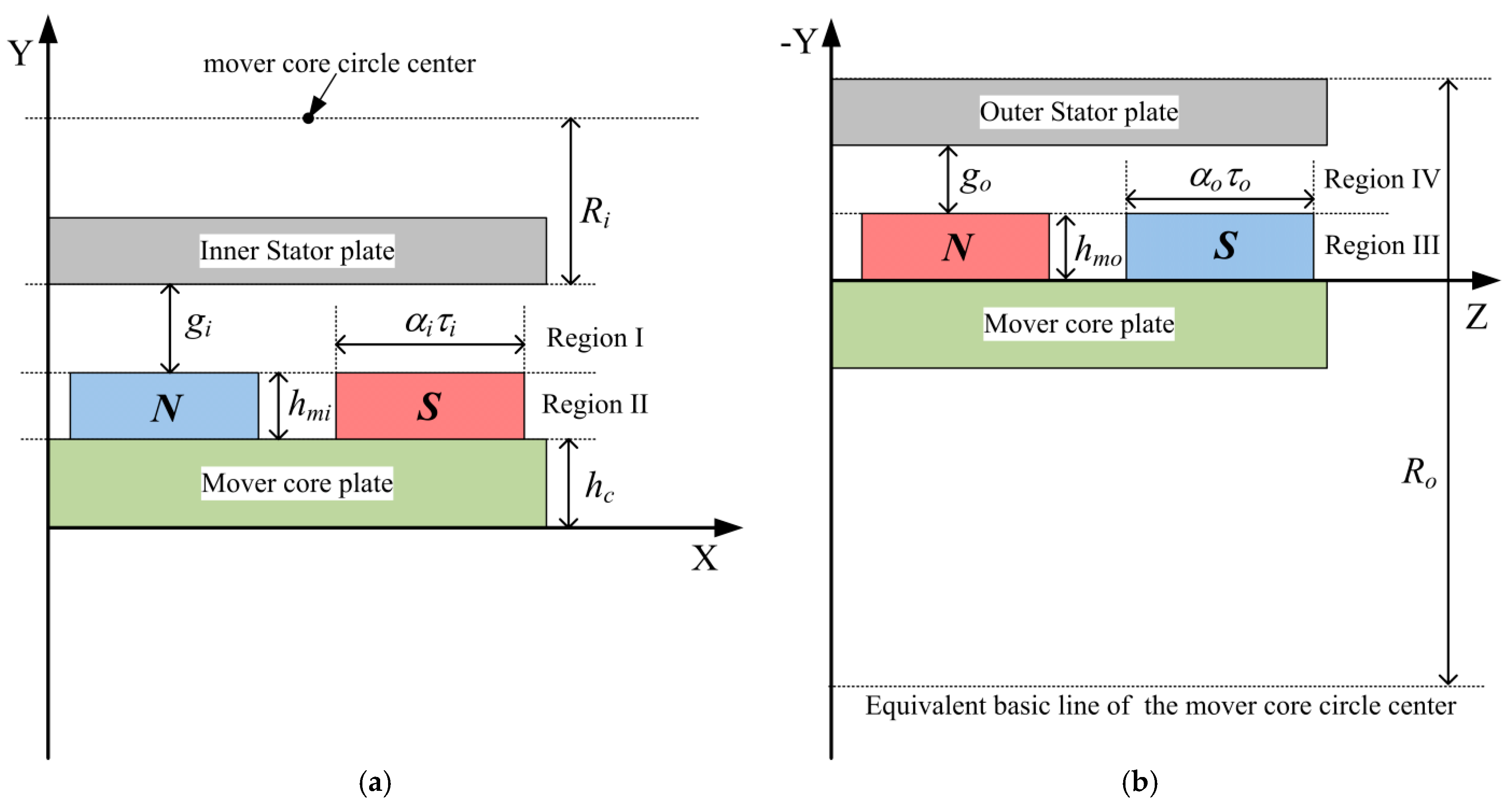
3.1. Model of the PMs
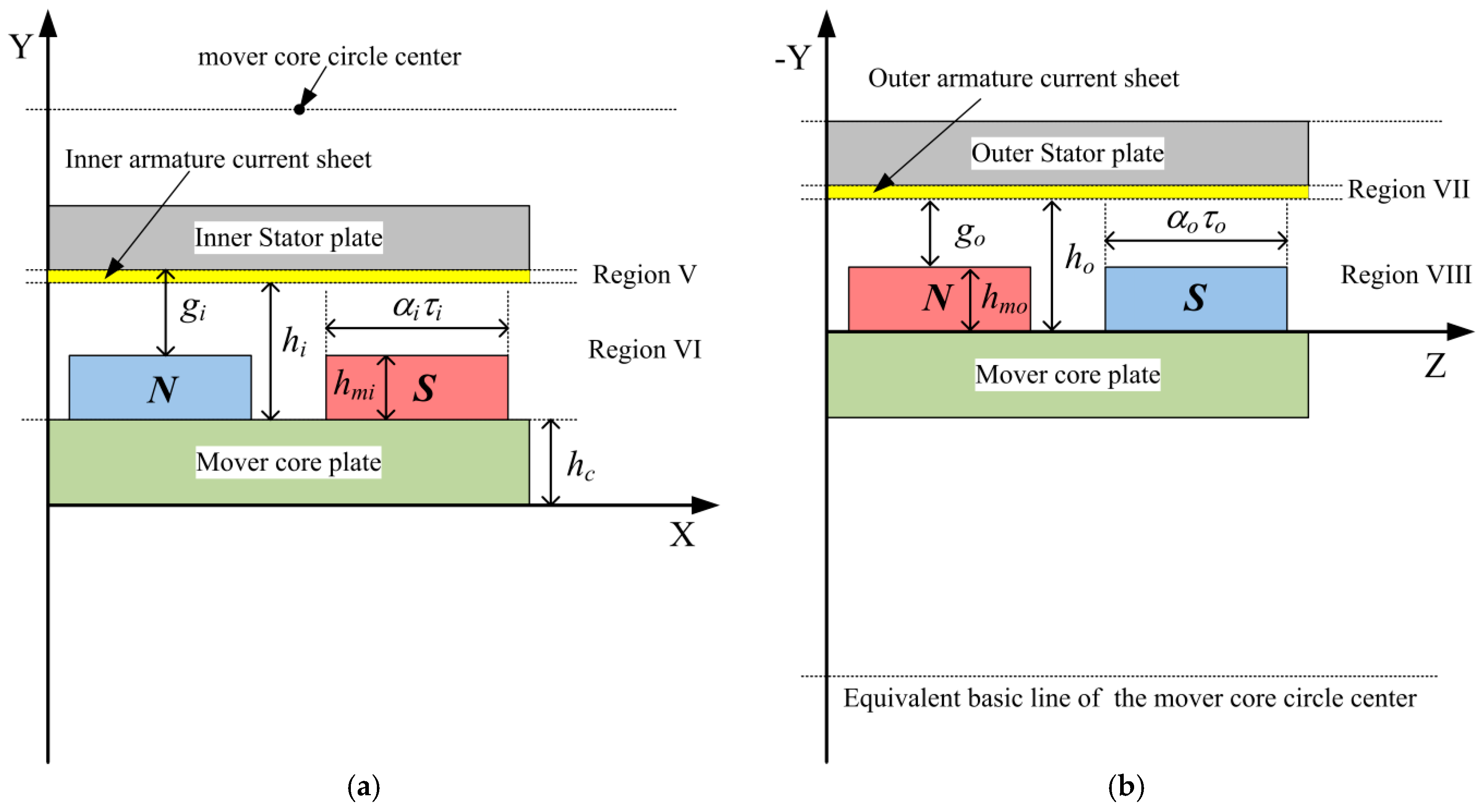
3.2. Model of Armature Reaction Current
3.3. Effect of Stator Slotting
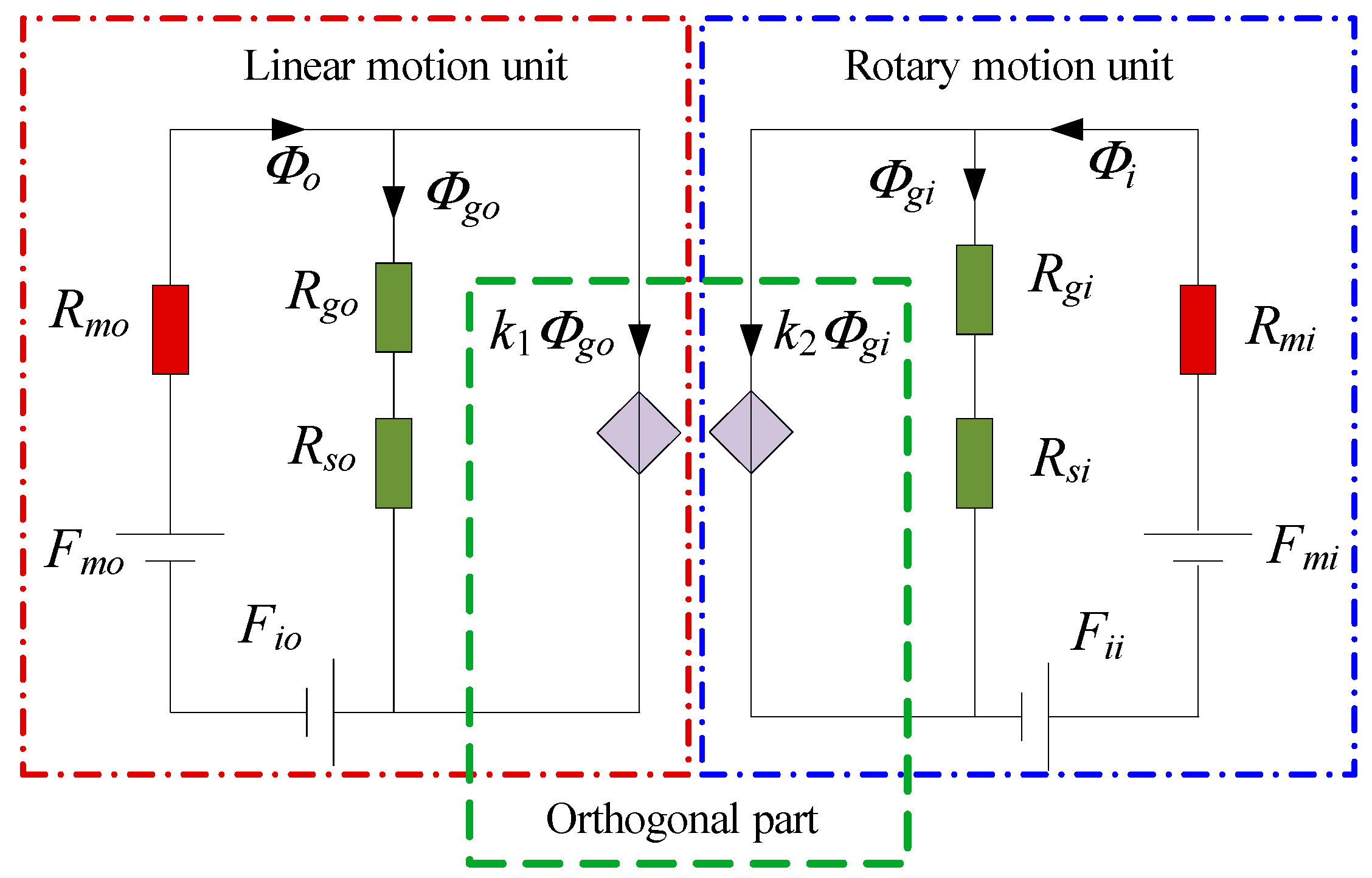
3.4. Effect of the Orthogonal Magnetic Field Coupling
3.5. Performances Prediction
3.5.1. Open-Circuit Conditions
3.5.2. On-Load Conditions
3.6. Process of the Calculation
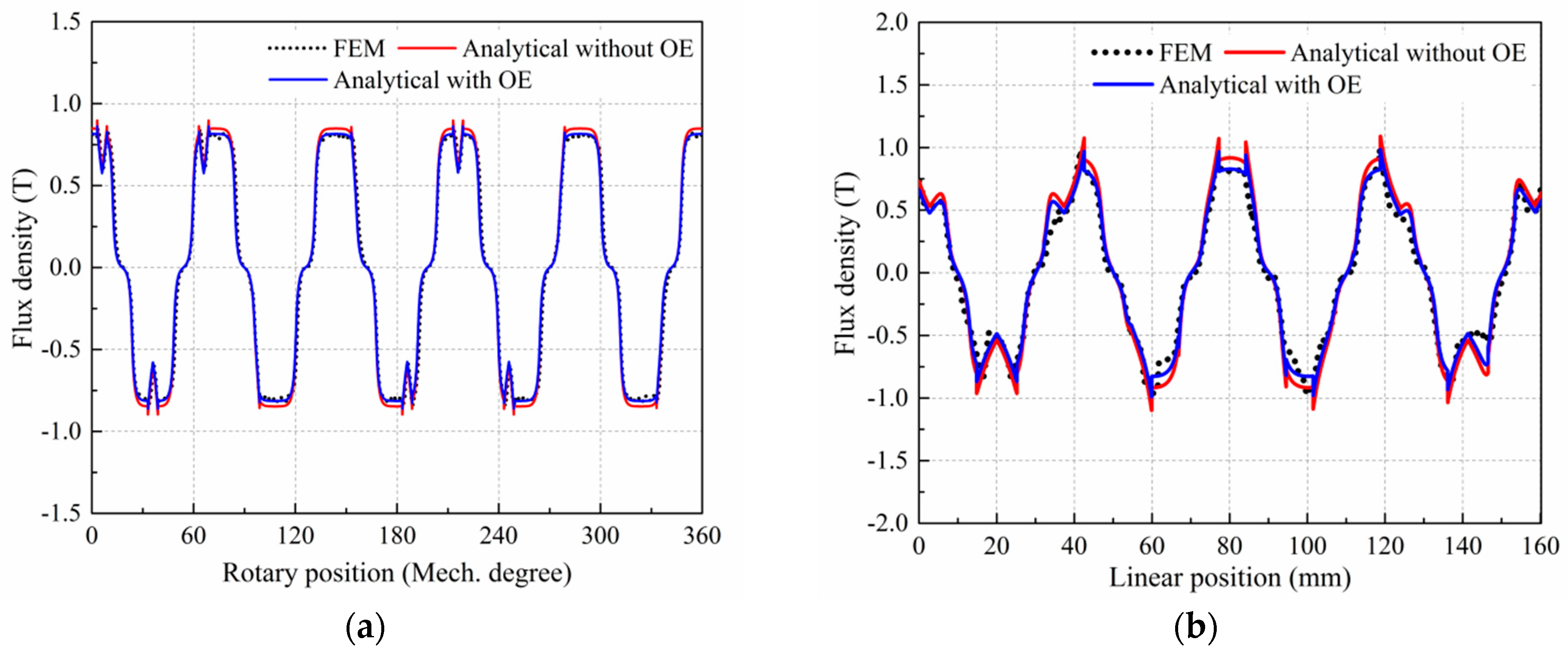
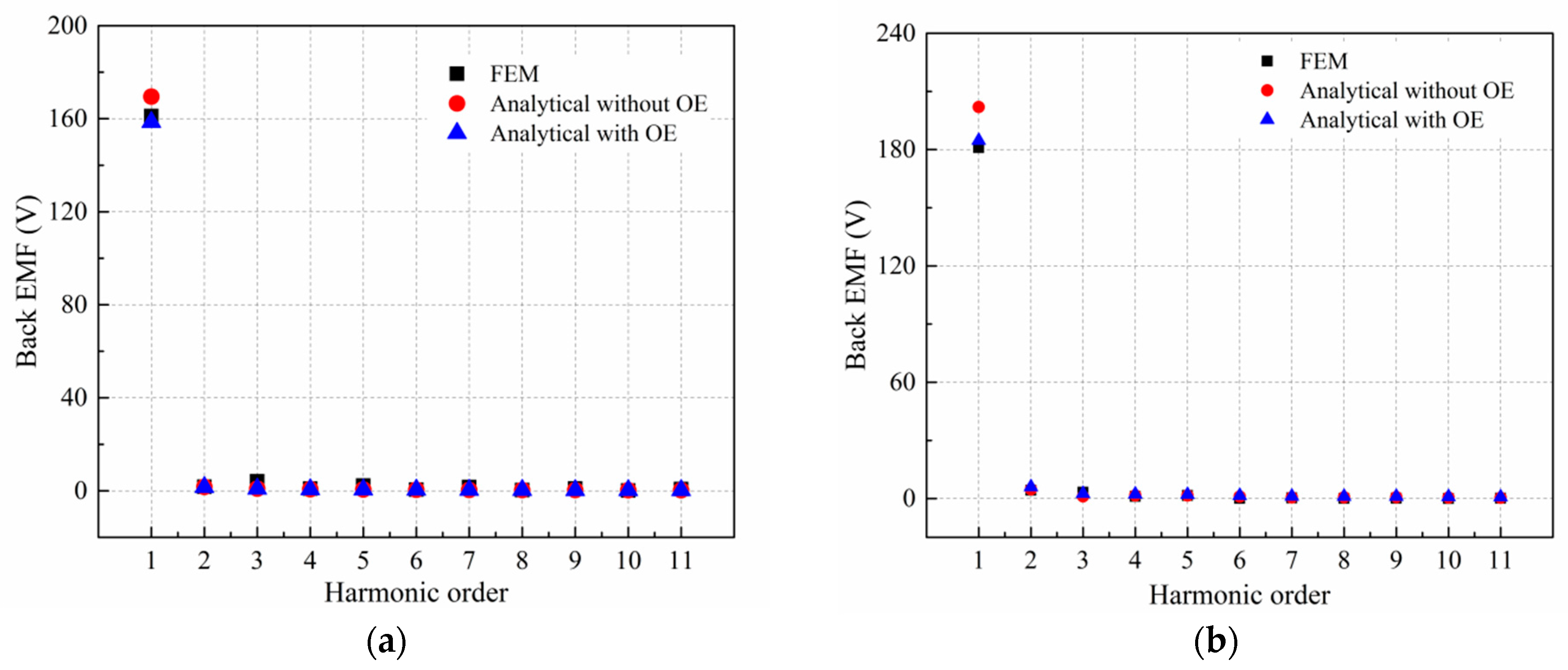
4. Comparison of Predictions with Finite Element Calculation
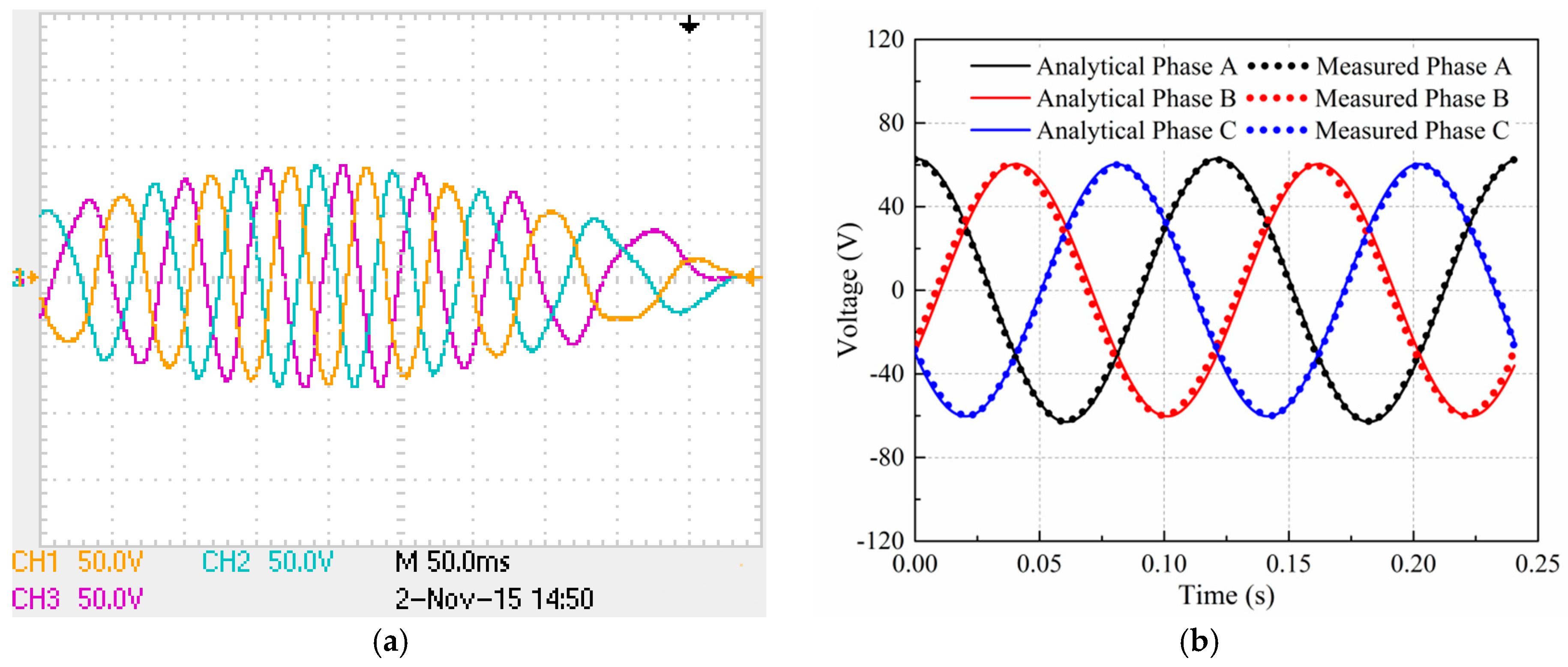
5. Experimental Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mendrela, E.A.; Gierczak, E.C. Double-winding rotary-linear induction motor. IEEE Trans. Energy Convers. 1987, EC-2, 47–54. [Google Scholar] [CrossRef]
- Jeon, W.J.; Tanabiki, M.; Onuki, T.; Yoo, J.Y. Rotary-linear induction motor composed of four primaries with independently energized ring-windings. In Proceedings of the IEEE Industry Application Society Annual Meeting, New Orleans, LA, USA, 5–9 October 1997; pp. 365–372. [Google Scholar]
- Jin, P.; Fang, S.H.; Lin, H.Y.; Wang, X.B.; Zhou, S.G. A novel linear and rotary halbach permanent magnet actuator with two degrees-of-freedom. J. Appl. Phys. 2012, 111. [Google Scholar] [CrossRef]
- Pan, J.F.; Zou, Y.; Cheung, N.C. Investigation of a rotary-linear switched reluctance motor. In Proceedings of the 2010 XIX International Conference on Electrical Machines(ICEM), Rome, Italy, 6–8 September 2010; pp. 1–4. [Google Scholar]
- Pan, J.F.; Zou, Y.; Cheung, N.C. Performance analysis and decoupling control of an integrated rotary linear machine with coupled magnetic paths. IEEE Trans. Magn. 2014, 50, 761–764. [Google Scholar] [CrossRef]
- Si, J.K.; Feng, H.C.; Ai, L.W.; Hu, Y.H.; Cao, W.P. Design and analysis of a 2-DOF split-stator induction motor. IEEE Trans. Energy Convers. 2015, 30, 1200–1208. [Google Scholar] [CrossRef]
- Jang, S.M.; Lee, S.H.; Cho, H.W.; Cho, S.K. Design and analysis of helical motion permanent magnet motor with cylindrical halbach array. IEEE Trans. Magn. 2003, 39, 3007–3009. [Google Scholar] [CrossRef]
- Bolognesi, P.; Taponecco, L. A novel 2-freedom-degree brushless motor. In Proceedings of the 2002 IEEE International Symposium on Industrial Electronics (ISIE), L’Aquila, Italy, 8–11 July 2002; pp. 863–868. [Google Scholar]
- Krebs, G.; Tounzi, A.; Pauwels, B.; Piriou, F. Modeling of a linear and rotary permanent magnet actuator. IEEE Trans. Magn. 2008, 44, 4357–4360. [Google Scholar] [CrossRef]
- Krebs, G.; Tounzi, A.; Pauwels, B.; Willemot, D.; Piriou, M.F. Design of a permanent magnet actuator for linear and rotary movements. Eur. Phys. J. Appl. Phys. 2008, 44, 77–85. [Google Scholar] [CrossRef]
- Jin, P.; Lin, H.Y.; Fang, S.H.; Yuan, Y.; Guo, Y.J.; Jia, Z. 3D Analytical linear force and rotary torque analysis of linear and rotary permanent magnet actuator. IEEE Trans. Magn. 2013, 49, 3989–3992. [Google Scholar] [CrossRef]
- Chen, L.; Hofmann, W. Design of one rotary-linear permanent magnet motor with two independently energized three phase windings. In Proceedings of the 7th IEEE International Conference on Power Electronics and Drive Systems (PEDS), Bangkok, Thailand, 26–30 November 2007; pp. 1372–1376. [Google Scholar]
- Meessen, K.J.; Paulides, J.J.H.; Lomonova, E.A. Analysis of a novel magnetization pattern for 2-DOF rotary-linear actuators. IEEE Trans. Magn. 2012, 48, 3867–3870. [Google Scholar] [CrossRef]
- Xu, L.; Lin, M.Y.; Fu, X.H.; Li, N. Analysis of a double stator linear rotary permanent magnet motor with orthogonally arrayed permanent magnets. IEEE Trans. Magn. 2016, 52. [Google Scholar] [CrossRef]
- Zheng, P.; Wu, Q.; Zhao, J.; Tong, C.D.; Bai, J.G.; Zhao, Q.B. Performance analysis and simulation of a novel brushless double rotor machine for power-split HEV applications. Energies 2012, 5, 119–137. [Google Scholar] [CrossRef]
- Tong, C.D.; Song, Z.Y.; Bai, J.G.; Liu, J.Q.; Zheng, P. Analytical investigation of the magnetic-field distribution in an axial magnetic-field-modulated brushless double-rotor machine. Energies 2016, 9, 589. [Google Scholar] [CrossRef]
- Huang, Y.K.; Guo, B.C.; Hemeida, A.; Sergeant, P. Analytical modeling of static eccentricities in axial flux permanent-magnet machines with concentrated windings. Energies 2016, 9, 892. [Google Scholar] [CrossRef]
- Bianchi, N. Analytical field computation of a tubular permanent-magnet linear motor. IEEE Trans. Magn. 2000, 36, 3798–3801. [Google Scholar] [CrossRef]
- Li, W.; Chau, K.T. Analytical field calculation for linear tubular magnetic gears using equivalent anisotropic magnetic permeability. Prog. Electromagn. Res. 2012, 127, 155–171. [Google Scholar] [CrossRef]
- Yu, Y.J.; Zhang, W.Y.; Sun, Y.X.; Xu, P.F. Basic characteristics and design of a novel hybrid magnetic bearing for wind turbines. Energies 2016, 9, 905. [Google Scholar] [CrossRef]
- Jin, P.; Fang, S.H.; Lin, H.Y.; Zhu, Z.Q.; Huang, Y.K.; Wang, X.B. Analytical magnetic field analysis and prediction of cogging force and torque of a linear and rotary. IEEE Trans. Magn. 2011, 47, 3004–3007. [Google Scholar] [CrossRef]
- Meessen, K.J.; Paulides, J.J.H.; Lomonova, E.A. Modeling of magnetization patterns for 2-DoF rotary-linear actuators. Int. J. Comput. Math. Electr. Electron. Eng. 2012, 31, 1428–1440. [Google Scholar] [CrossRef]
- Guo, K.K.; Fang, S.H.; Zhang, Y.; Yang, H.; Lin, H.Y.; Ho, S.L.; Feng, N.J. Irreversible demagnetization analysis of permanent magnet materials in a novel flux reversal linear-rotary permanent magnet actuator. IEEE Trans. Magn. 2016, 52. [Google Scholar] [CrossRef]
- O’Connell, T.C.; Krein, P.T. A Schwarz–Christoffel-based analytical method for electric machine field analysis. IEEE Trans. Energy Convers. 2009, 24, 565–577. [Google Scholar] [CrossRef]
- Hemeida, A.; Sergeant, P. Analytical modeling of surface PMSM using a combined solution of Maxwell’s equations and magnetic equivalent circuit. IEEE Trans. Magn. 2014, 50. [Google Scholar] [CrossRef]
- Zarko, D.; Ban, D.; Lipo, T.A. Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent magnet motor using complex relative air-gap permeance. IEEE Trans. Magn. 2004, 42, 1828–1837. [Google Scholar] [CrossRef]
- Gibbs, W.J. Conformal Transformations in Electrical Engineering; Chapman & Hall: London, UK, 1958; pp. 56–59. [Google Scholar]
- Barakat, G.; El-Meslouhi, T.; Dakyo, B. Analysis of the cogging torque behavior of a two-phase axial flux permanent magnet synchronous machine. IEEE Trans. Magn. 2001, 37, 2803–2805. [Google Scholar] [CrossRef]





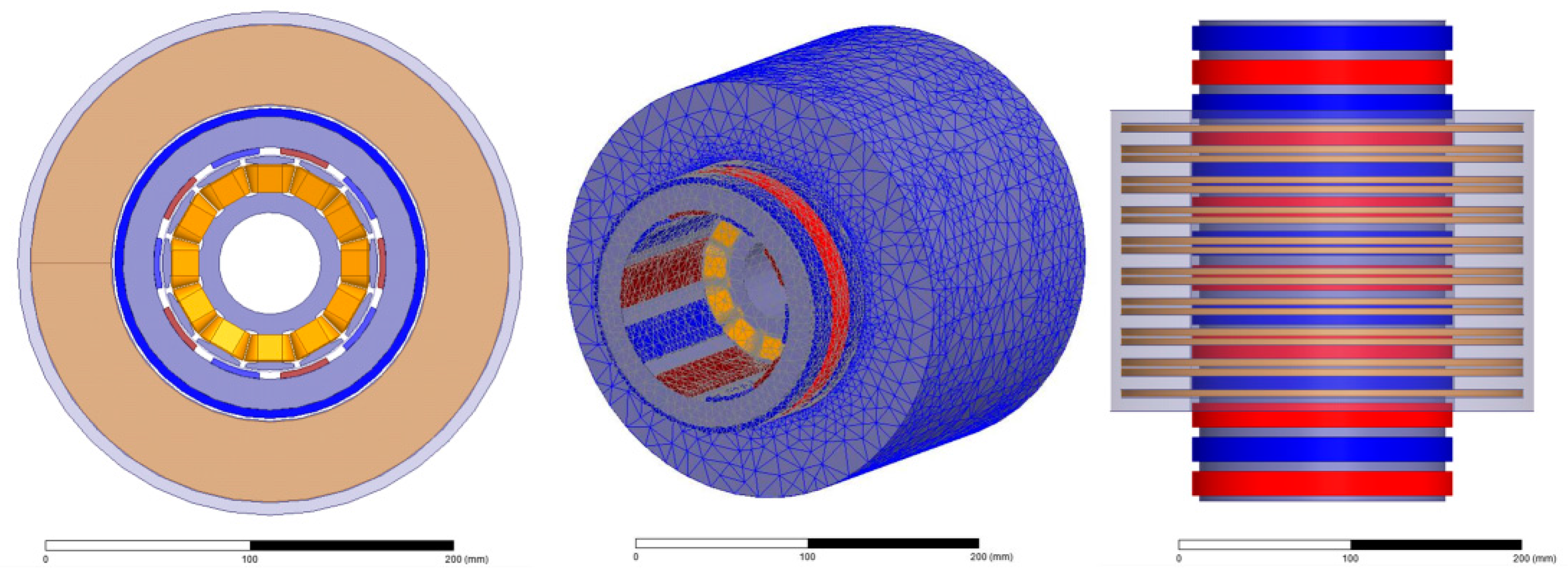






| Items | Value | Items | Value |
|---|---|---|---|
| Rated rotary motion power | 1 kW | Inside diameter of mover core | 114 mm |
| Rated linear motion power | 1 kW | Outside diameter of mover core | 144 mm |
| Rated rotational speed | 1000 r/min | Outer diameter of outer stator | 247 mm |
| Rated linear speed | 1 m/s | Inner diameter of inner stator | 50 mm |
| Inner PM thickness | 3 mm | Outer air-gap length | 1.5 mm |
| Outer PM thickness | 4 mm | Inner air-gap length | 1.5 mm |
| Axial length of the inner stator | 106 mm | Axial length of the outer stator | 175.4 mm |
| Item | Analytical Rotary | Analytical Linear | FEM Rotary | FEM Linear | Measured Rotary | Measured Linear |
|---|---|---|---|---|---|---|
| RMS value of back EMF (V) | 60.25 | 46.1 | 60.2 | 46 | 60 | 45.8 |
| Error in voltage | −0.42% | −0.66% | −0.33% | −0.44% | - | - |
| CPU time (h) | 0.15 | 24 | - | - | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Lin, M.; Fu, X.; Liu, K.; Guo, B. Analytical Calculation of the Magnetic Field Distribution in a Linear and Rotary Machine with an Orthogonally Arrayed Permanent Magnet. Energies 2017, 10, 493. https://doi.org/10.3390/en10040493
Xu L, Lin M, Fu X, Liu K, Guo B. Analytical Calculation of the Magnetic Field Distribution in a Linear and Rotary Machine with an Orthogonally Arrayed Permanent Magnet. Energies. 2017; 10(4):493. https://doi.org/10.3390/en10040493
Chicago/Turabian StyleXu, Lei, Mingyao Lin, Xinghe Fu, Kai Liu, and Baocheng Guo. 2017. "Analytical Calculation of the Magnetic Field Distribution in a Linear and Rotary Machine with an Orthogonally Arrayed Permanent Magnet" Energies 10, no. 4: 493. https://doi.org/10.3390/en10040493
APA StyleXu, L., Lin, M., Fu, X., Liu, K., & Guo, B. (2017). Analytical Calculation of the Magnetic Field Distribution in a Linear and Rotary Machine with an Orthogonally Arrayed Permanent Magnet. Energies, 10(4), 493. https://doi.org/10.3390/en10040493








