A Glowworm Swarm Optimization-Based Maximum Power Point Tracking for Photovoltaic/Thermal Systems under Non-Uniform Solar Irradiation and Temperature Distribution
Abstract
:1. Introduction
2. Characteristics of Solar Modules
2.1. PV Cell
2.2. PV Module
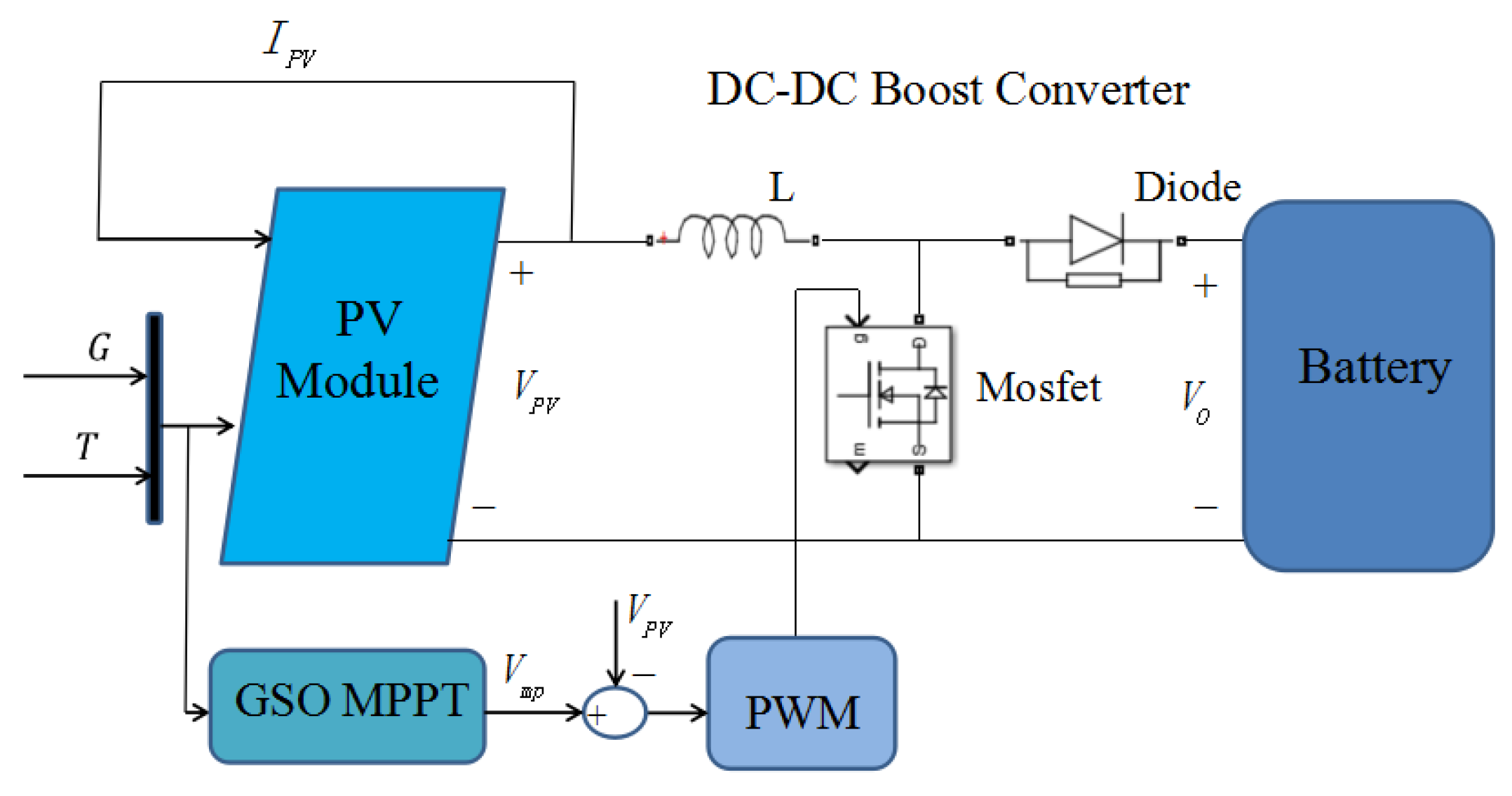
3. MPPT Algorithm
3.1. The Proposed GSO-Based MPPT
3.1.1. Luciferin Update Phase
3.1.2. Movement Phase
3.1.3. Local-Decision Range Update Phase
3.2. Perturbation and Observe Algorithm
3.3. Fractional Open-Circuit Voltage Technique
4. Simulation Results
- Case 1:
- Gradient temperature distribution condition
- Case 2:
- Fast variation in solar irradiation
- Case 3:
- Partial shading condition
- Case 4:
- Variation in the degree of shading.
4.1. Gradient Temperature Distribution Condition
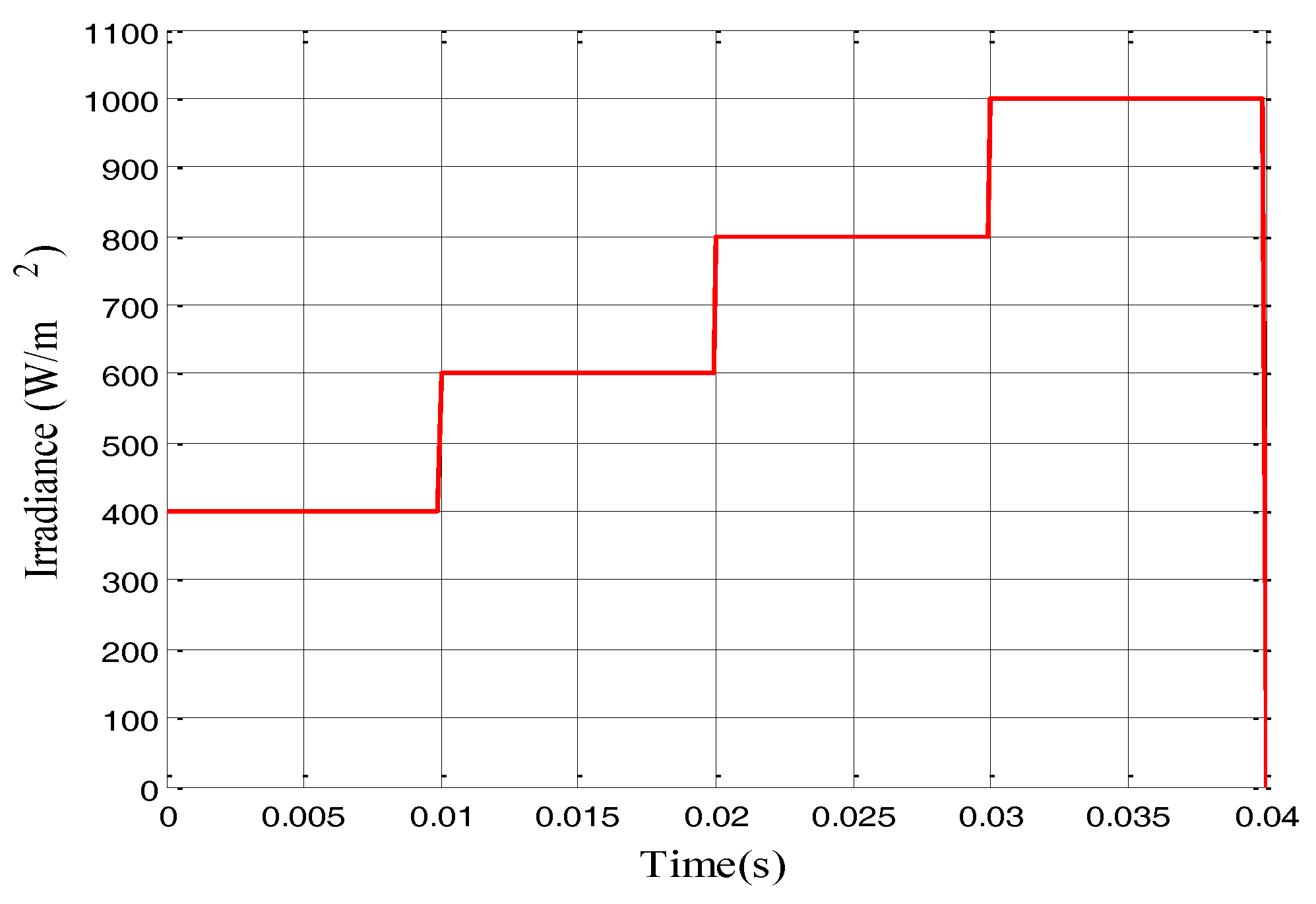
4.2. Fast Variation in Solar Irradiation
4.3. Partial Shading Condition
4.4. Variation in the Degree of Shading
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Diode ideality factor | Electronic charge (C) | ||
| Euclidean distance between and | Local decision radius | ||
| Band gap energy of semiconductor | Largest sensing radius | ||
| Objective function | Parallel resistance | ||
| PV cell output current (A) | Series resistance | ||
| Diode current (A) | Movement step size | ||
| Luciferin of glowworm | Solar radiation () | ||
| Current corresponding to the MPP | Iteration number | ||
| Diode reverse saturation current (A) | Temperature | ||
| Parallel resistance current (A) | Operating temperature (K) | ||
| Light-generated current (A) | Reference temperature (K) | ||
| Diode reverse saturation current at STC (A) | PV cell output voltage (V) | ||
| Short-circuit current (A) | Diode voltage | ||
| Boltzmann’s constant (J/K) | Voltage of the PV module | ||
| The coefficient of the proportionality | Voltage corresponding to the MPP | ||
| Number of outstanding individuals | Boost converter output voltage (V) | ||
| Neighborhood of agen | Open-circuit voltage | ||
| PV cell output power | Location of glowworm Greek symbols | ||
| Probability of glowworm moving to | The current temperature coefficient | ||
| PV maximum power (W) | Variation coefficient of decision radius | ||
| Probability of glowworm | Luciferin enhancement constant | ||
| PV module output power (W) | Luciferin decay constant |
References
- Sahoo, S.K. Renewable and sustainable energy reviews solar photovoltaic energy progress in India: A review. Renew. Sustain. Energy Rev. 2016, 59, 927–939. [Google Scholar] [CrossRef]
- Subudhi, B.; Pradhan, R. A comparative study on maximum power point tracking techniques for photovoltaic power systems. IEEE Trans. Sustain. Energy 2013, 4, 89–98. [Google Scholar] [CrossRef]
- Qin, L.; Lu, X. Matlab/Simulink-based research on maximum power point tracking of photovoltaic generation. Phys. Procedia 2012, 24, 10–18. [Google Scholar] [CrossRef]
- Bendib, B.; Belmili, H.; Krim, F. A survey of the most used MPPT methods: Conventional and advanced algorithms applied for photovoltaic systems. Renew. Sustain. Energy Rev. 2015, 45, 637–648. [Google Scholar] [CrossRef]
- Jubaer, A.; Zainal, S. An improved perturb and observe (P&O) maximum power point tracking (MPPT) algorithm for higher efficiency. Appl. Energy 2015, 150, 97–108. [Google Scholar]
- Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Assessment of perturb and observe MPPT algorithm implementation techniques for PV pumping applications. IEEE Trans. Sustain. Energy 2012, 3, 21–33. [Google Scholar] [CrossRef]
- Bangyin, L.; Shanxu, D.; Fei, L.; Pengwei, X. Analysis and improvement of maximum power point tracking algorithm based on incremental conductance method for photovoltaic array. Proceedinngs of the Seventh International Conference on Power Electronics and Drive Systems, Bangkok, Thailand, 27–30 November 2007; pp. 637–641. [Google Scholar]
- Mohammed, S.S.; Devaraj, D. Simulation of Incremental Conductance MPPT based two phase interleaved boost converter using MATLAB/Simulink. Proceedinngs of the IEEE International Conference Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 5–7 March 2015; pp. 1–6. [Google Scholar]
- Sivakumar, P.; Kader, A.A.; Kaliavaradhan, Y.; Arutchelvi, M. Analysis and enhancement of PV efficiency with incremental conductance MPPT technique under non-linear loading conditions. Renew. Energy 2015, 81, 543–550. [Google Scholar] [CrossRef]
- Chen, P.C.; Chen, P.Y.; Liu, Y.H.; Chen, J.H.; Luo, Y.F. A comparative study on maximum power point tracking techniques for photovoltaic generation systems operating under fast changing environments. Sol. Energy 2015, 119, 261–276. [Google Scholar] [CrossRef]
- Bayod-Rújula, Á.A.; Cebollero-Abián, J.A. A novel MPPT method for PV systems with irradiance measurement. Sol. Energy 2014, 109, 95–104. [Google Scholar] [CrossRef]
- Rezk, H.; Hasaneen, E.S. A new MATLAB/Simulink model of triple-junction solar cell and MPPT based on artificial neural networks for photovoltaic energy systems. Ain Shams Eng. J. 2015, 6, 873–881. [Google Scholar] [CrossRef]
- Zaghba, L.; Terki, N.; Borni, A.; Bouchakour, A. Intelligent control MPPT technique for PV module at varying atmospheric conditions using MATLAB/SIMULINK. In Proceedings of the 2014 International Renewable and Sustainable Energy Conference (IRSEC), Ouarzazate, Morocco, 17–19 October 2014; pp. 661–666. [Google Scholar]
- Guenounou, O.; Dahhou, B.; Chabour, F. Adaptive fuzzy controller based MPPT for photovoltaic systems. Energy Convers. Manag. 2014, 78, 843–850. [Google Scholar] [CrossRef]
- Chen, Y.T.; Jhang, Y.C.; Liang, R.H. A fuzzy-logic based auto-scaling variable step-size MPPT method for PV systems. Sol. Energy 2016, 126, 53–63. [Google Scholar] [CrossRef]
- Gounden, N.A.; Peter, S.A.; Nallandula, H.; Krithiga, S. Fuzzy logic controller with MPPT using line-commutated inverter for three-phase grid-connected photovoltaic systems. Renew. Energy 2009, 34, 909–915. [Google Scholar] [CrossRef]
- Kofinas, P.; Dounis, A.I.; Papadakis, G.; Assimakopoulos, M.N. An Intelligent MPPT controller based on direct neural control for partially shaded PV system. Energy Build. 2015, 90, 51–64. [Google Scholar] [CrossRef]
- Hadji, S.; Gaubert, J.P.; Krim, F. Theoretical and experimental analysis of genetic algorithms based MPPT for PV systems. Energy Procedia 2015, 74, 772–787. [Google Scholar] [CrossRef]
- Sarvi, M.; Ahmadi, S.; Abdi, S. A PSO-based maximum power point tracking for photovoltaic systems under environmental and partially shaded conditions. Prog. Photovolt. Res. Appl. 2015, 23, 201–214. [Google Scholar] [CrossRef]
- Soufyane Benyoucef, A.; Chouder, A.; Kara, K.; Silvestre, S. Artificial bee colony based algorithm for maximum power point tracking (MPPT) for PV systems operating under partial shaded conditions. Appl. Soft Comput. 2015, 32, 38–48. [Google Scholar] [CrossRef]
- Larbes, C.; Cheikh, S.M.A.; Obeidi, T.; Zerguerras, A. Genetic algorithms optimized fuzzy logic control for the maximum power point tracking in photovoltaic system. Renew. Energy 2009, 34, 2093–2100. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Palani, S. Application of a combined particle swarm optimization and perturb and observe method for MPPT in PV systems under partial shading conditions. Renew. Energy 2015, 75, 308–317. [Google Scholar] [CrossRef]
- Krishnanand, K.N.; Ghose, D. Glowworm swarm optimization for simultaneous capture of multiple local optima of multimodal functions. Swarm Intell. 2009, 3, 87–124. [Google Scholar] [CrossRef]
- Singh, A.; Deep, K. New variants of glowworm swarm optimization based on step size. Int. J. Syst. Assur. Eng. Manag. 2015, 6, 286–296. [Google Scholar] [CrossRef]













| Parameters | Value | Unit |
|---|---|---|
| Current temp. coefficient | 0.002086 | A/°C |
| Open-circuit Voltage (Voc) | 0.53 | V |
| Short-circuit Current (Isc) | 2.926 | A |
| Ideal Factor (A) | 1.3 | - |
| Electrical resistance | 0.0277 | Ω |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Y.; Hou, W.; Li, G.; Chen, X. A Glowworm Swarm Optimization-Based Maximum Power Point Tracking for Photovoltaic/Thermal Systems under Non-Uniform Solar Irradiation and Temperature Distribution. Energies 2017, 10, 541. https://doi.org/10.3390/en10040541
Jin Y, Hou W, Li G, Chen X. A Glowworm Swarm Optimization-Based Maximum Power Point Tracking for Photovoltaic/Thermal Systems under Non-Uniform Solar Irradiation and Temperature Distribution. Energies. 2017; 10(4):541. https://doi.org/10.3390/en10040541
Chicago/Turabian StyleJin, Yi, Wenhui Hou, Guiqiang Li, and Xiao Chen. 2017. "A Glowworm Swarm Optimization-Based Maximum Power Point Tracking for Photovoltaic/Thermal Systems under Non-Uniform Solar Irradiation and Temperature Distribution" Energies 10, no. 4: 541. https://doi.org/10.3390/en10040541
APA StyleJin, Y., Hou, W., Li, G., & Chen, X. (2017). A Glowworm Swarm Optimization-Based Maximum Power Point Tracking for Photovoltaic/Thermal Systems under Non-Uniform Solar Irradiation and Temperature Distribution. Energies, 10(4), 541. https://doi.org/10.3390/en10040541






