Performance Comparison between Selected Evaporative Air Coolers
Abstract
:1. Introduction
1.1. Subject of the Study
- -
- The typical counter-flow exchanger has separate intakes for primary and working air (Figure 1a,c). Therefore, both air streams can have different inlet parameters and different values of the airflow rate. This unit is not able to create a pre-cooling effect for the working air in the dry channel as regenerative unit (Figure 1b), but it can operate on the exhaust air in the systems with additional cooling coil (Figure 1c) and can have value of the airflow in the wet channel equal or higher to value of the airflow in the dry channel.
- -
- In the regenerative heat and mass exchanger a mixture of primary and working airflow is delivered to the dry channel (Figure 1b) and it passes the dry channel, where it is cooled. At the end of the dry channel primary and working airflow are separated, working airflow is delivered to the wet channel, while primary airflow is delivered to the occupants. Precooling of the working airflow in the dry channel allows to increase the efficiency of the exchanger, however, it also gives several disadvantages: regenerative unit cannot use exhaust air from the conditioned room, airflow delivered to the occupants is always smaller than the intake air (and airflow in the wet channel has to be smaller than the airflow in the wet channel. To increase the efficiency of the regenerative unit, a desiccant wheel can be added, to dehumidify the air before it passes the cooler (Figure 1e).
- -
- The perforated regenerative exchanger is similar to the regenerative exchanger, but in this unit, working air is delivered to the wet channel in portions instead of delivering whole value of the working air after it passes the dry channel as it is in case of the typical regenerative air cooler (Figure 1d). From the mathematical modeling standpoint, this unit requires additional algorithm describing the air streams mixing process (described in detail by authors in [5]).
- -
- The novel, modified exchanger is a combination of regenerative unit and a counter-flow unit (Figure 1f). It can operate on the exhaust air, but it can also return part of the airflow from the dry channel to the wet channel. Depending on the ambient and exhaust air conditions, proportions between air returned from the dry channel and the exhaust airflow can be changed to achieve highest effectiveness.
2. Methodologies
2.1. Model
- For the plate surface in the main air-flow channel (see Figure 3).Equation (4) can be converted using following set of equations:to the form presented below:
- For the plate surface in the working air channel (see Figure 3):This equation can be converted using the Equation (6) and the energy balance equation presented below:to the form:It should be noted that the iterative procedure of the boundary conditions assignment for the fin in the wet channel and local plate temperature computation at each node of integration step is considerably simplified using Equation (9).
- For the main air stream:
- For the working air stream:
- The boundary conditions for the fin in the working air-flow passage (Figure 4) are:
- And the boundary conditions for the fin in the main air-flow passage are:
2.2. Validation
3. Results and Discussion
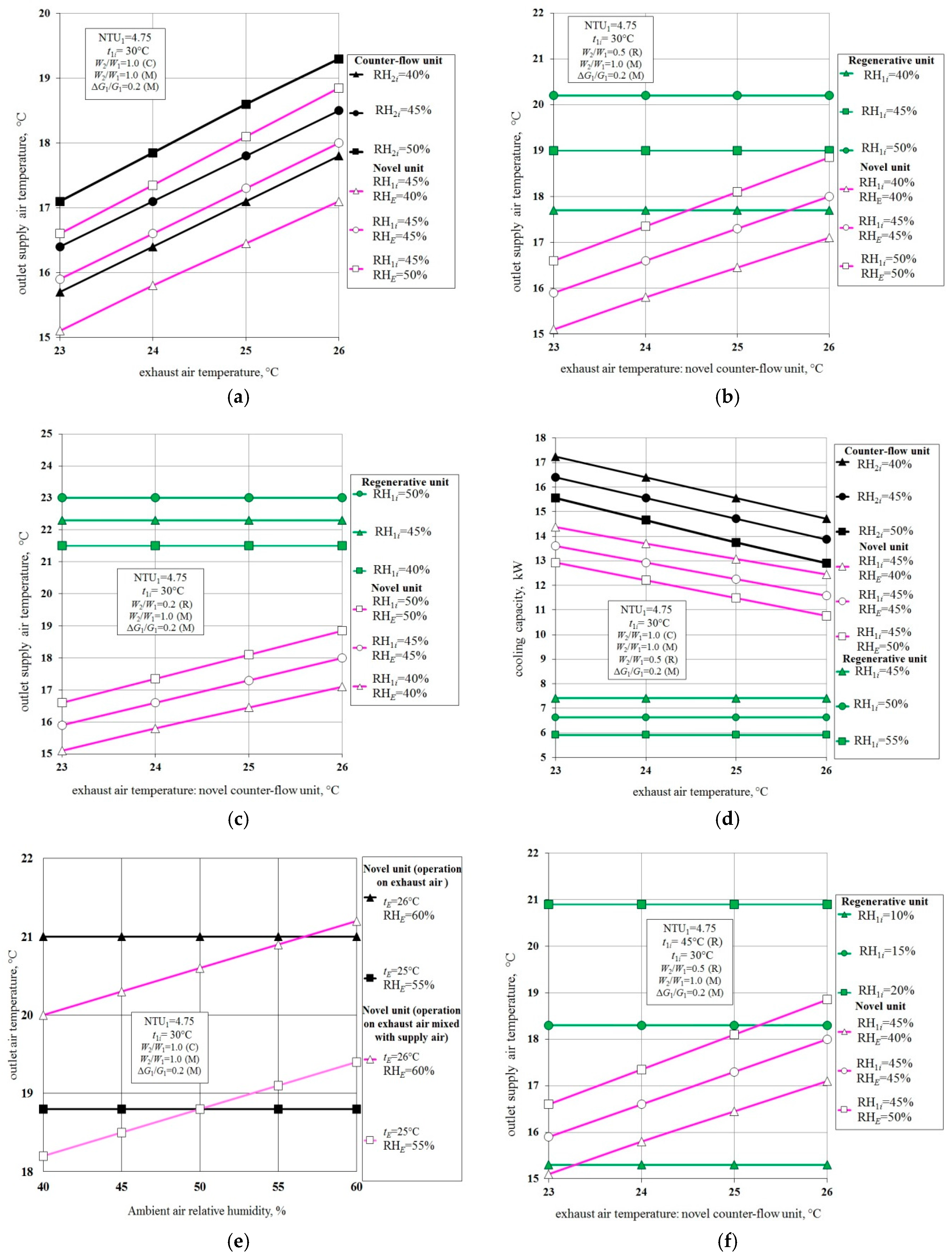
3.1. Comparision of Different Types of Evaporate Air Coolers
3.2. Annual Opeartion
3.2.1. Cooling Effectiveness during Summer Operation
3.2.2. Heat Recovery Effectiveness and Safe Working Conditions during Winter Operation
3.2.3. Problems Associated with Round-Year Operation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| cp | J/(kg K) | Specific heat capacity of moist air |
| cg | J/(kg K) | Specific heat capacity of water vapor |
| C | - | Counter-flow exchanger |
| E | - | Exhaust airflow |
| F | m2 | Surface area |
| h | m | Height |
| HR | - | Heat recovery exchanger |
| G | kg/s | Moist air mass flow rate |
| IEC | - | Indirect evaporative cooler |
| L, l | m | Streamwise length of cooler |
| M | - | Novel (Modified) counter-flow exchanger |
| kg/s | Water vapor mass flow rate (referenced to the elementary plate surface) | |
| q | W/m2 | Heat flux |
| kW | Cooling capacity respected to airflow rate equal 1 m3/s = (1 − W2/W1)·V·ρ·cp·(t1i − t1o), kW, where V is volumetric airflow rate equal 1 m3/s; and (1 − W2/W1) is correction coefficient including uneven values of the intake air and primary air delivered to the occupants in case of regenerative exchanger and the novel, modified exchanger (in case of the C unit it is not included) | |
| ro | kJ/kg | Specific heat of water evaporation |
| Q | W | Rate of heat transfer |
| R | - | Regenerative exchanger |
| RH | % | Relative humidity |
| s | m | Fin pitch |
| t | °C | Temperature |
| °C | Average temperature | |
| v | m/s | Air stream velocity |
| V | m3/s | Volumetric airflow rate |
| W | W/K | Heat capacity rate of the fluid |
| x | kg/kg | Humidity ratio |
| X | m | Coordinate along supply air flow direction |
| Y | m | Coordinate perpendicular to X coordinate |
| Z | m | Coordinate along fins direction |
| Special characters: | ||
| α | W/(m2 K) | Convective heat transfer coefficient |
| β | kg/(m2 s) | Mass transfer coefficient |
| δ | m | Thickness |
| ε | - | Effectiveness |
| εeqv | - | Equivalent effectiveness |
| εt | - | Temperature effectiveness |
| ρ | kg/m3 | Density |
| σ | - | Surface wettability factor, σ∈(0.01.0) |
| Non dimensional coordinates: | ||
| Le | - | Lewis factor Le = α/(βc_p) |
| NTU | - | Number of transfer units Le = α/(βc_p) |
| - | = X/lX—relative X coordinate | |
| - | = Y/lY—relative Y coordinate | |
| - | = Z/hfin—relative Z coordinate | |
| Subscripts/Superscripts: | ||
| 1 | Main (supply) airflow | |
| 2 | Working airflow in the wet channels | |
| cond | Thermal conductivity | |
| E | Exhaust airflow | |
| fin | Referenced to the fins | |
| i | Inlet | |
| l | Latent heat flow | |
| met | Metal foil (impenetrable cover of the plate) | |
| o | Outlet | |
| p | Referenced to the plate surface | |
| plt | Referenced to the channel plate | |
| s | Sensible heat flux | |
| swc | Safe working conditions | |
| w | Water film | |
| WB | Wet-bulb temperature | |
| X | Air streamwise in the dry channel | |
| Y | Air streamwise in the wet channel | |
| ’ | Conditions at the air/water interface temperature | |
| ” | Referenced to the plate surface | |
| ● | Referenced to the elementary surface | |
References
- Rogdakis, E.D.; Koronaki, I.P.; Tertipis, D.N. Experimental and computational evaluation of a Maisotsenko evaporative cooler at Greek climate. Energy Build. 2014, 70, 497–506. [Google Scholar] [CrossRef]
- Pandelidis, D.; Anisimov, S.; Worek, W.M. Performance study of the Maisotsenko Cycle heat exchangers in different air-conditioning applications. Int. J. Heat Mass Transf. 2015, 81, 207–221. [Google Scholar] [CrossRef]
- Pandelidis, D.; Anisimov, S. Numerical analysis of the heat and mass transfer processes in selected M-Cycle heat exchangers for the dew point evaporative cooling. Energy Convers. Manag. 2015, 90, 62–83. [Google Scholar] [CrossRef]
- Anisimov, S.; Pandelidis, D. Theoretical study of the basic cycles for indirect evaporative air cooling. Int. J. Heat Mass Transf. 2015, 84, 974–989. [Google Scholar] [CrossRef]
- Pandelidis, D.; Anisimov, S.; Worek, W.M. Comparison study of the counter-flow regenerative evaporative heat exchangers with numerical methods. Appl. Therm. Eng. 2015, 84, 211–224. [Google Scholar] [CrossRef]
- Miyazaki, T.; Akisawa, A.; Nikai, I. The cooling performance of a building integrated evaporative cooling system driven by solar energy. Energy Build. 2011, 43, 2211–2218. [Google Scholar] [CrossRef]
- Anisimov, S.; Jedlikowski, A. An influence of surface cross-flow plate–fin heat exchangers on efficiency of heat recovery units used in ventilation and air conditioning systems. In Proceedings of the XIIth International Scientific Conference on Quality of Indoor Air and Environment, Haifa, Israel, 23 March–3 April 2013; pp. 141–147. [Google Scholar]
- Pandelidis, D.; Anisimov, S. Numerical analysis of the selected operational and geometrical aspects of the M-Cycle heat and mass exchanger. Energy Build. 2015, 87, 413–424. [Google Scholar] [CrossRef]
- Danielewicz, J. The ecological and economic effects of thermal upgrading of buildings—The case of selected hospitals in Poland. Pol. J. Environ. Stud. 2007, 16, 90–92. [Google Scholar]
- Anisimov, S.; Pandelidis, D.; Danielewicz, J. Numerical analysis of selected evaporative exchangers with the Maisotsenko Cycle. Energy Convers. Manag. 2014, 88, 426–441. [Google Scholar] [CrossRef]
- Hsu, S.T.; Lavan, Z.; Worek, W.M. Optimization of wet-surface heat exchangers. Energy 1989, 14, 757–770. [Google Scholar] [CrossRef]
- Lee, J.; Lee, D.-Y. Experimental study of a counter flow regenerative evaporative cooler with finned channels. Int. J. Heat Mass Transf. 2013, 65, 173–179. [Google Scholar] [CrossRef]
- Alizadeh, S. Performance of a solar liquid desiccant air conditioner—An experimental and theoretical approach. Sol. Energy 2008, 82, 563–572. [Google Scholar] [CrossRef]
- Miyazaki, T.; Nikai, I.; Akisawa, A. Simulation analysis of open cycle adsorption air conditioning system—Numeral modeling of a fixed bed dehumidification unit and the Maisotsenko cycle cooling unit. Int. J. Energy Clean Environ. 2011, 12, 341–354. [Google Scholar] [CrossRef]
- Anisimov, S.; Jedlikowski, A.; Pandelidis, D. Frost formation in the cross-flow plate heat exchanger for energy recovery. Int. J. Heat Mass Transf. 2015, 90, 201–217. [Google Scholar] [CrossRef]
- Duan, Z.; Changhong, Z.; Zhang, X.; Mustafa, M.; Zhao, X.; Alimohammadisagvand, B.; Hasan, A. Indirect evaporative cooling: Past, present and future potentials. Renew. Sustain. Energy Rev. 2012, 16, 6823–6850. [Google Scholar] [CrossRef]











| Problem | Assumption |
|---|---|
| Heat exchange with the surroundings | Assumed as negligible |
| Operation | Steady state |
| Airflow physical properties | Ideal and incompressible gas |
| Water rate consumption | Used for evaporation and for keeping the plate surface at a saturated state. Air flow heat capacity is much larger than that of the water |
| Driving force of mass transfer | Humidity ratio gradient (gradient of partial pressure of the water vapor) |
| Kinetic properties of air stream and water | Constant and assumed as equal to bulk average values |
| Other important assumptions | The temperature of the water film, the sensible heat transfer coefficient α and the Lewis factor depend on the operating conditions [5] |
| Input Data | Values | Unit |
|---|---|---|
| Inlet air temperature | 27–32 | °C |
| Inlet relative humidity of air | 40–60 | % |
| Inlet air flow | 0.2 | kg/s |
| W2/W1 | 0.3 | - |
| Air velocity in the dry channel | 1.0 | m/s |
| Air velocity in the wet channel | 0.6 | m/s |
| NTUdry channel | 11.6 | - |
| NTUwet channel | 22.0 | - |
| External size | 550 × 690 × 350 | mm |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandelidis, D.; Anisimov, S.; Drąg, P. Performance Comparison between Selected Evaporative Air Coolers. Energies 2017, 10, 577. https://doi.org/10.3390/en10040577
Pandelidis D, Anisimov S, Drąg P. Performance Comparison between Selected Evaporative Air Coolers. Energies. 2017; 10(4):577. https://doi.org/10.3390/en10040577
Chicago/Turabian StylePandelidis, Demis, Sergey Anisimov, and Paweł Drąg. 2017. "Performance Comparison between Selected Evaporative Air Coolers" Energies 10, no. 4: 577. https://doi.org/10.3390/en10040577
APA StylePandelidis, D., Anisimov, S., & Drąg, P. (2017). Performance Comparison between Selected Evaporative Air Coolers. Energies, 10(4), 577. https://doi.org/10.3390/en10040577





