Performance Predictions of Dry and Wet Vapors Ejectors Over Entire Operational Range
Abstract
:1. Introduction
2. Preliminaries
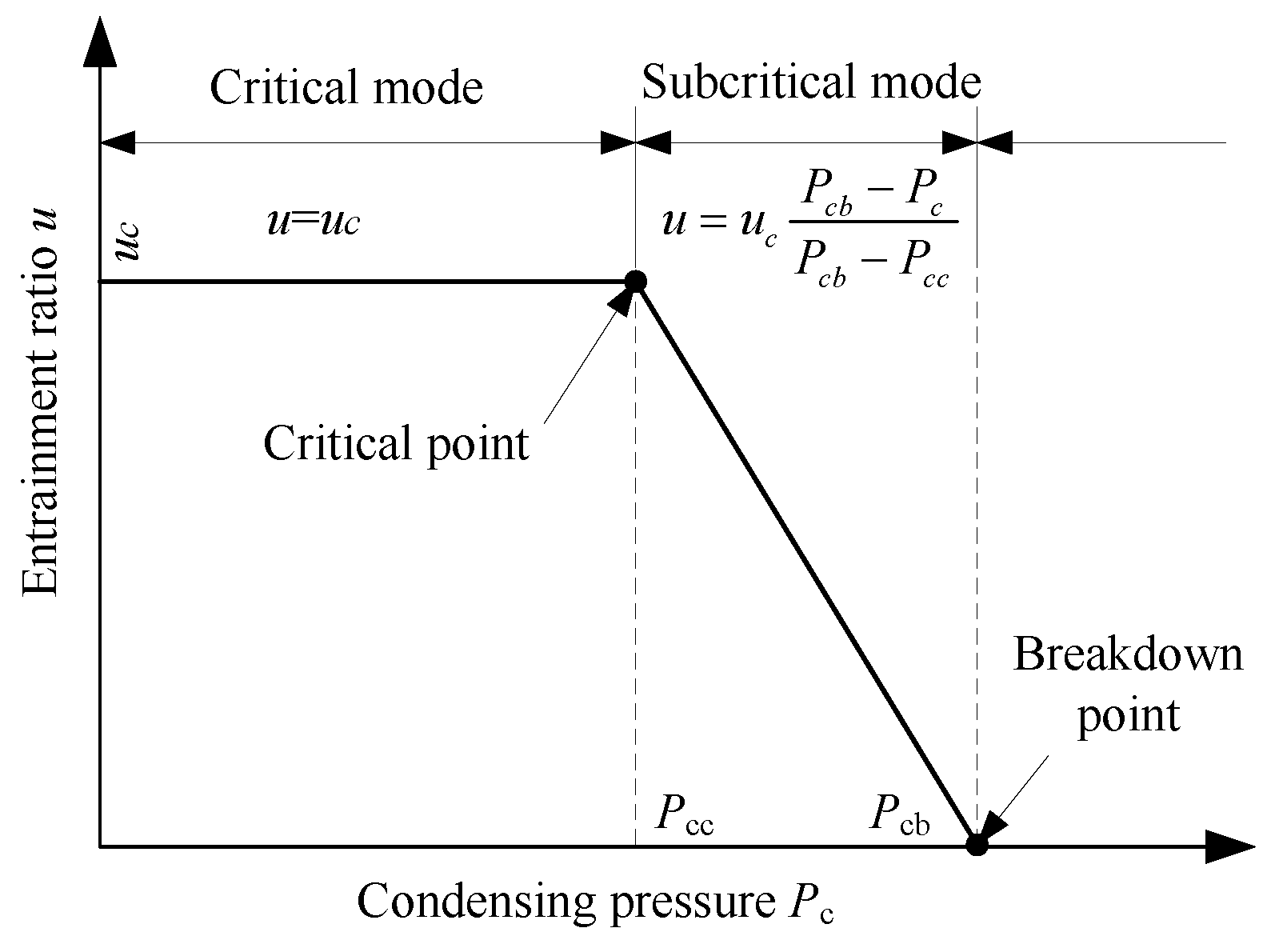
2.1. Operation Modes
- Critical mode: the primary flow and the secondary flow are choked at the nozzle throat and section y-y, respectively, and u is constant, as ;
- Subcritical mode: only the primary flow is choked at the nozzle throat and u decreases with as ;
- Back-flow mode: no choking phenomenon exists and as .
2.2. Assumptions
- The inner wall of the ejector is adiabatic and the flow is one dimensional and steady inside the ejector;
- The kinetic energy of the primary flow at the nozzle inlet, the secondary flow at the suction inlet and the mixing flow at the diffuser outlet are negligible;
- Constant-pressure mixing exists at critical point. After fanning out of the nozzle, the primary flow entrains but does not mix with the secondary flow before section y-y. The secondary flow is choked at section y-y and starts to mix with the primary flow with a uniform pressure, i.e., before the shock;
- Constant-pressure disturbing occurs at breakdown point. The primary and secondary flows do not mix before section x-x. Then, before the shock, the secondary flow disturbs the the primary flow by mixing in and out of the primary flow with a uniform pressure, i.e., .
3. Ejector Performance Modelling
3.1. Model for the Critical Point
3.1.1. Primary Flow from Inlet to Nozzle Throat
3.1.2. Primary Flow from Throat to Exit of Nozzle
3.1.3. Primary Flow from Nozzle Exit to Section y-y
3.1.4. Secondary Flow from Suction Inlet to Section y-y
3.1.5. Mixing and Shock in Constant Section
3.1.6. Diffuser
3.2. Model for the Breakdown Point
3.2.1. Primary Flow from Inlet to Nozzle Exit
3.2.2. Primary Flow from Nozzle Exit to Section x-x
3.2.3. Secondary flow at section x-x
3.2.4. Constant Pressure Disturbing
3.2.5. Diffuser
3.3. Speed of Sound of Wet Vapor
3.4. Model over Entire Operational Range
4. Experimental Verification
4.1. R134a Ejector
4.2. R141b Ejector
4.3. R245fa Ejector
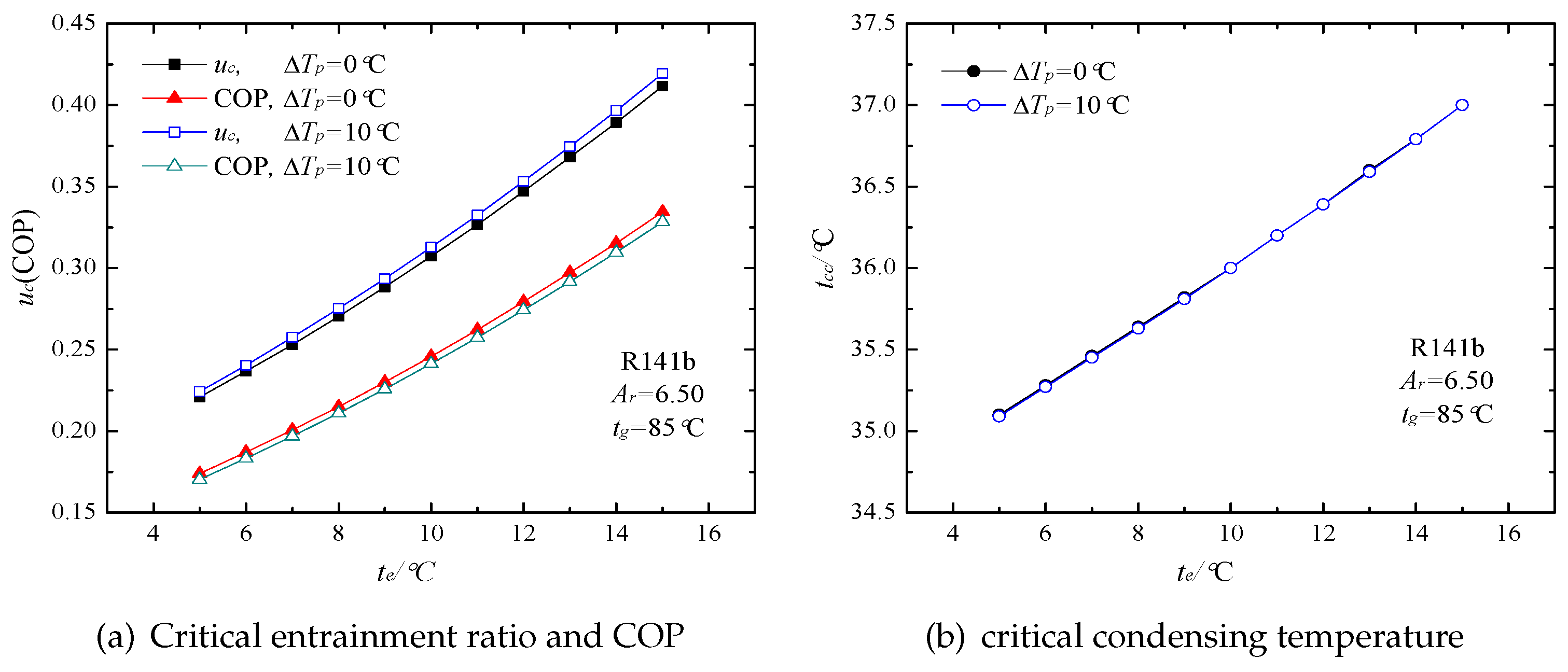
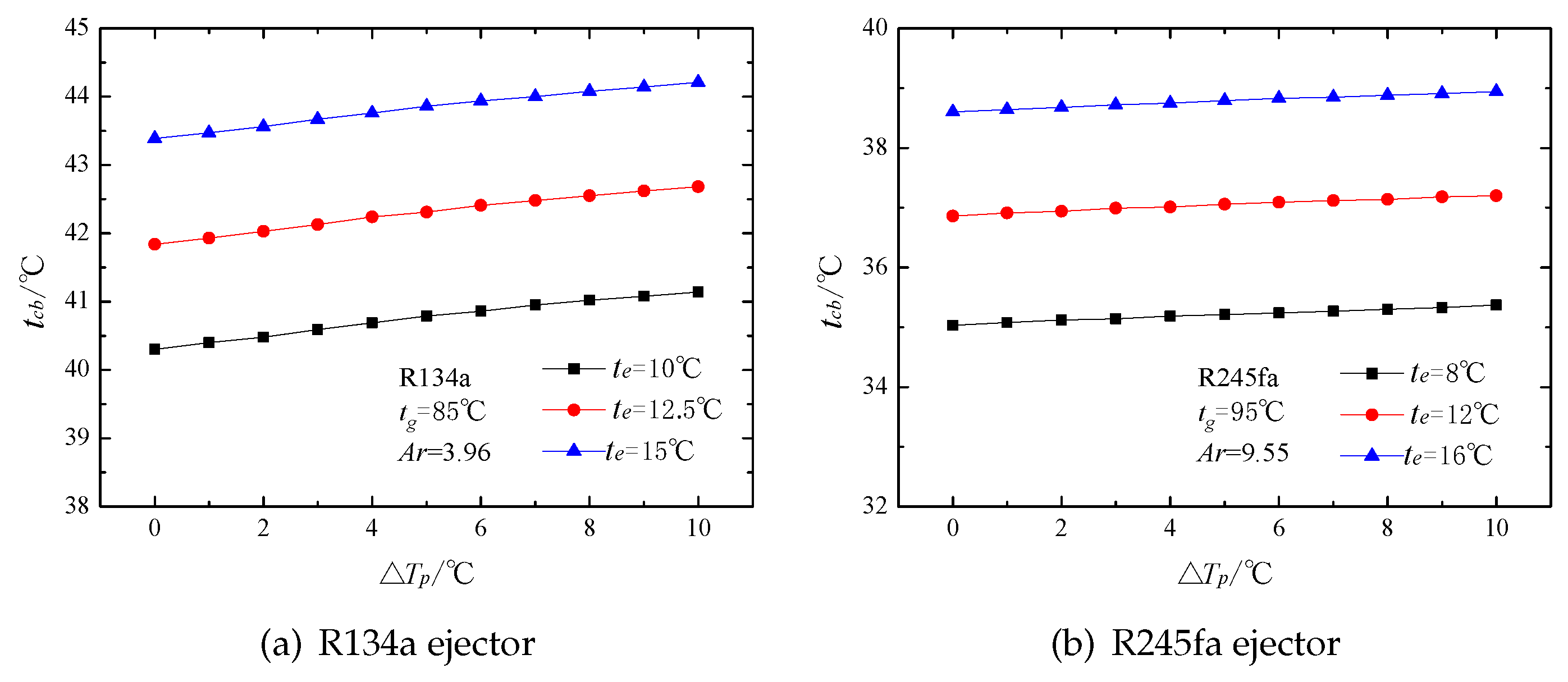
5. Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| COP | the coefficient of performance |
| CRS | compressor-based refrigeration system |
| EOC | the effect of the change (of efficiency) |
| ERS | ejector refrigeration system |
Nomenclature
| a | speed of sound (m/s) |
| A | area (m) |
| d | diameter (m) |
| h | enthalpy (kJ/kg) |
| K | bulk modulus of elasticity (N/m) |
| m | mass flow rate (kg/s) |
| P | pressure (MPa) |
| s | entropy (kJ/kg K) |
| t | temperature (°C) |
| T | temperature (K) |
| u | entrainment ratio |
| v | velocity (m/s) |
| void fraction of vapor | |
| strain | |
| efficiency relating to isentropic efficiency | |
| density (kg/m) | |
| stress (N/m) | |
| efficiency account for losses | |
| infinitesimal | |
| Subscripts | |
| b | breakdown |
| c | condensation, critical point |
| d | diffuser |
| e | expansion, evaporation |
| g | generation |
| l | liquid |
| m | mixing flow |
| p | primary flow |
| primary flow at inlet of ejector | |
| primary flow at nozzle exit | |
| r | ratio |
| s | secondary flow, isentropic process |
| secondary flow at inlet of ejector | |
| t | throat |
| v | vapor |
| y | position of the hypothetical throat |
References
- Shestopalov, K.; Huang, B.; Petrenko, V.; Volovyk, O. Investigation of an experimental ejector refrigeration machine operating with refrigerant R245fa at design and off-design working conditions. Part 1. Theoretical analysis. Int. J. Refrig. 2015, 55, 201–211. [Google Scholar] [CrossRef]
- Umair, M.; Akisawa, A.; Ueda, Y. Performance evaluation of a solar adsorption refrigeration system with a wing type compound parabolic concentrator. Energies 2014, 7, 1448–1466. [Google Scholar] [CrossRef]
- Akiloroaya, V.; Samali, B.; Fakhar, A.; Pishghadam, K. A review of different strategies for HVAC energy saving. Energy Convers. Manag. 2014, 77, 738–754. [Google Scholar] [CrossRef]
- Keenan, J.H.; Neumann, E.P. A simple air ejector. ASME J. Appl. Mech. 1942, 9, A75–A81. [Google Scholar]
- Keenan, J.H. An investigation of ejector design by analysis and experiment. J. Appl. Mech. 1950, 17, 299–309. [Google Scholar]
- Munday, J.T.; Bagster, D.F. A new ejector theory applied to steam jet refrigeration. Ind. Eng. Chem. Process. Des. Dev. 1977, 16, 442–449. [Google Scholar] [CrossRef]
- Eames, I.W.; Aphornratana, S.; Sun, D.W. The jet-pump cycle: A low cost refrigerator option powered by waste heat. Heat Recover. Syst. CHP 1995, 15, 711–721. [Google Scholar] [CrossRef]
- Huang, B.J.; Chang, J.M.; Wang, C.P.; Petrenko, V.A. A 1-D analysis of ejector performance. Int. J. Refrig. 1999, 22, 354–364. [Google Scholar] [CrossRef]
- Besagni, G.; Mereu, R.; Chiesa, P.; Inzoli, F. An integrated lumped parameter-CFD approach for off-design ejector performance evaluation. Energy Convers. Manag. 2015, 105, 697–715. [Google Scholar] [CrossRef]
- Khennich, M.; Sorin, M.; Galanis, N. Exergy flows inside a one phase ejector for refrigeration Systems. Energies 2016, 9, 212. [Google Scholar] [CrossRef]
- Chen, W.; Shi, C.; Zhang, S.; Chen, H.; Chong, D.; Yan, J. Theoretical analysis of ejector refrigeration system performance under overall modes. Appl. Energy 2017, 185, 2074–2084. [Google Scholar] [CrossRef]
- Lear, W.E.; Parker, G.M.; Sherif, S.A. Analysis of two-phase ejectors with Fabri choking. Arch. Proc. Inst. Mech. Eng. C-J. Mech. 2002, 216, 607–621. [Google Scholar] [CrossRef]
- Cardemil Cardemil, J.M.; Colle, S. A general model for evaluation of vapor ejectors performance for application in refrigeration. Energy Convers. Manag. 2012, 64, 79–86. [Google Scholar] [CrossRef]
- Chen, Y.M.; Sun, C.Y. Experimental study of the performance characteristics of a steam-ejector refrigeration system. Energy Convers. Manag. 1997, 15, 384–394. [Google Scholar] [CrossRef]
- Xu, X.; Chen, G.; Tang, L.; Zhu, Z.; Liu, S. Experimental evaluation of the effect of an internal heat exchanger on a transcritical CO2 ejector system. J. Zhejiang Univ.-Sci. A 2011, 12, 146–153. [Google Scholar] [CrossRef]
- Chen, W.; Liu, M.; Chong, D.; Yan, J.; Little, A.B.; Bartosiewicz, Y. A 1D model to predict ejector performance at critical and sub-critical operational regimes. Appl. Therm. Eng. 2013, 36, 1750–1761. [Google Scholar] [CrossRef]
- Li, F.; Tian, Q.; Wu, C.; Wang, X.; Lee, J.M. Ejector performance prediction at critical and subcritical operational modes. Appl. Therm. Eng. 2017, 115, 444–454. [Google Scholar] [CrossRef]
- Li, F.; Wu, C.; Wang, X.; Tian, Q.; Teo, K.L. Sparsity-enhanced optimization for ejector performance prediction. Energy 2016, 113, 25–34. [Google Scholar] [CrossRef]
- Chen, S.L.; Yen, J.Y.; Huang, M.C. Experimental investigation of ejector performance based upon different refrigerants. ASHRAE Trans. 1998, 104, 153–160. [Google Scholar]
- Lemmon, E.; Huber, M.; McLinden, M. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, version 9.1; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Anderson, J. Modern Compressible Flow, 2nd ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Ameur, K.; Aidoun, Z.; Ouzzane, M. Modeling and numerical approach for the design and operation of two-phase ejectors. Appl. Therm. Eng. 2016, 109, 809–818. [Google Scholar] [CrossRef]
- Wood, A.B. A Textbook of Sound, 3rd ed.; Neill and Co. Ltd: London, UK, 1957. [Google Scholar]
- Tao, B.; Chen, D.H.; Che, C.X.; Wang, X.M. Study on the sound velocity in a gas-liquid flow. J. Appl. Acoust. 2015, 34, 373–376. [Google Scholar]
- Henry, R.E.; Grolmes, M.A.; Fauske, H.K. Pressure-Pulse Propagation in Two-Phase One- and Two-Component Mixtures; ANL: Chicago, IL, USA, 1971. [Google Scholar]
- Besagni, G.; Mereu, R.; Leo, G.D.; Inzoli, F. A study of working fluids for heat driven ejector refrigeration using lumped parameter models. Int. J. Refrig. 2015, 58, 154–171. [Google Scholar] [CrossRef] [Green Version]
- Varga, S.; Oliveira, A.C.; Diaconu, B. Numerical assessment of steam ejector efficiencies using CFD. Int. J. Refrig. 2009, 32, 1203–1211. [Google Scholar] [CrossRef]
- Li, F. Study on Ejectors and a Solar Ejector-Refrigeration System with Dual Energy-Storage Tanks and Mulitiple Ejectors. Ph.D. Thesis, Taiyuan Univesity Technology, Taiyuan, China, 2016. [Google Scholar]


















| Refrigerant | Molecular Mass | Boiling Point | Critical Temperature | Critical Pressure | Safety Group | ODP | GWP |
|---|---|---|---|---|---|---|---|
| (°C) | (°C) | (MPa) | |||||
| R134a | 102.03 | −26.1 | 101.1 | 4.06 | A1 | 0 | 1370 |
| R141b | 116.95 | 32.0 | 204.4 | 4.21 | A2 | 0.12 | 717 |
| R245fa | 134.05 | 15.1 | 154.0 | 3.65 | B1 | 0 | 1050 |
| A | Theory | Experiment | Errors | Theory | Experiment | Errors | |||
|---|---|---|---|---|---|---|---|---|---|
| (°C) | (°C) | (MPa) | (MPa) | (%) | (%) | (m/s) | |||
| AA Ejector | |||||||||
| 2.77 | 75 | 10 | 0.8969 | 0.885 | 1.35 | 0.0844 | 0.0836 | 1.01 | 137.2 |
| 2.77 | 75 | 12.5 | 0.9203 | 0.8974 | 2.55 | 0.1149 | 0.1224 | −6.14 | 137.0 |
| 2.77 | 75 | 15 | 0.9426 | 0.9351 | 0.80 | 0.1472 | 0.1561 | −5.72 | 136.7 |
| BB Ejector | |||||||||
| 3.32 | 75 | 10 | 0.8461 | 0.8553 | −1.08 | 0.1929 | 0.1933 | −0.19 | 136.9 |
| 3.32 | 75 | 12.5 | 0.8685 | 0.8655 | 0.35 | 0.2325 | 0.2209 | 5.24 | 136.7 |
| 3.32 | 75 | 15 | 0.8906 | 0.8808 | 1.11 | 0.2749 | 0.257 | 6.97 | 136.5 |
| 3.32 | 80 | 10 | 0.9071 | 0.9278 | −2.23 | 0.1402 | 0.1411 | −0.65 | 134.8 |
| 3.32 | 80 | 12.5 | 0.9324 | 0.9354 | −0.32 | 0.1749 | 0.1757 | −0.45 | 134.5 |
| 3.32 | 80 | 15 | 0.9568 | 0.9598 | −0.31 | 0.2118 | 0.2055 | 3.08 | 134.2 |
| 3.32 | 85 | 12.5 | 0.9964 | 1.0049 | −0.85 | 0.1235 | 0.1172 | 5.35 | 131.9 |
| 3.32 | 85 | 15 | 1.024 | 1.035 | −1.06 | 0.1562 | 0.1532 | 1.97 | 131.6 |
| BA Ejector | |||||||||
| 3.96 | 75 | 10 | 0.7984 | 0.7994 | −0.12 | 0.3195 | 0.3248 | −1.64 | 136.6 |
| 3.96 | 75 | 12.5 | 0.8204 | 0.8074 | 1.62 | 0.3694 | 0.3744 | −1.32 | 136.4 |
| 3.96 | 75 | 15 | 0.8431 | 0.8129 | 3.71 | 0.4237 | 0.4446 | −4.71 | 136.3 |
| 3.96 | 80 | 10 | 0.8555 | 0.8649 | −1.08 | 0.2522 | 0.2635 | −4.29 | 134.4 |
| 3.96 | 80 | 12.5 | 0.8797 | 0.8818 | −0.23 | 0.2966 | 0.3177 | −6.63 | 134.2 |
| 3.96 | 80 | 15 | 0.9039 | 0.8855 | 2.07 | 0.3442 | 0.3546 | −2.94 | 134.0 |
| 3.96 | 85 | 10 | 0.9134 | 0.9453 | −3.37 | 0.193 | 0.206 | −6.31 | 131.8 |
| 3.96 | 85 | 12.5 | 0.9401 | 0.9647 | −2.55 | 0.2317 | 0.2381 | −2.68 | 131.5 |
| 3.96 | 85 | 15 | 0.9667 | 0.9648 | 0.19 | 0.2739 | 0.2782 | −1.53 | 131.3 |
| Experiment | Present | Errors | Experiment | Huang [8] | Present | Huang [8] | Present | |||
|---|---|---|---|---|---|---|---|---|---|---|
| (°C) | (°C) | (MPa) | (MPa) | (%) | Error (%) | Error (%) | (m/s) | |||
| AA Ejector | ||||||||||
| 95 | 8 | 0.1424 | 0.1404 | −1.39 | 0.1859 | 0.1554 | 0.1769 | −16.43 | −4.83 | 154.9 |
| 90 | 8 | 0.1287 | 0.1271 | −1.25 | 0.2246 | 0.2156 | 0.2169 | −3.99 | −3.43 | 154.4 |
| 84 | 8 | 0.1147 | 0.1124 | −2.03 | 0.288 | 0.288 | 0.2745 | 0.23 | −4.68 | 153.8 |
| 78 | 8 | 0.1027 | 0.0991 | −3.53 | 0.3257 | 0.3525 | 0.3442 | 8.24 | 5.68 | 153.2 |
| 95 | 12 | 0.1442 | 0.1438 | −0.27 | 0.235 | 0.2573 | 0.234 | 9.49 | −0.44 | 154.4 |
| 90 | 12 | 0.1312 | 0.1303 | −0.72 | 0.2946 | 0.3257 | 0.2824 | 10.54 | −4.14 | 154.0 |
| 84 | 12 | 0.1167 | 0.1154 | −1.15 | 0.3398 | 0.4147 | 0.352 | 22.04 | 3.59 | 153.5 |
| AB Ejector | ||||||||||
| 90 | 8 | 0.1229 | 0.1203 | −2.12 | 0.2718 | 0.2093 | 0.2551 | −22.99 | −6.13 | 154.2 |
| 84 | 8 | 0.1071 | 0.1065 | −0.59 | 0.3117 | 0.3042 | 0.319 | −2.39 | 2.33 | 153.6 |
| 78 | 8 | 0.0912 | 0.0939 | 3.00 | 0.3922 | 0.4422 | 0.3956 | 12.74 | 0.86 | 153.0 |
| AG Ejector | ||||||||||
| 95 | 8 | 0.1275 | 0.1242 | −2.58 | 0.2552 | 0.2144 | 0.2573 | −15.98 | 0.80 | 154.4 |
| 90 | 8 | 0.1196 | 0.1125 | −5.97 | 0.304 | 0.2395 | 0.3071 | −21.22 | 1.02 | 154.0 |
| 84 | 8 | 0.102 | 0.0996 | −2.35 | 0.3883 | 0.3704 | 0.3783 | −4.61 | −2.56 | 153.4 |
| 78 | 8 | 0.0897 | 0.088 | −1.88 | 0.4393 | 0.4609 | 0.464 | 4.93 | 5.62 | 152.9 |
| 95 | 12 | 0.1279 | 0.1273 | −0.46 | 0.3503 | 0.3434 | 0.3291 | −1.97 | −6.06 | 154.0 |
| 90 | 12 | 0.1167 | 0.1154 | −1.08 | 0.4034 | 0.4142 | 0.3887 | 2.67 | −3.65 | 153.6 |
| 84 | 12 | 0.1023 | 0.1025 | 0.21 | 0.479 | 0.4769 | 0.4729 | 12.09 | −1.27 | 153.2 |
| 78 | 12 | 0.0901 | 0.0908 | 0.82 | 0.6132 | 0.6659 | 0.5733 | 8.60 | −6.51 | 152.6 |
| AC Ejector | ||||||||||
| 95 | 8 | 0.1179 | 0.1185 | 0.49 | 0.2814 | 0.2983 | 0.292 | 6.01 | 3.75 | 154.2 |
| 90 | 8 | 0.1079 | 0.1073 | −0.53 | 0.3488 | 0.3552 | 0.3461 | 1.84 | −0.76 | 153.8 |
| 84 | 8 | 0.095 | 0.0952 | 0.17 | 0.4241 | 0.4605 | 0.4233 | 8.58 | −0.19 | 153.3 |
| 78 | 8 | 0.0816 | 0.0841 | 3.08 | 0.4889 | 0.5966 | 0.5144 | 22.03 | 5.21 | 152.8 |
| AD Ejector | ||||||||||
| 95 | 8 | 0.1071 | 0.1086 | 1.43 | 0.3457 | 0.3476 | 0.3625 | 0.56 | 4.87 | 153.9 |
| 90 | 8 | 0.0988 | 0.0985 | −0.27 | 0.4446 | 0.4178 | 0.4245 | −6.02 | −4.52 | 153.6 |
| 84 | 8 | 0.0856 | 0.0875 | 2.20 | 0.5387 | 0.5215 | 0.5126 | −3.19 | −4.84 | 153.1 |
| 78 | 8 | 0.0726 | 0.0775 | 6.73 | 0.6227 | 0.6944 | 0.6169 | 11.51 | −0.94 | 152.6 |
| 95 | 12 | 0.1107 | 0.1116 | 0.84 | 0.4541 | 0.4708 | 0.4527 | 3.67 | −0.31 | 153.6 |
| 90 | 12 | 0.1008 | 0.1015 | 0.65 | 0.5422 | 0.5573 | 0.5255 | 2.78 | −3.07 | 153.3 |
| 84 | 12 | 0.089 | 0.0903 | 1.48 | 0.635 | 0.6906 | 0.6283 | 8.75 | −1.05 | 152.8 |
| 78 | 12 | 0.0772 | 0.0803 | 3.97 | 0.7412 | 0.8626 | 0.7494 | 16.37 | 1.11 | 152.4 |
| EG Ejector | ||||||||||
| 95 | 8 | 0.1377 | 0.1366 | −0.83 | 0.2043 | 0.1919 | 0.1991 | −6.06 | −2.52 | 154.8 |
| EC Ejector | ||||||||||
| 95 | 8 | 0.1283 | 0.1303 | 1.54 | 0.2273 | 0.2078 | 0.2294 | −8.57 | 0.91 | 154.6 |
| 95 | 12 | 0.1304 | 0.1334 | 2.33 | 0.304 | 0.3235 | 0.296 | 6.41 | −2.64 | 154.1 |
| ED Ejector | ||||||||||
| 95 | 8 | 0.1212 | 0.1194 | −1.45 | 0.2902 | 0.2658 | 0.2911 | −8.39 | 0.32 | 154.2 |
| EE Ejector | ||||||||||
| 95 | 8 | 0.1095 | 0.1111 | 1.44 | 0.3505 | 0.3253 | 0.3482 | −7.20 | −0.67 | 154.0 |
| 95 | 12 | 0.1095 | 0.1141 | 4.20 | 0.4048 | 0.4894 | 0.436 | 10.55 | 7.70 | 153.6 |
| EF Ejector | ||||||||||
| 95 | 8 | 0.1047 | 0.106 | 1.24 | 0.3937 | 0.3774 | 0.3892 | −4.13 | −1.15 | 153.8 |
| 95 | 12 | 0.1051 | 0.109 | 3.68 | 0.4989 | 0.5482 | 0.4835 | 9.89 | −3.09 | 153.5 |
| EH Ejector | ||||||||||
| 95 | 8 | 0.0981 | 0.1004 | 2.37 | 0.4377 | 0.4627 | 0.4401 | 5.70 | 0.55 | 153.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Chang, Z.; Tian, Q.; Wu, C.; Wang, X. Performance Predictions of Dry and Wet Vapors Ejectors Over Entire Operational Range. Energies 2017, 10, 1012. https://doi.org/10.3390/en10071012
Li F, Chang Z, Tian Q, Wu C, Wang X. Performance Predictions of Dry and Wet Vapors Ejectors Over Entire Operational Range. Energies. 2017; 10(7):1012. https://doi.org/10.3390/en10071012
Chicago/Turabian StyleLi, Fenglei, Zhao Chang, Qi Tian, Changzhi Wu, and Xiangyu Wang. 2017. "Performance Predictions of Dry and Wet Vapors Ejectors Over Entire Operational Range" Energies 10, no. 7: 1012. https://doi.org/10.3390/en10071012
APA StyleLi, F., Chang, Z., Tian, Q., Wu, C., & Wang, X. (2017). Performance Predictions of Dry and Wet Vapors Ejectors Over Entire Operational Range. Energies, 10(7), 1012. https://doi.org/10.3390/en10071012




