Study on Electrode Potential of Zinc Nickel Single-Flow Battery during Charge
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Working Principle of a ZNB
2.2. Concentration of Active Substances in the Battery
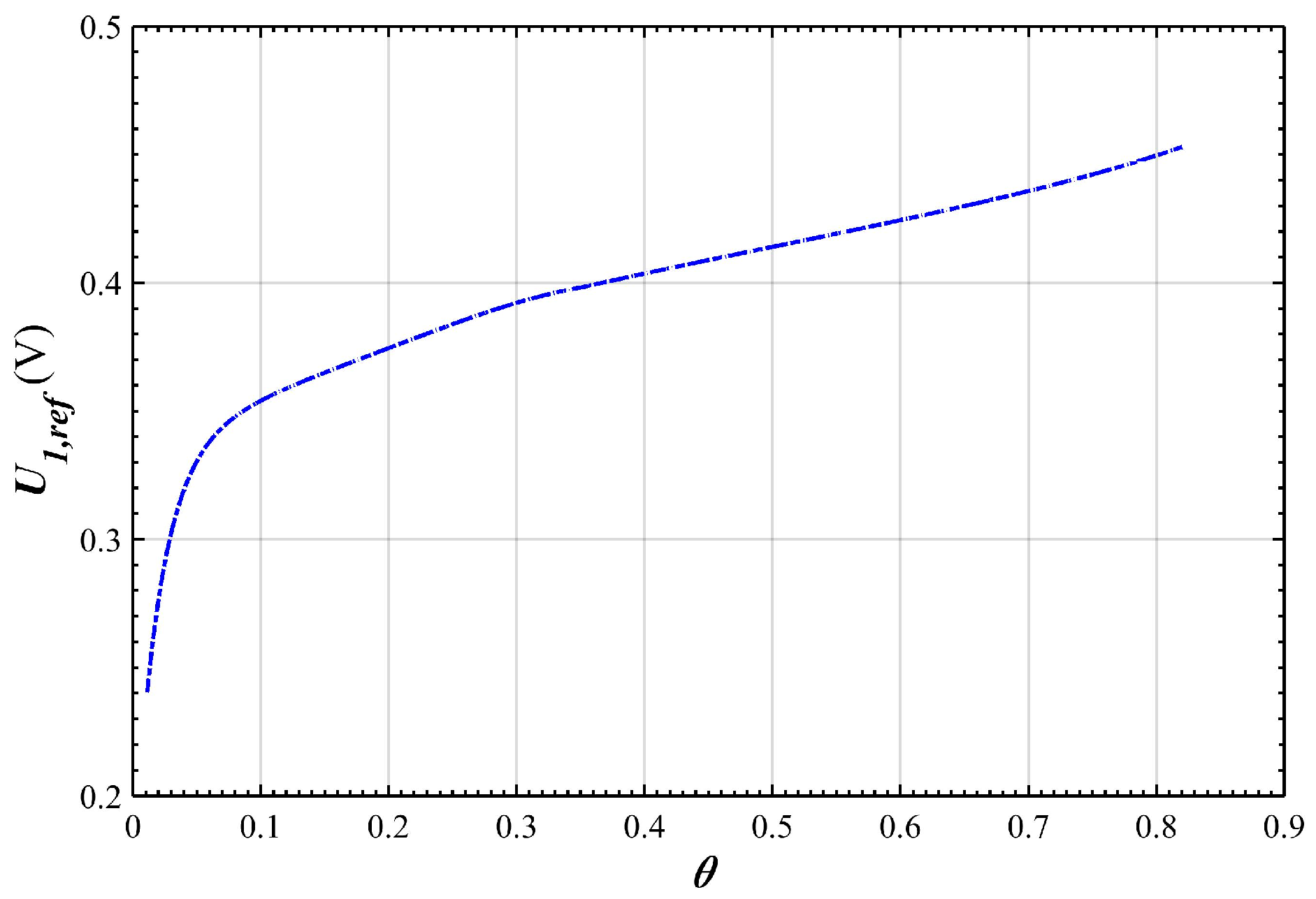
2.3. Over-Potential and Equilibrium-Potential of the Positive Electrode
2.4. Over-Potential and Equilibrium-Potential of the Negative Electrode
2.5. Battery Stack Voltage
3. Results and Discussion
Simulation Results and Analysis
4. Conclusions
- The simulated relative error of the stack voltage was kept below 0.62% of the ZNB under the 100 A charging condition, which indicates that the established stack voltage model accurately characterized the dynamic characteristics of the ZNB stack voltage during charging.
- In the stable charging stage, the over-potential of the positive electrode was rapidly reduced from 0.03 V to 0.01 V, and then stabilized at 0.007 V. This was mainly because the charge transfer rate of the electrode is lower than the mass transfer rate before charging stabilizes.
- In the stable charging stage, the over-potential of negative electrode tended to increase linearly from 1.9 mV to 4 mV, indicating that the polarization of the negative electrode gradually increased with the charging process, and that its change was very small with respect to the over-potential of the positive electrode.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cho, J.; Jeong, S.; Kim, Y. Commercial and research battery technologies for electrical energy storage applications. Prog. Energy Combust. 2015, 48, 84–101. [Google Scholar] [CrossRef]
- Skyllas-Kazacos, M.; Chakrabarti, M.H.; Hajimolana, S.A.; Mjalli, F.S.; Saleem, M. Progress in flow battery research and development. J. Electrochem. Soc. 2011, 158, R55. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, L.; Yang, Y.-S.; Wen, Y.-H.; Cao, G.-P.; Wang, X.-D. Preliminary study of single flow zinc-nickel battery. Electrochem. Commun. 2007, 9, 2639–2642. [Google Scholar] [CrossRef]
- Wen, Y.; Cheng, J.; Zhang, L.; Yan, X.; Yang, Y. The inhibition of the spongy electrocrystallization of zinc from doped flowing alkaline zincate solutions. J. Power Sources 2009, 193, 890–894. [Google Scholar] [CrossRef]
- Gu, W.B.; Wang, G.Q.; Wang, C.Y. Modeling the overcharge process of VRLA batteries. J. Power Sources 2002, 108, 174–184. [Google Scholar] [CrossRef]
- Wang, C.Y.; Srinivasan, V. Computational battery dynamics (CBD)—Electrochemical/thermal coupled modeling and multi-scale modeling. J. Power Sources 2002, 110, 364–376. [Google Scholar] [CrossRef]
- Al-Fetlawi, H.; Shah, A.A.; Walsh, F.C. Modelling the effects of oxygen evolution in the all-vanadium redox flow battery. Electrochim. Acta 2010, 55, 3192–3205. [Google Scholar] [CrossRef]
- Shah, A.A.; Al-Fetlawi, H.; Walsh, F.C. Dynamic modelling of hydrogen evolution effects in the all-vanadium redox flow battery. Electrochim. Acta 2010, 55, 1125–1139. [Google Scholar] [CrossRef]
- Xiao, M.; Wang, Y.; Yao, S.; Song, Y.; Cheng, J.; He, K. Analysis of internal reaction and mass transfer of zinc-nickel single flow battery. J. Renew. Sustain. Energy 2016, 8, 064102. [Google Scholar] [CrossRef]
- Yao, S.; Liao, P.; Xiao, M.; Cheng, J.; He, K. Modeling and simulation of the zinc-nickel single flow batteries based on MATLAB/Simulink. AIP Adv. 2016, 6, 125302. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, H.; Lai, Q.; Li, X.; Shi, D. Performance gains in single flow zinc–nickel batteries through novel cell configuration. Electrochim. Acta 2013, 105, 618–621. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, H.; Lai, Q.; Li, X.; Shi, D.; Zhang, L. A high power density single flow zinc–nickel battery with three-dimensional porous negative electrode. J. Power Sources 2013, 241, 196–202. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, H.; Lai, Q.; Li, X.; Zheng, Q.; Xi, X.; Ding, C. Effect of temperature on the performances and in situ polarization analysis of zinc–nickel single flow batteries. J. Power Sources 2014, 249, 435–439. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, H.; Zhao, P.; Yi, B. A comparative study of carbon felt and activated carbon based electrodes for sodium polysulfide/bromine redox flow battery. Electrochim. Acta 2006, 51, 6304–6312. [Google Scholar] [CrossRef]
- Fan, D.; White, R.E. A mathematical model of a sealed nickel-cadmium battery. J. Electrochem. Soc. 1991, 138, 17–25. [Google Scholar] [CrossRef]
- Mao, Z.; White, R.E. A mathematical model of the self-discharge of a Ni-H2 battery. J. Electrochem. Soc. 1991, 138, 3354–3361. [Google Scholar] [CrossRef]
- Mao, Z.; Vidts, P.D.; White, R.E. Theoretical analysis of the discharge performance of a NiOOH/H2 cell. J. Electrochem. Soc. 1994, 141, 54–64. [Google Scholar] [CrossRef]
- Paxton, B.; Newman, J. Modeling of nickel/metal hydride batteries. J. Electrochem. Soc. 1997, 144, 3818–3831. [Google Scholar] [CrossRef]
- Srinivasan, V.; Weidner, J.W.; White, R.E. Mathematical models of the nickel hydroxide active material. J. Solid State Eletrochem. 2000, 4, 367–382. [Google Scholar] [CrossRef]
- Pan, Y.H.; Srinivasan, V.; Wang, C.Y. An experimental and modeling study of isothermal charge/discharge behavior of commercial Ni-MH cells. J. Power Sources 2002, 112, 298–306. [Google Scholar] [CrossRef]
- Bourgault, P.L.; Conway, B.E. The electrochemical behavior of the nickel oxide electrode Part II: Quasi-equilibrium behavior. Can. J. Chem. 1960, 38, 1557–1575. [Google Scholar] [CrossRef]
- Mao, Z.; White, R.E. Mathematical modeling of a primary zinc/air battery. J. Electrochem. Soc. 1992, 139, 1105–1114. [Google Scholar] [CrossRef]
- Liu, X.; Xie, Z.; Cheng, J.; Zhao, P.; Gu, W. Mathematical modeling of the nickel electrode for the single flow zinc-nickel battery. In Proceedings of the World Non-Grid-Connected Wind Power and Energy Conference, Nanjing, China, 24–26 September 2009. [Google Scholar]








| Parameter | Symbol | Value |
|---|---|---|
| Current | I | 100 A |
| Faraday constant | F | 96,485 C/mol |
| Effective mass transfer area | A | 3 dm2 |
| Total volume of electrolyte | V | 8.5 L |
| Volume of the runner | V | 5.3 L |
| Flow rate | Q | 10 L/s |
| Initial concentration of hydroxide ions | 8.5 mol/L | |
| Initial concentration of zincate ions | 1 mol/L |
| Electrode | Parameter | Value | Unit | Source | |
|---|---|---|---|---|---|
| Positive electrode | ase | Specific electroactive surface area | 3864 | cm2/cm3 | [23] |
| iNi,ref | Reference exchange current density of nickel reaction | 1.04 × 10−4 | A/cm2 | [23] | |
| Anodic transfer coefficient for the nickel reaction | 0.5 | [23] | |||
| Maximum concentration of proton | 35.3 | mol/dm3 | ρavg/ | ||
| Reference concentration of hydroxide ion | 7 | mol/dm3 | [23] | ||
| Negative electrode | iZn,ref | Reference exchange current density of zinc reaction | 0.03 | A/cm2 | chosen |
| Anodic transfer coefficient for the zinc reaction | 0.5 | - | chosen | ||
| Reference concentration of Zn(OH)42− | 0.5 | mol/dm3 | chosen | ||
| U0 | Initial equilibrium potential of negative electrode | −1.215 | V | [3] | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, S.; Liao, P.; Xiao, M.; Cheng, J.; Cai, W. Study on Electrode Potential of Zinc Nickel Single-Flow Battery during Charge. Energies 2017, 10, 1101. https://doi.org/10.3390/en10081101
Yao S, Liao P, Xiao M, Cheng J, Cai W. Study on Electrode Potential of Zinc Nickel Single-Flow Battery during Charge. Energies. 2017; 10(8):1101. https://doi.org/10.3390/en10081101
Chicago/Turabian StyleYao, Shouguang, Peng Liao, Min Xiao, Jie Cheng, and Wenwen Cai. 2017. "Study on Electrode Potential of Zinc Nickel Single-Flow Battery during Charge" Energies 10, no. 8: 1101. https://doi.org/10.3390/en10081101
APA StyleYao, S., Liao, P., Xiao, M., Cheng, J., & Cai, W. (2017). Study on Electrode Potential of Zinc Nickel Single-Flow Battery during Charge. Energies, 10(8), 1101. https://doi.org/10.3390/en10081101




