Off-Design Performances of Subcritical and Supercritical Organic Rankine Cycles in Geothermal Power Systems under an Optimal Control Strategy
Abstract
:1. Introduction
2. ORC System
- 1–2: The high pressure working fluid vapor expands to do work in the turbine.
- 2–5: The exhausted vapor is condensed by cooling water in the condenser.
- 5–6: The subcooled liquid is pumped to a high pressure in the refrigerant pump.
- 6–1: The high pressure liquid is heated into vapor by geothermal water in the evaporator (vapor generator).
2.1. Thermodynamic Modeling
2.2. Thermodynamic Parameter Optimization on the Design Condition
- (1)
- The system is supposed in steady state.
- (2)
- The pressure drops in heat exchangers and pipelines are ignored.
- (3)
- The vapor quality of turbine outlet is restricted to not less than 1 to avoid the droplet wear phenomenon.
3. System Components Modeling and Design
3.1. Radial Inflow Turbine
3.2. Heat Exchangers
3.3. Pump
4. Results and Discussion
4.1. Off-Design Performance Optimization
4.2. Various Geothermal Water Mass Flow Rates
4.3. Various Geothermal Water Inlet Temperatures
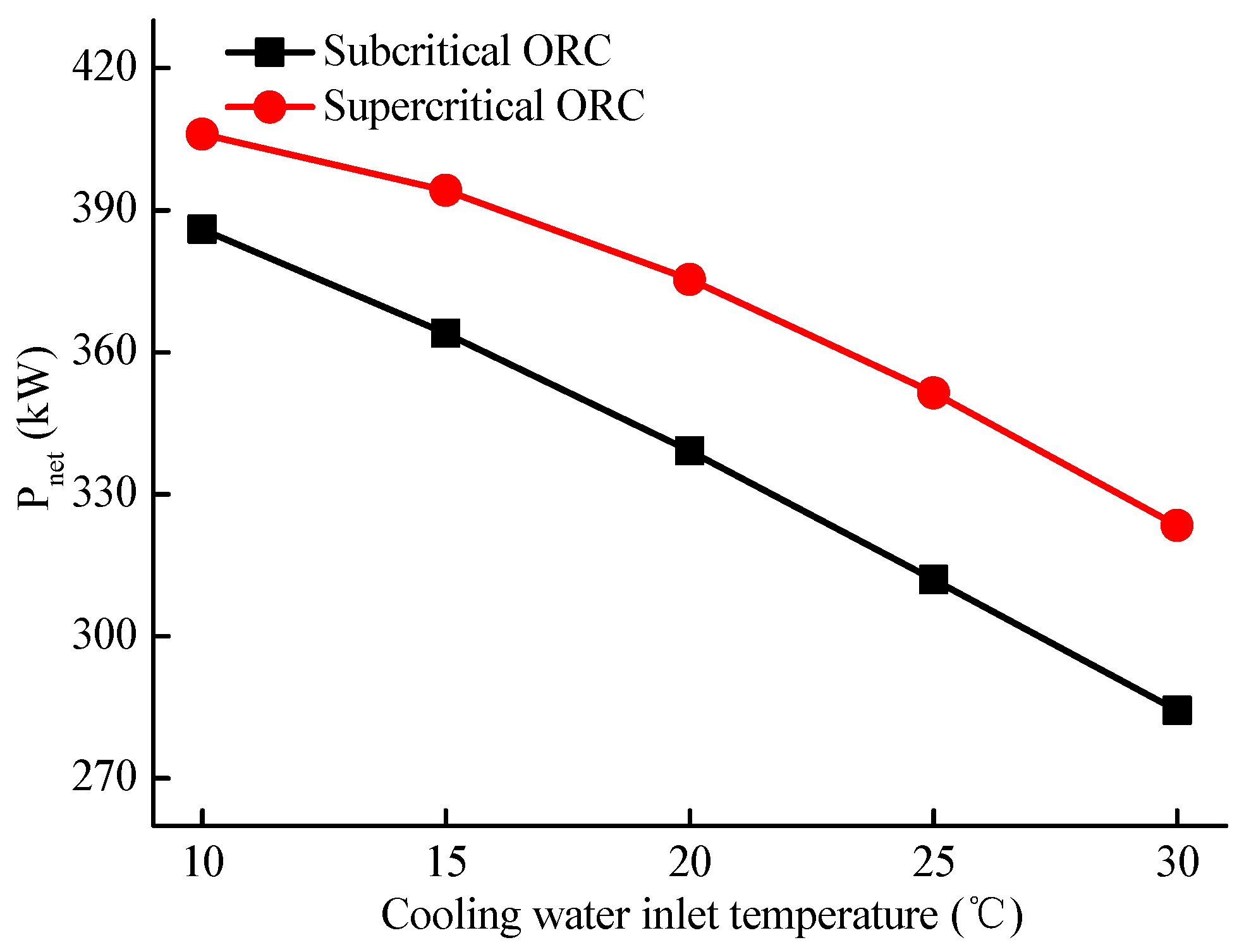
4.4. Various Cooling Water Inlet Temperatures
4.5. Various Geothermal Water Inlet Temperatures and Cooling Water Inlet Temperatures
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| A | area | [m2] |
| Bd | Bond number | [-] |
| Bo | Boiling number | [-] |
| b | blade height | [mm] |
| c | absolute velocity | [m/s] |
| cd | channel distance | [mm] |
| cp | constant pressure specific heat | [kJ/(kg-K)] |
| D | hydraulic diameter | [m] |
| g | gravitational acceleration | [m/s2] |
| G | mass velocity | [kg/s] |
| h | enthalpy | [J/kg] |
| H | pump head | [m] |
| K | loss coefficient | [-] |
| L | loss | [J/kg] |
| M | loss model multiplier | [-] |
| m | mass flow rate | [kg/s] |
| N | rotational speed | [rpm] |
| n | incidence angle | [°] |
| P | power | [kW] |
| pressure | [kPa] | |
| Pl | plate length | [m] |
| Pr | Prandtl number | [-] |
| Pt | Plate thickness | [mm] |
| Pw | Plate width | [m] |
| Q | heat transfer rate | [kW] |
| q | heat flux | [w/m2] |
| q | volumetric flow rate | [m3/s] |
| r | radius | [mm] |
| T | temperature | [°C] |
| U/C0 | velocity ratio | [-] |
| u | circular velocity | [m/s] |
| w | relative velocity | [m/s] |
| x | vapor quality; | [-] |
| Z | blade number | [-] |
| α | absolute fluid velocity angle | [°] |
| β | relative fluid velocity angle | [°] |
| γ | latent heat of vaporization | [J/kg] |
| δ | clearance | [m] |
| η | efficiency | [%] |
| θ | chevron angle | [°] |
| λ | thermal conductivity | [W/m-K] |
| μ | viscosity | [N-s/m2] |
| ρ | density | [kg/m3] |
Subscripts
| 1–8 | state points of ORCs |
| 01–04 | state points in turbine |
| b | bulk |
| cr | critical |
| cw | cooling water |
| de | design |
| df | disc friction |
| e | exit energy |
| eq | equivalent |
| g | gas |
| gw | geothermal water |
| i | incidence |
| in | inlet |
| l | liquid |
| m | mean |
| out | outlet |
| p | passage |
| RP | refrigerant pump |
| r | radial component |
| s | isentropic |
| u | tangential component |
| w | wall |
| wf | working fluid |
| WP | cooling water pump |
| st | stagnant |
References
- Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, H.; Tao, G.; Zhang, S.; Wang, H.; Tao, G. Performance comparison and parametric optimization of subcritical Organic Rankine Cycle (ORC) and transcritical power cycle system for low-temperature geothermal power generation. Appl. Energy 2011, 88, 2740–2754. [Google Scholar]
- Guo, C.; Du, X.; Goswami, D.Y.; Yang, L. Investigation on working fluids selection for organic rankine cycles with low-temperature heat sources. Int. J. Green Energy 2016, 13, 556–565. [Google Scholar] [CrossRef]
- Liu, C.; Gao, T.; Zhu, J.; Xu, J. Performance optimization and economic analysis of geothermal power generation by subcritical and supercritical Organic Rankine Cycles. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Sauret, E.; Rowlands, A.S. Candidate radial-inflow turbines and high-density working fluids for geothermal power systems. Energy 2011, 36, 4460–4467. [Google Scholar] [CrossRef]
- Pan, L.; Wang, H. Improved analysis of Organic Rankine Cycle based on radial flow turbine. Appl. Therm. Eng. 2013, 61, 606–615. [Google Scholar] [CrossRef]
- Baines, N.C. A meanline prediction method for radial turbine efficiency. In Proceedings of the International 6th Conference on Turbocharging and Air Management Systems, London, UK, 3–5 November 1998; Volume 11, pp. 45–56. [Google Scholar]
- Li, Y.; Ren, X.D. Investigation of the organic Rankine cycle (ORC) system and the radial-inflow turbine design. Appl. Therm. Eng. 2016, 96, 547–554. [Google Scholar] [CrossRef]
- Zheng, Y.; Hu, D.; Cao, Y.; Dai, Y. Preliminary design and off-design performance analysis of an Organic Rankine Cycle radial-inflow turbine based on mathematic method and CFD method. Appl. Therm. Eng. 2017, 112, 25–37. [Google Scholar] [CrossRef]
- Wang, J.; Wang, M.; Li, M.; Xia, J.; Dai, Y. Multi-objective optimization design of condenser in an organic Rankine cycle for low grade waste heat recovery using evolutionary algorithm. Int. Commun. Heat Mass Transf. 2013, 45, 47–54. [Google Scholar] [CrossRef]
- Calise, F.; Capuozzo, C.; Carotenuto, A.; Vanoli, L. Thermoeconomic analysis and off-design performance of an organic Rankine cycle powered by medium-temperature heat sources. Sol. Energy 2014, 103, 595–609. [Google Scholar] [CrossRef]
- Song, J.; Gu, C.W.; Ren, X. Parametric design and off-design analysis of organic Rankine cycle (ORC) system. Energy Convers. Manag. 2016, 112, 157–165. [Google Scholar] [CrossRef]
- Gabbrielli, R. A novel design approach for small scale low enthalpy binary geothermal power plants. Energy Convers. Manag. 2012, 64, 263–272. [Google Scholar] [CrossRef]
- Fu, B.R.; Hsu, S.W.; Lee, Y.R.; Hsieh, J.C.; Chang, C.M.; Liu, C.H. Effect of off-design heat source temperature on heat transfer characteristics and system performance of a 250-kW organic Rankine cycle system. Appl. Therm. Eng. 2014, 70, 7–12. [Google Scholar] [CrossRef]
- Fu, B.R.; Hsu, S.W.; Lee, Y.R.; Hsieh, J.C.; Chang, C.M.; Liu, C.H. Performance of a 250 kW organic Rankine cycle system for off-design heat source conditions. Energies 2014, 7, 3684–3694. [Google Scholar] [CrossRef]
- Ibarra, M.; Rovira, A.; Alarcón-Padilla, D.C.; Blanco, J. Performance of a 5 kW e Organic Rankine Cycle at part-load operation. Appl. Energy 2014, 120, 147–158. [Google Scholar] [CrossRef]
- Nusiaputra, Y.Y.; Wiemer, H.J.; Kuhn, D. Thermal-economic modularization of small, organic Rankine cycle power plants for mid-enthalpy geothermal fields. Energies 2014, 7, 4221–4240. [Google Scholar] [CrossRef]
- Mazzi, N.; Rech, S.; Lazzaretto, A. Off-design dynamic model of a real Organic Rankine Cycle system fuelled by exhaust gases from industrial processes. Energy 2015, 90, 537–551. [Google Scholar]
- Hu, D.; Li, S.; Zheng, Y.; Wang, J.; Dai, Y. Preliminary design and off-design performance analysis of an Organic Rankine Cycle for geothermal sources. Energy Convers. Manag. 2015, 96, 175–187. [Google Scholar] [CrossRef]
- Hu, D.; Zheng, Y.; Wu, Y.; Li, S.; Dai, Y. Off-design performance comparison of an organic Rankine cycle under different control strategies. Appl. Energy 2015, 156, 268–279. [Google Scholar] [CrossRef]
- Usman, M.; Imran, M.; Yang, Y.; Lee, D.H.; Park, B.S. Thermo-economic comparison of air-cooled and cooling tower based Organic Rankine Cycle (ORC) with R245fa and R1233zde as candidate working fluids for different geographical climate conditions. Energy 2017, 123, 353–366. [Google Scholar] [CrossRef]
- Rajabloo, T.; Bonalumi, D.; Iora, P. Effect of a partial thermal decomposition of the working fluid on the performances of orc power plants. Energy 2017, 133, 1013–1026. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, T.; Ma, J. Working fluid charge oriented off-design modeling of a small scale Organic Rankine Cycle system. Energy Convers. Manag. 2017, 148, 944–953. [Google Scholar] [CrossRef]
- Liu, Q.; Duan, Y.; Yang, Z. Performance analyses of geothermal organic Rankine cycles with selected hydrocarbon working fluids. Energy 2013, 63, 123–132. [Google Scholar] [CrossRef]
- Toffolo, A.; Lazzaretto, A.; Manente, G.; Paci, M. A multi-criteria approach for the optimal selection of working fluid and design parameters in Organic Rankine Cycle systems. Appl. Energy 2014, 121, 219–232. [Google Scholar] [CrossRef]
- Lecompte, S.; Huisseune, H.; Broek, M.V.D.; Schampheleire, S.D.; Paepe, M.D. Part load based thermo-economic optimization of the Organic Rankine Cycle (ORC) applied to a combined heat and power (CHP) system. Appl. Energy 2013, 111, 871–881. [Google Scholar] [CrossRef]
- Ge, Z.; Wang, H.; Wang, H.T.; Wang, J.J.; Li, M.; Wu, F.Z.; Zhang, S.Y. Main parameters optimization of regenerative organic Rankine cycle driven by low-temperature flue gas waste heat. Energy 2015, 93, 1886–1895. [Google Scholar] [CrossRef]
- Feidt, M.; Kheiri, A.; Pelloux-Prayer, S. Performance optimization of low-temperature power generation by supercritical ORCs (organic Rankine cycles) using low GWP (global warming potential) working fluids. Energy 2014, 67, 513–526. [Google Scholar]
- Vetter, C.; Wiemer, H.J.; Kuhn, D. Comparison of sub- and supercritical Organic Rankine Cycles for power generation from low-temperature/low-enthalpy geothermal wells, considering specific net power output and efficiency. Appl. Therm. Eng. 2013, 51, 871–879. [Google Scholar] [CrossRef]
- Lecompte, S.; Huisseune, H.; Broek, M.V.D.; Vanslambrouck, B.; Paepe, M.D. Review of organic Rankine cycle (ORC) architectures for waste heat recovery. Renew. Sustain. Energy Rev. 2015, 47, 448–461. [Google Scholar] [CrossRef]
- Marcuccilli, F.; Zouaghi, S. Radial inflow turbines for kalina and organic Rankine cycles. In Proceedings of the European Geothermal Congress 2007, Unterhaching, Germany, 30 May–1 June 2007. [Google Scholar]
- Wasserbauer, C.A.; Glassman, A.J. Fortran Program for Predicting Off-Design Performance of Radial-Inflow Turbines; National Aeronautics and Space Administration: Washington, DC, USA, 1975.
- Meitner, P.L.; Glassman, A.J. Computer Code for Off-Design Performance Analysis of Radial-Inflow Turbines with Rotor Blade Sweep; NASA Lewis Research Center: Cleveland, OH, USA, 1983.
- Ventura, C.A.M.; Jacobs, P.A.; Rowlands, A.S.; Petrie-Repar, P.; Sauret, E. Preliminary design and performance estimation of radial inflow turbines: An automated approach. J. Fluids Eng. 2012, 134. [Google Scholar] [CrossRef]
- Forooghi, P.; Hooman, K. Experimental analysis of heat transfer of supercritical fluids in plate heat exchangers. Int. J. Heat Mass Transf. 2014, 74, 448–459. [Google Scholar] [CrossRef]
- Klemeš, J.J. Compact Heat Exchangers for Energy Transfer Intensification: Low Grade Heat and Fouling Mitigation; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Bejan, A.; Kraus, A.D. Heat Transfer Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- García-Cascales, J.; Vera-García, F.; Corberán-Salvador, J.; Gonzálvez-Maciá, J. Assessment of boiling and condensation heat transfer correlations in the modelling of plate heat exchangers. Int. J. Refrig. 2007, 30, 1029–1041. [Google Scholar] [CrossRef]
- Amalfi, R.L.; Vakili-Farahani, F.; Thome, J.R. Flow boiling and frictional pressure gradients in plate heat exchangers. Part 2: Comparison of literature methods to database and new prediction methods. Int. J. Refrig. 2016, 61, 185–203. [Google Scholar] [CrossRef]
- Yan, Y.Y.; Lio, H.C.; Lin, T.F. Condensation heat transfer and pressure drop of refrigerant r-134a in a plate heat exchanger. Int. J. Heat Mass Transf. 1999, 42, 993–1006. [Google Scholar] [CrossRef]



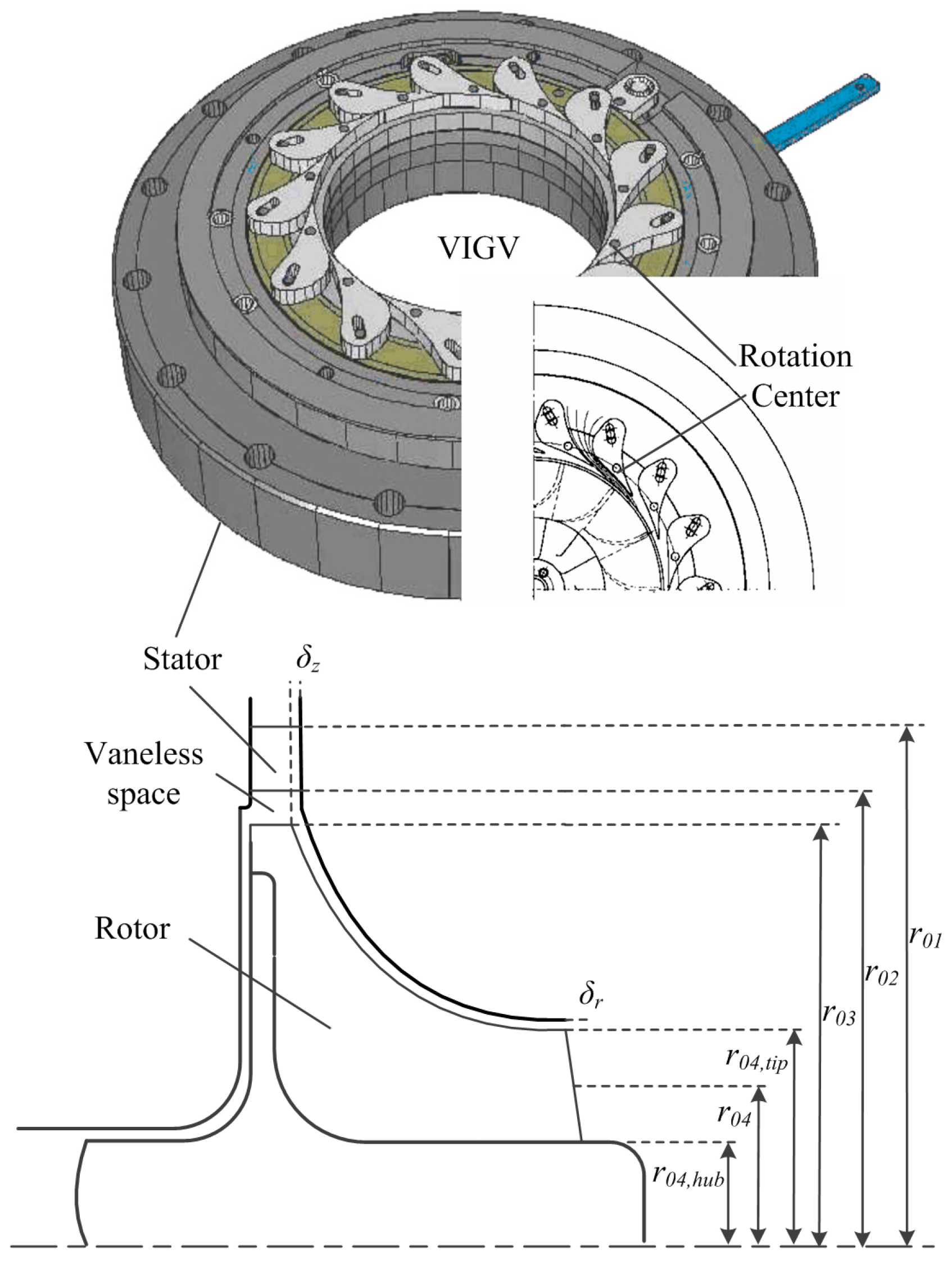















| Parameter | Value |
|---|---|
| Geothermal water inlet temperature (°C) | 150 |
| Geothermal water reinjection temperature (°C) | ≥70 |
| Geothermal water flow rate (kg/s) | 10 |
| Cooling water inlet temperature (°C) | 20 |
| Evaporator pinch temperature (°C) | 10 |
| Vapor generator pinch temperature (°C) | 10 |
| Condenser pinch temperature (°C) | 5 |
| Turbine isentropic efficiency (%) | 80 |
| Refrigerant pump isentropic efficiency (%) | 70 |
| Cooling water pump head (m) | 20 |
| Cooling water pump efficiency (%) | 80 |
| Parameter | Subcritical ORC | Supercritical ORC |
|---|---|---|
| Turbine inlet pressure (kPa) | 1787.1 | 5106.6 |
| Condensing pressure (kPa) | 400.7 | 769.7 |
| Turbine inlet temperature (°C) | 99.4 | 132.8 |
| Net power output (kW) | 330.4 | 371.2 |
| Mass flow rate of working fluid (kg/s) | 8.07 | 15.06 |
| Mass flow rate of cooling water (kg/s) | 136.6 | 127.5 |
| Parameter | Reference Data | Prediction Result | Deviation |
|---|---|---|---|
| Turbine efficiency (%) | 82.3 | 82.7 | 0.5% |
| Mass flow rate (kg/s) | 5.85 | 5.74 | 1.9% |
| Turbine outlet temperature (°C) | 47.3 | 46.9 | 0.9% |
| Power (kW) | 68.5 | 67.5 | 1.5% |
| Parameter | Subcritical Turbine | Supercritical Turbine |
|---|---|---|
| r01 (mm) | 159.8 | 119.3 |
| r02 (mm) | 135.8 | 101.4 |
| r03 (mm) | 123.5 | 92.2 |
| r04,tip (mm) | 85.8 | 52.7 |
| r04,hub (mm) | 60.2 | 25.8 |
| bstator (mm) | 5.9 | 4.1 |
| bin,rotor (mm) | 5.9 | 4.1 |
| α02 (°) | 19 | 17 |
| β04 (°) | 29 | 36 |
| Zstator (mm) | 14 | 14 |
| Zrotor (mm) | 11 | 11 |
| N (rpm) | 17000 | 19000 |
| PTurbine (kW) | 402.9 | 498 |
| ηTurbine (%) | 80.1 | 79.9 |
| Parameter | Evaporator (Subcritical ORC) | Condenser (Subcritical ORC) | Vapor Generator (Supercritical ORC) | Condenser (Supercritical ORC) |
|---|---|---|---|---|
| Plate width (m) | 0.46 | 0.87 | 0.75 | 0.67 |
| Plate length (m) | 0.7 | 1.3 | 1.5 | 1.38 |
| Plate thickness (mm) | 0.6 | 0.6 | 0.6 | 0.6 |
| Channel distance (mm) | 3.0 | 3.1 | 2.5 | 3.1 |
| Chevron angle (°) | 60 | 60 | 60 | 60 |
| Heat transfer area (m2) | 48.0 | 168.5 | 120.4 | 182.2 |
| Pressure drop (kPa) | 16.9 | 8.4 | 21.1 | 7.9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, T.; Liu, C. Off-Design Performances of Subcritical and Supercritical Organic Rankine Cycles in Geothermal Power Systems under an Optimal Control Strategy. Energies 2017, 10, 1185. https://doi.org/10.3390/en10081185
Gao T, Liu C. Off-Design Performances of Subcritical and Supercritical Organic Rankine Cycles in Geothermal Power Systems under an Optimal Control Strategy. Energies. 2017; 10(8):1185. https://doi.org/10.3390/en10081185
Chicago/Turabian StyleGao, Tieyu, and Changwei Liu. 2017. "Off-Design Performances of Subcritical and Supercritical Organic Rankine Cycles in Geothermal Power Systems under an Optimal Control Strategy" Energies 10, no. 8: 1185. https://doi.org/10.3390/en10081185
APA StyleGao, T., & Liu, C. (2017). Off-Design Performances of Subcritical and Supercritical Organic Rankine Cycles in Geothermal Power Systems under an Optimal Control Strategy. Energies, 10(8), 1185. https://doi.org/10.3390/en10081185




