Abstract
Research on the operation of the multiple microgrid (MMG) has been increasing as the power system is operated through the microgrid. Some of the studies related to MMG have introduced various operation strategies by introducing concepts such as power sharing and power trading for power exchange between microgrids. In this paper, a strategy for obtaining optimal scheduling of MMG systems with power sharing through coordination among microgrids that have no cost function of generation units is proposed. There are microgrid-energy management systems (MG-EMSs) in the lower level that determine individual schedules for each microgrid in a hierarchical system. In the upper level, the microgrid of microgrids center (MoMC) implements the coordination among microgrids. In order to achieve the optimal operation of the entire system, MoMC calculates the amount of power sharing based on a predetermined limit value and allocates the command for coordination to each MG-EMS. MG-EMS changes the individual schedule based on the command. These processes are repeatedly performed, and when the change of the total cost becomes smaller than a specified size, the process is terminated and the schedule is determined. The advantages of the proposed algorithm are as follows. (1) It is a power sharing strategy of multiple microgrids considering multiple feeder structures as well as a single feeder structure for minimizing the operation cost of the entire system; (2) it is a power sharing strategy between microgrids that can be applied in a microgrid where only units that do not have a cost function exist; (3) since it is the optimization of the distributed form, the computation time decreases sharply compared with the one performed at the central center. The verification of the proposed algorithm was performed through MATLAB.
1. Introduction
The microgrid has been studied in the last decade, focusing on new forms of the operation of power systems. Because of the microgrid, the power system has shifted away from the conventional centralized operation to a locally distributed form. Distributed generation (DG) such as the renewable energy source and the energy storage system (ESS), which are typical components of the microgrid, have also been continuously studied [1]. With emphasis on the importance of microgrids, the fields where the microgrid can be applied have been diversified, such as university campuses, military service areas, local communities, and commercial and industrial complexes. Since the above-mentioned areas are generally medium-scale or large-scale systems, if they are composed of one microgrid they become similar to a centralized operation method and increase the burden on management and operations. For medium and large scale systems, therefore, it is appropriate to construct multiple microgrids rather than a single microgrid. In accordance with this trend, in recent years there have been studies focusing on a large number of microgrids, extending from a single microgrid operating mode. A number of microgrid operation schemes have been proposed, including sharing or trading power between microgrids when multiple microgrids are implemented. The operation of multiple microgrids is based on extending a single microgrid operating scheme and is typically a hierarchical structure because it is an extension of the operating structure of a single microgrid. In [2], optimal operation of a single microgrid is proposed, but the system structure is hierarchical. Based on the model predictive control framework, the alternating direction method of multipliers method and the dual decomposition method are used. This means that the optimization problem of the microgrid is divided into N sub-problems and solved in parallel. Prox-average message passing is applied in the process of solving the problem. In this method, a specific system can be classified as net and device and handled in a hierarchical manner. It is based on updating the output of each device by exchanging information between net and device. Reference [3] also has a hierarchical structure using a decomposition method. The various components in the microgrid are considered as sub-problems, and the optimum solution for the entire microgrid is obtained while iteratively updating the multipliers. In [4], this hierarchical distributed optimization method is applied to a large number of microgrid systems. The main purpose here is to minimize the power loss due to the power sharing between the microgrids using Lagrange multipliers. Reference [5] deals with the scheduling of power transactions of the multiple microgrid with EVs. In this case, the potential price signals considering the dual variables are reflected in the time of use (TOU) price signal, and this price signal is allocated to the respective microgrids so that the power to deal with the utility grid is determined as the optimal value. As a result, the limit on the amount of power trading with the utility grid at the peak is reduced, thereby reducing the cost. References [6,7] have also proposed the method for the economic operation and power trading of multiple microgrids in community form. Reference [6] proposes the power coordination of multiple microgrids for the optimal operation of one community. Based on a hierarchical structure, the amount of power sharing is adjusted through communication between the microgrid agent at the lower level and the microgrid center agent at the upper level. Reference [7] proposes a power trading scheme in a community microgrid that includes the AC microgrid and the DC microgrid. It is proposed that the output of the microgrid and the amount of power trading between the utility grids by adjusting the droop curve of the converters be adjusted. While all of the previous literature considers the grid-connected operation, references [8,9] consider the islanded operation. In [8], a dual variable is assumed to be an electricity-selling price, and then a power-trading scheme between the microgrids is proposed. According to the law of supply and demand, the selling price of electricity among the microgrid is determined by considering the change of the price by the load. Reference [9] proposes a distributed power sharing scheme using the average consensus algorithm. Power sharing is performed only in an emergency and determines the amount of power to be shared in proportion to the available reserve power of each microgrid. Other studies that do not consider power sharing directly have proposed various operating strategies of multiple microgrid systems in grid-connected or stand-alone modes [10,11], and multi-DC microgrid operation and control strategies are also discussed recently [12,13].
Most of the studies on the operation of the multiple microgrid in the grid-connected, described above, assume the topology with one PCC, and the mathematical models and assumptions of the components used to solve the optimization problem are needed. Typically, it is assumed that the objective function of the battery is arbitrarily convex quadratic. In practice, however, the topology of multiple microgrids may have multiple feeders as well as a single feeder. For example, for two microgrids owned by different owners, if each microgrid has a different PCC, the operating method may be different in terms of power sharing.
Components with clearly defined mathematical models such as generators can be used as mathematical models for optimal operation, but the elements such as the energy storage system (ESS) are defined according to the user’s convenience, that is, they depend on the purpose of operation. In recent studies, by using the relationship between the output and the efficiency of the battery, the life-time cost or life-cycle cost of the battery can be modeled and the battery can be operated according to these models [14,15,16]. However, few studies have been conducted in the long-term, considering the life cycle cost of the battery. In addition, according to a report on energy storage trends published in 2017, the cost of utility-scale energy storage systems is expected to gradually decrease [17]. As a result, the operation of an ESS that considers lifetime costs is not necessarily considered effective, and it may be better to replace the battery after obtaining the maximum benefit because of the cost reduction of the ESS. For this reason, when an ESS runs in a microgrid, it cannot be guaranteed to have a cost function. When a microgrid is constructed only with elements that do not have a specified objective function, such as renewable generation or ESS, it is no longer possible to derive an optimal operating plan considering the power sharing based on the incremental cost of generating the components.
Therefore, a distributed operation scheme is proposed considering power sharing between multiple microgrids, consisting of components that have a multi-feeder topology and components that cannot have power generation costs, and cost optimization for the entire system. The proposed operation scheme for the multi-microgrids system has a hierarchical structure. It consists of an upper system that manages the entire microgrid called the microgrid of microgrids (MoMC) and the microgrid energy management system (MG-EMS) that exist for each microgrid operation and management. The proposed operating scheme achieves distributed optimal operation of the multiple microgrid through appropriate coordination between the upper and lower systems. The purpose of each microgrid located in the lower ones is to adjust the peak power of the microgrid, and the purpose of the upper system is to adjust the optimum point for the entire system. In addition, in the case of islanded operation, the scheme for performing power sharing within this hierarchical structure can be used to increase the reliability of the multiple microgrid system. Power sharing can be accomplished through the coordination of each microgrid EMS with the upper system, MoMC, providing power from a microgrid with sufficient reserve power to a microgrid with deficient power.
In summary, this paper differs from previous studies in the following points.
- (1)
- It includes a power sharing strategy among microgrids applied in multiple microgrid systems with a single feeder as well as multiple feeders. Due to the power sharing achieved through the proposed coordination algorithm in the MoMC, the peaks of each feeder are adjusted to achieve a total cost savings.
- (2)
- For units that do not have an objective function, it is difficult to achieve power sharing by updating dual variables such as Lagrange multipliers or by matching the incremental cost of the objective function through the consensus algorithm. Therefore, there is a need for a way that power sharing can be performed between microgrids in a multiple microgrids system that is connected to the utility grid. That is, when the power sharing is performed, if the microgrid includes only power generation units, which cannot determine the cost function, the power sharing can be achieved by applying the proposed algorithm.
- (3)
- The proposed power sharing strategy is based on the distributed optimization of multiple microgrid systems in a hierarchical structure. Based on the optimization results performed by each microgrid, a coordination algorithm in the MoMC is performed and the results are reflected in each microgrid. The coordination algorithm performed in MoMC is a simple operation as opposed to solving complex problems such as optimization problems, and since each microgrid performs local optimization, the time required for determining the schedule of the entire system is reduced significantly.
Section 2 describes the definition of power sharing and the types of power sharing. Section 3 describes the hierarchical structure of multiple microgrid systems and describes the functions and roles of MG-EMS and MoMC, which are responsible for the operation of the system. Section 4 describes the algorithm for distributed optimal operation for the grid connected operation of multiple microgrids, and Section 5 shows the simulation results for the proposed algorithm. Finally, Section 6 describes the conclusion and the possibility that this algorithm can be applied in practice.
2. Definition of Power Sharing
Before an algorithm for optimal operation in multiple microgrid conditions is proposed, power sharing or power exchange, which are key parts of the algorithm, are defined and the need for power sharing and the kind of power sharing is also defined. It is possible to consider various situations that can occur when operating multiple microgrids by understanding the form of power sharing according to situations where power sharing is required.
2.1. Definition and Necessity of Power Sharing
Power sharing or power exchange is implemented to achieve economic or reliability objectives. This means sending power from one microgrid to another or to multiple microgrids. Conversely, it is possible to send power from multiple microgrids to one microgrid. In an AC system that constitutes a current power system, it is impossible to directly send power from one place to another, but it can be considered that power sharing is achieved by indirectly changing the flow of power. The form of power sharing can vary depending on how the topology for a single microgrid or multiple microgrid system is configured. Also, as mentioned earlier, the form of power sharing may vary depending on the number of feeders in the system.
There are two main cases that require power sharing. Multiple microgrid systems are operated in connection with the utility grid, and the system is disconnected from the utility grid and islanded operation is performed. When operated in connection with the utility grid, the main objective is to improve the economics of the overall system. In other words, the overall cost should be minimized considering the operating cost of each microgrid. The cost for peak power can be reduced through power sharing between the microgrids when peak power is expected in some microgrids. In addition, economic efficiency can be improved through coordination between a generator with a high incremental cost and a generator with a low one. On the other hand, during islanded operation, the main purpose is to improve the reliability of the entire system. For this purpose, the reliability of the overall system is improved by carrying out power sharing from the microgrid, which can share sufficient reserve power, to the microgrid with the deficiency. For this reason, power sharing is required for multiple microgrid operations.
2.2. Types of Power Sharing
The power sharing scheme can be classified into four cases according to the conditions. The first condition is the number of grid feeders connected with the microgrid and the second condition is the form of power sharing. The power sharing method can be divided into a single feeder and multiple feeders depending on the number of feeders, and can be divided into direct power sharing or indirect power sharing depending on the form of power sharing. In the case of a single feeder, it means that there is only one point which is connected with the utility grid in the microgrid or multiple microgrid systems, and in the case of multiple feeders, there are several such points. On the other hand, indirect power sharing in the form of power sharing is a common form, and this indirect power sharing implies the power flow that changes as some power sources reduce generation and other sources increase generation. In the case of direct power sharing, this means that power is directly shared as a form of point-to-point (PTP) between microgrids. For example, a back-to-back (BTB) structure is constructed between two AC systems using a power electronics facility such as a converter, and the facility can be used to share the power directly. In a single feeder, power sharing can occur indirectly because there is only one feeder, whereas in many feeders, if there is no physical connection through the transmission lines between the microgrids constituting the multiple microgrid systems, it can be regarded as indirect power sharing. If there is no connection, it can be regarded as a virtual power plant (VPP) in multiple feeders. It is defined as VPP because it determines the optimal schedule for the whole system and it is not the case that power sharing is implemented actually. If there is a physical connection, the system structure must be able to change so that the connection line does not form the entire ring system.
Figure 1 shows an example of the form of power sharing in an MMG system with two feeders. In this way, the system structures for the multiple feeders are also taken into consideration. Table 1 shows the result of classifying the power sharing method according to the economy or reliability of the power sharing purpose mentioned above. It shows whether the form of power sharing is indirect or direct, depending on the number of feeders and the purpose of the power sharing.
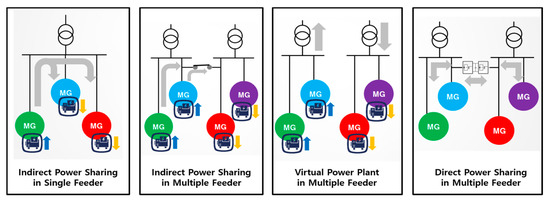
Figure 1.
An example of the form of power sharing in a multiple microgrid (MMG) system structure with two feeders.

Table 1.
Types of power sharing based on various conditions.
3. Configuration of System Structure for Multiple Microgrid
This section describes the system architecture and the main components of system required for the operation of multiple microgrids. It also defines the function and role of each system component according to system structure.
3.1. Structure of Multiple Microgrid Systems
Multiple microgrid is the system consisting of several single microgrids. Multiple microgrid systems can be distinguished in two cases, depending on whether each microgrid owns one or only one owner for the entire system. If there is a microgrid owner, each microgrid can perform its own optimal operation or perform power sharing in the form of power trading with another microgrid. It is also possible to cooperatively operate microgrids for the purpose of solving problems on the grid side, including congestion in the utility grid. On the other hand, when there is a single owner, one medium-scale or large-scale power system is composed of multiple microgrids. In practice, it is similar to the operating form of a single microgrid, but because it manages the whole system in a distributed manner, it can compensate for the drawbacks of centralized operation such as the processing burden of operations. In both cases, a hierarchical structure can be utilized for multiple microgrid operations. Figure 2 shows a hierarchical structure for multiple microgrids. This hierarchical structure consists of MoMC located in the upper layer and MG-EMS located in each microgrid of the lower layer. The distributed operation of the entire system is possible through a cooperative operation or specific coordination between MoMC and MG-EMS. In the existing centralized operation, MoMC manages and operates all the internal elements of each microgrid, but in the proposed distributed operation, MoMC has a simple coordination function and monitoring function of the whole system. MoMC basically monitors the microgrid states in the MMG system and gives orders to each MG-EMS under certain circumstances. When the schedule is determined, the optimization problem is solved in the MG-EMS of each microgrid, not the MoMC. Therefore, all the conditions considered when the schedule is determined are handled in the MG-EMS. As a result, the MoMC does not solve the large-scale optimization problem, but merely performs the simple coordination by receiving the schedule obtained in the MG-EMS and sends the coordinated result to the MG-EMS. In addition, in the distributed operation mode, the plug and play function of the microgrid is easy to expand the system, and it is easy to construct a multi-microgrid platform.
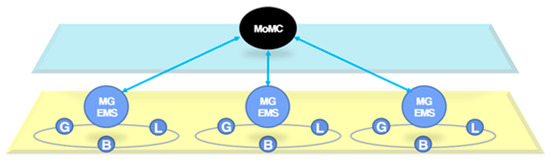
Figure 2.
Hierarchical structure diagram of multiple microgrid.
3.2. Definition of MoMC and MG-EMS Functions
Since the multiple microgrid system has a common hierarchical structure for both cases which are the grid-connected mode and the islanded mode, the MoMC in the upper layer and the MG-EMS in the lower layer have basically unique functions and roles regardless of the operation mode, respectively. Since the MG-EMS is located in each microgrid, the optimal schedule is determined only for each microgrid. In the case of the grid-connected mode, the optimal schedule is set for the purpose of cost reduction and the schedule is set for the purpose of improving the reliability when operating in islanded mode. As a measure of reliability, the cost of power outage is used and the schedule is configured to minimize power outage costs. One of the main functions of the MoMC is to collect the data associated with the schedule after each microgrid schedule has been determined. Based on the collected data, MoMC performs a specific coordination and assigns the data reflecting the coordination to each MG-EMS again. The data exchanged between MoMC and MG-EMS depends on the mode of operation. In the case of the grid-connected operation, the data to be exchanged is the transaction power with the utility grid and net-demand of each microgrid system, and MoMC coordinates net-demand data based on the peak penalty cost. On the other hand, in the case of the islanded operation, the data exchanged is the amount of reserve power or the amount of deficiency power and net-demand data of each microgrid, and then MoMC directly coordinates the net-demand data by comparing the reserve power and the deficiency. Based on the modified data, each MG-EMS determines its own schedule again. The re-scheduling of the MG-EMS changes the power flow and, consequently, the indirect power sharing. Table 2 shows the functions and roles of MoMC and MG-EMS and the criteria for power sharing.

Table 2.
Definition of microgrid of microgrids (MoMC) and microgrid energy management system (MG-EMS) functions.
4. Power Sharing Algorithm for Grid-Connected Operation
This section describes the power-sharing algorithm for the grid-connected operation of multiple microgrids. When operated as grid-connected, the amount of power sharing is indirectly calculated by scheduling coordination rather than directly calculating the amount of power sharing. In other words, the schedule of each microgrid is changed through adjustment at the upper level based on the individual optimal schedule in each MG-EMS. Then, the difference from the individual optimal schedule is determined as the power shares. First of all, the difference between the optimization and power sharing algorithm of the microgrid with convex form of objective function and the algorithm proposed in this paper is described, and the proposed algorithm will then be described in detail.
4.1. Differences in the Operating Conditions of the Proposed Algorithm
Generally, the components that consist of the microgrid are generators, the battery energy storage system (BESS), renewable energy sources, and loads. When calculating the optimal schedule of controllable distributed sources, such as generators or BESS, the objective function of these components is usually assumed to be a convex function, such as the quadratic function. If the objective function is quadratic, it can be regarded as an economic dispatch problem, which means that the solution to the problem is the coincidence of the incremental cost of the cost function. In the case of power sharing, and considering the general multi-microgrid situation, it means converging all of the incremental costs of each power source into the same value. Within the hierarchical operating structure described above, all MG-EMSs build their respective schedules and send the individual incremental cost to the higher-level MoMC. The incremental cost values collected from all MG-EMS to MoMC are adjusted by the MoMC, and the adjusted values are again assigned to each MG-EMS. The MG-EMS coordinates its schedule through the allocated values. As the process is repeated, the output of each microgrid is changed, and the amount of power sharing is determined according to the changed output. The details are presented in our previous studies [18].
Unlike the situation mentioned above, the algorithm proposed in this paper deals with the case where there is no convex objective function. In other words, there is no distributed source such as a generator, and only renewable sources and BESS exist. Also, in the case of BESS, it does not have any convex cost function, such as the life-cycle cost of the batteries. A description of the variables used in the following equations is summarized in Table 3.

Table 3.
A description of the variable notation.
4.2. Optimization in MG-EMS
Since there is no component that has the incremental cost, it is impossible to adjust the schedule based on the change of the incremental cost. Therefore, the main objective of BESS is set to achieve peak shaving and peak control by minimizing the power supplied from the system in accordance with the peak load and utility price. An arbitrary limit value is set for the power supplied from the utility according to the user’s intention, and the penalty cost is set to be paid when the supplied power exceeds the limit value. This penalty cost may be regarded as the increasing fundamental cost based on the peak power increased, and in this paper, the penalty cost is set equivalent to 10 times the utility price. As will be described later, the power sharing is determined according to the set limit values. As shown in Equation (1), the objective function is set to obtain the schedule for 24 h at intervals of 1 h. The objective function includes terms for minimizing the cost of power supplied from the grid and minimizing the peak increase.
, , and are the utility price, the power supplied from the utility grid, the penalty cost, and the preset power limit value, respectively. The penalty cost was set at 10 times the utility price. represents a scale factor, which determines the degree of weighting for the penalty terms.
The decision variable in the optimization problem is , the power supplied by the grid, but another variable determined by the constraints is the output of BESS. That is, as a result of the scheduling, the discharge power or the charge power of BESS and are determined. Therefore, constraints must be constructed for this decision variable. However, since can be determined depending on the output of BESS, constraints include those for BESS. The BESS constraint includes the output constraints for charging or discharging and the constraints on state-of-charge (SOC), as well as state constraints that indicate states for charging and discharging.
where,
Equations (2) and (3) are constraints on the battery output, and and denote the charging power of the battery and the discharging power of the battery, respectively. Equation (4) is the upper and lower limit for SOC, and Equation (5) is the equality constraint for SOC. In Equation (5), and refer to charging and discharging efficiency, respectively, and refers to battery capacity. Also, means time-step, which is set to 1 h generally. Equation (6) is the inequality constraint that indicates the state of the battery. If is one in Equation (6), the battery performs discharging. If is one, the battery performs charging, and there is no case in which and become equal. In addition to the constraints of BESS, Equation (7) also includes general equality constraints on the balance between generation and demand. In Equation (7), means net-demand, which is the value obtained by subtracting the renewable power from the predicted load value . With the above objective function and constraints, each MG-EMS solves its own optimization problem and sends the data resulted in and to the MoMC. Since the objective function is basically a nonlinear function, the optimization problem to be solved in MG-EMS is a problem defined as nonlinear programming. Furthermore, since the charge/discharge status of the battery must be determined, binary variables consisting of 0 and 1 must be included. Therefore, this problem can be considered as a mixed integer nonlinear programming problem and can be solved by NLP solver such as IPOPT or Bonmin [19,20].
4.3. Coordination in MoMC
In the MoMC, the coordination algorithm is performed using and the data of each microgrid received from MG-EMS. It is assumed that the MoMC already knows information about the peak limits of all microgrids. As shown in Equations (8) and (9), the excess power value and the margin power value for each time interval can be obtained based on the limit values as threshold values. is the index of the microgrid that has the margin up to the limit, and is the index of the microgrid that has exceeded the limit.
Equation (10) shows the calculation of the average power by using the obtained margin power and excess power. Here, the average value can be used to determine the criteria for power sharing and the power sharing value can be calculated according to this criterion as in Equations (11) and (12).
In Equation (13), the power sharing value determined for each time slot is applied to the data received from each MG-EMS and then allocated to the MG-EMS.
The coordinated assigned to the MG-EMS is used to solve the optimization problem defined above. The result is sent back to the MoMC and the same procedure described so far is repeated until the difference between the total cost of the current step and the previous step is within the tolerance. If the iteration is terminated, the schedule of the power supplied from the grid and the ESS in each microgrid are finally determined.
The processes described so far are summarized in the flow chart of Figure 3. In Figure 3, represents the total cost of the multiple microgrid system at the step and means a small number. In the MoMC, the utility transaction power exceeding the limit value set in each microgrid is distributed to another microgrid, and the coordination is carried out in the net-demand. That is, the coordinated schedule means the result of power sharing between microgrids. In this paper, the results of power sharing when the schedule is planned through penalty terms are shown. However, the proposed algorithm is effective without penalty terms. Even if a real-time schedule is applied instead of a full-day schedule, the algorithm is considerably effective because the computation burden is small and the time required for obtaining the result is small. The verification of the algorithm for these parts, including the basic verification of the proposed algorithm, is also presented in the next section.
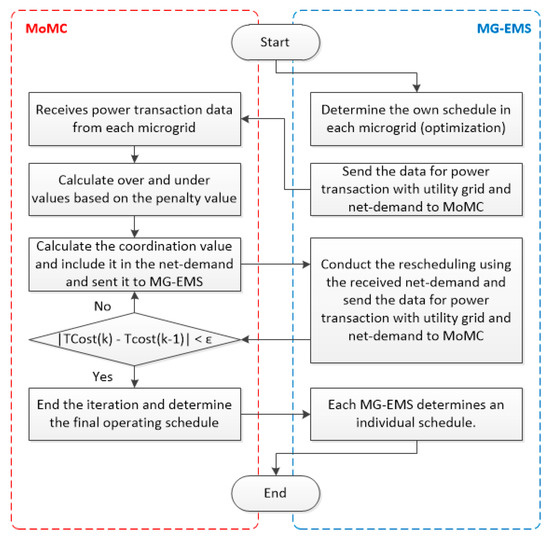
Figure 3.
The flowchart of the proposed algorithm.
5. Numerical Results
In this section, algorithm verification is performed on multiple microgrids. The multiple microgrid system can be assumed to have a system structure with a PCC as shown in Figure 4a, or a system structure with multiple feeders as shown in Figure 4b. In the case of multiple feeder systems like Figure 4b, there must be a separate line for power sharing. In this case, the connections between the microgrids must be electrically isolated through the power electronics in order to prevent the problem of system stability, such as protection cooperation according to the ring topology. The number of the microgrid set is three, to verify the basic performance of the algorithm. As mentioned earlier, each microgrid has only renewable energy sources and battery energy storage systems because the microgrid that does have the units without the cost function is focused. For simplicity of analysis, each microgrid was assumed to have one photovoltaic (PV) generation and one battery energy storage system (BESS). The PV curve of each microgrid is shown in Figure 5. The system price parameter is based on PJM market data [21], and Figure 6 shows the price curve. The load curves are shown in Figure 7 and the load capacities are summarized in Table 4. The parameters such as the rated output power and the rated capacity of the power sources are set appropriately for the loads and are listed in Table 4 together with the other parameter values. All simulations are done with 1-h time step size and all parameters set above can be changed according to the system configuration. The simulation was also performed using a computer with an Intel Core i7-6800K 3.4GHz CPU and 32GB memory and MATLAB (2016a, Mathworks, Natick, MA, USA). Bonmin was used as an optimization solver and the settings for the solver are summarized in Table 5.
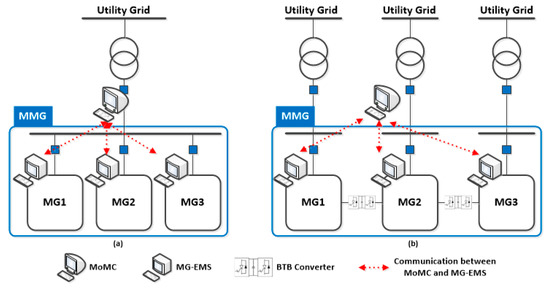
Figure 4.
Examples of multiple microgrid system architecture for application of the proposed algorithm. (a) Multiple microgrids with a single feeder; and (b) Multiple microgrids with multiple feeders.
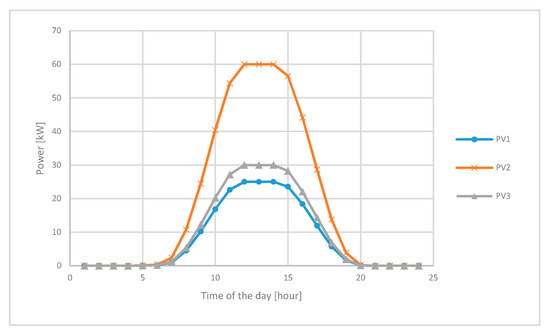
Figure 5.
Renewable generation photovoltaic (PV) profile.
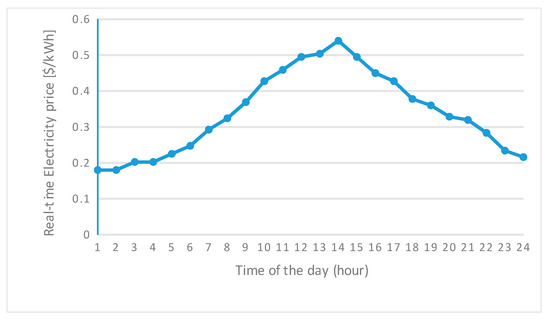
Figure 6.
Real-time price profile.
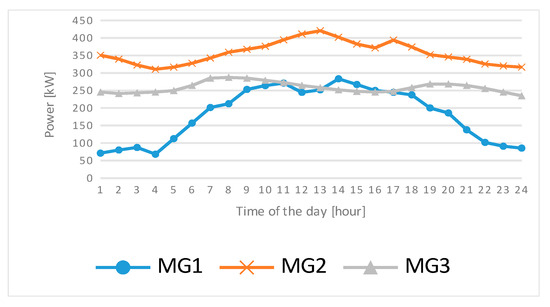
Figure 7.
Load profiles of each microgrid.

Table 4.
Parameter setting of each microgrid.

Table 5.
Parameter settings for the solver.
Figure 8 shows the daily schedule results of the power supplied from the utility grid for each microgrid. The solid bars are the results before the coordination are applied, the shaded bars show the results of the coordination applied, and the dotted line is the predetermined limit value for each microgrid. In the figure of the schedule without the coordination, in the case of MG1, the schedule is configured to be smaller than the limit value at all times, and only the amount of the power transaction with utility grid at 1:00, 2:00, and 24:00 are exceeded the limits in MG2, and the limit was exceeded in most of the times except for 12:00 to 15:00 in MG3. This result shows that MG1 has some margin in all times until the limit is exceeded and MG2 has a margin in most time periods, including peak time, and MG3 needs the power sharing from other MGs in the majority of the times. In other words, since MG3 pays a penalty for exceeding the limit, it has a cost loss. The expected losses are resolved somewhat through power sharing between the microgrids, as shown in Figure 8 (shaded bars). Since each microgrid determines the schedule in consideration of the price curve of the utility system, the result of the coordination in MoMC can be interpreted as follows. (1) Net-demand is small in most of the time including peak time, so that MG2, which has enough margin from the limit, changes the schedule and shares some or all of the power supplied from 3:00 to 23:00 to other MGs as power sharing; (2) in the case of MG1, it is supplied from the grid at the lowest price of 24:00, 1:00, and 2:00, and is shared with other MGs; (3) in case of MG3, since it exceeds the limit in most of the time, it does not pay the penalty cost at all times except 24:00, 1:00, and 2:00 through power shared from MG1 and MG2. Figure 9 shows the state of power sharing by time for each microgrid. Each microgrid constructs a schedule according to its own limit line and calculates a value for power sharing by varying its schedule according to coordination from the MoMC, and performs power sharing according to these values. When the schedule is changed through coordination, the schedule of the ESSs belonging to each microgrid also changes. Figure 10 and Figure 11 show the change of SOC and the output of each ESS.
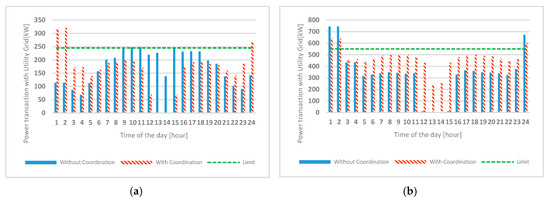
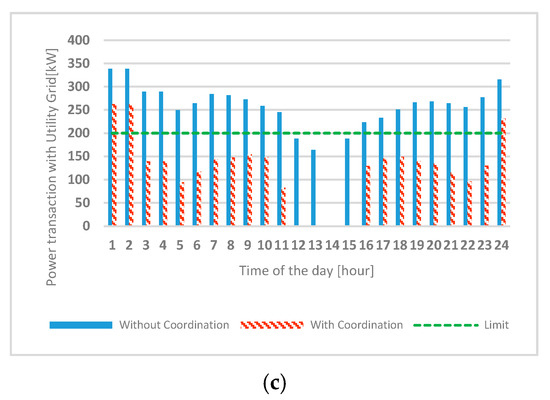
Figure 8.
Power transaction with utility grid (a) MG1, (b) MG2, (c) MG3.
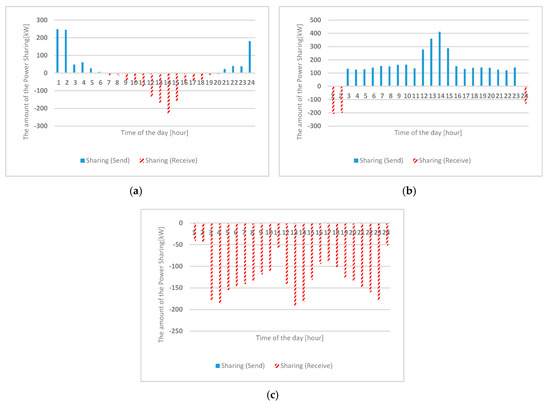
Figure 9.
The amount of the power sharing in each microgrid (a) MG1, (b) MG2, (c) MG3.
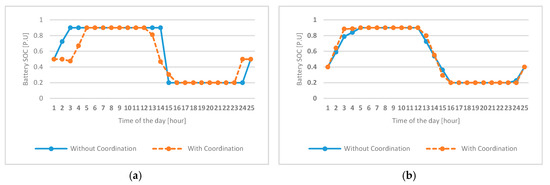
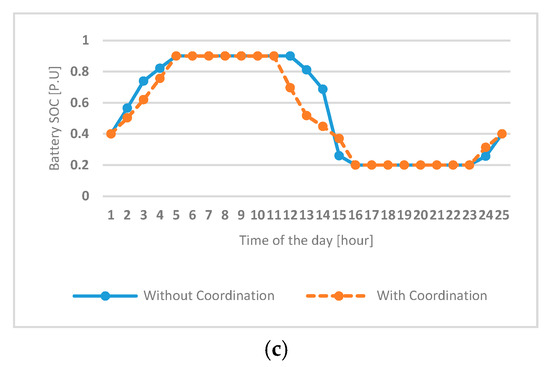
Figure 10.
Battery SOC in each microgrid (a) MG1, (b) MG2, (c) MG3.
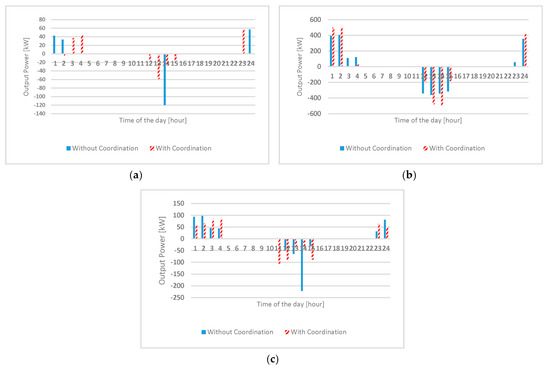
Figure 11.
Battery output in each microgrid (a) MG1, (b) MG2, (c) MG3.
The change in the schedule of each microgrid through this coordination is due to the change of the net-demand shown in Figure 12. The MoMC calculates the amount of the power sharing and reflects these values to the net-demand of each MG; it delivers the coordinated net-demand to each MG-EMS, and then the MG-EMS uses the coordinated net-demand to change its own schedule. Therefore, the amount of the power sharing shown in Figure 9 reflects the change of the power schedule supplied from the utility grid and the change of the ESS schedule.
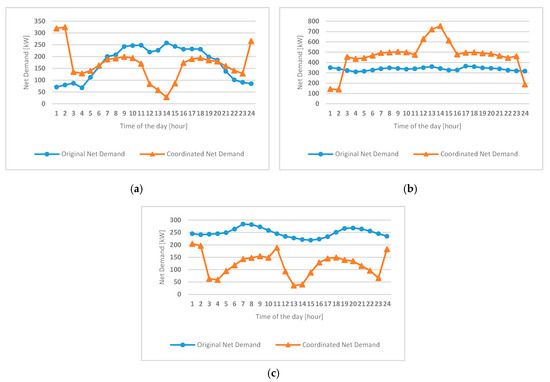
Figure 12.
Changes in net-demand for each microgrid (a) MG1, (b) MG2, (c) MG3.
Table 6 shows the cost for each microgrid and the total MMG according to the conditions. The cost results before and after the coordination are applied, and the cost results of the centralized method considering all the microgrids are compared. This table shows two things. First, the results before and after the coordination is applied are different for each microgrid. In the case of MG1 and MG2, the cost was reduced due to coordination and the cost for MG2 increased. However, the cost of the entire MMG is reduced by about 1.34% when the coordination is applied. In other words, the cost of some microgrids will increase, but other microgrids will benefit, which will benefit the entire MMG system. Secondly, the difference between the cost of the coordinated MMG and the cost of the centralized method is only about 0.3%. That is, even if an optimal schedule is constructed in a distributed form, it is close to the result of the centralized method and achieves a near optimum.

Table 6.
A summary of the results comparison with penalty term.
Table 7 shows the results of applying the same algorithm, except for the penalty term, in the objective function defined in the previous section. Since the penalty was not applied here, the MMG cost after coordination was about 0.16% higher. The proposed algorithm stops the iteration when the difference of total cost in the iteration is within a convergence criterion. Since it is set to 0.01, the error can be canceled if it is set to a smaller value. As in Table 5, the difference from the centralized method is about 0.3% in Table 6, which can be regarded as having an approximate optimal value.

Table 7.
A summary of the results comparison without penalty term.
Figure 13 shows the computation time as the number of microgrids increases. As a result, the conventional central optimization method increases the computation time dramatically as the number of microgrids increases. On the other hand, in the case of the proposed algorithm, the computation time does not increase significantly even if the number of microgrids increases. When the proposed algorithm is applied, it can be achieved within a few minutes because it is computed in parallel and in a distributed manner. As a result of the analysis under the same solver, the computation time was about 66 s for the seven microgrids, whereas the conventional centralized method took about 21 h. Even if considering the actual data communication time, the required time is within a few minutes. Therefore, the proposed algorithm is more effective because it does not increase the burden of computation even if the number of microgrids increases in multiple microgrid systems.
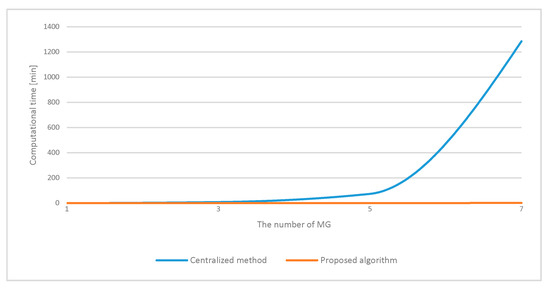
Figure 13.
Computation time according to the number of microgrids using centralized method.
6. Conclusions
In this paper, a distributed coordination strategy is proposed between microgrids for the optimal operation of the whole system under a hierarchical multiple microgrid system. The optimal operation of the entire microgrid system is achieved through the determination of individual schedules in each microgrid and the iterative execution of coordination is performed in terms of the overall system. The proposed algorithm is verified by simulation using MATLAB. As a result of the simulation, it is shown that the total cost has been reduced by paying less penalty cost after coordination at MoMC. Compared with the results of applying the centralized method, the difference between the total cost of the proposed algorithm and that of the centralized method is less than 1%, regardless of the penalty term of the objective function of each microgrid. This means that the proposed power sharing algorithm through the coordination is valid without a special penalty cost function, which is practical in multiple microgrids consisting of only ESSs or renewable energy resources without an energy cost function. Finally, comparing the computation time with the increase of the number of microgrids shows that the proposed algorithm has a considerable advantage in terms of computational burden and time required. Therefore, this algorithm can be applied not only to determine the day-ahead schedule but also to determine the real-time schedule. In summary, the advantages of the proposed algorithm are as follows: (1) it is a power sharing strategy of multiple microgrids considering multiple feeder structures as well as a single feeder structure for minimizing the operation cost of the entire system; (2) it is a power sharing strategy between microgrids that can be applied in a microgrid where only units that do not have a cost function exist; (3) since it is the optimization of the distributed form, the computation time decreases sharply compared with the one performed at the central center. In future works, we will study the operational strategy of improving the economics through power sharing for peak power control when constructing real-time schedules.
Acknowledgments
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy (MOTIE) of the Korea (No. 20151210200080). This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education, Science and Technology (Grant no. NRF-2013R1A1A1012667).
Author Contributions
Won-Poong Lee carried out the main research tasks and wrote the full manuscript, and Jin-Young Choi provided technical support to verify the proposed algorithm in simulation software. Dong-Jun Won validated and double-checked the proposed algorithm, the results, and the whole manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Canizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Wang, T.; Neill, D.O.; Kamath, H. Dynamic Control and Optimization of Distributed Energy Resources in a Microgrid. IEEE Trans. Smart Grid 2015, 6, 2884–2894. [Google Scholar] [CrossRef]
- Yang, Z.; Wul, R.; Yang, J.; Long, K.; You, P. Economical Operation of Microgrid with Various Devices Via Distributed Optimization. IEEE Trans. Smart Grid 2016, 7, 857–867. [Google Scholar] [CrossRef]
- Wang, Y.; Wul, R.; Mao, S.; Nelms, R.M. On Hierarchical Power Scheduling for the Macrogrid and Cooperative Microgrids. IEEE Trans. Ind. Inform. 2015, 11, 1574–1584. [Google Scholar] [CrossRef]
- Wang, D.; Guan, X.; Wu, J.; Li, P.; Zan, P.; Xu, H. Integrated Energy Exchange Scheduling for Multimicrogrid System With Electric Vehicles. IEEE Trans. Smart Grid 2016, 7, 1762–1774. [Google Scholar] [CrossRef]
- Tian, P.; Xiao, X.; Wang, K.; Ding, R. A Hierarchical Energy Management System Based on Hierarchical Optimization for Microgrid Community Economic Operation. IEEE Trans. Smart Grid 2016, 7, 2230–2241. [Google Scholar] [CrossRef]
- Che, L.; Shahidehpour, M.; Alabdulwahab, A.; Al-Turki, Y. Hierarchical Coordination of a Community Microgrid with AC and DC Microgrids. IEEE Trans. Smart Grid 2015, 6, 3042–3051. [Google Scholar] [CrossRef]
- Gregoratti, D.; Matamoros, J. Distributed Energy Trading: The Multiple-Microgrid Case. IEEE Trans. Ind. Electron. 2015, 62, 2551–2559. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Chen, C. Networked Microgrids for Self-Healing Power Systems. IEEE Trans. Smart Grid 2016, 7, 310–319. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J. Self-Healing Resilient Distribution Systems Based on Sectionalization into Microgrids. IEEE Trans. Power Syst. 2015, 30, 3139–3149. [Google Scholar] [CrossRef]
- Liu, W.; Gu, W.; Sheng, W.; Meng, X.; Xue, S.; Chen, M. Pinning-Based Distributed Cooperative Control for Autonomous Microgrids under Uncertain Communication Topologies. IEEE Trans. Power Syst. 2016, 31, 1320–1329. [Google Scholar] [CrossRef]
- Moayedi, S.; Davoudi, A. Distributed Tertiary Control of DC Microgrid Clusters. IEEE Trans. Power Electron. 2016, 31, 1717–1733. [Google Scholar] [CrossRef]
- Meng, L.; Dragicevic, T.; Roldan-Perez, J.; Vasquez, J.C.; Guerrero, J.M. Modeling and Sensitivity Study of Consensus Algorithm-Based Distributed Hierarchical Control for DC Microgrids. IEEE Trans. Smart Grid 2016, 7, 1504–1515. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, W.; Hug, G.; Kar, S.; Li, Z. Cooperative control of distributed energy storage systems in a microgrid. IEEE Trans. Smart Grid 2015, 6, 238–248. [Google Scholar] [CrossRef]
- He, G.; Chen, Q.; Kang, C.; Pinson, P.; Xia, Q. Optimal Bidding Strategy of Battery Storage in Power Markets Considering Performance-Based Regulation and Battery Cycle Life. IEEE Trans. Smart Grid 2016, 7, 2359–2367. [Google Scholar] [CrossRef]
- Shen, J.; Dusmez, S.; Khaligh, A. Optimization of Sizing and Battery Cycle Life in Battery/Ultracapacitor Hybrid Energy Storage Systems for Electric Vehicle Applications. IEEE Trans. Ind. Inform. 2014, 10, 2112–2121. [Google Scholar] [CrossRef]
- Eller, A.; Gauntlett, D. Energy Storage Trends and Opportunities in Emerging Markets; Energy Sector Management Assistance Program, International Finance Corporation World Bank Group: Washington, DC, USA, 2017; pp. 10–11. [Google Scholar]
- Choi, B.R.; Lee, W.P.; Choi, J.Y.; Shin, Y.H.; Won, D.J. Optimal Power Exchange of Multi-Microgrids with Hierarchical Coordination. In Proceedings of the 6th International Youth Conference on Energy 2017, Budapest, Hungary, 21–24 June 2017. [Google Scholar]
- Ipopt Home Page. Available online: https://projects.coin-or.org/Ipopt (accessed on 2 June 2017).
- Bonmin Home Page. Available online: https://projects.coin-or.org/Bonmin (accessed on 2 June 2017).
- Website of the Regional Transmission Organization PJM. Available online: http://www.pjm.com (accessed on 2 June 2017).
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).