An Anonymous Authentication and Key Establish Scheme for Smart Grid: FAuth

Abstract

The smart meters in electricity grids enable fine-grained consumption monitoring. Thus, suppliers could adjust their tariffs. However, as smart meters are deployed within the smart grid field, authentication and key establishment between smart grid parties (smart meters, aggregators, and servers) become an urgency. Besides, as privacy is becoming a big concern for smart meters, smart grid parties are reluctant to leak their real identities during the authentication phase. In this paper, we analyze the recent authentication schemes in smart grids and other applied fields, and propose an anonymous authentication and key establishment scheme between smart grid parties: FAuth. The proposed scheme is based on bilinear maps and the computational Diffie–Hellman problem. We changed the way the smart meter parties registered at Key Generation Center, making the proposed scheme robust against various potential attacks that could be launched by the Key Generation Center, as the scheme could avoid the private key of the smart meter parties from leaking to the Key Generation Center. Besides, the proposed scheme reduced the computational load, both at the smart meter side and at the aggregator side, which make it perfectly suitable for computation-constrained devices. Security proof results show the proposed scheme is secure under the BAN logic and random oracle model.

1. Introduction

The internet of things is now applied into many parts of our daily life. Smart meters are one of these. The European Commission has formulated the goal to provide 80% of all households with smart electricity meters by the year 2020 [1]. As a smart meter can report its measurements periodically to the utility supplier instantaneously, the utility supplier can dynamically change the supplement according to the reported data. With more and more smart meters applied, authentication and key establishment have become an important issue in the smart grid area. According to Sanjab et al. (2016) [2], “a robust authentication protocol is needed while communicating between smart grid parties.” According to the Report on Workshop on Security & Privacy in IoT of Europe (2016) [3], “identification and authentication of end-devices, gateways and servers as very first requirement.” is considered to help manage scalability, evolutivity and risk assessment of the overall IoT system. Authentication enables the parties in the smart grid to authenticate each other and establish a shared key. But as privacy becomes a concern, people start trying to find ways that smart grid parties could authenticate each other without leaking their identity to adversaries.

First, as a smart meter is installed beside the house of inhabitants, as stated in [4], “this malicious attacker might be able to forge sensed data such as the amount of electricity usage at this house before sending these forged data back to the corresponding service server.” Passive attacks are easily launched by an attacker, such as eavesdrop attack, and some other attacks launched by the attackers. Authentication and encryption methods should be applied in this scenario.

Second, electricity usage naturally includes personal information of the inhabitants, according to the electricity consumption, it is easy to judge if inhabitants are at home or not, and with fine-grained electricity consumption reporting instantly, privacy-sensitive information, regarding which appliances are active, can be obtained. Also, by data mining or static methods, according to the electricity consumption, the status and income of the inhabitants may be revealed, so anonymous authentication is needed; in FAuth, the identity of the smart meter is encrypted before sending.

Third, as smart meters have constrained computability compared to aggregators, it is necessary to try to lower the computation cost at the smart meter side; in FAuth, the computation cost at the smart meter side is the lowest compared to other schemes.

So, in this paper, we proposed an anonymous authentication scheme based on bilinear maps and the computational Diffie–Hellman problem: FAuth, which totally meets the above three requirements as stated. The contributions of this paper include the following three points:

• We changed the way smart meter parties register at the Key Generation Center, detailed in Section 6.3, and prevent the Key Generation Center from knowing the private key of the smart grid parties. Thus, some security problems are prevented, detailed in Section 8.
• Based on the methods of Tsai-Lo [4] and Odelu [5], we proposed FAuth, and the comparison results show that the proposed scheme greatly reduced the computation costs of smart grid parties at the authentication phase.
• Security analyses of BAN logic and random oracle model are conducted to show that the proposed scheme is safe.

This paper is organized as follows: We discuss the related works in Section 2. Some preliminary knowledge is described in Section 3. A review of Odelu’s scheme is presented in Section 4. The security limitations of Odelu’s scheme are discussed at Section 5. The scheme: FAuth is proposed in Section 6. We conduct two separate security analyses using BAN logic and random oracle model in Section 7 and Section 8. We provide a comparison with the related schemes in Section 9. A brief introduction of the I3RES Project is given in Section 10. We conclude the paper with a summary of the contributions in Section 11.

2. Related Work

Tsai-Lo and Nai-Wei Lo proposed an authentication scheme based on bilinear map, and the computational Diffie–Hellman problem [4]. The advantage of their scheme is that a smart meter can be quickly authenticated without involving the trust anchor because of the two identity based cryptosystems. Odelu et al. (2016) provide a scheme with security functionalities, including strong credentials’ privacy and SK-security under the CK-adversary model [5]. Their scheme provided a variety of security functionalities, and reduced computational costs for both the smart meter and service provider. Xia and Wang proposed a key distribution scheme for smart grid network [6]. They used a trusted third party which can conduct key revocation, and the third party can be easily duplicated in case power outages occur. Jo et al. (2016) proposed efficient and privacy-preserving protocols for a smart grid in [7]. The proposed protocols were shown to be robust against attacks of data collection unit (DCU) compromise attacks. Further, in their protocol, the response of messages were more efficient by the adoption of the distributed verification method.

Zhang et al. (2017) proposed a new, efficient, certificate-less, generalized signcryption (CLGSC) scheme, and a lightweight and robust security-aware (LRSA) D2D-assist data transmission protocol that was proposed based on CLGSC [8]. Their security analysis demonstrated that the LRSA protocol can achieve data confidentiality and integrity, mutual authentication, contextual privacy, anonymity, and so on. Their experimental results show that the LRSA protocol outperforms the existing schemes in terms of computational and communication overhead. Liu et al. (2014) proposed a certificate-less signature scheme based on bilinear pairings [9]. And based on this scheme, they proposed two certificate-less remote anonymous schemes for wireless body area networks. A client could anonymously be authenticated and establish a key with the application provider. He et al. (2016) provided an improved scheme where the application provider does not have to store any information for the authenticating users [10]. Li et al. (2013) also proposed an authentication scheme based on bilinear pairings [11]. Tsai-Lo and Lo proposed a new anonymous authentication scheme based on nonce and bilinear pairing [12], which supports mutual authentication, key exchange, user anonymity, and user untraceability. It is claimed that their scheme withstands all major security threats and meets general security requirements. In addition, no verification table is required to be implemented at service providers or the trusted SCG service.

He et al. (2017) proposed a data aggregation scheme [13] that can thwart internal attacks for the smart grid environment. They claimed their scheme is provably secure and can meet the security requirements, and incurs lower communication costs.

H. Xiong briefly described the work of [9] in [14], and according to their opinion, certificate managements, scalability, and forward security are the three parts that can be improved in the scheme of the work of [9]. In his scheme, only registered users can authenticate each other and build a shared key, besides, this shared key is only known by the two registered users and the network manager would not know this shared key. Also, according to the public information transmitted between the two users, an adversary is unable to learn this shared key. However, in this scheme, the server does not check the validity of incoming users. Li and J. Hong proposed a modified BDCPS scheme [15], which is an efficient certificate-less access control for wireless body area networks. In this scheme, every user first generates a public key pair ($x_U,y_U=g^{x_U}$), and then registers at a key generating center (KGC), to get a partial private key $D_U=\frac{1}{H_2\left(y_U,I{D}_U\right)+S}P$. After the user gets this partial private key, he can generate his public key pair ($y_U,h_U,T_U$). As only registered user could generate this public key pair, this public key pair can be used as a measure to test if a user is legal or not, as only the public key is transferred, so the identity of the user is hidden.

Liu et al. (2016) proposed an authentication scheme [16] which could well protect the identity and privacy of the user, while the scheme is very cost-effective compared to [9]. Islam and Khan proposed a partial public key method [17], where a user registers at the server several times in order to get more than one authentication keys, then the user uses different keys for authentication to achieve anonymity. He et al. (2015) applied the partial key concept to the vehicular ad hoc networks, and proposed an efficient identity-based privacy preserving authentication scheme, and their scheme enables batch verification of multiple messages [18]. Further, they applied a similar method into public auditing in cloud-based body area networks in [19], by D. He, S. Zeadally, and L. Wu.

Porambage et al. (2014) proposed a pervasive authentication protocol and key establishment scheme [20], their scheme is also based on a partial public key method. But in their scheme, $Cer{t}_U$ is a fixed value, so the user in this scheme could be tracked by $Cer{t}_U$. The registration phase of FAuth is similar to those of [13,20].

Zhang et al. (2014) proposed a scheme based on ECC public key infrastructure [21], but they do not take into account the anonymity of the user, as the user names are sent directly. In [22], Tu et al. (2015) improved the scheme [21], but the username is sent without processing, too. Odelu et al. (2015) [23] proposed an authentication scheme between two users, with the help of a server node, the scheme is also based on a partial public key by elliptic curve cryptography (ECC). They also proposed a similar authentication scheme between two users, but their scheme does not need there to be a trusted server to help the two users to finish the authentication process, as the scheme uses the ECC based El-Gammal type signature [24].

The scheme in [25] is the first one that defines a formal model to capture the feature of user untraceability, and that highlights the damaging threat of de-synchronization attacks on privacy-preserving two-factor authentication schemes.

The schemes in [26,27,28,29], and [30] use elliptic curve cryptography (ECC) to generate a shared key with the server. The scheme in [30] suffers from impersonation attacks in the registration phase, offline password guessing attacks in the login phase, and offline password guessing attacks in the password change phase. The schemes in [31,32] provide a lightweight scheme based on ECC, but they do not protect the privacy of the user, since the user names are sent transparently. Huang et al. (2015) provides an ECC-based authentication scheme between user and server [33], while their scheme is found to be vulnerable to inner side impersonate attacks by [34] by Chaudhry et al. (2016). Li et al. (2015) [35] provide an authentication between user and cloud server, as they use a symmetric key as a way of authentication, and an asymmetric key to establish the shared key, but the $UI{D}_i$ of a user is transferred transparently, so a user could be tracked. The method in [11] is similar to [35], only their shared key is based on a symmetric key, and the scheme in [11] suffers from inner side user attacks, as they shared a same key. Jiang et al. (2016) built their scheme based on the knowledge of chaotic maps [27].

The proposed scheme: FAuth is an improvement of the schemes of [4,5,36], which specially focused on the smart meter authentication problem. The second scheme of [36] could not provide smart meter anonymity at the authentication phase, and suffers from “unknown key share attacks” according to [4]. According to [5], scheme [4] fails to protect the smart secret credentials if the ephemeral secret is revealed as an adversary. The registration manner of smart meters and aggregators in the proposed scheme are changed to provide better security endurance, compared to [5]; besides, a detailed computation of computation and communication costs were conducted, and all the results show the proposed scheme is more suitable for smart grid environments.

3. Preliminary

In this section, an introduction to basic knowledge bilinear maps and the computational Diffie–Hellman problem is introduced.

3.1. Bilinear Map

Central to pairing-based cryptosystems is a bilinear nondegenerate map, originally given as $e:G_1\times G_1\to G_2$, where $G_1$, $G_2$ are both cyclic groups of prime order $q$, and the discrete log problem is hard in $G_1$. $G_1$ is a cyclic additive group, and $G_2$ is a cyclic multiplicative group. Bilinear maps have the following properties:

• Bilinearity: $e\left(aP,bQ\right)=e{\left(aP,bQ\right)}^{ab}$ for $\forall P,\forall Q\in G_1$, for $\forall a,b\in Z_q^{\ast }$.
• Computability: there is an efficient algorithm to compute $P,Q$, for $\forall P,\forall Q\in G_1$.
• Non-degeneracy: $\exists P,Q\in G_1$ with $e\left(P,Q\right)\ne 1$, where $1$ is the multiplicative identity of $G_2$.

3.2. Computational Diffie-Hellman Problem

Given $P,xP,yP\in G_1$, for $\forall x,y\in Z_q^{\ast }$. It is infeasible to compute $xyP$.

4. Review of Odelu’s Scheme

In this section, the authentication scheme proposed by Vanga Odelu, Ashok Kumar Das, Mohammad Wazid, and Mauro Conti for smart grids is evaluated. Some notions used in their scheme are listed in Table 1.

Table 1. Symbols used in Odelu’s scheme.

Symbol	Description
$G_1,G_2$	Bilinear groups
$P$	Generator of $G_1$
$g$	Generator of $G_2$: $g=e(P,P)$
$q$	Prime order of $G_1$ and $G_2$
$KGC$	Key Generation Center
$(k_x,R_x)$	Private and public key pair of $KGC$; $R_x=k_x·P$
$(S_j,I{d}_j)$	jth service provider and its identity
$(k_j,K_j)$	The public key pair of $S_j$:$k_j=H_5(SI{D}_j,K_j)$
$(M_i,I{d}_i)$	ith smart meter and its identity
$(k_i,R_i)$	Key pair of $M_i$, where $k_i$ is kept secret
$(x\stackrel{}{\leftarrow }{}_{R}X)$	$x$ is randomly picked from a set $X$
||	String connection symbol

4.1. Setup Phase of Odelu’s Scheme

In this phase, $KGC,$ which is a trust key generation center, sets up the parameters using the following steps:

Step 1

$KGC$ chooses bilinear map groups $\left(G_1,G_2\right)$ with a prime order, $q,$ and generators $P\in G_1$, and $g=e\left(P,P\right)\in G_2$, where $e:G_1\times G_1\to G_2$ is the bilinear map.

Step 2

$KGC$ chooses the cryptographic one way hash functions $H_1:{\left\{0,1\right\}}^{\ast }\to Z_q^{\ast }$, $H_2:G_2\times {\left\{0,1\right\}}^{\ast }\to {\left\{0,1\right\}}^m,H_3:{\left\{0,1\right\}}^{\ast }\to {\left\{0,1\right\}}^n,H_4:G_2\to Z_q^{\ast },and{H}_5:{\left\{0,1\right\}}^{\ast }\times G_2\to Z_q^{\ast }$, where $m=n+w$, and $w$ is a constant and it is also fixed during the setup phase as in [37], which is based on the input length of an encryption algorithm used in our authentication and key agreement phase. Note that in their proposed scheme, $w$ is calculated such that $n+w=2|q|+|G_1|$ bits, where $|X|$ denotes the bit length of string $X$.

Step 3

$KGC$ then chooses its master private key $k_x\stackrel{}{\leftarrow }{}_R{}^{}X{}_q^{\ast }$ and computes the corresponding public key $R_x=k_x·P\in G_1$.

Step 4

finally, $KGC$ declares the public parameter $\left\{G_1,G_1,q,e,P,P_{pub},g,H_1,H_2,H_3,H_4,H_5\right\}$.

4.2. Smart Meter Registration of Their Scheme

First, we have to make it clear that the registration phase is under a secure channel. Suppose a smart meter $M_i$ wants to register with the $KGC$. $M_i$ sends its identity, $I{d}_i$, to $KGC$ via secure channel. After receiving the identity $I{d}_i$, $KGC$ conducts the following steps:

• Selects a random number $r_m\stackrel{}{\leftarrow }{}_R{}^{}X{}_q^{\ast }$, $R_m=r_m·P$
• Computes $k_i=H_5\left(I{d}_i,R_m\right)k_x+r_m\left(modq\right)$ (El-Gamal type signature on $I{d}_i$)
• Sends $\left(k_i,R_m\right)$ to $M_i$

When smart meter $M_i$ receives $\left(k_i,R_m\right)$, it stores them in the tamper-proof module. The whole process is depicted in Table 2.

Table 2. Registration phase of smart meter in Odelu’s scheme.

Smart Meter ${\mathit{M}}_{\mathit{i}}$	$\mathit{K}\mathit{G}\mathit{C}$
Identity $I{d}_i$	$(k_x,R_x)$
Sends $\left\{I{d}_i\right\}$ to $TA$
$\left\{I{d}_i\right\}$	Random $r_m$, $R_m=r_m·P$ $k_i=H_5(I{d}_i,R_m)k_x+r_m$
Stores $\left\{k_i,R_m\right\}$	$\left\{k_i,R_m\right\}$

4.3. Service Provider Registration of Their Scheme

When a service provider $S_j$ wants to join the system, it has to first register at $KGC$. $S_j$ sends its identity, $I{d}_j$, to $KGC$. After receiving the identity $I{d}_j$, $KGC$ calculates the private key $K_j=\frac{1}{k_x+H_1\left(I{d}_j\right)}·P$, and sends $K_j$ to $S_j$. When smart meter $S_j$ receives $K_j$, it computes $k_j=H_5\left(I{d}_j,K_j\right)$, and stores $\left(k_j,K_j\right)$ into the tamper-proof module. The whole process is depicted in Table 3.

Table 3. Registration phase of service provider in Odelu’s scheme.

Service Provider ${\mathit{S}}_{\mathit{j}}$	$\mathit{K}\mathit{G}\mathit{C}$
Identity $I{d}_j$	$(k_x,R_x)$
Sends $\left\{I{d}_j\right\}$ to $TA$
$\left\{I{d}_j\right\}$	$K_j=\frac{1}{k_x+H_1(I{d}_j)}·P$
$k_j=H_5(I{d}_j,K_j)$ Stores $\left\{k_j,K_j\right\}$	$\left\{K_j\right\}$

4.4. Authentication and Key Establishment Phase of Their Scheme

In the authentication phase of their scheme, smart meter $M_i$ and service provider $S_j$ could authenticate each other without the help of $KGC$.

• $M_i$ chooses two random numbers $x_1,n_1\stackrel{}{\leftarrow }{}_R{}^{}Z{}_q^{\ast }$, and then computes $T_1=(x_1+k_i)(H_1(I{d}_j)P+R_x))$, $g_1=g^{x_1+k_i}$, $C_1=H_2(g_1,I{d}_j)⨁(I{d}_i,R_m,n_1)$ and $A_1=H_3(T_1||I{d}_i||R_m||n_1||g_1)$. $M_i$ sends request message $Message1=\left\{T_1,C_1,A_1\right\}$ to $S_j$.
• Upon receiving the message $\left\{T_1,C_1,A_1\right\}$ from $M_i$, $S_j$ derives $g_1=e(T_1,K_j)$, using its own private key $K_j$. Then, it computes $(I{d}_i,R_m,n_1)=C_1⨁H_2(g_1,I{d}_j)$. $S_j$ then checks if $A_1=H_3(T_1||I{d}_i||R_m||n_1||g_1)$; if it does not hold, $S_j$ terminates the session, otherwise, $S_j$ chooses a random number $x_2\stackrel{}{\leftarrow }{}_R{}^{}X{}_q^{\ast }$ and computes $g_2=e((x_2+k_j)P,H_5(I{d}_i,R_m)R_x+R_m)=g^{(x_2+k_j)k_i}$, the session key $sk=H_4(g_1^{x_2+k_j})$ and $A_2=H_3(sk||g_2||I{d}_j||I{d}_i||n_1||g_1)$, and $S_j$ then sends $Message2=\left\{g_2,A_2\right\}$ to $M_i$.
• After receiving $\left\{g_2,A_2\right\}$ from $S_j$, $M_i$ computes the session key $sk=H_4(g_2^{(x_1+k_i)/k_i})$. Next $M_i$ checks if $A_2=H_3(sk||g_2||I{d}_j||I{d}_i||n_1||g_1)$. If it does not hold, $M_i$ terminates the session. Otherwise, $M_i$ authenticates $S_j$ as a valid target server, and sets $sk$ as the session key. $M_i$ then computes $A_3=H_3(sk||I{d}_i||n_1||g_1||g_2||I{d}_j)$ and sends $Message3=\left\{A_3\right\}$ to $S_j$.
• Upon receiving $\left\{A_3\right\}$, $S_j$ checks if $A_3=H_3(sk||I{d}_i||n_1||g_1||g_2||I{d}_j)$. It this does not hold, $S_j$ terminates the session. Otherwise, $S_j$ confirms that $M_i$ is a legitimate registered smart meter, and agrees with the session key $sk$.

Now both $S_j$ and $M_i$ agree on the shared key, $sk$, and the information flow is depicted in the following Table 4.

Table 4. Authentication phase of Odelu’s scheme.

Smart Meter ${\mathit{M}}_{\mathit{i}}$	Provider ${\mathit{S}}_{\mathit{j}}$.
$(k_i,R_i)$	$(k_j,K_j)$
Random numbers $x_1,n_1\stackrel{}{\leftarrow }{}_R{}^{}X{}_q^{\ast }$.
$T_1=(x_1+k_i)(H_1(I{d}_j)P+R_x)$
$g_1=g^{x_1+x_i}$
$C_1=H_2(g_1,I{d}_j)⨁(I{d}_i,R_m,n_1)$
$A_1=H_3(T_1||I{d}_i||R_m||n_1||g_1)$
$\left\{T_1,C_1,A_1\right\}$	$g_1=e(T_1,K_j)$$(I{d}_i,R_m,n_1)=C_1⨁H_2(g_1,I{d}_j)$
	Checks if $A_1=H_3(T_1||I{d}_i||R_m||n_1||g_1)$
	Random number $x_1\stackrel{}{\leftarrow }{}_R{}^{}X{}_q^{\ast }$
	$g_2=e\left((x_2+k_j)P,H_5(I{d}_i,R_m)R_x+R_m\right)$ $=g^{(x_2+k_j)s_i}$
	$sk=H_4(g_1^{x_2+k_j})$
	$A_2=H_3(sk||g_2||I{d}_j||I{d}_i||n_1||g_1)$
$sk=H_4(g_2^{(x_1+k_i)/k_i})$ Checks if $A_2=H_3(sk||g_2||I{d}_j||I{d}_i||n_1||g_1)$	$\left\{g_2,A_2\right\}$
$A_3=H_3(sk||I{d}_i||n_1||g_1||g_2||I{d}_j)$
$\left\{A_3\right\}$	Checks if $A_3=H_3(sk||I{d}_i||n_1||g_1||g_2||I{d}_j)$
Both agree on session key $sk$

5. Security Limitations of Odelu’s Scheme

In the registration phase of Odelu’s scheme, the private key of the smart meter $M_i$ is $k_i=H_5\left(I{d}_i,R_m\right)k_x+r_m$, which is generated by $KGC$, so $KGC$ knows this private key of the smart meter $M_i$. It is the same with the private key of the service provider $S_j$. So as $KGC$ knows the private keys of the smart meter parties, although $KGC$ is trust worthy, a curious $KGC$ can launch various attacks.

5.1. Impersonate Attack by $KGC$

It is obviously that with the private key of smart meters or service provider $S_j$, $KGC$ could easily impersonate as a smart meter $M_i$ or a service provider $S_j$.

5.2. Tracked by $KGC$

Besides, the private key of the smart meter $M_i$ and the service provider $S_j$ are all known by $KGC$. This means in the authentication phase, the smart meter $M_i$ could be tracked by $KGC$. For a smart meter, it would send $\left\{T_1,C_1,A_1\right\}$ to a service provider $S_j$, and $KGC$ has the private key of $S_j$, so $KGC$ could decrypt $C_1$ to get the identity of $M_i$, which is $I{d}_i$. In this way, smart meter $M_i$ could tracked by $KGC$.

6. The Proposed Authentication Protocol for Smart Grid

In this section, an introduction of the structure of the system was given, and then we propose FAuth. A detailed description of the registration phase and the authentication phase is given in this section.

6.1. Structure of the Scheme

The model is depicted in Figure 1. The structure is divided into three layers, the first layer is the server layer, the second layer is the aggregator layer, and the third layer is the smart meter layer, the smart meters report their reading to the aggregator, the aggregator adds all the smart meters’ reading in its range and reports that to the server.

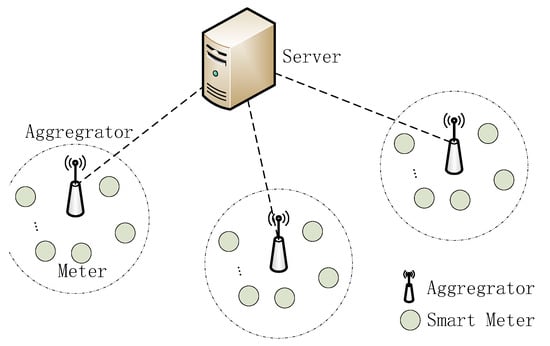
Figure 1. The structure of the model.

In order for the smart meters and aggregators to authenticate each other, we introduce a Key Generation Center, which works like the Trusted Anchor in [5], which is in charge of the registration of the smart meter and the aggregators.

The abstract structure is depicted in Figure 2. The Key Generation Center is in charge of the key generation for the smart meter parties, the smart meters, and the aggregators, and the server has to register to the KGC before they enter the network.

Figure 2. The abstract structure of the model.

• All the members of the scheme, i.e., server, smart meter, and aggregator, have to register at KGC to get their public key pairs.
• The aggregator and smart meters have to authenticate each other and build a shared key for the smart meters to report their reading to the aggregator. The same process happens between the aggregator and the server. In this paper, we only analyze the first part, because the mutual authentication process between the aggregator and the server is the same.

The proposed scheme is an anonymous mutual authentication scheme between the smart meter and the aggregator, or the aggregator and the server, and by the proposed scheme, the two parties could build a shared key for farther communication.

6.2. Setup of the Scheme

The setup phase in the proposed scheme is the same as that in [5], as we have discussed in 4.1. $KGC$ generates its public key pair $\left(k_x,R_x\right)$ and sends these parameters to all the members of the scheme. The symbols we will use in the next section are summarized in Table 5.

Table 5. Symbols used in the proposed scheme.

Symbols	Description
$KGC$	Key Generation Center
$A{G}_j$	The jth aggregator
$M_i$	The ith smart meter
$I{d}_x$	$KGC$’s identity
$I{d}_i$	The ith smart meter’s identity
$I{d}_j$	The jth aggregator’s identity
$(k_x,R_x)$	The private key and public key of $KGC$
$(k_j,R_j)$	The private key and public key of Aggregator
$(k_i,R_i)$	The private key and public key of Smart meter
$T{S}_1$	Timestamp
$H_1,H_2,H_3,H_4,H_5$	Hash function
||	String connection symbol

6.3. Registration Phase of Smart Meter

The registration phase of $M_i$ in the proposed scheme is similar to that of the scheme [20], as depicts in Table 6. When a smart meter wants to join, it has to register first. A smart meter with identity $I{d}_i$ first generates a random number $k_u\stackrel{}{\leftarrow }{}_R{}^{}X{}_q^{\ast },R_u=k_u·P$. Then, $M_i$ sends the registration request $\left\{I{d}_i,R_u\right\}$ to $KGC$, and $KGC$ generates a random number, $k_n\stackrel{}{\leftarrow }{}_R{}^{}X{}_q^{\ast }$, and calculates $R_n=k_n·P$, $R_{in}=\left(R_u+R_n\right)$, $e_i=H(R_{in}||I{d}_i)$, $s_i=e_i·k_n+k_x$. Then, $KGC$ sends $\{e_i,s_i,R_n\}$ back to the smart meter. The smart meter calculates its own private $k_i=s_i+e_i·k_u=e_i·k_n+e_i·k_u+k_x$, and public key $R_i=e_i·R_{in}+R_x=e_i·R_u+e_i·R_n+R_x$. Now the registration phase of the smart meter is finished, and the private key of the smart meter is only known by the smart meter itself.

Table 6. Registration phase of the smart meter.

Smart Meter ${\mathit{M}}_{\mathit{i}}$	$\mathit{K}\mathit{G}\mathit{C}$
Identity $I{d}_i$	$(k_x,R_x)$
Random number $R_u=k_u·P$
Sends $\left\{I{d}_i,R_u\right\}$ to $KGC$
$\left\{I{d}_i,R_u\right\}$	Random $k_n$, $R_n=k_n·P$ $R_{in}=(R_u+R_n)$
	$e_i=H(R_{in}||I{d}_i)$
	$s_i=e_i·k_n+k_x$
$R_{in}=(R_u+R_n)$ $k_i=e_i·k_n+e_i·k_u+d_x$	$\left\{e_i,s_i,R_n\right\}$
$R_i=e_i·R_{in}+R_x$
Stores $\left\{k_i,R_i,R_{in}\right\}$

6.4. Registration Phase of Aggregator

The registration phase of an aggregator, $A{G}_j$, is the same as with the smart meter $M_i$, the process is depicts in Table 7. Finally, an aggregator will get a public key pair: private key $k_j=s_j+e_j·k_c=e_j·k_m+e_j·k_c+k_x$, and public key $R_j=e_j·R_{jm}+R_x$.

Table 7. Registration phase of the aggregator.

Aggregator $\mathit{A}{\mathit{G}}_{\mathit{j}}$	$\mathit{K}\mathit{G}\mathit{C}$
Identity $I{d}_j$	$(k_x,R_x)$
Random number $R_c=k_c·P$
Sends $\left\{I{d}_j,R_c\right\}$ to $KGC$
$\left\{I{d}_j,R_c\right\}$	Random $k_m$, $R_m=k_m·P$ $R_{jm}$ = $(R_c+R_m)$ $e_j=H(R_{jm}||I{d}_j)$
	$s_j=e_j·k_m+k_x$
$R_{jm}=(R_c+R_m)$ $k_j=e_j·k_m+e_j·k_c+k_x$	$\left\{s_j,e_j,R_m\right\}$
$R_j=e_j·R_{jm}+R_x$
Stores $\left\{k_j,R_{jm},R_j\right\}$

6.5. Request and Authentication Phase

Smart meter, $M_i$, with identity, $I{d}_i$, first has to perform the following steps to be anonymously authenticated by an aggregator. Only after mutual authentication, can the smart meter then report its reading to the aggregator.

• Smart meter, $M_i$, with identity, $I{d}_i$, chooses a random number $x_1\stackrel{}{\leftarrow }{}_{R}X{}_q^{\ast }$, and calculates $T_1=\left(x_1+k_i\right)·R_j,g_1=g^{\left(x_1+k_i\right)}$.
• Using the hashed value of $g_1$ to encrypt its identity, $I{d}_i$, and $R_{in}$: $C_1=H_2\left(g_1\right)⨁\left(I{d}_i,R_{in}\right)$.
• Gets the timestamp $T{S}_1$.
• Calculates the hashed value: $A_1=H_3\left(T_1||I{d}_i||R_{in}||T{S}_1\right)$.
• Sends Message 1 = {$T_1,C_1,A_1,T{S}_1$} to the aggregator.

When aggregator $A{G}_j$ receives the data {$T_1,C_1,A_1,T{S}_1$} from a smart meter, $M_i$, $A{G}_j$ will conduct the following steps to authenticate the meter $M_i$:

• Checks the freshness of the $T{S}_1$, if $T{S}_1$ is not fresh, $A{G}_j$ abandons the message.
• Calculates $g_1^{\prime }=e{\left(T_1,P\right)}^{1/k_j}$ using its private key $k_j$.
• Decrypts $C_1$ to get $\left(I{d}_i^{\prime },R_{in}^{\prime }\right)=C_1⨁H_2\left(g_1^{\prime }\right)$.
• Checks if $A_1=H_3\left(T_1||I{d}_i^{\prime }||R_{in}^{\prime }||T{S}_1\right)$; if they are not equal, aborts here.
• Calculates the public key of $M_i:R_i^{\prime }=H_5\left(I{d}_i^{\prime },R_{in}^{\prime }\right)·R_{in}^{\prime }+R_x$.
• Chooses a random number $x_2\stackrel{}{\leftarrow }{}_R{}^{}X{}_q^{\ast }$.
• Calculates $T_2=\left(x_2+k_j\right)·k_j^{-1}·T_1$.
• Calculates $T_3=\left(x_2+k_j\right)·R_i^{\prime }$.
• Calculates $sk=H_4\left(T_2\right)=H_4(\left(x_2+k_j\right)·k_j^{-1}·T_1)=H_4\left(k_i^{-1}\left(x_1+k_i\right)·T_3\right)$.
• Calculates $A_2=H_3\left(sk||T_3||I{d}_j||I{d}_i^{\prime }||T{S}_1||g_1^{\prime }\right)$.
• Sends Message 2 = {$T_3,A_2$} to the client $M_i$.

When smart meter $M_i$ gets the data {$T_3,A_2$}, $M_i$ will do the following steps to authenticate this message.

6.

$M_i$ computes the shared key using its private key $k_i$: $s{k}^{\prime }=H_4(k_i^{-1}·\left(x_1+k_i\right)·T_3)=H_4(\left(x_2+k_j\right)·k_j^{-1}·T_1)$.

7.

$M_i$ checks if $A_2=H_3\left(s{k}^{\prime }||T_3||I{d}_j||I{d}_i||T{S}_1||g_1\right)$; if they are not equal, aborts here, otherwise calculates $A_3=H_3\left(s{k}^{\prime }||I{d}_i||g_1||T_3||I{d}_j\right)$; now $M_i$ has accepted the shared key $s{k}^{\prime }$.

8.

Sends Message 3 = {$A_3$} to $A{G}_j$.

When aggregator $A{G}_j$ gets the data {$A_3$}, $A{G}_j$ will check if $A_3=H_3\left(sk||I{d}_i^{\prime }||g_1^{\prime }||T_3||I{d}_j\right)$; if they are equal, $A{G}_j$, accepts the key $sk$. Now the smart meter $M_i$, and aggregator $A{G}_j$, have authenticated each other and build a shared key. The whole process is depicted in Table 8.

Table 8. Request and authentication phase of the proposed scheme.

Smart Meter ${\mathit{M}}_{\mathit{i}}$	Aggregator $\mathit{A}{\mathit{G}}_{\mathit{j}}$
$(k_i,R_i)$	$(k_j,R_j)$
random numbers $x_1\stackrel{}{\leftarrow }{}_R{}^{}X{}_q^{\ast }$
$T_1=(x_1+k_i)·R_j$
$g_1=g^{(x_1+k_i)}$
$C_1=H_2(g_1)⨁(I{d}_i,R_{in})$
$A_1=H_3(T_1||I{d}_i||R_{in}||T{S}_1)$
$\left\{T_1,C_1,A_1,T{S}_1\right\}$	$g_1^{\prime }=e{(T_1,P)}^{1/k_j}$ $(I{d}_i^{\prime },R_{in}^{\prime })=C_1⨁H_2(g_1^{\prime })$
	checks if $A_1=H_3(T_1||I{d}_i^{\prime }||R_{in}^{\prime }||T{S}_1)$
	$R_i^{\prime }=H_5(I{d}_i^{\prime },R_{in}^{\prime })·R_{in}^{\prime }+R_x$
	random number $x_2\stackrel{}{\leftarrow }{}_R{}^{}X{}_q^{\ast }$
	$T_2=(x_2+k_j)·k_j^{-1}·T_1$
	$T_3=(x_2+k_j)·R_i^{\prime }$
	$sk=H_4(T_2)$
	$A_2=H_3(sk||T_3||I{d}_j||I{d}_i^{\prime }||T{S}_1||g_1)$
$s{k}^{\prime }=H_4(k_i^{-1}(x_1+k_i)·T_3)$ checks if $A_2=H_3(s{k}^{\prime }||T_3||I{d}_j||I{d}_i||T{S}_1||g_1)$	$\left\{T_3,A_2\right\}$
$A_3=H_3(s{k}_{}^{\prime }||I{d}_i||g_1||T_3||I{d}_j)$
$\left\{A_3\right\}$	checks if $A_3=H_3(sk||I{d}_i^{\prime }||g_1||T_3||I{d}_j)$
Both agree on session key $sk$

7. Security Analysis Using BAN Logic

A security analysis of the proposed scheme by using Burrows–Abadi–Needham logic (BAN logic) [38] was conducted. With the help of BAN logic, we can determine whether the exchanged information is trustworthy, and secured against eavesdropping. Now we are going to give a brief overview of the BAN logic. First some symbols used in the BAN logic are described in the Table 9, and some primary BAN logic postulates are given in Table 10. We suppose there are only two entities, smart meter $M_i$, and aggregator $A{G}_j$, in the scheme.

Table 9. Symbols of BAN logic.

Symbol	Meaning
P|≡X	P believes X
P$⨞$X	P sees/receives X
P|∼X	P once said X (or P sent X)
P|⇒X	P controls X
#(X)	X is fresh
P$\stackrel{k}{\leftrightarrow }$Q	P and Q communicate using shared key K
$\stackrel{k}{\to }$Q	K is the public key of Q
${\left\{X\right\}}_k$	the message X is encrypted by K
${\left\{X\right\}}_{k^{-1}}$	the message X is encrypted by private key K

Table 10. Some primary BAN logic postulates.

Name	Rule
$⨞$ rule	$\frac{P|\equiv \stackrel{k}{\to }P,P⨞{\left\{X\right\}}_k}{P⨞X}$, $\frac{P|\equiv P\stackrel{k}{\leftrightarrow }Q,P⨞{\left\{X\right\}}_k}{P⨞X}$, $\frac{P|\equiv \stackrel{k}{\to }Q,P⨞{\left\{X\right\}}_{k^{-1}}}{P⨞X}$
|∼ introduction rule	$\frac{P|\equiv \stackrel{k}{\to }Q,P⨞{\left\{X\right\}}_{k^{-1}}}{P|\equiv Q|~X}$, $\frac{P|\equiv P\stackrel{k}{\leftrightarrow }Q,P⨞{\left\{X\right\}}_k}{P|\equiv Q|~X}$
|∼ elimination rule	$\frac{P|\equiv \#(X),P|\equiv Q|~X}{P|\equiv Q|\equiv X}$
Jurisdiction or control rule	$\frac{P|\equiv Q⨞X,P|\equiv Q|\equiv X}{P|\equiv X}$
$\stackrel{\mathrm{k}}{\leftrightarrow }$ introduction rule	$\frac{P|\equiv \#(k),P|\equiv Q|\equiv X}{P|\equiv P\stackrel{k}{\leftrightarrow }Q}$
Elimination of multipart messages rule	$\frac{P|\equiv Q|~(X,Y)}{P|\equiv Q|~X}$, $\frac{P|\equiv Q|\equiv (X,Y)}{P|\equiv Q|\equiv X}$, $\frac{P|\equiv (X,Y)}{P|\equiv X}$, $\frac{P⨞(X,Y)}{P⨞X}$, $\frac{P|\equiv \#(X,Y)}{P|\equiv \#(X)}$
Freshness rule	$\frac{P|\equiv \#(X)}{P|\equiv \#(X,Y)}$

7.1. The Goal of the Proposed Scheme

The goals of the proposed scheme in BAN logic are depicted in the following, and these goals could ensure $M_i$ and $A{G}_j$ agree on the shared key, $sk$, between them.

1. $M_i|\equiv M_i\stackrel{sk}{\leftrightarrow }A{G}_j$

2. $A{G}_j|\equiv M_i\stackrel{sk}{\leftrightarrow }A{G}_j$

3. $M_i|\equiv A{G}_j|\equiv M_i\stackrel{sk}{\leftrightarrow }A{G}_j$

4. $A{G}_j|\equiv M_i|\equiv M_i\stackrel{sk}{\leftrightarrow }A{G}_j$

7.2. Idealization of the Message

The messages of the proposed scheme, in idealized form in terms of the messages exchanged, is given in Table 11.

Table 11. The idealized form of the messages.

Message	Flow	Idealization Form
1	$M_i\to A{G}_j$	$\{T_1,{\{T_1,I{d}_i,R_{in},T{S}_1\}}_{g_1},T{S}_1\}$
2	$A{G}_j\to M_i$	$\{T_3,{\left\{sk,I{d}_i,T_3,I{d}_j,T{S}_1\right\}}_{g_1}\}$
3	$M_i\to A{G}_j$	$\{{\left\{sk,I{d}_i,T_3,I{d}_j\right\}}_{g_1}\}$

7.3. The Initial State Assumptions

In order to prove the proposed scheme, we first have to make the following initial state assumptions:

A1

$M_i|\equiv \#\left(T{S}_1\right)$

A2

$A{G}_j|\equiv \#\left(T{S}_1\right)$

A3

$M_i|\equiv M_i\stackrel{g_1}{\leftrightarrow }A{G}_j$

A4

$A{G}_j|\equiv M_i\stackrel{g_1}{\leftrightarrow }A{G}_j$

A5

$M_i|\equiv A{G}_j⟾T_1$

A6

$A{G}_j|\equiv M_i⟾T_3$

7.4. The Proof of the Proposed Scheme

7.4.1. Analysis of Message 1

1. According to Message 1, we get:

$$A{G}_j⨞\{T_1,{\{T_1,I{d}_i,R_{in},T{S}_1\}}_{g_1},T{S}_1\}$$

(1)

2. According to the “Elimination of multipart messages” rule and (1), we get:

$$A{G}_j⨞{\{T_1,I{d}_i,R_{in},T{S}_1\}}_{g_1}$$

(2)

3. According to the “$|~$ introduction rule”, (2), and A4, we get:

$$A{G}_j|\equiv M_i|\sim \{T_1,I{d}_i,R_{in},T{S}_1\}$$

(3)

4. According to the “Freshness rule”, (3), and A2, we get:

$$A{G}_j|\equiv \#\left(T_1,I{d}_i,R_{in},T{S}_1\right)$$

(4)

5. According to the “Elimination of multipart messages rule”, and (4), we get:

$$A{G}_j|\equiv \#\left(T_1\right)$$

(5)

6. According to the “$|\sim$ elimination rule”, (4), and (3), we get:

$$A{G}_j|\equiv M_i|\equiv \left(T_1,I{d}_i,R_{in},T{S}_1\right)$$

(6)

7. According to the “Elimination of multipart messages rule”, and (6), we get:

$$A{G}_j|\equiv M_i|\equiv T_1$$

(7)

8. According to the “Jurisdiction rule”, (7), and A6, we get:

$$A{G}_j|\equiv T_1$$

(8)

9. As “$x_2$” is a random number generated by $A{G}_j$, we get:

$$A{G}_j|\equiv \#\left(x_2\right)$$

(9)

10. According to “#()- promotion rule”, (5), and (9), we get:

$$A{G}_j|\equiv \#\left(sk\right),sk=h(\left(x_2+k_j\right)·k_j^{-1}·T_1)$$

(10)

11. According to the “$\stackrel{k}{\leftrightarrow }$ introduction rule”, (10) and (7), we get:

$$A{G}_j|\equiv A{G}_j\stackrel{sk}{\leftrightarrow }{M}_i$$

(11)

7.4.2. Analysis of Message 2

12. According to Message 2, we get:

$$M_i⨞\{T_3,{\left\{sk,I{d}_i,T_3,I{d}_j,T{S}_1\right\}}_{g_1}\}$$

(12)

13. According to the “Elimination of multipart messages rule”, and (12), we get:

$$M_i⨞{\{sk,I{d}_i,T_3,I{d}_j,T{S}_1\}}_{g_1}$$

(13)

14. According to the “$|~$ introduction rule”, (13), and A3, we get:

$$M_i|\equiv A{G}_j|\sim \{sk,I{d}_i,T_3,I{d}_j,T{S}_1\}$$

(14)

15. According to “Freshness rule”, (14), and A1, we get:

$$M_i|\equiv \#\left(sk,I{d}_i,T_3,I{d}_j,T{S}_1\right)$$

(15)

16. According to the “$\mathrm{Elimination}\mathrm{of}\mathrm{multipart}\mathrm{messages}$ rule”, (15), we get:

$$M_i|\equiv \#\left(T_3\right)$$

(16)

17. According to the “$|\sim$ elimination rule”, (15), and (14), we get:

$$M_i|\equiv A{G}_j|\equiv \left(sk,I{d}_i,T_3,I{d}_j,T{S}_1\right)$$

(17)

18. According to the “Elimination of multipart messages rule”, and (17), we get:

$$M_i|\equiv A{G}_j|\equiv T_3$$

(18)

19. According to the “Jurisdiction rule”, (18), and A5, we get:

$$M_i|\equiv T_3$$

(19)

20. As “$x_1$” is a random number generated by $M_i$, we get:

$$M_i|\equiv \#\left(x_1\right)$$

(20)

21. According to the “#()- promotion rule”, (16), and (20), we get:

$$M_i|\equiv \#\left(sk\right),sk=h\left(k_i^{-1}·\left(x_1+k_i\right)·T_3\right)$$

(21)

22. According to the “$\stackrel{k}{\leftrightarrow }$ introduction rule”, (21) and (18) we get:

$$M_i|\equiv A{G}_j\stackrel{sk}{\leftrightarrow }{M}_i$$

(22)

23. According to the “Elimination of multipart messages rule”, and (17), we get:

$$M_i|\equiv A{G}_j|\equiv sk$$

(23)

7.4.3. Analysis of Message 3

24. According to Message 3 we get:

$$A{G}_j⨞\{{\left\{sk,I{d}_i,T_3,I{d}_j\right\}}_{g_1}\}$$

(24)

25. According to the “$|~$ introduction rule”, (24), and A4, we get:

$$A{G}_j|\equiv M_i|\sim \{sk,I{d}_i,T_3,I{d}_j\}$$

(25)

26. According to “Freshness rule”, (10), and (25) we get:

$$A{G}_j|\equiv \#\left(sk,I{d}_i,T_3,I{d}_j,T{S}_1\right)$$

(26)

27. According to the “$|\sim$ elimination rule”, (25), and (26), we get:

$$A{G}_j|\equiv M_i|\equiv \left(sk,I{d}_i,T_3,I{d}_j\right)$$

(27)

28. According to the “Elimination of multipart messages rule”, and (27), we get:

$$A{G}_j|\equiv M_i|\equiv sk$$

(28)

Now we have accomplished all the goals of our proof; based on (11), (22), (23), and (28), we can say the proposed scheme is provably safe under BAN logic.

8. Security Analysis Using Random Oracle

In this section, a security proof of random oracle is provided, based on the model of [5,30]. In order to simplify, it is supposed that only two entities are in FAuth: a smart meter $M$, and an aggregator $AG$.

While each entity has many instances, using $M^i$ stands for the ith smart meter, and $A{G}^j$ for the jth aggregator. $\zeta$ can be used as $M^i$ or $A{G}^j$. An instance is considered as an oracle, and a simulator is used to answer the input message. Under this model, $\zeta$ is considered as a participant or an oracle [5]. To crack the scheme, an adversary could use a simulator to ask for the following queries:

Send ($\mathit{\zeta },\mathit{m}$): this oracle $\zeta$ receives a message, $m$, from an entity, and answers this query with the corresponding message.

Execute (${\mathit{M}}^{\mathit{i}},\mathit{A}{\mathit{G}}^{\mathit{j}}$): this query simulates the passive attack, and the adversary, A, can learn the message transmitted between $M^i,A{G}^j$.

ReveralSerrsion ($\mathit{\zeta }$): the adversary A can learn the session specific information, and the answer of this query doesn’t include the private key of $M^i$ or $A{G}^j$.

ReveralSk ($\mathit{\zeta }$): the adversary, A, can learn the session key of the oracle $\zeta$.

Corrupt ($\mathit{\zeta }$): the adversary, A, can learn the private key of the entity $\zeta$.

Expire ($\mathit{\zeta }$): this query erases the session key of a completed session held by the oracle $\zeta$.

Test ($\mathit{\zeta }$): returns a session key or a random key, only before any of the ReveralSerrsion ($\zeta$), ReveralSk ($\zeta$) and Corrupt ($\zeta$) have been asked.

Lemma 1 (Difference Lemma).

Let $R_1,R_{2}and{R}_3$ represent the events defined in some probability distribution. If $R_1\bigwedge \neg R_3\iff R_2\bigwedge \neg R_3$, we have $|Pr\left[R_1\right]-Pr\left[R_2\right]|\le Pr\left[R_3\right]$.

Theorem 1.

Let A be a t polynomial time adversary against the semantic security, and make no more than $q_s$ send queries, $q_e$ execute queries, and $q_h$ hash queries. The advantage of A in our scheme is given by $Ad{v}_{FAuth}(A)\le \frac{O({(q_s+q_e)}^2)}{(q-1)}+\frac{O(q_h^2)}{2^l}+\frac{O(q_s+q_h)}{2^{l-1}}+O(q_h·(Ad{v}_A^{CDH}(t^{\prime })))$, where $t^{\prime }=O(t+(q_h+q_h)·T_m)$, and $T_m$ is the time for multiplication operation in group.

In order to prove Theorem 1, we introduce four games, $G_i$, and the first game represents the real attack, $Suc{c}_i$ is the event that in Game $G_i$ the adversary correctly guesses the result of the Test ($\zeta$).

Game $G_0$: This game simulates the real scheme under random oracle, according to sematic security, and it is clear that:

$$Ad{v}_{FAuth}\left(A\right)=|2\mathrm{Pr}\left[Suc{c}_0\right]-1|$$

Game $G_1$: This game simulates all the oracles, $L_H$ stores all the answers to hash queries, if the hash query is asked by adersary, then the answer is sotred in $L_A$, and $L_P$ stores the transcripts of all the messages, all oracles are demonstrated in in Table 12 and Table 13, and an adversary is unable to distinguish between the two games:

$$\mathrm{Pr}\left[Suc{c}_0\right]=\mathrm{Pr}\left[Suc{c}_1\right]$$

Table 12. Simulation of send queries.

Simulation of Send Queries
For a Send ($M^i$, init) query, the simulator does the following steps:
Selects random number $x_1\stackrel{}{\leftarrow }{}_R{}^{}X{}_q^{\ast }$,
Computes $T_1=(x_1+k_i)·R_j,g_1=g^{(x_1+k_i)}$, $C_1=H_2(g_1)⨁(I{d}_i,R_{in})$, get timestamp $T{S}_1$, and Calculates $A_1=H_3(T_1||I{d}_i||R_{in}||T{S}_1)$
Returns $M1=${$T_1,C_1,A_1,T{S}_1$} as the answer
For a Send ($M^i$,$A{G}^j$, $M1$) query, the simulator does the following steps:
Computes $g_1^{\prime }=e{(T_1,P)}^{1/k_j}$, and check if $A_1=H_3(T_1||I{d}_i^{\prime }||R_{in}^{\prime }||T{S}_1)$, if they are not equal, terminates here.
Selects random number $x_2\in \stackrel{}{\leftarrow }{}_R{}^{}X{}_q^{\ast }$,
Computes $T_2=(x_2+k_j)·k_j^{-1}·T_1$, $T_3=(x_2+k_j)·R_i^{\prime }$, $sk=H_4(T_2)$, and $A_2=H_3(sk||T_3||I{d}_j||I{d}_i^{\prime }||T{S}_1||g_1^{\prime })$
Returns $M2=${$T_3,A_2$} as the answer
For a Send ($A{G}^j$,$M^i$, $M2$) query, the simulator does the following steps:
Computes $s{k}^{\prime }=H_4(k_i^{-1}·(x_1+k_i)·T_3)$, and checks if $A_2=H_3(s{k}^{\prime }||T_3||I{d}_j||I{d}_i||T{S}_1||g_1)$, if they are not equal, aborts here, otherwise calculates $A_3=H_3(s{k}^{\prime }||I{d}_i||g_1||T_3||I{d}_j)$.
Returns $M3=${$A_3$} as the answer
For a Send ($M^i$,$A{G}^j$,$M3$) query, the simulator does the following steps:
$A{G}_j$ will check if $A_3=H_3(sk||I{d}_i^{\prime }||g_1^{\prime }||T_3||I{d}_j)$, if they are equal, then the two parties built the shared key.

Table 13. Simulation of other queries.

Simulation of Other Queries
For a Hash($i$, s, $\omega$) query, which $i=1,2,3,4,5$, if the record ($i$, s, $\omega$) is found in $L_{\mathrm{H}}$, return $\omega$ as result. Otherwise, chooses a random string from ${\left\{0,1\right\}}^l$ and add the record ($i$, s, $\omega$) to $L_{\mathrm{H}}$.
If this query is asked by adversary, A, then the record is added to $L_{\mathrm{A}}$.
For a Execute($A{G}^j$,$M^i$) query, it proceeds with the Send queries successively, and outputs the matching transcripts. $M1=${$T_1,C_1,A_1,T{S}_1$}, $M2=${$T_3,A_2$}, $M3=${$A_3$}
For a Corrupt ($\zeta$) query, the simulator returns private key owned by entity $\zeta$.
For a RevealSession ($\zeta$) query, the simulator returns session state information $\left\{x_1,g_1=g^{(x_1+k_i)},T_1=(x_1+k_i)·a·P\right\}$ of $M^i$, or $\left\{x_2,T_3=(x_2+k_j)·b·P\right\}$ for instance $A{G}^j$.
For a RevealSK ($\zeta$) query, the simulator returns session key sk, if $\zeta$ has formed an session key and the instance $\zeta$ has not been aksed by a Test query, otherwise, null is returned.
For a Test ($\zeta$) query, first obtains the shared key from a RevealSK ($\zeta$) query, and then flips a coin b, if b = 1, returns the shared key, otherwise returns an random string from ${\left\{0,1\right\}}^l$.

The difference lemma was imported from [39,40] for the formal security proof.

Game $G_2$: This game simulates all the oracles in Game $G_1$, but two kinds of collisions are trying to be avoided here, and the results are obtained by the birthday paradox:

• Random numbers of $x_1$ and $x_2$ should be different in different sessions, and the probability is bounded by: $\frac{O({\left(q_s+q_e\right)}^2)}{2\left(q-1\right)}$.
• The probability of a hash result collision is bounded by $\frac{O\left(q_h^2\right)}{2^{l+1}}$, where $l$ is the length of a result of a hash function.

These two kinds of collisions should be avoided, so the two games differ by:

$$|\mathrm{Pr}\left[Suc{c}_2\right]-\mathrm{Pr}\left[Suc{c}_1\right]|\le \frac{O({\left(q_s+q_e\right)}^2)}{2\left(q-1\right)}+\frac{O\left(q_h^2\right)}{2^{l+1}}$$

Game $G_3$: This game simulates the situation where an adversary may guess the result of a hash function $A_1,A_2$ and $A_3$ without asking the random oracle.

For a Send $(M^i$, $A{G}^j$, $M1$) query, $A{G}^j$ has to check if $M1$ belongs to the transcripts, and check if $A_1\in L_{\mathrm{A}}$; if either of them fails, $A{G}^j$ terminates the session, the probability is bounded by $\frac{O\left(q_s\right)}{2^l}$; for the checking of if $H_2\left(g_1\right)\in L_{\mathrm{A}}$, and the probability is bounded by $\frac{O\left(q_h\right)}{2^l}$, so for a Send $(M^i$, $A{G}^j$, $M1$) query, the probability is bounded by $\frac{O\left(q_s+q_h\right)}{2^l}$. For a Send ($A{G}^j$, $M^i$, $M2$) or Send ($M^i$, $A{G}^j$, $M3$) query, the probability is bounded by $\frac{O\left(q_s+q_h\right)}{2^l}$, too.

This game and the previous one are indistinguishable unless the smart meter and aggregator reject valid authentication information:

$$|\mathrm{Pr}\left[Suc{c}_3\right]-\mathrm{Pr}\left[Suc{c}_2\right]|\le \frac{O\left(q_s+q_h\right)}{2^l}$$

Game $G_4$: The CDH problem is brought in this game. In order to win the game, A should ask the query $H_4$ and broke the CDH problem; the adversary’s goal is to compute the session key by asking Execute ($A{G}^j$,$M^i$) query and the corresponding hash query, and the adversary can also get the transcripts. The proposed scheme fits the SK-security [5] in the following four cases.

Case 1 RevealSession ($M^i$) and RevealSession ($A{G}^j$):

Adversary can get the session state information $\left\{x_1,g_1=g^{\left(x_1+k_i\right)},T_1=\left(x_1+k_i\right)·a·P\right\}$ of $M^i$, and $\left\{x_2,T_3=\left(x_2+k_j\right)·b·P\right\}$ for the matching instance $A{G}^j$. Where $a=H(R_{jm}||I{d}_j)·\left(k_m+k_c\right)+k_x$ and $b=H(R_{in}||I{d}_i)\left(k_n+k_u\right)+k_x$.

Case 2 RevealSession ($M^i$) and Corrupt ($A{G}^j$):

Adversary can get the session state information $\left\{x_1,g_1=g^{\left(x_1+k_i\right)},T_1=\left(x_1+k_i\right)·a·P\right\}$ of $M^i$, the private key $\left\{k_j\right\}$ for the matching instance $A{G}^j$ without session information.

Case 3 Corrupt ($M^i$) and RevealSession ($A{G}^j$):

Adversary can get the private key $\left\{k_i\right\}$ of $M^i$, but could not get the session information of $M^i$, and can get $\left\{x_2,T_3=\left(x_2+k_j\right)·b·P\right\}$ for the matching instance $A{G}^j$.

Case 4 Corrupt ($M^i$) and Corrupt ($A{G}^j$):

Adversary can get the private key $\left\{k_i\right\}$ of $M^i$, but could not get the session information, and can get the private key $\left\{k_j\right\}$ for the matching instance $A{G}^j$ without session information, too.

However, in all the above four cases, adversary A is unable to solve the CDH problem given the information it gets in the four cases. The shared key sk can be gotten with the probability $\frac{1}{q_h}$ in the list of $L_A$, $t^{\prime }=O\left(t+\left(q_h+q_h\right)·T_m\right)$ be the running time in all, then it is not hard to get:

$$|\mathrm{Pr}\left[Suc{c}_4\right]-\mathrm{Pr}\left[Suc{c}_3\right]|\le O\left(q_h\left(Ad{v}_A^{CDH}\left(t^{\prime }\right)\right)\right)$$

Until now, through the games and using the lemma 1, theorem 1 is proven.

9. Comparison

9.1. Computational Performance Analysis

In this section, we compared the computation cost of the proposed scheme with [4,5], and the second scheme in [36], and we use the following symbols to stand for different time costs. In order for comparison, we use the experimental results from [41], the same as in Odelu’s scheme, and the results are shown in Table 14. We also “omit the modular multiplication $T_m$. as it requires very low execution time than that for execution time of a modular exponentiation operation” [41]. We also ignore the point addition and XOR operations, as the time consumption is marginal, at the same time, we “assume $T_h\approx T_s$”. The final results are shown in Table 15 and Table 16.

Table 14. Time comparison of various cryptographic operations.

Calculations	Server (ms)	Client (s)
Exponentiation in $G_2$	<1	<0.1
Multiplication operation in $G_1$	1.17	0.13
Bilinear map pairing	3.16	0.38
Map to point	<1	<0.1
General hash function	0.01	0.001

Table 15. Computation cost of different types of calculations at the authentication phase.

Schemes	Smart Meter						Aggregator *
	${\mathit{T}}_{\mathit{b}\mathit{p}}$	${\mathit{T}}_{\mathit{e}\mathit{x}\mathit{p}}$	${\mathit{T}}_{\mathit{m}\mathit{u}\mathit{l}}$	${\mathit{T}}_{\mathit{s}}$	${\mathit{T}}_{\mathit{H}}$	${\mathit{T}}_{\mathit{h}}$	${\mathit{T}}_{\mathit{b}\mathit{p}}$	${\mathit{T}}_{\mathit{e}\mathit{x}\mathit{p}}$	${\mathit{T}}_{\mathit{m}\mathit{u}\mathit{l}}$	${\mathit{T}}_{\mathit{s}}$	${\mathit{T}}_{\mathit{H}}$	${\mathit{T}}_{\mathit{h}}$
Y. Wang et al. [36]	1	0	3	1	2	5	1	1	3	1	2	5
Odelu et al. [5]	0	1	3	0	0	6	2	2	1	0	0	6
Tsai-Lo et al. [4]	0	1	4	0	0	5	2	1	3	0	0	5
The proposed scheme	0	1	2	0	0	5	1	1	3	0	0	5

Aggregator * The smart meters are divided into different aggregation areas in the smart grid, the role of service provider in schemes of [4,5,36] are similar to the role of the aggregator in our scheme in an aggregation area.

Table 16. Computation cost at the authentication phase.

Schemes	Smart Meter		Aggregator
	Total (s)	Compare (s)	Total (ms)	Compare * (ms)
Y. Wang et al. [36]	<0.976	+0.611	<8.73	+1.01
Odelu et al. [5]	<0.496	+0.131	<9.72	+2
Tsai-Lo et al. [4]	<0.625	+0.26	<10.88	+3.16
The proposed scheme	<0.365	0	<7.72	0

Compare * mean compare with the proposed scheme.

• $T_{exp}$ the execution time of a modular exponentiation operation in $G_2$
• $T_{mul}$ the execution time of a scalar multiplication operation in $G_1$
• $T_{bp}$ the execution time of bilinear map pairing $e:G_1\times G_1\to G_2$
• $T_s$ the execution time of a symmetric encryption/decryption
• $T_H$ the execution time of map to point
• $T_h$ the execution time of general one-way hash function

9.2. Communication Performance Analysis

In this section, we compared the proposed scheme’s computation cost with Tsai-Lo’s scheme [4], Odelu’s scheme [5], and Y. Wang et al. [36]. According to Odelu et al., “the random number/nonce is 128 bits, the identity and hash output of all hash functions $H_1$, $H_3$, $H_4$ and $H_5$ (except the hash function $H_2$) are 160 bits each, the elements in group $G_1$ and $G_2$ are 320 bits and 512 bits, respectively, and the timestamp is 32 bits” [5]. We get the following computation cost in Table 17, and for $C_1$, its length is calculated as the length of $\left(I{d}_i,R_{in}\right)$, which is 480 bits.

Table 17. Communication comparison.

Schemes	M1	M2	M3	M4	Total	Compare *
Y. Wang et al. [36]	320	320	160	160	960	−672
Odelu et al. [5]	1088	672	160	0	1920	+288
Tsai-Lo et al. [4]	608	480	320	0	1408	−224
The proposed scheme	992	480	160	0	1632	0

Compare * mean compare with the proposed scheme. M1 for message 1. M2 for message 2, M3 for message 3, M4 for message 4 only in [36].

9.3. Comparison of the Schemes

In this part, we compare the security features with the other schemes [4,5,36]. As we discussed in Section 5, Odelu’s scheme [5] suffers from $KGC$ impersonate attacks and $KGC$ track attacks; in Tsai-Lo’s scheme [4], the private key of the smart meter and service provider is also known by $KGC$, so their scheme suffers from these two attacks, too. Besides, as $KGC$ knows the private key, $KGC$ could find out the shared key, so $KGC$ could launch an eavesdrop attack. The second scheme of [36] does not have a $KGC$, but instead, a card maker, and the card maker knows the private key of the card owner. Besides, according to [4], the second scheme of [36] “does not support anonymity as it uses (smart meter) identity through its authentication process” and suffers from “unknown key share attack”.

According to [5], Tsai-Lo scheme in [4] “fails to protect the smart secret credentials when the ephemeral secret is revealed to $\mathcal{A}$ (adversary).” We name this attack “session exposure attacks when ephemeral secrets leaked”. We get Table 18 based on the security analysis in Section 5, Table 15 and Table 16.

Table 18. System comparison.

Schemes	F1	F2	F3	F4	F5	F6	F7
Y. Wang et al. [36]	×	×	×	-	−672 bit	+0.611 s	+1.01 ms
Odelu et al. [5]	×	×	√	√	+288 bit	+0.131 s	+2 ms
Tsai-Lo et al. [4]	×	×	×	×	−224 bit	+0.26 s	+3.16 ms
The proposed scheme	√	√	√	√	0	0	0

F1—KGC impersonate attack, F2—KGC track attack, F3—KGC eavesdrop attack, F4—session exposure attacks if ephemeral secrets are unexpectedly revealed under the CK–adversary, F5—comparison of communication cost, F6—comparison of computation cost at smart meter side (s), F7—comparison of computation cost at aggregator side (ms).

10. I3RES Project

Our work is part of the I3RES project (ICT-based intelligent management of integrated RES for the optimal operation of smart grid), which manages the grid capabilities, supports the deployment of services, and eases the development of user applications. The computational view of the I3RES is defined by the development of an open platform based on standardized and commercial off-the-shelf technologies, supporting the deployment of new services and decision-making mechanisms (1) to support tasks associated to monitoring in the context of the medium and low voltage network; (2) to manage the distribution of RES production in the distribution network associated to the stakeholders; and (3) to manage and control generation–consumption balance from the consumer point of view (DSM).

Our research group proposed a common middleware architecture for smart grids [42], which contributed to the standardization of designing and implementation of semantic middle architecture. It has been proven that sematic middleware architecture is a key element to create business models where new actors can join a new scenario, and where energy access and trade are democratized and more distributed than before. The general structure is depicted in Figure 3. The security component is a key part of the middleware, since it provides the required security mechanisms for the different application domains. The proposal presented in this paper was embedded within this security component, offering the security mechanisms needed for a smart grid application in an efficient way. Thus, it was feasible to deploy the security component in the different devices in smart grid.

Figure 3. Components of the common middleware architecture [42].

11. Conclusions

In this paper, we introduced an anonymous authentication scheme based on bilinear pairing and the computational Diffie–Hellman problem. First, we improved the registration phase, so that a smart meter’s private key will not be leaked to the Key Generation Center. Thus, the proposed scheme is immune to various potential attacks launched by the Key Generation Center. Besides, we greatly improved the efficiency of the scheme, the computation cost at both the smart meter side and aggregator side is much lower compared to the existing schemes. We also use the BAN logic and random oracle model to prove that the proposed scheme is secure. As data privacy of the smart meter is becoming an urgency, in future, we want to focus on data aggregation methods in smart grids to protect the privacy of the smart meter consumption. Finally, the proposal was fitted into the security component of a common middleware architecture, in order to provide the required security mechanisms for a smart grid application.