Control of Variable Speed Wind Turbines with Doubly Fed Asynchronous Generators for Stand-Alone Applications

Abstract

This paper addresses the design and implementation of a novel control of a variable speed wind turbine with doubly fed induction generator for stand-alone applications. In opposition to grid-tied applications, in stand-alone systems the voltage and frequency must be generated by the doubly fed induction generator. Therefore, a voltage and frequency controller is required for supplying the load at constant voltage and frequency. This controller is implemented by orientation of the generator stator flux vector along a synchronous reference axis. In this way, constant voltage and frequency is obtained and the generator will supply the active and reactive power demanded by the load, while the wind turbine will be responsible for achieving power balance in the system. Then, power control is assumed by the pitch actuator controlling the rotational speed of the wind turbine for power balancing. A load shedding mechanism is needed if the load power exceeds the maximum available wind power. Detailed simulation results are presented and discussed to demonstrate the capabilities and contributions of the proposed control scheme.

1. Introduction

Traditionally, wind farms have been operated to extract maximum energy yield, assuming certain conditions of voltage and frequency in the grid without contributing to its support [1]. So far, wind power plants are not connected massively in weak networks, and even less in isolated systems. However, recent innovations in micro-grids have aroused the interest in the standalone operation of the wind turbine (WT), as part of isolated grids, or as distributed generators in weak networks [2,3,4]. Another interesting area of application is in offshore wind farms connected to grid through an high-voltage direct current (HVdc) link. In these systems, the offshore wind farm is isolated from the grid. While in voltage-sourced converter (VSC)-HVdc technology the wind farm voltage is supplied by the VSC rectifier, if a line-commutated converter (LCC)-HVdc rectifier is employed the voltage must be generated by the wind turbine generators, which are now operating in the isolated grid of the wind farm feeding the LCC rectifier [5,6].

Unlike in grid-connected systems, WT in stand-alone and islanding operation must impose and maintain voltage and frequency while matching generation and load, despite of varying rotor speed due to wind speed variations and varying loads. When generation exceeds demanded load, generation must be reduced by controlling the pitch angle of blades. On the other hand, if generation is not enough to supply the load, a load shedding mechanism must be employed [7]. Thus, standalone operation requirements imply that WT must have active power control through aerodynamic control and power electronic converters control [8,9]. WT technologies that meet these requirements are those based on variable speed generators and pitch control. Among these technologies, the doubly fed induction generator (DFIG) arises as an attractive option, as this is the dominant technology in the market nowadays [10,11,12,13].

The grid-tied control of the DFIG has been extensively treated in literature. [14] presents an overview of control systems for DFIG, which includes a large amount of references. Nevertheless, the stand-alone operation of DFIG-based wind turbines has not been investigated much in the literature. In [15] the control of a DFIG supplying an isolated load is presented. In this paper an indirect stator-oriented vector control scheme is used to provide constant voltage and frequency for variations in both load and wind speed. Further studies on this topic when the DFIG is connected to an unbalanced load using sensorless control have been published by the same authors in [16], and more recently by other authors in [17]. A similar indirect control approach is proposed in [18], but using rotor flux control instead of rotor current.

In [19] a direct voltage control for a stand-alone DFIG is presented. This proposal uses the polar coordinates of the stator voltage vector for controlling the voltage magnitude and frequency. The proposed technique employs the rotor current magnitude and frequency to control the stator voltage magnitude and frequency, respectively. The same approach has also been proposed in [20,21].

This paper presents a new control strategy to regulate the voltage and frequency of the DFIG in stand-alone operation. While in [15] indirect control is used for flux orientation, here flux orientation is achieved by direct control of the flux angle in a very reliable and robust way. A direct voltage and frequency controller (DVFC) is used to maintain constant voltage and frequency during stand-alone operation. Voltage and frequency control is based on the orientation of the stator flux vector along a synchronous axis rotating at the reference synchronous speed. The ability of the DVFC to maintain the stator flux oriented toward the synchronous reference axis means that constant voltage and frequency is obtained, which in turn it means that the load active and reactive power is supplied by the DFIG.

Another important improvement is that while in [15] a dummy load is used to match the load power and the WT power following the maximum power point tracking (MPPT) strategy, here the WT power control (WTPC) assures that the WT produces just the power demanded by the load. The DVFC implies a load tracking strategy where the DFIG torque is imposed by the load. Therefore, this affects the rotational speed of the WT which in turn is controlled by the blade pitch actuator. By controlling the rotational speed, the power drawn from the WT is equal to the generator power and in turn to the load power.

Simulation results in a 2 MW WT are presented and discussed to demonstrate the capabilities of the proposed control scheme for stand-alone operation.

The paper is organized as follows. In Section 2, first the overall system is presented, and the WT and DFIG models are introduced, from which the proposed control scheme is obtained in Section 3. In Section 4, simulation results are presented and discussed and finally conclusions are established in Section 5.

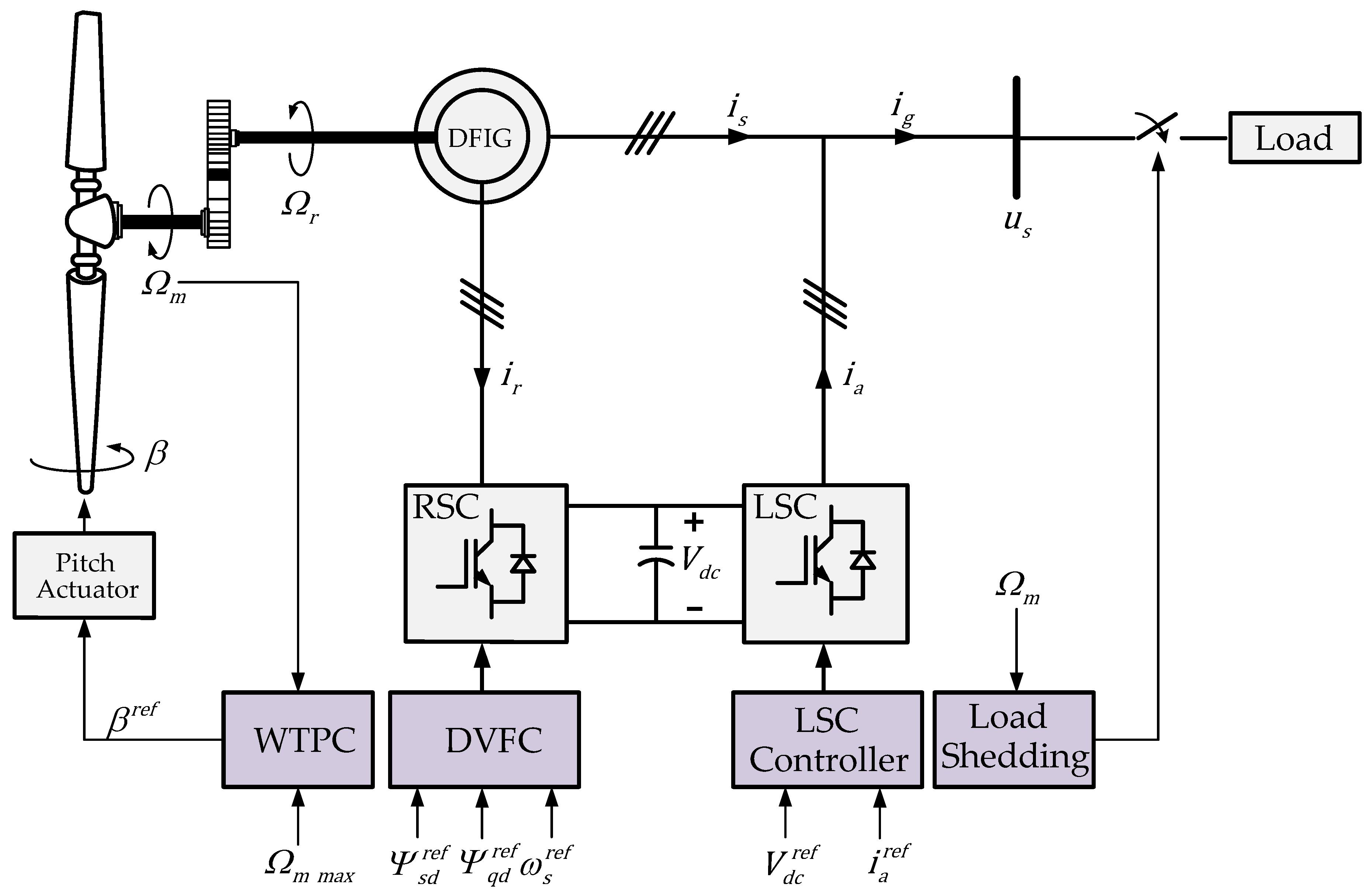
2. Stand-Alone DFIG Based Variable Speed Wind Turbine

The DFIG-based wind turbine configuration for stand-alone operation is shown in Figure 1. It consists of a variable speed wind turbine coupled to a wound rotor induction generator with its stator directly connected to the load and its rotor connected through a back-to-back converter.

In this configuration, the control system has two main components: the DVFC responsible for obtaining constant voltage and frequency at the generator terminals, and the WT power controller responsible for balancing power through the system. On the other hand, the operation of the DFIG also requires the control of the grid side converter, but this is done as conventional and therefore it is not going to be presented through the paper, as it is based on the well-known control of the DC link voltage for injecting the rotor power to the line [22]. The main difference here is that the line voltage must be created first by generator stator. Also, a load shedding controller is necessary for regulating the load when it is higher than the available wind power.

Finally, it has to be remarked again that the stator angular frequency, ω_s, of the DFIG in stand-alone operation is obtained from a control reference and not from the grid by a phase-locked loop (PLL), as in grid-connected operation. This is the angular frequency of the synchronous reference frame where the stator flux vector will be aligned by control, as presented in Section 3.

2.1. Wind Turbine Model

The simple and well-known one-mass mechanical model [22] is proposed to study the dynamics of the mechanical system and to derive the stability of the system.

$$T_m-T_g=J\frac{d{\Omega }_m}{dt}+D{\Omega }_m$$

(1)

where Ω_m is the wind turbine rotational speed, T_m and T_g are the wind turbine and the generator torque, respectively, and J and D are the inertia moment and friction coefficient, respectively.

The wind turbine model provides the turbine mechanical torque, T_m, based on the well-known steady-state power characteristics of the wind turbine [10,22]. The mechanical power, P_m, of the wind turbine is given by:

$$P_m=\frac{1}{2}\rho A{v}^3{C}_p(\lambda ,\beta )$$

(2)

where ρ is the air density; C_p is the performance coefficient of the wind turbine which is a function of the tip speed ratio, λ, and the blade pitch angle, β. In this model, the wind speed v represents the mean value of the upstream wind and A is the area swept by the turbine blades.

Therefore, the WT torque can be expressed as follows:

$$T_m=\frac{P_m}{{\Omega }_m}$$

(3)

The function C_p(λ, β) in (2) has been modeled by using the equation proposed in [23]. The maximum power point is obtained at C_{p max} = 0.48, with optimum tip speed ratio λ_B = 8.1, and for a minimum blade pitch angle β_min = 0. Figure 2 shows the WT power characteristics, for various wind speed values as a function of the rotational speed.

As will be shown in Section 3, maximum power locus (curve B-C-D) is particularly relevant because it defines the stability limit of the WT supplying an isolated load. This curve will be used in the control strategy of the WT to obtain the maximum active power that the generator can produce that guarantees a stable operation. The wind speed at point C, where maximum mechanical rotational speed, Ω_{m max}, is achieved, is also important, and it is defined as the base wind speed, v_B, as follows.

$$v_B=\frac{{\Omega }_{m\max }R}{{\lambda }_B}$$

(4)

where R is the turbine radius.

On the other hand, in a WT with active power control, the blade pitch angle β is controlled by a pitch servo mechanism [10,22]. The WT power control (WTPC, see Section 3.3) produces a blade angle set-point β^ref, followed by means of the pitch servo mechanism, turning the WT blades to control the mechanical power output.

2.2. DFIG Model

The DFIG stator and rotor voltage vector equations in a synchronous reference frame ω_s [10,22] are defined as:

$$-u_s=R_s{i}_s+\frac{d{\mathsf{\psi }}_s}{dt}+j{\omega }_s{\mathsf{\psi }}_s$$

(5)

$$-u_r=R_r{i}_r+\frac{d{\mathsf{\psi }}_r}{dt}+js{\omega }_s{\mathsf{\psi }}_r,$$

(6)

Being the stator and rotor flux linkages in the synchronous reference frame expressed as

$${\mathsf{\psi }}_s=L_s{i}_s+L_m{i}_r$$

(7)

$${\mathsf{\psi }}_r=L_m{i}_s+L_r{i}_r,$$

(8)

The electromagnetic torque can be expressed using the d-q components as follow:

$$T_g=\frac{3}{2}p\frac{L_m}{L_s}(i_{rd}{\psi }_{sq}-i_{rq}{\psi }_{sd})$$

(9)

where u_s, u_r, i_s, i_r, ψ_s, ψ_r are the space phasor of the stator and rotor voltages, currents and fluxes, respectively, and L_s, L_r and L_m are the stator, rotor and mutual inductance, respectively; R_s and R_r are the stator and rotor resistances, respectively; ω_s the stator angular frequency; s is the slip; and p is number of pole pairs.

3. System Control and Operation

The objective of the control system of a DFIG-based wind turbine operating in stand-alone mode is to maintain constant voltage and frequency at the generator terminals. The starting of the DIFG requires the pre-charge of the DC bus of the back-to-back converters. In grid-connected DFIG this is done from the grid through the line-side converter (LSC). In an islanded DFIG an external voltage source is needed for excitation because it is not possible charging the dc capacitor from the grid through the LSC. For pre-charging the DC bus, a reduced capacity battery system or even a small permanent magnet synchronous generator (PMSG) mechanically coupled to the DFIG shaft can be used, as proposed in [22].

Once the DC bus is pre-charged, the DFIG is controlled through the rotor-side converter (RSC) to obtain nominal voltage and frequency at the generator terminals at not-load. At this moment, the LSC will charge the DC bus at nominal voltage V_dc and the exciter is automatically blocked.

3.1. Direct Voltage and Frequency Control (DVFC)

The control of the stand-alone DFIG is based on the orientation of the stator flux vector along a synchronous reference frame (d-axis whose rotational speed is ${\omega }_s^{ref}$ = 2π⋅50 rad/s) generated by the controller. As long as the control is able to maintain the stator flux vector orientated along the d-axis, the frequency (50 Hz) is kept constant. Note that this principle is different from the conventional stator flux oriented control (FOC) employed in grid-tied DFIG [22]. In FOC the quadrature component of the flux is zero by definition, while in this new proposal it is the objective of the control system to make this component zero. Also, while in FOC the quadrature component of the flux zero, the quadrature component of the current is free, and it is used to set torque as desired. In contrast, here the quadrature component of the flux has to be taken to zero, and in order to achieve this, the quadrature component of the current will be used, as demonstrated below, that is, it is not free, as the generator torque cannot be set because it will be forced by the load power.

For such purposes, a DVFC based in the following principle is employed. In steady state, the stator flux vector will be aligned along the d-axis and therefore ψ_sd = |ψ_s^ref| and ψ_sq = 0. In order to achieve these references, two control channels are implemented. The first one to obtain constant stator flux and the second one to obtain constant frequency, i.e., ψ_sq = 0 (see Figure 3).

In Figure 4, the reference stator flux is compared to the d-axis component of the actual stator flux vector while the q-axis component of the actual stator flux vector is compared to zero. The reference d-axis is obtained by integration of the desired angular frequency ${\omega }_s^{ref}$.

Stator flux can be controlled by means of the rotor currents imposed by the RSC. Using (5) and (8) in d-q components, the following expressions can be obtained:

$${\tau }_s\frac{d{\psi }_{sd}}{dt}+{\psi }_{sd}=+L_m\cdot i_{rd}\underset{C_{ird}}{\underbrace{-{\tau }_s\cdot u_{sd}+{\omega }_s\cdot {\tau }_s\cdot {\psi }_{sq}}},$$

(10)

$${\tau }_s\frac{d{\psi }_{sq}}{dt}+{\psi }_{sq}=+L_m\cdot i_{rq}\underset{C_{irq}}{\underbrace{-{\tau }_s\cdot u_{sq}+{\omega }_s\cdot {\tau }_s\cdot {\psi }_{sd}}},$$

(11)

where ${\tau }_s=L_s/R_s$.

These expressions show that ψ_sd can be controlled by the d-axis component of the rotor current, i_rd, while ψ_sq can be controlled by the q-axis component of the rotor current, i_rq. There is also one coupling term in each equation (c_ird and c_irq) that can be compensated using the corresponding feed-forward terms as is shown in Figure 4.

Finally, two d-q current regulators will impose the desired current components through the d-q component of the rotor voltage, as shown in the following expressions, obtained from (6) and (8):

$$\sigma \cdot L_r\frac{d{i}_{rd}}{dt}+R_r{i}_{rd}=-u_{rd}\underset{C_{urd}}{\underbrace{-\frac{L_m}{L_s}\frac{d{\psi }_{sd}}{dt}+s{\omega }_s\frac{L_m}{L_s}\cdot {\psi }_{sq}-s{\omega }_s\sigma L_r{i}_{rq}}},$$

(12)

$$\sigma \cdot L_r\frac{d{i}_{rq}}{dt}+R_r{i}_{rq}=-u_{rq}\underset{C_{urq}}{\underbrace{-\frac{L_m}{L_s}\frac{d{\psi }_{sq}}{dt}-s{\omega }_s\frac{L_m}{L_s}\cdot {\psi }_{sd}-s{\omega }_s\sigma L_r{i}_{rd}}},$$

(13)

where $\sigma =1-L_m^2/(L_s{L}_r)$ and c_urd, and c_urq are also feed-forward compensation terms in the current control loops.

Figure 4 shows the complete voltage and frequency control (DVFC) scheme for the DFIG in stand-alone operation.

On the other hand, a stator flux estimator based on (7) is used for feeding-back the actual stator flux components, which requires the rotor and stator current measurements.

Also, note that because the whole control is oriented to a synchronous axis obtained directly by integration of the desired angular frequency (${\omega }_s^{ref}$), this signal is not subjected to any measurement noise or grid disturbance, which would be the case if a PLL was needed.

Another important consideration is that with controlled stator flux, the voltage deviation due to the load current is only due to the voltage drop in the stator resistance, as given by (5), which it is usually very small (between 0.005 and 0.02 p.u., depending on the generator rating). This means that the proposed DVFC does not require a voltage regulator to maintain voltage within acceptable margins.

3.2. Line Side Converter (LSC) Control

The line side converter is used for controlling the back-to-back converters DC voltage, as in grid-tied DFIG. By doing this, the control automatically assures that the rotor power is instantaneously transferred to the grid [22]. Moreover, the decoupled control of the LSC active and reactive current also allows for the adjustment of the LSC reactive current, that here it is set to zero following a minimum current strategy.

3.3. Wind Turbine Power Control (WTPC)

In the previous section, it has been shown how the DVFC will supply constant voltage and frequency to the load, being the generator power equal to the load power. Nevertheless, in steady state, power balance can only be achieved if the WT supplies to the generator exactly the active power demanded by the load (obviously, adding mechanical, magnetic and electric losses). In order to do so a WT power control (WTPC) is required.

From (1), neglecting the rotational losses for the sake of simplicity, in steady state the WT driving torque T_m must equal the braking torque of the generator T_g, or, by multiplying by the rotational speed (Ω_m), the WT power P_m equals the generator power P_g. On the other hand, if P_g is equal to the load power, P_l, the former relationship implies that if P_m is higher than P_l, Ω_m will increase, or decrease if P_m is lower than P_l. Therefore, power balance can be achieved by means of a speed control loop: only when P_m = P_l, Ω_m is kept constant. This speed control loop is shown in the Figure 5.

The speed control loop will ensure that the WT Ω_{m max} is not exceeded by acting on the pitch control system. The blade pitch angle β is adjusted reducing or increasing P_m until it matches P_l. Note that this control system is similar to the one used grid-tied WTs for limiting power when the wind speed is higher than rated. The only difference is that here Ω_{m max} can be achieved at any wind speed, depending on the load power value.

The pitch actuator block represents the dynamics of the pitch servo mechanism. The pitch actuator has been modeled as a first order function [23] defined by a gain parameter, k_b, and a time constant τ_b (see Appendix), where the input is the error signal between the pitch reference angle and the actual pitch angle. The output of this block is the pitch angle rate, which must be limited to the maximum and minimum allowable pitch angle rates (${\dot{\beta }}_{max}$,${\dot{\beta }}_{min}$). The actual pitch angle is then calculated by integrating the pitch angle rate and limited between the maximum and minimum allowable pitch angles (β_max, β_min).

The WT power control (WTPC) follows P_m by regulating the pitch angle. Figure 6a shows P_m output achieved for two values of β , at Ω_{m max}. Starting at P_m1, if P_l is gradually increased, β will be gradually decreased until the minimum pitch angle is achieved (β = β_min = 0). When the minimum pitch angle is achieved, the speed controller output reaches saturation, as the WT cannot longer increase the power extraction from the wind by adjusting β. From this point, two different situations could be derived if load power is increased even more.

For v > v_B (Figure 6a), P_m cannot be increased any further (point 2), because this requires increasing Ω_m and the WT is already rotating at maximum speed. Therefore, the maximum power of the WT has been achieved for the incoming wind, as given by the power curve of the WT. In Figure 2, this situation is given by the segment C-D, where, for example, the intersection point of the v = 11 m/s curve and the segment C-D would represent the maximum power that can be supplied at that wind speed (point 2 in Figure 6a).

For v < v_B (Figure 6b), when the minimum pitch angle is reached (point 1), and P_l is higher than P_m, the turbine will decelerate. But in this case, the deceleration of the WT will produce an adjustment of P_m until the power balance is met. Starting from a balanced power point 1 with minimum pitch angle and Ω_{m max}, if P_l increases up to point 2, the turbine will decelerate until the new power balance is met, that is, the power-speed characteristic of the turbine will ensure that any load power can be supplied until the maximum power point is achieved in point 3. When the maximum power point is reached, P_m cannot be increased any more as the maximum power of the WT has been achieved for the incoming wind. Load shedding is then required to maintain the power balance. In Figure 2, this situation is given by the curve B-C, where, for example, the intersection point of the v = 9 m/s curve and the curve B-C would represent the maximum power that can be supplied at that wind speed (point 3 in Figure 6b).

Note that the reasoning above is also valid in the case of a variation of P_m, due to a change in v. For example, if v decreases while supplying a given load, Ω_m will decrease, increasing C_p and therefore compensating the reduction in power due to a lower v.

3.4. Load Shedding

In order to assure that the maximum power that the WT can deliver (as given by the power-speed curve A-B-C-D of Figure 2) is not exceeded by the generator, leading to an unstable operation of the WT, a load regulation has to be implemented, which will be a function of Ω_m. When the WT reaches the stability limit, the load regulation scheme avoids falling into instability: a reduction in Ω_m that will lead to a further reduction of the WT power. This load regulation scheme could be a simple load shedding mechanism or a continuous load regulation mechanism, if the load can be regulated in such way, like in pumping stations or battery charging [24].

4. Simulation Results

The simulation results and analysis of the proposed DVFC and WTPC are discussed in this section. A detailed simulation in PSIM© software (UC3M, Leganés, Spain) [25] has been used for the validation, using the parameters of a 2 MW WT. The simulation workbench parameters are given in the Appendix.

4.1. Results With Constant Wind Speed and Variable Load

During this test wind speed is kept constant at 11 m/s. The WT is initially running at maximum speed (2000 rpm at the generator axis) at not-load as is shows in Figure 7. The rotational speed is controlled by adjusting the pitch angle through the speed controller of Figure 5. In this scheme the pitch actuator rate has been limited to 10°/s as a realistic value for simulation.

At t = 5 s, a 1 MW load is applied to the generator. In order to supply such load the blade pitch angle is decreased, increasing P_m while maintaining maximum rotational speed (see Figure 7). Following, at t = 10 s, the load is increased up to 2 MW and the blades are now pitched to the optimum position (β = 0) to increase P_m. At this point, the turbine is not supplying enough power to the load, producing a reduction of the rotational speed up to 1770 rpm. This reduction of the speed in turn produces an increase of C_p, which allows for supplying the load power.

Finally, at t = 15 s, a reactive load is connected. It is shown in Figure 8. The reactive power is automatically supplied by the generator by adjusting the d-axis rotor current and does not require any adjustment by the WTPC as is observed in Figure 7.

Figure 8 shows the load active and reactive power and the DFIG stator flux. Stator flux is presented in per unit because it is easier to understand regarding the proposed control system. Base value is given in the appendix. This figure shows the capability of the DVFC to control the stator flux as required, that is, maintaining constant d-axis flux equal to nominal, which in turn means maintaining nearly constant voltage, and maintaining constant q-axis flux equal to zero, which in turn means maintaining constant frequency. It has to be remarked that frequency control does not require frequency measurement, but the stator flux in the reference synchronous axis. Figure 8 also shows that the stator flux, and therefore the stator voltage, is gradually increased from zero to rated at the beginning of the simulation for starting-up (from 0 until 1 s). Figure 9 shows a zoom-in of the generated instantaneous voltage in one phase from 0 to 1.5 s.

On the other hand, Figure 10 shows a zoom of the instantaneous load voltages and currents around the active power step. As stated before, voltage is maintained nearly constant by the DVFC. Also, note that frequency is not affected by the rotational speed change at t = 10 s (see Figure 7), due to the fast electrical magnitudes control in opposition to the slower mechanical magnitudes control, showing a total decoupling between both control system.

Finally, Figure 11 shows a zoom-in of the instantaneous load voltage and current around t = 15 s (when a reactive load is applied to generator). This figure shows that the reactive load produces a transient voltage drop, but this disturbance is quickly compensated by the proposed voltage and frequency control system.

4.2. Results with Variable Wind Speed and Constant Load

In this simulation case, wind speed changes from 11 m/s to 15 m/s at t = 4 s, while supplying a constant 2 MW load. The test starts with the ending conditions of the previous one, when the WT is supplying the rated load at a rotational speed bellow maximum (1770 rpm approx.), and the pitch angle is adjusted to zero. Then, wind speed increases, producing an excess of power and increasing the rotational speed (see Figure 12). Nevertheless, the increase of the rotational speed (which produces a C_p reduction) is not enough for reducing the mechanical power, in order to balance the mechanical and the load power. So, when maximum rotational speed is achieved the pitch angle increases to reduce the WT power while maintaining maximum speed, which means that the mechanical power generated by the WT equals the power demanded by the load.

In this case, the electrical variables do not show any interesting behavior because the increase of wind speed mainly disturbs the mechanical system, and the small disturbance in the electrical system is quickly compensated for by the DVFC. Therefore, the load power is kept constant as the DVFC is able to maintain constant voltage and frequency during this test.

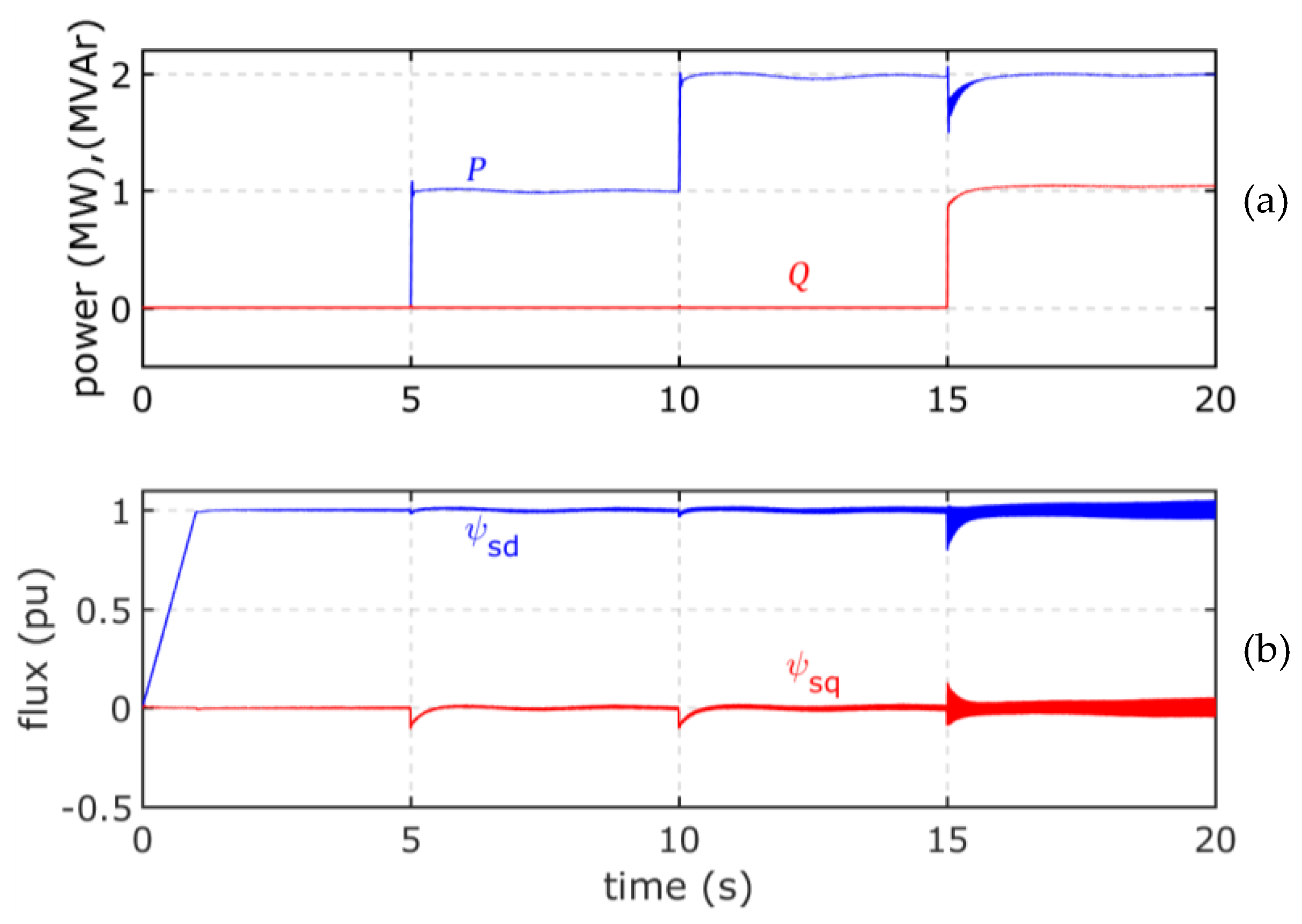
4.3. Results Under a Change in the Reference Signals with Constant Wind Speed and Constant Load

In this simulation case, wind speed and load are maintained constant, but a change is applied to the reference signals, that is, a change is applied to the reference frequency and also to the reference flux magnitude. Although this case does not represent any operational case, it is interesting for demonstrating the capabilities of the proposed control system.

This test starts with the ending conditions of the previous one. The WT is supplying rated power to a resistive load. Wind speed is 15 m/s and rotational speed is maximum (2000 rpm) with β = 14° approx. It is important to remark that although the resistive load is not affected by the frequency, the change in the flux frequency will produce a proportional increment of the voltage, which in turn will produce a change in the load power, proportional to the square of the voltage.

At t = 0.5 s, a frequency step from 50 Hz to 55 Hz is applied. This new frequency is quickly adjusted by the DVFC, as shown in Figure 13. This frequency adjustment produces only a small disturbance in the quadrature component of the stator flux, while no disturbance can be appreciated in the direct component of the stator flux. As a result, while maintaining constant rotational speed, the voltage frequency is increased by decreasing the frequency of the impressed rotor currents, as can be seen in Figure 14.

In the following test the stator flux magnitude is increased by 10%. Figure 15 shows the simulation results. The increase of the stator flux produces a proportional increase of the generated stator voltage. Which, on the other hand, produces an increment of the power demanded by the load (with a resistive load, power is proportional to the square of the voltage magnitude). Figure 16 shows the resulting stator voltage change.

5. Conclusions

This paper has presented a novel control scheme for the stand-alone operation of a variable speed wind turbine with DFIG. For such purpose the DFIG voltage and frequency, and also the WT power, have to be controlled in order to supply just the power demanded by the load.

The voltage and frequency control (DVFC) is based on the stator flux orientation along a synchronous reference axis. The rotational speed of this synchronous reference axis is generated by control and therefore is not subjected to any measurement disturbance. The magnitude and angular frequency of the stator flux is controlled through the rotor current components by the rotor voltages imposed by the RSC. With constant stator flux magnitude and frequency, the stator voltage is only subjected to a small disturbance due to the voltage drop in the stator resistance, and therefore a voltage regulator is not required.

On the other hand, the power drawn from the WT (WTPC) is controlled by means of a speed control loop relying on the pitch control of the WT. By controlling rotational speed, the power drawn from the WT is maintained equal to the generator power, and in turn to the load power.

The proposed control scheme has been validated in a simulated workbench. Simulation results show the response of proposed control system under varying load, wind speed and reference signals, demonstrating the capability of the proposed control system to maintain constant voltage and frequency under varying loads and wind velocities with an excellent dynamic response.