A Survey of WEC Reliability, Survival and Design Practices
Abstract
:1. Introduction
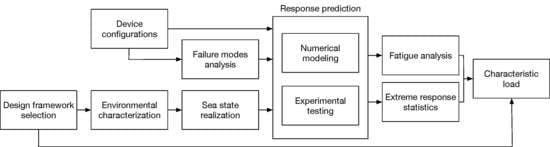
2. Device Configuration
3. Failure Modes Analysis
4. Design Frameworks
5. Environmental Characterization
6. Sea State Realization
7. Response Prediction
7.1. Numerical Modeling
7.2. Experimental Testing
8. Determining a Characteristic Load
8.1. Fatigue
8.2. Extreme Response Statistics
9. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ABS | American Bureau of Shipping |
| ACER | average conditional exceedance rate |
| CEC | current energy converter |
| CFD | computational fluid dynamics |
| CMS | conditional monitoring system |
| DNV | Det Norske Veritas |
| FEA | finite element analysis |
| FMEA | failure modes and effects analysis |
| FMECA | failure mode, effects and criticality analysis |
| IEC | International Electrotechnical Commission |
| I-FORM | inverse first-order reliability method |
| ITTC | International Towing Tank Conference |
| LCOE | levelized cost of energy |
| LEC | life extending control |
| NDBC | National Data Buoy Center |
| PCA | principle component analysis |
| PTO | power take-off |
| RM3 | Reference Model 3 |
| TEC | tidal energy converter |
| TS | technical specification |
| WEC | wave energy converter |
References
- Coe, R.G.; Neary, V.S.; Lawson, M.J.; Yu, Y.H.; Weber, J. Extreme Conditions Modeling Workshop Report; Technical Report NREL/TP-5000-62305 SNL/SAND2014-16384R; Sandia National Laboratories: Albuquerque, NM, USA, 2014.
- International Electrotechnical Commission. Marine Energy—Wave, Tidal and Other Water Current Converters—Part 2: Design Requirements for Marine Energy Systems; IEC TS 62600-2:2016; IEC: Geneva, Switzerland, 2016. [Google Scholar]
- NORSOK. Actions and Action Effects (N-003); N-003; Standards Norway: Oslo, Norway, 2007. [Google Scholar]
- Det Norske Veritas. Environmental Conditions and Environmental Loads; DNV-RP-C205; Det Norske Veritas: Oslo, Norway, 2007. [Google Scholar]
- American Bureau of Shipping. Design Standards for Offshore Wind Farms; M10PC00105; American Bureau of Shipping: Houston, TX, USA, 2011. [Google Scholar]
- Det Norske Veritas. Design of Offshore Wind Turbine Structures; DNV-OS-J101; Det Norske Veritas: Oslo, Norway, 2014. [Google Scholar]
- International Electrotechnical Commission. Design Requirements for Offshore Wind Turbines; IEC 61400-3:2009; International Electrotechnical Commission: Geneva, Switzerland, 2014. [Google Scholar]
- Coe, R.G.; Neary, V.S. Review of Methods for Modeling Wave Energy Converter Survival in Extreme Sea States. In Proceedings of the 2nd Marine Energy Technology Symposium, Seattle, WA, USA, 15–17 April 2014. [Google Scholar]
- Whittaker, T.; Collier, D.; Folley, M.; Osterried, M.; Henry, A.; Crowley, M. The development of Oyster—A shallow water surging wave energy converter. In Proceedings of the 7th European Wave and Tidal Energy Conference (EWTEC2007), Porto, Portugal, 11–14 September 2007. [Google Scholar]
- Beatty, S.J.; Hiles, C.E.; Nicoli, R.S.; Adamson, J.E.; Buckham, B.J. Design Synthesis of a Wave Energy Converter. In Proceedings of the 28th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2009), Honolulu, HI, USA, 31 May–5 June 2009. [Google Scholar]
- Yu, Y.H.; Li, Y. Preliminary results of a RANS simulation for a floating point absorber wave energy system under extreme wave conditions. In Proceedings of the 30th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2011), Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar]
- Stillinger, C.; Brekken, T.; von Jouanne, A. Furthering the study of real-time life extending control for ocean energy conversion. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Tom, N.M.; Yu, Y.H.; Wright, A.D.; Lawson, M.J. Pseudo-spectral control of a novel oscillating surge wave energy converter in regular waves for power optimization including load reduction. Ocean Eng. 2017, 137, 352–366. [Google Scholar] [CrossRef]
- Hals, J.; Falnes, J.; Moan, T. A Comparison of Selected Strategies for Adaptive Control of Wave Energy Converters. J. Offshore Mech. Arct. Eng. 2011, 133, 031101. [Google Scholar] [CrossRef]
- Wang, L.; Engström, J.; Göteman, M.; Isberg, J. Constrained optimal control of a point absorber wave energy converter with linear generator. J. Renew. Sustain. Energy 2015, 7, 043127. [Google Scholar] [CrossRef]
- Coe, R.G.; Bacelli, G.; Wilson, D.; Abdelkhalik, O.; Korde, U.A.; Robinett, R.D., III. A comparison of control strategies for wave energy converters. Int. J. Mar. Energy 2017, 20, 45–63. [Google Scholar]
- Retzler, C.H.; Pizer, D.J. The hydrodynamics of the PELAMIS wave energy device: experimental and numerical results. In Proceedings of the 20th International Conference on Offshore Mechanics and Arctic Engineering (OMAE2001), Rio de Janeiro, Brazil, 3–8 June 2001. [Google Scholar]
- Stallard, T.J.; Weller, S.D.; Stansby, P.K. Limiting heave response of a wave energy device by draft adjustment with upper surface immersion. Appl. Ocean Res. 2009, 31, 282–289. [Google Scholar] [CrossRef]
- Palm, J.; Eskilsson, C.; Moura Paredes, G.; Bergdahl, L. CFD Simulation of a Moored Floating Wave Energy Converter. In Proceedings of the 10th European Wave and Tidal Energy Conference (EWTEC), Aalborg, Denmark, 2–6 September 2013. [Google Scholar]
- Parmeggiani, S.; Kofoed, J.P.; Friis-Madsen, E. Extreme Loads on the Mooring Lines and Survivability Mode for the Wave Dragon Wave Energy Converter. In Proceedings of the World Renewable Energy Congress (WREC), Linköping, Sweden, 8–13 May 2011. [Google Scholar]
- Parmeggiani, S.; Muliawan, M.J.; Gao, Z.; Moan, T.; Friis-Madsen, E. Comparison of Mooring Loads in Survivability Mode on the Wave Dragon Wave Energy Converter Obtained by a Numerical Model and Experimental Data. In Proceedings of the 31st International Conference on Ocean, Offshore and Arctic Engineering (OMAE2012), Rio de Janeiro, Brazil, 1–6 July 2012; pp. 341–350. [Google Scholar]
- Pecher, A.; Kofoed, J.P.; Larsen, T. Design Specifications for the Hanstholm WEPTOS Wave Energy Converter. Energies 2012, 5, 1001–1017. [Google Scholar] [CrossRef]
- Wan, L.; Gao, Z.; Moan, T. Experimental and numerical study of hydrodynamic responses of a combined wind and wave energy converter concept in survival modes. Coast. Eng. 2015, 104, 151–169. [Google Scholar] [CrossRef]
- Zurkinden, A.S.; Damkilde, L.; Gao, Z.; Moan, T. Structural modeling and analysis of a wave energy converter applying dynamical substructuring method. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering (OMAE2013), Nantes, France, 9–14 June 2013. [Google Scholar]
- Kenny, C.J.; Findlay, D.; Lazakis, I.; Shek, J.; Thies, P.R. Development of a Condition Monitoring System for an Articulated Wave Energy Converter. In Proceedings of the European Safety and Reliability Conference (ESREL 2016), Glasgow, Scotland, 25–29 September 2016. [Google Scholar]
- Kenny, C.J.; Findlay, D.; Thies, P.R.; Shek, J.; Lazakis, I. Lessons Learned from 3 Years of Failure: Validating an FMEA with Historical Failure Data. In Proceedings of the 12th European Wave and Tidal Energy Conference (EWTEC2017), Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Okoro, U.; Kolios, A.; Cui, L. Multi-criteria risk assessment approach for components risk ranking—The case study of an offshore wave energy converter. Int. J. Mar. Energy 2017, 17, 21–39. [Google Scholar]
- Coe, R.G.; Michelen, C.; Eckert-Gallup, A.; Sallaberry, C. Full long-term design response analysis of a wave energy converter. Renew. Energy 2018, 116, 356–366. [Google Scholar] [CrossRef]
- Muliawan, M.J.; Gao, Z.; Moan, T. Application of the Contour Line Method for Estimating Extreme Responses in the Mooring Lines of a Two-Body Floating Wave Energy Converter. J. Offshore Mech. Arct. Eng. 2013, 135, 031301. [Google Scholar]
- Winterstein, S.R.; Ude, T.C.; Cornell, C.A.; Bjerager, P.; Haver, S. Environmental parameters for extreme response: Inverse FORM with omission factors. In Proceedings of the 6th International Conference on Structural Safety & Reliability (ICOSSAR), Innsbruck, Austria, 9–13 August 1993. [Google Scholar]
- Haver, S.; Winterstein, S.R. Environmental contour lines: A method for estimating long term extremes by a short term analysis. Trans. Soc. Nav. Archit. Mar. Eng. 2009, 116, 116–127. [Google Scholar]
- Yu, Y.H.; Van Rij, J.; Coe, R.; Lawson, M. Preliminary Wave Energy Converters Extreme Load Analysis. In Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2015), St. John’s, NL, Canada, 19–24 June 2015. [Google Scholar]
- Baarholm, G.S.; Haver, S.; ∅kland, O.D. Combining contours of significant wave height and peak period with platform response distributions for predicting design response. Mar. Struct. 2010, 23, 147–163. [Google Scholar] [CrossRef]
- Haver, S.; Sagli, G.; Gran, T. Long term response analysis of fixed and floating structures. In Proceedings of the 1998 International OTRC Symposium, Houston, TX, USA, 30 April–1 May 1998. [Google Scholar]
- Rendon, E.A.; Manuel, L. Long-term loads for a monopile-supported offshore wind turbine. Wind Energy 2014, 17, 209–223. [Google Scholar] [CrossRef]
- Ren, N.; Gao, Z.; Moan, T.; Wan, L. Long-term performance estimation of the Spar-Torus-Combination (STC) system with different survival modes. Ocean Eng. 2015, 108, 716–728. [Google Scholar] [CrossRef]
- Michelen, C.; Coe, R. Comparison of Methods for Estimating Short-Term Extreme Response of Wave Energy Converters. In Proceedings of the OCEANS 2015—MTS/IEEE Washington, Washington, DC, USA, 19–22 October 2015. [Google Scholar]
- Fonseca, N.; Pascoal, R.; Morais, T.; Dias, R. Design of a mooring system with synthetic ropes for the FLOW wave energy converter. In Proceedings of the 28th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2009), Honolulu, HI, USA, 31 May–5 June 2009; pp. 1189–1198. [Google Scholar]
- Agarwal, P. Structural Reliability of Offshore Wind Turbines. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2008. [Google Scholar]
- Ruggiero, P.; Komar, P.D.; Allan, J.C. Increasing wave heights and extreme value projections: The wave climate of the U.S. Pacific Northwest. Coast. Eng. 2010, 57, 539–552. [Google Scholar] [CrossRef]
- Young, I.; Zieger, S.; Babanin, A.V. Global trends in wind speed and wave height. Science 2011, 332, 451–455. [Google Scholar] [CrossRef] [PubMed]
- Reeve, D.; Chen, Y.; Pan, S.; Magar, V.; Simmonds, D.; Zacharioudaki, A. An investigation of the impacts of climate change on wave energy generation: The Wave Hub, Cornwall, UK. Renew. Energy 2011, 36, 2404–2413. [Google Scholar] [CrossRef] [Green Version]
- Haver, S. On the joint distribution of heights and periods of sea waves. Ocean Eng. 1987, 14, 359–376. [Google Scholar] [CrossRef]
- Silva-González, F.; Heredia-Zavoni, E.; Montes-Iturrizaga, R. Development of environmental contours using Nataf distribution model. Ocean Eng. 2013, 58, 27–34. [Google Scholar] [CrossRef]
- Huseby, A.B.; Vanem, E.; Natvig, B. A new approach to environmental contours for ocean engineering applications based on direct Monte Carlo simulations. Ocean Eng. 2013, 60, 124–135. [Google Scholar] [CrossRef]
- Vanem, E.; Bitner-Gregersen, E.M. Alternative environmental contours for marine structural design—A comparison study. J. Offshore Mech. Arct. Eng. 2015, 137, 051601. [Google Scholar]
- Eckert-Gallup, A.C.; Sallaberry, C.J.; Dallman, A.R.; Neary, V.S. Application of principal component analysis (PCA) and improved joint probability distributions to the inverse first-order reliability method (I-FORM) for predicting extreme sea states. Ocean Eng. 2016, 112, 307–319. [Google Scholar] [CrossRef]
- Coe, R.G.; Michelen, C.; Eckert-Gallup, A.C.; Yu, Y.H.; van Rij, J. WDRT: A toolbox for design-response analysis of wave energy converters. In Proceedings of the 4th Marine Energy Technology Symposium, Washington, DC, USA; 2016. [Google Scholar]
- Ochi, M.K. Ocean Waves: The Stochastic Approach; Cambridge University Press: Cambridge, UK, 2005; Volume 6. [Google Scholar]
- Faltinsen, O. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1993; Volume 1. [Google Scholar]
- Ochi, M.K. Wave statistics for the design of ships and ocean structures. Trans. Soc. Nav. Archit. Mar. Eng. 1978, 86, 47–76. [Google Scholar]
- Tromans, P.S.; Anaturk, A.R.; Hagemeijer, P. A new model for the kinematics of large ocean waves-application as a design wave. In Proceedings of the 1st International Offshore and Polar Engineering Conference, Edinburgh, UK, 11–16 August 1991; pp. 64–71. [Google Scholar]
- Orszaghova, J.; Rafiee, A.; Wolgamot, H.; Draper, S.; Taylor, P. Experimental Study of Extreme Responses of a Point Absorber Wave Energy Converter. In Proceedings of the 20th Australasian Fluid Mechanics Conference, Perth, Australia, 1–8 December 2016. [Google Scholar]
- Weller, S.; Stallard, T.; Stansby, P. Experimental measurements of the complex motion of a suspended axisymmetric floating body in regular and near-focused waves. Appl. Ocean Res. 2013, 39, 137–145. [Google Scholar] [CrossRef]
- Rafiee, A.; Wolgamot, H.; Draper, S.; Orszaghova, J.; Fiévez, J.; Sawyer, T. Identifying the design wave group for the extreme response of a point absorber wave energy converter. In Proceedings of the Asian Wave and Tidal Energy Conference (AWTEC), Singapore, 24–28 October 2016. [Google Scholar]
- Santo, H.; Taylor, P.; Moreno, E.C.; Stansby, P.; Taylor, R.E.; Sun, L.; Zang, J. Extreme motion and response statistics for survival of the three-float wave energy converter M4 in intermediate water depth. J. Fluid Mech. 2017, 813, 175–204. [Google Scholar] [CrossRef]
- Hann, M.; Greaves, D.; Raby, A.; Howey, B. Use of constrained focused waves to measure extreme loading of a taut moored floating wave energy converter. Ocean Eng. 2018, 148, 33–42. [Google Scholar] [CrossRef]
- Quon, E.; Platt, A.; Yu, Y.H.; Lawson, M. Application of Most Likely Extreme Response Method for Wave Energy Converters. In Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2016), Busan, Korea, 19–24 June 2016. [Google Scholar]
- Taylor, P.H.; Jonathan, P.; Harland, L.A. Time domain simulation of jack-up dynamics with the extremes of a Gaussian process. J. Vib. Acoust. 1997, 119, 624–628. [Google Scholar] [CrossRef]
- Göteman, M.; Engström, J.; Eriksson, M.; Hann, M.; Ransley, E.; Greaves, D.; Leijon, M. Wave loads on a point-absorbing wave energy device in extreme waves. In Proceedings of the 25th International Ocean and Polar Engineering Conference, Kona, HI, USA, 21–26 June 2015. [Google Scholar]
- Topper, M.B. Guidance for Numerical Modelling in Wave and Tidal Energy; SuperGen Marine; The University of Edinburgh: Edinburgh, Scotland, 2010. [Google Scholar]
- Penalba, M.; Giorgi, G.; Ringwood, J.V. Mathematical modelling of wave energy converters: A review of nonlinear approaches. Renew. Sustain. Energy Rev. 2017, 78, 1188–1207. [Google Scholar] [CrossRef]
- Folley, M.; Babarit, A.; Child, B.; Forehand, D.; O’Boyle, L.; Silverthorne, K.; Spinneken, J.; Stratigaki, V.; Troch, P. A Review of Numerical Modelling of Wave Energy Converter Arrays. In Proceedings of the 31st International Conference on Ocean, Offshore and Arctic Engineering (OMAE2012), Rio de Janeiro, Brazil, 1–6 July 2012; pp. 535–545. [Google Scholar]
- Li, Y.; Yu, Y.H. A synthesis of numerical methods for modeling wave energy converter-point absorbers. Renew. Sustain. Energy Rev. 2012, 16, 4352–4364. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Newman, J.N. Marine Hydrodynamics; MIT Press: Cambridge, MA, USA, 1978. [Google Scholar]
- WAMIT. WAMIT User Manual, 7th ed.; WAMIT: Chestnut Hill, MA, USA, 2012. [Google Scholar]
- Babarit, A.; Delhommeau, G. Theoretical and numerical aspects of the open source BEM solver NEMOH. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC2015), Nantes, France, 6–11 September 2015. [Google Scholar]
- Bacelli, G.; Coe, R.G.; Patterson, D.; Wilson, D. System Identification of a Heaving Point Absorber: Design of Experiment and Device Modeling. Energies 2017, 10, 472. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, J.H.; Kim, Y. Time series prediction of nonlinear ship structural responses in irregular seaways using a third-order Volterra model. J. Fluids Struct. 2014, 49, 322–337. [Google Scholar] [CrossRef]
- Gkikas, G.; Athanassoulis, G. Development of a novel nonlinear system identification scheme for the pressure fluctuation inside an oscillating water column-wave energy converter Part I: Theoretical background and harmonic excitation case. Ocean Eng. 2014, 80, 84–99. [Google Scholar] [CrossRef]
- Cummins, W.E. The Impulse Response Function and Ship Motions; Technical Report DTNSDRC 1661; Department of the Navy, David Taylor Model Basin: Bethesda, MD, USA, 1962. [Google Scholar]
- Lawson, M.; Yu, Y.H.; Nelessen, A.; Ruehl, K.; Michelen, C. Implementing Nonlinear Buoyancy and Excitation Forces in the WEC-Sim Wave Energy Converter Modeling Tool. In Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering (OMAE2014), San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Penalba, M.R.; Mérigaud, A.; Gilloteaux, J.C.; Ringwood, J. Nonlinear Froude-Krylov force modelling for two heaving wave energy point absorbers. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC2015), Nantes, France, 6–11 September 2015. [Google Scholar]
- Merigaud, A.; Gilloteaux, J.C.; Ringwood, J. A nonlinear extension for linear boundary element methods in wave energy device modelling. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering (OMAE2012), Rio de Janeiro, Brazil, 1–6 July 2012. [Google Scholar]
- Gilloteaux, J.C.; Bacelli, G.; Ringwood, J. A non-linear potential model to predict large-amplitudes-motions: Application to a multi-body wave energy converter. In Proceedings of the 10th World Renewable Energy Congress (WREC), Glasgow, Scotland, 19–25 July 2008; Sayigh, A., Ed.; WREC: Brighton, UK, 2008; pp. 934–939. [Google Scholar]
- Zurkinden, A.S.; Ferri, F.; Beatty, S.; Kofoed, J.P.; Kramer, M. Non-linear numerical modeling and experimental testing of a point absorber wave energy converter. Ocean Eng. 2014, 78, 11–21. [Google Scholar] [CrossRef]
- Sirnivas, S.; Yu, Y.H.; Hall, M.; Bosma, B. Coupled mooring analyses for the WEC-Sim wave energy converter design tool. In Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2016), Busan, Korea, 19–24 June 2016. [Google Scholar]
- Giorgi, G.; Ringwood, J.V. Nonlinear Froude-Krylov and viscous drag representations for wave energy converters in the computation/fidelity continuum. Ocean Eng. 2017, 141, 164–175. [Google Scholar] [CrossRef]
- Bharath, A.; Nader, J.R.; Penesis, I.; Macfarlane, G. Nonlinear hydrodynamic effects on a generic spherical wave energy converter. Renew. Energy 2018, 118, 56–70. [Google Scholar] [CrossRef]
- Kring, D.C. Time Domain Ship Motions by a Three-Dimensional Rankine Panel Method. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1994. [Google Scholar]
- Shin, Y.; Belenky, V.; Lin, W.; Weems, K.; Engle, A. Nonlinear Time Domain Simulation Technology for Seakeeping and Wave-Load Analysis for Modern Ship Design. Trans. Soc. Nav. Archit. Mar. Eng. 2003, 111, 557–583. [Google Scholar]
- Letournel, L.; Ferrant, P.; Babarit, A.; Ducrozet, G.; Harris, J.C.; Benoit, M.; Dombre, E. Comparison of fully nonlinear and weakly nonlinear potential flow solvers for the study of wave energy converters undergoing large amplitude motions. In Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering (OMAE2014), San Francisco, CA, USA, 8–13 June 2014; p. 23912. [Google Scholar]
- Greenhow, M.; Vinje, T.; Brevig, P.; Taylor, J. A theoretical and experimental study of the capsize of Salter’s duck in extreme waves. J. Fluid Mech. 1982, 118, 221–239. [Google Scholar] [CrossRef]
- Guerber, E.; Benoit, M.; Grilli, S.T.; Buvat, C. A fully nonlinear implicit model for wave interactions with submerged structures in forced or free motion. Eng. Anal. Bound. Elem. 2012, 36, 1151–1163. [Google Scholar] [CrossRef] [Green Version]
- International Towing Tank Conference. Practical Guidelines for Ship CFD Applications; Technical Report 7.5-03-02-03; International Towing Tank Conference: Rio de Janeiro, Brazil, 2011. [Google Scholar]
- Ransley, E.; Greaves, D.; Raby, A.; Simmonds, D.; Hann, M. Survivability of wave energy converters using CFD. Renew. Energy 2017, 109, 235–247. [Google Scholar] [CrossRef]
- Yu, Y.H.; Li, Y. Reynolds-Averaged Navier-Stokes simulation of the heave performance of a two-body floating-point absorber wave energy system. Comput. Fluids 2013, 73, 104–114. [Google Scholar] [CrossRef]
- Neary, V.S.; Lawson, M.; Previsic, M.; Copping, A.; Hallett, K.C.; Labonte, A.; Rieks, J.; Murray, D. Methodology for Design and Economic Analysis of Marine Energy Conversion (MEC) Technologies; Technical Report SAND2014-9040; Sandia National Laboratories: Albuquerque, NM, USA, 2014.
- Sjökvist, L.; Göteman, M. Peak Forces on Wave Energy Linear Generators in Tsunami and Extreme Waves. Energies 2017, 10, 1323. [Google Scholar]
- Westphalen, J.; Greaves, D.M.; Raby, A.; Hu, Z.Z.; Causon, D.M.; Mingham, C.G.; Omidvar, P.; Stansby, P.K.; Rogers, B.D. Investigation of Wave-Structure Interaction Using State of the Art CFD Techniques. Open J. Fluid Dyn. 2014, 4, 18–43. [Google Scholar] [CrossRef]
- Madhi, F.; Yeung, R.W. On survivability of asymmetric wave-energy converters in extreme waves. Renew. Energy 2017, in press. [Google Scholar]
- Holmes, B. Tank Testing of Wave Energy Conversion Systems: Marine Renewable Energy Guides; European Marine Energy Centre: Orkney, Scotland, 2009. [Google Scholar]
- International Towing Tank Conference. Wave Energy Converter Model Test Experiments; 7.5-02-07-03.7; International Towing Tank Conference: Rio de Janeiro, Brazil, 2011. [Google Scholar]
- International Towing Tank Conference. Final Report and Recommendations to the 23rd ITTC—The Specialist Committee on Waves; International Towing Tank Conference: Rio de Janeiro, Brazil, 2002. [Google Scholar]
- Payne, G. Guidance for the Experimental Tank Testing of Wave Energy Converters; SuperGen Marine; University of Strathclyde: Glasgow, Scotland, 2008. [Google Scholar]
- Henry, A.; Kimmoun, O.; Nicholson, J.; Dupont, G.; Wei, Y.; Dias, F. A two dimensional experimental investigation of slamming of an oscillating wave surge converter. In Proceedings of the Twenty-Fourth International Ocean and Polar Engineering Conference, Busan, Korea, 15–20 June 2014. [Google Scholar]
- Blommaert, C.; Van Paepegem, W.; Dhondt, P.; De Backer, P.G.; Degrieck, J.; De Rouck, J.; Vantorre, M.; Van Slycken, J.; De Baere, I.; De Backer, H. Large scale slamming tests on composite buoys for wave energy applications. In Proceedings of the 17th International Conference on Composite Materials (ICCM), Edinburgh, UK, 27–31 July 2010. [Google Scholar]
- Van Paepegem, W.; Blommaert, C.; De Baere, I.; Degrieck, J.; De Backer, G.; De Rouck, J.; Degroote, J.; Vierendeels, J.; Matthys, S.; Taerwe, L. Slamming wave impact of a composite buoy for wave energy applications: Design and large-scale testing. Polym. Compos. 2011, 32, 700–713. [Google Scholar] [CrossRef]
- Hughes, O.F.; Paik, J.K. Ship Structural Analysis and Design; Society of Naval Architects and Marine Engineers: Jersey City, NJ, USA, 2010. [Google Scholar]
- Lewis, E. Principles of Naval Architecture: Stability and Strength; Principles of Naval Architecture, Society of Naval Architects and Marine Engineers: Jersey City, NJ, USA, 1989. [Google Scholar]
- Veldkamp, D. Chances in Wind Energy: A Probabilistic Approach to Wind Turbine Fatigue Design. Ph.D. Thesis, Delft University of Technology (TU Delft), Delft, The Netherlands, 2006. [Google Scholar]
- Downing, S.D.; Socie, D. Simple rainflow counting algorithms. Int. J. Fatigue 1982, 4, 31–40. [Google Scholar] [CrossRef]
- Ambühl, S.; Ferri, F.; Kofoed, J.P.; Sørensen, J.D. Fatigue reliability and calibration of fatigue design factors of wave energy converters. Int. J. Mar. Energy 2015, 10, 17–38. [Google Scholar] [CrossRef]
- Ambühl, S.; Kramer, M.; Sørensen, J.D. Reliability-based Calibration of Partial Safety Factors for Wave Energy Converters. In Proceedings of the International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP12), Vancouver, BC, Canada, 12–15 July 2015. [Google Scholar]
- Ambühl, S.; Kramer, M.; Sørensen, J.D. Reliability-Based Structural Optimization of Wave Energy Converters. Energies 2014, 7, 8178–8200. [Google Scholar] [CrossRef]
- Sørensen, J.D. Reliability and Maintenance for Offshore Wind Turbines and Wave Energy Devices. In Renewable Energies Offshore; CRC Press: Boca Raton, FL, USA, 2015; pp. 39–46. [Google Scholar]
- Thies, P.R.; Johanning, L.; Harnois, V.; Smith, H.C.; Parish, D.N. Mooring line fatigue damage evaluation for floating marine energy converters: Field measurements and prediction. Renew. Energy 2014, 63, 133–144. [Google Scholar] [CrossRef] [Green Version]
- Ferri, F.; Ambühl, S.; Fischer, B.; Kofoed, J.P. Balancing power output and structural fatigue of wave energy converters by means of control strategies. Energies 2014, 7, 2246–2273. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Naess, A.; Moan, T. Stochastic Dynamics of Marine Structures; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Naess, A. Extreme value estimates based on the envelope concept. Appl. Ocean Res. 1982, 4, 181–187. [Google Scholar] [CrossRef]
- Naess, A.; Gaidai, O. Estimation of extreme values from sampled time series. Struct. Saf. 2009, 31, 325–334. [Google Scholar] [CrossRef]
- Vazquez-Hernandez, A.O.; Sagrilo, L.V.S.; Ellwanger, G.B. On the Extreme Analysis Applied to Moored Floating Platforms. In Proceedings of the 22nd International Conference on Ocean, Offshore and Arctic Engineering (OMAE2003), Cancun, Mexico, 8–13 June 2003; pp. 241–247. [Google Scholar]
- Lian, G.; Haver, S.K. Estimating long term extreme slamming from breaking waves. In Proceedings of the 34th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2015), St. Johns, NL, Canada, 31 May–5 June 2015. [Google Scholar]





© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coe, R.G.; Yu, Y.-H.; Van Rij, J. A Survey of WEC Reliability, Survival and Design Practices. Energies 2018, 11, 4. https://doi.org/10.3390/en11010004
Coe RG, Yu Y-H, Van Rij J. A Survey of WEC Reliability, Survival and Design Practices. Energies. 2018; 11(1):4. https://doi.org/10.3390/en11010004
Chicago/Turabian StyleCoe, Ryan G., Yi-Hsiang Yu, and Jennifer Van Rij. 2018. "A Survey of WEC Reliability, Survival and Design Practices" Energies 11, no. 1: 4. https://doi.org/10.3390/en11010004
APA StyleCoe, R. G., Yu, Y.-H., & Van Rij, J. (2018). A Survey of WEC Reliability, Survival and Design Practices. Energies, 11(1), 4. https://doi.org/10.3390/en11010004