Modeling Aggregate Hourly Energy Consumption in a Regional Building Stock
Abstract
:1. Introduction
1.1. Background
1.2. Methods for Modeling Aggregate Hourly Energy Consumption
1.3. Objectives
2. Data and Methods
2.1. Model Setup
2.2. Decomposing Hourly Electricity Consumption
2.3. Modeling Hourly Electricity Consumption
2.4. Modeling Hourly District Heat Consumption
2.5. Modeling Aggregate Regional Hourly Energy Consumption
3. Input Data
3.1. Number and Size of Buildings and Dwellings
3.2. Heating Systems
4. Results
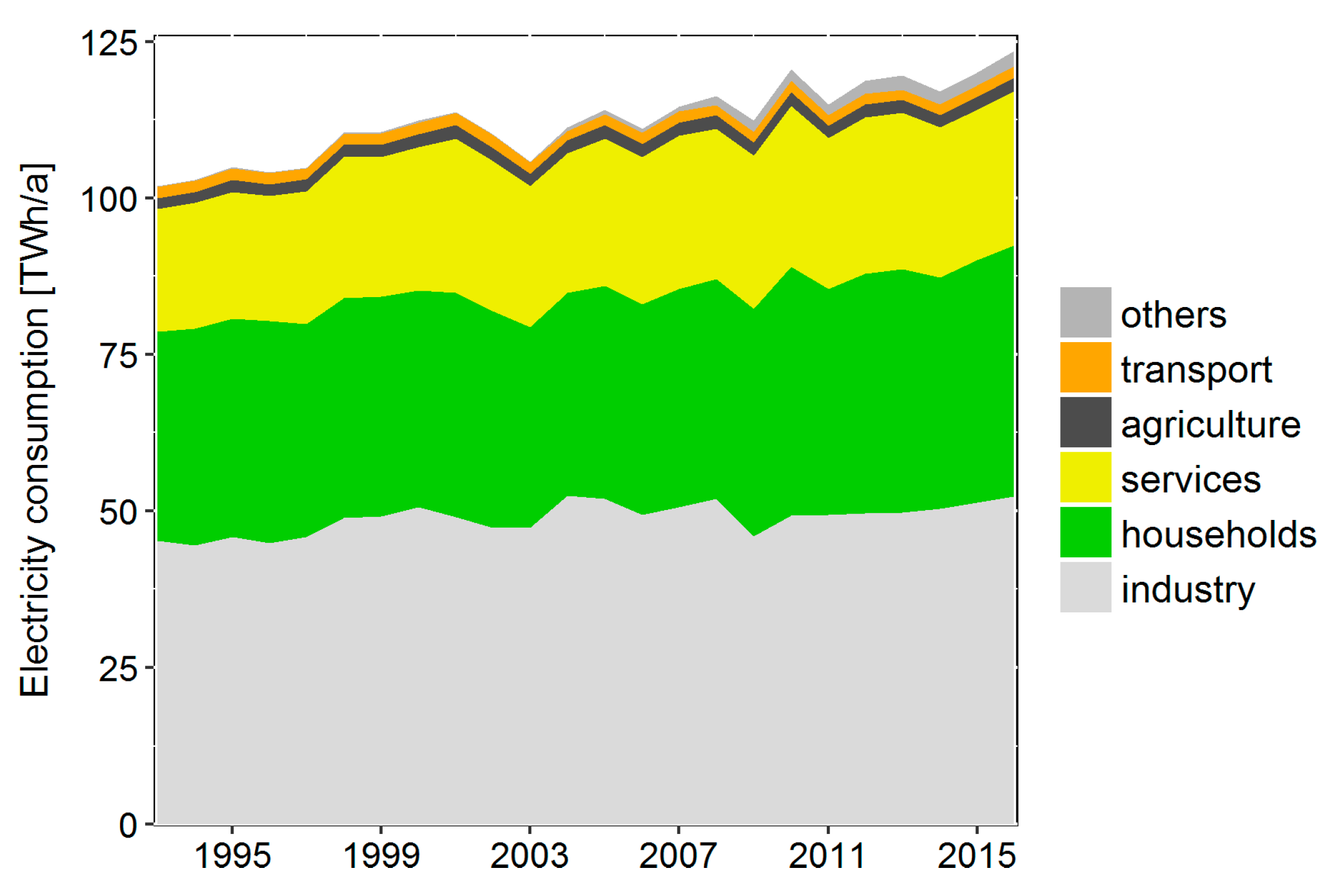
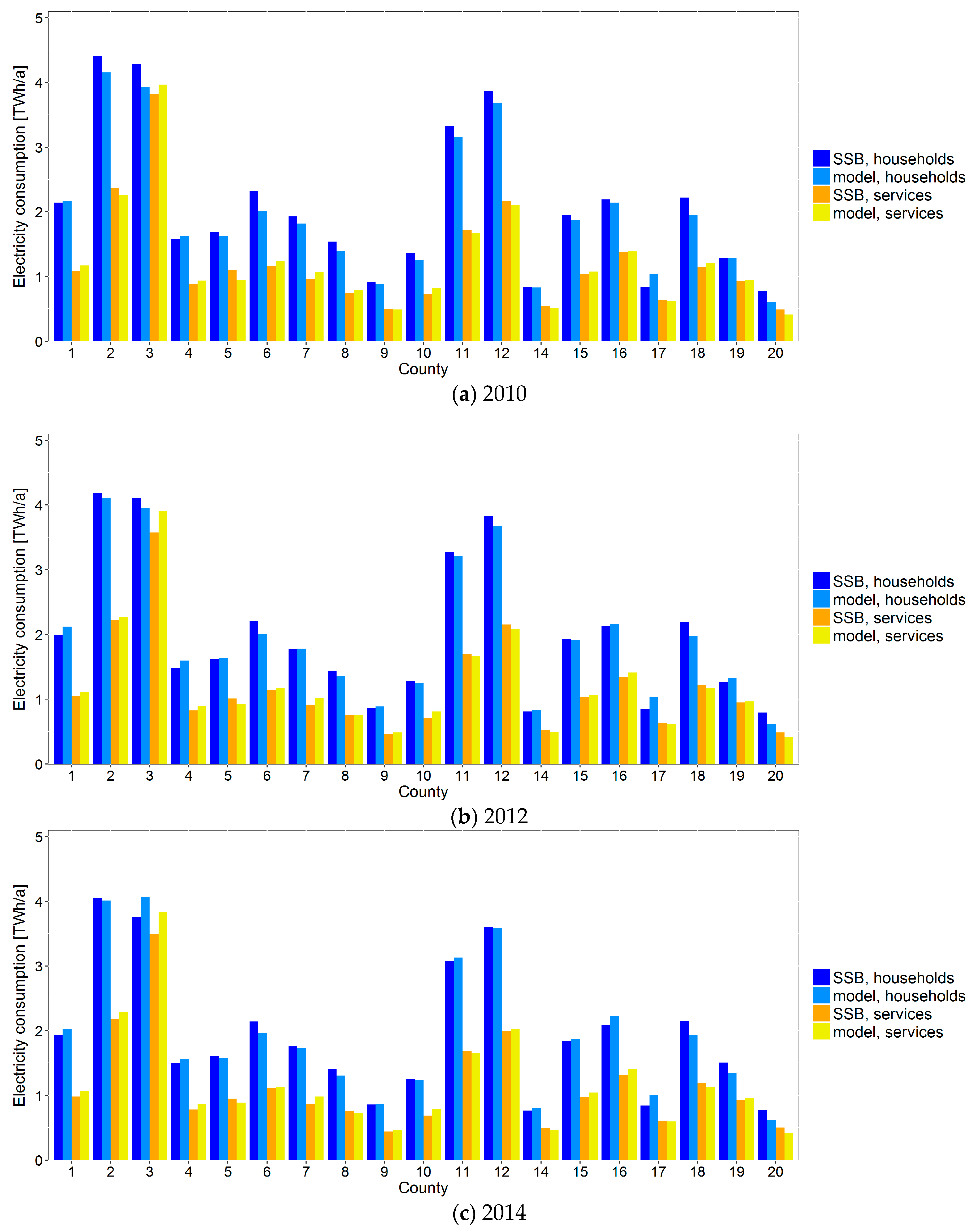
4.1. Electricity Consumption per County, Sector, and Year
4.2. Hourly Electricity Consumption per Sector and Nord Pool Region
4.3. Case Study of Hourly District Heat Consumption in Oslo
5. Discussion
5.1. Modeling Approach
5.2. Uncertainties Regarding Input Data and Model Validation
5.3. Further Suggested Improvements
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Explanatory Variables
| Variable | Symbol/Description | Type | Reference Group |
|---|---|---|---|
| x1 | dwelling group = attached | dummy | dwelling group = detached |
| x2,…,4 | number of adults = 2, 3, >3 | dummy | adults = 1 |
| x5,…,7 | number of children (<16 years) = 1, 2, >2 | dummy | children = 0 |
| x8 | senior resident = yes × (daytype = workday) | dummy | senior resident = no |
| x9 | (resident more than 20 h at home = yes) (daytype = workday) | dummy | resident more than 20 h at home = no |
| x10 | weekend resident = yes × (daytype = workday) | dummy | weekend resident = no |
| x11,…,13 | daytype = Saturday but no holiday, Sunday or holiday, workday within school-holidays | dummy | daytype = workday |
| x14 | cold storage = yes | dummy | cold storage = no |
| x15 | other electricity-intensive appliances = yes | dummy | appliances = no |
| x16,…,24 | month = 2, 3, 4, 5, 8, 9, 10, 11, 12 | dummy | month = 1 (January) |
| x25 | HDD | continuous | - |
| x26 | HDD1st | continuous | - |
| x27 | HDD × floor space | continuous | - |
| x28 | HDD × (dwelling group = attached) | cont./dummy | dwelling group = detached |
| x29 | HDD × (heat pump = yes) | cont./dummy | heat pump = no |
| x30 | HDD × (central electric boiler = yes) | cont./dummy | central electric boiler = no |
| x31 | HDD × (central heat pump = yes) | cont./dummy | central heat pump = no |
| x32 | HDD × (age = ≥2000) | cont./dummy | age = <2000 |
| x33 | HDD × (wood burning = supplementary) | cont./dummy | wood burning = no or only for coziness |
| x34 | HDD × (wood burning = mainly) | cont./dummy | wood burning = no or only for coziness |
| Variable | Symbol | Description | Type | Reference Group |
|---|---|---|---|---|
| x1 | A | average floor space | continuous | - |
| x2 | HDD | heating degree day | continuous | - |
| x3 | HDD1st | 1st differences in HDD | continuous | - |
| x4 | CDD | cooling degree day | continuous | - |
| x5,…,15 | month | month = 2, …, 12 | dummy | month = 1 (January) |
| x16 | free | d is a non-workday day | dummy | free = no |
| x17 | Sat | d is a Saturday but no holiday | dummy | Sat = no |
| x18 | Sun | d is a Sunday or holiday | dummy | Sun = no |
| x19 | school-holidays | d is within school-holidays, but not weekend or holiday | dummy | school-holidays = no |
| Variable | Offices, el. | Offices, Non-el. | Schools, el. | Schools, Non-el. | Kinder-Gartens | Shops | Health | Others |
|---|---|---|---|---|---|---|---|---|
| A | x | x | x | x | x | x | x | x |
| HDD | x | - | x | - | x | x | x | x |
| HDD1st | x | - | x | - | x | x | x | x |
| month | - | x | - | - | - | - | - | - |
| free | x | x | x | x | x | - | - | - |
| school-holidays | - | - | x | x | x | - | - | - |
| Sat | - | - | - | - | - | x | - | - |
| Sun | - | - | - | - | - | x | - | - |
| A × month | x | - | x | x | x | x | x | x |
| A × free | x | x | x | x | x | - | x | x |
| A × school-holidays | x | x | - | - | - | - | - | - |
| A × HDD | x | - | x | - | x | x | x | x |
| A × Sat | - | - | - | - | - | x | - | - |
| A × Sun | - | - | - | - | - | x | - | - |
| A × HDD × free | x | - | x | - | x | - | - | - |
| A × CDD × free | x | x | - | - | - | - | - | - |
| A × HDD × Sun | - | - | - | - | - | x | - | - |
| A × CDD × Sun | - | - | - | - | - | x | - | - |
| Variable | Offices | Schools | Apartment Buildings |
|---|---|---|---|
| A | x | x | - |
| HDD | x | x | - |
| HDD1st | x | x | - |
| A × old | x | x | - |
| A × month | x | x | - |
| A × HDD | x | x | x |
| A × HDD1st | - | - | x |
| A × HDD·old | x | x | - |
| A × HDD·free | x | x | - |
| A × HDD × school-holidays | x | x | - |
| apartments | - | - | x |
| apartments·free | - | - | x |
| apartments·month | - | - | x |
References
- Statistics Norway (SSB), Energy Balance, Table 11561. Available online: https://www.ssb.no/statistikkbanken/selectvarval/Define.asp?subjectcode=&ProductId=&MainTable=EnergiBalanse2&nvl=&PLanguage=0&nyTmpVar=true&CMSSubjectArea=energi-og-industri&KortNavnWeb=energibalanse&StatVariant=&checked=true (accessed on 18 November 2017).
- Bøeng, A.C.; Holstad, M. Fakta om Energi—Utviklingen i Energibruk i Norge. Available online: https://www.ssb.no/energi-og-industri/artikler-og-publikasjoner/_attachment/104473?_ts=13d86acd6f8 (accessed on 28 December 2017).
- Statistics Norway (SSB), Energy Balance, Table 08311. Available online: https://www.ssb.no/statistikkbanken/selectvarval/Define.asp?subjectcode=&ProductId=&MainTable=NtoForbKraftGrupp&nvl=&PLanguage=1&nyTmpVar=true&CMSSubjectArea=energi-og-industri&KortNavnWeb=elektrisitet&StatVariant=&checked=true (accessed on 15 December 2017).
- Statistics Norway (SSB), Energy Accounting, Table 04372. Available online: https://www.ssb.no/statistikkbanken/selectvarval/Define.asp?subjectcode=&ProductId=&MainTable=AndreFormal&nvl=&PLanguage=0&nyTmpVar=true&CMSSubjectArea=energi-og-industri&KortNavnWeb=energiregnskap&StatVariant=&checked=true (accessed on 15 December 2017).
- Statistics Norway (SSB). Share of Heating Equipment Used, Per Dwelling Type, Table 10568. Available online: https://www.ssb.no/statistikkbanken/selectvarval/Define.asp?subjectcode=&ProductId=&MainTable=HusenVarmutstyr&nvl=&PLanguage=1&nyTmpVar=true&CMSSubjectArea=energi-og-industri&KortNavnWeb=husenergi&StatVariant=&checked=true (accessed on 15 December 2017).
- Rosenberg, E.; Lind, A.; Espegren, K.A. The impact of future energy demand on renewable energy production—Case of Norway. Energy 2013, 61, 419–431. [Google Scholar] [CrossRef]
- Seljom, P.; Rosenberg, E.; Fidje, A.; Haugen, J.E.; Meir, M.; Rekstad, J.; Jarlset, T. Modelling the effects of climate change on the energy system—A case study of Norway. Energy Policy 2011, 39, 7310–7321. [Google Scholar] [CrossRef]
- Andersen, F.; Larsen, H.; Boomsma, T. Long-term forecasting of hourly electricity load: Identification of consumption profiles and segmentation of customers. Energy Convers. Manag. 2013, 68, 244–252. [Google Scholar] [CrossRef]
- Andersen, F.; Larsen, H.; Gaardestrup, R. Long term forecasting of hourly electricity consumption in local areas in Denmark. Appl. Energy 2013, 110, 147–162. [Google Scholar] [CrossRef]
- Swan, L.G.; Ugursal, V.I. Modeling of end-use energy consumption in the residential sector: A review of modeling techniques. Renew. Sustain. Energy Rev. 2009, 13, 1819–1835. [Google Scholar] [CrossRef]
- Kavgic, M.; Mavrogianni, A.; Mumovic, D.; Summerfield, A.; Stevanovic, Z.; Djurovic-Petrovic, M. A review of bottom-up building stock models for energy consumption in the residential sector. Build. Environ. 2010, 45, 1683–1697. [Google Scholar] [CrossRef]
- Richardson, I.; Thomson, M.; Infield, D.; Clifford, C. Domestic electricity use: A high-resolution energy demand model. Energy Build. 2010, 42, 1878–1887. [Google Scholar] [CrossRef] [Green Version]
- Yao, R.; Steemers, K. A method of formulating energy load profile for domestic buildings in the UK. Energy Build. 2005, 37, 663–671. [Google Scholar] [CrossRef]
- McLoughlin, F.; Duffy, A.; Conlon, M. Characterising domestic electricity consumption patterns by dwelling and occupant socio-economic variables: An Irish case study. Energy Build. 2012, 48, 240–248. [Google Scholar] [CrossRef]
- Widén, J.; Wäckelgård, E. A high-resolution stochastic model of domestic activity patterns and electricity demand. Appl. Energy 2010, 87, 1880–1892. [Google Scholar] [CrossRef]
- Foucquier, A.; Robert, S.; Suard, F.; Stéphan, L.; Jay, A. State of the art in building modelling and energy performances prediction: A review. Renew. Sustain. Energy Rev. 2013, 23, 272–288. [Google Scholar] [CrossRef]
- Brøgger, M.; Wittchen, K. Estimating the energy-saving potential in national building stocks—A methodology review. Renew. Sustain. Energy Rev. 2018, 82, 1489–1496. [Google Scholar] [CrossRef]
- Aydinalp, M.; Ugursal, V.I.; Fung, A.S. Modeling of the appliance, lighting, and space-cooling energy consumptions in the residential sector using neural networks. Appl. Energy 2002, 71, 87–110. [Google Scholar] [CrossRef]
- Aydinalp, M.; Ugursal, V.I.; Fung, A.S. Modeling of the space and domestic hot-water heating energy-consumption in the residential sector using neural networks. Appl. Energy 2004, 79, 159–178. [Google Scholar] [CrossRef]
- Beccali, M.; Cellura, M.; Brano, V.L.; Marvuglia, A. Forecasting daily urban electric load profiles using artificial neural networks. Energy Convers. Manag. 2004, 45, 2879–2900. [Google Scholar] [CrossRef]
- Beccali, M.; Cellura, M.; Brano, V.L.; Marvuglia, A. Short-term prediction of household electricity consumption: Assessing weather sensitivity in a mediterranean area. Renew. Sustain. Energy Rev. 2008, 12, 2040–2065. [Google Scholar] [CrossRef]
- Rodrigues, F.; Cardeira, C.; Calado, J. The daily and hourly energy consumption and load forecasting using artificial neural network method: A case study using a set of 93 households in Portugal. Energy Procedia 2014, 62, 220–229. [Google Scholar] [CrossRef]
- Chae, Y.T.; Horesh, R.; Hwang, Y.; Lee, Y.M. Artificial neural network model for forecasting sub-hourly electricity usage in commercial buildings. Energy Build. 2016, 111, 184–194. [Google Scholar] [CrossRef]
- Magalhães, S.; Leal, V.; Horta, I. Modelling the relationship between heating energy use and indoor temperatures in residential buildings through Artificial Neural Networks considering occupant behavior. Energy Build. 2017, 151, 332–343. [Google Scholar] [CrossRef]
- Fels, M.F. PRISM: An introduction. Energy Build. 1986, 9, 5–18. [Google Scholar] [CrossRef]
- Pedersen, L.; Stang, J.; Ulseth, R. Load prediction method for heat and electricity demand in buildings for the purpose of planning for mixed energy distribution systems. Energy Build. 2008, 40, 1124–1134. [Google Scholar] [CrossRef]
- Braun, M.; Altan, H.; Beck, S. Using regression analysis to predict the future energy consumption of a supermarket in the UK. Appl. Energy 2014, 130, 305–313. [Google Scholar] [CrossRef]
- Amiri, S.; Mottahedi, M.; Asadi, S. Using multiple regression analysis to develop energy consumption indicators for commercial buildings in the U.S. Energy Build. 2015, 109, 209–216. [Google Scholar] [CrossRef]
- Fumo, N.; Biswas, M.R. Regression analysis for prediction of residential energy consumption. Renew. Sustain. Energy Rev. 2015, 47, 332–343. [Google Scholar] [CrossRef]
- Pulido-Arcas, J.; Pérez-Fargallo, A.; Rubio-Bellido, C. Multivariable regression analysis to assess energy consumption and CO2 emissions in the early stages of offices design in Chile. Energy Build. 2016, 133, 738–753. [Google Scholar] [CrossRef]
- Oh, S.; Ng, K.; Thu, K.; Chun, W.; Chua, K. Forecasting long-term electricity demand for cooling of Singapore’s buildings incorporating an innovative air-conditioning technology. Energy Build. 2016, 127, 183–193. [Google Scholar] [CrossRef]
- Arregi, B.; Garay, R. Regression analysis of the energy consumption of tertiary buildings. Energy Procedia 2017, 122, 9–14. [Google Scholar] [CrossRef]
- Wang, L.; Kubichek, R.; Zhou, X. Adaptive learning based data-driven models for predicting hourly building energy use. Energy Build. 2018, 159, 454–461. [Google Scholar] [CrossRef]
- Kipping, A.; Trømborg, E. Hourly electricity consumption in norwegian households—Assessing the impacts of different heating systems. Energy 2015, 93 Pt 1, 655–671. [Google Scholar] [CrossRef]
- Kipping, A.; Trømborg, E. Modeling and disaggregating hourly electricity consumption in Norwegian dwellings based on smart meter data. Energy Build. 2016, 118, 350–369. [Google Scholar] [CrossRef]
- Kipping, A.; Trømborg, E. Modeling hourly consumption of electricity and district heat in non-residential buildings. Energy 2017, 123, 473–486. [Google Scholar] [CrossRef]
- Statistics Norway (SSB). Dwelling Types and Floor Space, Table 06513. Available online: https://www.ssb.no/statistikkbanken/SelectVarVal/define.asp?SubjectCode=al&ProductId=al&MainTable=BoligBygnBruks&contents=Boliger5&PLanguage=0&Qid=0&nvl=True&mt=1&pm=&SessID=8116073&FokusertBoks=1&gruppe1=Hele&gruppe2=Hele&gruppe3=Hele&gruppe4=Hele&VS1=Fylker&VS2=Bygninger06&VS3=Bruksareal7&VS4=&CMSSubjectArea=&KortNavnWeb=boligstat&StatVariant=&Tabstrip=SELECT&aggresetnr=1&checked=true (accessed on 26 July 2016).
- Statistics Norway (SSB). Table 06266: Dwellings, by Type of Building and Year of Construction. Available online: https://www.ssb.no/statistikkbanken/SelectVarVal/define.asp?SubjectCode=al& ProductId=al&MainTable=BoligerB&contents=Boliger&PLanguage=0&Qid=0&nvl=True&mt=1& pm=&SessID=8353112&FokusertBoks=1&gruppe1=Hele&gruppe2=Hele&gruppe3=Hele&gruppe4=Hele&VS1=Fylker&VS2=Bygninger05&VS3=BygnAr&VS4=&CMSSubjectArea=&KortNavnWeb=boligstat&StatVariant=&Tabstrip=SELECT&aggresetnr=1&checked=true (accessed on 24 August 2016).
- Statistics Norway (SSB). Population, Table 06913. Available online: https://www.ssb.no/statistikkbanken/SelectVarVal/Define.asp?MainTable=Folkemengd1951&KortNavnWeb=folkemengde& PLanguage=0&checked=true (accessed on 26 July 2016).
- Statistics Norway (SSB). Population and Housing Census, Table 09810. Available online: https://www.ssb.no/statistikkbanken/SelectVarVal/Define.asp?MainTable=FOBbolAldBAarByg&KortNavnWeb= fobbolig&PLanguage=0&checked=true (accessed on 26 July 2016).
- Statistics Norway (SSB). Families and Households, Table 10986. Available online: https://www.ssb.no/statistikkbanken/SelectVarVal/define.asp?SubjectCode=al&ProductId=al&MainTable=HushTypRegion&contents=Personer&PLanguage=0&Qid=0&nvl=True&mt=1&pm=&SessID=8073068&FokusertBoks=2&gruppe1=Hele&gruppe2=Hele&gruppe3=Hele&VS1=FylkerFastland&VS2=HusholdType2006niv2&VS3=&CMSSubjectArea=&KortNavnWeb=familie&StatVariant=&Tabstrip=SELECT&aggresetnr=2&checked=true (accessed on 26 July 2016).
- Statistics Norway (SSB). Employment, Table 09315. Available online: https://www.ssb.no/statistikkbanken/SelectVarVal/Define.asp?MainTable=SysselAldNar&KortNavnWeb=regsys&PLanguage=0& checked=true (accessed on 26 July 2016).
- Statistics Norway (SSB). Number of Buildings per County and Building Type 2006–2016. Available online: https://www.ssb.no/en/bygg-bolig-og-eiendom/statistikker/byggeareal/aar/2016-02-15?fane=tabell#content (accessed on 30 March 2016).
- Norwegian Energy Labels for Buildings. Available online: http://www.energimerking.no/ (accessed on 1 August 2016).
- Statistics Norway (SSB). Electricity Consumption in the Service Sector per Category and County. Available online: http://ec.europa.eu/eurostat/statistics-explained/index.php/Electricity_and_heat_statistics (accessed on 19 May 2016).
- Statistics Norway (SSB). Electricity, Annual Figures per Consumer Group and Region, 2011–2014, Table 10314. Available online: https://www.ssb.no/statistikkbanken/SelectVarVal/Define.asp?MainTable=NtoForbKraftGrKom&KortNavnWeb=elektrisitet&PLanguage=0&checked=true (accessed on 1 August 2016).
- Hourly Electricity Consumption Data. Available online: http://www.nordpoolspot.com/historical-market-data/ (accessed on 15 August 2016).
- Hourly Meter Data of Aggregate District Heat Consumption in Oslo. Available online: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/267585/Sub-national_electricity_consumption_factsheet_2012.pdf (accessed on 8 March 2017).









| Sector | Consumer Category | Building Category (Meter Data) | Separate Models for Electric/Non-Electric Heating | References |
|---|---|---|---|---|
| households | households | dwellings | no | [34,35] |
| services | offices | office buildings | yes | [36] |
| services | education | schools, universities | yes | [36] |
| services | education | kindergartens | no | - |
| services | trade | shops, stores | no | - |
| services | health | nursing homes | no | - |
| services | others | hotels, museums | no | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kipping, A.; Trømborg, E. Modeling Aggregate Hourly Energy Consumption in a Regional Building Stock. Energies 2018, 11, 78. https://doi.org/10.3390/en11010078
Kipping A, Trømborg E. Modeling Aggregate Hourly Energy Consumption in a Regional Building Stock. Energies. 2018; 11(1):78. https://doi.org/10.3390/en11010078
Chicago/Turabian StyleKipping, Anna, and Erik Trømborg. 2018. "Modeling Aggregate Hourly Energy Consumption in a Regional Building Stock" Energies 11, no. 1: 78. https://doi.org/10.3390/en11010078
APA StyleKipping, A., & Trømborg, E. (2018). Modeling Aggregate Hourly Energy Consumption in a Regional Building Stock. Energies, 11(1), 78. https://doi.org/10.3390/en11010078





