A Novel Model Incorporating Geomechanics for a Horizontal Well in a Naturally Fractured Reservoir
Abstract
:1. Introduction
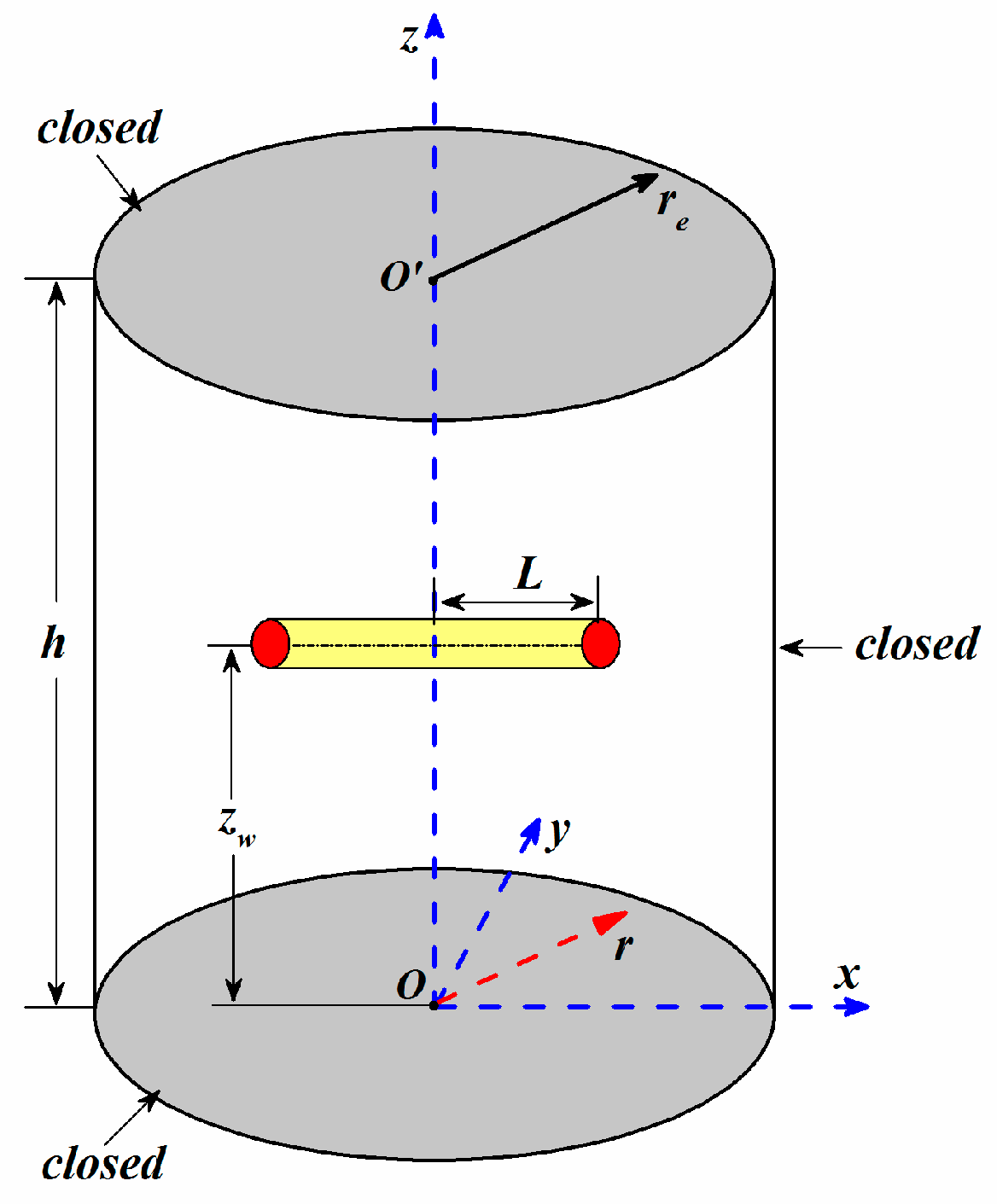
2. Physical Model
- (1)
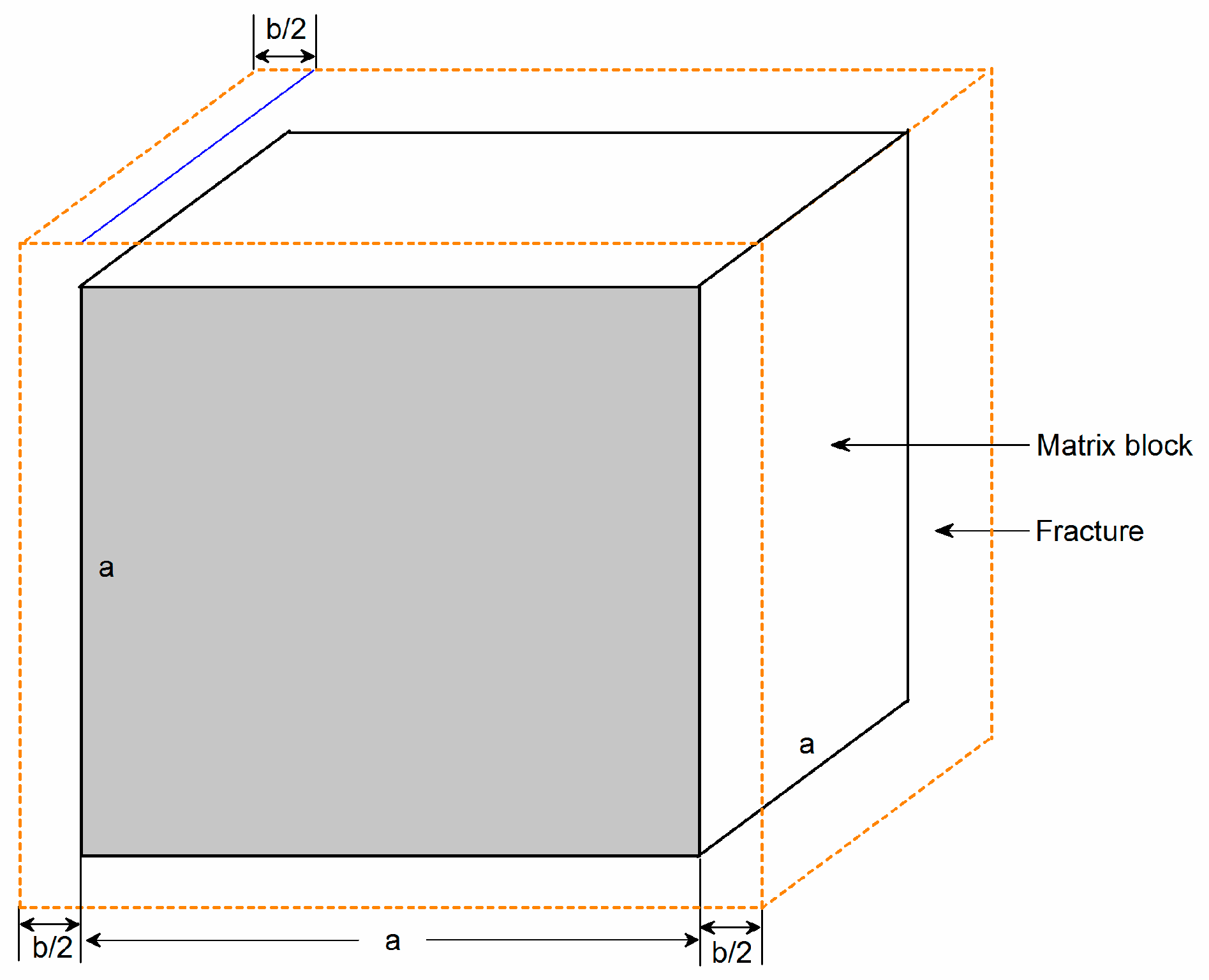
- This formation consists of two systems, including natural fracture system and matrix system, and can be represented by Warren-Root model. Two kinds of porous media are homogeneous, and the closure of natural fractures caused by reservoir pressure depletion is taken into account.
- (2)
- This reservoir is circular and closed at the external boundary of side and bounded by upper and lower impermeable formation, and has a uniform thickness.
- (3)
- Flow in this reservoir is considered to be a slightly compressible and single-phase fluid with constant viscosity and obeys Darcy’s law. Pseudo-steady flow from matrix system to natural fracture system is assumed.
- (4)
- This horizontal well is produced at a constant rate and no fluid is assumed to flow at the tip of the horizontal wellbore.
- (5)
- Gravity and capillary effects are neglected.
3. Fracture Permeability vs. Mechanical Elasticity
4. Point Sink Model in the Closed Cylindrical System
4.1. Mathematical Model in the Closed Cylindrical System
4.1.1. Governing Equations
4.1.2. Initial Conditions and Boundary Conditions
4.2. Point Sink Model Solution
4.2.1. Pedrosa Transform and Perturbation Transform
4.2.2. Laplace Transform and Fourier Transform
4.2.3. Model Solution
5. Horizontal Well Model Incorporating Geomechanics
6. Results and Discussion
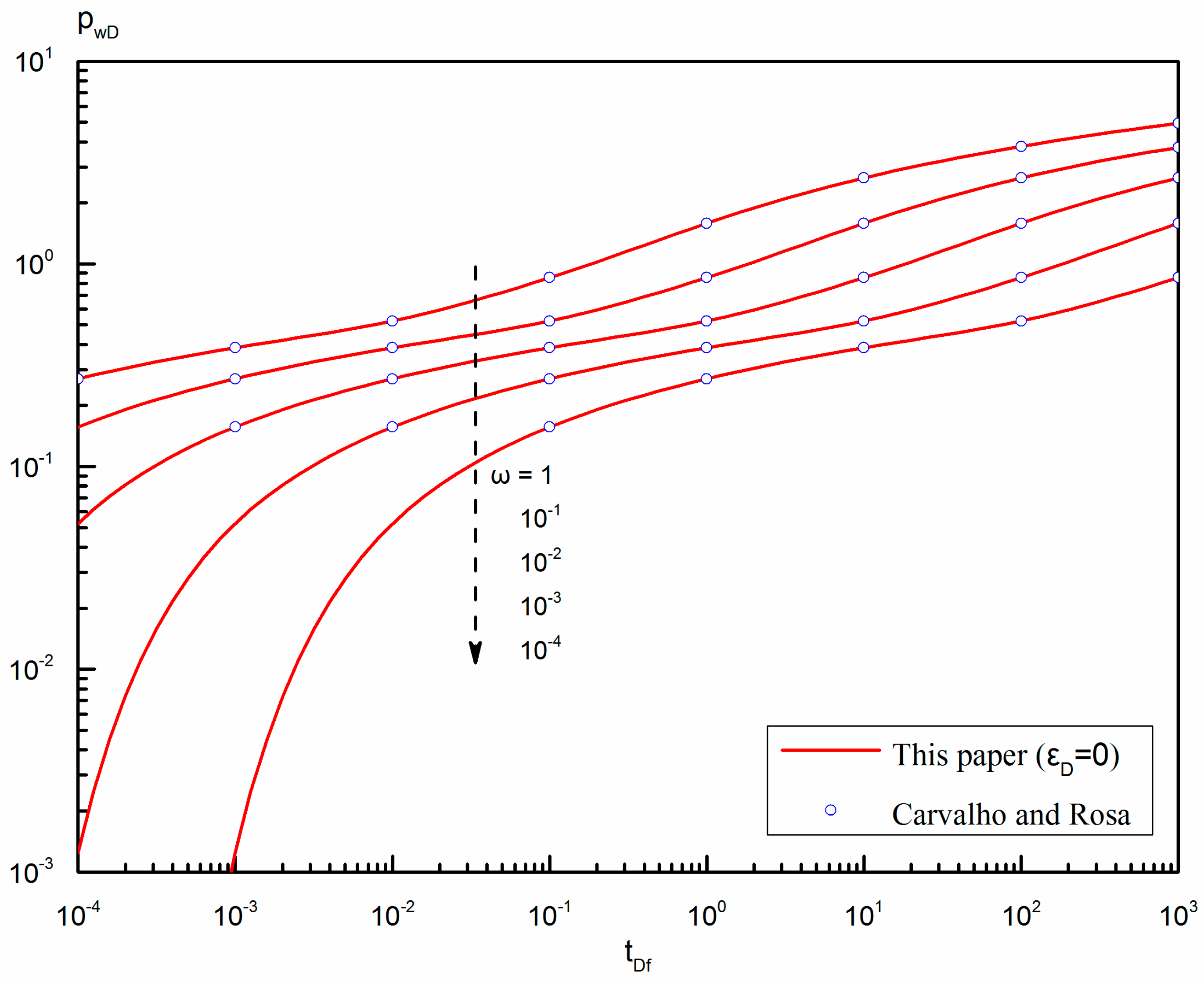
6.1. Verification of the Solution
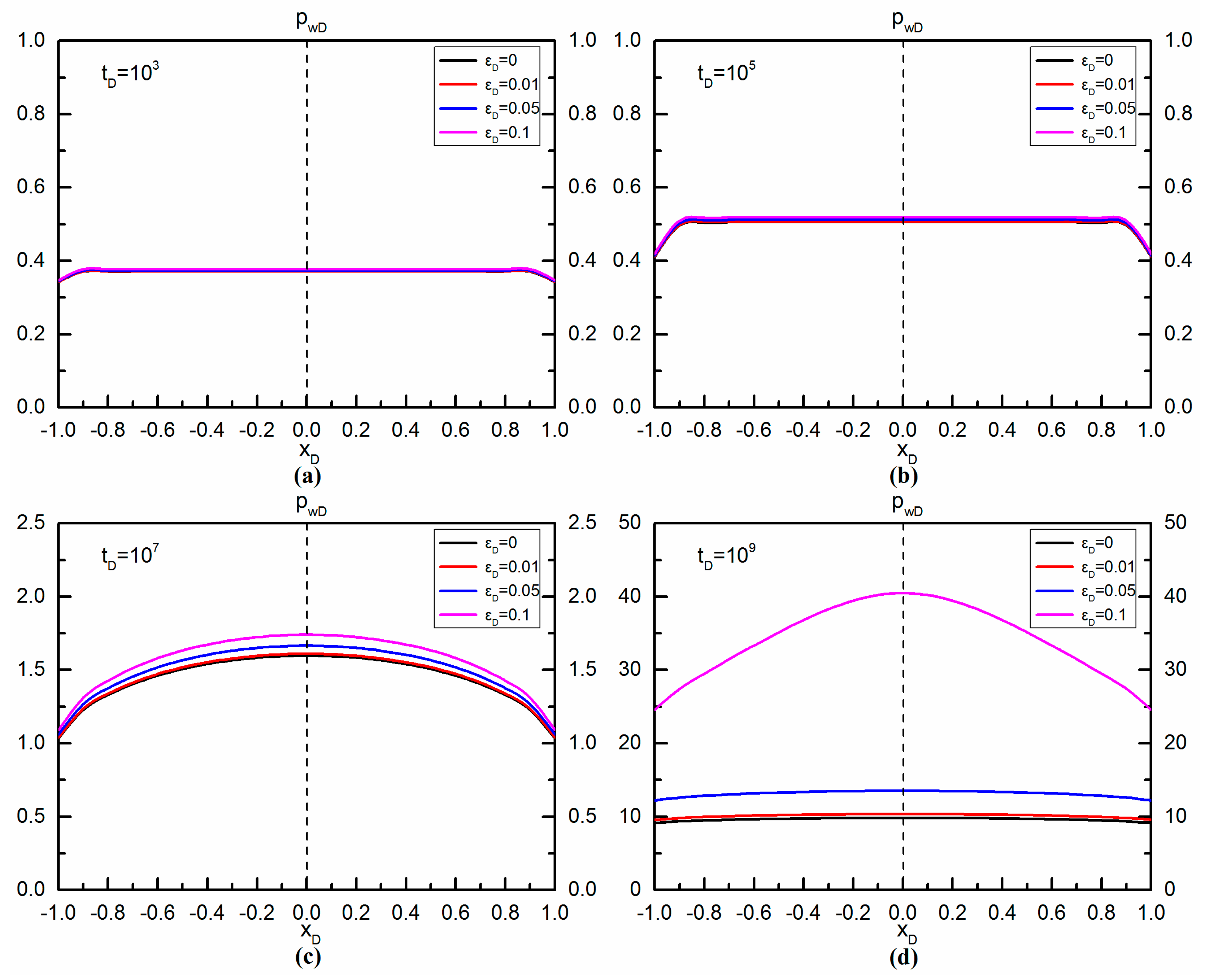
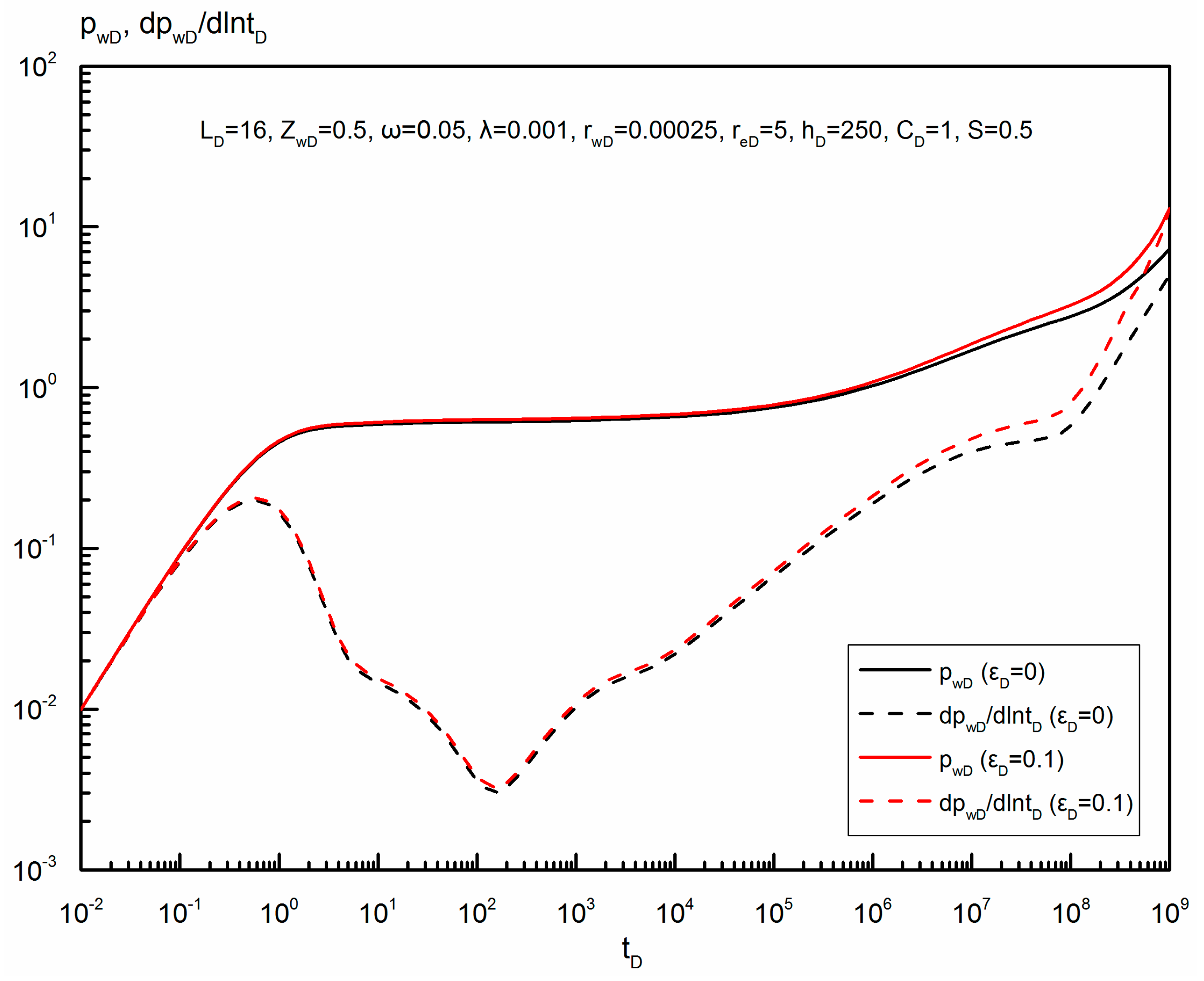
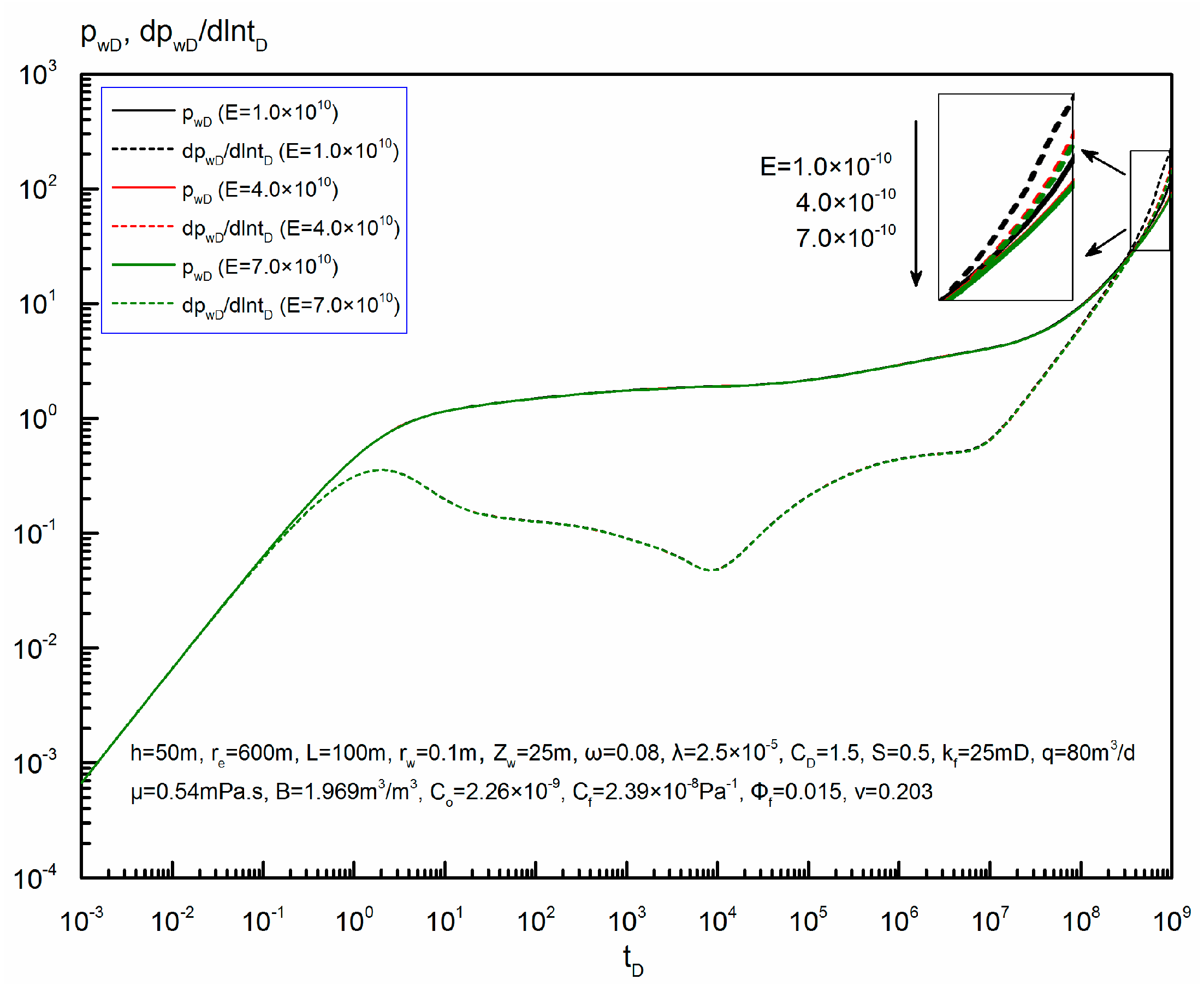
6.2. Effect of Dimensionless Elasticity Parameter on Horizontal Wellbore Pressure-Drop Profiles
6.3. Comparison with a Model Not Considering Geomechanics
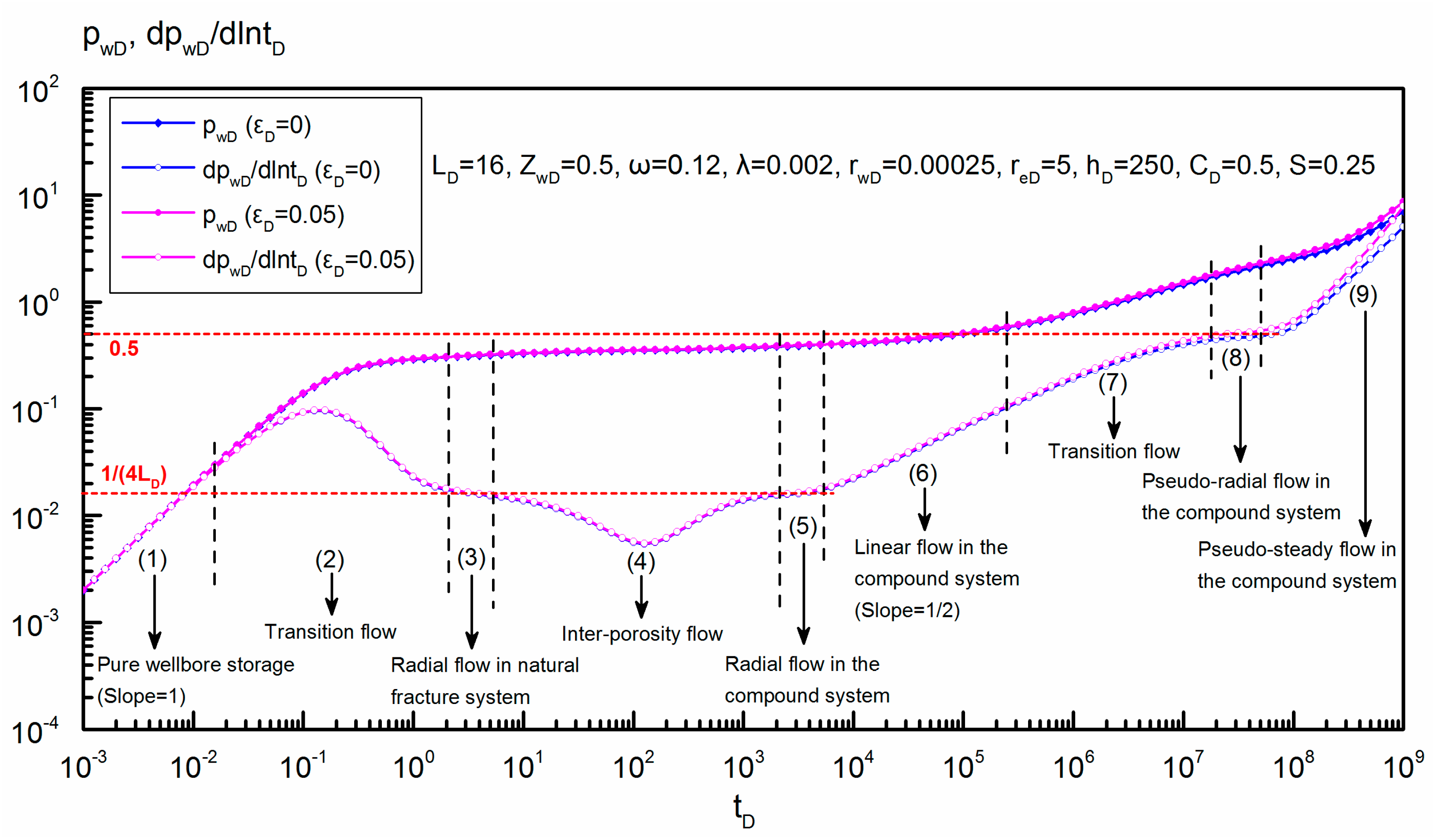
6.4. Flow Regime Recognition on Transient Wellbore Pressure Curves
- (1)
- Pure wellbore storage regime. At small dimensionless time, flow is mainly governed by the wellbore storage effect, and the transient pressure and pressure derivative curves align in an upward straight line with a unit slope.
- (2)
- First transition flow. This regime is marked by a hump on the pressure derivative curve.
- (3)
- Radial flow in the natural fracture system. A short radial flow may occur after a transition flow if the reserve ratio in the natural fracture system is large enough. As presented in Figure 6, the pressure derivative curve in this regime is a horizontal line with a value of “” and the corresponding streamline distribution in the reservoir is shown in Figure 7a.
- (4)
- Inter-porosity flow. This regime represents the cross flow from matrix system to natural fracture system. The pressure derivative curve in this regime shows a concave-shaped segment, which is the main characteristic of naturally fractured reservoirs.
- (5)
- Radial flow in the compound system. When the inter-porosity flow finishes, fluid flow in two systems reaches a dynamic balance, and a second radial flow begins to occur in the compound system. A horizontal line with a value of “” can be also observed on the pressure derivative curve in this regime and its streamline distribution is the same with that in the third flow regime (as shown in Figure 7a).
- (6)
- Linear flow in the compound system. In this regime, the dominating flow is linear flow in the horizontal plane, and the streamlines are parallel to the upper and lower boundary (as shown in Figure 7b). Its pressure derivative curve shows an upward straight line with a half slope.
- (7)
- Second transition flow. As the drainage area expands, a second transition flow may occur in the reservoir before it reaches a pseudo-radial flow in the horizontal plane.
- (8)
- Pseudo-radial flow in the compound system. When reservoir radius is large enough, a pseudo-radial flow in the horizontal plane may be formed after the second transition flow (as shown in Figure 7c). Unlike the conventional reservoir, due to the effect of stress sensitivity, the pressure derivative curve is not a horizontal line with a value of “0.5” but exhibits an upward tendency.
- (9)
- Pseudo-steady flow in the compound system. When the transient wave reaches the outer boundary, both the transient pressure curve and pressure derivative curves go up rapidly, and their slopes are greater than “1” due to stress sensitivity (as shown in Figure 6).
6.5. Analysis of Parameters’ Influence on Transient Pressure Behavior
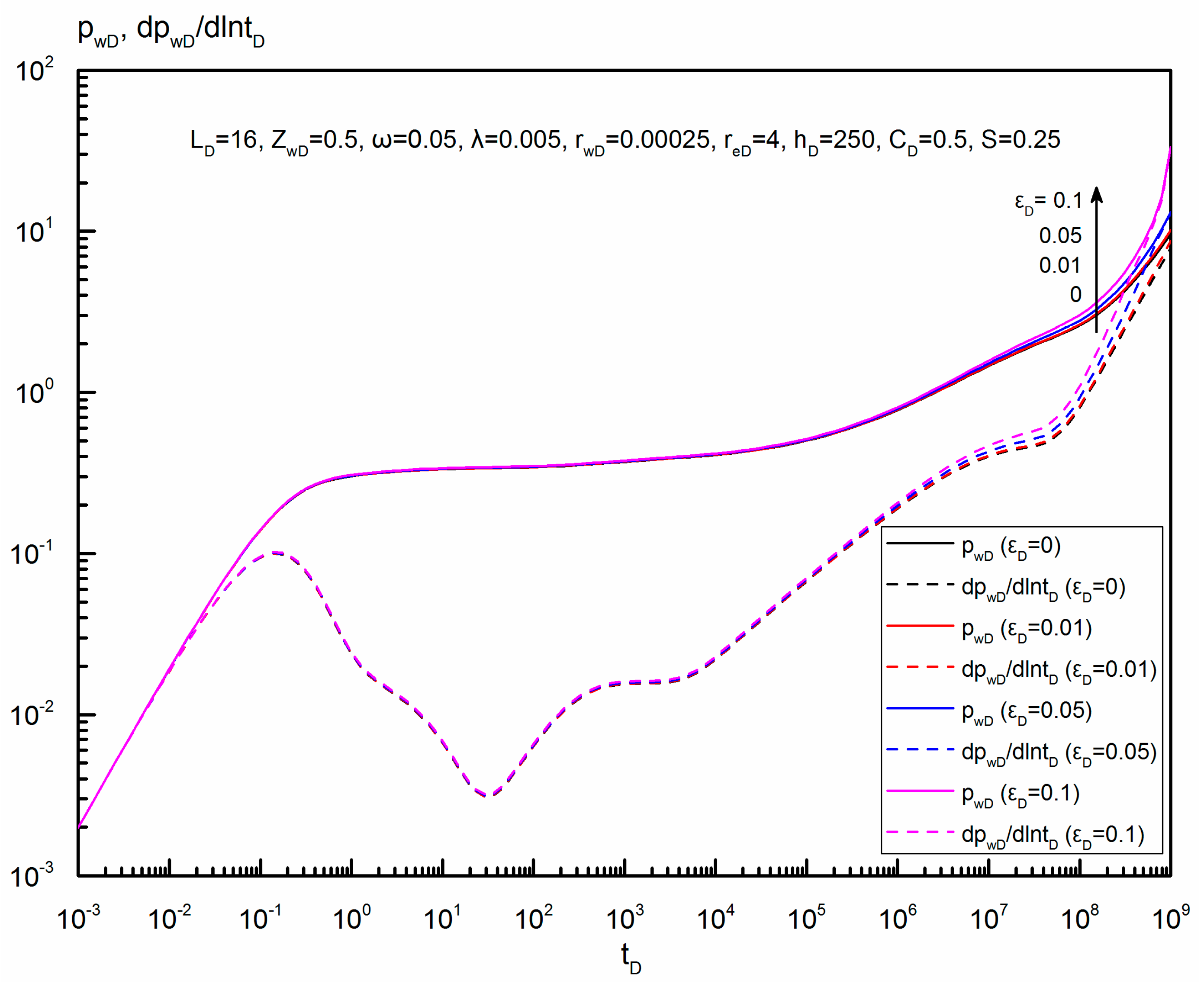
6.5.1. Dimensionless Elasticity Parameter
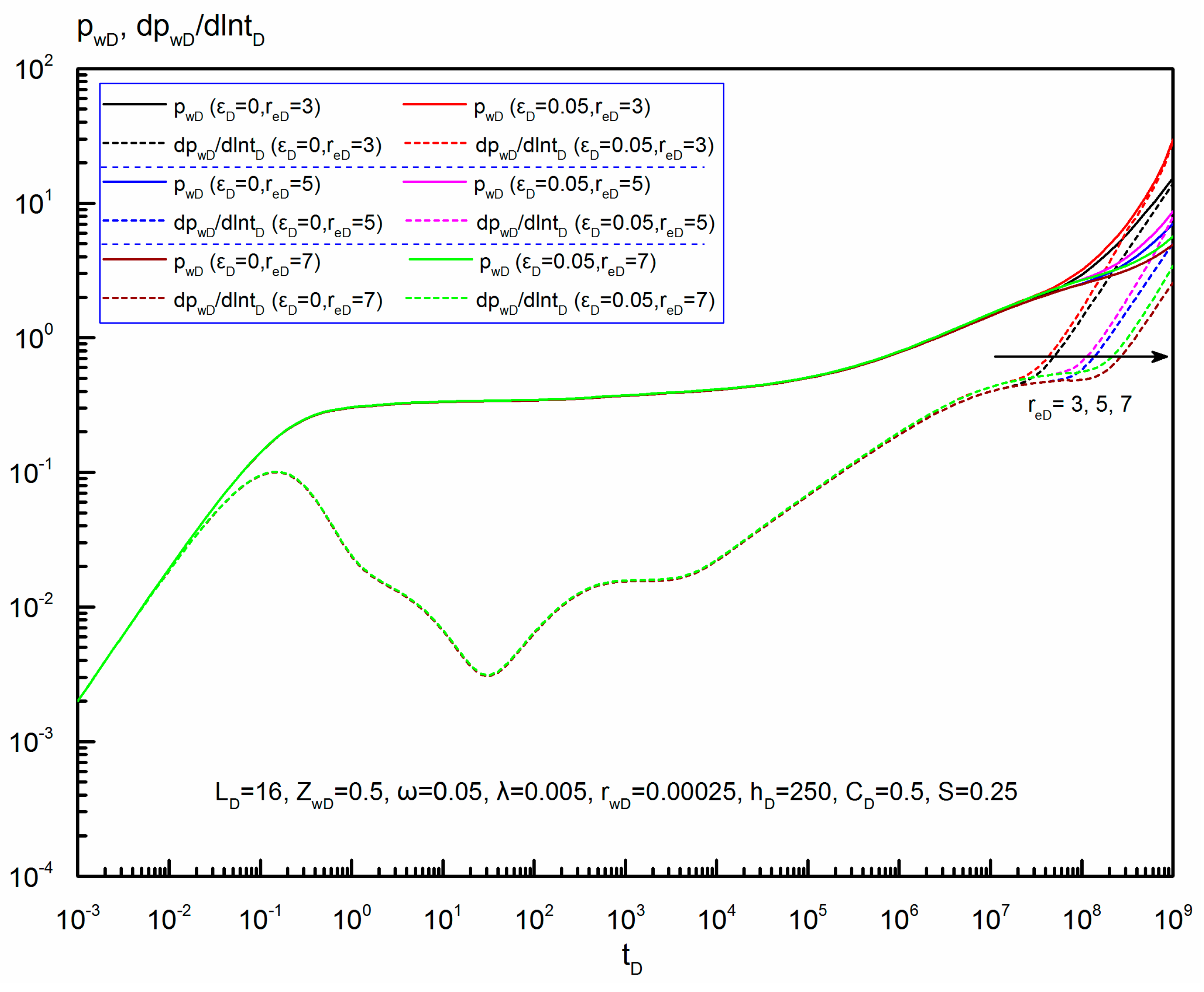
6.5.2. Dimensionless Reservoir Radius
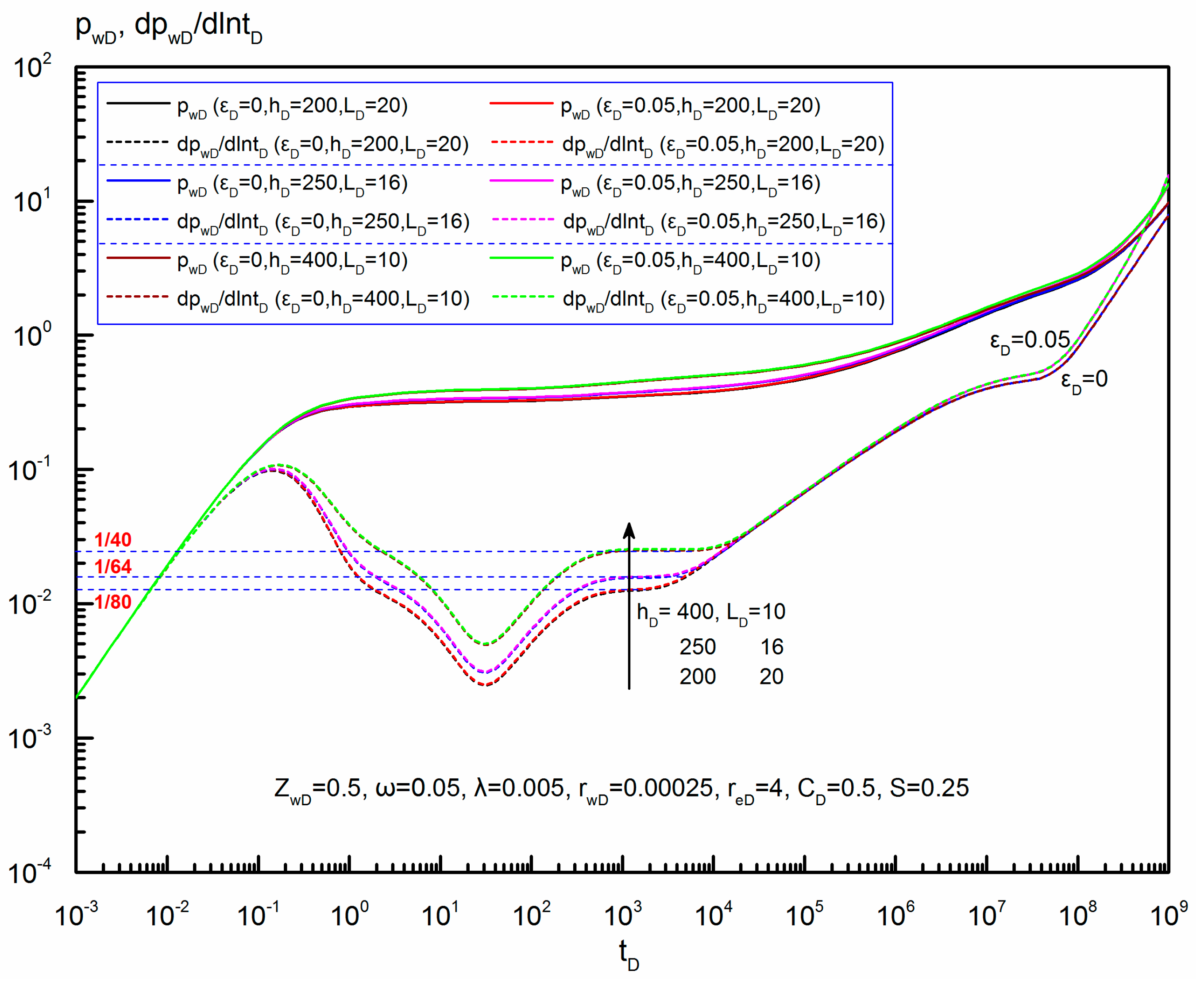
6.5.3. Dimensionless Reservoir Thickness
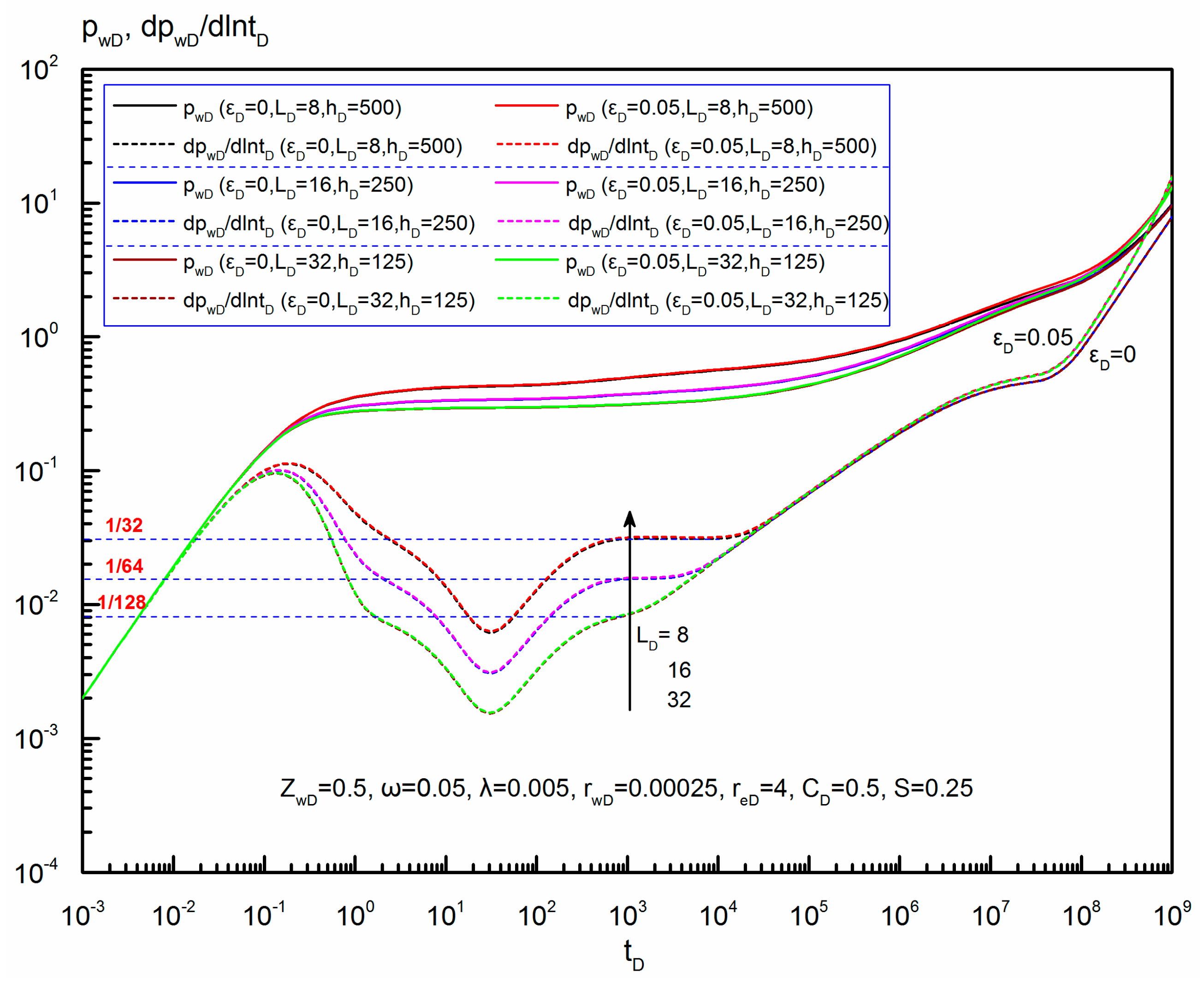
6.5.4. Dimensionless Horizontal Wellbore Length
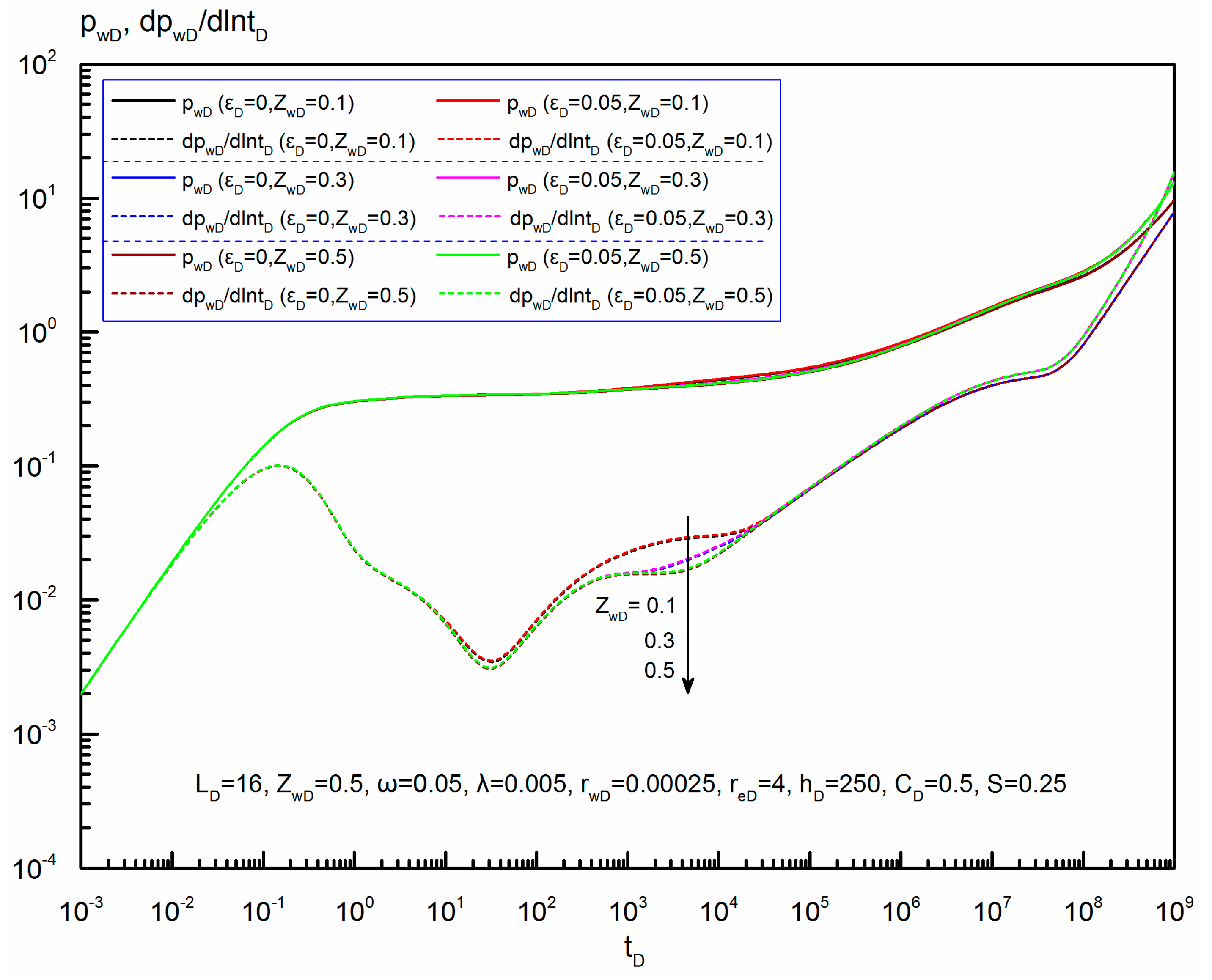
6.5.5. Dimensionless Wellbore Vertical Position
6.6. Analysis of the Influence of Geomechanical Parameters in North Truva Field
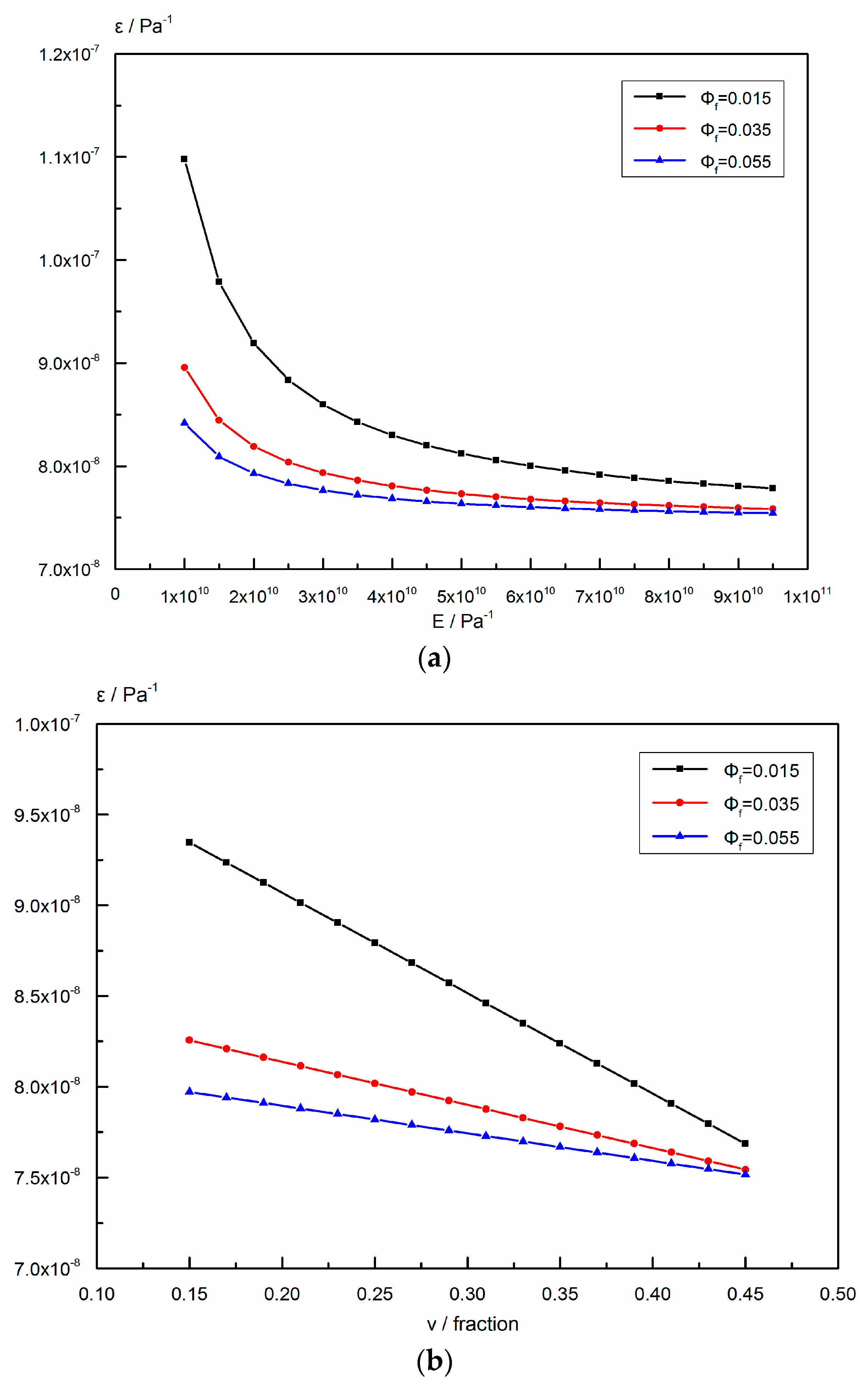
6.6.1. Influence of Geomechanical Parameters on the Elasticity Parameter
6.6.2. Influence of Geomechanical Parameters on the Transient Response of H519
7. Conclusions
- (1)
- For a uniform-flux horizontal well, the effect of dimensionless elasticity parameter on the pressure drop profiles becomes stronger as the production time gets longer, due to a larger fracture permeability reduction caused by the closure of natural fractures. When the effect of dimensionless elasticity parameter is strong enough, the profile looks like a bow, and a farther position away from the center of the horizontal wellbore corresponds to a lower pressure drop.
- (2)
- For an infinite-conductivity horizontal well, while the production going on, especially in the late-flow period, the pressure drop of the model incorporating geomechanics becomes larger than that not incorporating geomechanics, and more reservoir energy will be consumed to produce the same amount of oil.
- (3)
- Nine typical flow regimes can be observed on the transient response of the infinite-conductivity horizontal well incorporating geomechanics. The differences between the models incorporating and not incorporating this property lie in the final flow regimes. Due to the stress sensitivity, the pressure derivative curve is not a horizontal line with a value of “0.5” but exhibits an upward tendency in the pseudo-radial flow in the compound system, and in the pseudo-steady flow regime, both the transient pressure curve and the pressure derivative curve rise quickly and their slope is greater than “1”.
- (4)
- Analysis of parameters’ influence on the transient pressure behavior shows that dimensionless elasticity parameter and dimensionless reservoir radius mainly affect the late-flow period, but dimensionless reservoir thickness, dimensionless wellbore length and dimensionless wellbore vertical position mainly influence the early-flow period. There is a larger pressure drop with the increase of dimensionless elasticity parameter or the decrease of dimensionless reservoir radius in the late-flow period.
- (5)
- For the KT-I formation of the North Truva field, the elasticity parameter decreases with the increase of Young’s modulus or Poisson’s ratio at a given fracture porosity and this parameter ranges from Pa−1 to Pa−1 in this formation. Calculation results show that the transient response of H519 has a slight negative correlation with Young’s modulus and Poisson’s ratio in the late-flow period, especially in the pseudo-steady flow regime.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Field variables | |
| matrix block side length, m | |
| fracture width, m | |
| fracture width change caused by fracture compressibility, m | |
| fracture width change caused by matrix elasticity, m | |
| permeability of natural fracture system, mD | |
| permeability of matrix system, mD | |
| fluid viscosity, cp | |
| formation volume factor, dimensionless | |
| shape factor, m−2 | |
| porosity of natural fracture system, fraction | |
| porosity of matrix system, fraction | |
| porosity of natural fracture system under the initial condition, fraction | |
| porosity of matrix system under the initial condition, fraction | |
| oil compressibility, Pa−1 | |
| fracture compressibility, Pa−1 | |
| matrix compressibility, Pa−1 | |
| Poisson’s ratio, dimensionless | |
| average velocity, m/s | |
| Young’s modulus, Pa | |
| fluid density, kg/m3 | |
| reservoir pressure, Pa | |
| initial reservoir pressure, Pa | |
| pressure in natural fracture system, Pa | |
| pressure in matrix system, Pa | |
| pressure drop caused by skin effect, Pa | |
| pressure change in natural fracture system, Pa | |
| overburden pressure, Pa | |
| time, s | |
| total wellbore flow rate, kg/s | |
| inter-porosity flow from matrix to natural fracture, kg/s | |
| production rate of the point sink, kg/s | |
| wellbore storage coefficient, m3/Pa | |
| fracture storage capacity, fraction | |
| inter-porosity flow coefficient, dimensionless | |
| elasticity parameter, Pa−1 | |
| distance in the x axis, m | |
| distance in the y axis, m | |
| distance in the z axis, m | |
| distance of a point sink in the x axis, m | |
| distance of a point sink in the y axis, m | |
| distance of a point sink or a horizontal well in the z axis, m | |
| reservoir radius distance, m | |
| wellbore radius, m | |
| reservoir boundary radius, m | |
| reservoir thickness, m | |
| half-length of horizontal wellbore, m | |
| infinitesimal vertical distance, m | |
| Dimensionless variables: real domain | |
| dimensionless pressure in natural fracture system | |
| dimensionless pressure in matrix system | |
| dimensionless pressure in natural fracture system after Pedrosa transform | |
| i-order dimensionless pressure in natural fracture system after perturbation transform, i = 0, 1, 2, 3… | |
| dimensionless time | |
| dimensionless distance in the x axis | |
| dimensionless distance in the y axis | |
| dimensionless distance in the z axis | |
| dimensionless radius distance | |
| dimensionless distance of a point sink in the x axis, m | |
| dimensionless distance of a point sink in the y axis, m | |
| dimensionless distance of a point sink or a horizontal well in the z axis, m | |
| dimensionless wellbore radius | |
| dimensionless reservoir boundary radius | |
| dimensionless z-coordinate of horizontal wellbore | |
| dimensionless length of horizontal wellbore | |
| dimensionless reservoir thickness | |
| dimensionless infinitesimal vertical distance | |
| dimensionless elasticity parameter | |
| dimensionless wellbore storage coefficient | |
| skin factor | |
| dimensionless production rate of point sink | |
| Dimensionless variables: Laplace domain | |
| dimensionless time variable in Laplace domain | |
| dimensionless pressure in natural fracture system in Laplace domain | |
| dimensionless pressure in matrix system in Laplace domain | |
| i-order dimensionless pressure in natural fracture system in Laplace domain | |
| Special functions | |
| modified Bessel function (2nd kind, zero order) | |
| modified Bessel function (2nd kind, first order) | |
| modified Bessel function (1st kind, zero order) | |
| modified Bessel function (1st kind, first order) | |
| Special subscripts | |
| fracture property | |
| matrix property | |
| horizontal wellbore | |
| dimensionless variable | |
| Laplace transform | |
| Fourier transform | |
References
- Ozkan, E.; Raghavan, R.; Joshi, S.D. Horizontal well pressure analysis. In Proceedings of the SPE California Regional Meeting, Ventura, CA, USA, 8–10 April 1987. Paper No. 16378. [Google Scholar] [CrossRef]
- Ozkan, E. Performance of Horizontal Wells. Ph.D. Thesis, Tulsa University, Tulsa, OK, USA, 1988. [Google Scholar]
- De Carvalho, R.S.; Rosa, A.J. Transient pressure behavior for horizontal wells in naturally fractured reservoir. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 2–5 October 1988. Paper No. 18302. [Google Scholar] [CrossRef]
- Rosa, A.J.; de Carvalho, R.S. A mathematical model for pressure evaluation in an lnfinite-conductivity horizontal well. SPE Form. Eval. 1989, 4, 559–566. [Google Scholar] [CrossRef]
- Jones, F.O.; Owens, W.W. A laboratory study of low-permeability gas sands. J. Pet. Technol. 1980, 32, 1631–1640. [Google Scholar] [CrossRef]
- Economides, M.J.; Buchsteiner, H.; Warpinski, N.R. Step-pressure test for stresssensitive permeability determination. In Proceedings of the SPE Formation Damage Control Symposium, Lafayette, LA, USA, 7–10 February 1994. Paper No. 27380. [Google Scholar]
- Farquhar, R.A.; Smart, B.G.D.; Todd, A.C.; Tompkins, D.E.; Tweedie, A.J. Stress sensitivity of lowpermeability sandstones from the rotliegendes sandstone. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1993. Paper No. 26501. [Google Scholar] [CrossRef]
- Xu, W.; Wang, X.; Hou, X.; Clive, K.; Zhou, Y. Transient analysis for fractured gas wells by modified pseudo-functions in stress-sensitive reservoirs. J. Nat. Gas Sci. Eng. 2016, 35, 1129–1138. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Guo, J.; Zhang, L. A semi-analytical model for multilateral horizontal wells in low-permeability naturally fractured reservoirs. J. Petrol. Sci. Eng. 2017, 149, 564–578. [Google Scholar] [CrossRef]
- Barenblatt, G.I.; Zheltov, Y.P. Fundamental equations for the flow of homogeneous fluids through fissured rocks. Dokl. Akad. Nauk SSSK 1960, 132, 545–548. [Google Scholar]
- Barenblatt, G.I.; Zheltov, Y.P.; Kochina, I.N. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Nelson, R. Geologic Analysis of Naturally Fractured Reservoirs; Gulf Professional Publishing: Houston, TX, USA, 1985. [Google Scholar]
- Vasilev, I.; Alekshakhin, Y.; Kuropatkin, G. Pressure transient behavior in naturally fractured reservoirs: Flow anaysis. In Proceedings of the SPE Annual Caspian Technical Conference & Exhibition, Astana, Kazakhstan, 1–3 November 2016. Paper No. 182562. [Google Scholar] [CrossRef]
- Warren, J.E.; Root, P.J. The behavior of naturally fractured reservoirs. SPE J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Kazemi, H. Pressure transient analysis of naturally fractured reservoirs with uniform fracture distribution. SPE J. 1969, 9, 451–462. [Google Scholar] [CrossRef]
- De Swaan, O.A. Analytic solutions for determining naturally fractured reservoir properties by well testing. SPE J. 1976, 16, 117–122. [Google Scholar] [CrossRef]
- Nur, A.; Yilmaz, O. Pore Pressure in Fronts in Fractured Rock Systems; Department of Geophysics, Stanford University: Stanford, CA, USA, 1985. [Google Scholar]
- Kikani, J.; Pedrosa, O.A. Perturbation analysis of stress-sensitive reservoirs. SPE Form. Eval. 1991, 6, 379–386. [Google Scholar] [CrossRef]
- Chen, M.; Bai, M. Modeling stress-dependent permeability for anisotropic fractured porous rocks. Int. J. Rock Mech. Min. 1998, 35, 1113–1119. [Google Scholar] [CrossRef]
- Raghavan, R.; Chin, L.Y. Productivity changes in reservoirs with stress-dependent permeability. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002. Paper No. 77535. [Google Scholar] [CrossRef]
- Oluyemi, G.F.; Ola, O. Mathematical modelling of the effects of in-situ stress regime on fracture-matrix flow partitioning in fractured reservoirs. In Proceedings of the Nigeria Annual International Conference and Exhibition, Tinapa, Calabar, Nigeria, 31 July–7 August 2010. Paper No. 136975. [Google Scholar] [CrossRef]
- Jabbari, H.; Zeng, Z.; Ostadhassan, M. Impact of in-situ stress change on fracture conductivity in naturally fractured reservoirs: Bakken case study. In Proceedings of the 45th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011. Paper No. ARMA-11-239. [Google Scholar]
- Celis, V.; Silva, R.; Ramones, M.; Guerra, J.; Da Prat, G. A new model for pressure transient analysis in stress sensitive naturally fractured reservoirs. SPE Adv. Technol. Ser. 1994, 2, 126–135. [Google Scholar] [CrossRef]
- Samaniego, V.F.; Villalobos, L.H. Transient pressure analysis of pressure dependent naturally fractured reservoirs. J. Petrol. Sci. Eng. 2003, 39, 45–56. [Google Scholar] [CrossRef]
- Yao, S.; Zeng, F.; Liu, H. A semi-analytical model for hydraulically fractured wells with stress-sensitive conductivities. In Proceedings of the SPE Unconventional Resources Conference Canada, Calgary, AB, Canada, 5–7 November 2013. Paper No. 167230. [Google Scholar] [CrossRef]
- Zhang, Z.; He, S.; Liu, G.; Guo, X.; Mo, S. Pressure buildup behavior of vertically fracturedwells with stress-sensitive conductivity. J. Petrol. Sci. Eng. 2014, 122, 48–55. [Google Scholar] [CrossRef]
- Rosalind, A. Impact of stress sensitive permeability on production data analysis. In Proceedings of the SPE Unconventional Reservoirs Conference, Keystone, CO, USA, 10–12 February 2008. Paper No. 114166. [Google Scholar] [CrossRef]
- Robertson, E.P.; Christiansen, R.L. A permeability model for coal and other fractured, sorptive-elastic media. In Proceedings of the SPE Eastern Regional Meeting, Canton, OH, USA, 11–13 October 2006. Paper No. 104380. [Google Scholar] [CrossRef]
- Janna, W.S. Introduction to Fluid Mechanics; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Zhang, J.; Bai, M.; Roegiers, J.C.; Liu, T. Determining stress-dependent permeability in the laboratory. In Proceedings of the 37th U.S. Symposium on Rock Mechanics, Vail, CO, USA, 7–9 June 1999; Volume 37, pp. 341–347. [Google Scholar]
- McKee, C.R.; Bumb, A.C.; Koenig, R.A. Stress-dependent permeability and porosity of coal and other geologic formations. SPE Form. Eval. 1988, 3, 81–91. [Google Scholar] [CrossRef]
- Pedrosa, O.A. Pressure transient response in stress-sensitive formations. In Proceedings of the SPE California Regional Meeting, Oakland, CA, USA, 2–4 April 1986. Paper No. 15115. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Non-Linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramey, H.J., Jr. The use of source and Green’s functions in solving unsteady-flow problems in reservoirs. SPE J. 1973, 13, 285–296. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramey, H.J., Jr.; Raghavan, R. Unsteady-state pressure distributions created by a well with a single infinite-conductivity vertical fracture. SPE J. 1974, 14, 347–360. [Google Scholar] [CrossRef]
- Clonts, M.D.; Ramey, H.J., Jr. Pressure-transient analysis for wells with horizontal drainholes. In Proceedings of the SPE California Regional Meeting, Oakland, CA, USA, 2–4 April 1986. Paper No. 15116. [Google Scholar] [CrossRef]
- Daviau, F.; Mouronval, G.; Bourdarot, G.; Curutchet, P. Pressure analysis for horizontal wells. SPE Form. Eval. 1988, 3, 716–724. [Google Scholar] [CrossRef]
- Kuchuk, F.J.; Goode, P.A.; Wilkinson, D.J.; Thambynayagam, R.K.M. Pressure-transient behavior of horizontal wells with and without gas cap or aquifer. SPE Form. Eval. 1991, 6, 86–94. [Google Scholar] [CrossRef]
- Van Everdingen, A.F. The skin effect and its influence on the productive capacity of a well. J. Pet. Technol. 1953, 5, 171–176. [Google Scholar] [CrossRef]
- Kucuk, F.; Ayestaran, L. Analysis of simultaneously measured pressure and sandface flow rate in transient well testing. J. Pet. Technol. 1985, 37, 323–334. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]


| Parameters | Definitions |
|---|---|
| Dimensionless time | |
| Dimensionless pressure | |
| Dimensionless x-, y-, z-coordinate | , , |
| Dimensionless x-, y-, z-coordinate of wellbore | , , |
| Dimensionless radius distance | |
| Dimensionless wellbore radius | |
| Dimensionless reservoir boundary radius | |
| Dimensionless z-coordinate of wellbore | |
| Dimensionless wellbore length | |
| Dimensionless reservoir thickness | |
| Dimensionless infinitesimal vertical distance | |
| Dimensionless elasticity parameter | |
| Interporosity flow coefficient | |
| Fracture storage capacity | |
| Dimensionless production rate of point sink | |
| Dimensionless wellbore storage coefficient | |
| Skin factor |
| Parameters in this Work | Values | Parameters in Figure 5 of SPE 18302 [3] | Values |
|---|---|---|---|
| 100~10−4 | 100~10−4 | ||
| 10−9 | 10−3 | ||
| 100,000 | infinite | ||
| 200 | 0.2 | ||
| 0.68 | 0.68 | ||
| 0.001 | 0.001 | ||
| 0.001 | 0.001 | ||
| 0.5 | 0.5 | ||
| 0 | 0 | ||
| 0 | 0 | ||
| 5 | |||
| 0 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 0.1 | 0.00025 | ||
| 0.003 | 0.5 | ||
| 4 | 16 | ||
| 250 | 0.5 | ||
| −1~1 | 0.25 | ||
| 0 | 0, 0.01, 0.05, 0.1 |
| Formation Parameters | Values |
|---|---|
| Poisson’s ratio | 0.15–0.45 |
| Young’s modulus | 1.0 × 1010–9.5 × 109 Pa |
| Fracture porosity | 0.015–0.055 |
| Fracture compressibility | 2.39 × 10−8 Pa−1 |
| Oil compressibility | 2.26 × 10−9 Pa−1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Xing, G.; Fan, Z.; Zhao, W.; Zhao, L.; Song, H. A Novel Model Incorporating Geomechanics for a Horizontal Well in a Naturally Fractured Reservoir. Energies 2018, 11, 2584. https://doi.org/10.3390/en11102584
Wang M, Xing G, Fan Z, Zhao W, Zhao L, Song H. A Novel Model Incorporating Geomechanics for a Horizontal Well in a Naturally Fractured Reservoir. Energies. 2018; 11(10):2584. https://doi.org/10.3390/en11102584
Chicago/Turabian StyleWang, Mingxian, Guoqiang Xing, Zifei Fan, Wenqi Zhao, Lun Zhao, and Heng Song. 2018. "A Novel Model Incorporating Geomechanics for a Horizontal Well in a Naturally Fractured Reservoir" Energies 11, no. 10: 2584. https://doi.org/10.3390/en11102584
APA StyleWang, M., Xing, G., Fan, Z., Zhao, W., Zhao, L., & Song, H. (2018). A Novel Model Incorporating Geomechanics for a Horizontal Well in a Naturally Fractured Reservoir. Energies, 11(10), 2584. https://doi.org/10.3390/en11102584





