Frequency-Adaptive Current Controller Design Based on LQR State Feedback Control for a Grid-Connected Inverter under Distorted Grid
Abstract
:1. Introduction
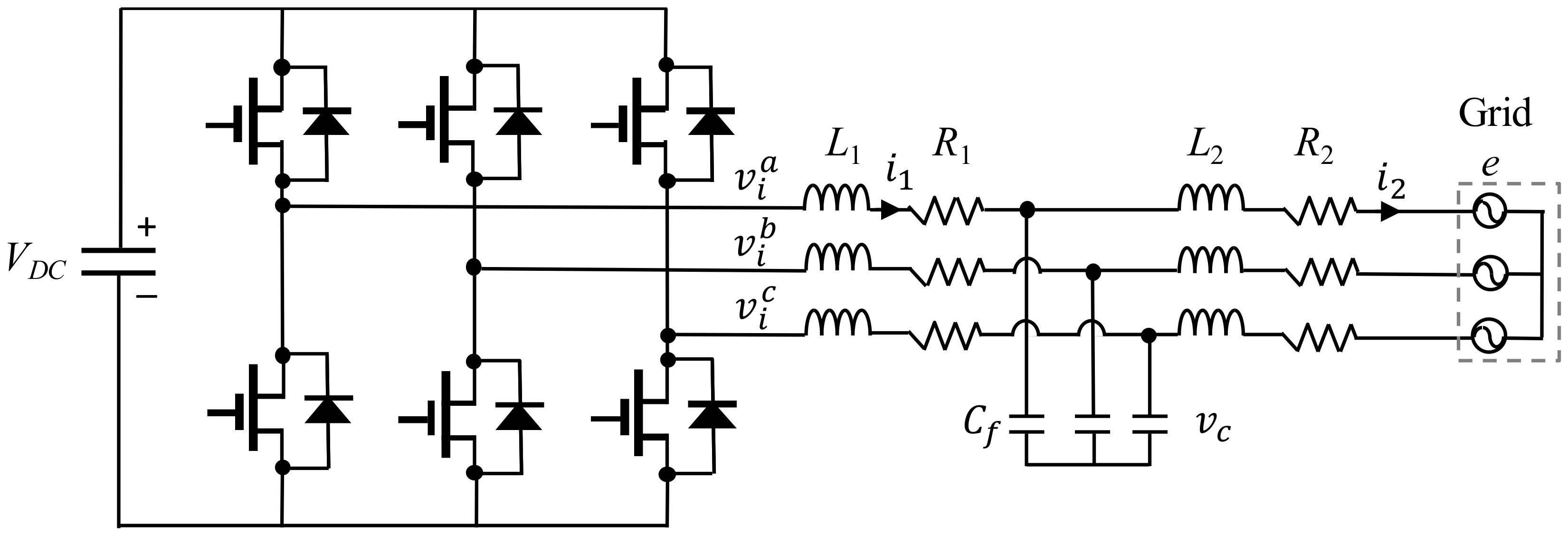
2. System Model of an LCL-Filtered Grid-Connected Inverter
2.1. Modeling of a Grid-Connected Inverter in the Synchronous Reference Frame
2.2. Discretization of the System Model
3. Proposed Frequency-Adaptive Current Control Scheme
3.1. Frequency Detection under Distorted Grid Voltage
3.2. Optimal Feedback Current Control Design Based on IM
3.3. Design of the Discrete-Time Observer in the Stationary Reference Frame
4. Simulation Results
4.1. Control Performance without Frequency Variation
4.2. Control Performance with Frequency Variation
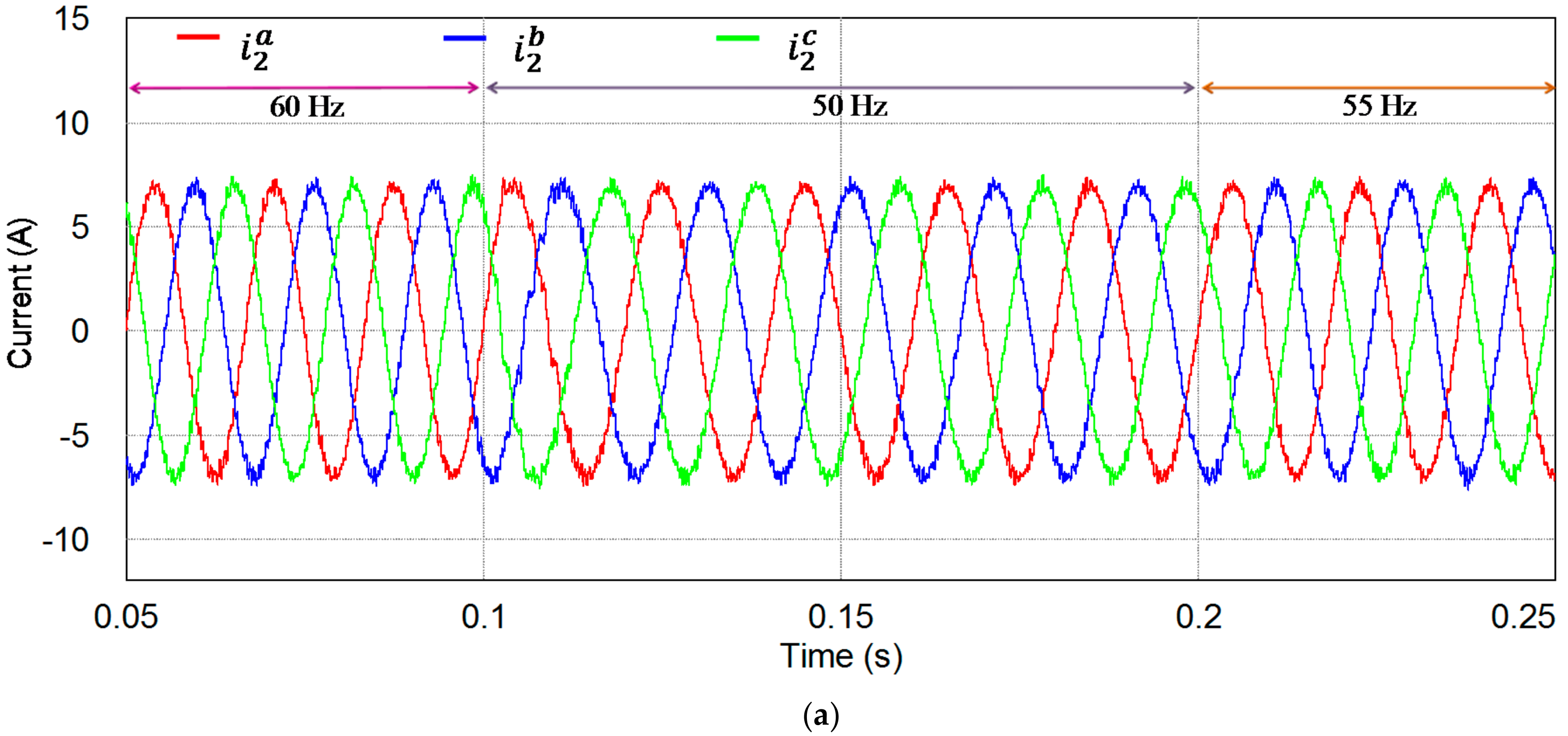
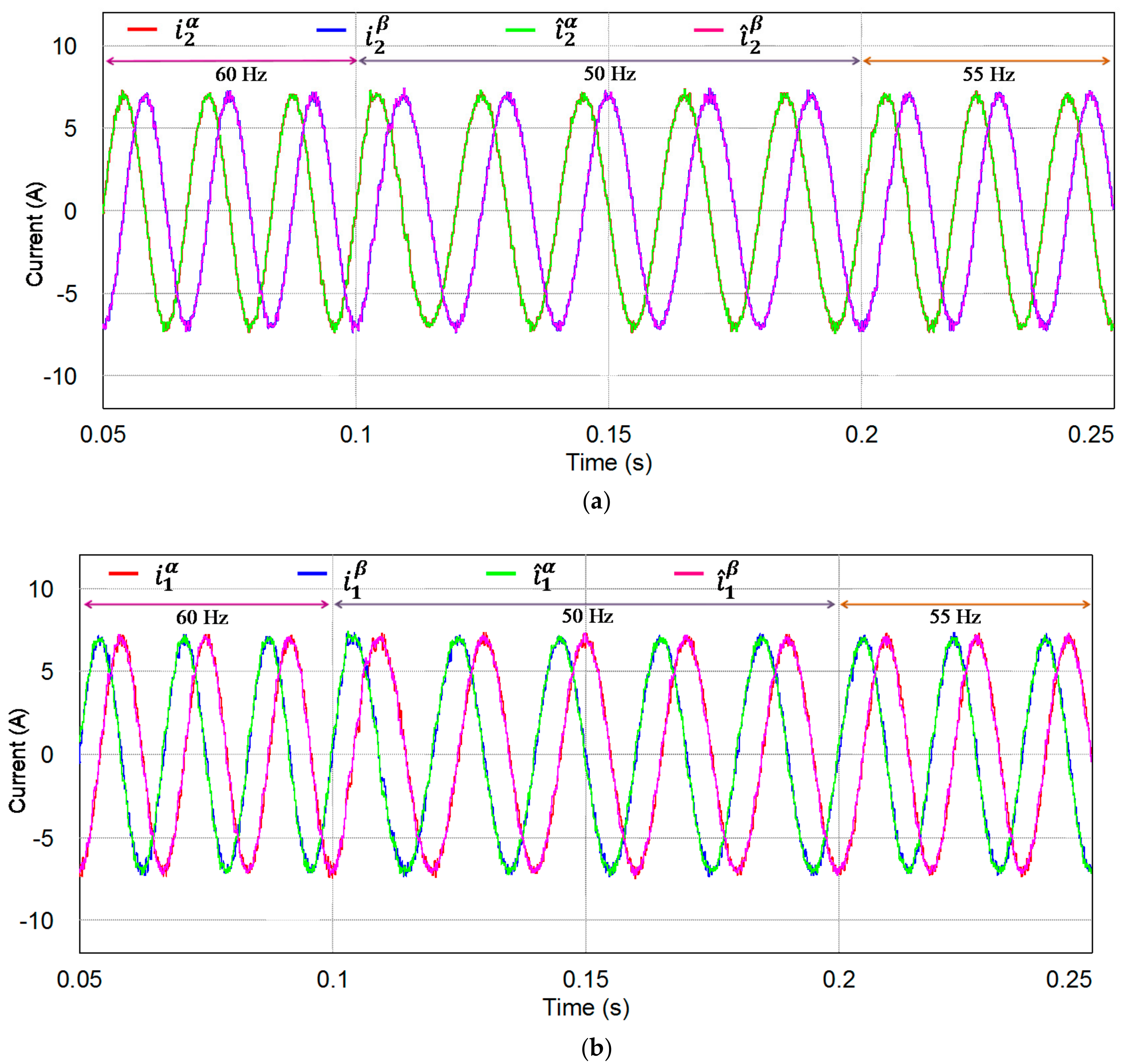
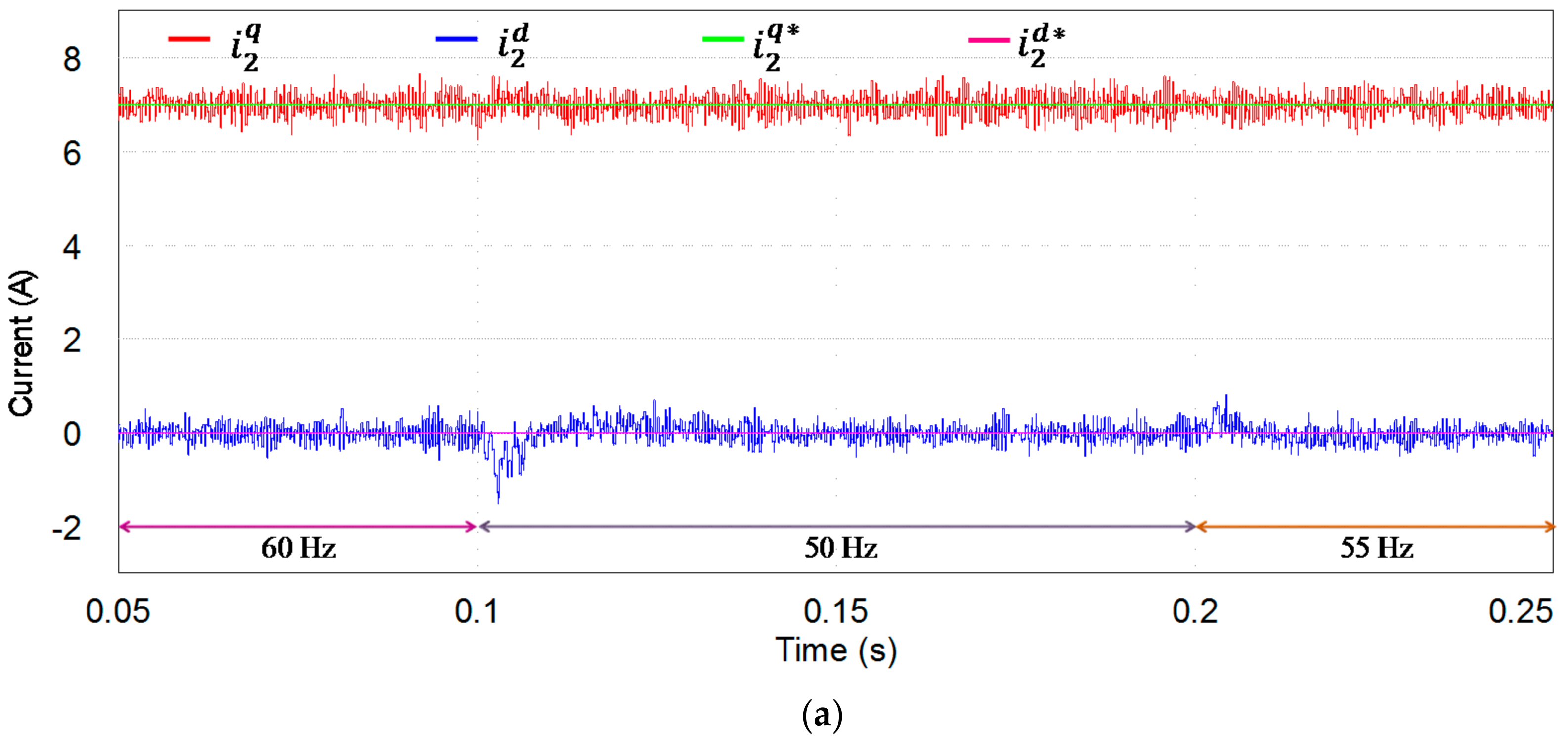
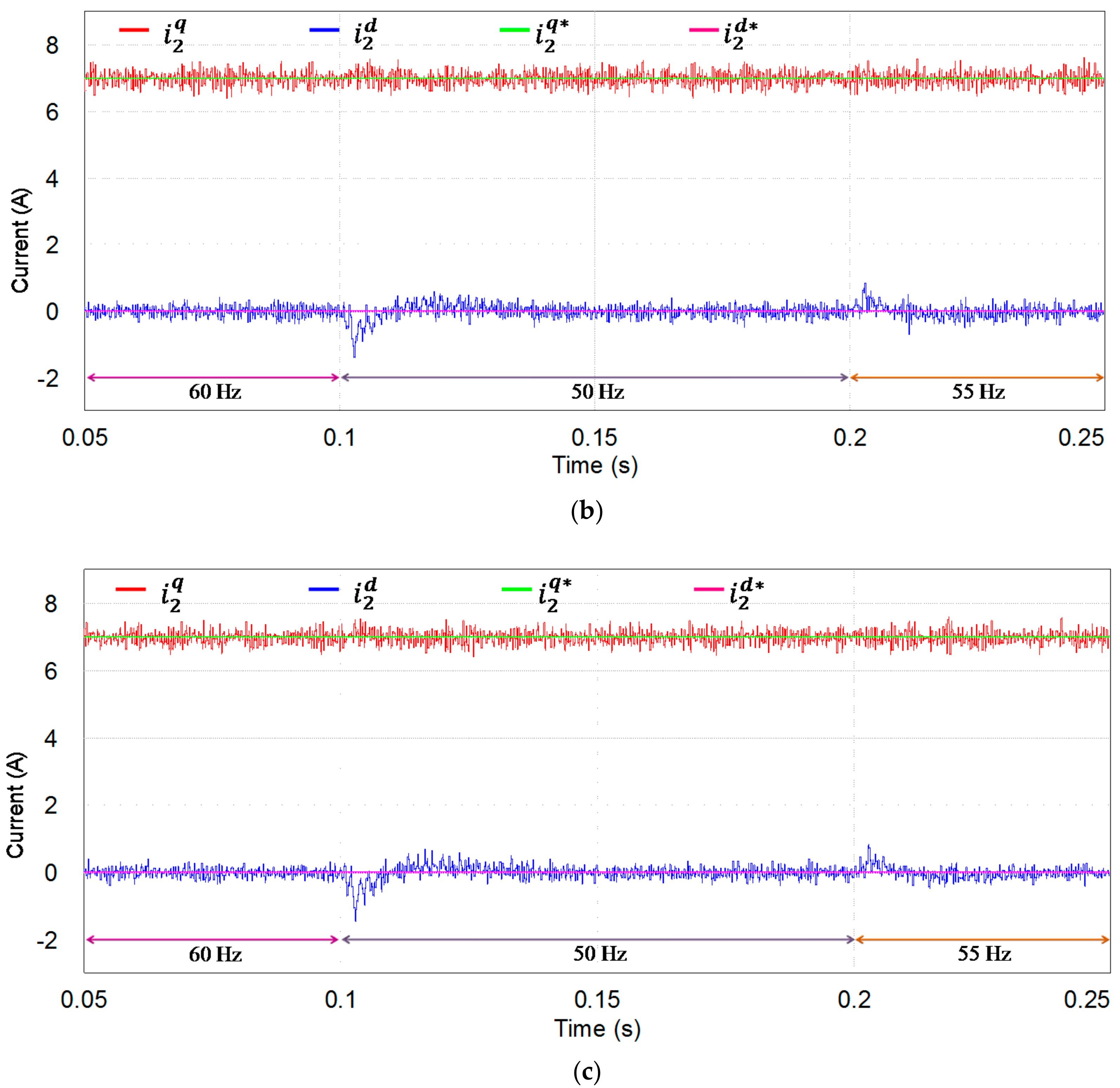
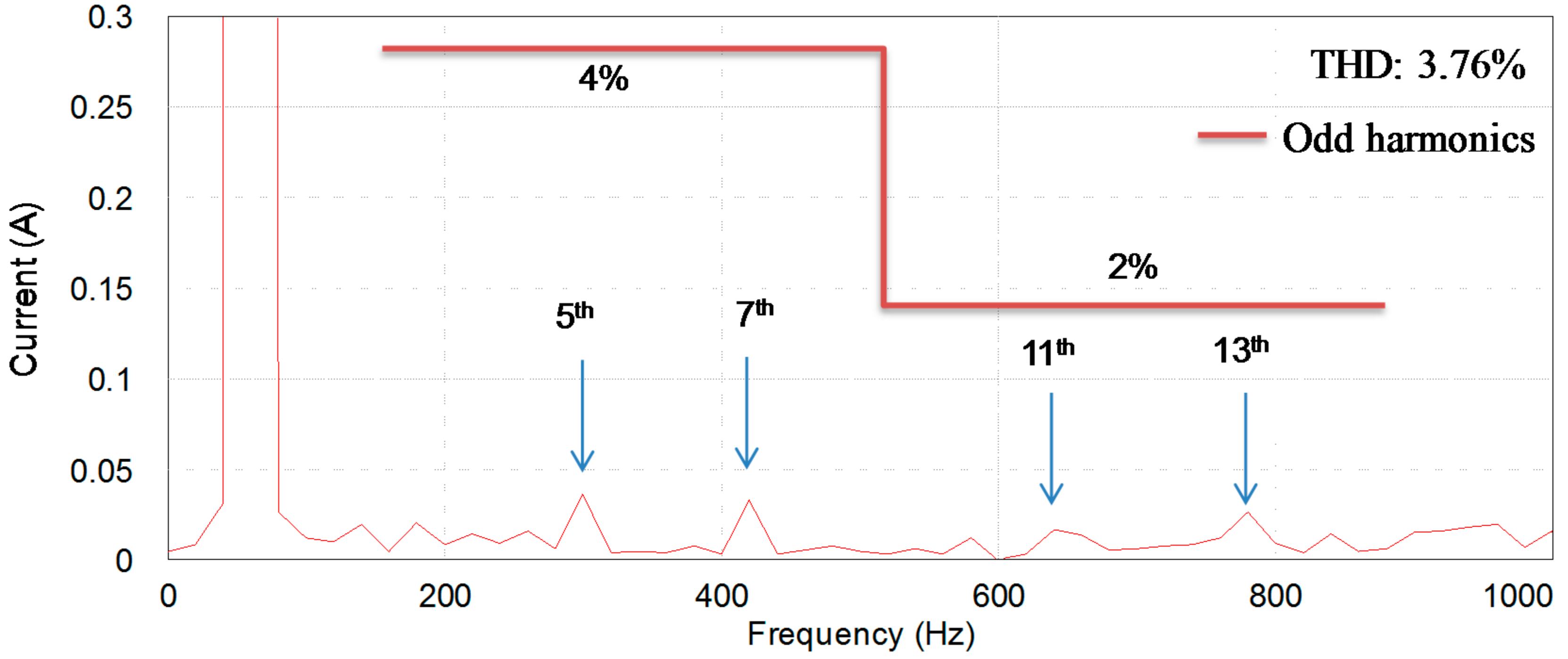
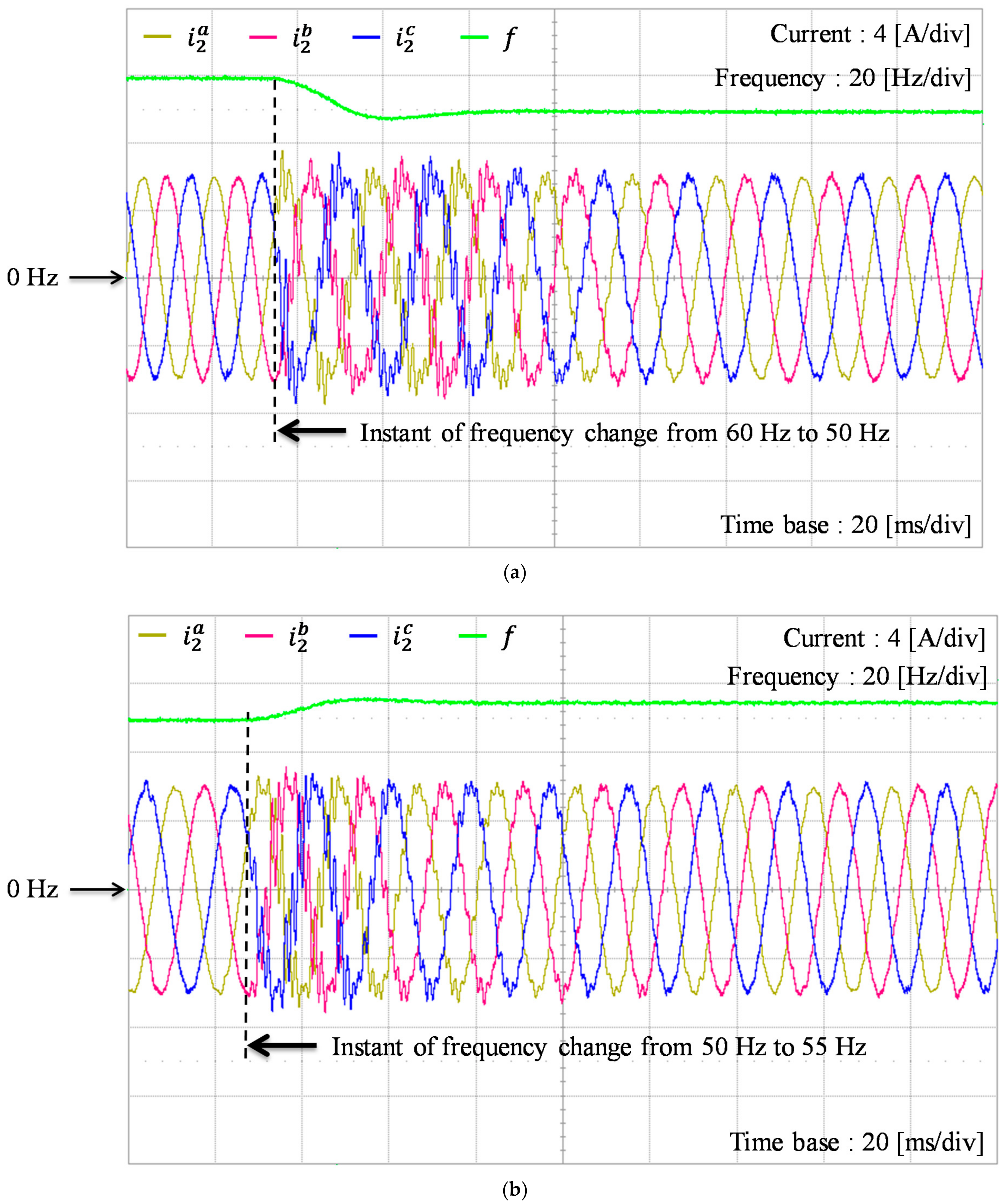
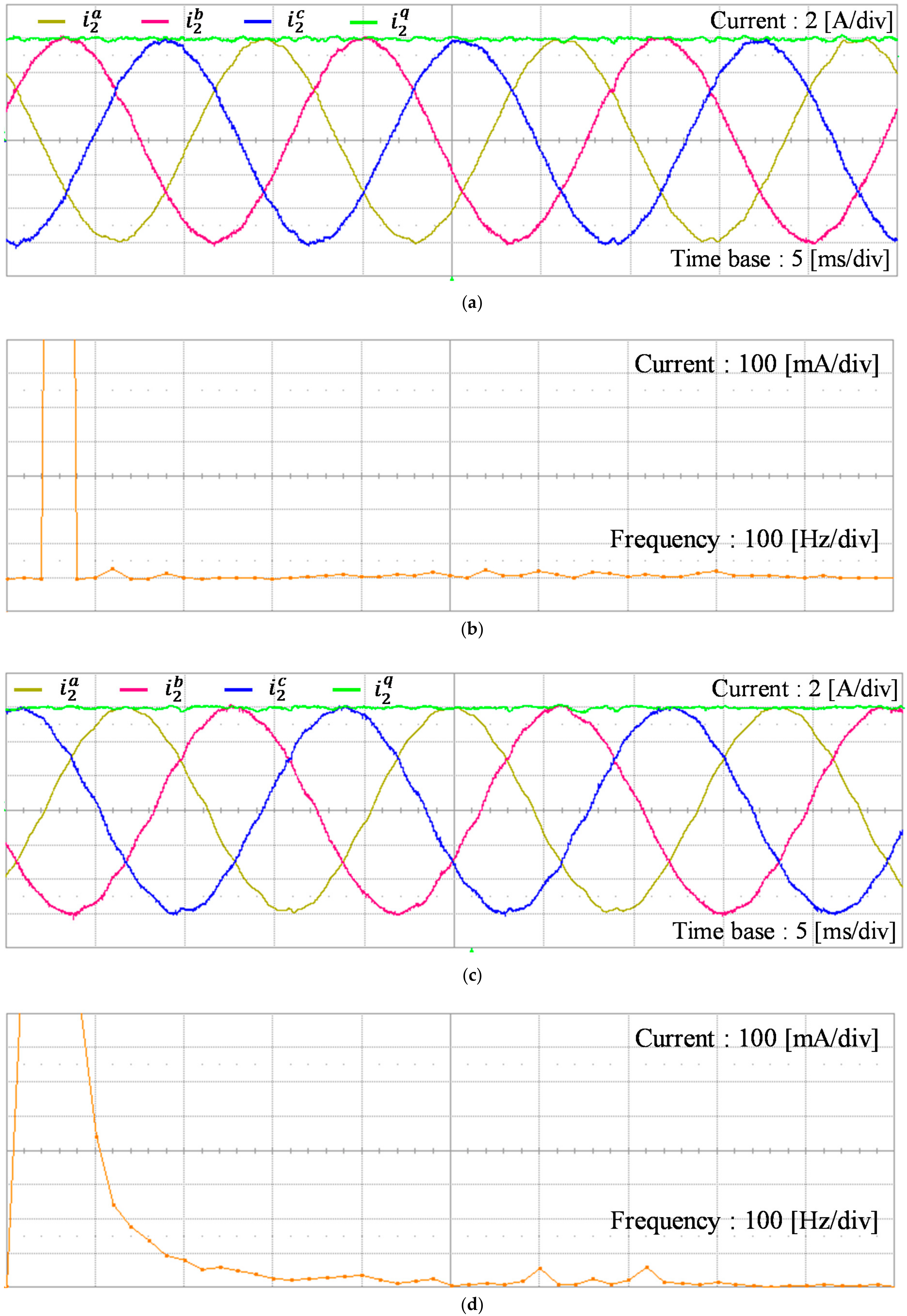
5. Experimental Results
5.1. Configuration of the Experimental System
5.2. The Observer’s Estimation Performance
5.3. Control Performance with Frequency Variation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, D.; Zhang, J.; Qian, Z. An improved repetitive control scheme for grid-connected inverter with frequency-adaptive capability. IEEE Trans. Ind. Electr. 2013, 60, 814–823. [Google Scholar] [CrossRef]
- Trinh, Q.N.; Lee, H.H. An advanced current control strategy for three-phase shunt active power filters. IEEE Trans. Ind. Electr. 2013, 60, 5400–5410. [Google Scholar] [CrossRef]
- Jiang, S.; Cao, D.; Li, Y.; Liu, J.; Peng, F.Z. Low-THD, fast-transient, and cost-effective synchronous-frame repetitive controller for three-phase UPS inverters. IEEE Trans. Power Electr. 2012, 27, 2994–3005. [Google Scholar] [CrossRef]
- Castilla, M.; Miret, J.; Matas, J.; Garcia de Vicuna, L.; Guerrero, J.M. Linear current control scheme with series resonant harmonic compensator for single-phase grid-connected photovoltaic inverters. IEEE Trans. Ind. Electr. 2008, 55, 2724–2733. [Google Scholar] [CrossRef]
- Dou, X.; Yang, K.; Quan, X.; Hu, Q.; Wu, Z.; Zhao, B.; Li, P.; Zhang, S.; Jiao, Y. An optimal PR control strategy with load current observer for a three-phase voltage source inverter. Energies 2015, 11, 1–21. [Google Scholar] [CrossRef]
- Schiesser, M.; Waterlain, S.; Marchesoni, M.; Carpita, M. A simplified design strategy for multi-resonant curent control of a grid-connected voltage source inverter with an LCL filter. Energies 2018, 11, 1–15. [Google Scholar] [CrossRef]
- Shen, G.; Zhu, X.; Zhang, J.; Xu, D. A new feedback method for PR current control of LCL-filter-based grid-connected inverter. IEEE Trans. Ind. Electr. 2010, 57, 2033–2041. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Multiple harmonics control for three-phase grid converter systems with the use of PI-RES current controller in a rotating frame. IEEE Trans. Power Electr. 2006, 21, 836–841. [Google Scholar] [CrossRef]
- Li, W.; Ruan, X.; Pan, D.; Wang, X. Full-feedforward schemes of grid voltage for a three-phase LCL-type grid-connected inverter. IEEE Trans. Ind. Electr. 2013, 60, 2237–2249. [Google Scholar] [CrossRef]
- Huerta, F.; Pérez, J.; Cóbreces, S. Frequency-adaptive multiresonant LQG state-feedback current controller for LCL-filtered VSCs under distorted grid voltages. IEEE Trans. Ind. Electr. 2018, 65, 8433–8444. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, K.; Wang, H.; Blaabjerg, F.; Wang, D.; Zhang, B. Frequency adaptive selective harmonic control for grid-connected inverters. IEEE Trans. Ind. Electr. 2015, 30, 3912–3924. [Google Scholar] [CrossRef]
- Jorge, S.G.; Busada, C.A.; Solsona, J.A. Frequency-adaptive current controller for three-phase grid-connected converters. IEEE Trans. Ind. Electr. 2013, 65, 4169–4177. [Google Scholar] [CrossRef]
- Eren, S.; Pahlevani, M.; Bakhshai, A.; Jain, P. A digital current control technique for grid-connected AC/DC converters used for energy storage systems. IEEE Trans. Power Electr. 2017, 32, 3970–3988. [Google Scholar] [CrossRef]
- Hogan, D.J.; Gonzalez-Espin, F.J.; Hayes, J.G.; Lightbody, G.; Foley, R. An adaptive digital-control scheme for improved active power filtering under distorted grid conditions. IEEE Trans. Ind. Electr. 2018, 65, 988–999. [Google Scholar] [CrossRef]
- Golestan, S.; Ebrahimzadeh, E.; Guerrero, J.M.; Vasquez, J.C. An adaptive resonant regulator for single-phase grid-tied VSCs. IEEE Trans. Power Electr. 2018, 33, 1867–1873. [Google Scholar] [CrossRef]
- Kukkola, J.; Hinkkanen, M.; Zenger, K. Observer-based state-space current controller for a grid converter equipped with an LCL filter: Analytical method for direct discrete-time design. IEEE Trans. Ind. Appl. 2015, 51, 4079–4090. [Google Scholar] [CrossRef]
- Yoon, S.J.; Lai, N.B.; Kim, K.H. A systematic controller design for a grid-connected inverter with LCL filter using a discrete-time integral state feedback control and state observer. Energies 2018, 11, 1–20. [Google Scholar]
- Kukkola, J.; Hinkkanen, M. Observer-based state-space current control for a three-phase grid-connected converter equipped with an LCL filter. IEEE Trans. Ind. Appl. 2014, 50, 2700–2709. [Google Scholar] [CrossRef]
- Perez-Estevez, D.; Doval-Gandoy, J.; Yepes, A.; Lopez, O. Positive- and negative-sequence current controller with direct discrete-time pole placement for grid-tied converters with LCL filter. IEEE Trans. Power Electr. 2017, 32, 7207–7221. [Google Scholar] [CrossRef]
- Tran, T.V.; Yoon, S.J.; Kim, K.H. An LQR-based controller design for an LCL-filtered grid-connected inverter in discrete-time state-space under distorted grid environment. Energies 2018, 11, 1–28. [Google Scholar] [CrossRef]
- Miskovic, V.; Blasko, V.; Jahns, T.M.; Smith, A.H.C.; Romenesko, C. Observer-based active damping of LCL resonance in grid-connected voltage source converters. IEEE Trans. Ind. Appl. 2014, 50, 3977–3985. [Google Scholar] [CrossRef]
- Francis, B.; Wonham, W. The internal model principle of control theory. Automatica 1976, 12, 457–465. [Google Scholar] [CrossRef]
- Lai, N.B.; Kim, K.H. Robust control scheme for three-phase grid-connected inverters with LCL-filter under unbalanced and distorted grid conditions. IEEE Trans. Energy Convers. 2018, 33, 506–515. [Google Scholar] [CrossRef]
- Lim, J.S.; Park, C.; Han, J.; Lee, Y.I. Robust tracking control of a three-phase DC–AC inverter for UPS applications. IEEE Trans. Ind. Electr. 2014, 61, 4142–4151. [Google Scholar] [CrossRef]
- Maccari, L.A.; Massing, J.R.; Schuch, L.; Rech, C.; Pinheiro, H.; Oliveira, R.C.L.F.; Montagner, V.F. LMI-based control for grid-connected converters with LCL filters under uncertain parameters. IEEE Trans. Power Electr. 2014, 29, 3776–3785. [Google Scholar] [CrossRef]
- Gabe, I.J.; Montagner, V.F.; Pinheiro, H. Design and implementation of a robust current controller for VSI connected to the grid through an LCL filter. IEEE Trans. Power Electr. 2009, 24, 1444–1452. [Google Scholar] [CrossRef]
- Franklin, G.; Workman, M.; Powell, J. Digital Control of Dynamic Systems; Ellis-Kagle Press: Half Moon Bay, CA, USA, 2006. [Google Scholar]
- Golestan, S.; Ramezani, M.; Guerrero, J.M.; Freijedo, F.D.; Monfared, M. Moving average filter based phase-locked loops: Performance analysis and design guidelines. IEEE Trans. Power Electr. 2014, 29, 2750–2763. [Google Scholar] [CrossRef]
- Orellana, M.; Grino, R. Some consideration about discrete-time AFC controllers. In Proceedings of the 52nd IEEE Conf. on Decision and Control, Florence, Italy, 10–13 December 2013; pp. 6904–6909. [Google Scholar]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems, 7th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Phillips, C.L.; Nagle, H.T. Digital Control System Analysis and Design, 3rd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Ogata, K. Discrete Time Control Systems, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Huerta, F.; Pizarro, D.; Cóbreces, S.; Rodríguez, F.J.; Girón, C.; Rodríguez, A. LQG servo controller for the current control of LCL grid-connected voltage-source converters. IEEE Trans. Ind. Electr. 2012, 59, 4272–4284. [Google Scholar] [CrossRef]
- IEEE. IEEE Standard for Interconnecting Distributed Resources with Electric Power System; IEEE Std.1547; IEEE: New York, NY, USA, 2003. [Google Scholar]
- Texas Instrument. TMS320F28335 Digital Signal. Controller (DSC)—Data Manual; Texas Instrument: Dallas, TX, USA, 2008. [Google Scholar]

















| Parameters | Value | Units |
|---|---|---|
| DC link voltage | 420 | V |
| Resistance (load bank) | 24 | |
| Filter resistance | 0.5 | |
| Filter capacitance | 4.5 | µF |
| Inverter-side filter inductance | 1.7 | mH |
| Grid-side filter inductance | 1.7 | mH |
| Grid voltage (line-to-line root mean square (rms)) | 220 | V |
| Grid frequency | 50, 55, 60 | Hz |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bimarta, R.; Tran, T.V.; Kim, K.-H. Frequency-Adaptive Current Controller Design Based on LQR State Feedback Control for a Grid-Connected Inverter under Distorted Grid. Energies 2018, 11, 2674. https://doi.org/10.3390/en11102674
Bimarta R, Tran TV, Kim K-H. Frequency-Adaptive Current Controller Design Based on LQR State Feedback Control for a Grid-Connected Inverter under Distorted Grid. Energies. 2018; 11(10):2674. https://doi.org/10.3390/en11102674
Chicago/Turabian StyleBimarta, Rizka, Thuy Vi Tran, and Kyeong-Hwa Kim. 2018. "Frequency-Adaptive Current Controller Design Based on LQR State Feedback Control for a Grid-Connected Inverter under Distorted Grid" Energies 11, no. 10: 2674. https://doi.org/10.3390/en11102674






