Recursive Method for Distribution System Reliability Evaluation

Abstract

This paper proposes a novel hybrid recursive method for distribution system reliability evaluation to deal with the computational limit and low-efficiency problem which exist in previously developed techniques as the system becomes larger. This method includes a bottom-up process and a top-down process, which are developed on the basis of a recursive principle, and the synthesis of both processes yield the reliability performance of each bus of the system. The bottom-up process considers the effects of downstream failures on upstream customers, and the top-down process considers the effects of upstream failures on downstream customers. In addition, a novel switch zone concept is defined and introduced into the bottom-up recursive process to save the computation cost. Besides, section technique (ST) and shortest path method (SPM) are employed to effectively simplify the recursive path and thus, the computation efficiency can be improved. The most significant feature of the proposed method over ST, SPM, failure mode and effect analysis (FMEA) is that it provides a more generalized equivalent approach to maximally simplify the network for reliable evaluation irrespective of the network topology. The effectiveness of the proposed method has been validated through comprehensive tests on Roy Billinton test system (RBTS) bus 6 and a practical-sized distribution system in China.

1. Introduction

Reliability evaluation is one of the essential functions required in the planning and operating stage of energy systems [1,2,3]. So far, considerable methodologies, such as Monte Carlo simulation (MCS), minimal cut set approach, and FMEA have evolved over the past 50 years to develop various reliability techniques [4,5,6,7]. However, those methodologies usually involve iterative computations, and hence are time-consuming and hard to be implemented in high-level analyses, such as risk analysis and sensitivity analysis [8]. Therefore, section technique (ST) [9,10], reliability network equivalent approach (RNEA) [11,12], shortest path method (SPM) [13] and zone-branch method [14], have been proposed to reduce the calculation complexity for reliability evaluation. Nevertheless, those methods are generally based on a sub-feeder equivalent approach, where, depending on the original topology, the network may not maximally be simplified. In other words, the equivalent path of those methods mainly depends on the network topology and, consequently, the computation cost involved in the subsequent reliability assessment is limited, which is the main drawback of those methods. Furthermore, these methods may fail to provide or even lose the reliability performance of some critical buses in the system, and thus cannot offer sufficient information required for system expansion and reinforcement [15].

It is clear that when a failure happens, the interruption effects spread over the entire network step by step since the elements in the system are closely connected with each other [16]. In other words, considering a certain element, the effect of all its downstream failures on any upstream load point (LP), as well as the effect of its upstream failures on downstream LP, will more or less depend on the operation state of the element. As comprehensively analyzed in this paper, those effects can be determined accurately using the recursive principles of reliability information for interlinked elements and adjacent buses. Accordingly, a novel recursive method for distribution system reliability evaluation is proposed in this paper as to improve the algorithm efficiency and to retain the calculation accuracy. It should be noted that several recursive algorithms have been developed in the literatures as existing reliability solutions [17,18,19,20]. However, they cannot be directly implemented in real distribution system because of the differences between power distribution systems and generalized series-parallel multi-state systems [18]. The differences can be mainly summarized as: (1) The power flow direction should be considered in distribution system reliability evaluation; (2) the effect of alternative supplies (AS) on reliability performance should also be considered in power systems; (3) the network of distribution system is more complex because of the hand-in-hand loop structure. Therefore, this work is further devoted to investigate the recursive principles that power networks exhibit and a recursive algorithm that can improve reliability evaluation efficiency. The main contributions of this paper include:

• Comprehensive analysis on the bottom-up and top-down recursive principles of reliability performance for interconnected elements and adjacent buses.
• The development of an novel hybrid recursive method for distribution system reliability evaluation based on the analyzed recursive principles.
• The definition of switch zone concept, which has been introduced in the proposed method for efficiency improvement.

The proposed recursive method has been thoroughly tested and benchmarked on RBTS bus 6 and a practical-sized distribution system under various operational scenarios.

2. General Model for Distribution System

2.1. General Data Structure for Basic Elements

The basic element in the distribution system is a tie connecting any two adjacent buses. A tie may be a transformer, a piece of line, or protective device. Generally, the reliability performance of line and transformer can be statistically described as two independent indices, including failure rate and outage duration. In addition, the performance of protective devices can be represented as operation probability and (replacing) time. Therefore, all the basic elements in the distribution system can be summarized as a general data structure [21], as follows,

$$e=\left\{i,j,a,\lambda ,p,t\right\}$$

(1)

where e denotes a certain element whose parent bus and offspring bus are represented as i and j; a denotes the type of the element; λ and r are the failure rate and outage duration; p is the probability of the element operating unsuccessfully; t is the repair time or replacing time for non-switch devices or operation time for the switch device.

2.2. Section of a Branch

A distribution system can be decomposed into several independent sections by protective devices. In any section, the protective devices that should be acted and the out-of-service duration for all LPs are irrespective of where the failure happens in this section. Therefore, the whole section, termed as section of a branch, can be treated as an equivalent unit to reduce the computation events for reliability evaluation. The reliability performances of an equivalent section can be determined as,

$${\lambda }_s={\displaystyle {\sum }_{k=1}^{N_s}{\lambda }_k}$$

(2)

$$r_s={\displaystyle {\sum }_{k=1}^{N_s}{\lambda }_k{r}_k}/{\lambda }_s$$

(3)

where λ_s and r_s denote the equivalent failure rate and outage duration for one section, respectively; N_s is the total number of elements;

The determination of equivalent sections involves the following steps: (1) Select one non-marked element randomly in the distribution system; (2) choose one feasible search direction and examine the successive elements along the selected direction as to identify the type of the elements until a protective device is encountered or it ends with the terminal of a feeder; (3) the search procedure terminates if all existing directions have been checked once, and then the area surrounded by the protective devices forms one equivalent section; (4) go to step (1) until all elements in distribution system are marked.

2.3. General Model for Distribution System

Using the general data structure and equivalent sections, a distribution system can be represented as a simplified tree data structure in which the components are related to each other through parent and offspring relationships [22,23]. One such equivalent process for a small-scale distribution system is illustrated in Figure 1. It is shown that the components in the simplified lower subfigure consist of equivalent sections and protective devices since all the section of branches in the upper subfigure are replaced with corresponding independent components in the lower subfigure.

Generally, there is a breaker between the main supply and the distribution system. The breaker is used to isolate the outages occurring in the distribution system from the rest of the power utility. Assuming the protective devices are perfectly coordinated, then all the components, in which a permanent fault occurred only results in the main breaker recognizing and isolating the fault, are categorized as 1st level components. Accordingly, 2nd level components are those ones in which when a fault occurs, will result in the protective devices that are connected to 1st level components recognizing and triggering. Therefore, any component in the distribution system can always be hierarchically classified as one of the nth level components, where n represents the number of protective devices between the main supply and the components. Take the lower subfigure in Figure 1 as an example, the 1st level components contain breaker B1 and line 1–2, the 2nd level contain switch S1, fuses 2–3 and 2–5, and equivalent sections 3–4, 5–6 and 7–8, and so on.

It can be found that when a fault occurred, both of its upstream LPs and downstream LPs will be affected to some degree conditionally. The degree relies on the operations state of the involving protective devices and AS [24,25]. In other words, considering a particular component, the effect of its downstream failures on its upstream LPs will more or less depend on its own operation state. As analyzed in the following Section 3 and Section 4, this kind of effect can be recursively determined using bottom-up recursive principles. Similarly, the effect of its upstream failures on downstream LPs can be determined using top-down recursive principles. Synthesizing both of the effects yields the reliability performances for any bus and LP.

In addition, the concept and formation of the proposed recursive algorithm are based upon the following assumptions,

(1)

All faults are permanent.

(2)

Overlapping failures are not considered in this paper because those effects are negligible in practical power system.

The protective devices are perfectly coordinated, i.e., the protective device closest to the fault needs to operate first.

3. Recursive Principles

3.1. Bottom-Up Recursive Principle

Generally, the protective devices used in distribution systems can be classified into two categories: The ones with an instantaneous response and the ones with a delayed response [26,27]. The former can isolate downstream failures immediately subject to an operation probability, and the latter includes switches, and can be used to reduce the restoration time when required. Considering a general case, two components are arranged as shown in Figure 2 where the arrow indicates the direction of power flow. e_T denotes the failure component and both of the terminals for e_S, i.e., i and j, will be affected. Therefore, the interruption effect of e_T on bus i can be determined using the effect of e_T on bus j, described as follows,

Condition A: e_S is a breaker, fuse, relay or other protective device with instantaneous response.

Condition B: e_S is the closest upstream switch to the failure e_T, which is used to isolate the fault from upstream LPs.

$${\lambda }^{bu}{}_{iT}=\{\begin{array}{l}{\lambda }^{bu}{}_{jT}\mathrm{Condition}A\mathrm{not}\mathrm{satisfied}\\ {\lambda }^{bu}{}_{jT}{p}_S\mathrm{Condition}A\mathrm{satisfied}\end{array}$$

(4)

$$r^{bu}{}_{iT}=\{\begin{array}{l}{r}^{bu}{}_{jT}\mathrm{Condition}B\mathrm{not}\mathrm{satisfied}\\ \min \left(r^{bu}{}_{jT},t_S\right)\mathrm{Condition}B\mathrm{satisfied}\end{array}$$

(5)

where λ^bu_jT, r^bu_jT are bottom-up interruption effect from e_T to bus j of e_S; Similarly, λ^bu_iT, r^bu_iT are that from e_T to bus i of e_S; t_s is the switching time of e_S.

In summary, the interruption effect of e_T on bus i can be recursively determined using the effect of e_T on bus j. Specifically, if condition A is satisfied, then the equivalent failure rate of e_T on bus i equals to the product of p_S and λ^bu_jT. It can be easily concluded that the service of upstream LPs will not be interrupted by downstream failures when e_S functions perfectly. Otherwise, the failure rate stays unchanged. If condition B is satisfied, the outage duration of e_T on bus i selects the minimal of t_S, and r^bu_jT. This is because switch e_S is responsible for acting to restore the service of upstream LPs. Otherwise, the duration remains the same. In addition, it can be summarized that the bottom-up recursive principles are irrespective of the location and the type of the failure component e_T.

3.2. Top-Down Recursive Principle

It is clear that when a failure happens, the services of the entire downstream LPs will undoubtedly be interrupted, and part of that needs to be restored through AS. This is usually the case in the modern distribution system in which feeders are in the form of hand-in-hand loop. Top-down recursive principle is to address the interruption effect of upstream failures on downstream LPs. Similarly, consider a general case as shown in Figure 3, where e_S and e_T have the same meaning with Figure 2. Therefore, the interruption effect of e_T on bus i can be determined using the effect of e_T on bus j, described as follows,

Condition C: No AS exists on e_T’s downstream area or no switching device sits between e_T and e_S.

Condition D: At least one switching device exists between e_T and e_S, and meanwhile at least one AS exists on the downstream area of the closest downstream switch to e_T.

$${\lambda }^{td}{}_{jT}={\lambda }^{td}{}_{iT}$$

(6)

$$r^{td}{}_{jT}=\{\begin{array}{l}{r}^{td}{}_{iT}\mathrm{Condition}C\mathrm{satisfied}\\ \min \left(r^{td}{}_{iT},\max (t_o,t_{\mathrm{AS}})\right)\mathrm{Condition}D\mathrm{satisfied}\end{array}$$

(7)

where λ^td_jT and r^td_jT denote the top-down equivalent effect from e_T on bus j of e_S, and λ^td_iT and r^td_iT denote the effect from e_T on bus i of e_S; t_AS is the switching time of an AS and t_o is the operation time of the responsible isolating switch.

To summarize, the interruption effect of e_T on bus j can also be recursively determined using the effect of e_T on bus i. Specifically, the equivalent failure rate of e_T on bus j equals that of e_T on bus i, and the equivalent outage duration depends on the location of switching devices and available AS. If condition C is satisfied, the outage duration of e_T on bus j equals the repair time of e_T. If condition D is satisfied, the duration chooses the minimum of the accessing time of corresponding AS and r^bu_iT.

4. The Proposed Recursive Algorithm

The proposed recursive algorithm consists of bottom-up and top-down recursive processes. The former considers the effect of downstream interruptions on upstream buses within a network, while the latter considers the impact of upstream interruptions on downstream buses. The synthesis of both procedures can generate the reliability indices of any bus and LP.

4.1. Bottom-Up Recursive Process

According to the bottom-up recursive principle, the interruption effect of one failure on its upstream buses differs with the type of the recursive component e_S, that is whether e_S is a switching device or not.

Definition 1: The zone surrounded by switches is defined as a switch zone, each of which contains only one upstream switch and several downstream switches, as shown in Figure 1. It should be stressed that the switch zone is distinguished from the section of a branch because of different definitions and objectives. The switch zone is classified based on switching devices and is used to simplify the recursive process and thus to offer facilities for recursive process. While the section of a branch is classified based on protective devices in any form and is employed to reduce the basic components, thereby simplifying the distribution system [28].

(1) e_S denotes a switching device: In this case, e_S is the upstream switch of a certain switch zone, denoted as Ω. Hence, when a fault occurs in Ω, the service of upstream LPs can be restored through opening e_S. That means the outage duration for upstream LPs is not more than the operation time of e_S. And then, according to (4)–(5), the bottom-up recursive process from e_S’s bus j to its bus i can be summarized as follows,

$${\lambda }^{bu}{}_{iS}={\lambda }^{bu}{}_{iS}+{\lambda }^{bu}{}_{jS}+{\lambda }^{bu}{}_{j\mathsf{\Omega }}$$

(8)

$$r^{bu}{}_{iS}=\left({\lambda }^{bu}{}_{iS}{r}^{bu}{}_{iS}+{\lambda }^{bu}{}_{jS}{r}^{bu}{}_{jS}+\min \left(r^{bu}{}_{j\mathsf{\Omega }},t_S\right){\lambda }^{bu}{}_{j\mathsf{\Omega }}\right)/{\lambda }^{bu}{}_{iS}$$

(9)

where λ^bu_jΩ and r^bu_jΩ denote the aggregated interruption effects of downstream failures in Ω on bus j, and those effects can be mitigated via opening e_S. While λ^bu_jS and r^bu_jS denote the interruptions of failures occurring in other downstream areas on bus j, indicating that these interruptions cannot be mitigated by opening e_S. Other symbols involving subscript i have similar meanings.

(2) e_S denotes a non-switching device: In this case, bus i and bus j are in the same switch zone, and thus the bottom-up recursive process from e_S’s bus j to bus i can be summarized as,

$${\lambda }^{bu}{}_{iS}={\lambda }^{bu}{}_{iS}+{\lambda }^{bu}{}_{jS}{p}_S$$

(10)

$$r^{bu}{}_{iS}=\left({\lambda }^{bu}{}_{iS}{r}^{bu}{}_{iS}+{\lambda }^{bu}{}_{jS}{r}^{bu}{}_{jS}{p}_S\right)/{\lambda }^{bu}{}_{iS}$$

(11)

$${\lambda }^{bu}{}_{i\mathsf{\Omega }}={\lambda }^{bu}{}_{i\mathsf{\Omega }}+{\lambda }^{bu}{}_{j\mathsf{\Omega }}{p}_S$$

(12)

$$r^{bu}{}_{i\mathsf{\Omega }}=\left({\lambda }^{bu}{}_{i\mathsf{\Omega }}{r}^{bu}{}_{i\mathsf{\Omega }}+{\lambda }^{bu}{}_{j\mathsf{\Omega }}{r}^{bu}{}_{j\mathsf{\Omega }}{p}_S\right)/{\lambda }^{bu}{}_{i\mathsf{\Omega }}$$

(13)

where p_S is the operation probability for e_S, and adopts 1 for any equivalent component.

In order to maximally improve the calculation efficiency, the reliability performance of buses at lthe owest-level should be determined as a priority, and then the performance of buses at higher-level can be calculated recursively. In other words, the calculation events on the higher-level can only be achieved as long as all components on the current level have been computed once.

4.2. Top-Down Recursive Process

Definition 2: The network whose components are on the shortest path from the main supply to any AS is referred to as the main network and the rest of the independent sections are referred to as lateral networks [29].

As presented in Section 3.2, the top-down recursive principle differs with the location of ASs and switching devices. Consequently, two general cases are considered in this paper: The current recursive component e_S is on the main network or not. This is because the service to the downstream subarea of e_S can be restored via closing one available AS if e_S sits on the main network, otherwise the service cannot be restored [30].

(1) e_S on Main Network: As shown in Figure 3, assuming e_T and e_S are two longitudinally connected switches on the main network, then the recursive rules from bus b of e_T to bus j of e_S can be described as follows,

$${\lambda }^{td}{}_{j\mathsf{\Omega }}={\lambda }^{bu}{}_{b\mathsf{\Omega }}-{\lambda }^{bu}{}_{i\mathsf{\Omega }}$$

(14)

$$r^{td}{}_{j\mathsf{\Omega }}=\min \{\begin{array}{c}\max \left(t_S,\min \left(t_{AS1},t_{AS1}\dots \right)\right)\\ \left({\lambda }^{bu}{}_{b\mathsf{\Omega }}{r}^{bu}{}_{b\mathsf{\Omega }}-{\lambda }^{bu}{}_{i\mathsf{\Omega }}{r}^{bu}{}_{i\mathsf{\Omega }}\right)/{\lambda }^{td}{}_{j\mathsf{\Omega }}\end{array}$$

(15)

$${\lambda }^{td}{}_{jS}={\lambda }^{td}{}_b+{\lambda }^{bu}{}_{bS}-{\lambda }^{bu}{}_{iS}$$

(16)

$$r^{td}{}_{jS}=\left({\lambda }^{td}{}_b{r}^{td}{}_b+{\lambda }^{bu}{}_{bS}{r}^{bu}{}_{bS}-{\lambda }^{bu}{}_{iS}{r}^{bu}{}_{iS}/{\lambda }^{td}{}_{jS}\right)$$

(17)

$${\lambda }^{td}{}_j={\lambda }^{td}{}_{jS}+{\lambda }^{td}{}_{j\mathsf{\Omega }}$$

(18)

$$r^{td}{}_j=\left({\lambda }^{td}{}_{jS}{r}^{td}{}_{jS}+{\lambda }^{td}{}_{j\mathsf{\Omega }}{r}^{td}{}_{j\mathsf{\Omega }}\right)/{\lambda }^{td}{}_j$$

(19)

where t_AS1 and t_AS2 represent the operation time of available AS1, AS2, respectively, and the one with minimal time should be chosen to restore the service, and thus to minimize the outage duration; λ^td_j and r^td_j are the synthesized interruption effects of e_S’s upstream failures; λ^td_jΩ and r^td_jΩ are synthesized effects of failures happened in Ω (here, it is the switch zone between e_S and e_T) on bus j, and λ^td_jS and r^td_jS denote the effect of failures in e_T’s upstream areas on bus j.

If a fault occurs in Ω, the service to downstream LPs can be restored by opening e_S, and thereby the top-down outage duration is not more than the accessing time of available AS, as presented in (15). Otherwise, e_S should not be involved in the restoration process.

(2) e_S on Lateral Network: In this case, the top-down equivalent failure rate stays the same with the case of the main network since service restoration cannot avoid outage. In addition, when a failure happens in Ω, its downstream LPs cannot be restored until the fault has been cleared since no AS exists on lateral networks, and thus the top-down equivalent duration can be described as follows,

$$r^{td}{}_{j\mathsf{\Omega }}=\left({\lambda }^{bu}{}_{b\mathsf{\Omega }}{r}^{bu}{}_{b\mathsf{\Omega }}-{\lambda }^{bu}{}_{i\mathsf{\Omega }}{r}^{bu}{}_{i\mathsf{\Omega }}\right)/{\lambda }^{td}{}_{j\mathsf{\Omega }}$$

(20)

It can be easily observed that only the switching devices are selected to go through the top-down recursive process. This is designed to maximally simplify the recursive path and thus the efficiency can be improved. The top-down recursive process begins with any switch at the highest-level, and terminates when all switches have been recursively calculated once. Similarly, in this process, the breadth-first search method is also employed to guarantee the high efficiency.

Note that only the top-down reliability performances of both terminals of the switch have been computed in the top-down recursive process. Thereby, the reliability performance of other buses can be determined using top-down recursive principles.

4.3. The Synthesis of Two Recursive Process

The service interruptions for any bus and LP can be attributed to failures in its upstream or downstream networks. Based on the recursive principles presented above, considering any LP, the reliability performance can be determined by synthesizing its bottom-up recursive process and the top-down recursive process, described as,

$${\lambda }_k={\lambda }^{bu}{}_{k\mathsf{\Omega }}+{\lambda }^{bu}{}_{kS}+{\lambda }^{td}{}_k$$

(21)

$$r_k=\left({\lambda }^{bu}{}_{k\mathsf{\Omega }}{r}^{bu}{}_{k\mathsf{\Omega }}+{\lambda }^{bu}{}_{kS}{r}^{bu}{}_{kS}+{\lambda }^{td}{}_k{r}^{td}{}_k\right)/{\lambda }_k$$

(22)

where λ^td_k and r^td_k denote the interruptions caused by failures on load point k’s upstream area; λ^bu_kΩ and r^bu_kΩ denote interruptions caused by faults occurred in downstream Ω; and λ^bu_kS and r^bu_kS denote the interruptions that happened on other downstream areas.

4.4. Procedures

In summary, the main execution steps for reliability evaluation using the proposed recursive method can be illustrated as a flowchart in Figure 4. Initialization block is to initialize the variables required in both recursive processes. In the bottom-up recursive process, set variables λ^bu_jS, r^bu_jS, λ^bu_iS, r^bu_iS to zero, and λ^bu_jΩ and r^bu_jΩ to the reliability indices of the component whose offspring node is j. In the top-down recursive process, λ^td_jS and r^td_jS at the highest-level are determined based on top-down recursive principles.

5. System Studies

The performance of the proposed recursive method has been fully evaluated through the following two case studies. The two test systems are the commonly used RBTS-BUS6 [31] and a practical industrial distribution system in Henan province, China [32].

5.1. RBTS-BUS6

As a typical mixed rural/urban distribution network with residential, commercial and agricultural customers, RBTS-BUS6 consists of 4 feeders, 40 load points, 82 lines, 40 fuses and 28 transformers, 9 breakers and 17 disconnect switches [31]. Normally, the tie-switch connecting feeder 1 and feeder 2 is assumed to be opened and other switches are set to be closed. The peak load and average load of this system are 20 MW and 10.72 WM, respectively. The reliability parameters for protective devices are given in

Table 1. Reliability Parameters for Protective Devices.

Element	λ (f/year)	r (h)	Element	λ (f/year)	r (h)
Breaker	0.006	4	Transformer	0.015	10
Line	0.065	5	Fuse	0.002	3
Switch	0.006	4

λ-failure rate, r-repair time, for lines (year·km⁻¹).

, other system parameters and the network topology are referred to in Reference [31].

In order to comprehensively explore the benefits of the proposed method, three different cases have been considered:

• Case 1: The operation time of all tie-switches is set to 1.5 h and that of other disconnect switches is set to 1 h. In addition, the fuses, breakers and relays are assumed to be 100% reliable, i.e., they belongs to ideal protective devices;
• Case 2: All the fuses, breakers and relays are assumed to be 90% reliable and other conditions are set as the same with case 1;
• Case 3: An AS has been installed at the terminal of feeder 4, and other conditions are set as the same with case 2.

Based on the reliability parameters presented in Table 1, the reliability performance of all LPs can be calculated using the proposed recursive method. The results are partly listed in

Table 2. Calculation Events Using Several Algorithms.

Feeders	FMEA	RNEA	ST	SPM	Recursive Method
F1	180	180	135	102	91
F2	245	245	179	133	106
F3	72	72	60	50	68
F4	1863	774	992	725	231
System	2360	1271	1366	1010	496

. The experiment reveals that the results obtained from the proposed recursive method are completely consistent with the results obtained from FMEA/RNEA/ST/SPM in all three cases. Thus, it can be readily conferred that the system reliability performances obtained from the proposed method are also consistent with the system performance obtained from FMEA, RNEA, ST and SPM, which demonstrates the computation accuracy of the proposed method.

In addition, the results in Table 2 also demonstrate that the operation state of protective devices can more or less affect the reliability performances for each LP since the reliability results in case 2 are worse than the results in case 1. Moreover, with reference to case 1–3 or case 2–3, it can be concluded that ASs could largely improve the reliability performance for related LPs since they can shorten the interruptions via service restoration.

The significance of the proposed recursive method is its element-by-element equivalent principles, which result in computation efficiency improvement. In References [9,33], the efficiency of the distribution system is measured by calculation events. One unit of calculation event is defined as the time taken for calculating both λ and r once. The calculation event neglects the differences of each computing platform, i.e., the hardware and software aspects, and thus the efficiency of the reliability algorithm can be expressed more relatively. Considering case 3, the calculation events for FMEA, RNEA, ST, SPM and the proposed recursive method are tabulated in

Table 3. The Execution Time for Several Algorithms.

Feeders	FMEA	RNEA	ST	SPM	Recursive Method
F1(s)	0.0327	0.0327	0.0251	0.0226	0.0203
F2(s)	0.0366	0.0366	0.0320	0.0247	0.0222
F3(s)	0.0151	0.0151	0.0127	0.0113	0.0138
F4(s)	0.4431	0.2097	0.2693	0.1836	0.0593
System	0.5277	0.2943	0.3393	0.2423	0.1156

. It can be found that the calculation events of the overall system using the proposed method amount to 496, and are 21.02% of that required by FMEA, 39.02% of RNEA, 49.11% of ST, and 36.31% of the SPM, which indicates the proposed method exhibits the highest computation efficiency.

Moreover, considering case 3, the run time using FMEA, RNEA, ST, SPM and the recursive algorithm for the overall system are listed in

Table 4. Reliability Performance in RBTS-BUS 6 System.

	FMEA/RNEA/ST/SPM						The Proposed Recursive Method
	Case 1		Case 2		Case 3			Case 1		Case 2		Case 3
	λ (f/year)	r (h)	λ (f/year)	r (h)	λ (f/year)	r (h)		λ (f/year)	r (h)	λ (f/year)	r (h)	λ (f/year)	r (h)
LP1	0.3683	2.3795	0.3225	2.5751	0.3225	2.5751		0.3683	2.3795	0.3225	2.5751	0.3225	2.5751
LP3	0.3780	2.5790	0.3752	2.6075	0.3752	2.6075		0.3780	2.5790	0.3752	2.6075	0.3752	2.6075
LP5	0.3780	2.6207	0.4019	2.5550	0.4019	2.5550		0.3780	2.6207	0.4019	2.5550	0.4019	2.5550
LP7	0.4133	2.2293	0.3506	2.4491	0.3506	2.4491		0.4133	2.2293	0.3506	2.4491	0.3506	2.4491
LP10	0.4035	2.3417	0.4107	2.3429	0.4107	2.3429		0.4035	2.3417	0.4107	2.3429	0.4107	2.3429
LP14	0.2685	2.8920	0.2523	3.0132	0.2523	3.0132		0.2685	2.8920	0.2523	3.0132	0.2523	3.0132
LP18	1.6865	3.3131	1.8572	3.3563	1.8572	3.3563		1.6865	3.3131	1.8572	3.3563	1.8572	3.3563
LP23	1.7255	3.3512	1.8923	3.3868	1.8923	3.3868		1.7255	3.3512	1.8923	3.3868	1.8923	3.3868
LP26	1.7255	5.0342	1.9801	5.0658	1.9801	3.1844		1.7255	5.0342	1.9801	5.0658	1.9801	3.1844
LP31	2.5570	3.8850	2.6530	3.8594	2.6530	3.8594		2.5570	3.8850	2.6530	3.8594	2.6530	3.8594
LP37	2.5798	5.0205	2.7610	5.0568	2.7610	3.7075		2.5798	5.0205	2.7610	5.0568	2.7610	3.7075
LP40	2.5310	5.0209	2.7171	5.0577	2.7171	3.6866		2.5310	5.0209	2.7171	5.0577	2.7171	3.6866

, as to make the conclusion concerning the efficiency of the proposed method more convincing. The simulations are carried out with an Intel(R) Core i7-3612QM 2.1-GHz CPU and 16.00 GB of RAM. From Table 4, it can be seen that the execution time of the recursive method is 1.1564 s, which is 21.92% of that required by FMEA, 39.30% of RNEA, 34.08% of ST, and 47.73% of the SPM. This also indicates that the proposed recursive method exhibits the highest calculation efficiency amongst these listed algorithms. In addition, the execution time using ST takes 0.3393 s, which is 64.30% of that executed by FMEA. This is consistent with the conclusion in Reference [9] that ST takes 76.3% of the time using FMEA, considering the base case of RBTS-Bus6.

5.2. An Industrial Distribution System

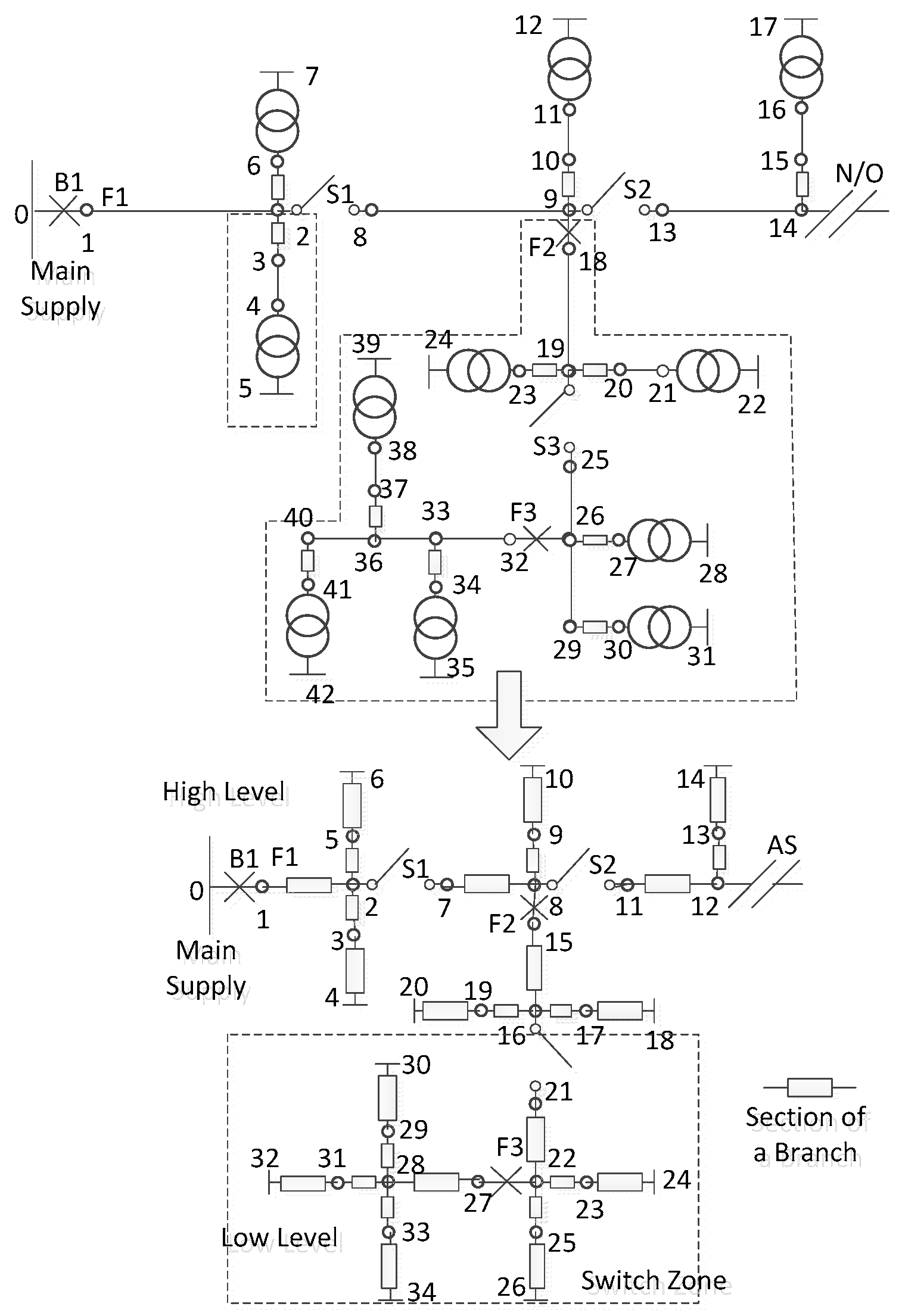
For an in-depth investigation into the efficiency benefits of the proposed recursive method, a practical 362-bus urban distribution system newly upgraded in Henan province [31], China, is adopted as the benchmark system. The distribution system, shown in Figure 5, consists of five 10-kV feeders, 242 branches and 186 load transformers. In addition, many types of protective devices, such as 98 normally closed disconnect switches, 5 normally opened tie-switches, 21 fuse cutouts and 14 circuit breakers, are also contained in the system. The length and capacity for feeders F1–F5 are 7.242 km & 3.5 MVA, 15.806 km & 26.1 MVA, 5.502 km & 2.9 MVA, 6.654 km & 5.7 MVA, and 7.441 km & 6.3 MVA, respectively. Each feeder contains industrial, office building, government, residential and commercial customers. The reliability data for the circuit equipment is listed in

Table 5. Reliability Data for Transformers and Lines.

Transformer Size (kVA)	λ (f/year)	r (h)	Line Type	λ (f/year)	r (h)
80–200	0.0039	49.2	YJV-70/120	1.09 × 10−6	10.5
200–315	0.0043	60.8	YJV-240/300	1.05 × 10−6	12.9
315–500	0.0047	65.6	YJLV-120	1.16 × 10−6	14.1
500–800	0.0049	70.1	YJLV-400	1.33 × 10−6	15.7
800–1200	0.0055	74.2	LGJ-185/240	7.86 × 10−6	3.6
1200–∞	0.0059	79.5	LGJ-300	6.13 × 10−6	5.5

and

Table 6. Reliability Data for protection devices.

Element	λ (f/year)	r (h)	Element	λ (f/year)	r (h)
Breaker	0.006	4	Fuse-cutout	0.384	3.5
Fuse	0.002	3	Disconnect	0.006	1
Tie switch	0.005	0.5	Automatic switch	0.006	1

. Based on the reliability data for circuit equipments, the reliability performance for each feeder can be calculated.

Similarly, three different cases are simulated to demonstrate the benefits of the proposed recursive algorithm, described as follows,

• Case 1: All types of protective devices, such as fuses, breakers and fuse cutouts are assumed to be 100% reliable.
• Case 2: All types of protective devices are assumed to be 80% reliable.
• Case 3: The operation time of all tie-switch is set to 1.5 h, and other conditions are set as the same as case 2.

The reliability performances for each feeder under three cases are shown in

Table 7. System Reliability Performance under Three Cases.

	Feeders		SAIFI (int/cus.year)	SAIDI (hr/cus.year)	CAIDI (h/int)	ASAI (%)	EENS (GWh/year)
FA		Case 1	1.6042	6.2784	3.9137	99.9283	19.2620
		Case 2	1.7315	8.0894	4.6719	99.9077	23.3609
		Case 3	1.7315	11.1293	6.4276	99.8730	34.1682
FB		Case 1	1.7036	7.8975	4.6358	99.9098	49.0729
		Case 2	1.8718	10.7834	5.7610	99.8769	75.8316
		Case 3	1.8718	16.6630	8.9021	99.8098	109.1904
FC		Case 1	1.1416	2.6276	2.3017	99.9700	9.0762
		Case 2	1.2048	4.1288	3.4270	99.9529	12.2648
		Case 3	1.2048	5.4838	4.5516	99.9374	21.3651
FD		Case 1	1.8892	10.4182	5.5146	99.8811	43.1673
		Case 2	2.1326	16.9168	7.9325	99.8069	69.8013
		Case 3	2.1326	21.8815	10.2605	99.7502	101.3390
FE		Case 1	1.0327	1.6354	1.5836	99.9813	26.0794
		Case 2	1.1650	2.8440	2.4412	99.9675	42.2841
		Case 3	1.1650	5.6226	4.8263	99.9358	50.0943
System		Case 1	1.5264	3.8134	2.4983	99.9565	146.6578
		Case 2	1.6377	7.3089	4.4629	99.9166	223.5427
		Case 3	1.6377	11.8669	7.2461	99.8645	316.1570

Notations: SAIFI is system average interruption frequency index; SAIDI is system average interruption duration index; CAIDI denotes customer average interruption duration index; ASAI denotes system average availability index; EENS denotes the electric energy not supplied each year.

.

It can be seen from the results that the SAIDI of all five feeders ranges from a minimal of 1.6354 to a high of 10.4182 with an average of 5.7714 in case 1. However, if the breakers and fuses operate successfully at a probability of 0.8, the SAIDI of the whole system would jump to 7.3089 in case 2, indicating that breaker/fuse have a large effect on the system reliability performance. The changing trends of other reliability indices also support this conclusion. Therefore, more reliable protective equipments are crucial for minimizing the frequency and duration of interruptions, and so the system reliability performance can be accordingly enhanced. In other words, the system reliability performance for industrial distribution systems would deteriorate hugely if the protective equipment lacked adequate maintenance and inspection.

Moreover, with reference to case 2–3, it can be founded that SAIDI of the system jumps to 11.8669 when the operation time of all tie-switches is set to 1.5 h, which is far beyond 7.3089 in case 2. This indicates that the AS has a significant impact on the improvement of system reliability performance. This is why the modern distribution system is usually upgraded as a hand-in-hand loop structure in which a Tie-Line Switch (Sectionalizer) is located at the end and middle of these feeders.

The calculation events as well as the run time of FMEA, RNEA, ST, SPM and the proposed recursive method are tabulated in

Table 8. Calculation Events Using Several Algorithms.

Feeders	FMEA	RNEA	ST	SPM	Recursive Method
FA	6592	2401	2862	882	496
FB	15,620	11,067	6719	2561	1158
FC	4730	1624	2261	1020	377
FD	12,608	8226	4068	1592	448
FE	11,051	7620	3913	1375	407
System	50,601	30,938	19,823	7430	2886

and

Table 9. The Execution Time for Several Algorithms.

Feeders	FMEA	RNEA	ST	SPM	Recursive Method
FA(s)	2.0432	0.7052	0.8062	0.2715	0.1468
FB(s)	4.4627	3.7593	1.6470	0.7680	0.3014
FC(s)	1.7301	0.6028	0.7523	0.3007	0.0925
FD(s)	3.5644	2.0671	1.2368	0.4682	0.1359
FE(s)	3.3029	2.1536	1.1162	0.4416	0.1137
System(s)	15.1033	9.288	5.5585	2.25	0.7903

. As seen, the calculation events for FA-FE using the proposed method are 7.52%, 7.41%, 7.97%, 3.55%, and 3.68% of that required for FMEA. The run time for FA-FE using the recursive method is 7.18%, 6.75%, 5.34%, 3.81%, and 3.44% of that required for FMEA. The results also demonstrate that the proposed method exhibits the highest efficiency over RNEA, ST and SPM, which is consistent with the conclusions obtained in Section 5.1.

5.3. Discussions

The proposed recursive algorithm mainly consists of a bottom-up and a top-down recursive process, which have been discussed in Section 3 and Section 4. The former quantifies the effect of downstream failures on certain upstream bus. This effect is similar to the effect of an equivalent lateral section on the bus in Reference [12]. The latter considers the effect of upstream failures on certain downstream bus, and this effect is similar to the effect of an equivalent series component on the bus in Reference [12]. The reliability indices of the equivalent lateral section and equivalent series component can be determined by using the recursive algorithm presented in Formulas (8)–(22). To any bus, there is always one equivalent series component and several equivalent lateral sections, and the synthesis of reliability indices of those components and sections yields the reliability performance of that bus.

With the above analysis, it is clear that the top-down or bottom-up recursive process is not only applied to the nodes in the lateral network, but also to the nodes in the main network. Also, the reliability indices of any node can be recursively obtained based on those of neighboring nodes only, while reliability information of the rest of network is not required at all. This is because the combined effect of downstream failures on a certain node is considered in analyzing the reliability performance of its connected downstream nodes in the proposed recursive method. Similarly, the combined effect of upstream failures on the node is accounted for in the reliability analysis of its connected upstream nodes. Therefore, the proposed recursive method provides a more generalized element-by-element equivalent principle, with which the network simplification for reliability evaluation can be fully realized. Compared to the sub-feeder-based approach in many existing methods, where network simplification has to be designed according to specific network topology involving excessive computational costs, the proposed recursive method can maximally simplify the network and thus minimize the computation cost accordingly due to its element-by-element recursive principles. Moreover, the computation cost of the proposed recursive method is further minimized using several techniques, as follows,

(1)

Section of a branch is utilized to reduce the number of equivalent process, and thus the distribution system can be simplified.

(2)

The upstream recursive process adopts SPM [13], in which the components in other branches are treated as a lateral equivalent section, and so the computation cost can be further mitigated.

Therefore, theoretically, it can be concluded that the proposed recursive method exhibits higher calculation efficiency than FMEA, RNEA, ST and SPM, which is consistent with the simulation results presented in Section 5.1 and Section 5.2.

It should be noted that the proposed recursive method can also be used in bidirectional power flow case and non-radial network’s structures, due to the emergency of sustainable energy and the requirement of high reliability in recent years. First, the distribution system has several typical operation scenarios. Here, operation scenario indicates the operational status of the distribution system at a given moment. Each scenario has a fixed power flow with a unique direction and different scenarios may exhibit different power flow directions. We can use our method to calculate the reliability indices at any operational scenario. Synthesizing these indices at all scenarios generates the final reliability indices of the distribution system. Second, the energy in the distribution system generally flows from the transmission system to load points. Any non-radial structure, such as a circular, can be viewed as a basic component in (1). Its equivalent failure rate and outage duration are calculated in Formulas (2) and (3), As a result, the reliability indices of the not-radial distribution system can be evaluated by taking the non-radial structure as an equivalent component. Therefore, our recursive method has wide application in distribution systems.

6. Conclusions

In this paper, a computationally effective recursive method is proposed for distribution system reliability evaluation. The bottom-up and top-down recursive processes are firstly investigated and developed on the basis of stringent recursive principles. In addition, a novel switch zone is embedded in the bottom-up equivalent process to save the computation cost. In addition, section technique and shortest path method are also introduced in the proposed method for network simplification. The proposed method has been successfully tested on a practical 362-bus distribution system in Henan province, China.

The primary advantage of the proposed approach over other methods is the superior calculation efficiency and applicability for large-scale distribution networks. This paper also demonstrated that the lack of maintenance and inspection for protective devices could significantly deteriorate the system reliability performance. Moreover, the hand-in-hand loop distribution structure could reduce the outage duration because of the restoration process.