Optimal Design of Rated Wind Speed and Rotor Radius to Minimizing the Cost of Energy for Offshore Wind Turbines
Abstract
:1. Introduction
2. Design Process of Wind Turbines
- Step 1: Conception stage. As the first stage of a turbine design, the conception design involves the definitions of the nominal parameters of the wind turbine, such as the nominal power output, rotor diameter, electrical energy conversion system and so on.
- Step 2: Blade design. The blade design step defines the aerodynamics and structural concepts of the blades, which are determined by the overall conception in the step 1 and the controller development in the step 3, respectively.
- Step 3: Control development and preliminary design models. During this step, the preliminary design models, which are typically based on multibody models, are employed to estimate the loads acting on major components of the turbine during its life cycle. When the loads are beyond limitations, the controller and blade structural designs will be required to be redesigned. Thus, steps 2 and 3 depend on each other, and the final design of blades and controller will be finished after several iterations.
- Step 4: Design engineering and strength calculation. During this step, a strength calculation of the major components is carried out, so that it can be verified that the designed components are able to withstand the loads calculated during the life cycle.
- Step 5: Construction and erection of the prototype. During this step, the prototype of the wind turbine is manufactured and erected on the wind farm site.
- Step 6: Measurements on the prototype. As a final step, it aims at proving the predicted property of the designed turbine within a measurement campaign.
3. COE Model of Offshore Turbines
3.1. AEP Model of the Offshore Turbines
3.1.1. Power Curve Modeling of the Offshore Turbines
3.1.2. Weibull Distribution of the Offshore Wind Statistics
3.2. Cost Model of the Offshore Turbines
3.2.1. The Initial Capital Cost
3.2.2. The Annual Operating Expense
3.3. COE Model of the Offshore Turbines
4. COE Optimization for Offshore Turbines
4.1. Optimizaiton Method
- Step 1: Initialize the wind statistics of the offshore site: , , ;
- Step 2: Define the ranges of the design parameters: , ;
- Step 3: Evaluate the COE using different and , and save the smallest value of COE and its corresponding and ;
- Step 4: Repeat step 3 until all design parameters sets of and have been evaluated;
- Step 5: Output minimal COE and the corresponding design parameters.
4.2. Parameter Settings
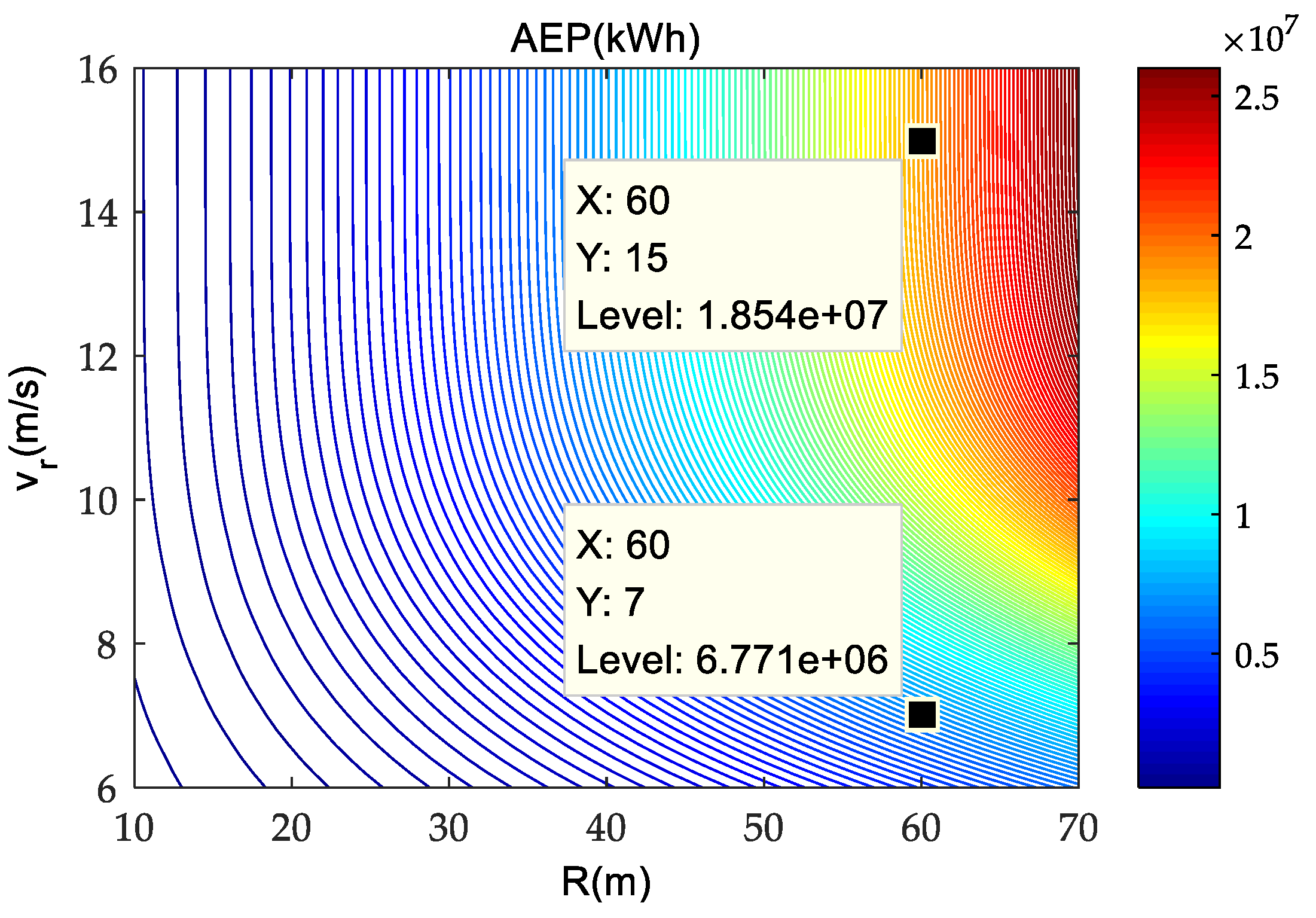
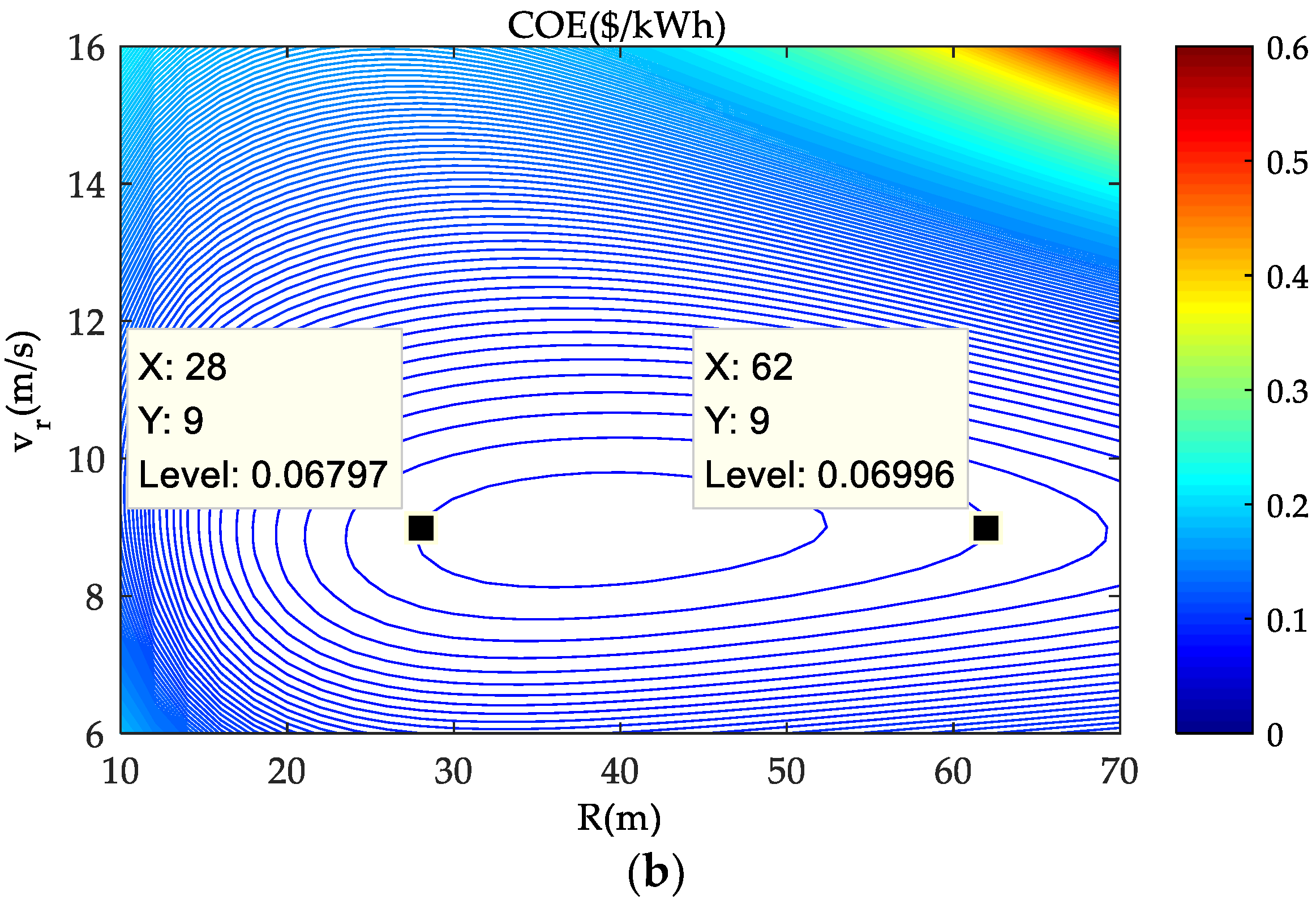
4.3. Optimizaiton Results and Discussions
4.4. Result Analysis on a Typical Case
5. Conclusions
- Considering is an acceptable COE value to exploit the wind energy, the offshore wind turbines should be installed at the sea with the wind class III or above.
- The offshore wind turbines with a large capacity and long blades may not absolutely bring the COE down, as their optimal capacities depend on the offshore wind conditions.
- The COE is more sensitive to the rated wind speed than the rotor size, so it is critical to bring the COE down by selecting the suitable rated wind speed.
- The COE of offshore turbines is less sensitive to the power coefficient than to the rated wind speed and the rotor size, which justify the significance of the conception design optimization.
- The optimal rated wind speed of the offshore wind turbines should be designed around 1.5 times more than the annual mean wind speed, while the optimal rotor can be designed towards big-size, as the offshore wind turbines having a low COE appear with long blades and a large capacity.
Author Contributions
Funding
Conflicts of Interest
References
- Global Wind Report. 2017. Available online: http://www.gwec.net/global-figures/graphs/ (accessed on 3 September 2018).
- Dai, J.C.; Yang, X.; Wen, L. Development of wind power industry in China: A comprehensive assessment. Renew. Sustain. Energy Rev. 2018, 97, 156–164. [Google Scholar] [CrossRef]
- Willis, D.J.; Niezrecki, C.; Kuchma, D. Wind energy research: State-of-the-art and future research directions. Renew. Energy 2018, 125, 133–154. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons: West Sussex, UK, 2011. [Google Scholar]
- Zhu, Y.; Cheng, M.; Hua, W.; Wang, W. A novel maximum power point tracking control for permanent magnet direct drive wind energy conversion systems. Energies 2012, 5, 1398–1412. [Google Scholar] [CrossRef]
- Song, D.; Yang, J.; Cai, Z.L.; Dong, M.; Su, M.; Wang, Y.H. Wind estimation with a non-standard extended Kalman filter and its application on maximum power extraction for variable speed wind turbines. Appl. Energy 2017, 190, 670–685. [Google Scholar] [CrossRef]
- Song, D.; Yang, J.; Su, M.; Liu, A.; Liu, Y.; Joo, Y. A comparison study between two MPPT control methods for a large variable-speed wind turbine under different wind speed characteristics. Energies 2017, 10, 613. [Google Scholar] [CrossRef]
- Song, D.; Yang, J.; Cai, Z.; Dong, M.; Joo, Y.H. Model predictive control with finite control set for variable-speed wind turbines. Energy 2017, 126, 564–572. [Google Scholar] [CrossRef]
- Scholbrock, A.; Fleming, P.; Schlipf, D. Lidar-enhanced wind turbine control: Past, present, and future. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 1399–1406. [Google Scholar]
- Zhang, X.L.; Huang, C.; Hao, S.P.; Chen, F.; Zhai, J.J. An Improved Adaptive-Torque-Gain MPPT Control for Direct-Driven PMSG Wind Turbines Considering Wind Farm Turbulences. Energies 2016, 9, 977. [Google Scholar] [CrossRef]
- Huang, C.; Li, F.; Jin, Z. Maximum power point tracking strategy for large-scale wind generation systems considering wind turbine dynamics. IEEE Trans. Ind. Electron. 2015, 62, 2530–2539. [Google Scholar] [CrossRef]
- Yin, M.H.; Li, W.J.; Chung, C.Y.; Chen, Z.Y.; Z, Y. Inertia Compensation Scheme of WTS Considering Time Delay for Emulating Large-Inertia Turbines. IET Renew. Power Gener. 2017, 11, 529–538. [Google Scholar] [CrossRef]
- Martínez-Lucas, G.; Sarasúa, J.I.; Sánchez-Fernández, J.Á. Frequency Regulation of a Hybrid Wind–Hydro Power Plant in an Isolated Power System. Energies 2018, 11, 239. [Google Scholar] [CrossRef]
- Martínez-Lucas, G.; Sarasúa, J.I.; Sánchez-Fernández, J.Á. Eigen analysis of wind–hydro joint frequency regulation in an isolated power system. Int. J. Electr. Power Energy Syst. 2018, 103, 511–524. [Google Scholar] [CrossRef]
- Song, D.; Yang, J.; Fan, X.; Liu, Y.; Liu, A.; Chen, G.; Joo, Y. Maximum power extraction for wind turbines through a novel yaw control solution using predicted wind directions. Energy Convers. Manag. 2018, 157, 589–599. [Google Scholar] [CrossRef]
- Song, D.; Fan, X.; Yang, J.; Liu, A.; Chen, S.; Joo, Y. Power extraction efficiency optimization of horizontal-axis wind turbines through optimizing control parameters of yaw control systems using an intelligent method. Appl. Energy 2018, 224, 267–279. [Google Scholar] [CrossRef]
- Chehouri, A.; Younes, R.; Ilinca, A.; Jean, P. Review of performance optimization techniques applied to wind turbines. Appl. Energy 2015, 142, 361–388. [Google Scholar] [CrossRef]
- Fuglsang, P.; Madsen, H.A. Optimization method for wind turbine rotors. J. Wind Eng. Ind. Aerodyn. 1999, 80, 191–206. [Google Scholar] [CrossRef]
- Shen, X.; Chen, J.G.; Zhu, X.C. Multi-objective optimization of wind turbine blades using lifting surface method. Energy 2015, 90, 1111–1121. [Google Scholar] [CrossRef] [Green Version]
- Ferdoues, M.S.; Ebrahimi, S.; Vijayaraghavan, K. Multi-objective optimization of the design and operating point of a new external axis wind turbine. Energy 2017, 125, 643–653. [Google Scholar] [CrossRef]
- Tang, C.; Soong, W.L.; Freere, P.; Pathmanathan, M.; Ertugrul, N. Dynamic wind turbine output power reduction under varying wind speed conditions due to inertia. Wind Energy 2013, 16, 561–573. [Google Scholar] [CrossRef]
- Yin, M.H.; Yang, Z.Q.; Xu, Y.; Liu, J.K.; Zhou, L.J.; Zou, Y. Aerodynamic optimization for variable-speed wind turbines based on wind energy capture efficiency. Appl. Energy 2018, 221, 508–521. [Google Scholar] [CrossRef]
- Bortolotti, P.; Bottasso, C.L.; Croce, A. Combined preliminary–detailed design of wind turbines. Wind Energy Sci. 2016, 1, 71–88. [Google Scholar] [CrossRef] [Green Version]
- Arias-Rosales, A.; Osorio-Gómez, G. Wind turbine selection method based on the statistical analysis of nominal specifications for estimating the cost of energy. Appl. Energy 2018, 228, 980–998. [Google Scholar] [CrossRef]
- Villena-Ruiz, R.; Ramirez, F.J.; Honrubia-Escribano, A.; Gomez-Lazaro, E. A techno-economic analysis of a real wind farm repowering experience: The Malpica case. Energy Conver. Manag. 2018, 172, 182–199. [Google Scholar] [CrossRef]
- Gualtieri, G. Improving investigation of wind turbine optimal site matching through the self-organizing maps. Energy Conver. Manag. 2017, 143, 295–311. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Chen, J.; Pang, X. Wind Turbine Optimization for Minimum Cost of Energy in Low Wind Speed Areas Considering Blade Length and Hub Height. Appl. Sci. 2018, 8, 1202. [Google Scholar] [CrossRef]
- Diveux, T.; Sebastian, P.; Bernard, D. Horizontal axis wind turbine systems: Optimization using genetic algorithms. Wind Energy Int. J. Prog. Appl. Wind Power Conver. Technol. 2001, 4, 151–171. [Google Scholar] [CrossRef]
- Mirghaed, M.R.; Roshandel, R. Site specific optimization of wind turbines energy cost: Iterative approach. Energy Conver. Manag. 2013, 73, 167–175. [Google Scholar] [CrossRef]
- Eminoglu, U.; Ayasun, S. Modeling and design optimization of variable-speed wind turbine systems. Energies 2014, 7, 402–419. [Google Scholar] [CrossRef]
- Chen, J.; Wang, F.; Stelson, K.A. A mathematical approach to minimizing the cost of energy for large utility wind turbines. Appl. Energy 2018, 228, 1413–1422. [Google Scholar] [CrossRef]
- Fingersh, L.J.; Hand, M.M.; Laxson, A. Wind Turbine Design Cost and Scaling Model; Technical Report NREL/TP-500-40566; National Renewable Energy Laboratory (NREL): Gold, CO, USA, 2006. [Google Scholar]
- Zierath, J.; Jassmann, U.; Abel, D.; Weber, F. Introduction of model predictive control for load reduction on a 3,0 mw wind turbine. In Proceedings of the Brazil Windpower 2015, Rio de Janeiro, Brazil, 1–3 September 2015. [Google Scholar]
- Moné, C.; Hand, M.; Bolinger, M. 2015 Cost of Wind Energy Review; Technical Report NREL/TP-500-40566; National Renewable Energy Laboratory (NREL): Gold, CO, USA, 2017. [Google Scholar]
- Teyabeen, A.A.; Akkari, F.R.; Jwaid, A.E. Power Curve Modelling for Wind Turbines. In Proceedings of the 2017 UKSim-AMSS 19th International Conference on Computer Modelling & Simulation (UKSim), Cambridge, UK, 5–7 April 2017. [Google Scholar]
- Goudarzi, A.; Davidson, I.E.; Ahmadi, A. Intelligent analysis of wind turbine power curve models. In Proceedings of the 2014 IEEE Symposium on Computational Intelligence Applications in Smart Grid (CIASG), Orlando, FL, USA, 9–12 December 2014; pp. 1–7. [Google Scholar]
- Justus, C.G.; Hargraves, W.R.; Mikhail, A. Methods for estimating wind speed frequency distributions. J. Appl. Meteorol. 1978, 17, 350–353. [Google Scholar] [CrossRef]
- Tar, K. Some statistical characteristics of monthly average wind speed at various heights. Renew. Sustain. Energy Rev. 2008, 12, 1712–1724. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, D.; Yi, Q. Wind Profiles and Wave Spectra for Potential Wind Farms in South China Sea. Part I: Wind Speed Profile Model. Energies 2017, 10, 125. [Google Scholar] [CrossRef]
- Hsu, S.A.; Meindl, E.A.; Gilhousen, D.B. Determining the power-law wind-profile exponent under near-neutral stability conditions at sea. J. Appl. Meteorol. 1994, 33, 757–765. [Google Scholar] [CrossRef]
- Seguro, J.V.; Lambert, T.W. Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis. J. Wind Eng. Ind. Aerodyn. 2000, 85, 75–84. [Google Scholar] [CrossRef]
- European Wind Energy Association. Wind Energy-The Facts: A Guide to the Technology, Economics and Future of Wind Power; Routledge: Landon, UK, 2012. [Google Scholar]
- Sedaghat, A.; Hassanzadeh, A.; Jamali, J.; Mostafaeipour, A. Determination of rated wind speed for maximum annual energy production of variable speed wind turbines. Appl. Energy 2017, 205, 781–789. [Google Scholar] [CrossRef]








| Type | Cost Model (Unit: $) |
|---|---|
| Mechanical System | |
| Blade | |
| Gearbox | |
| low speed shaft | |
| Main bearings | |
| Mechanical brake | |
| Electrical System | |
| Generator | |
| Power converter | |
| Electrical connection | |
| Control System | |
| Pitch system | |
| Yaw system | |
| Control safety system | 55,000 |
| Auxiliary System | |
| Hydraulic cooling system | |
| Hub | |
| Nose cone | |
| Mainframe | |
| Nacelle cover | |
| Tower | |
| Type | Cost Model (Unit: $) |
|---|---|
| Marinization | |
| Offshore support structure | |
| Offshore transportation | |
| Offshore turbine installation | |
| Offshore electrical interface and connection | |
| Offshore engineering permits | |
| Port and staging equipment | |
| Personnel access equipment | 60,000 |
| Scour protection | |
| Surety bond | |
| Offshore warranty premium |
| Type | Cost Model (Unit: $) |
|---|---|
| Offshore Levelized replacement cost | |
| Offshore bottom lease cost | |
| Offshore O&M |
| Wind Power Class | Mean Annual Wind Speed (m/s) | Power Density (W/m2) |
|---|---|---|
| I | 0–4.4 | 0–100 |
| II | 4.4–5.1 | 100–150 |
| III | 5.1–5.6 | 150–200 |
| IV | 5.6–6.0 | 200–250 |
| V | 6.0–6.4 | 250–300 |
| VI | 6.4–7.0 | 300–400 |
| VII | 7.0–9.4 | 400–1000 |
| Parameter | Values or Ranges |
|---|---|
| [4, 7] with a step of 1 | |
| [1.2, 3.6] with a step of 0.4 | |
| 10 | |
| 0.1 | |
| 1.225 | |
| [10, 70] with a step of 2 | |
| [6, 16] with a step of 0.2 | |
| 3 | |
| 25 | |
| 0.17 | |
| 0.42 |
| Wind Class | ||||||
|---|---|---|---|---|---|---|
| I, II | 4.0 | 1.2 | 0.1660 | 8.2 | 38 | 643.45 |
| 1.6 | 0.1595 | 7.6 | 38 | 512.29 | ||
| 2.0 | 0.1566 | 7.2 | 38 | 435.58 | ||
| 2.4 | 0.1550 | 6.8 | 38 | 366.94 | ||
| 2.8 | 0.1540 | 6.6 | 40 | 371.76 | ||
| 3.2 | 0.1532 | 6.4 | 40 | 338.97 | ||
| 3.6 | 0.1527 | 6.2 | 38 | 278.13 | ||
| II, III, IV | 5.0 | 1.2 | 0.1253 | 9 | 38 | 850.75 |
| 1.6 | 0.1170 | 8.4 | 38 | 691.69 | ||
| 2.0 | 0.1127 | 8.2 | 38 | 643.45 | ||
| 2.4 | 0.1099 | 7.8 | 38 | 553.80 | ||
| 2.8 | 0.1080 | 7.6 | 38 | 512.29 | ||
| 3.2 | 0.1066 | 7.4 | 38 | 472.90 | ||
| 3.6 | 0.1055 | 7.4 | 40 | 523.99 | ||
| IV, V, IV | 6.0 | 1.2 | 0.1044 | 9.6 | 38 | 1032.49 |
| 1.6 | 0.0956 | 9.2 | 38 | 908.73 | ||
| 2.0 | 0.0911 | 9 | 38 | 850.75 | ||
| 2.4 | 0.0883 | 8.8 | 40 | 881.20 | ||
| 2.8 | 0.0862 | 8.6 | 40 | 822.47 | ||
| 3.2 | 0.0847 | 8.4 | 38 | 691.69 | ||
| 3.6 | 0.0835 | 8.4 | 40 | 766.41 | ||
| VI, VII | 7.0 | 1.2 | 0.0925 | 10 | 38 | 1167.00 |
| 1.6 | 0.0833 | 9.8 | 38 | 1098.38 | ||
| 2.0 | 0.0789 | 9.6 | 38 | 1032.49 | ||
| 2.4 | 0.0761 | 9.6 | 38 | 1032.49 | ||
| 2.8 | 0.0741 | 9.4 | 38 | 969.30 | ||
| 3.2 | 0.0727 | 9.2 | 38 | 908.73 | ||
| 3.6 | 0.0715 | 9.2 | 38 | 908.73 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, L.; Zhang, X.; Song, D.; Tang, W.; Yang, J.; Li, L.; Tian, X.; Wen, W. Optimal Design of Rated Wind Speed and Rotor Radius to Minimizing the Cost of Energy for Offshore Wind Turbines. Energies 2018, 11, 2728. https://doi.org/10.3390/en11102728
Luo L, Zhang X, Song D, Tang W, Yang J, Li L, Tian X, Wen W. Optimal Design of Rated Wind Speed and Rotor Radius to Minimizing the Cost of Energy for Offshore Wind Turbines. Energies. 2018; 11(10):2728. https://doi.org/10.3390/en11102728
Chicago/Turabian StyleLuo, Longfu, Xiaofeng Zhang, Dongran Song, Weiyi Tang, Jian Yang, Li Li, Xiaoyu Tian, and Wu Wen. 2018. "Optimal Design of Rated Wind Speed and Rotor Radius to Minimizing the Cost of Energy for Offshore Wind Turbines" Energies 11, no. 10: 2728. https://doi.org/10.3390/en11102728
APA StyleLuo, L., Zhang, X., Song, D., Tang, W., Yang, J., Li, L., Tian, X., & Wen, W. (2018). Optimal Design of Rated Wind Speed and Rotor Radius to Minimizing the Cost of Energy for Offshore Wind Turbines. Energies, 11(10), 2728. https://doi.org/10.3390/en11102728





