Control of Current Phase Advancing in Single-Leg Power Converters with the Use of Switched Capacitors

Abstract

This paper deals with the control of current phase advancing in single-leg voltage source inverters (VSI) and matrix converters with a two-phase output. The phase shift of the current in the auxiliary phase is set with the use of switched capacitors. Two distinctive control methods are used for the current phase advancing, open-loop control and closed-loop control. In addition, a new averaging method is derived for the calculation of the switched capacitance used in the open-loop control. The practical use of the designed control methods with the switched capacitor is shown in simulations and experimental verifications on a single-leg matrix converter with a passive and active load (induction motor).

1. Introduction

A topology of the single-leg matrix converter (MxC) is derived from a single-leg VSI converter system with input rectifier [1,2,3]. The analysis of such a MxC topology scheme has been done [4,5]. The advantages of those schematics are presented by the absence of the input rectifier and bulky filtering capacitor and consequently higher efficiency. This is possible by switching of both reversible connected switches (metal-oxide-semiconductor field-effect transistors ), [6]. Using switched capacitors for creating of quadrature supply or two/phase induction motor fed by VSI converter is described in [7]. For IM fed by single-leg MxC, please refer to the following works [8,9].

The use of switched capacitors has been previously published for VSI supply systems in [10,11,12], for single-leg VSI in [7], and for single-phase VSI in [7,11]. All these applications with switched capacitors are derived for steady state with real-time closed-loop control. The use of switched capacitor control for single-leg VSI has not yet been published. For a single-leg matrix converter, the use of switched capacitors is described in the authors’ recent work [8,9].

These MxC or VSI converters require controlling the capacitance due to the single-leg output of the converter when using two-phase passive or active loads. The auxiliary phase is connected in series with switched capacitors to the converter output in comparison to the main phase which is connected directly to converter output. Multiple topologies of switched capacitors exist with different configurations of switches and capacitors with different properties.

This paper deals with phase shift control of current in a single-leg matrix converter with a two-phase output. A known topology of two parallel connected capacitors and switches is used. Two different control methods are used for the current phase advancing. The first method uses open-loop control, where the required 90 degrees phase shift between the current in the main and auxiliary phase is calculated based on the parameters of the load (resistance and inductance). A novel method for control of the desired variable switched capacitance is also derived for the use in the open-loop control. The closed-loop control of current phase shift is inspired by the phase-locked loop.

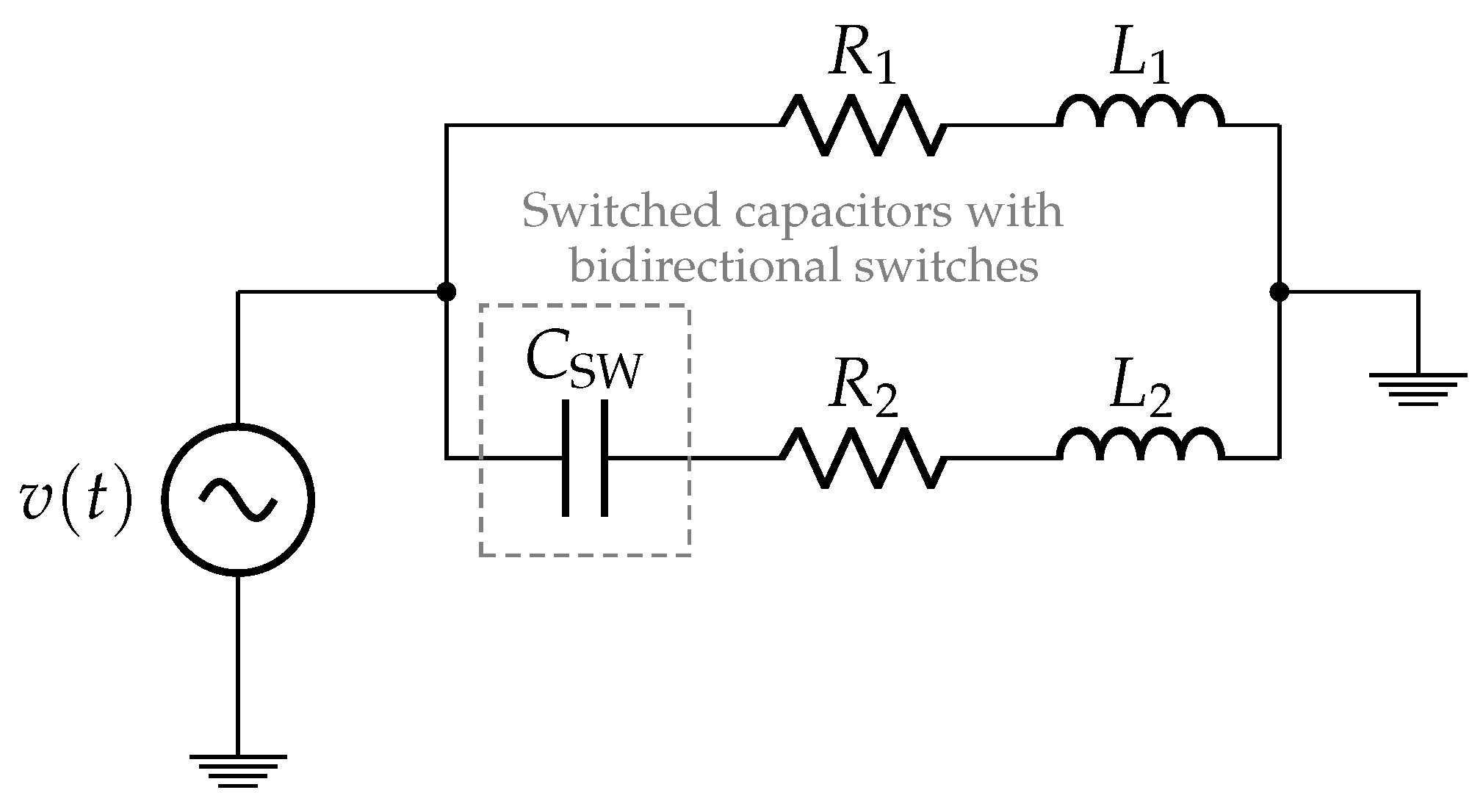
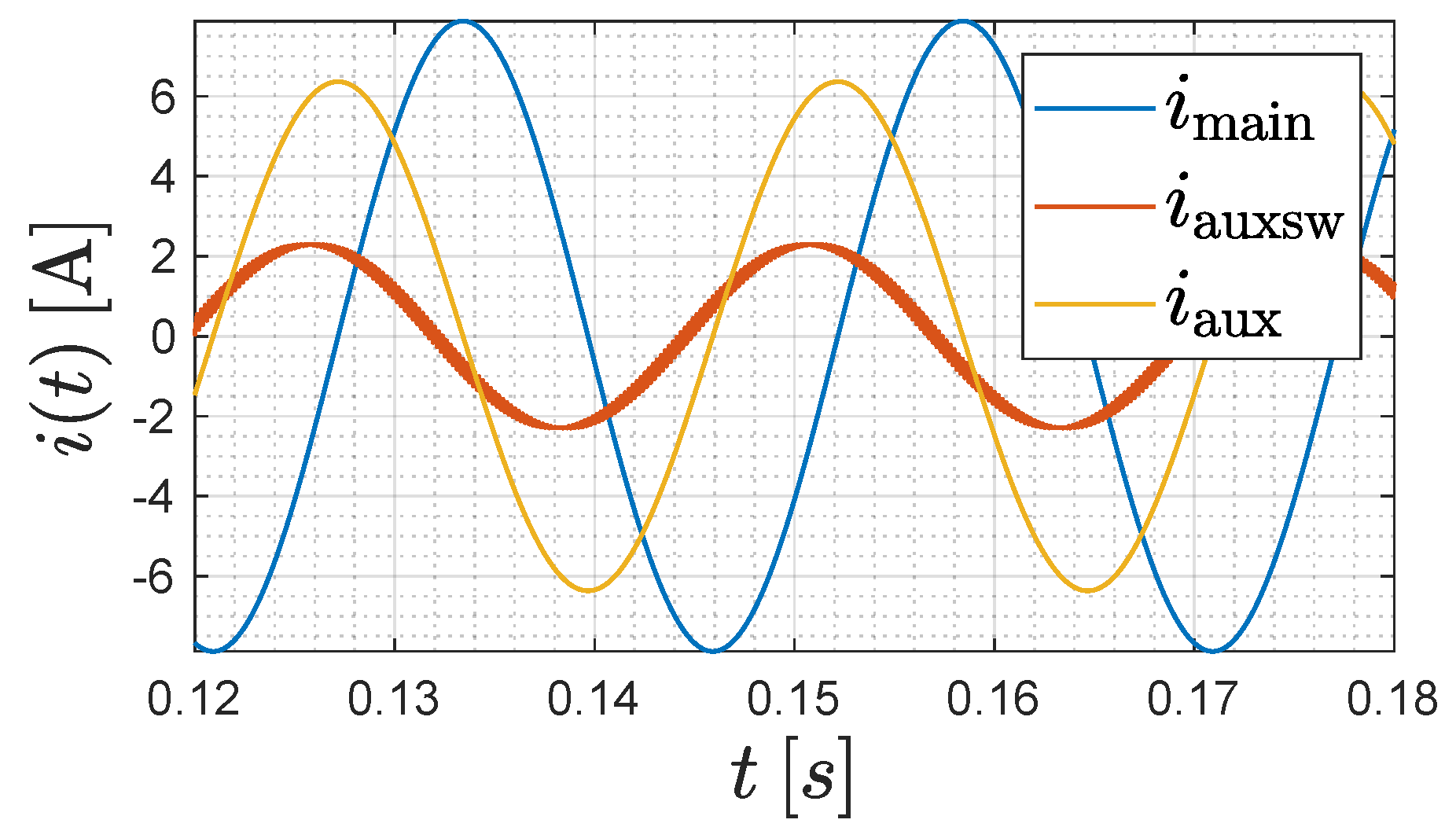
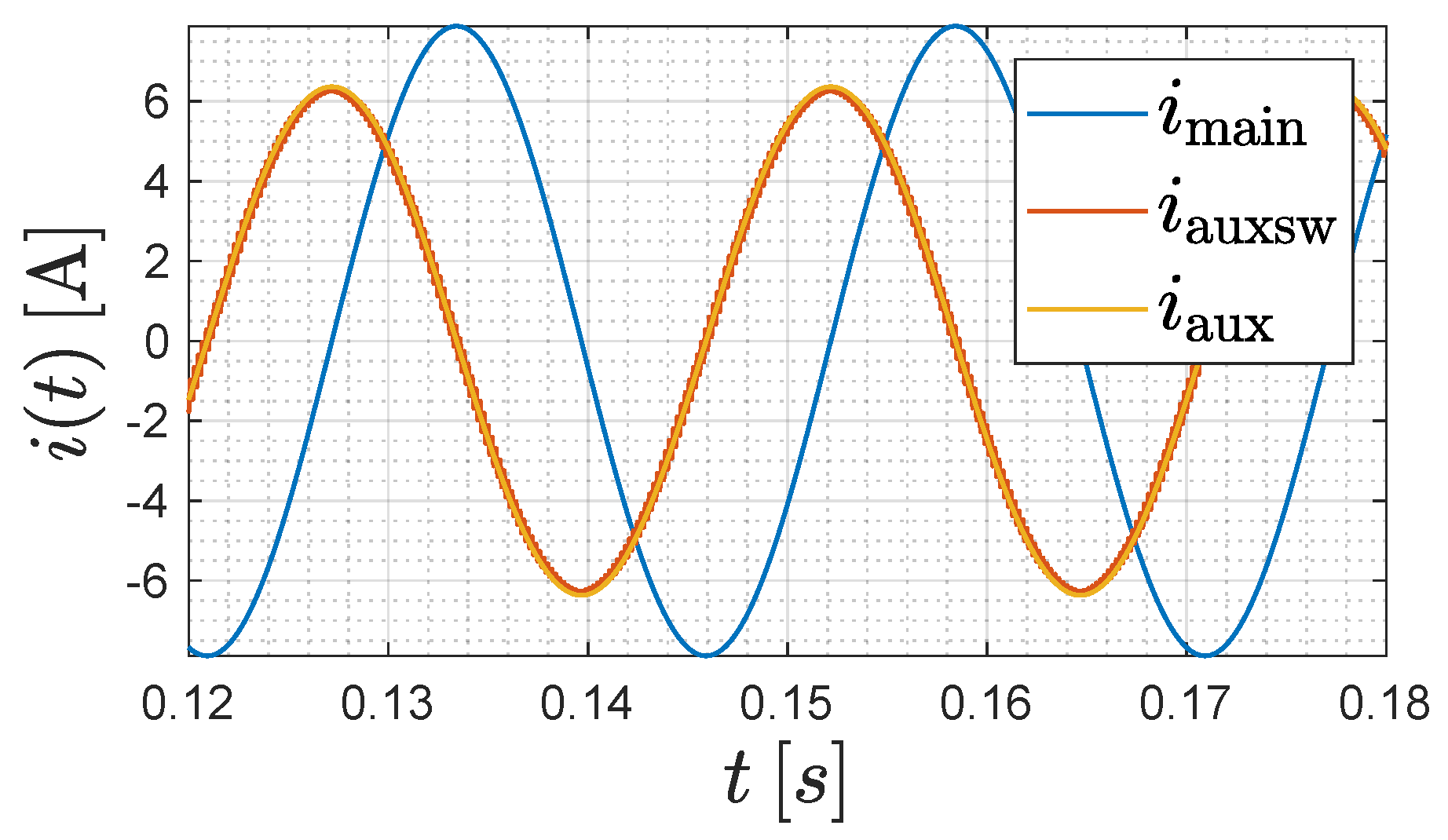
2. Principle of Operation

The switched capacitors are comprised of one large capacitor and one small capacitor and two switches (Figure 1a). During the operation, only one switch is in the on-state at a time. A single-pole-double-throw switch is used in our analysis and modeling of the switched capacitors (Figure 1b).

The switch needs to be able to block the voltage of both polarities and conduct the current in both directions. One of this type of switch, two anti-series emitter connected insulated-gate bipolar transistors (IGBT), with the equivalent symbol used in this paper, is shown in Figure 2.

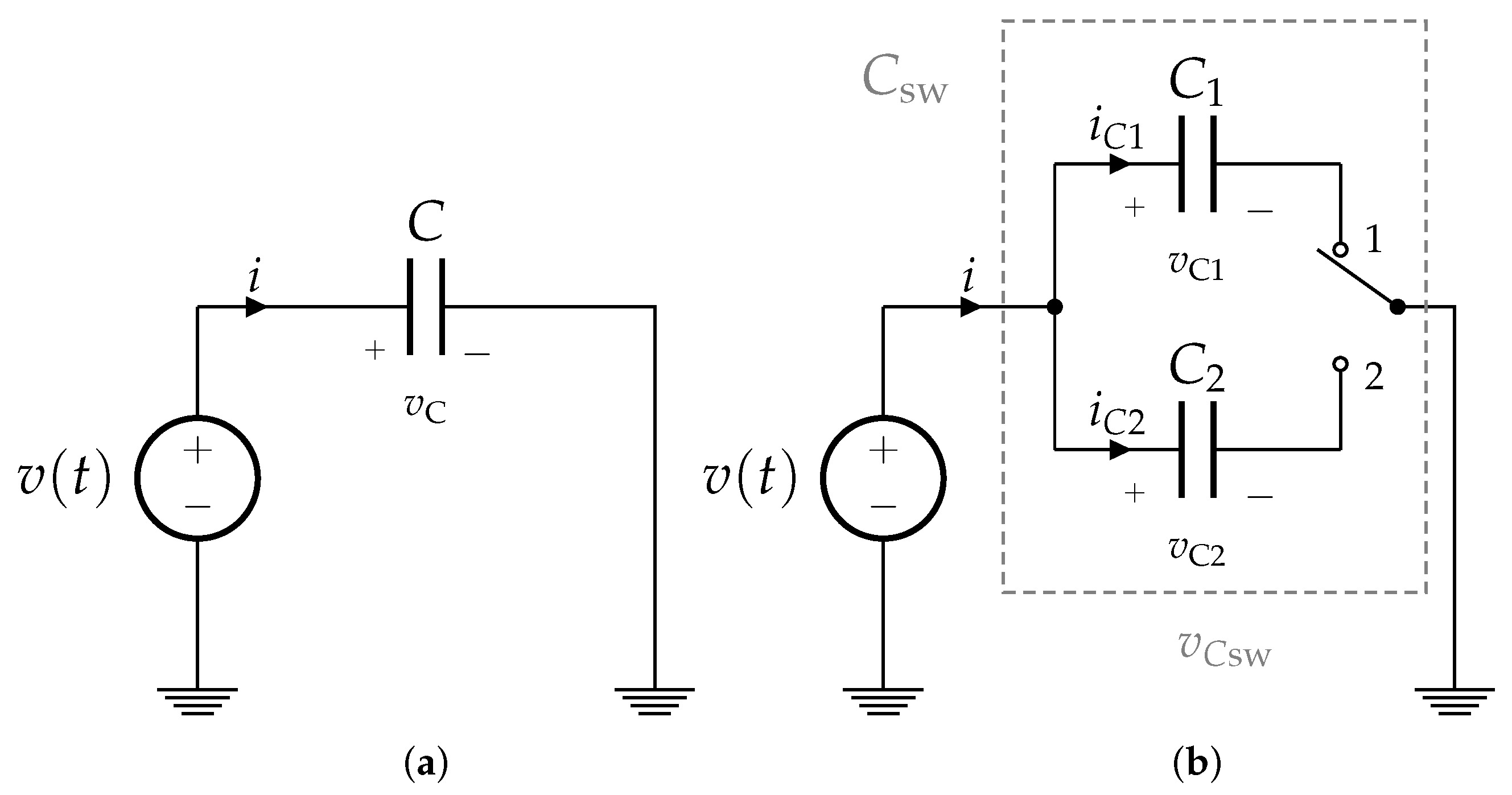
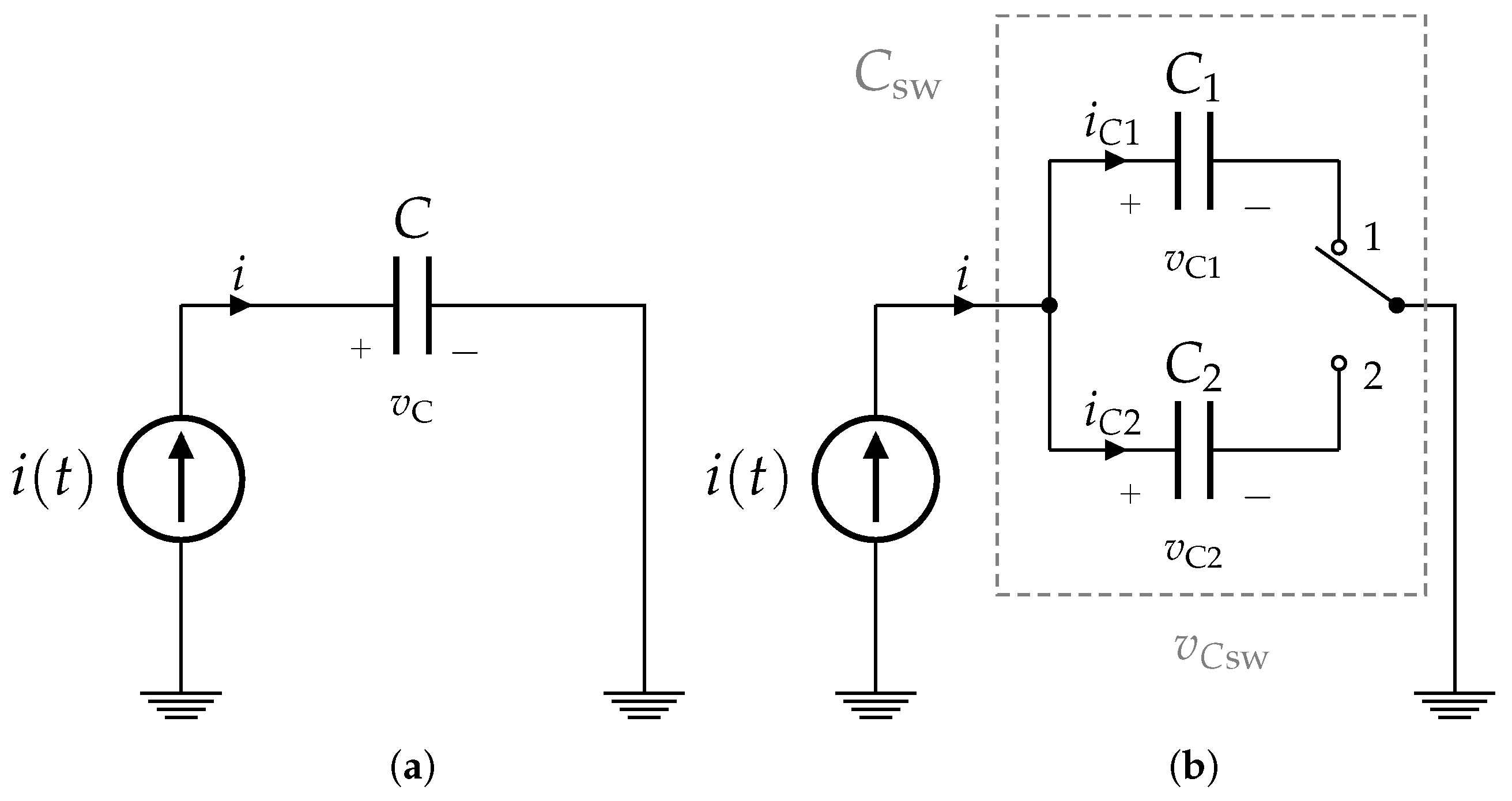
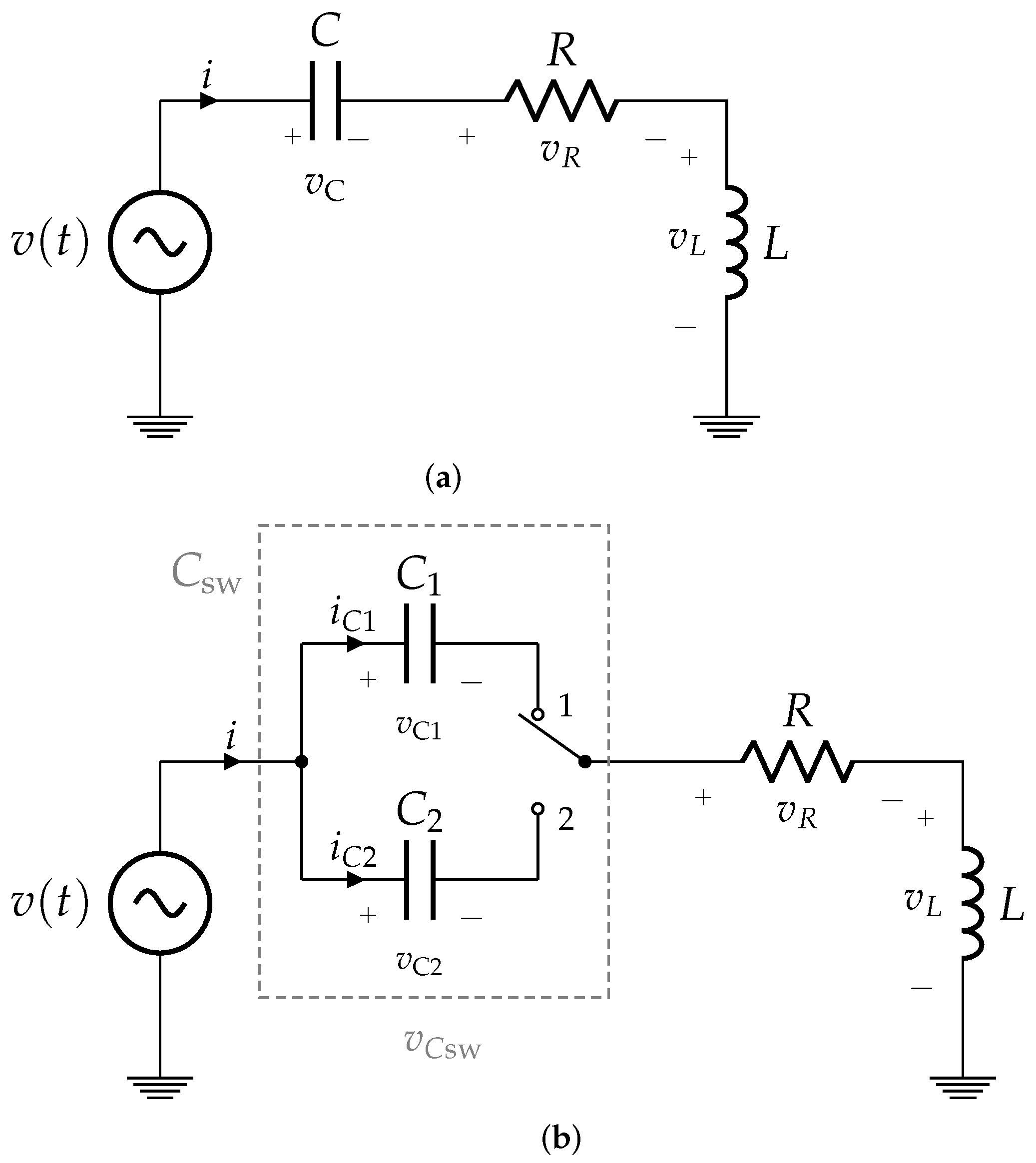
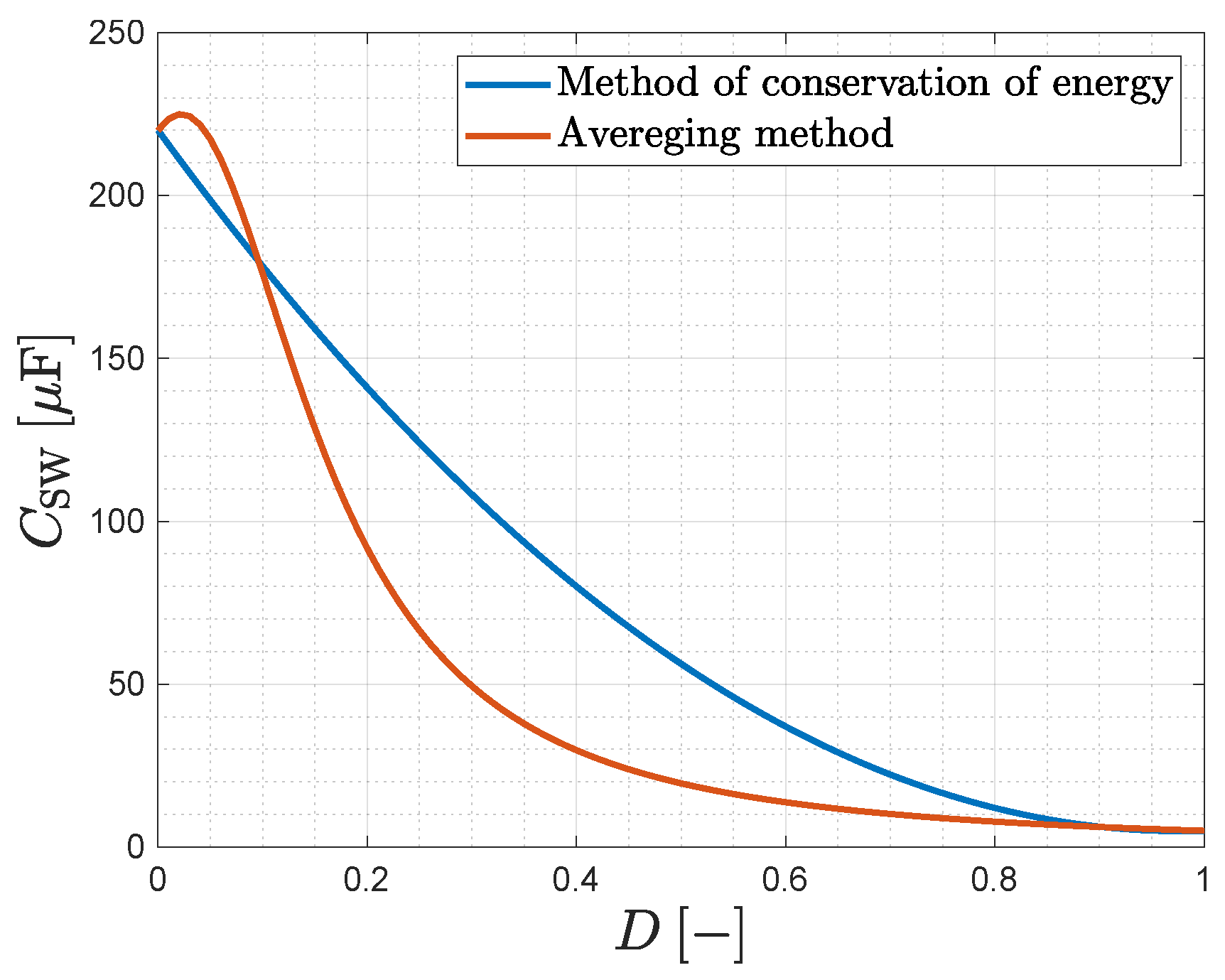
2.1. Method of Conservation of Energy

From the potential energy stored in the capacitors can be deduced the equation for the controlled switched capacitance [7]. The capacitors potential energy is

$$\begin{array}{c}\hfill E={\displaystyle \frac{1}{2}}C{v}^2,\end{array}$$

(1)

where E is the energy stored in the capacitor, C is the capacitance, and v the voltage of the capacitor. The schematic in Figure 3a shows the voltage source connected with the capacitor.

The average voltages on the capacitors are

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill 〈v_{C1}〉& =DV,\hfill \\ \hfill 〈v_{C2}〉& =(1-D)V,\hfill \end{array}\end{array}$$

(2)

where D is the duty cycle, V is the constant voltage on the voltage source, and $\langle v_{C1}\rangle$ and $\langle v_{C2}\rangle$ are the average voltages on the capacitors.

Then, the total energy stored in the two capacitors is

$$\begin{array}{c}\hfill E=E_1+E_2.\end{array}$$

(3)

Combining Equations (1)–(3) yields the value of the switched capacitance as

$$\begin{array}{c}\hfill C_{\mathrm{SW}}=C_1{D}^2+C_2({1-D)}^2.\end{array}$$

(4)

The equivalent switched capacitance $C_{\mathrm{SW}}$ with voltage source is shown in Figure 3b. The capacitance $C_{\mathrm{SW}}$ needs to equal C.

From Equation (4), the value of duty cycle can be derived as

$$\begin{array}{c}\hfill D={\displaystyle \frac{C_2\pm \sqrt{C_{\mathrm{SW}}\left(C_1+C_2\right)-C_1{C}_2}}{C_1+C_2}}.\end{array}$$

(5)

2.2. Averaging Method

We now use a current source as shown in Figure 4 [9,13]. The voltage on capacitor is given as

$$\begin{array}{c}\hfill v_C\left(t\right)={\displaystyle \frac{1}{C}}\int i\left(t\right)\mathrm{d}t,\end{array}$$

(6)

where $i\left(t\right)$ is the current in the capacitor C. We can consider the capacitor current as constant values at sufficient high switching frequency $i\left(t\right)=I$.

In the first interval, as shown in Figure 4b, the average current flowing in the capacitor $C_1$ is given as

$$\begin{array}{c}\hfill \langle i_{C1}\rangle =DI,\end{array}$$

(7)

where I is the value of a constant current source. During the second interval, the average current on the capacitor $C_2$ is given as

$$\begin{array}{c}\hfill \langle i_{C2}\rangle =(1-D)I.\end{array}$$

(8)

We can now derive the voltages on the capacitors $C_1$ and $C_2$ from Equations (6)–(8) as

$$\begin{array}{c}\hfill v_{C1}\left(t\right)={\displaystyle \frac{1}{C_1}}DIt,\end{array}$$

(9)

$$\begin{array}{c}\hfill v_{C2}\left(t\right)={\displaystyle \frac{1}{C_2}}\left(1-D\right)It,\end{array}$$

(10)

where t is time. We can look at the capacitor voltages as constant values at sufficient high switching frequency $v_{C1}\left(t\right)=V_{C1}$, $v_{C2}\left(t\right)=V_{C2}$.

The average voltage during one switching period from capacitor $C_1$ is

$$\begin{array}{c}\hfill 〈v_{C1}〉=D{V}_{C1},\end{array}$$

(11)

and from the capacitor $C_2$

$$\begin{array}{c}\hfill 〈v_{C2}〉=(1-D)V_{C2}.\end{array}$$

(12)

The average voltage on the switched capacitor is then

$$\begin{array}{c}\hfill 〈v_{C\mathrm{sw}}〉=D{V}_{C1}+(1-D)V_{C2}.\end{array}$$

(13)

The voltage on the single capacitor C needs to equal the voltage on the switched capacitor $C_{\mathrm{SW}}$

$$\begin{array}{c}\hfill v_C\left(t\right)=v_{C\mathrm{sw}}\left(t\right),\end{array}$$

(14)

which is equal to the average voltage

$$\begin{array}{c}\hfill v_C\left(t\right)=〈v_{C\mathrm{sw}}〉.\end{array}$$

(15)

Voltage on the capacitor C is given as

$$\begin{array}{c}\hfill v_C\left(t\right)={\displaystyle \frac{1}{C}}It.\end{array}$$

(16)

Substituting Equations (9), (10), (13) and (16) into Equation (15) yields

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{C_{\mathrm{SW}}}}={\displaystyle \frac{1}{C_1}}{D}^2+{\displaystyle \frac{1}{C_2}}{(1-D)}^2\end{array}$$

(17)

The duty cycle can be calculated from Equation (17) as

$$\begin{array}{c}\hfill D={\displaystyle \frac{C_1+{\displaystyle \frac{{C_{1}C}_2}{2}}\sqrt{{\displaystyle \frac{4}{{C_2}^2}}-\left({\displaystyle \frac{4}{C_1}}+{\displaystyle \frac{4}{C_2}}\right)\left({\displaystyle \frac{1}{C_2}}-{\displaystyle \frac{1}{C_{\mathrm{SW}}}}\right)}}{C_1+C_2}}.\end{array}$$

(18)

Let us now look at Figure 5, where we have an RL load connected in series with the capacitor and a harmonic voltage source. The differential equation, describing the RLC circuit in Figure 5a, is

$$\begin{array}{c}\hfill v\left(t\right)=Ri\left(t\right)+L{\displaystyle \frac{\mathrm{d}i\left(t\right)}{\mathrm{d}t}}+v_C\left(t\right),\end{array}$$

(19)

and in the integrodifferential form as

$$\begin{array}{c}\hfill v\left(t\right)=Ri\left(t\right)+L{\displaystyle \frac{\mathrm{d}i\left(t\right)}{\mathrm{d}t}}+{\displaystyle \frac{1}{C}}\int i\left(t\right)\mathrm{d}t.\end{array}$$

(20)

A similar equation applies for the circuit with the switched capacitor in Figure 5b.

$$\begin{array}{c}\hfill v\left(t\right)=Ri\left(t\right)+L{\displaystyle \frac{\mathrm{d}i\left(t\right)}{\mathrm{d}t}}+〈v_{C\mathrm{sw}}〉,\end{array}$$

(21)

where the voltage $v_C\left(t\right)$ equals $\langle v_{C\mathrm{sw}}\rangle$, when we neglect the switching ripple. The capacitors $C_1$ and $C_2$ voltages are substituted into Equation (21) as

$$\begin{array}{c}\hfill v\left(t\right)=Ri\left(t\right)+L{\displaystyle \frac{\mathrm{d}i\left(t\right)}{\mathrm{d}t}}+D{v}_{C1}\left(t\right)+\left(1-D\right)v_{C2}\left(t\right).\end{array}$$

(22)

Using Equations (9) and (10), we get the integrodifferential equation as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill v\left(t\right)& =Ri\left(t\right)+L{\displaystyle \frac{\mathrm{d}i\left(t\right)}{\mathrm{d}t}}+{\displaystyle \frac{D^2}{C_1}}\int i\left(t\right)\mathrm{d}t+{\displaystyle \frac{{(1-D)}^2}{C_2}}\int i\left(t\right)\mathrm{d}t\hfill \\ & =Ri\left(t\right)+L{\displaystyle \frac{\mathrm{d}i\left(t\right)}{\mathrm{d}t}}+\left({\displaystyle \frac{D^2}{C_1}}+{\displaystyle \frac{{(1-D)}^2}{C_2}}\right)\int i\left(t\right)\mathrm{d}t.\hfill \end{array}\end{array}$$

(23)

Substituting Equation (17) into Equation (23) yields

$$\begin{array}{c}\hfill v\left(t\right)=Ri\left(t\right)+L{\displaystyle \frac{\mathrm{d}i\left(t\right)}{\mathrm{d}t}}+{\displaystyle \frac{1}{C_{\mathrm{SW}}}}\int i\left(t\right)\mathrm{d}t.\end{array}$$

(24)

Equation (24) (Figure 5b) with switched capacitors is equivalent to Equation (20) (Figure 5a) with a single capacitor. The average value of the capacitance $C_{\mathrm{SW}}$ in the switching capacitors is the same as the value of capacitance C in a single capacitor.

The current i stays almost constant thanks to the inductance L for one switching period. The switching frequency is much larger than the frequency of the harmonic voltage source $f_s\gg f$, and therefore the current i can be expressed as constant. Because of this, we can use the derived equations also with RLC circuit and a harmonic voltage source.

2.3. Comparison of the Methods

The circuit in Figure 6 was simulated in MATLAB/Simulink (R2018a, MathWorks, Natick, MA, USA) environment with the following parameters: $R_1=70.53\Omega ,R_2=52.9\Omega ,L_1=170\mathrm{mH},L_1=120\mathrm{mH},C_1=5\mathsf{\mu }\mathrm{F}$ and $C_2=220\mathsf{\mu }\mathrm{F}.$ The calculated value for the capacitor is $C_{\mathrm{SW}}=33.867\mathsf{\mu }\mathrm{F}$ for the frequency $f=40\mathrm{Hz}$.

The first simulation results, shown in Figure 7, were gained using the method of conservation of energy. The simulation shown in Figure 8 was conducted using the averaging method. The calculation of the capacitance needed for the phase shift is described in the next section. The variables in the figures are as follows: $i_{\mathrm{main}}$ is the current in the main phase, $i_{\mathrm{aux}}$ is the current in the auxiliary phase with a normal capacitor (Figure 5a) and $i_{\mathrm{auxsw}}$ is the current in auxiliary phase with switched capacitors (Figure 5b).

As we can see, the first method does not have an exact phase shift of 90 degrees between the two currents. On the other hand, the second method has an exact phase shift of 90 degrees.

The current in auxiliary phase with a single capacitor matches the current with switched capacitors.

The difference in the value of the set (calculated) capacitance can be seen in Figure 9. The current i does not charge the capacitors $C_1$ and $C_2$ to the same voltage value and this is the reason the first method fails, as it assumes the same voltage on both capacitors.

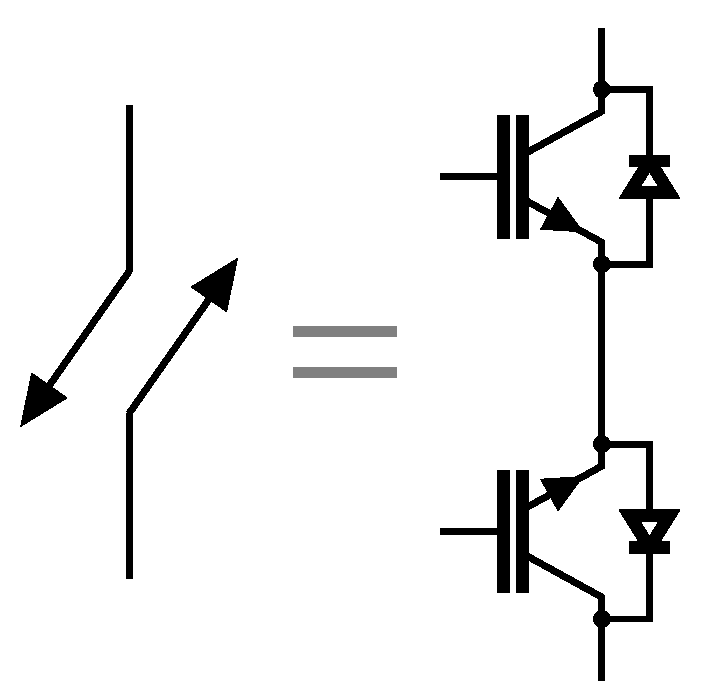
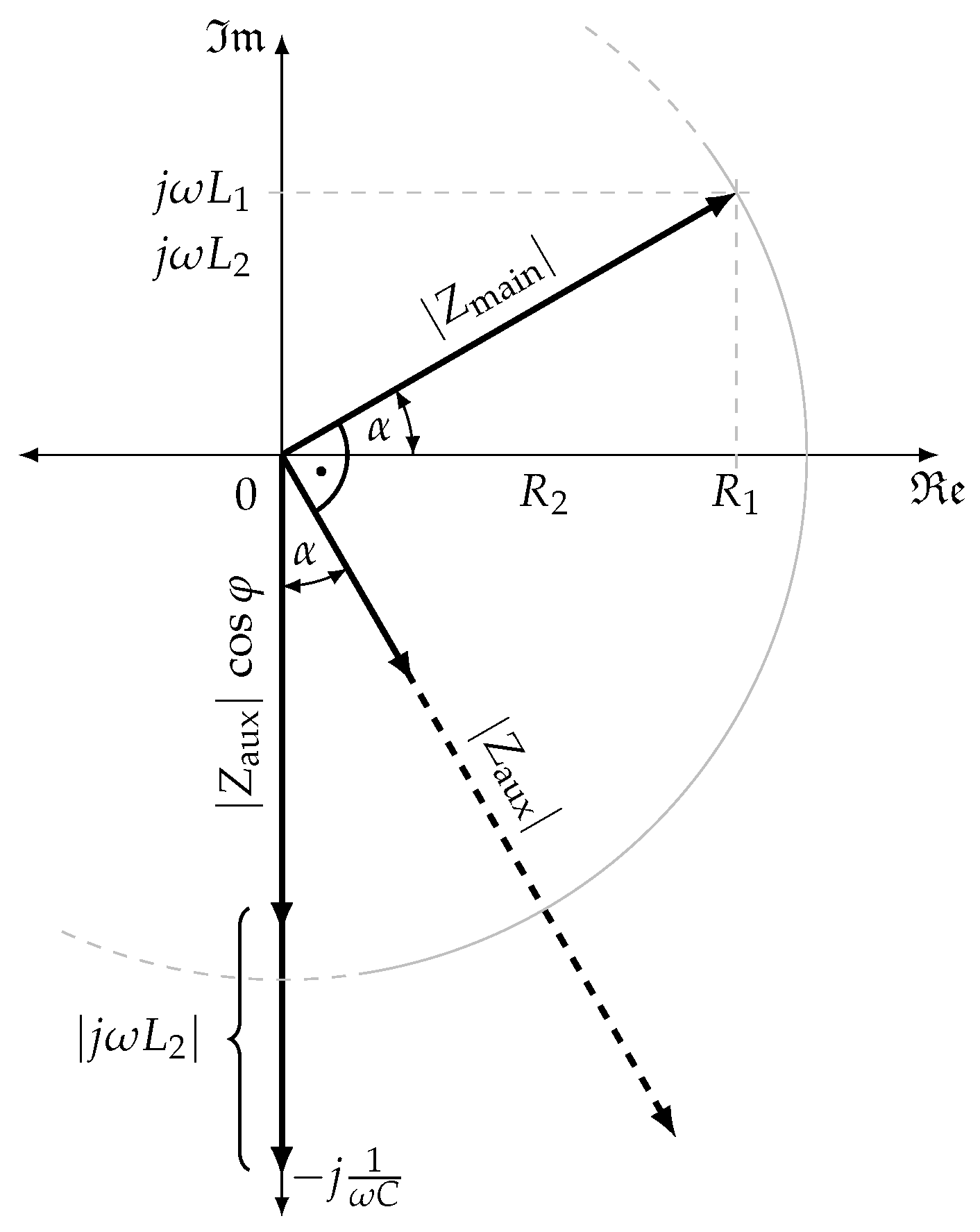
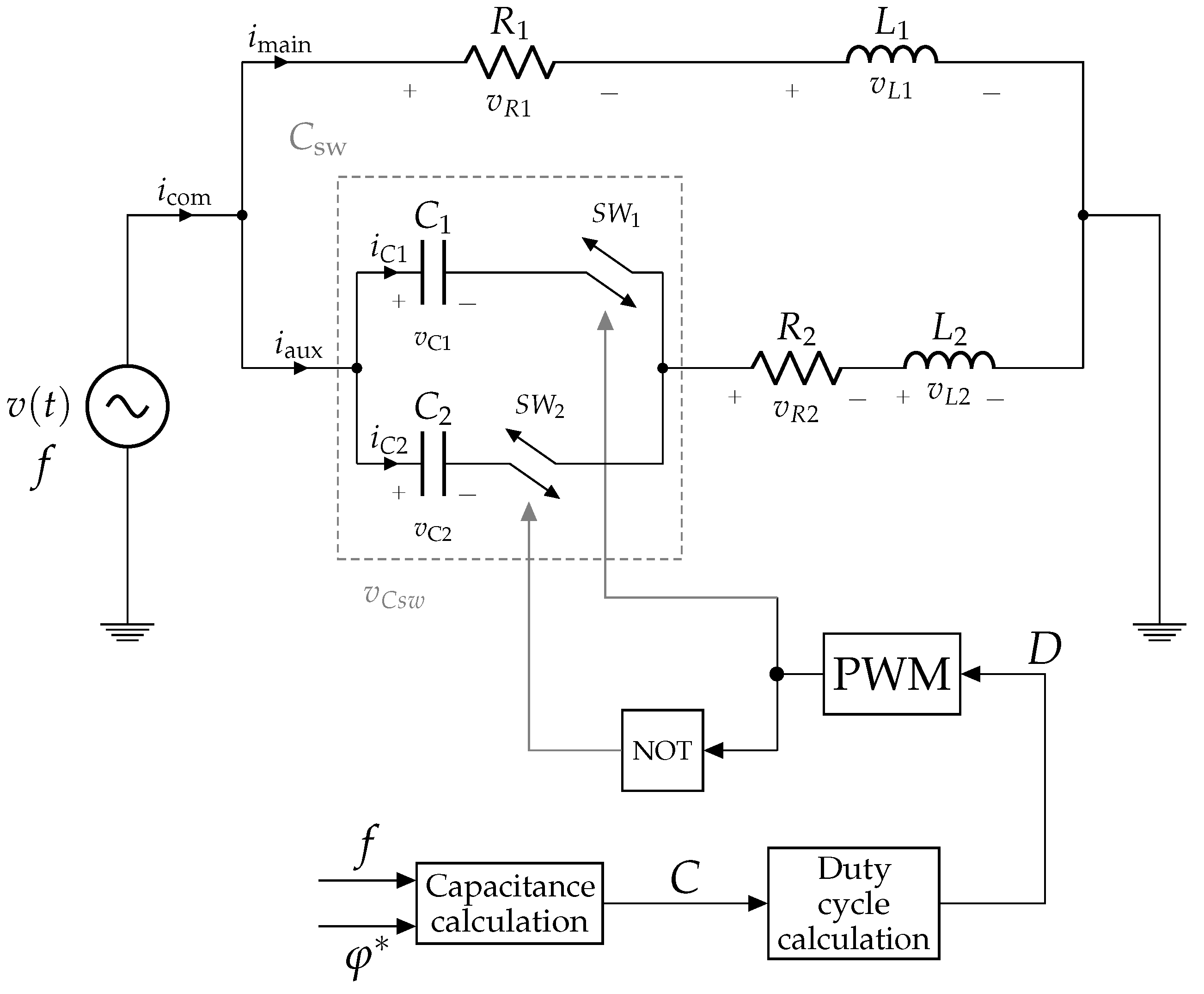
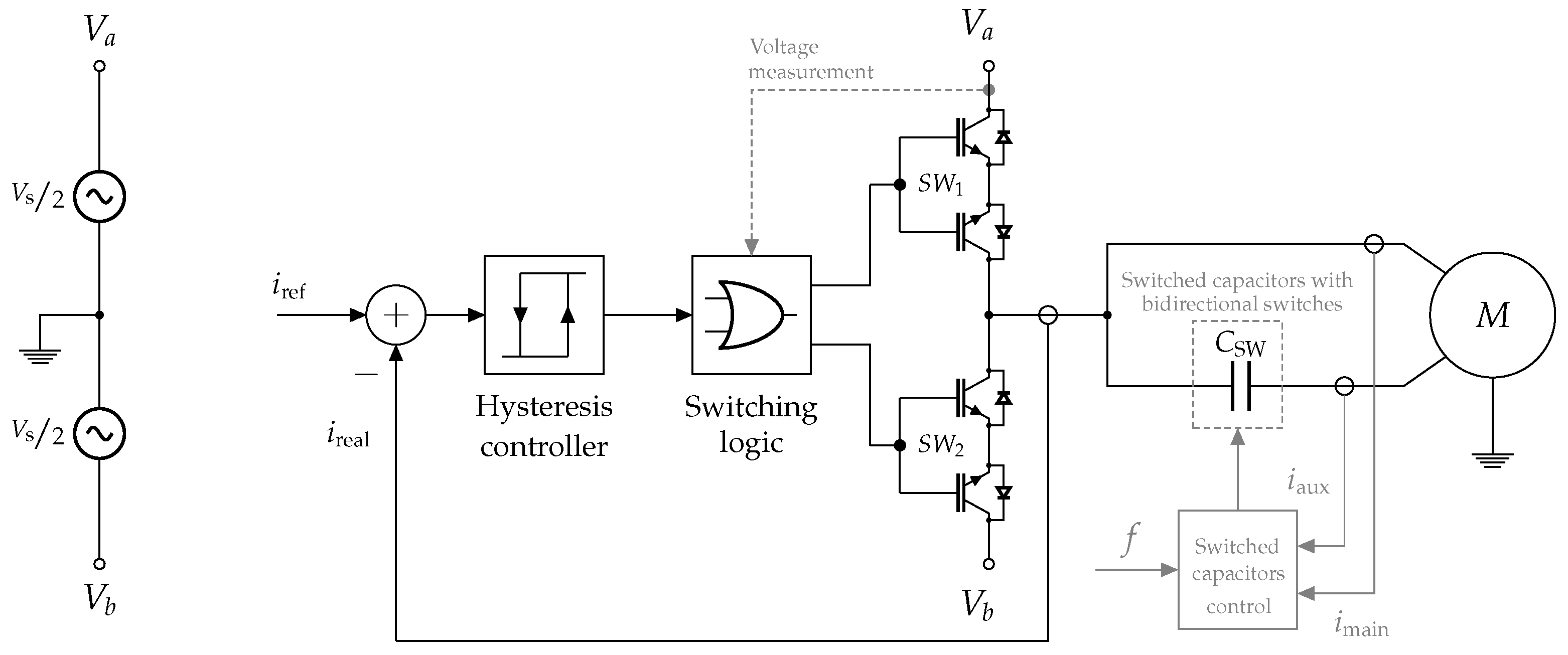
3. Control of Phase Advancing with Switched Capacitors

The equations for the switched capacitors are now used to control the phase shift of the current. Figure 6 shows a harmonic voltage source with two-phase RL load (main phase $R_1{L}_1$ and auxiliary phase $R_2{L}_2$) and a switched capacitor connected in series with the auxiliary phase. During the change of frequency, the phase shift is always constant at 90 degrees. The following equations describe the calculation of the capacitance

$$\begin{array}{c}\hfill \alpha =\arctan {\displaystyle \frac{\omega L_1}{R_1}},\end{array}$$

(25)

where $\omega$ is the angular frequency.

$$\begin{array}{c}\hfill Z_{\mathrm{aux}}={\displaystyle \frac{R_2}{sin\alpha }},\end{array}$$

(26)

where $Z_{\mathrm{aux}}$ is the impedance of the auxiliary phase.

The value of the capacitance is then calculated as

$$\begin{array}{c}\hfill C={\displaystyle \frac{1}{\omega (Z_{\mathrm{aux}}\cos \alpha +\omega L_2)}}.\end{array}$$

(27)

The calculation of the capacitance for 90 degrees phase shift is also shown in the vector diagram in Figure 10.

For a variable phase shift, as shown in Figure 11, the following equation can be used for the calculation of capacitance

$$\begin{array}{c}\hfill \beta =\phi -\alpha ,\end{array}$$

(28)

$$\gamma =\{\begin{array}{cc}{\displaystyle \frac{\pi }{2}}-\beta ,\hfill & \beta >0\hfill \\ \left|\beta \right|,\hfill & \beta <0,\hfill \end{array}$$

(29)

$$C=\{\begin{array}{cc}{\displaystyle \frac{1}{\omega (Z_{\mathrm{aux}}cos\gamma +\omega L_2)}},\hfill & \beta >0\hfill \\ {\displaystyle \frac{1}{\omega (Z_{\mathrm{aux}}sin\gamma +\omega L_2)}},\hfill & \beta <0\hfill \\ {\displaystyle \frac{1}{{\omega }^2{L}_2}},\hfill & \beta =0.\hfill \end{array}$$

(30)

3.1. Open Loop Control

In open-loop control, the 90-degree phase shift is calculated from precise values of the system parameters (frequency, inductance, and resistance) [9]. We can see the open-loop scheme and simplified control diagram in Figure 12 and Figure 13. First, the value of the capacitance is calculated based on these parameters. Second, the value of the duty cycle which controls the value of the switched capacitor is calculated based on the required capacitance and the values of the capacitors that are switched. These methods were described in previous chapters. The advantage is that there are no stability issues as in a feedback loop, and also no dynamics response of the control output (duty cycle). The disadvantage is that we need to know the parameters of the system, and, if the parameters of the system (inductance and resistance) change over time, the phase shift will also change from the set value of 90 degrees. The method of open-loop control is used in Section 2.3.

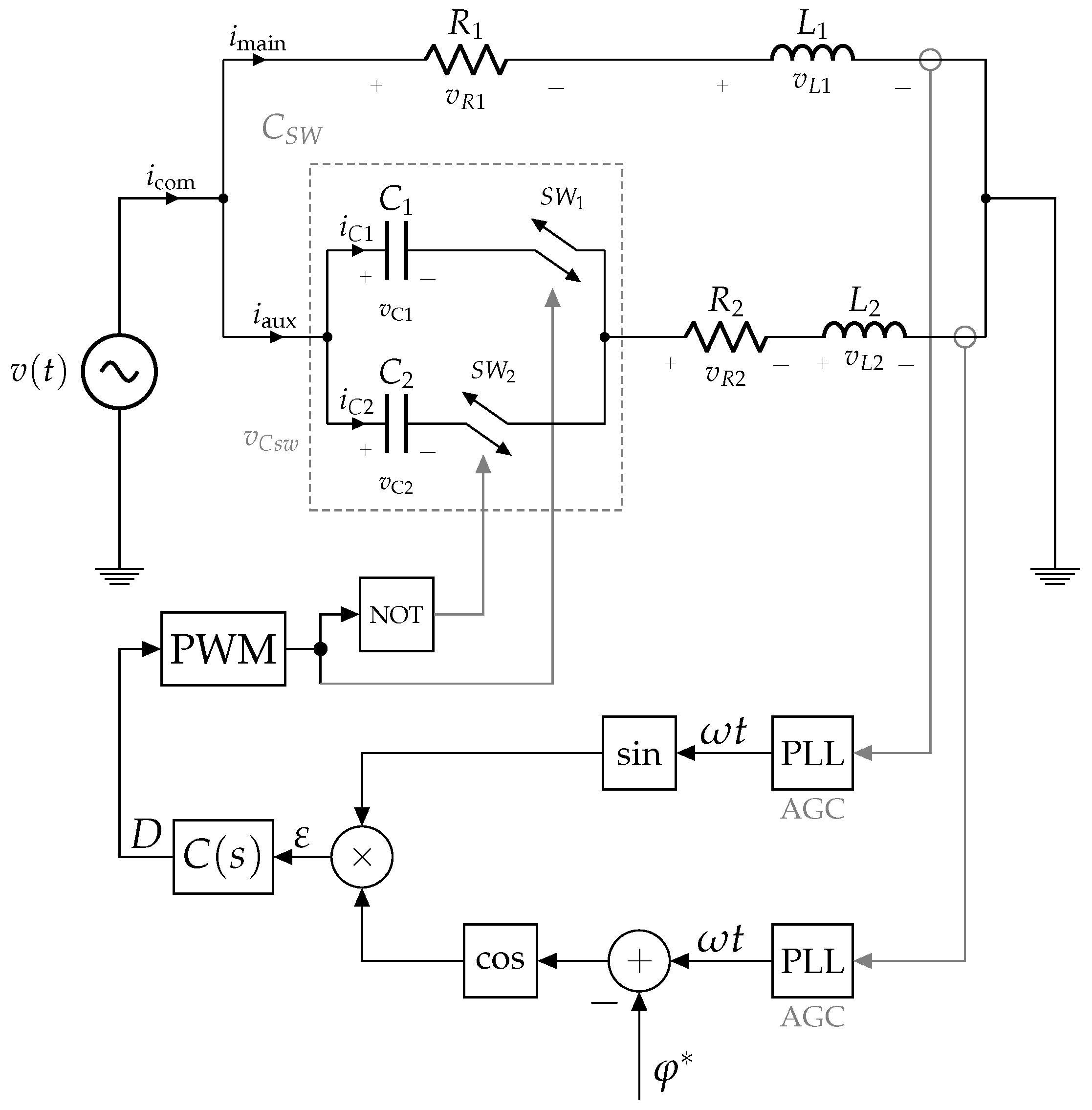
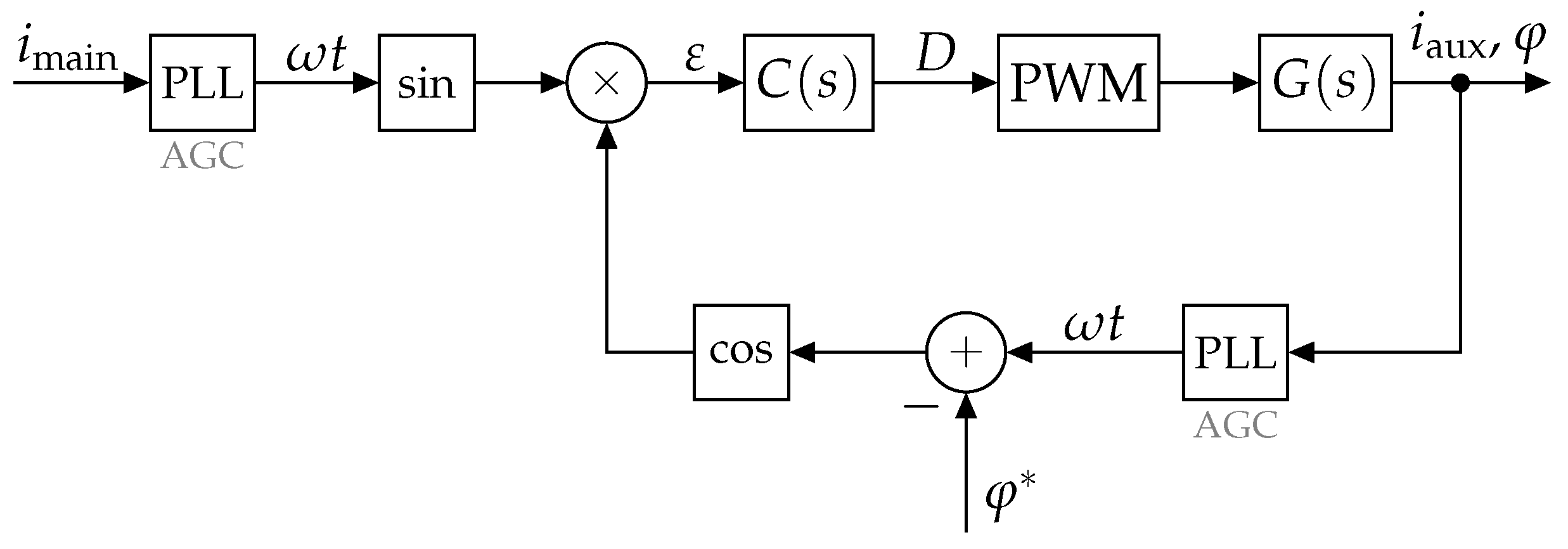
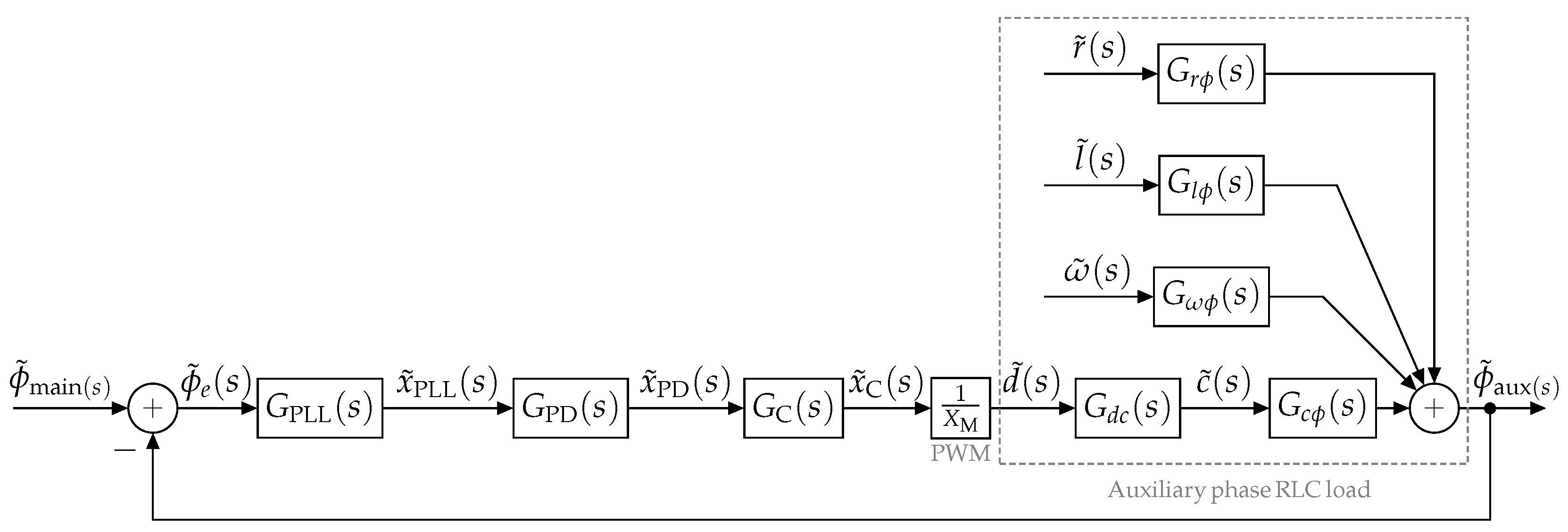
3.2. Closed-Loop Control

The closed-loop (feedback) control [14] of the phase shift was inspired by an analog phase-locked loop PLL [15]. We can see the complete control scheme with the circuit in Figure 14. The simplified block diagram is shown in Figure 15. Similar to a PPL, we also require a phase detector to compare the phase shift between main and auxiliary phase currents. A simple mixer (multiplication) is used as the phase detector to compare the phase signals. The current signals in the main and auxiliary phase have different magnitudes. This, however, would also affect the phase detector output, and we want to compare only the phase shift. To solve this problem, two PLLs with automatic gain control AGC are used for measurement of the current signals. The PLLs have unity magnitude outputs thanks to AGC. Another benefit of the PLLs is the removal of noise and current ripple from the signal.

3.2.1. Linearization of the Phase Detector

The large signal phase detector output in Figure 15 can be written as follows

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\varphi }_{\mathrm{e}}& =sin(\omega t+{\varphi }_{\mathrm{main}})cos(\omega t+{\varphi }_{\mathrm{aux}}-{\phi }^{*})\hfill \\ & =sin(\omega t+{\varphi }_{\mathrm{main}})cos\left(\omega t+{\varphi }_{\mathrm{aux}}-{\displaystyle \frac{\pi }{2}}\right)\hfill \\ & =sin(\omega t+{\varphi }_{\mathrm{main}})sin(\omega t+{\varphi }_{\mathrm{aux}}),\hfill \end{array}\end{array}$$

(31)

where t is time, $\omega$ is angular frequency, ${\varphi }_{\mathrm{main}}$ is the current phase shift in the main phase, ${\varphi }_{\mathrm{aux}}$ is the current phase shift in auxiliary phase, and ${\phi }^{*}=\pi /2$ is the desired phase shift difference between phases.

The phase shift variables can be written as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\varphi }_{\mathrm{main}}& ={\overline{\varphi }}_{\mathrm{main}}+{\tilde{\varphi }}_{\mathrm{main}},\hfill \\ \hfill {\varphi }_{\mathrm{aux}}& ={\overline{\varphi }}_{\mathrm{aux}}+{\tilde{\varphi }}_{\mathrm{aux}},\hfill \\ \hfill {\varphi }_{\mathrm{e}}& ={\overline{\varphi }}_{\mathrm{e}}+{\tilde{\varphi }}_{\mathrm{e}},\hfill \end{array}\end{array}$$

(32)

where ${\overline{\varphi }}_{\mathrm{main}}$, ${\overline{\varphi }}_{\mathrm{aux}}$, and ${\overline{\varphi }}_{\mathrm{e}}$, are the large signal components at the operating point and ${\tilde{\varphi }}_{\mathrm{main}}$, ${\tilde{\varphi }}_{\mathrm{aux}}$, and ${\tilde{\varphi }}_{\mathrm{e}}$, are the small signal components (perturbations) around the operating point at equilibrium.

We can substitute the variables from Equarion (32) into Equation (31) of the phase detector. For simplification, we assume in our derivation of the linear phase detector that the large signal phase shift in the main phase is ${\overline{\varphi }}_{\mathrm{aux}}=0$ and in the auxiliary phase ${\overline{\varphi }}_{\mathrm{aux}}=\pi /2$ at equilibrium, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\varphi }_{\mathrm{e}}& =sin(\omega t+{\overline{\varphi }}_{\mathrm{main}}+{\tilde{\varphi }}_{\mathrm{main}})sin(\omega t+{\overline{\varphi }}_{\mathrm{aux}}+{\tilde{\varphi }}_{\mathrm{aux}})\hfill \\ & =sin(\omega t+{\tilde{\varphi }}_{\mathrm{main}})sin\left(\omega t+{\displaystyle \frac{\pi }{2}}+{\tilde{\varphi }}_{\mathrm{aux}}\right).\hfill \end{array}\end{array}$$

(33)

The solution of Equation (33) yields

$$\begin{array}{c}\hfill {\varphi }_{\mathrm{e}}={\displaystyle \frac{1}{2}}\left[sin(2\omega t+{\tilde{\varphi }}_{\mathrm{main}}+{\tilde{\varphi }}_{\mathrm{aux}})+sin({\tilde{\varphi }}_{\mathrm{main}}-{\tilde{\varphi }}_{\mathrm{aux}})\right].\end{array}$$

(34)

As we can see, our solution has only small signal components, but also two nonlinearities.

The first nonlinearity with double frequency ac component

$$sin(2\omega t+{\tilde{\varphi }}_{\mathrm{main}}),$$

can be removed with a low-pass loop filter.

The second nonlinearity can be removed if we assume that the small-signal phase shift difference is sufficiently small ${\tilde{\varphi }}_{\mathrm{main}}-{\tilde{\varphi }}_{\mathrm{aux}}\approx 0$, then we can write

$$\begin{array}{c}\hfill sin({\tilde{\varphi }}_{\mathrm{main}}-{\tilde{\varphi }}_{\mathrm{aux}})\approx {\tilde{\varphi }}_{\mathrm{main}}-{\tilde{\varphi }}_{\mathrm{aux}}.\end{array}$$

(35)

Then, in the steady state (equilibrium), is the small signal output (error signal) around the operation point of the phase detector equal to

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tilde{\varphi }}_{\mathrm{e}}& =K_{\mathrm{PD}}({\tilde{\varphi }}_{\mathrm{main}}-{\tilde{\varphi }}_{\mathrm{aux}})\hfill \\ & ={\displaystyle \frac{1}{2}}({\tilde{\varphi }}_{\mathrm{main}}-{\tilde{\varphi }}_{\mathrm{aux}}),\hfill \end{array}\end{array}$$

(36)

where $K_{\mathrm{PD}}$ is the phase detector gain.

3.2.2. Linearization of the Controlled System

To be able to use classical control system theory, we need to have a linear dynamic system. One way to achieve this is to use linearization [16]. We use Taylor series expansion around a specific quiescent operating point. Only the first order term in the series can be used because of the linearity requirement, i.e. higher order terms represent nonlinearities.

The equation for the switching capacitor is derived in the previous section (Equation (17)). The phase shift of the auxiliary phase current is calculated as

$$\begin{array}{c}\hfill {\varphi }_{\mathrm{aux}}=-arctan{\displaystyle \frac{\omega L_2-{\displaystyle \frac{1}{\omega C}}}{R_2}}\end{array}$$

(37)

As we can see, the phase shift is a function of the angular frequency $\omega$, capacitance C, inductance $L_2$, and resistance $R_2$. We control the phase shift with the change in the capacitance C which is again controlled by the duty cycle D. The changes in angular frequency $\omega$, inductance $L_2$, and resistance $R_2$ represent disturbances in our control system output which is the phase shift ${\varphi }_{\mathrm{aux}}$.

We linearize about one variable in the case of the switching capacitor

$$\begin{array}{c}\hfill D=\overline{D}+\tilde{d},\end{array}$$

(38)

and about four variables in the case of the phase shift of the auxiliary phase

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \omega & =\overline{\omega }+\tilde{\omega },\hfill \\ \hfill C& =\overline{C}+\tilde{c},\hfill \\ \hfill L_2& ={\overline{L}}_2+{\tilde{l}}_2,\hfill \\ \hfill R_2& ={\overline{R}}_2+{\tilde{r}}_2,\hfill \end{array}\end{array}$$

(39)

where $\overline{D}$, $\overline{\omega }$, $\overline{C}$, ${\overline{L}}_2$, and ${\overline{R}}_2$ are the equilibrium operating point variables and $\tilde{d}$, $\tilde{\omega }$, $\tilde{c}$, ${\tilde{l}}_2$, and ${\tilde{r}}_2$ are the small signal perturbation variables around the operating point.

The first order Taylor series approximation for the equation of the switching capacitance (Equation (17)) is

$$\begin{array}{cc}\hfill C& =C\left(\overline{D}\right)+{\left.{\displaystyle \frac{\partial C\left(D\right)}{\partial D}}\right|}_{\overline{D}}·\tilde{d}+\begin{array}{c}\mathrm{higher}\mathrm{order}\mathrm{terms}\\ \left(\mathrm{nonlinearities}\right)\end{array},\hfill \end{array}$$

(40)

where the equilibrium operating point of the calculated switching capacitance is

$$\begin{array}{c}\hfill C\left(\overline{D}\right)={\displaystyle \frac{C_1{C}_2}{C_2{\overline{D}}^2+C_1{(1-\overline{D})}^2}}\end{array}$$

(41)

and the slope (tangent line) for the linear small signal value of $\tilde{c}$, which is dependent on the small change of the duty cycle $\tilde{d}$, is

$$\begin{array}{c}\hfill {\left.{\displaystyle \frac{\partial C\left(D\right)}{\partial D}}\right|}_{\overline{D}}={\displaystyle \frac{-2C_1{C}_2(C_2\overline{D}-C_1(1-\overline{D}))}{{(C_1(1-\overline{D})+C_2\overline{D})}^2}}.\end{array}$$

(42)

Again, we use Taylor series and linearize the equation of phase shift (37) about four variables and neglect the higher order terms.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\varphi }_{\mathrm{aux}}& ={\varphi }_{\mathrm{aux}}(\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2)\hfill \\ & +{\left.{\displaystyle \frac{\partial {\varphi }_{\mathrm{aux}}(\omega ,C,L_2,R_2)}{\partial C}}\right|}_{\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2}·\tilde{c}\hfill \\ & +{\left.{\displaystyle \frac{\partial {\varphi }_{\mathrm{aux}}(\omega ,C,L_2,R_2)}{\partial \omega }}\right|}_{\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2}·\tilde{\omega }\hfill \\ & +{\left.{\displaystyle \frac{\partial {\varphi }_{\mathrm{aux}}(\omega ,C,L_2,R_2)}{\partial L_2}}\right|}_{\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2}·{\tilde{l}}_2\hfill \\ & +{\left.{\displaystyle \frac{\partial {\varphi }_{\mathrm{aux}}(\omega ,C,L_2,R_2)}{\partial R_2}}\right|}_{\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2}·{\tilde{r}}_2\hfill \\ & +\begin{array}{c}\mathrm{higher}\mathrm{order}\mathrm{terms}\\ \left(\mathrm{nonlinearities}\right)\end{array},\hfill \end{array}\end{array}$$

(43)

where the equilibrium operating point of the phase shift is

$$\begin{array}{c}\hfill {\varphi }_{\mathrm{aux}}(\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2)=-arctan{\displaystyle \frac{\overline{\omega }{\overline{L}}_2-{\displaystyle \frac{1}{\overline{\omega }\overline{C}}}}{{\overline{R}}_2}}.\end{array}$$

(44)

The small signal phase shift is a function of the linear combination of small signal changes in capacitance $\tilde{c}$, angular frequency $\tilde{\omega }$, inductance ${\tilde{l}}_2$, and resistance ${\tilde{r}}_2$. These variables represent four independent inputs.

The slope of the contribution of capacitance $\tilde{c}$ to phase shift is

$$\begin{array}{c}\hfill {\left.{\displaystyle \frac{\partial {\varphi }_{\mathrm{aux}}(\omega ,C,L_2,R_2)}{\partial C}}\right|}_{\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2}={\displaystyle \frac{-1}{\overline{\omega }{\overline{R}}_2{\overline{C}}^2\left[{\left({\displaystyle \frac{\overline{\omega }{\overline{L}}_2}{{\overline{R}}_2}}-{\displaystyle \frac{1}{\overline{\omega }{\overline{R}}_2{\overline{C}}_2}}\right)}^2+1\right]}}.\end{array}$$

(45)

The slope of the contribution of angular frequency $\tilde{\omega }$ to phase shift is

$$\begin{array}{c}\hfill {\left.{\displaystyle \frac{\partial {\varphi }_{\mathrm{aux}}(\omega ,C,L_2,R_2)}{\partial \omega }}\right|}_{\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2}=\left({\displaystyle \frac{{\overline{L}}_2}{{\overline{R}}_2}}+{\displaystyle \frac{1}{{\overline{\omega }}^2{\overline{R}}_2{\overline{C}}_2}}\right){\displaystyle \frac{-1}{{\left({\displaystyle \frac{\overline{\omega }{\overline{L}}_2}{{\overline{R}}_2}}-{\displaystyle \frac{1}{\overline{\omega }{\overline{R}}_2{\overline{C}}_2}}\right)}^2+1}}.\end{array}$$

(46)

The slope of the contribution of inductance ${\tilde{l}}_2$ to phase shift is

$$\begin{array}{c}\hfill {\left.{\displaystyle \frac{\partial {\varphi }_{\mathrm{aux}}(\omega ,C,L_2,R_2)}{\partial L_2}}\right|}_{\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2}={\displaystyle \frac{-\overline{\omega }}{{\overline{R}}_2\left[{\left({\displaystyle \frac{\overline{\omega }{\overline{L}}_2}{{\overline{R}}_2}}-{\displaystyle \frac{1}{\overline{\omega }{\overline{R}}_2{\overline{C}}_2}}\right)}^2+1\right]}}.\end{array}$$

(47)

The slope of the contribution of resistance ${\tilde{r}}_2$ to phase shift is

$$\begin{array}{c}\hfill {\left.{\displaystyle \frac{\partial {\varphi }_{\mathrm{aux}}(\omega ,C,L_2,R_2)}{\partial R_2}}\right|}_{\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2}=\left({\displaystyle \frac{1}{\overline{\omega }{\overline{R}}_2^2{\overline{C}}_2}}-{\displaystyle \frac{\overline{\omega }{\overline{L}}_2}{{\overline{R}}_2^2}}\right){\displaystyle \frac{-1}{{\left({\displaystyle \frac{\overline{\omega }{\overline{L}}_2}{{\overline{R}}_2}}-{\displaystyle \frac{1}{\overline{\omega }{\overline{R}}_2{\overline{C}}_2}}\right)}^2+1}}.\end{array}$$

(48)

From these equations can be derived the transfer functions for control and the disturbances.

Phase shift capacitance to output transfer function:

$$G_{c\varphi }\left(s\right)={\left.{\displaystyle \frac{\tilde{\varphi }\left(s\right)}{\tilde{c}\left(s\right)}}\right|}_{\begin{array}{c}\tilde{\omega }=0\\ {\tilde{l}}_2=0\\ {\tilde{r}}_2=0\end{array}}={\left.{\displaystyle \frac{\partial {\varphi }_{\mathrm{aux}}(\omega ,C,L_2,R_2)}{\partial C}}\right|}_{\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2}.$$

(49)

Phase shift duty cycle to capacitance transfer function:

$$G_{dc}\left(s\right)={\displaystyle \frac{\tilde{c}\left(s\right)}{\tilde{d}\left(s\right)}}={\displaystyle \frac{-2C_1{C}_2(C_2\overline{D}-C_1(1-\overline{D}))}{{(C_1(1-\overline{D})+C_2\overline{D})}^2}}.$$

(50)

Phase shift control to output transfer function:

$$G_{d\varphi }\left(s\right)={\displaystyle \frac{\tilde{\varphi }\left(s\right)}{\tilde{d}\left(s\right)}}=G_{dc}\left(s\right)G_{c\varphi }\left(s\right).$$

(51)

Phase shift angular frequency to output transfer function:

$$\begin{array}{c}\hfill G_{\omega \varphi }\left(s\right)={\left.{\displaystyle \frac{\tilde{\varphi }\left(s\right)}{\tilde{\omega }\left(s\right)}}\right|}_{\begin{array}{c}\tilde{c}=0\\ {\tilde{l}}_2=0\\ {\tilde{r}}_2=0\end{array}}={\left.{\displaystyle \frac{\partial {\varphi }_{\mathrm{aux}}(\omega ,C,L_2,R_2)}{\partial \omega }}\right|}_{\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2}.\end{array}$$

(52)

Phase shift inductance to output transfer function:

$$\begin{array}{c}\hfill G_{l\varphi }\left(s\right)={\left.{\displaystyle \frac{\tilde{\varphi }\left(s\right)}{\widetilde{l_2}\left(s\right)}}\right|}_{\begin{array}{c}\tilde{\omega }=0\\ \tilde{c}=0\\ {\tilde{r}}_2=0\end{array}}={\left.{\displaystyle \frac{\partial {\varphi }_{\mathrm{aux}}(\omega ,C,L_2,R_2)}{\partial L_2}}\right|}_{\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2}.\end{array}$$

(53)

Phase shift resistance to output transfer function:

$$\begin{array}{c}\hfill G_{r\varphi }\left(s\right)={\left.{\displaystyle \frac{\tilde{\varphi }\left(s\right)}{\widetilde{r_2}\left(s\right)}}\right|}_{\begin{array}{c}\tilde{\omega }=0\\ {\tilde{l}}_2=0\\ \tilde{c}=0\end{array}}={\left.{\displaystyle \frac{\partial {\varphi }_{\mathrm{aux}}(\omega ,C,L_2,R_2)}{\partial R_2}}\right|}_{\overline{\omega },\overline{C},{\overline{L}}_2,{\overline{R}}_2}.\end{array}$$

(54)

The small signal variables $\tilde{\omega }\left(s\right)$, $\widetilde{l_2}\left(s\right)$, and $\widetilde{r_2}\left(s\right)$ represent disturbances of the controlled system and propagate to the output ${\tilde{\varphi }}_{\mathrm{aux}}\left(s\right)$ through the transfer function (gain) of $G_{\omega \varphi }\left(s\right)$, $G_{l\varphi }\left(s\right)$, and $G_{r\varphi }\left(s\right)$.

The phase shift variation ${\tilde{\varphi }}_{\mathrm{aux}}\left(s\right)$ can be expressed as a linear combination of four independent inputs

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tilde{\varphi }}_{\mathrm{aux}}\left(s\right)& =G_{c\varphi }\left(s\right)\tilde{c}\left(s\right)+G_{\omega \varphi }\tilde{\omega }\left(s\right)+G_{l\varphi }\left(s\right)\widetilde{l_2}\left(s\right)+G_{r\varphi }\left(s\right)\widetilde{r_2}\left(s\right)\hfill \\ & =G_{c\varphi }\left(s\right)G_{dc}\left(s\right)\tilde{d}\left(s\right)+G_{\omega \varphi }\tilde{\omega }\left(s\right)+G_{l\varphi }\left(s\right)\widetilde{l_2}\left(s\right)+G_{r\varphi }\left(s\right)\widetilde{r_2}\left(s\right).\hfill \end{array}\end{array}$$

(55)

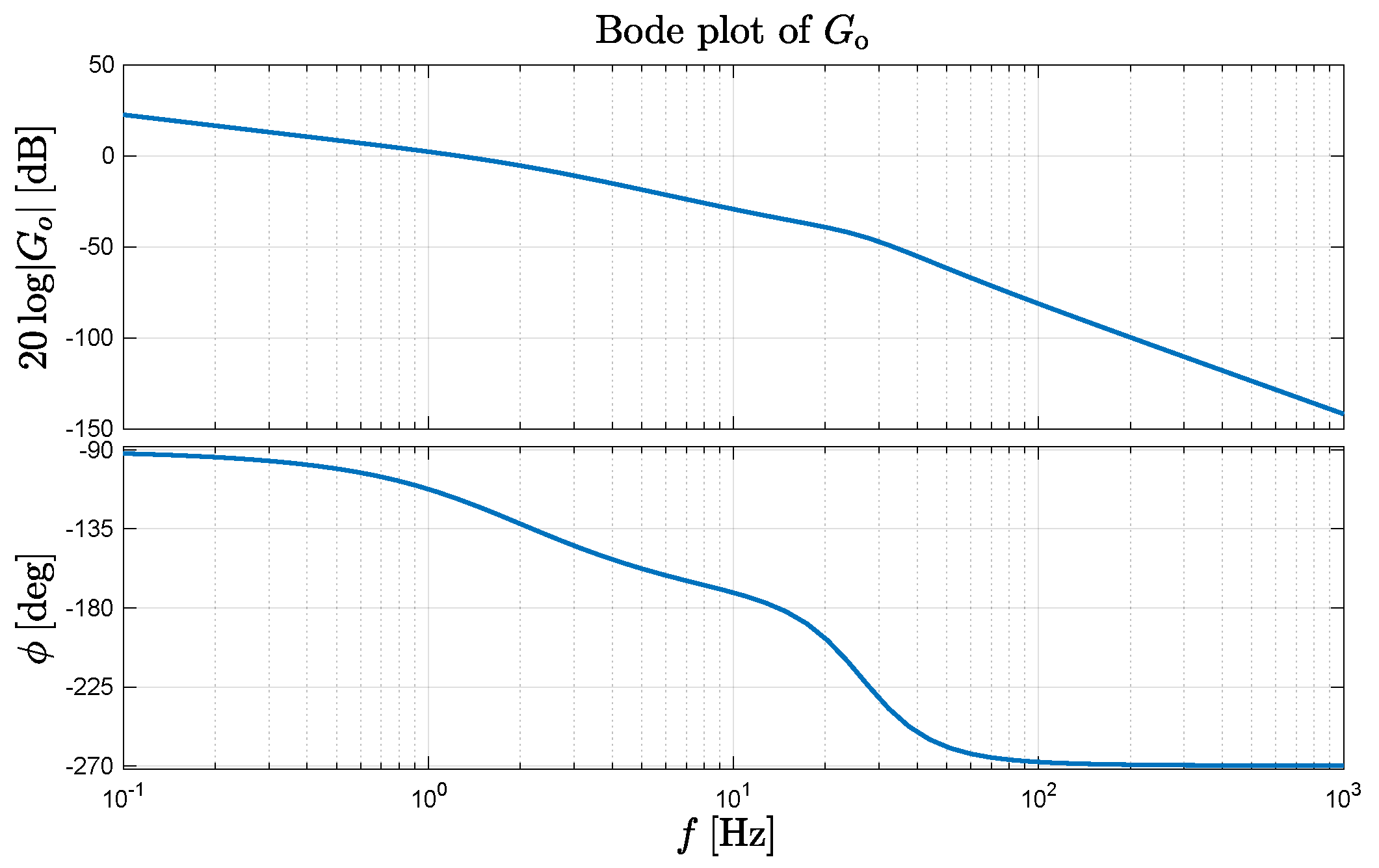
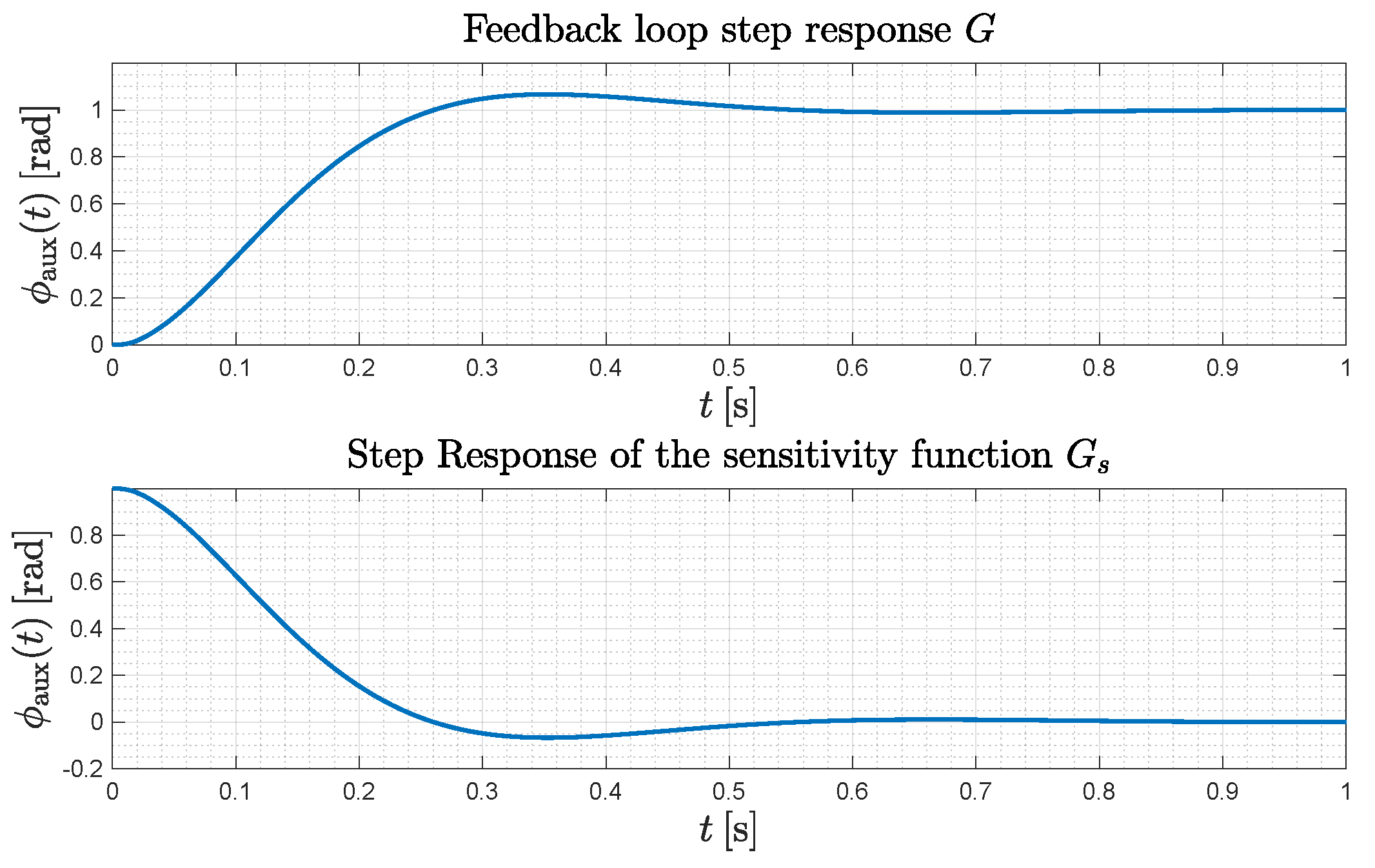
3.2.3. Control Loop Design

The gain of the phase detector is

$$\begin{array}{c}\hfill G_{\mathrm{PD}}\left(s\right)={\displaystyle \frac{1}{2}}.\end{array}$$

(56)

The designed compensator consists of a low pass filter, which is used for removal of the ac component (second harmonics) from the phase detector output (error signal) and a PI controller.

The transfer function of the second order low pass filter:

$$\begin{array}{c}\hfill G_{\mathrm{F}}\left(s\right)={\displaystyle \frac{K_{\mathrm{F}}}{{\left({\tau }_{\mathrm{F}}s+1\right)}^2}},\end{array}$$

(57)

where $K_{\mathrm{F}}=2$ is the filter gain and ${\tau }_{\mathrm{F}}=0.1\mathrm{s}$ is the filter time constant.

The transfer function of the used PLLs is

$$G_{\mathrm{PLL}}\left(s\right)={\displaystyle \frac{{\varphi }_{out}\left(s\right)}{{\varphi }_{in}\left(s\right)}}={\displaystyle \frac{K_{\mathrm{P}}s+K_{\mathrm{I}}}{s^2+K_{\mathrm{P}}s+K_{\mathrm{I}}}},$$

(58)

where $K_{\mathrm{P}}=166.6$ and $K_{\mathrm{I}}=27,755.55$ are the coefficients of the function.

The transfer function of PI controller is

$$\begin{array}{c}\hfill G_{\mathrm{PI}}\left(s\right)=K_{\mathrm{P}}+K_{\mathrm{I}}{\displaystyle \frac{1}{s}},\end{array}$$

(59)

where $K_{\mathrm{P}}=0.05$ is the proportional coefficient, and $K_{\mathrm{I}}=0.35$ is the integral coefficient.

The controller and the whole compensation network are designed with sufficient amplitude and phase margin for robustness of the control feedback loop in the case of changes in the parameters of the system and good rejection of the disturbances.

The open-loop gain transfer function is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill G_o\left(s\right)& =G_{\mathrm{PLL}}\left(s\right)G_{\mathrm{PD}}\left(s\right)G_{\mathrm{c}}\left(s\right)G_{d\varphi }\left(s\right)\hfill \\ & =G_{\mathrm{PLL}}\left(s\right)G_{\mathrm{PD}}\left(s\right)G_{\mathrm{F}}\left(s\right)G_{\mathrm{PI}}\left(s\right)G_{dc}\left(s\right)G_{c\varphi }\left(s\right)\hfill \end{array}\end{array}$$

(60)

The closed-loop control transfer function is

$$\begin{array}{c}\hfill G\left(s\right)={\displaystyle \frac{{\tilde{\varphi }}_{\mathrm{aux}}\left(s\right)}{{\tilde{\varphi }}_{\mathrm{main}}\left(s\right)}}={\displaystyle \frac{G_{d\varphi }\left(s\right)}{1+G_o\left(s\right)}}={\displaystyle \frac{G_{dc}\left(s\right)G_{c\varphi }\left(s\right)}{1+G_o\left(s\right)}}.\end{array}$$

(61)

The negative feedback reduces the influence of disturbances in the controlled system.

The closed-loop transfer function of angular speed disturbance rejection is

$$\begin{array}{c}\hfill G_{\omega }\left(s\right)={\displaystyle \frac{{\tilde{\varphi }}_{\mathrm{aux}}\left(s\right)}{\tilde{\omega }\left(s\right)}}={\displaystyle \frac{G_{\omega \varphi }}{1+G_o\left(s\right)}}.\end{array}$$

(62)

The closed-loop transfer function of inductance disturbance rejection is

$$\begin{array}{c}\hfill G_l\left(s\right)={\displaystyle \frac{{\tilde{\varphi }}_{\mathrm{aux}}\left(s\right)}{{\tilde{l}}_2\left(s\right)}}={\displaystyle \frac{G_{l\varphi }}{1+G_o\left(s\right)}}.\end{array}$$

(63)

The closed-loop transfer function of resistance disturbance rejection is

$$\begin{array}{c}\hfill G_r\left(s\right)={\displaystyle \frac{{\tilde{\varphi }}_{\mathrm{aux}}\left(s\right)}{{\tilde{r}}_2\left(s\right)}}={\displaystyle \frac{G_{r\varphi }}{1+G_o\left(s\right)}}.\end{array}$$

(64)

The sensitivity transfer function is

$$\begin{array}{c}\hfill G_{\mathrm{s}}\left(s\right)={\displaystyle \frac{1}{1+G_o\left(s\right)}}.\end{array}$$

(65)

The phase shift variation ${\tilde{\varphi }}_{\mathrm{aux}}\left(s\right)$ with negative feedback and all disturbances is then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tilde{\varphi }}_{\mathrm{aux}}\left(s\right)& =G\left(s\right){\tilde{\varphi }}_{\mathrm{main}}\left(s\right)+G_{\omega }\left(s\right)\tilde{\omega }\left(s\right)+G_l\left(s\right){\tilde{l}}_2\left(s\right)+G_r\left(s\right){\tilde{r}}_2\left(s\right)\hfill \\ & ={\displaystyle \frac{G_{dc}\left(s\right)G_{c\varphi }\left(s\right)}{1+G_o\left(s\right)}}{\tilde{\varphi }}_{\mathrm{main}}\left(s\right)+{\displaystyle \frac{G_{\omega \varphi }}{1+G_o\left(s\right)}}\tilde{\omega }\left(s\right)+{\displaystyle \frac{G_{l\varphi }\left(s\right)}{1+G_o\left(s\right)}}{\tilde{l}}_2\left(s\right)+{\displaystyle \frac{G_{r\varphi }\left(s\right)}{1+G_o\left(s\right)}}{\tilde{r}}_2\left(s\right)\hfill \end{array}\end{array}$$

(66)

The closed-loop performance of the system can be seen from the Bode plot of the open-loop gain $G_o$, shown in Figure 16, and from the step response G of feedback systems, shown in Figure 17. The rejection of the feedback system to disturbances can be seen in the step response of the sensitivity transfer function $G_{\mathrm{s}}$.

A linearized block diagram of the feedback system is shown in Figure 18 and parameters of the system are shown in

Table 1. Parameters of the controlled system.

Parameters	Values	Units
f	25	$\mathrm{Hz}$
$R_1$	59.58	$\Omega$
$R_2$	67.38	$\Omega$
$L_1$	1210	$\mathrm{mH}$
$L_2$	2045	$\mathrm{mH}$
$C_1$	2.5	$\mathsf{\mu }\mathrm{F}$
$C_2$	200	$\mathsf{\mu }\mathrm{F}$

. The calculated gain functions for the operating point are shown in

Table 2. Gain functions of the linearized control system.

Parameters	Values	Units
$G_{dc}$	$-9.7265\times {10}^{-5}$	F
$G_{c\varphi }$	$-2.4878\times {10}^5$	$\mathrm{rad}/\mathrm{F}$
$G_{d\varphi }$	$24.1979$	$\mathrm{rad}$
$G_{\omega \varphi }$	−0.0571	$\mathrm{s}$
$G_{l\varphi }$	−2.1227	$\mathrm{rad}/\mathrm{H}$
$G_{r\varphi }$	0.0580	$\mathrm{rad}/\Omega$

.

The robustness of the designed PI controller and the whole feedback loop to changes of the system parameters can be seen on the Gain margins $Gm$ and phase margins $Pm$, in

Table 3. Gain margin at different parameters of the system.

$\mathit{Gm}$ (dB)		${\mathit{L}}_2$ (mH)
		$-10\%$	2045	$+10\%$
f (Hz)	5	54.1	51	49.3
	25	34.6	34.2	33.7
	45	34	33.5	33.1

and

Table 4. Phase margin at different parameters of the system.

$\mathit{Pm}$ (deg)		${\mathit{L}}_2$ (mH)
		$-10\%$	2045	$+10\%$
f (Hz)	5	87.2	86	85.1
	25	63.1	61.9	60.8
	45	61.4	60.2	59.1

.

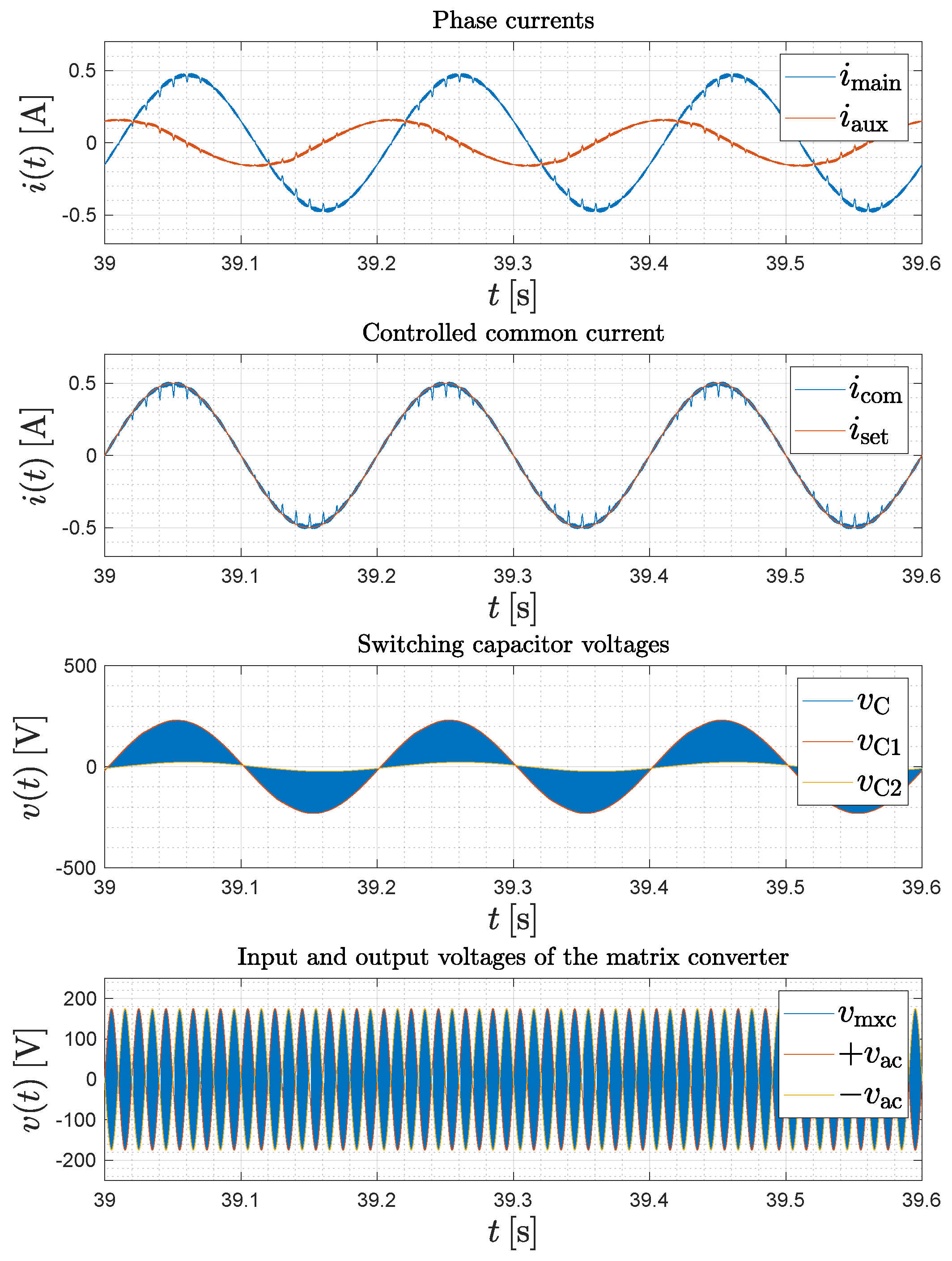
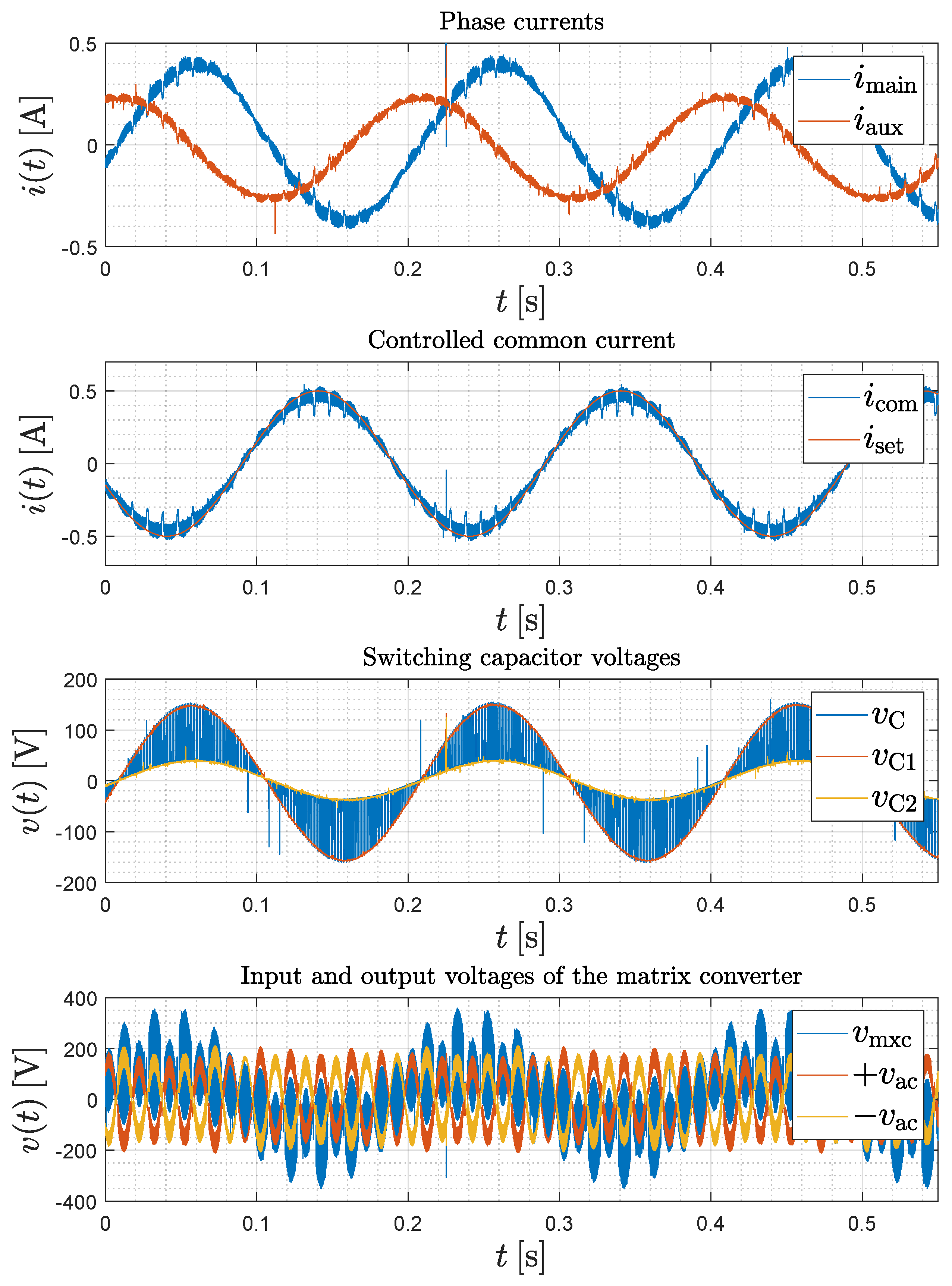
4. Simulation of the System with an Active IM Load

Simulation of single-leg two-phase matrix converter has been done with an active two-phase induction motor load using MATLAB/Simulink environment. The principal scheme is shown in Figure 19 [1,2,3,17,18,19,20]. We have two feedback loops. The first feedback loop controls the common current of both phases with a hysteresis controller. The second control loop controls the phase shift of the currents in both phases. The control methods are described in previous sections. The simulation results are shown in Figure 20, Figure 21 and Figure 22. The calculation time step of the simulation is $T_{\mathrm{s}}=1\times {10}^{-5}\mathrm{s}$.

The parameters for the two-phase induction motor used in simulation and experimental verification are shown in

Table 5. Parameters of the induction motor.

Parameters	Values	Units
$P_{\mathrm{n}}$	150	$\mathrm{VA}$
$V_{\mathrm{rms}}$	230	$\mathrm{V}$
f	50	$\mathrm{Hz}$
$R_{\mathrm{s}}$	59.58	$\Omega$
$R_{\mathrm{S}}$	67.38	$\Omega$
$L_{\mathrm{ss}}$	1210	$\mathrm{mH}$
$L_{\mathrm{SS}}$	2045	$\mathrm{mH}$
$L_{\mathrm{ms}}$	1120	$\mathrm{mH}$
$L_{\mathrm{mS}}$	1471	$\mathrm{mH}$
J	$488\times {10}^{-6}$	$\mathrm{kg}·{\mathrm{m}}^2$
F	$10\times {10}^{-6}$	$\mathrm{N}·\mathrm{m}·\mathrm{s}$
$p_{\mathrm{p}}$	1	−
$N_{\mathrm{s}}/N_{\mathrm{S}}$	$1.6$	−

.

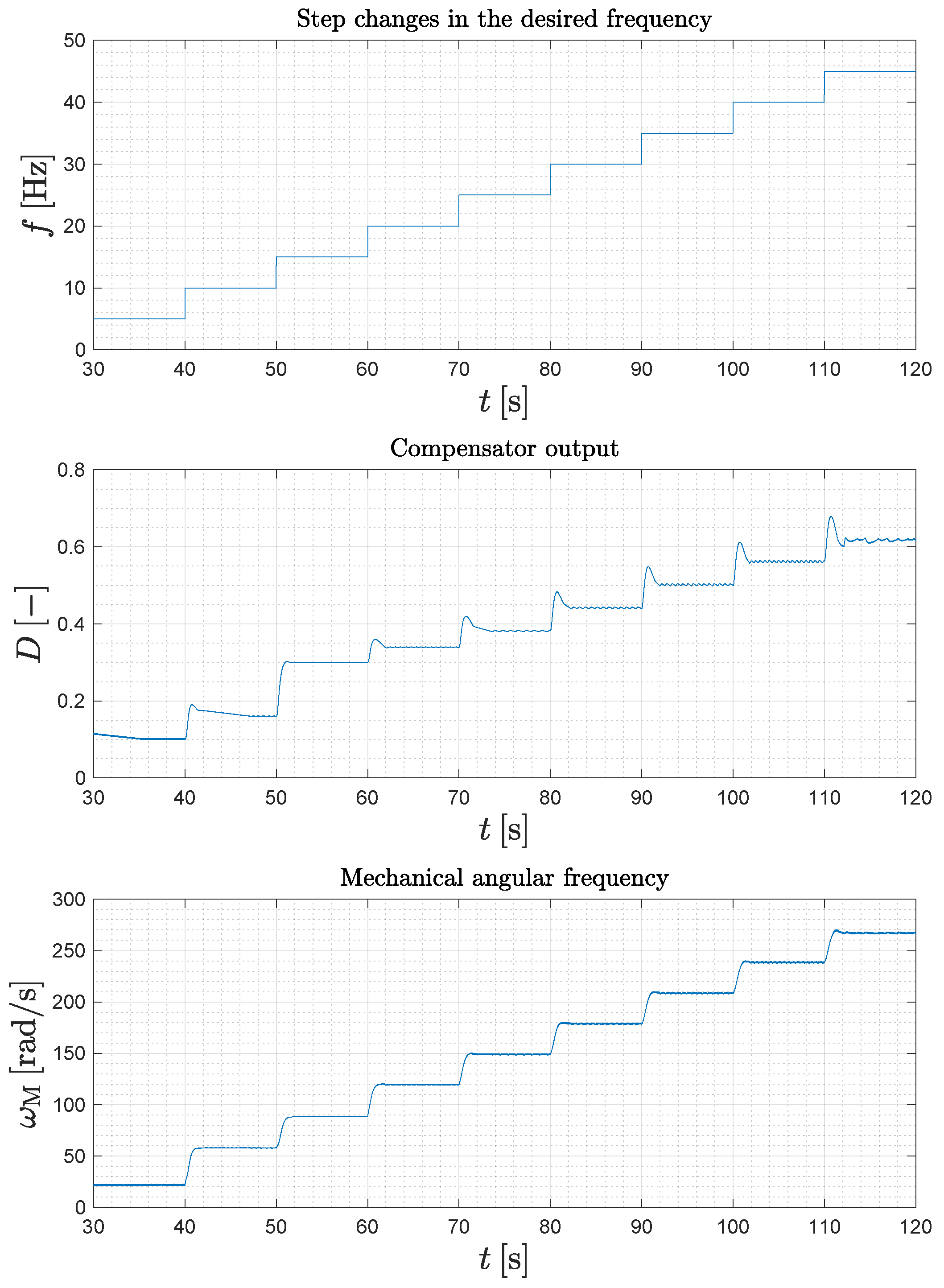
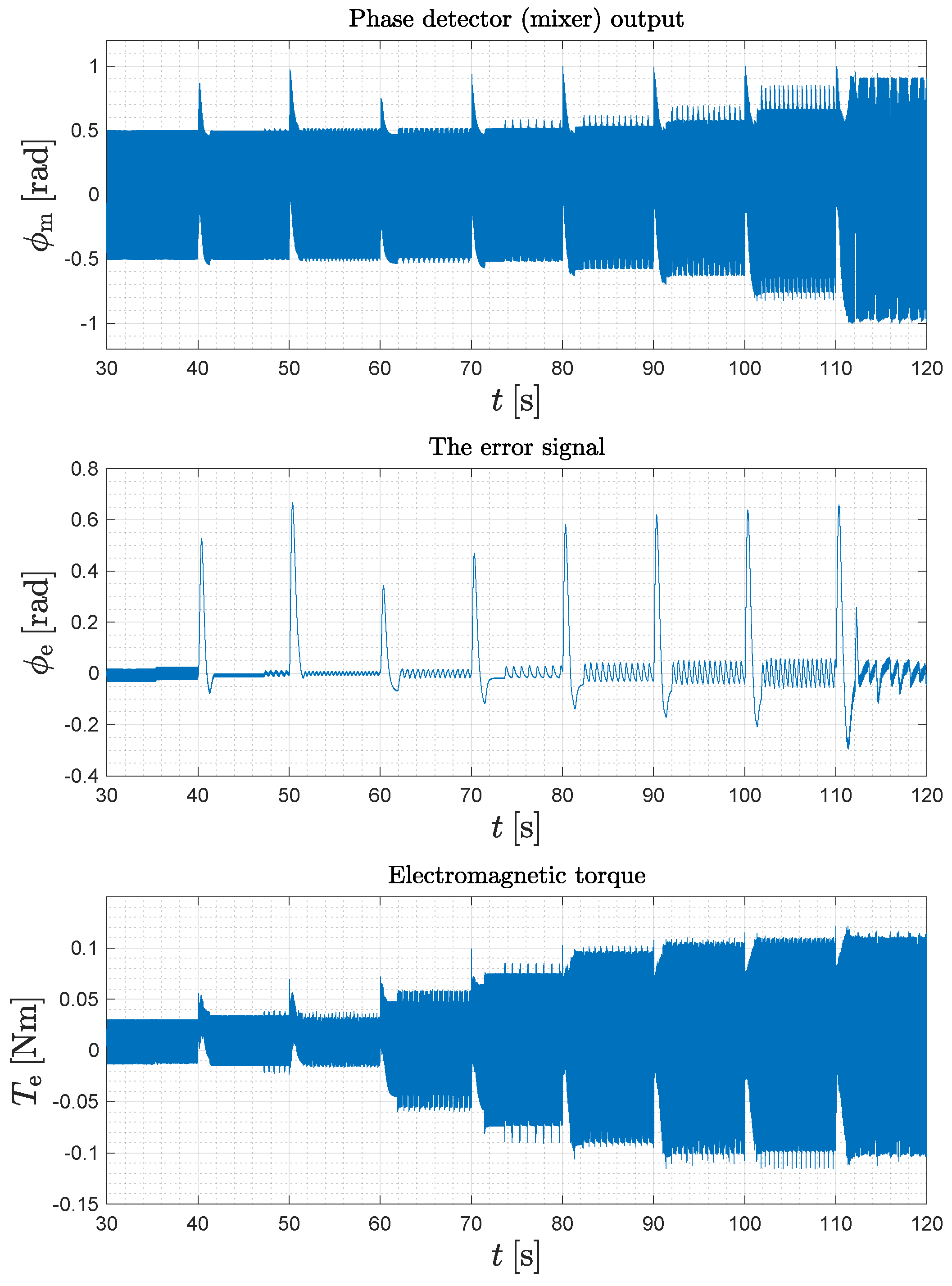
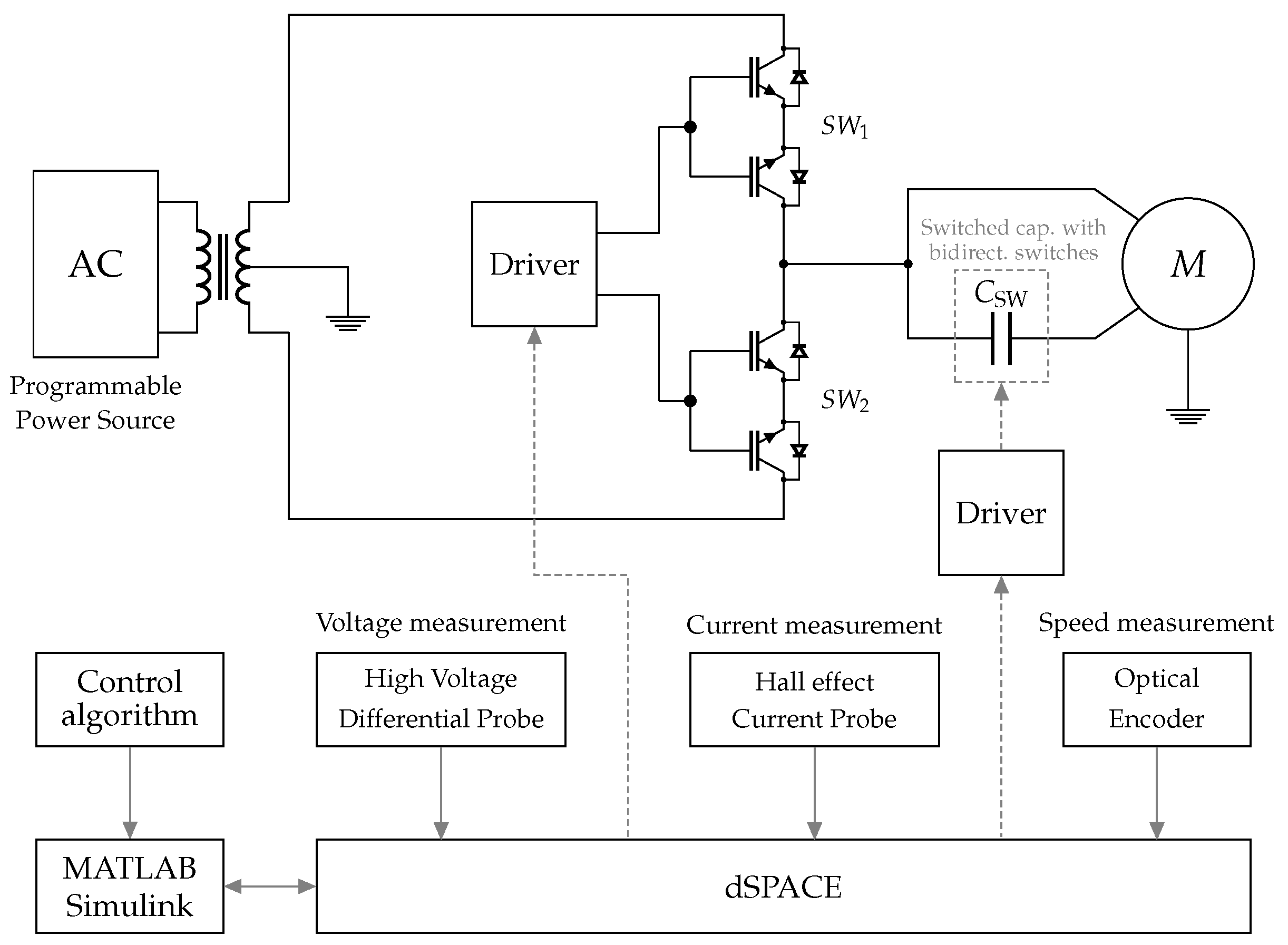
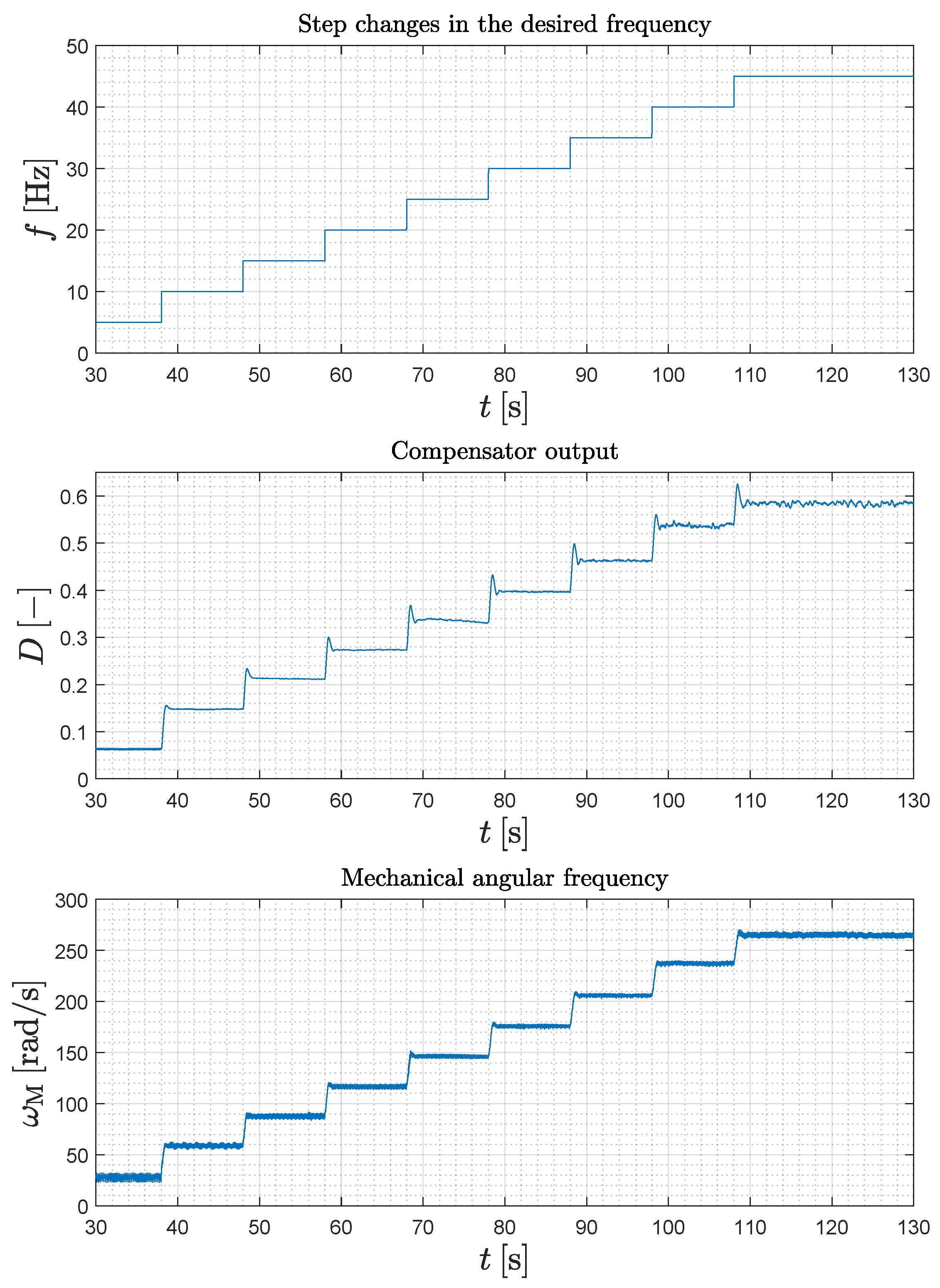
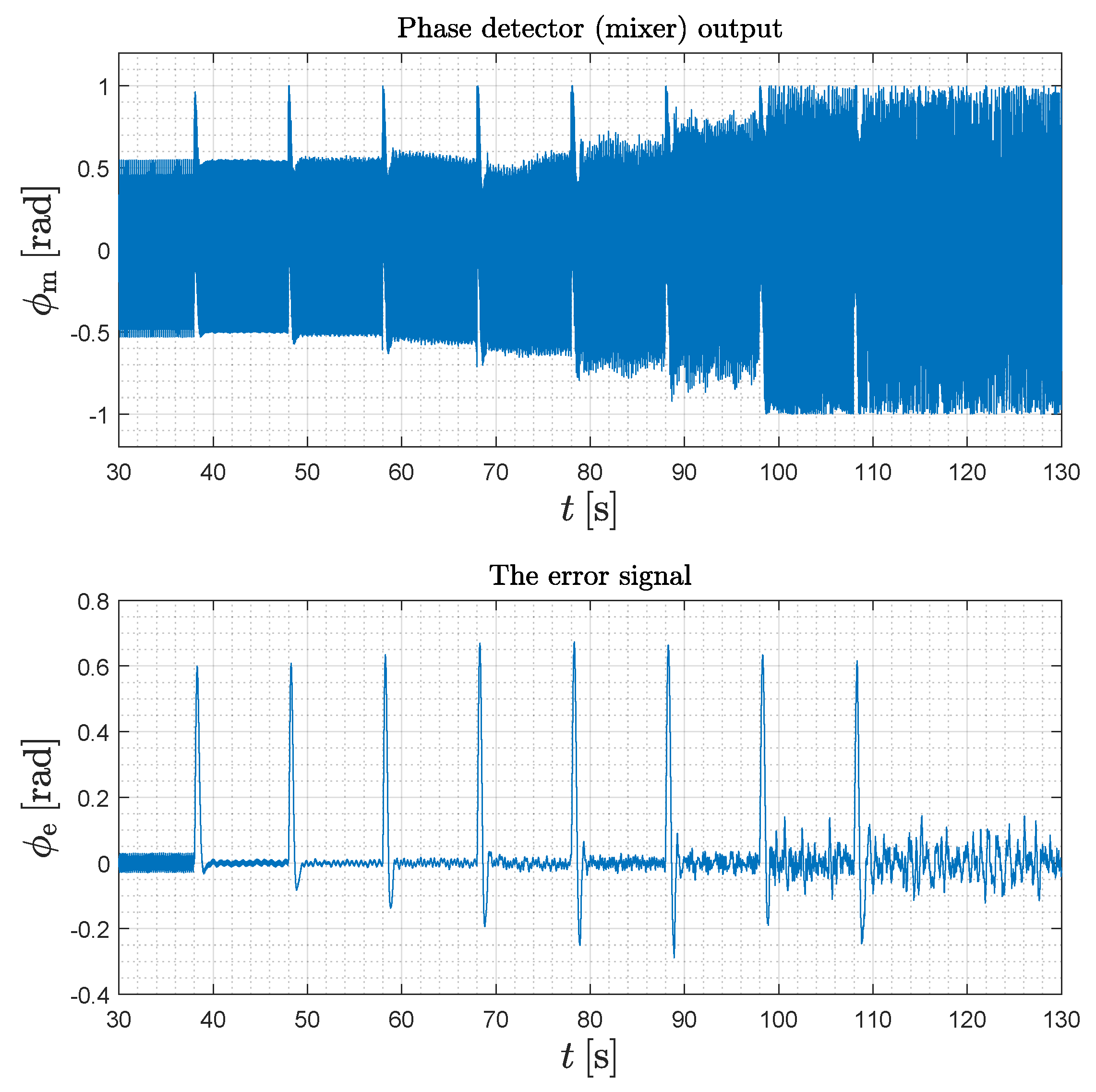
5. Experimental Verification and Measurement

Experimental verification was done with the help of dSPACE hardware interface. The connection with a physical matrix converter and induction motor can be seen in the block scheme in Figure 23. Hall effect current probes with amplifier where used for current measurement and differential voltage probes for voltage measurement. The current and voltage probes were connected to the analog input of dSPACE hardware. The digital outputs of dSPACE were used as the control outputs for the switched capacitors current phase control and hysteresis current control and connected to the transistor drivers. Emitter connected IGBT transistors were used as bidirectional switches for the single-leg matrix converter output and for the switched capacitors. The complete real-time control and measurement were done thru the dSPACE hardware and MATLAB/Simulink, ControlDesk software. The control algorithms were set up in the MATLAB/Simulink environment, and after compilation used in dSPACE. The measured data were saved and then plotted in MATLAB. The calculation time step of dSPACE was $T_{\mathrm{s}}=2\times {10}^{-5}\mathrm{s}$. The calculation time step affects the hysteresis band, that is the reason that the current ripple is higher in real measurement than in the simulation. The experimental results are shown in Figure 24, Figure 25 and Figure 26.

6. Conclusions

This paper brings analysis, modeling, computer simulation, and experimental verification of an enhanced one-leg two-phase matrix converter by a switched capacitor supplied by a symmetrical two-phase network with a neutral point. One of the main contributions is the combined control of the auxiliary phase advancing with 90 degrees phase shift under the entire range of the load operation. Against works with single-leg VSI converters (e.g., [1,2,3]), this paper also completes the topology by switched capacitors controlled to obtain quadrature current for the two-phase output.

Two new methods for controlling the phase shift with the auxiliary phase capacitor have been developed. The first method uses the open-loop control where the phase shift is controlled with a calculated value of capacitance for known parameters of the load (resistance and inductance) and the frequency. The value of capacitance is then set in the switched capacitor. The second method uses a negative feedback loop, where the phase shift automatically tunes to 90 degrees. Improved design of the switching capacitor has also been done with the use of the averaging method to get precise values of the switched capacitance.

Regarding electromagnetic interfacing and compatibility, the solving of those is a demanding problematic [21,22], and was not the subject of this article. Supposed applications of this investigated type of MxC converter are in the field of supply of two-phase induction motors for, e.g., pumps, compressors, etc. in a resident environment. A measurement of electromagnetic interference (EMI)/electromagnetic compatibility (EMC) is important for the prototype version of the converter. We are preparing the infrastructure for such a measurement on real prototype completed by EMI filter at the EMI/EMC chamber in the near future.

The simulations have been done in the MATLAB/Simulink environment. Due to simplification, a passive RL load and harmonic voltage source were first used for the analysis, modeling, and simulation with the switched capacitor. However, we realize that in a real situation is the switched capacitor used with a matrix converter and an active motoric load. Therefore, the final simulation and experimental verification with dSPACE are done with the matrix converter and induction motor as the active load.

The derived control methods with the switched capacitor can also be used with a different type of power converter such as the single-leg two-phase voltage source inverter.

References