Prediction of the Maximum Erosion Rate of Gas–Solid Two-Phase Flow Pipelines
Abstract
:1. Introduction
2. Gas–Solid Two-Phase Pipeline Erosion Model
2.1. Erosion Physical Model
2.2. Fluid Dynamics Theory
2.2.1. Gas Phase Equations
2.2.2. Solid Phase Equations
2.3. Finite Element Model
2.3.1. Finite Element Model and Grid Division
2.3.2. Boundary Conditions
2.3.3. Numerical Calculation
2.4. Erosion Rate Calculation Method
2.5. Analysis of Grid Independence
2.6. Model Validation
3. Simulation Results and Discussions
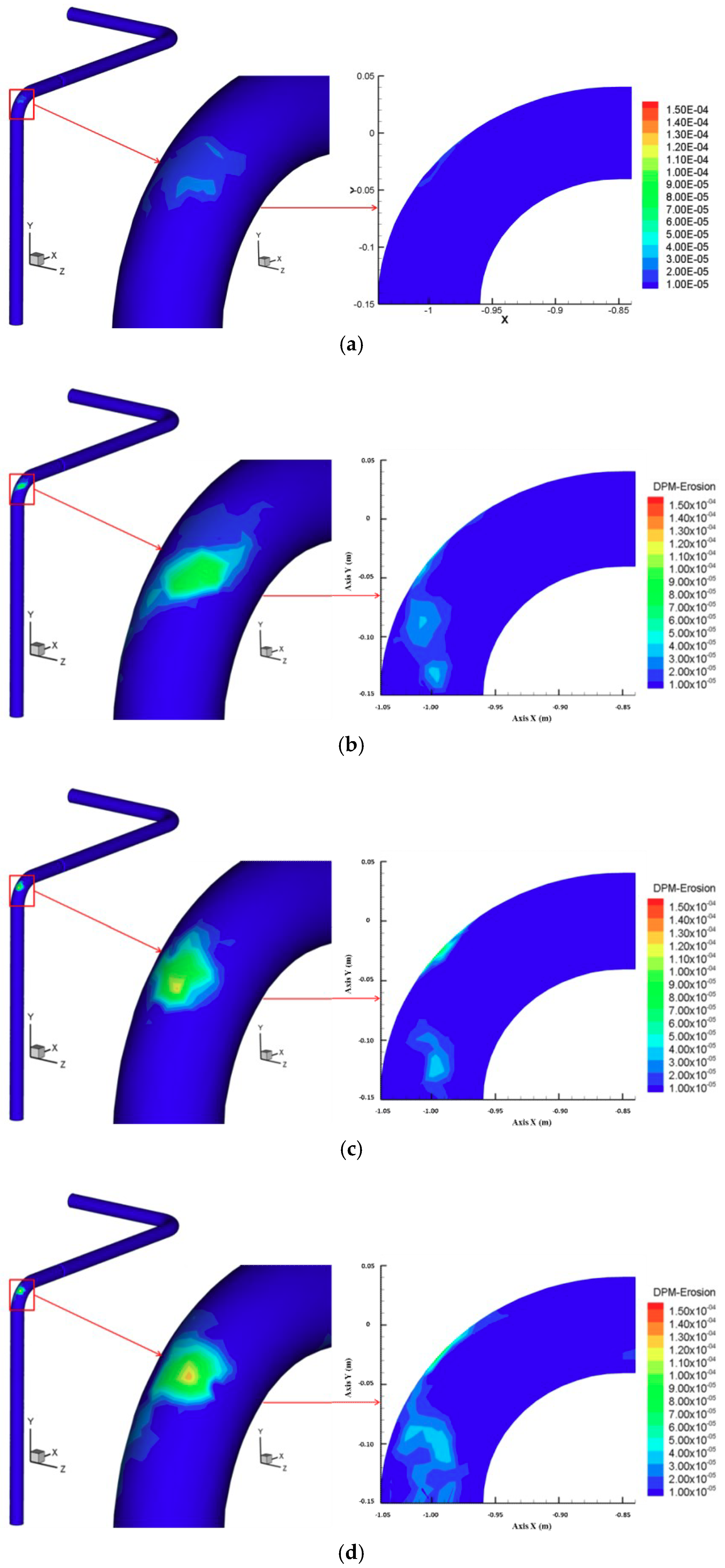
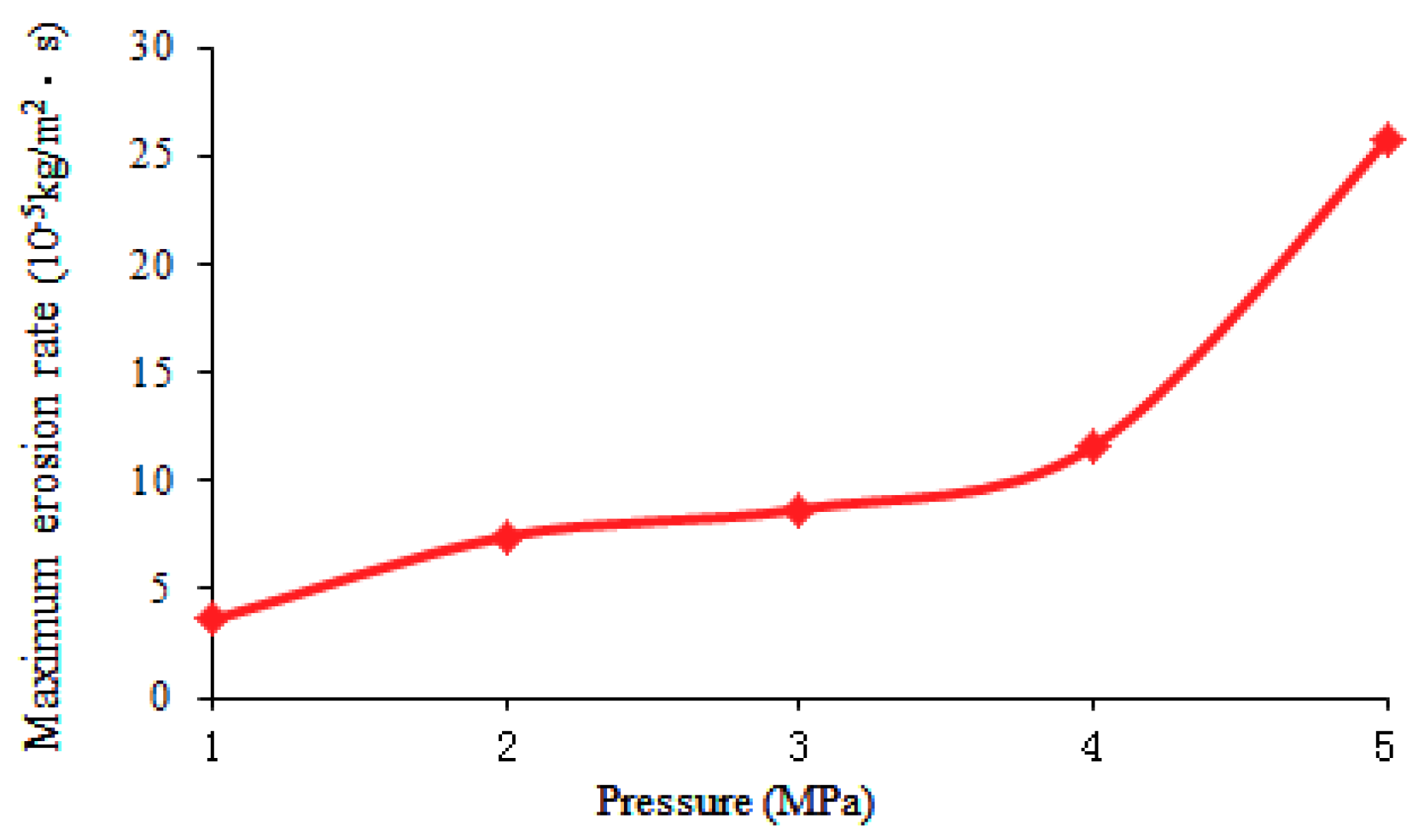
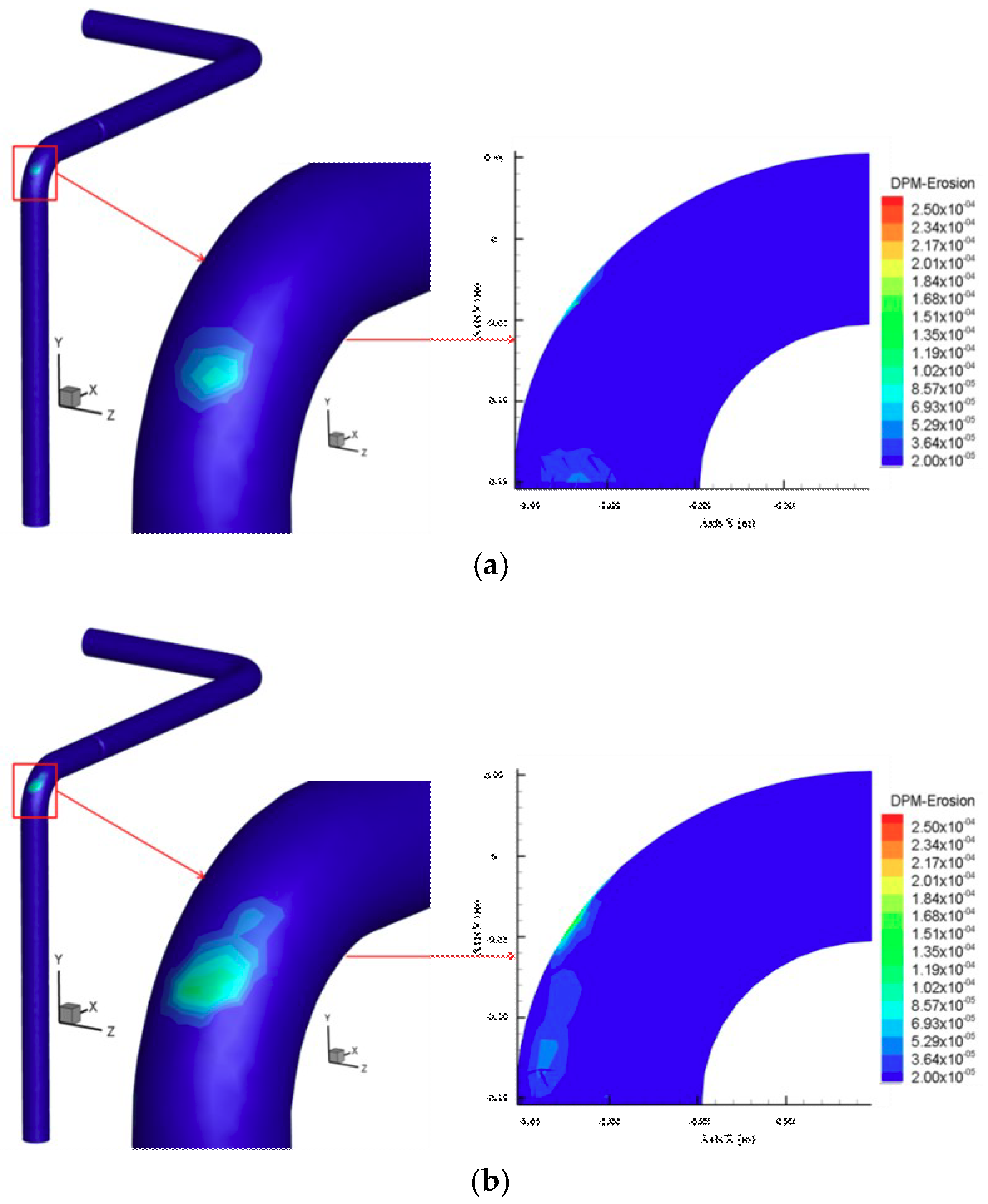
3.1. Influence of Pressure
3.2. Influence of Solid Content
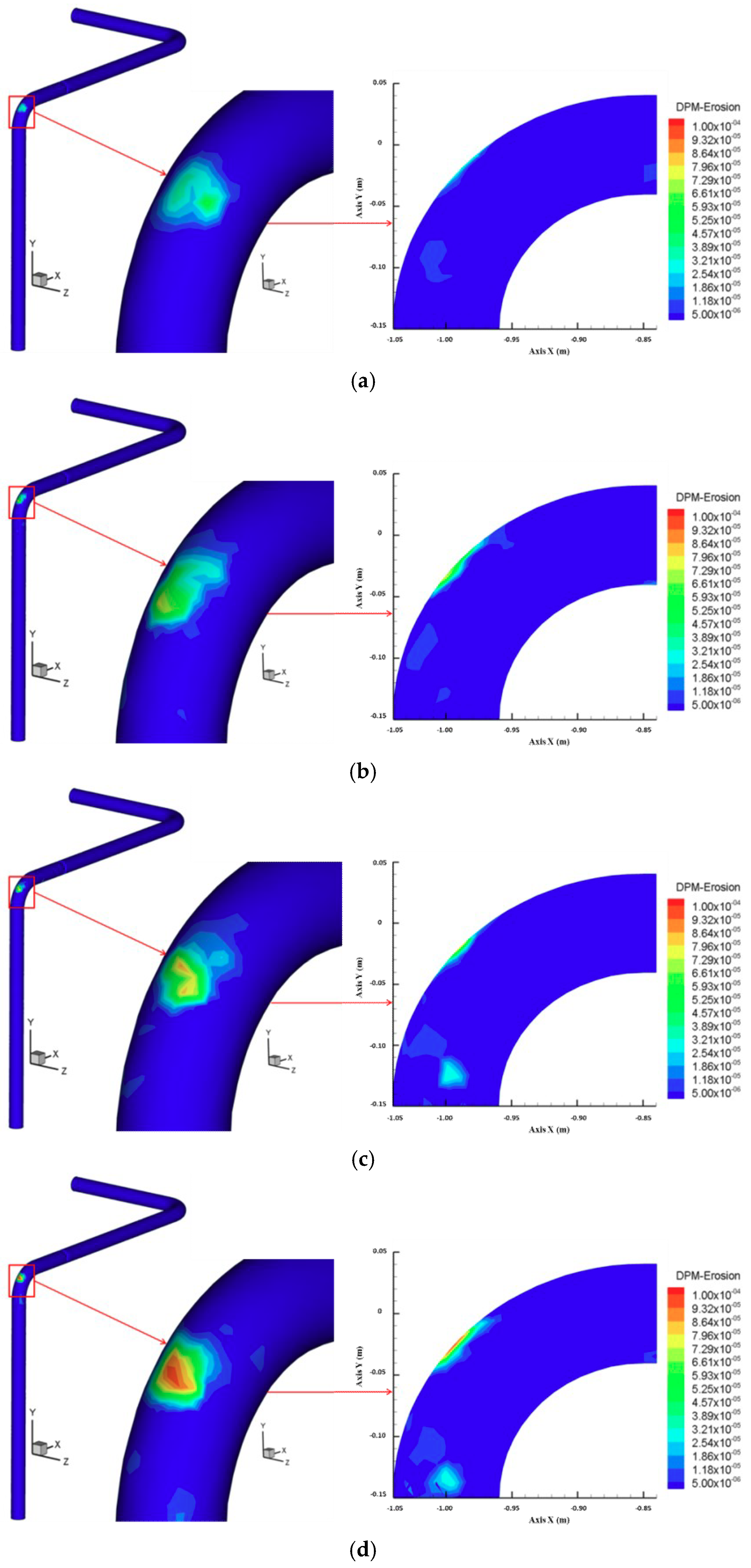
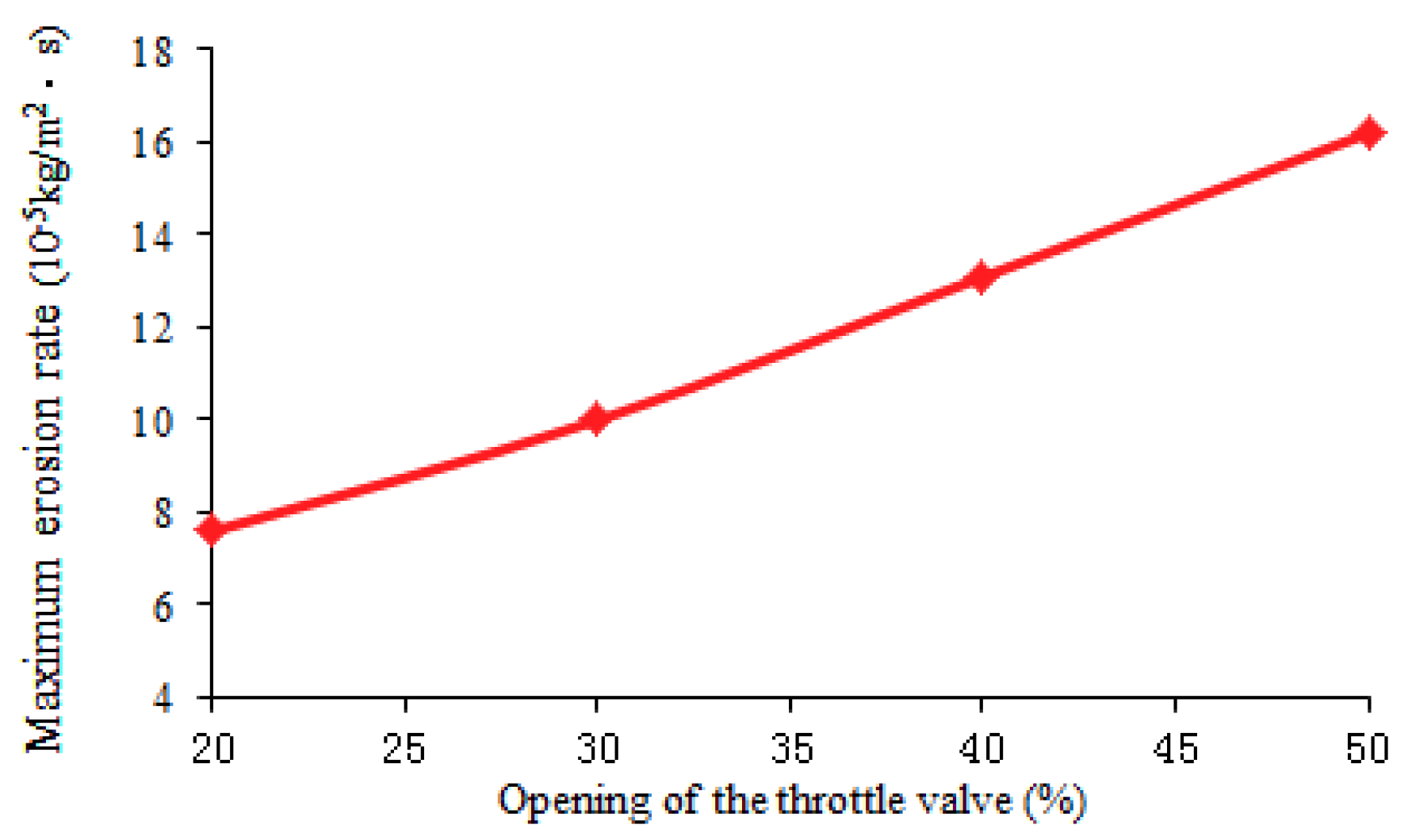
3.3. Influence of the Throttle Valve Opening
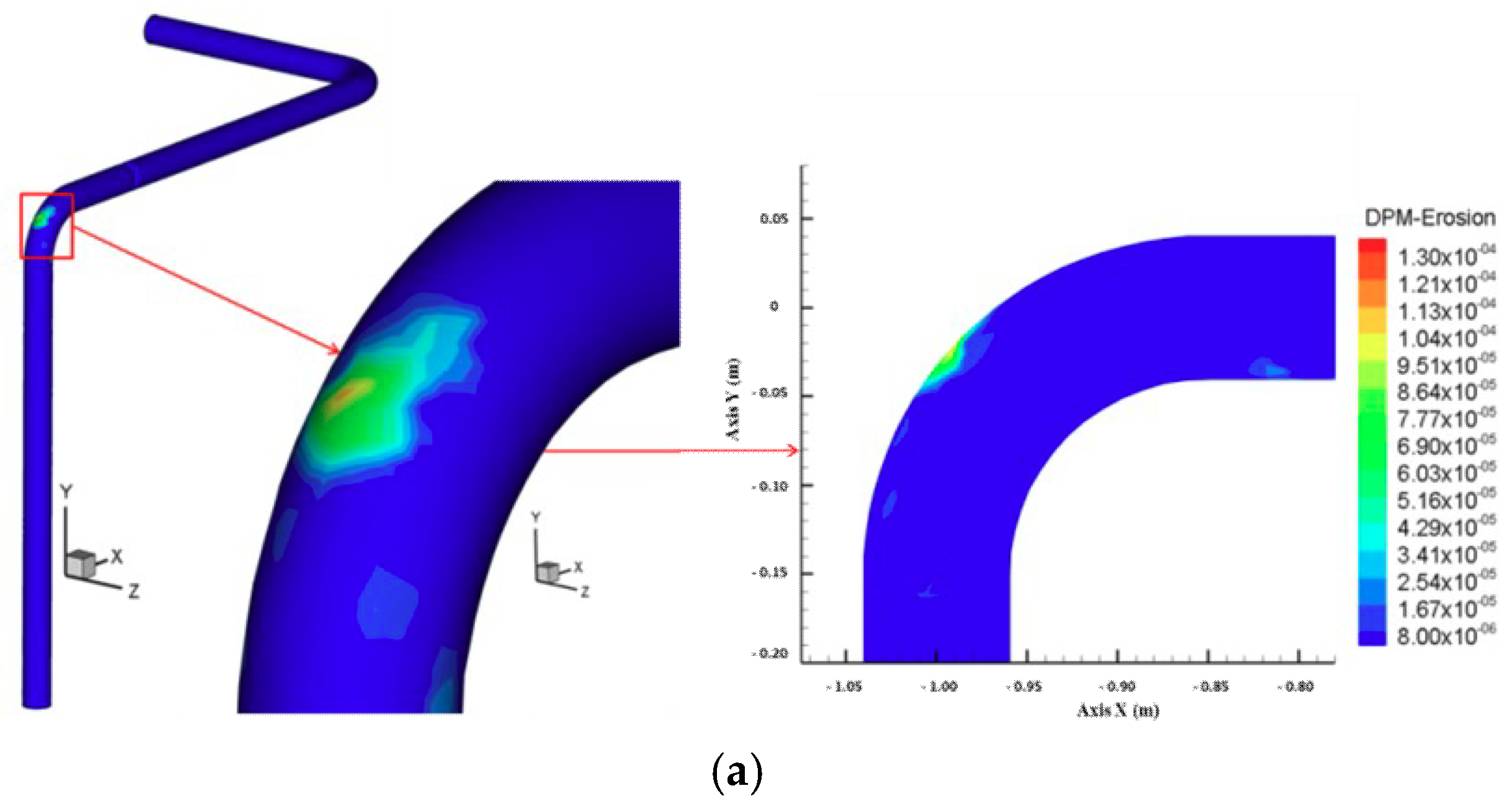
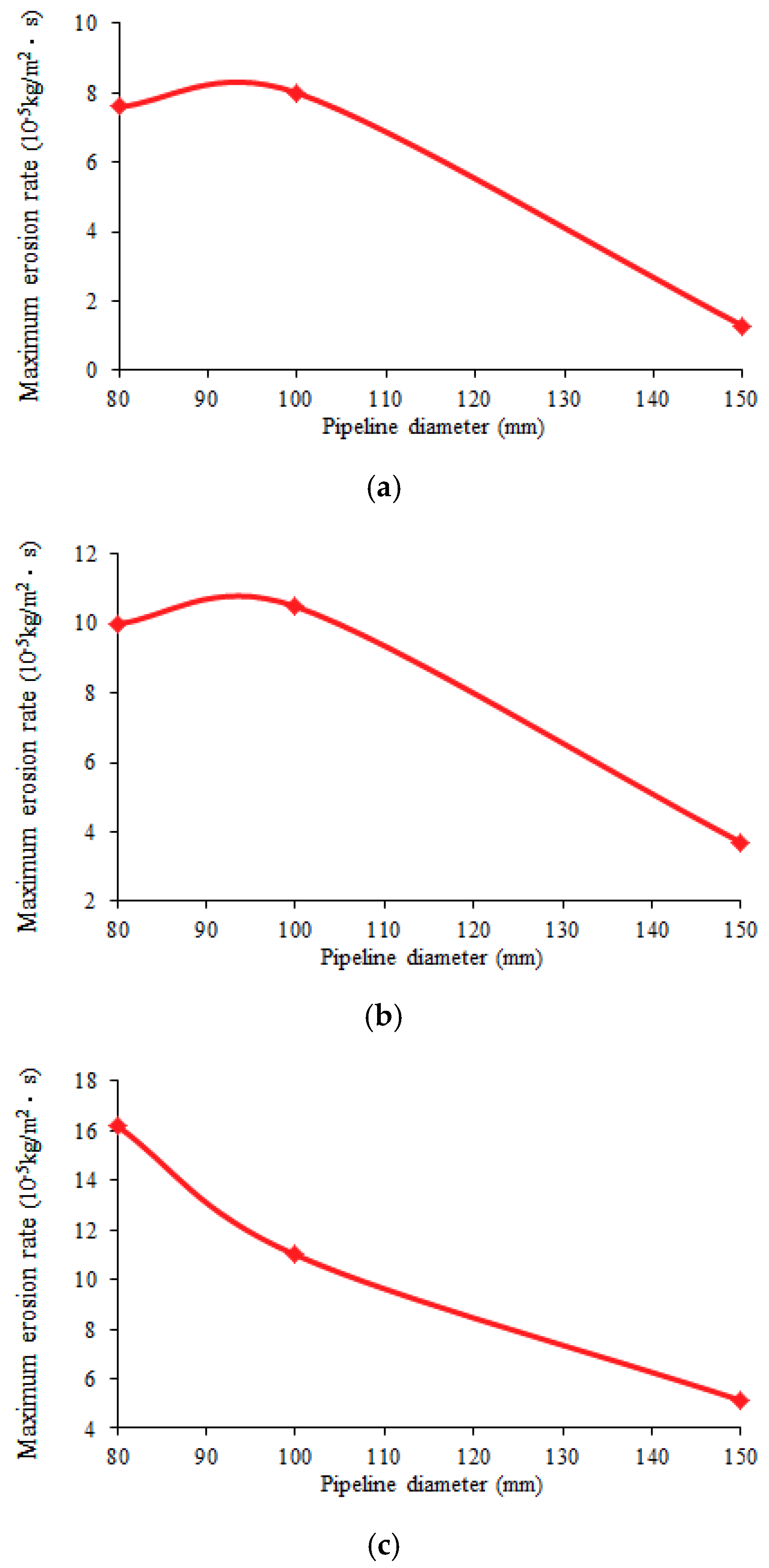
3.4. Influence of Pipe Diameter
4. Prediction of Maximum Erosion Rate
4.1. Prediction Equation for the Maximum Erosion Rate
4.2. Verification of the Maximum Erosion Rate Prediction Equation
5. Conclusions
- (1)
- The gas–solid two-phase flow pipe erosion finite element model established in this paper was validated combining with field test data. Verification results show that the absolute percentage error in the maximum erosion rate between the model results and the test datum is ≤10.75%.
- (2)
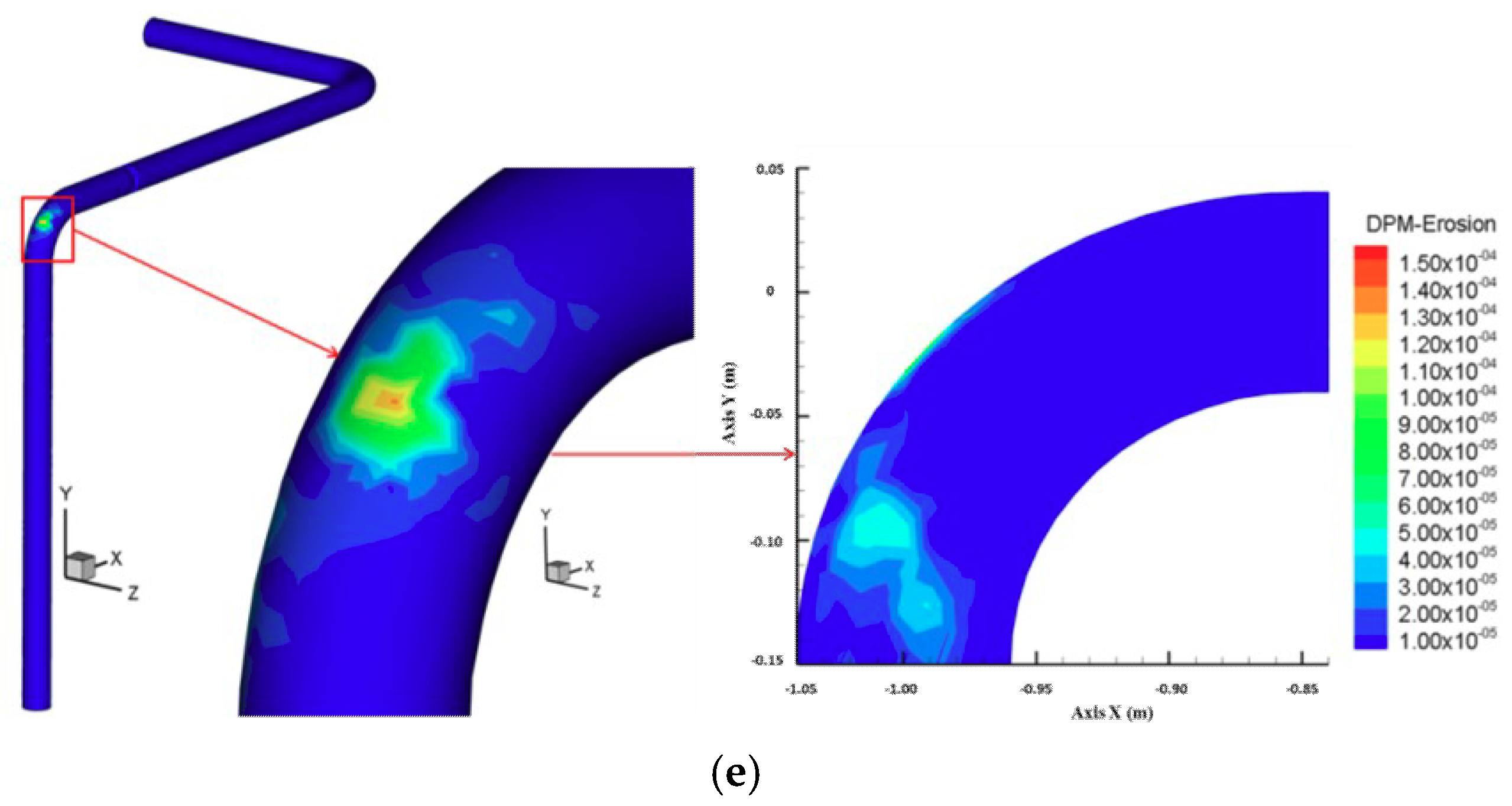
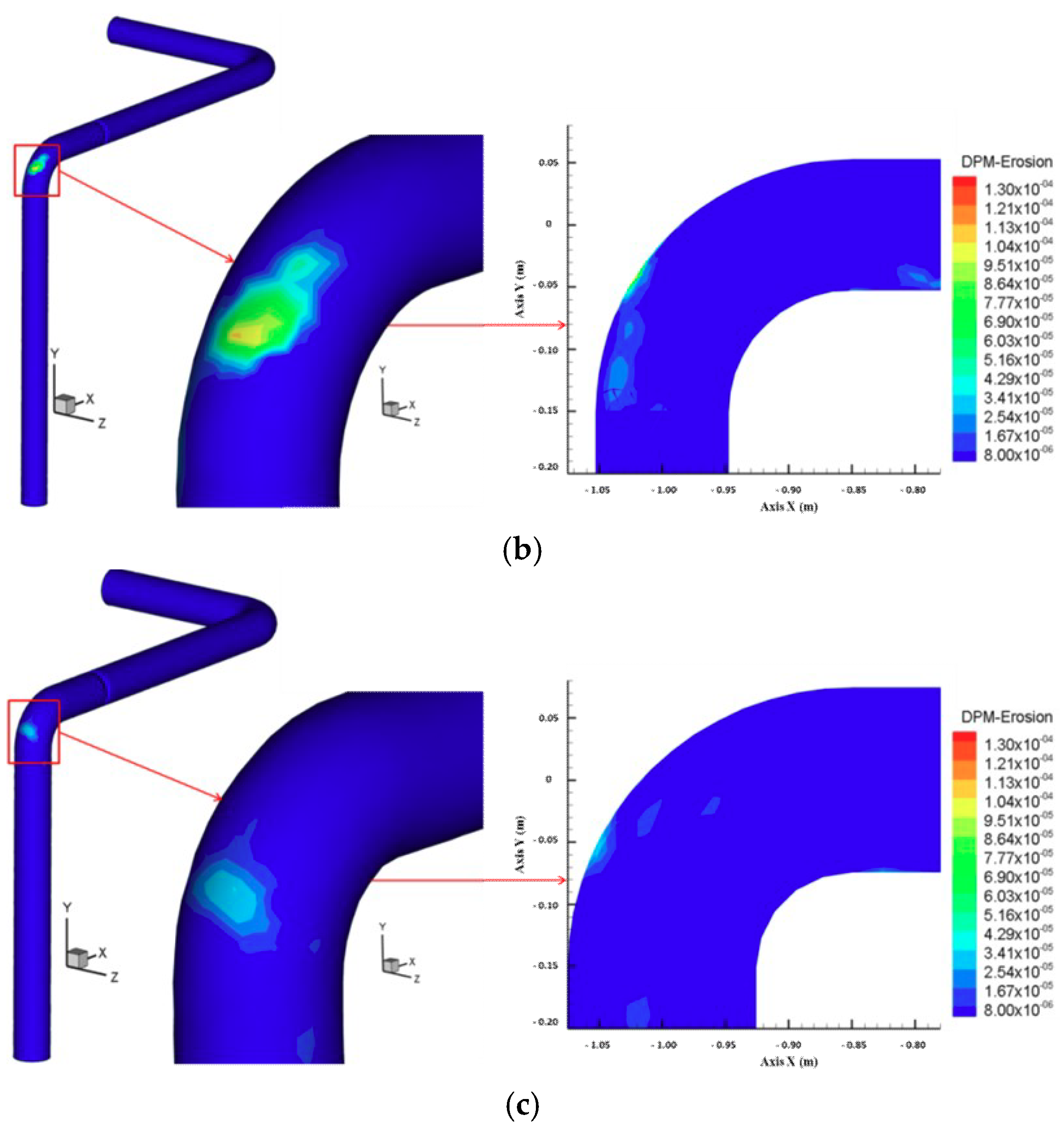
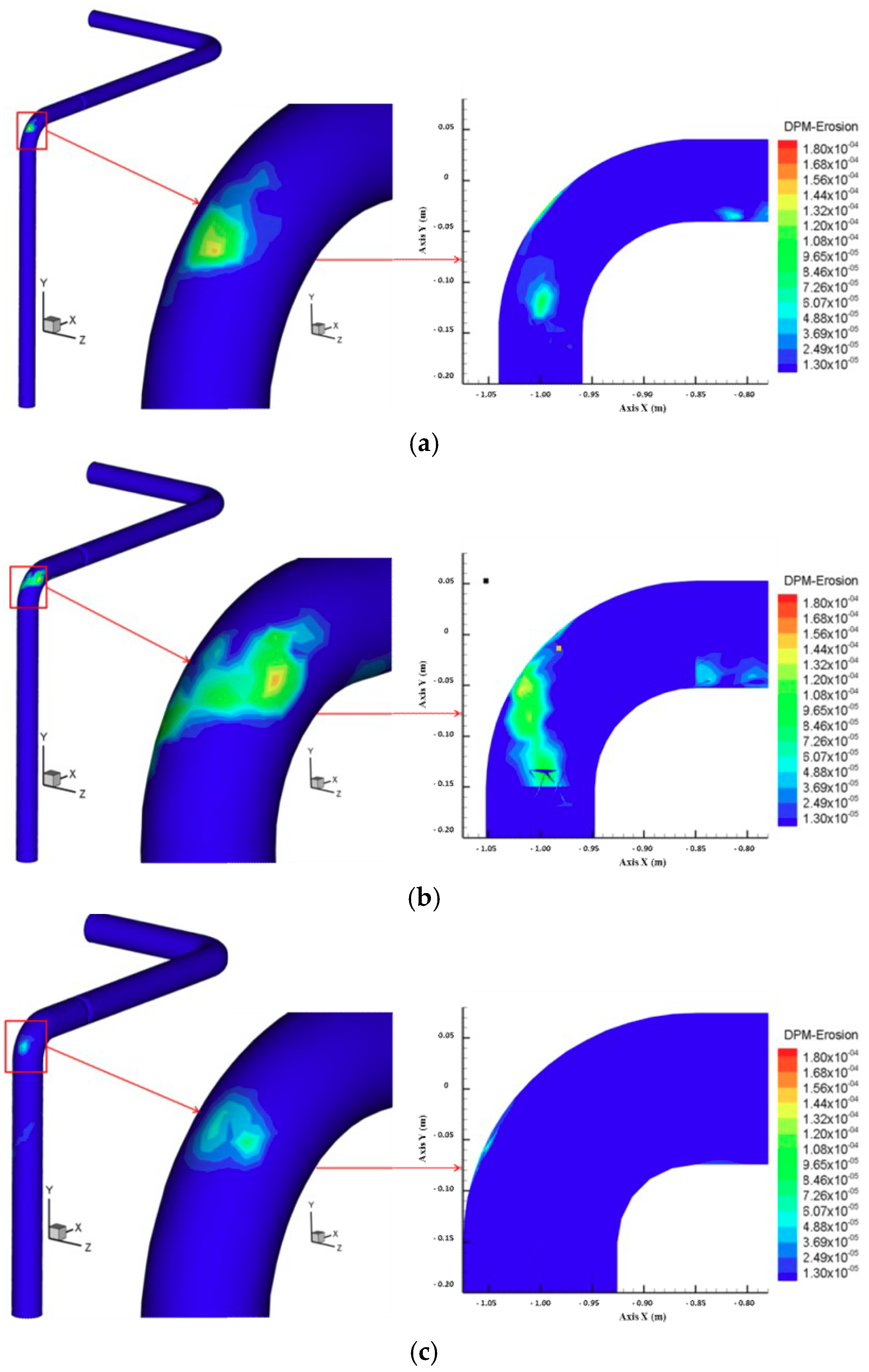
- When the solid emission force is coming from the real-time operational pressure of the equipment and the emission rate is controlled by adjusting the opening of the throttle valve while the brake valve is fully open, the outer cambered surface of the bend after the throttle valve is the most serious erosion area for gas–solid two-phase flow pipeline in a gas transmission station.
- (3)
- When the solid emission force is coming from the real-time operational pressure of the equipment and the emission rate is controlled by adjusting the opening of the throttle valve while the brake valve is fully open, the maximum erosion rate increases with increasing pressure, solid content, and opening of the throttle valve, but, along with the change in the pipe diameter, the maximum erosion rate increases at first and then decreases with increasing pipe diameter for throttle valve openings of 20% and 30%, and it decreases with increasing pipe diameter for a throttle valve opening of 50%.
- (4)
- The maximum erosion rate prediction equation, a function of four parameters (pressure, solid content, opening of the throttle valve, and pipe diameter), yields an absolute percentage error with the field test datum of ≤11.11%. The equation can be effectively used to improve the accuracy of predicting the gas–solid two-phase flow pipeline erosion rate in a gas transmission station.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Original Testing Data for Field K
| No. | Wall Thickness (mm) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| F-1 | 4.584 | 4.675 | 4.820 | / | / | / | 4.823 | 4.678 |
| F-2 | 4.623 | 4.676 | 4.817 | / | / | / | 4.818 | 4.673 |
| F-3 | 4.619 | 4.677 | 4.816 | / | / | / | 4.814 | 4.675 |
Appendix B. Original Testing Data for Fields A–J
| No. | Wall Thickness (mm) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| A | 4.14 | 4.66 | 4.81 | / | / | / | 4.84 | 4.67 |
| B | 4.98 | 5.84 | 6.05 | / | / | / | 6.1 | 5.86 |
| C | 5.92 | 6.3 | 6.42 | / | / | / | 6.46 | 6.36 |
| D | 4.49 | 4.65 | 4.85 | / | / | / | 4.86 | 4.62 |
| E | 5.68 | 5.88 | 6.11 | / | / | / | 6.16 | 5.94 |
| F | 6.06 | 6.16 | 6.33 | / | / | / | 6.30 | 6.17 |
| No. | Wall Thickness (mm) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| G | 4.08 | 4.68 | 4.80 | / | / | / | 4.81 | 4.66 |
| H | 5.58 | 5.86 | 6.07 | / | / | / | 6.14 | 5.87 |
| I | 5.90 | 6.31 | 6.41 | / | / | / | 6.45 | 6.37 |
| J | 4.44 | 4.67 | 4.83 | / | / | / | 4.85 | 4.65 |
References
- Ying, H. The solution of oil and gas two phase flow pipeline internal corrosion rate prediction model. J. Oil Gas Technol. 2009, 31, 364–366. [Google Scholar]
- Li, L.; Ji, Z.; Xu, Q.; Xiong, Z.; Li, F.; Kan, G. A novel on-line detector for solid particles in natural gas pipelines under high pressure: A case study. Nat. Gas Ind. 2012, 32, 81–84. [Google Scholar]
- Achebo, J.I. Pipeline using the drift flux models based on eulerian continuum equations. In Proceedings of the World Congress on Engineering, London, UK, 1–3 July 2009; Int Assoc Engineers-iaeng, UNIT1, 1-F, 37-39 Hung to Road: Kwun Tong, Hong Kong, China, 2009. [Google Scholar]
- Zhu, H.; Zhao, H.; Pan, Q.; Li, X. Coupling analysis of fluid-structure interaction and flow erosion of Gas–Solid flow in elbow pipe. Adv. Mech. Eng. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Bitter, J.G.A. A study of erosion phenomena. Wear 1963, 6, 5–21. [Google Scholar] [CrossRef]
- Finnie, I. On the velocity dependence of the erosion of ductile metals by solid particles at low angles of incidence. Wear 1978, 48, 181–190. [Google Scholar] [CrossRef]
- Levy, A. Solid Particle Erosion and Erosion-Corrosion of Materials; ASM International: Material Park, OH, USA, 1995. [Google Scholar]
- Tilly, G.P. A two stage mechanism of ductile erosion. Wear 1973, 23, 87–96. [Google Scholar] [CrossRef]
- Oka, Y.; Okamura, K.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact: Part 1: Effects of impact parameters on a predictive equation. Wear 2005, 259, 95–101. [Google Scholar] [CrossRef]
- Oka, Y.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact: Part 2: Mechanical properties of materials directly associated with erosion damage. Wear 2005, 259, 102–109. [Google Scholar] [CrossRef]
- Nan, L. Research of Effect of Particle Properties and Flow Field on Erosion in Gas Pipelines. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2017. [Google Scholar]
- API Recommended Practice 14E. Recommended Practice for Design and Installation of Offshore Production Platform Piping Systems; American Petroleum Institute: Washington, DC, USA, 2007. [Google Scholar]
- Desale, G.R.; Gandhi, B.K.; Jain, S.C. Particle size effects on the slurry erosion of aluminum alloy (AA 6063). Wear 2009, 266, 1066–1071. [Google Scholar] [CrossRef]
- Ou, G.; Xu, G.; Zhu, Z.; Yang, J.; Wang, Y. Fluid-structure interaction mechanism and numerical simulation of elbow erosion failure. J. Mech. Eng. 2009, 45, 119–124. [Google Scholar] [CrossRef]
- Ou, G.; Qiu, J.; Zhu, Z.; Wang, Y.; Xu, G. Fluid-structure interactional numerical simulation of erosion-corrosion failure of reducer in multiphase flow. Chin. J. Theor. Appl. Mech. 2010, 42, 197–204. [Google Scholar]
- Lian, Z.; Chen, X.; Lin, T.; Ming, X.; Zheng, J. Study on erosion mechanism of bending joint in blooey line. J. Southwest Pet. Univ. (Sci. Technol. Ed.) 2014, 36, 150–156. [Google Scholar]
- Gnanavelu, A.; Kapur, N.; Neville, A.; Flores, J.F. An integrated methodology for predicting material wear rates due to erosion. Wear 2009, 267, 1935–1944. [Google Scholar] [CrossRef]
- Lester, D.R.; Graham, L.A.; Wu, J. High precision suspension erosion modeling. Wear 2010, 269, 449–457. [Google Scholar] [CrossRef]
- Feng, L.; Wang, J.; Mao, Y.; Zhang, G.; Wang, J. Numerical simulation of liquid-solid erosion in sudden expansion and contraction tube. Acta Petrolei Sinica (Pet. Process. Sect.) 2014, 30, 1080–1085. [Google Scholar]
- Zhang, S.; Cao, H.; Liu, Y.; Gao, C. Numerical simulation of liquid-solid two-phase flow and erosion-collision in a syphon. J. Hebei Univ. Technol. 2008, 37, 48–54. [Google Scholar]
- Li, G.; Wang, Y.; Sun, H.; Kang, L.; Wang, Y.; He, R. Numerical simulation on solid particle erosion of solid-liquid two-phase fluid in flow controller. Acta Petrolei Sinica 2009, 30, 145–148. [Google Scholar]
- Ran, Y. Study on Structure Optimization of Two Cluster Hydraulic Injector Based on Erosion Analysis. Master’s Thesis, Xi’an Petroleum University, Xi’an, China, 2017. [Google Scholar]
- Qian, D. Study on Erosion Rule of Panyu 35-2 Submarine Gas Pipeline. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2015. [Google Scholar]
- Jia, Q. Erosion Failure Numerical Simulation of Sediment Delivery Pipeline in Gas Drilling. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2013. [Google Scholar]



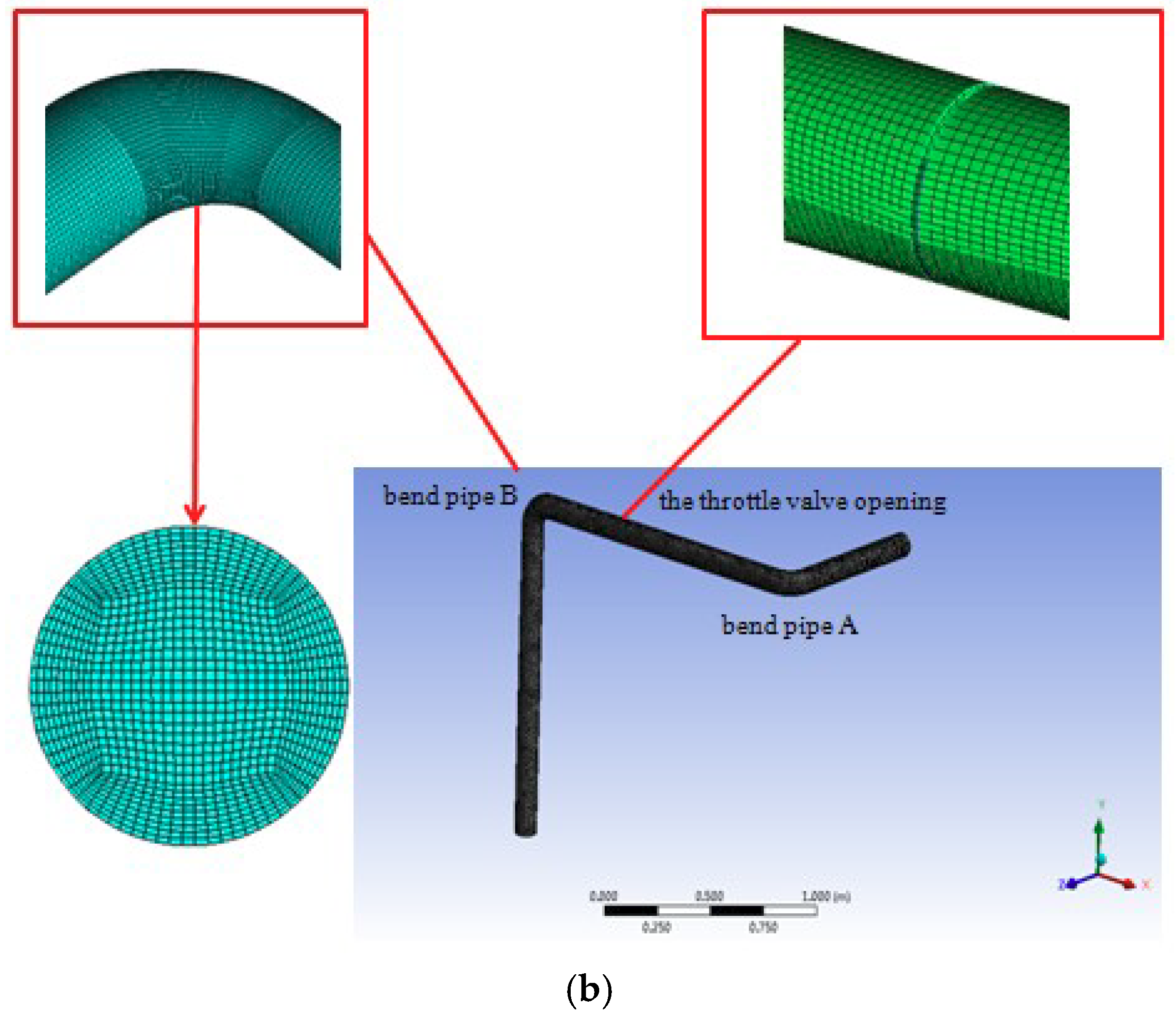






| L1 (cm) | L2 (cm) | L3 (cm) | L4 (cm) | L5 (cm) |
|---|---|---|---|---|
| 80 | 40 | 80 | 40 | 140 |
| No. | Max. Erosion Rate (mm/year) | Error (%) | Remarks | |
|---|---|---|---|---|
| Test Data | Calculation Results | |||
| F-1 | 0.1650 | 0.1541 | 6.61 | In the initial operation stage, openings of 20%, pressure of 3.77 MPa, solid content of 2.63 kg, blowdown period of 8min, blowdown operation of 48 times, the most serious erosion area occurred at the outer cambered surface of bend after throttle valve |
| F-2 | 0.1230 | 0.1346 | −9.43 | In the middle operation stage, openings of 30%, pressure of 3.75 MPa, solid content of 2.2 kg, blowdown period of 6.5 min, blowdown operation of 32 times, the most serious erosion area occurred at the outer cambered surface of bend after throttle valve |
| F-3 | 0.1265 | 0.1401 | −10.75 | In the middle operation stage, openings of 50%, pressure of 3.74 MPa, solid content of 2.0 kg, blowdown period of 5.7 min, blowdown operation of 32 times, the most serious erosion area occurred at the outer cambered surface of bend after throttle valve |
| Pipe Diameter | a | b | c | d |
|---|---|---|---|---|
| DN80 | 0.0127 | −0.0087 | 0.0019 | 9 × 10−6 |
| DN100 | 0.0159 | −0.0101 | 0.0018 | 3 × 10−5 |
| DN150 | 0.002 | −0.0015 | 0.0004 | 1 × 10−6 |
| Field | Test Results (mm) | Calculation Results (mm) | Error (%) | Remarks |
|---|---|---|---|---|
| A | 0.61 | 0.59 | −3.28 | operation for 8 years, solid content of 3 kg, particle size of 20 μm, openings of 20%, DN80, pressure of 2.5 MPa |
| B | 0.98 | 1.00 | 2.04 | operation for 7 years, solid content of 4 kg, particle size of 20 μm, openings of 20%, DN100, pressure of 3.5 MPa |
| C | 0.47 | 0.43 | −8.51 | operation for 14 years, solid content of 2.5 kg, particle size of 20 μm, openings of 30%, DN150, pressure of 3.5 MPa |
| D | 0.26 | 0.27 | 3.85 | operation for 5 years, solid content of 1 kg, particle size of 20 μm, openings of 35%, DN80, pressure of 1.6 MPa |
| E | 0.34 | 0.36 | 5.88 | operation for 11 years, solid content of 1 kg, particle size of 20 μm, openings of 20%, DN100, pressure of 2.5 MPa |
| F | 0.18 | 0.20 | 11.11 | operation for 10 years, solid content of 4.7 kg, particle size of 20 μm, openings of 20%, DN150, pressure of 2 MPa |
| Field | Test Results (mm) | Calculation Results (mm) | Error (%) | Remarks |
|---|---|---|---|---|
| G | 0.66 | 0.64 | −3.03 | operation for 8 years, solid content of 3 kg, particle size of 20 μm, openings of 20%, DN80, pressure of 3 MPa |
| H | 0.41 | 0.43 | 4.88 | operation for 3 years, solid content of 4 kg, particle size of 20 μm, openings of 20%, DN100, pressure of 3.5 MPa |
| I | 0.48 | 0.53 | 10.42 | operation for 13 years, solid content of 3.5 kg, particle size of 20 μm, openings of 30%, DN150, pressure of 3 MPa |
| J | 0.31 | 0.33 | 6.45 | operation for 6 years, solid content of 1 kg, particle size of 20 μm, openings of 40%, DN80, pressure of 1 MPa |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Lian, Z.; Hu, J.; Luo, M. Prediction of the Maximum Erosion Rate of Gas–Solid Two-Phase Flow Pipelines. Energies 2018, 11, 2773. https://doi.org/10.3390/en11102773
Xu J, Lian Z, Hu J, Luo M. Prediction of the Maximum Erosion Rate of Gas–Solid Two-Phase Flow Pipelines. Energies. 2018; 11(10):2773. https://doi.org/10.3390/en11102773
Chicago/Turabian StyleXu, Jingyuan, Zhanghua Lian, Jian Hu, and Min Luo. 2018. "Prediction of the Maximum Erosion Rate of Gas–Solid Two-Phase Flow Pipelines" Energies 11, no. 10: 2773. https://doi.org/10.3390/en11102773
APA StyleXu, J., Lian, Z., Hu, J., & Luo, M. (2018). Prediction of the Maximum Erosion Rate of Gas–Solid Two-Phase Flow Pipelines. Energies, 11(10), 2773. https://doi.org/10.3390/en11102773




