1. Introduction
Internationally coordinated efforts to set renewable energy targets have enhanced interest in the marine renewable energy (MRE) sector [
1,
2]. Tidal energy converter (TEC) technologies that transfer kinetic energy of tidal stream currents into electrical power are moving from the testing and feasibility stage [
2] to commercial scale array deployments. Notably, NOVA Innovation have three 100 kW devices deployed in Shetland, and Meygen have four 1.5 MW devices in the Pentland Firth, UK. Prior to large-scale development, it is crucial that we understand the physical feedbacks of energy extraction with the resource itself and the surrounding environment (e.g., [
3,
4]). Ocean models can aid this process, although uncertainties in the way that energy extraction is represented in models should be robustly quantified and minimized.
A TEC array contains multiple turbines that operate independently based on the local flow passing each turbine rotor. A technique to reduce feedbacks between devices (i.e., increase performance) is to adopt a staggered array design. Common array configurations (e.g., [
5]) lack any technical basis and fail to account for device and site-specific features, such as intra-array wake effects and misalignment to the flow [
6,
7]. Improved understanding of such feedbacks and impacts through accurate model simulations could strengthen investor confidence in the sector [
1,
8].
Tidal stream energy extraction is often implemented as an enhanced momentum sink or decelerating seabed stress term in coastal modelling studies (e.g., [
4,
9,
10,
11,
12,
13,
14,
15,
16,
17]), and Neill and Hashemi [
18] provided a detailed review of techniques and applications. TECs are commonly parameterized in depth-averaged models as an enhanced seabed frictional force applied over a defined area (e.g., [
13,
19,
20]). As this stress term denotes a decelerating momentum sink, valid results are produced when the drag parameterization is directly related to the total system energy lost, similar in effect to applying spatially varying seabed roughness to account for variations in seabed composition. As drag is implemented as a quadratic function of flow velocity, the area over which the force is applied is crucial, and will influence subsequent flow calculations.
Present guidance regarding resource assessment suggests incorporating energy extraction following resource characterization, where potential installed capacity may exceed 10 MW or extraction is greater than 2% of the available theoretical resource [
21]. Many shelf-scale studies typically use a mesh size in the order of hundreds of meters or kilometers (e.g., [
14]), which would fail to resolve the dynamics of typical individual turbines (<20 m). Industry standard resource assessment (stage 2a) suggests 200–500 m at pre-feasibility stage [
5]. For full-feasibility (stage 2b) and design development (stage 3) assessments, which include device feedbacks, models become more computationally expensive and care must be taken when discretizing to prevent instability [
22]. The inclusion of turbine dynamics enables stage 3 assessment and the prediction of potential impacts based on development size. However, the derivation of enhanced terms for modelling energy extraction must be sufficiently justified [
21].
In situ observations or computational fluid dynamics (CFD) modelling (e.g., [
23]) should inform intra-array feedbacks. Assessments of mid to far-field impacts can only be addressed realistically using a numerical coastal modelling framework. Thus, a staged approach to specification of technique is suggested by the International Electrotechnical Commission (IEC [
21]), involving:
Actual energy captured by TECs requiring consideration of device ‘water to wire’ efficiency factor that accounts for hydrodynamic, mechanical and electrical losses.
Intra-array spacing of devices relative to the plan area of model cells.
Support structure form drag associated with each TEC.
Any associated energy losses in downstream wake mixing and free stream velocity interaction between devices.
The combination of these factors ensures that macro-scale system feedbacks are captured. This enables confident determination of hydrodynamic interaction curves that link inflow velocities to levels of energy extraction and array capacity potential within a system. Simulations of energy extraction that average the enhanced stress term across the seabed area of an entire array fail to capture the intra-array wake effects and misrepresent the power density delivered to each turbine rotor within the array by as much as 21% [
24].
An issue noted by Shives et al. [
25] is that when considering an array-averaging approach versus a device-scale approach, there is difficulty defining the free stream velocity profile applicable to each device. The velocity experienced at the face of the array will differ from that in the lee of the array, where flow retardation over a large area is significant due to the decelerating force. Therefore, wake ‘recovery’, or mixing length, is misrepresented using an array-averaging approach, because energy extraction by a single device will induce a flow wake effect that disturbs the currents available to downstream devices, thus influencing the performance of surrounding devices. This phenomenon is ignored in array-averaging studies and ultimately results in uncertainties in simulations [
7,
26]. Further complications arise due to a lack of availability in validation data for mid to far field wakes from full-scale device arrays; therefore, CFD models may help improve coastal modelling simulations [
27]. The ability to upscale this information to simulate regional scale environmental feedbacks provides essential detailed calibration and validation of methods.
Individual TECs influence the local flow field and adjacent devices as flow velocity reduces immediately in the lee of a turbine, is enhanced at the rotor periphery, and creates a backpressure or thrust effect immediately upstream [
28]. TEC wake velocity reduction is a function of rotor operating state values, such as thrust; therefore, the rate of downstream velocity recovery will depend upon mixing between flow recirculation and the device wake. In unbounded flow, the velocity remains close to that of the incident regime; however, in the presence of bounding surfaces formed by the seabed, free surface and wakes from other devices, a pressure drop forms across each turbine. The fluid will accelerate in the regions of restriction, causing localized velocity increases in accordance with Bernoulli principles [
28].
In this study, we investigate whether coastal models discretized at individual device-scale, sufficiently capture more hydrodynamic feedbacks compared with array-averaged models. To achieve this, the mesh density should, as a minimum, sufficiently resolve each ‘installed’ device area, and resolve the flow in-between devices. This approach requires sensitivity analysis of mesh size and careful consideration of the applied model turbulence closure scheme (TCS). Furthermore, appropriate modification of applied formulae is needed to account for the proportional influence of the device on depth varying flow [
21,
29].
We implement a self-modified energy extraction method, using a depth-averaged coastal model (Telemac-2D) that solves the Shallow Water Equations (SWE). The use of 2D modelling strategies is justified by the IEC [
21]. However, in regions of rapid flow divergence and convergence, where vertical velocities are greatly enhanced, the hydrostatic assumption is no longer valid. The use of 3D models may provide better approximations in these cases, particularly those with higher order turbulence resolving schemes. In either case, authors should report and justify in sufficient detail the derivation of the additional extraction term applied [
21]. The aim here is to ascertain a validated method of energy extraction that improves upon an array-averaged approach in depth-averaged simulations. The usefulness of this 2D model application is tested in anticipation of future work involving coupled wave and sediment dynamics across large spatial and temporal scales that would prove difficult using 3D modelling of arrays at device-scale.
Our objectives are:
To incorporate tidal energy extraction at device scale.
To test the performance of the modelled hydrodynamics.
To compare array-averaging with device-scale results.
To quantify associated uncertainty.
Objectives are achieved by utilizing published empirical scaled turbine tank test and CFD studies to apply a validation of the methodology. We then utilize the validated device-scale approach to implement multiple devices, for various small-scale array configurations and compare this approach with an equivalent array-averaging technique. A determinant error threshold is suggested, beyond which it becomes important to account for intra-array turbine wake dynamics in coastal environmental impact studies caused by device-wake interactions. In doing this, we present a validated approach to shelf-scale turbine array implementation at device-scale. The inclusion of intra-array dynamics improves confidence in hydrodynamic resource assessment. This becomes significant when project feasibility studies scale up from single devices (<3 MW) and small (3–20 MW) or medium (20–50 MW) arrays, to full-scale (>50 MW) commercial array farms.
4. Discussion
Simulated tidal energy extraction at individual device-scale (i.e., representing a typical horizontal axis turbine) is analyzed in a 2D model using an idealized channel domain. Discretization is designed to replicate physical tank test conditions and thus emulate published empirical experimental scaled turbine data for validation. Analysis of centerline velocity deficit and transverse wake profiles are considered. Other modelling studies use similar approaches, for example, Roc et al. [
57] compared simulated results to porous disc analysis. How analogous this method is in replicating actual turbine dynamics is unclear. Our results show that the Telemac
k-Ɛ TCS provides simulated axial velocity deficit profiles with an accuracy ranging from 0.58 to 0.69 (R
2). The subsequent RMSE is 7.16%, 8.28% and 8.02% dependent upon mesh resolution (1, 5 and 10 m respectively). Simulations are based on a 20 m rotor diameter, ensuring that a minimum of two computational nodes fall within the defined device seabed area for the coarse mesh and twenty at finest resolution.
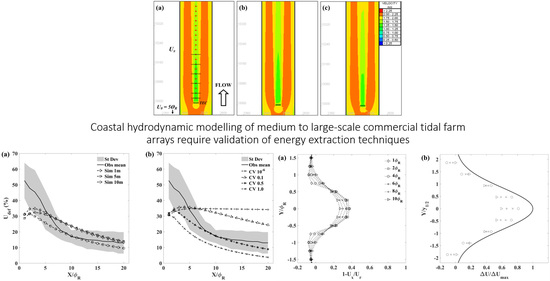
The depth-averaged simulation of near wake dynamics, i.e., within a few meters in lee of a device, exhibits greatest deviation from both empirical values (14–22%) and CFD simulations (
Figure 8 and
Figure 9). Where the magnitude of vertical velocity increases and becomes similar to horizontal velocity, the hydrostatic approximations are no longer valid. Furthermore, low-order TCS in 2D models fail to effectively resolve complex flow divergence and convergence. This is an inherent restriction for coastal modelling simulations utilizing this technique; Masters et al. [
23] report similar findings. This is highlighted in
Figure 8, where simulated velocity deficit within two rotor diameters downstream is almost half that expected, based on mean empirical values. However, in the mid to far wake profile the simulated momentum sink improves. At quasi steady state values approximately 20 rotor diameters downstream the velocity deficit is within ±1 s.d for all mesh dependent simulations using the
k-Ɛ TCS (
Table 3) and is achieved for the CV TCS on a 1 m grid when a velocity diffusivity coefficient value of 0.5 is applied (
Appendix B). By utilizing the generic device subroutine formulation and validation methodology presented here, the inherent accuracy of simulations can therefore be implied when upscaling to commercial array scales. Therefore, misrepresentation of phenomena such as wake turbulence in simulations that add to inaccuracies is both minimized and quantified, as both mesh dependency and TCS coefficient can be calibrated and optimized where necessary.
Analysis suggests that intra-array effects remain negligible when seabed shear stress and device structural drag are the contributing factors to flow deceleration. The influence of turbine feedbacks on dynamics is significantly enhanced (approximately four times greater) following device cut-in as power generation begins, and thus channel power density take-off increases. The impact peaks at rated speed (
Figure 3c and
Figure 10). This implies that turbine thrust (
CT), (i.e., the backpressure exerted on flow) and the associated intra-array device wake interactions that result, greatly influence turbulent mixing and energy dissipation and transfer within the hydrokinetic system. Comparison of the difference between undisturbed inflow conditions to the downstream, disturbed flux for device-scale and array-averaged simulations, illustrates that wake interactions enhance impacts as the number of devices in the array increases.
To consider difference in hydrokinetic system losses, the error induced into simulations when applying array-averaged energy extraction versus the device-scale method presented here was analyzed based on differential along channel flux (
Figure 10). In each configuration, simulated devices were aligned perpendicular to the incoming flow direction (i.e., simulating a non-yawing device that has no misalignment to flow). When linear interpolation and extrapolation is applied, the difference in channel flux (and hence flow velocity and subsequent power density) increases to 0.5% when
nTECs ≈ 25 devices for inline and staggered rows of turbines.
Power extracted from flow reduces when device rotor face is offset to flow direction [
6,
16]. The ability to orientate the angle of individual devices to ambient flow direction when device-scale approaches are adopted allows models to capture this effect. Results based on CF suggest that an initial 0.04% and 1.00% reduction in power captured by a single device occurs, due to a 10° and 20° offset to flow, respectively. This CF change alters when device numbers increase due to intra-array flow changes. The results are configuration-dependent, with an enhanced reduction in CF of 0.18% and 1.71% when five inline devices are simulated and 0.42% and 1.81% for fifteen (
Table 4,
Video S1). Staggering rows of TECs takes advantage of enhanced flow at the periphery of upstream devices to counter act power availability losses. Configuring turbines in this manner effectively negates (<0.02% for five devices) or improves (−0.11% and −0.45% for fifteen devices) any change in CF. However, ultimately, power take off is related to velocity change via
CP. Flow velocity is affected by system feedbacks from energy extraction terms based on drag (
CD) and thrust (
CT) parameterization. Therefore, individual device power capture is independent of the overall associated energy loss.
Given the limitations of the TCS available in Telemac, the approach presented here offers a robust improvement to array-averaged simulations by including intra-array wake effects. Improvements to this study might include extending the simulated transverse and longitudinal velocity deficit profile comparisons to full-scale deployed coastal observations where available. The use of effective validation against empirical observations and CFD simulations is key to improving confidence in results. Implementing this approach when up-scaling to large arrays therefore ensures induced model errors are minimized. The method presented provides a generalized approach that accounts for axial turbine thrust [
49], turbine proximity to boundaries and turbulent intensity levels [
49,
53,
56] for various rotor design types. Further improvements necessitate device field measurements, combined with CFD analysis to alter turbulence terms and improve 2D wake dynamics in coastal models. Reliable assessment of environmental resource impacts (e.g., combining sediment dynamics that include morphological changes [
12] and wave-tide interactions [
58]) can be made using 2D ocean-scale models that include this intra-array wake technique.
5. Conclusions
The aim of this study was to establish a device-scale approach to energy extraction in depth-averaged simulations that improves upon present techniques. The goal was to create an automated, validated and calibrated methodology, which improves upon array-averaging simulations when implementing energy extraction as an enhanced seabed friction term. This modelling study has implemented energy extraction at individual device-scale into a depth-averaged coastal numerical model (Telemac-2D). It was hypothesized that array-averaged energy extraction simulations do not account for intra-array wake effects and hence misrepresent device-resource interaction and feedbacks. This was investigated by adapting an irregular unstructured model mesh of an idealized tidal channel, capable of resolving individual turbines using a fine resolution regular sub-mesh (10, 5 and 1 m). In doing so, we determine that results are mesh size-dependent; however, the adapted formulae, produces repeatable results. Using the k-Ɛ TCS, a centerline axial wake velocity deficit profile accuracy of 0.58–0.69 (R2) and 7.16–8.28% (RMSE) was achieved when compared with empirical, scaled tank tests. If using a constant viscosity TCS, a velocity diffusivity coefficient of 0.5 must be assigned to achieve similar accuracy.
The estimated TEC power captured from the flow alters with device offset to flow orientation and array layout configuration. An increase in CF difference from 0.04% to 0.18% and 0.42% occurs when single rows of five and fifteen turbines are offset by 10° to the flow. This increases from 1.00% to 1.71% and 1.81% when the offset is 20°. However, power captured by an array is independent of energy extraction governed by drag and thrust terms, but dependent upon intra-array dynamics and associated velocity manipulation from device-wake feedbacks. Difference in CF is negated or improved (0.02%, 0.01% and −0.11%, −0.45% for five and fifteen devices, respectively) when devices are configured in staggered rows.
The calibrated and validated device-scale energy extraction methodology is compared to an array-averaged approach based on channel flux differential. Various configurations are analyzed, based on generic turbine characteristics and array configurations, with turbines simulated perpendicular to flow (i.e., no misalignment offset). Linear interpolation and extrapolation of these results identifies that the flux differential increases to >0.5% when nTECs ≈ 24–26 devices. This suggests that quantification of the uncertainty associated with utilizing an array-averaging approach, particularly when upscaling to commercial tidal array configurations, may be pertinent. Our results indicate that the uncertainty associated with upscaling must necessarily be established for environmental assessments that negate intra-array effects, as this will exceed 2% error when nTECs ≥100 devices.