Dynamic Programming for Optimal Energy Management of Hybrid Wind–PV–Diesel–Battery

Abstract

With the dramatic development of renewable energy resources all over the world, Vietnam has started to apply them along with the conventional resources to produce the electrical power in recent years. Visually, the aim of this action is to improve the economic as well as the environmental benefits. Therefore, a vast of hybrid systems that combine Wind turbine, Photovoltaic (PV), Diesel generator and battery have been considered with different configurations. According to this topic, there are lots of research trends in the literature. However, we aim to the optimal energy management of this hybrid system. In particular, in this paper, we propose an optimization method to deal with it. The interesting point of the proposed method is the usage of the information of sources, loads, and electricity market as an embedded forecast step to enhance the effectiveness of the actual operation via minimizing the operation cost by scheduling distributed energy resources (DER) while regarding emission reduction in the hybrid system is considered as the objective function. In this optimization problem, the constraints are determined by two terms, namely: the balance of power between the supply and the load demand, and also the limitations of each DER. Thus, to solve this problem, we make use of the dynamic programming (DP) to transform a system into a multi-stage decision procedure with respect to the state of charge (SOC), resulting in the minimum system cost (CS). In order to highlight the pros of the proposed method, we implement the comparison to a rule-based method in the same context. The simulation results are examined in order to evaluate the effectiveness of the developed methodology, which is a so-called global optimization.

1. Introduction

Nowadays, electricity demand has been increased significantly and massively while the environment is getting to be more and more harmful due to the emission gases from the conventional resources. Accompanying the remarkable improvement of technologies in the field of renewable energy, the clean energy resources have been utilized to supply the power. Some renewable resources like wind, solar, water have their own characteristics that depend on the locations, regional potential, etc.. However, in general, due to their unstable and discontinuous natures, they are supposed to be integrated in a hybrid system as power suppliers. A hybrid power generating system is conceptually composed of the PV panel, wind turbines, diesel generators, batteries and converters which are related to the size, capital cost, replacement cost and operation and maintenance cost [1,2,3].

There are a lot of publications that are based on the hybrid generating system in the literature. For instance, in [4], a model of the operation problem of microgrids (MGs) was proposed with respect to the economical, technical and environmental issues, as well as uncertainties related to loads, wind speed and solar radiation. The advantage of this paper is that the authors applied the proposed method to the Bisheh village in Iran. The problem was reformulated as a Mixed-Integer Nonlinear Programming (MINLP). The results showed that, considering load curtailment costs, the power losses of the main grid, the penalties of pollutant gasses emissions and the elimination of energy subsides will have tremendous impact on the operation of MGs. In [5], a novel tool for realistic modeling and efficient simulation have been developed. In [6], the authors present a study on a hybrid stand-alone system in Algeria to determine the feasibility of such systems via the optimization task considering both technical and economical factors. The results revealed that both factors have promising potentials. Unlike these topics, we aim to develop the energy management method to improve the economic efficiency and reliability of the overall system for a Wind–PV–Diesel hybrids with battery energy storage (BESS) by considering this problem as an optimization problem.

In the literature, there are several optimization approaches to optimize the energy management. For instance, in [7], a rule-based energy management system (EMS) has been developed in which the operation of the system depends on predefined rules. However, the optimal outcome has not been assured. Furthermore, the improved rule-based strategy has been proposed by embedding a low complexity Fuzzy logic controller in an EMS to minimize the grid power profile fluctuations while keeping the Battery SOC within secure limits in [8] with the controllable assumption for neither the renewable sources nor the load and to control the power flows in [9] through using linear programming. Furthermore, in [10], the authors have paid attention to the modeling of a consumer characteristic in the demand response. A multiperiod artificial bee colony optimization algorithm was employed for economic dispatch considering generation, storage and responsive load offers while an artificial neural network combined with a Markov chain approach is developed to predict a nondispatchable power generation and load demand according to uncertainties. In addition, the optimal energy management is achieved by using the linear programming (LP) and mix integer linear programming (MILP) methods that are described in [11,12]. For instance, in [12], the day-ahead scheduling feature of electric power and energy systems shared with renewable resources as an MILP problem for solving the hourly economic dispatch-constraint unit commitment. As a result, the generated power cost has reduced by almost 21% in comparison with conventional EMS. As we can see that, the common cons of the proposed methods above are the long computation times and the lack of the global optimal solution. On the other hand, the particle swarm optimization (PSO) method also has been utilized in [13,14,15]. In particular, in [15], the stochastic economic load dispatch (SELD) is considered as an optimization problem constrained by stochastic variables. An improved PSO has been proposed to solve the cost-minimization subproblem of MG SELD. In [16,17], the quadratic programming (QP) has been deployed to establish the optimal energy control strategy for a network containing PV/battery and electric vehicles. Despite achieving favorable results, this approach is affected by the fact that the objective function is required to be convex. In [18,19], the optimal energy management of a microgrid is solved by using Game Theory and multi-objective optimization techniques. The operating cost and the emission level are considered as two objective functions. In [20], a new method for the MG energy management problem through introducing a continuous-time, rolling horizon formulation. In this paper, the authors have applied two methods that so-called direct and Dynamic Programming Principle (DDP). The results figured out that DDP methods is perfectly suited to this problem. Furthermore, this method can reach the global optimum in less than one second of CPU time.

In our paper, with the purpose to improve the economic efficiency as well as the reliability of the system simultaneously, we consider the energy management as a multi-objective optimization problem. Generally speaking, the energy management system receives the forecast values of load demand, the distributed energy resources and the market electricity price in each hour on the next day to produce the scheduled output power of DER, the costs and the emissions. In order to bring down the costs of operation and decrease the release of disposal waste, the dynamic programming (DP) is deployed. The constraints are considered as the matching of generation and load in every period of time, the rating of DER, and the operating condition of the system. By this scene, we can obviously obtain the global solution. To show the effectiveness of the proposed method, a comparison between the DP-based proposed method and the rule-based method is also taken into account.

This paper is organized as follows. Section 2 demonstrates the configuration of studied system that will be used to optimize with the proposed method. In Section 3, the paper introduces the methodology in which the objective function and the constraints are clearly presented and explained. Moreover, the cost of system (CS) is expressed as an objective function. A rule-based energy management strategy is shown in Section 4. Section 5 describes the proposed method, which is DP application in energy management. In this part, the objective function is defined by employing the Bellman–Ford algorithm to determine the optimal order for the state of charge (SOC) from the first moment to the final moment. The simulation and results are demonstrated in Section 6 before concluding this work in Section 7.

2. Configuration of the Hybrid System

A hybrid system that includes PV, Wind, Diesel and Battery energy storage system (BESS) is shown in Figure 1:

The BESS operations depend on the operation strategy of this system. When the supplies are greater than the loads, the BESS will be charged. On the other hand, if the consumption exceeds the production, the BESS will discharge to meet the remaining power. The following equation describes the state of charge (SOC):

$$SOC\left(t\right)=\frac{C\left(t\right)}{C_{ref}},$$

(1)

where $C\left(t\right)$ is the battery capacity at t, and $C_{ref}$ is the reference battery capacity.

The stage of charge at the instant of time $SOC\left(t\right)$ is calculated based on the previous instant one $SOC(t-1)$, the produced power and load demand during the period of time from $(t-1)$ to t. Over the charging time, the state of charge at time t could be expressed as follows:

$$SOC\left(t\right)=SOC\left(t-1\right)+\frac{P_{PV}\left(t\right){+P}_{wind}\left(t\right){+P}_D\left(t\right){-P}_L\left(t\right)}{C_{ref}}\Delta t,$$

(2)

where:

• $P_L\left(t\right)$ is the load power at t;
• $P_{PV}\left(t\right)$ is the PV system power at t;
• $P_{wind}\left(t\right)$ is the wind power at t;
• $P_D\left(t\right)$ is the diesel power at time t.

In this paper, we denote $\Delta t$ as a unit time interval: $\Delta t=1$ (1 h) and $C_{ref}$ as BESS capacity (kWh).

A diesel generator set is installed in order to meet the whole load in case of shortage of power supplied by the PV, wind system and BESS. The diesel unit is initiated to adapt the load requirement and may be tripped whenever the overall production by other generating units is assured.

3. Methodology

In this part, the optimal energy management for the studied hybrid system is introduced. The objective function is described in Section 3.1 and the summary of the constraints is detailed in Section 3.2.

3.1. Objective Function

The aim of this methodology is to reduce the cost of system (CS) including the fuel costs (FC), the emission costs (EC) and the batteries replacement costs (BrC) to a minimum value. Here, the objective function can be expressed as follows:

$$CS=\sum _{t=1}^{24}FC\left(t\right)+EC\left(t\right)+BrC\left(t\right),$$

(3)

in which,

• the FC is determined by:

  $${FC\left(t\right)=C}_f.F\left(t\right),$$

  (4)

  where:
  • $C_f$ is the fuel price,
  • $F\left(t\right)$ is the diesel generator consumption per hour.

    $$F\left(t\right)=0.246\times P_D\left(t\right)+0.08415\times P_R,$$

    (5)

    where: $P_R$ is the rated power of diesel generators.
• The EC is expressed as follows:

  $$EC\left(t\right)=\frac{E_t{\times E}_{cf}{\times P}_D\left(t\right)}{1000},$$

  (6)

  where:
  • $E_f$ is the function of release of toxic gases (kg/kWh);
  • $E_{cf}$ is the factor of spending on emission;
• and the replacing batteries cost (BrC).
  The applied BrC in this paper at each time period corresponds to the cost of the capacity lost during the time interval. Its calculation is conducted based on the variation of $SOH$ $(\Delta SOH)$ at every time step. The variation of state of health $(\Delta SOH)$ between two states $x_i$ and $x_j$ during one time step is estimated in Equation (7). On the other hand, the $\Delta SOH$ can be estimated by (8) which is a linear function of the variation of the state of charge ($\Delta SOC$) and the ageing coefficient $\left(Z\right)$. The $(\Delta SOH)$ is calculated only during the discharge process:

  $$\Delta SOH{x}_i,x_j\left(t\right)=SOH{\left(x\right)}_i(t-\Delta t)-SOH{x}_j\left(t\right),$$

  (7)

  $${\Delta SOH(x}_i{,x}_j{t)=Z.(SOCx}_i{(t-\Delta t)-SOCx}_j\left(t\right)).$$

  (8)
  The BrC is expressed as follows [16]:

  $$BrC\left(t\right)=BiC\frac{\Delta SOH\left(t\right)}{{1-SOH}_{min}},$$

  (9)

  where:
  • $BiC$ is the batteries’ investment cost;
  • ${SOH}_{min}$ is the minimum state of health.

One thing to note here in this paper is that the Z is equal to ${3.1}^{-4}$ [21].

From the Equations (4)–(9), the objective function can be rewritten as follows:

$$min\sum _{t=1}^{24}{C}_f·({0.246·P}_D\left(t\right)+{0.08415·P}_R)+\frac{E_t{·E}_{cf}{P}_D\left(t\right)}{1000}+BiC\frac{{Z·(SOCx}_i{(t-\Delta t)-SOCx}_j\left(t\right))}{{1-SOH}_{min}}.$$

(10)

3.2. Constraints

The constraints of this optimization problem include:

• Power balance constraint:

  $$P_L\left(t\right)=P_{PV}\left(t\right)+P_{wind}\left(t\right)+P_B\left(t\right)+P_D\left(t\right),$$

  (11)

  where: $P_B\left(t\right)$ is the BESS power at t.
• BESS power output:

  $$P_{Bmin}\le P_B\left(t\right)\le P_{Bmax}.$$

  (12)
  The BESS power $P_B\left(t\right)$ corresponds to a transition between two operating conditions over one time step. Thus, the constraint to the SOC variation constraint is shown as follows:

  $${\Delta SOC}_{min}\le \Delta SOC\left(t\right)\le {\Delta SOC}_{max}.$$

  (13)
• Battery state of charge (SOC) constraint is limited by its predefined maximum and minimum values:

  $${SOC}_{min}\le SOC\left(t\right)\le {SOC}_{max}.$$

  (14)
• Battery state of health (SOH) constraint:

  $$SOH\left(t\right)\ge {SOH}_{min}.$$

  (15)
• Diesel generator constraint:
  The diesel generators should not be operated when the generated power below the minimum power recommended by the manufacturer. The diesel power at time t is bounded by:

  $$P_{die\_min}\le P_D\left(t\right)\le P_{die\_max},$$

  (16)

  where $P_{die}{}_{\_min}$, $P_{die\_max}$ are the minimum, maximum power operation of diesel generator, respectively.

4. A Rule-Based Energy Management Strategy

In this section, Figure 2 shows that a ‘constraint’ management strategy is developed on the basis of the pre-set rules. The system operation is implemented depending on the PV power and the consumption. This method is restricted due to the fact that the state of battery is not taken into account in the predefined rules.

The primary regulations that are the foundation of rule-based energy management are described as follows:

• Renewable energy is primarily sources to cover the loads;
• The BESS discharge in case of insufficient production;
• The BESS is charged whenever the generation exceeds the consumption.

The rule-based energy management algorithm should satisfy the following requirements:

$$P_L\left(t\right)=P_{PV}\left(t\right)+P_{wind}\left(t\right)+P_B\left(t\right)+P_D\left(t\right),$$

$${SOC}_{min}\le SOC\left(t\right)\le {SOC}_{max},$$

$$P_{Bmin}\le P_B\left(t\right)\le P_{Bmax},$$

$$P_{die\_min}\le P_D\left(t\right)\le P_{die\_max}.$$

The technique is carried out as detailed below:

• The diesel power output is given as the function of renewable energy power and the load demand;
• The BESS power is derived from the power balance rule;
• The compliance with the BESS and Diesel constraints (12)–(16) is required to be confirmed.

5. DP in Energy Management Issues

The program includes sub-problems, such that a system is categorized into a multi-stage decision procedure. A set of condition variables is cited as the system state at each time and is discretized by a phase dimension $\Delta SOC$. The first state of charge $\left(SO{C}_0\right)$ is expressed as an operation mode without any preceding node. Likewise, the last state of charge $\left(SO{C}_T\right)$ is also decided. All margins are determined in one order from t to t + $\Delta t$. Therefore, the shift of $SOC$ is depicted as a sequencing chart from the starting stage $\left(SO{C}_0\right)$ to the eventual phase (${SOC}_T$). Thus, the Bellman technique is deployed in order to find out the $SOC$ state resulting in the minimum system cost (CS) in Figure 3.

A condition of charge variation $(\Delta SOC)$ between two stages $x{}_i$ and $x{}_j$ over one state is detailed below [16]:

$$\Delta SOC(x_i,x_j,t)=SOC(x_j,t)-SOC(x_i,t-\Delta t).$$

(17)

• If $\Delta SOC<0$, then BESS dischargse.
• If $\Delta SOC>0$, then BESS is charged.
• If $\Delta SOC=0$, then BESS rests.

From the objective function (10), we can observe that the cost of system (CS) now is described as a relation of the $SOC$ change. The most appropriate value (CS) therefore can be gained by using the Bellman algorithm presented in Figure 3 to find the most suitable order (the quickest way) of state of charge $\left(SOC\right)$ from the starting instant to the last one. In Figure 4, a flowchart of the Bellman method with detailed computation of the weight of the edges is shown. In this figure, the Bellman method flowchart is described inside the red line rectangle. In this flowchart, there is a step that is to calculate the weight, which is described in the blue circle. The procedure on the left side of this figure, which is described in the blue dash circle, is used to calculate this weight.

The $SOC$ variation $(\Delta SOC)$ is expressed as a function of the battery power $\left(P{}_B\right)$. Thus, for each $\Delta SOC(x_i$,$x_j,t$), the $P_B\left(t\right)$ is calculated. Then, the diesel power ($P{}_D\left(t\right)$) is calculated based on the $P{}_B\left(t\right)$, the predicted value of $P_{PV}\left(t\right)$, $P_{wind\left(t\right)}$, and $P_L\left(t\right)$.

6. Simulation and Results

This section is to illustrate the optimal energy management of the Wind–PV–diesel–BESS hybrid system. This task is implemented by solving the optimization problem to define the minimum of cost of system, the most suitable plan of the diesel generator and BESS simultaneously. The optimal problem is described as following objective function:

$$min\sum _{t=1}^{24}{C}_f·({0.246·P}_D\left(t\right)+{0.08415·P}_R)+\frac{E_t{\times E}_{cf}{\times P}_D\left(t\right)}{1000}+BiC\frac{{Z·(SOCx}_i{(t-\Delta t)-SOCx}_j\left(t\right))}{{1-SOH}_{min}},$$

Subject to

$$P_L\left(t\right)=P_{PV}\left(t\right)+P_{wind}\left(t\right)+P_B\left(t\right)+P_D\left(t\right),$$

$$P_{Bmin}\le P_B\left(t\right)\le P_{Bmax},$$

$${SOC}_{min}\le SOC\left(t\right)\le {SOC}_{max},$$

$$SOH\left(t\right)\ge {SOH}_{min},$$

$$P_{die\_min}\le P_D\left(t\right)\le P_{die\_max}.$$

In order to solve this constrained optimization problem, we make use of the initial data such as the day-ahead forecast values of loads, PV and wind that are shown in Figure 5. Figure 5a says that the PV system starts to supply the energy at 5:00 a.m. and stops working at 9:00 p.m, in which the most supplied power is of 55 kW at around 3:00 p.m. Additionally, the load is fluctuated from 30 kW to 46 kw as shown in Figure 5c. The maximum power of load is at 12 p.m. Finally, Figure 5b describes that the power related to the wind speed is changing in the interval from 5 kW to 22 kW. As can be seen in this subfigure, the power is large in the morning and the night.

The simulation parameter values are shown in

Table 1. The simulation parameter values.

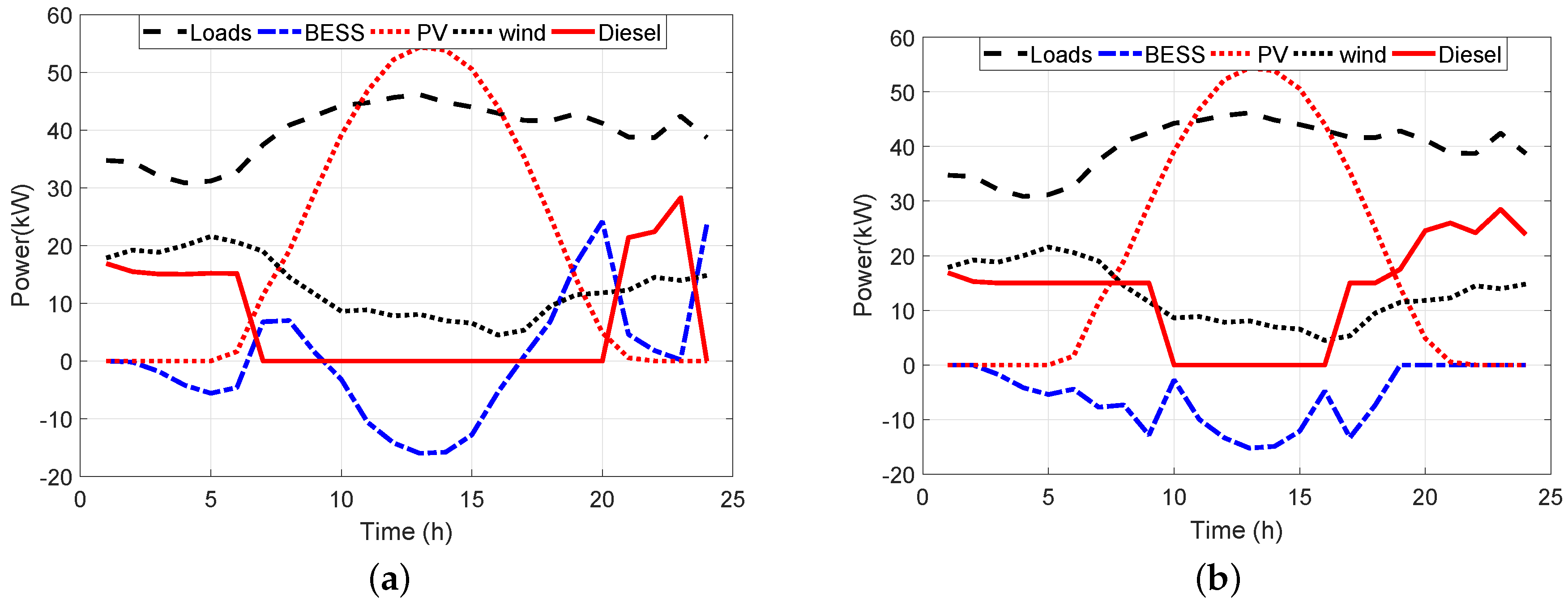
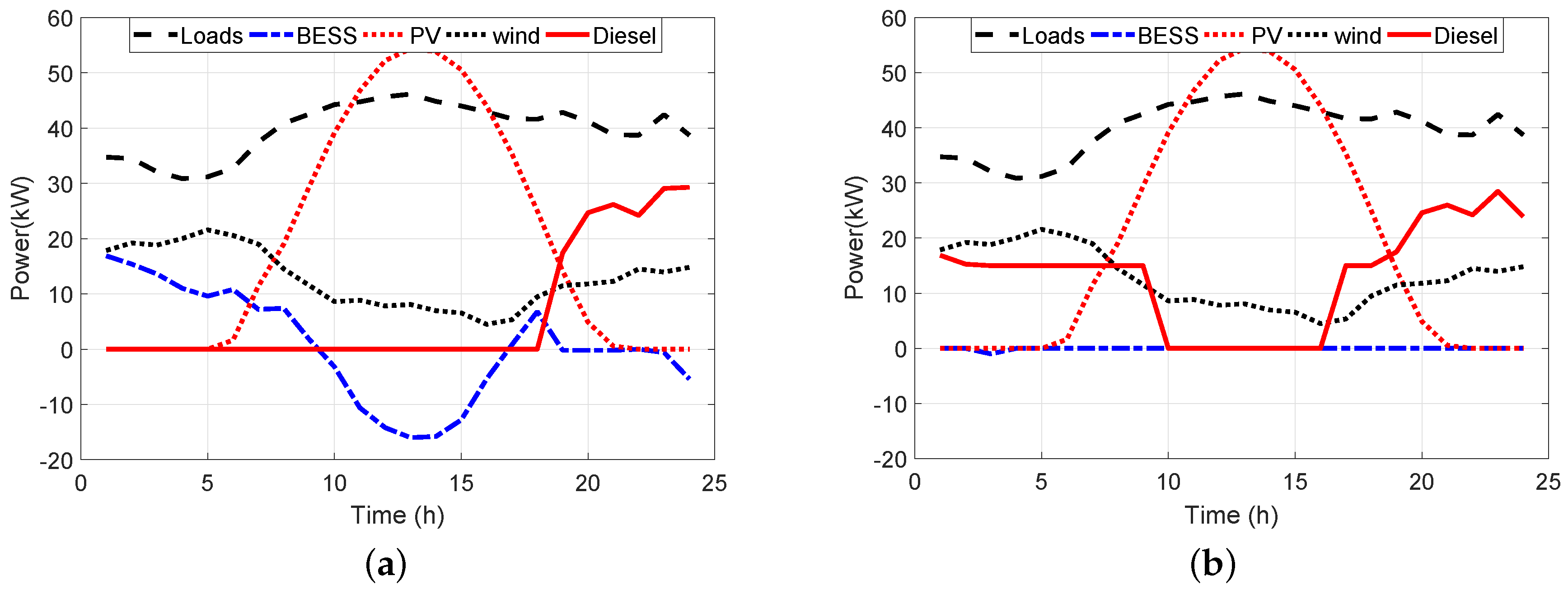
Name	Value	Unit
T	24	h
$\Delta t$	1	h
$\delta SOC$	0.001
$SO{C}_{min}$/$SO{C}_{max}$	0.2/0.9
$\Delta SO{C}_{min}$/$\Delta SO{C}_{max}$	−0.7/0.7
${SOH}_{min}$	0.7
Minimum/Maximum power of diesel	15/50	kW
BESS capacitor	200	kWh

.

One thing to note here is that the simulation results are cultivated by the proposed method and the rule-based method in three simulations, namely:

• Simulation 1: initial state of charge $SOC\left(t{}_0\right)=0.5$,
• Simulation 2: initial state of charge $SOC\left(t{}_0\right)=0.2$,
• Simulation 3: initial state of charge $SOC\left(t{}_0\right)=0.9$.

1. Simulation 1: $SOC\left(t_0\right)=0.5$

In this case, the load consumption is covered by the main generating units. Figure 6 differentiates by two methods: DP programming and ruled-based methods. The main purpose of these two methods is to define the relevant time for diesel to stop supplying for the load demand. For both methods, the requirements of load are adapted by the diesel and the wind power at the beginning of the day. In Figure 6a, the BESS discharges to supply the power to the load when the power from the wind park is insufficient. In addition, the diesel starts to stop working at 3:00 a.m. On the contrary, the Diesel keeps working to feed the load and BESS as shown in Figure 6b. Briefly speaking, while the DP method estimates that the diesel ceases to operate for 16 h (from 3:00 a.m. to 7:00 p.m.), the rule-based method shows that 7 h (from 10:00 a.m. to 4:00 p.m.) is the optimal value. In the first time of this process, the load receives power from the PV system or the BESS and wind parks. When the total of renewable power supplied the load is plenty, the power excess will charge the BESS. As can be seen from Figure 6, the DP method coordinates the diesel unit with the BESS and renewable source in order to adapt the load demand, whereas there is no coordination between the diesel unit and the BESS according to the rule-based technique, meaning that the BESS charge all the time possible. Figure 7a shows that the state of charge at the end of day turns back to the starting value (SOC = 0.5) to prepare for the next day. Otherwise, the SOC at the end of the day is given as larger than this value at the beginning (Figure 7b).

The simulation results in Figure 6 and Figure 7 reveal that non-operation of the diesel generation for 16 h each day can lead to the operation mode improving the lifespan of diesel gensets as well as cutting the expense of fuel and the release of greenhouse gases. Additionally, the equality of the first and the last SOC can make the performance of the charge operation at the commencement of the subsequent day easier. For the rule- based approach, due to the absence of the next day forecast, the regulation law is to maintain the BESS power in full as possible. Therefore, the final SOC is larger than the initial one (in Figure 7b). Therefore, the following day energy management strategy is limited because it is practically the full charge of BESS. As the result, the charging process will not be executed at the commencement of the following day. Therefore, this leads to the conclusion that the rule-based technique possesses several drawbacks when applied for day-ahead supervision.

The last values of the objective function for optimizing the DP and the rule-based control strategy are detailed as in

Table 2. The final value in simulation 1.

	DP	Rule-Based
Final value ($)	78.3	146.21

. The value obtained by using the DP technique is smaller than that derived from the rule-based approach. Thus, the DP method offers the optimal result.

2. Simulation 2: $SOC\left(t_0\right)=0.2$

The optimal generating plan in the hybrid system is depicted in Figure 8. In this operating scenario, the starting condition of charge SOC is 0.2. The system commences operating with the empty BESS. At the commencement of the day, the load consumption is covered by the wind power and the diesel, which almost operate at the minimum level. Subsequently, the BESS will charge for immediate use for supplying power to the load. In Figure 8a, at t = 7:00 a.m., the loads receive power from the PV, wind, and BESS. Thus, the diesel unit stops working from 9:00 a.m. to 8:00 p.m. In this period, the power exceeded is charged by the BESS. Afterwards, the BESS totally discharges to feed the loads. At the final stage, the diesel genset will start working to maintain the load operation at 9:00 p.m. The operation of the system obtained by the rule-based approach provides a similar result to the above calculation. The battery SOC characteristic is described as in Figure 9, which are always located in the range limited by the highest, and the lowest values over a period of 24 h.

The final value of the objective function for the two methods in this simulation is detailed in

Table 3. The final value in simulation 2.

	DP	Rule-Based
Final value ($)	89.45	146.21

. The simulation results derived from the rule-based technique are similar to those in the simulation 1. The proposed method offers the better results compared to the remaining technique.

3. Simulation 3: $SOC\left(t{}_0\right)=0.9$

Figure 10 and Figure 11 present the simulation results in case 3. This case differs from the two previous studies by the full charge of BESS in the first hours of the day. In general, the system operating condition in this case is similar to those in the two preceding simulations. Nevertheless, the diesel unit stops operating at the commencement of the day due to full charge of BESS in this period. Furthermore, at 6:00 p.m., the BESS is practically full in charge for the following day. As can be observed from Figure 10b, the BESS does not absorb the redundant power from PV because of its full charge. Therefore, a significant proportion of PV power fails to fulfill its daily duty cycle.

The final values for the DP and the rule-based approaches in this simulation are described in

Table 4. The final value in scenario 3.

	DP	Rule-Based
Final value ($)	80.31	130.21

. The number for the rule-based technique is lower than those for the two mentioned before cases because of non-operation of BESS for a day.

The simulation results detailed in Table 2, Table 3 and Table 4 have validated the optimal effectiveness of the DP approach when applied for energy management of the PV–wind–diesel–BESS hybrid system. Moreover, according to the DP technique, the simulation 1 (SOC = 0.5) has offered the best outcome in

Table 5. The final value by DP in scenarios.

	SOC = 0.5	SOC = 0.2	SOC = 0.9
CS${}_{optimal}$($)	78.3	89.45	80.31

.

7. Conclusions

In this study, we have proposed the Dynamic Programming method to manage the optimal energy management of the PV–wind–diesel–BESS hybrid system with respect to both economic benefits and its reliability. In particular, the DP approach is used to establish the optimal schedule of power sources. Clearly speaking, this method can minimize the operation cost of the hybrid system (CS) and CO2 emission while satisfying the technical conditions such as reliability, safety, etc. in three scenarios with the different initial states of charge. In this work, the comparison between the achieved final values from the DP method and those obtained by the Rule-based technique has been carried out to light up the contribution of the proposed method. The simulation results reveal that the proposed method has not only provided the global optimization technique of energy management but also determined the optimal initial stage of charge that leads to the best result in both operation and management of PV–wind–diesel–BESS hybrid system. In the near future, we will study extensively to build an optimal energy management rule dealing with a group of Microgrids that are associated together under a cooperative control method.