Life Cycle Estimation of Battery Energy Storage Systems for Primary Frequency Regulation
Abstract
:1. Introduction
- new control laws of the converters of the RES-based generation plants;
- integration of grid-connected battery energy storage systems (BESSs).
2. Literature Review and Contribution of the Paper
- all aspects related to the battery operation for primary frequency regulation are analyzed to highlight, in a feasible and effective way, the main issues affecting planning and operation;
- a simulation setup implementing the main features of the BESS control for primary frequency regulation is proposed;
- an autoregressive model based on actually measured data is tailored to accurately represent effective frequency patterns which are then used in statistical analyses;
- by analyzing the real frequency measures, an efficient method is adopted to estimate the parameters of the autoregressive model based on a Logistic underlying distribution assumption;
- a tool is proposed for the statistical prediction of the lifetime duration based on an accurate analysis of the charging/discharging cycles of the BESS provided by the rain-flow method and by a consolidated method used to model the lifetime degradation of the batteries;
- a sensitivity analysis is proposed in order to show the effect of the control features on the battery lifetime duration.
3. Primary Frequency Regulation with BESS
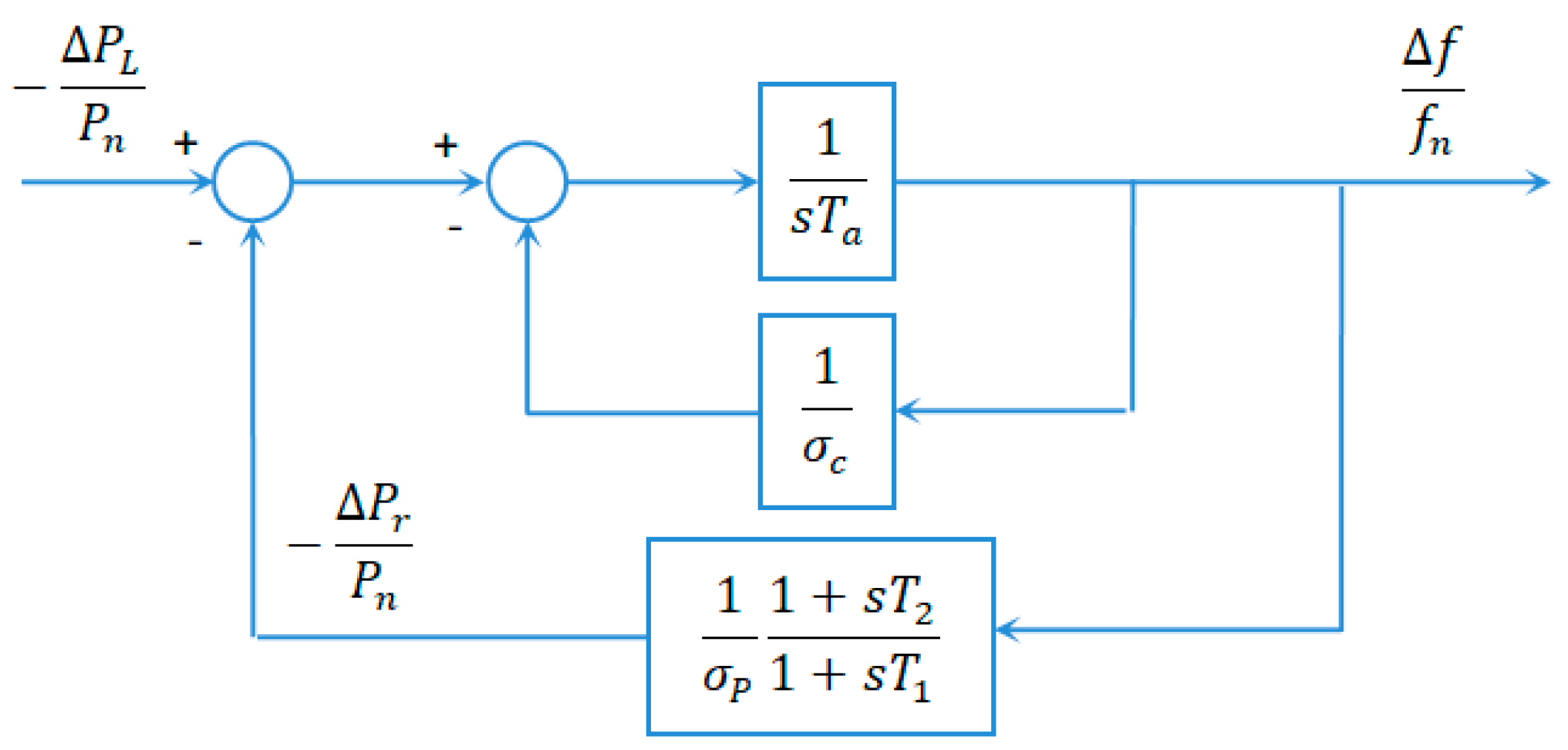
3.1. Basic Concepts on the Primary Frequency Regulation
3.2. Batteries for the Primary Frequency Regulation
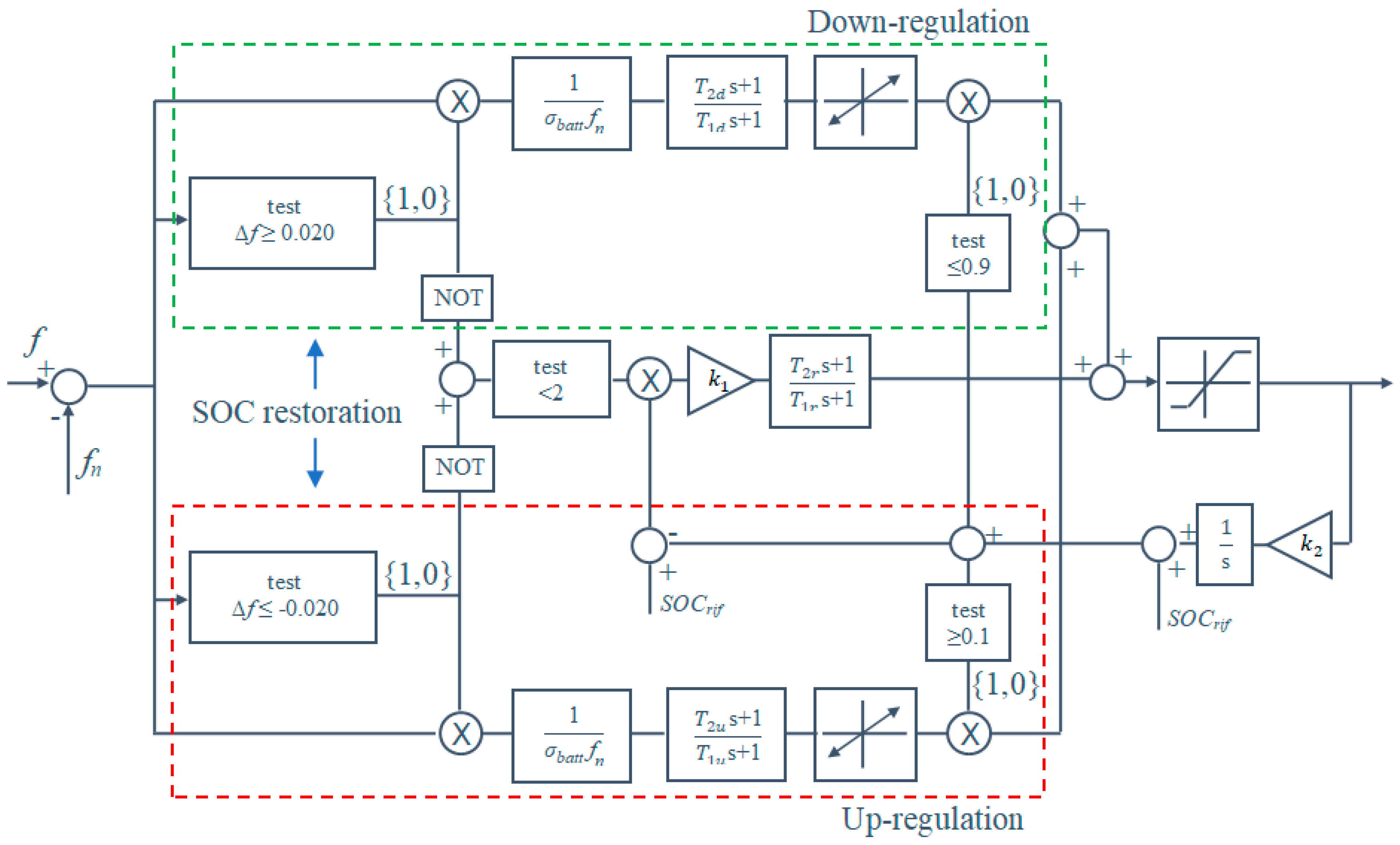
3.3. Battery Control for the Primary Frequency Regulation
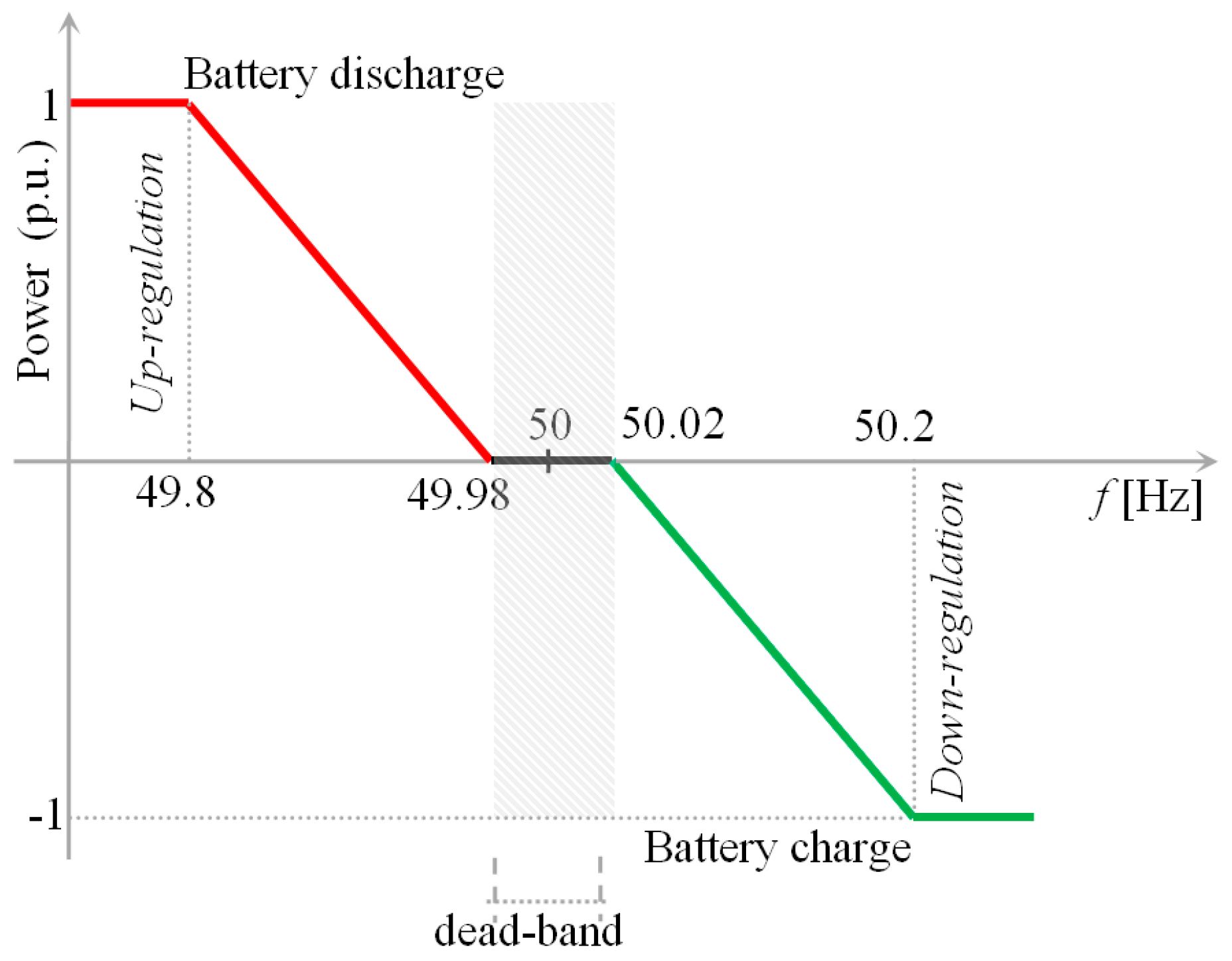
- provide the charging/discharging power according to the up- and down- regulation reported in Figure 3;
- restore the at a reference value, when frequency falls within the dead-band; the reference value is typically set at 0.5 p.u.;
- keep the within the range p.u., in order to preserve the battery lifetime.
4. Battery Lifetime Degradation Estimation
5. Representation of the Frequency Patterns through an Autoregressive Model
6. Numerical Applications
6.1. Battery Control for the Primary Frequency Regulation
6.2. Data analysis to Represent Frequency Patterns through an Autoregressive Model
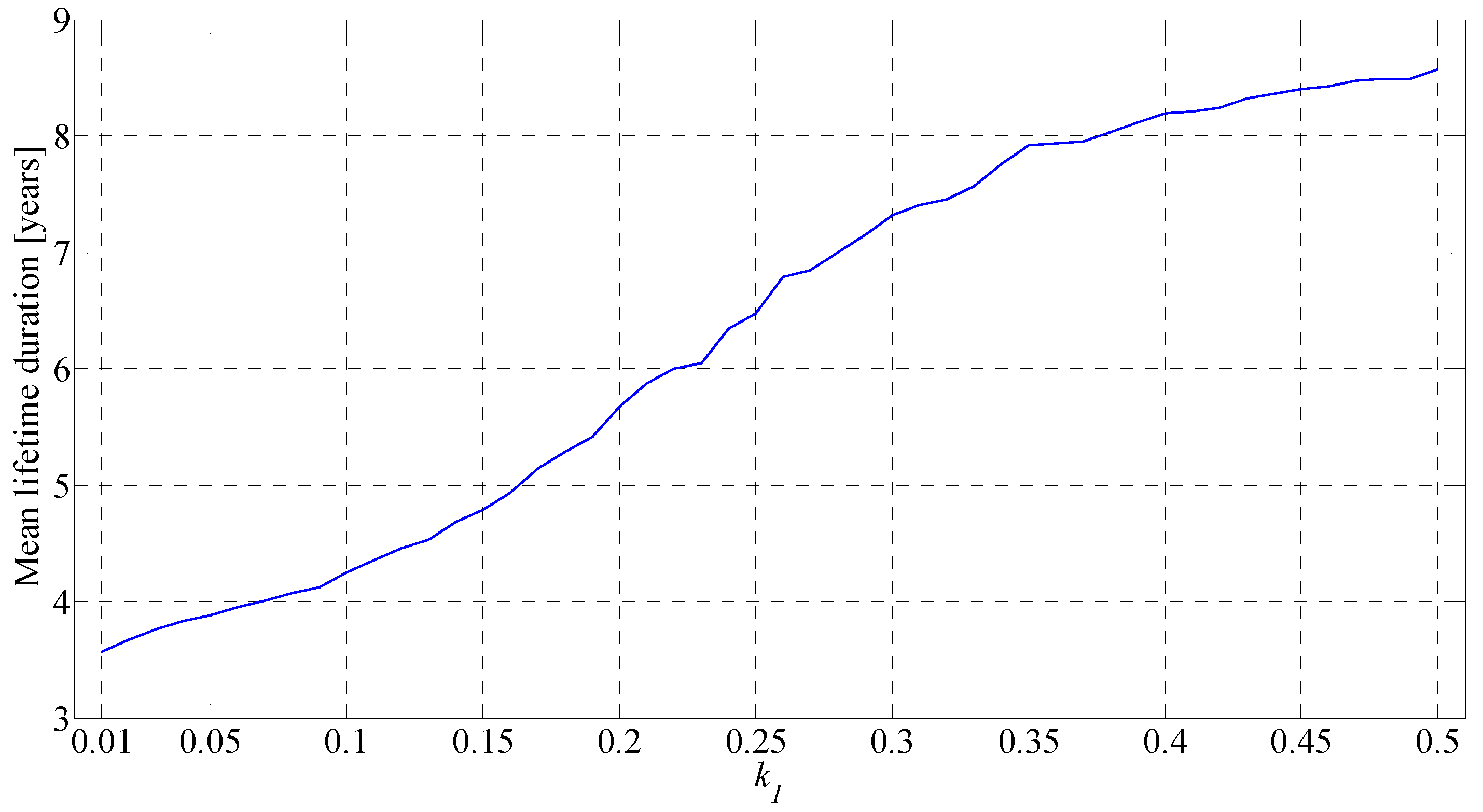
6.3. Statistical Analysis of the Battery Lifetime Duration and Impact of the Control Law
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| AC | alternating current |
| BESS | battery energy storage system |
| capacity fade in per cent value representing the end of the life | |
| DC | direct current |
| BESS energy capacity | |
| permanent regulating energy | |
| inertia constant | |
| number of different depths of discharge | |
| likelihood function | |
| battery life consumption | |
| number of cycles to the battery failure at the jth depth of discharge | |
| BESS power at time | |
| rated power of the BESS | |
| power delivered by the jth group at the time of the perturbation | |
| nominal active power of the jth group | |
| rotating reserve | |
| RES | renewable energy source |
| state of charge | |
| initial SOC value | |
| starting time of the generation unit | |
| estimated parameter at distributed according to a specific distribution | |
| depth of discharge characterizing the jth cycle | |
| frequency | |
| reference value of the frequency | |
| BESS restoration factor | |
| number of groups in service after the perturbation | |
| number of cycles performed at the jth depth of discharge | |
| number of samples | |
| time | |
| time series value at | |
| step load perturbation | |
| regulating power | |
| parameter of the autoregressive model’s polynomial approximation | |
| parameter estimated value of autoregressive model’s polynomial approximation | |
| mean value of the frequency deviation | |
| mean value estimation of the frequency deviation | |
| standard deviation of the frequency deviation | |
| Estimation of the standard deviation of the frequency deviation | |
| average value of the SOC level of jth cycle | |
| BESS setting droop | |
| permanent load droop | |
| permanent droop |
Appendix A. The Summary of the Literary Contributions
| Ref. | Main Investigated Items and Parameters | Object/Contribution |
|---|---|---|
| [14] |
|
|
| [15] |
|
|
| [22] |
|
|
| [23] |
|
|
| [24] |
|
|
| [25] |
|
|
| [26] |
|
|
| [27] |
|
|
| [28] |
|
|
| [29] |
|
|
| [30] |
|
|
| [31] |
|
|
| [32] |
|
|
| [33] |
|
|
| [34] |
|
|
| [35] |
|
|
| [36] |
|
|
| [37] |
|
|
| [38] |
|
|
| [39] |
|
|
| [40] |
|
|
| [41] |
|
|
| [42] |
|
|
| [43] |
|
|
| [44] |
|
|
| [45] |
|
|
| [46] |
|
|
| [47] |
|
|
References
- Bevrani, H.; Ghosh, A.; Ledwich, G. Renewable energy sources and frequency regulation: Survey and new perspectives. IET Renew. Power Gener. 2010, 4, 438–457. [Google Scholar] [CrossRef]
- Weissbach, T.; Welfonder, E. High frequency deviations within the European Power System: Origins and proposals for improvement. In Proceedings of the IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–6. [Google Scholar]
- Saarinen, L.; Norrlund, P.; Yang, W.; Lundin, U. Linear synthetic inertia for improved frequency quality and reduced hydropower wear and tear. Int. J. Electr. Power Energy Syst. 2018, 98, 488–495. [Google Scholar] [CrossRef]
- Adrees, A.; Papadopoulos, P.N.; Milanovic, J.V. A framework to assess the effect of reduction in inertia on system frequency response. In Proceedings of the IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Ulbig, A.; Borsche, T.S.; Andersson, G. Impact of low rotational inertia on power system stability and operation. IFAC Proc. Vol. 2014, 47, 7290–7297. [Google Scholar] [CrossRef]
- Chiodo, E.; Lauria, D.; Mottola, F. On-line bayes estimation of rotational inertia for power systems with high penetration of renewables. Part I: Theoretical methodology. In Proceedings of the 24th International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Amalfi Coast, Italy, 20–22 June 2018. [Google Scholar]
- Chiodo, E.; Lauria, D.; Mottola, F. On-line bayes estimation of rotational inertia for power systems with high penetration of renewables. Part II: Numerical experiments. In Proceedings of the 24th International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Amalfi Coast, Italy, 20–22 June 2018. [Google Scholar]
- Canevese, S.; Ciapessoni, E.; Gatti, A.; Rossi, M. Monitoring of frequency disturbances in the European continental power system. In Proceedings of the AEIT International Annual Conference (AEIT), Capri, Italy, 5–7 October 2016; pp. 1–6. [Google Scholar]
- Frizera Encarnação, L.; Carletti, D.; de Angeli Souza, S.; de Barros, O., Jr.; CorneauBroedel, D.; Trivilin Rodrigues, P. Virtual inertia for power converter control. Adv. Renew. Energies Power Technol. 2018, 2, 377–411. [Google Scholar] [CrossRef]
- Hirase, Y.; Abe, K.; Sugimoto, K.; Sakimoto, K.; Bevrani, H.; Ise, T. A novel control approach for virtual synchronous generators to suppress frequency and voltage fluctuations in microgrids. Appl. Energy 2018, 210, 699–710. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y.; Watanabe, M.; Küfeoğlu, S. Robust virtual inertia control of an islanded microgrid considering high penetration of renewable energy. IEEE Access 2018, 6, 625–636. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y. Virtual inertia control application to enhance frequency stability of interconnected power systems with high renewable energy penetration. Energies 2018, 11, 981. [Google Scholar] [CrossRef]
- Carpinelli, G.; Caramia, P.; Mottola, F.; Proto, D. Exponential weighted method and a compromise programming method for multi-objective operation of plug-in vehicle aggregators in microgrids. Int. J. Electr. Power Energy Syst. 2014, 56, 374–384. [Google Scholar] [CrossRef]
- Oudalov, A.; Chartouni, D.; Ohler, C. Optimizing a battery energy storage system for primary frequency control. IEEE Trans. Power Syst. 2007, 22, 1259–1266. [Google Scholar] [CrossRef]
- Knap, V.; Chaudhary, S.K.; Stroe, D.I.; Swierczynski, M.; Craciun, B.I.; Teodorescu, R. Sizing of an energy storage system for grid inertial response and primary frequency reserve. IEEE Trans. Power Syst. 2016, 31, 3447–3456. [Google Scholar] [CrossRef]
- Akram, U.; Khalid, M. A Coordinated frequency regulation framework based on hybrid battery-ultracapacitor energy storage technologies. IEEE Access 2018, 6, 7310–7320. [Google Scholar] [CrossRef]
- Continental Europe Operation Handbook. Available online: https://docstore.entsoe.eu/publications/system-operations-reports/operation-handbook/Pages/default.aspx (accessed on 13 September 2018).
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of lithium-ion battery degradation for cell life assessment. IEEE Trans. Smart Grid 2018, 9, 1131–1140. [Google Scholar] [CrossRef]
- Laresgoiti, I.; Käbitz, S.; Ecker, M.; Sauer, D.U. Modeling mechanical degradation in lithium ion batteries during cycling: Solid electrolyte interphase fracture. J. Power Sources 2015, 300, 112–122. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, B.; Tan, Y.; Kirschen, D.; Zhang, B. Optimal battery control under cycle aging mechanisms in pay for performance settings. IEEE Trans. Autom. Control. 2018, in press. [Google Scholar] [CrossRef]
- Xu, B.; Zhao, J.; Zheng, T.; Litvinov, E.; Kirschen, D.S. Factoring the cycle aging cost of batteries participating in electricity markets. IEEE Trans. Power Syst. 2018, 33, 2248–2259. [Google Scholar] [CrossRef]
- Kottick, D.; Blau, M.; Edelstein, D. Battery energy storage for frequency regulation in an island power system. IEEE Trans. Energy Convers. 1993, 8, 455–459. [Google Scholar] [CrossRef]
- Aditya, S.K.; Das, D. Application of battery energy storage system to load frequency control of an isolated power system. Int. J. Energy Res. 1999, 23, 247–258. [Google Scholar] [CrossRef]
- Aditya, S.K.; Das, D. Battery energy storage for load frequency control of an interconnected power system. Electr. Power Syst. Res. 2001, 58, 179–185. [Google Scholar] [CrossRef]
- Delille, G.; François, B.; Malarange, G. Dynamic frequency control support: A virtual inertia provided by distributed energy storage to isolated power systems. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenberg, Sweden, 11–13 October 2010. [Google Scholar]
- Hollinger, R.; Diazgranados, L.M.; Wittwer, C.; Engel, B. Optimal provision of primary frequency control with battery systems by exploiting all degrees of freedom within regulation. Energy Procedia 2016, 99, 204–214. [Google Scholar] [CrossRef]
- Fleer, J.; Stenzel, P. Impact analysis of different operation strategies for battery energy storage systems providing primary control reserve. J. Energy Storage 2016, 8, 320–338. [Google Scholar] [CrossRef]
- Greenwood, D.M.; Lim, K.Y.; Patsios, C.; Lyons, P.F.; Lim, Y.S.; Taylor, P.C. Frequency response services designed for energy storage. Appl. Energy 2017, 203, 115–127. [Google Scholar] [CrossRef]
- Gatta, F.M.; Geri, A.; Lamedica, R.; Lauria, S.; Maccioni, M.; Palone, F.; Rebolini, M.; Ruvio, A. Application of a lifepo4 battery energy storage system to primary frequency control: simulations and experimental results. Energies 2016, 9, 887. [Google Scholar] [CrossRef]
- Borsche, T.S.; Ulbig, A.; Andersson, G. Impact of frequency control reserve provision by storage systems on power system operation. IFAC Proc. Vol. 2014, 47, 4038–4043. [Google Scholar] [CrossRef]
- Brivio, C.; Mandelli, S.; Merlo, M. Battery energy storage system for primary control reserve and energy arbitrage. Sustain. Energy Grids Netw. 2016, 6, 152–165. [Google Scholar] [CrossRef] [Green Version]
- Fleer, J.; Zurmühlen, S.; Badeda, J.; Stenzel, P.; Hake, J.-F.; Uwe Sauer, D. Model-based economic assessment of stationary battery systems providing primary control reserve. Energy Procedia 2016, 99, 11–24. [Google Scholar] [CrossRef]
- Wen, Y.; Li, W.; Huang, G.; Liu, X. Frequency dynamics constrained unit commitment with battery energy storage. IEEE Trans. Power Syst. 2016, 31, 5115–5125. [Google Scholar] [CrossRef]
- Karagiannopoulos, S.; Rigas, A.; Hatziargyriou, N.; Hug, G.; Oudalov, A. Battery energy storage capacity fading and control strategies for deterministic and stochastic power profiles. In Proceedings of the Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016. [Google Scholar]
- Stroe, D.I.; Knap, V.; Swierczynski, M.; Stroe, A.I.; Teodorescu, R. Operation of a grid-connected lithium-ion battery energy storage system for primary frequency regulation: A battery lifetime perspective. IEEE Trans. Ind. Appl. 2017, 53, 430–438. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, B.; Wang, D.; Zhang, B. Using battery storage for peak shaving and frequency regulation: Joint optimization for superlinear gains. IEEE Trans. Power Syst. 2018, 33, 2882–2894. [Google Scholar] [CrossRef]
- Jia, H.; Mu, Y.; Qi, Y. A statistical model to determine the capacity of battery-supercapacitor hybrid energy storage system in autonomous microgrid. Int. J. Electr. Power Energy Syst. 2014, 54, 516–524. [Google Scholar] [CrossRef]
- Orihara, D.; Saitoh, H. Evaluation of battery capacity required for assist of balancing control. J. Int. Counc. Electr. Eng. 2017, 7, 119–124. [Google Scholar] [CrossRef]
- Pan, X.; Xu, H.; Song, J.; Lu, C. Capacity optimization of battery energy storage systems for frequency regulation. In Proceedings of the IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, 24–28 August 2015; pp. 1139–1144. [Google Scholar]
- Li, J.; Ma, Y.; Mu, G.; Feng, X.; Yan, G.; Guo, G.; Zhang, T. Optimal configuration of energy storage system coordinating wind turbine to participate power system primary frequency regulation. Energies 2018, 11, 1396. [Google Scholar] [CrossRef]
- Benato, R.; Dambone Sessa, S.; Musio, M.; Palone, F.; Polito, R.M. Italian experience on electrical storage ageing for primary frequency regulation. Energies 2018, 11, 2087. [Google Scholar] [CrossRef]
- Lian, B.; Sims, A.; Yu, D.; Wang, C.; Dunn, R.W. Optimizing LiFePO4 battery energy storage systems for frequency response in the UK system. IEEE Trans. Sustain. Energy 2017, 8, 385–394. [Google Scholar] [CrossRef]
- Alharbi, H.; Bhattacharya, K. Stochastic optimal planning of battery energy storage systems for isolated microgrids. IEEE Trans. Sustain. Energy 2018, 9, 211–227. [Google Scholar] [CrossRef]
- Johnston, L.; Díaz-González, F.; Gomis-Bellmunt, O.; Corchero-García, C.; Cruz-Zambrano, M. Methodology for the economic optimisation of energy storage systems for frequency support in wind power plants. Appl. Energy 2015, 137, 660–669. [Google Scholar] [CrossRef] [Green Version]
- Aghamohammadi, M.R.; Abdolahinia, H. A new approach for optimal sizing of battery energy storage system for primary frequency control of islanded Microgrid. Int. J. Electr. Power Energy Syst. 2014, 54, 325–333. [Google Scholar] [CrossRef]
- Ramírez, M.; Castellanos, R.; Calderón, G.; Malik, O. Placement and sizing of battery energy storage for primary frequency control in an isolated section of the Mexican power system. Electr. Power Syst. Res. 2018, 160, 142–150. [Google Scholar] [CrossRef]
- Zhang, Y.J.A.; Zhao, C.; Tang, W.; Low, S.H. Profit-maximizing planning and control of battery energy storage systems for primary frequency control. IEEE Trans. Smart Grid 2018, 9, 712–723. [Google Scholar] [CrossRef]
- Marconato, R. Electric Power Systems Vol. 3. Dynamic Behaviour, Stability and Emergency Controls; Hoepli: Milan, Italy, 2004. [Google Scholar]
- Matsuishi, M.; Endo, T. Fatigue of metals subjected to varying stress. Jpn. Soc. Mech. Eng. 1968, 68, 37–40. [Google Scholar]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, A159–A164. [Google Scholar]
- Han, H.; Li, Q.; Lu, Z.; Yang, X. Energy storage frequency response control considering battery aging of electric vehicle. In Proceedings of the IEEE International Conference on Energy Internet, Beijing, China, 17–21 April 2017; pp. 72–76. [Google Scholar]
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Kallas, M.; Honeine, P.; Richard, C.; Francis, C.; Amoud, H. Prediction of time series using Yule-Walker equations with kernels. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 2185–2188. [Google Scholar]
- Hassanzadeh, M.; Evrenosoğlu, C.Y.; Mili, L. A Short-term nodal voltage phasor forecasting method using temporal and spatial correlation. IEEE Trans. Power Syst. 2016, 31, 3881–3890. [Google Scholar] [CrossRef]
- Andrenacci, N.; Pede, G.; Chiodo, E.; Lauria, D.; Mottola, F. Tools for life cycle estimation of energy storage system for primary frequency reserve. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 1008–1013. [Google Scholar]
- RTE, Network Frequency. Available online: http://clients.rte-france.com/lang/an/visiteurs/vie/vie_frequence.jsp (accessed on 13 September 2018).
- Tiku, M.L.; Wong, W.K.; Bian, G. Estimating parameters in autoregressive models in non-normal situations: Symmetric innovations. Commun. Stat. Theory Methods 1999, 28, 315–341. [Google Scholar] [CrossRef]
- Wong, W.K.; Bian, G. Estimating parameters in autoregressive models with asymmetric innovations. Stat. Probab. Lett. 2005, 71, 61–70. [Google Scholar] [CrossRef]

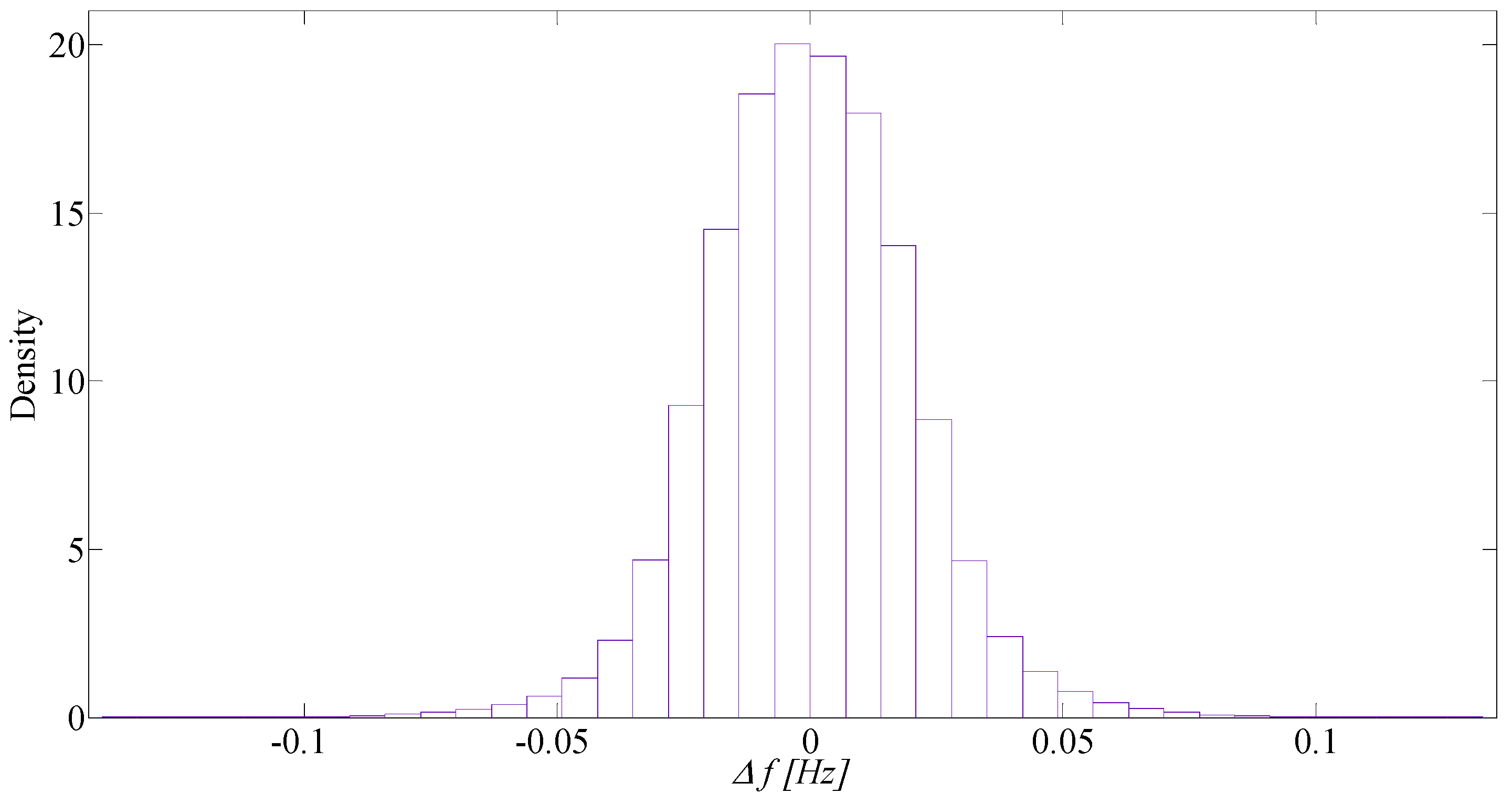

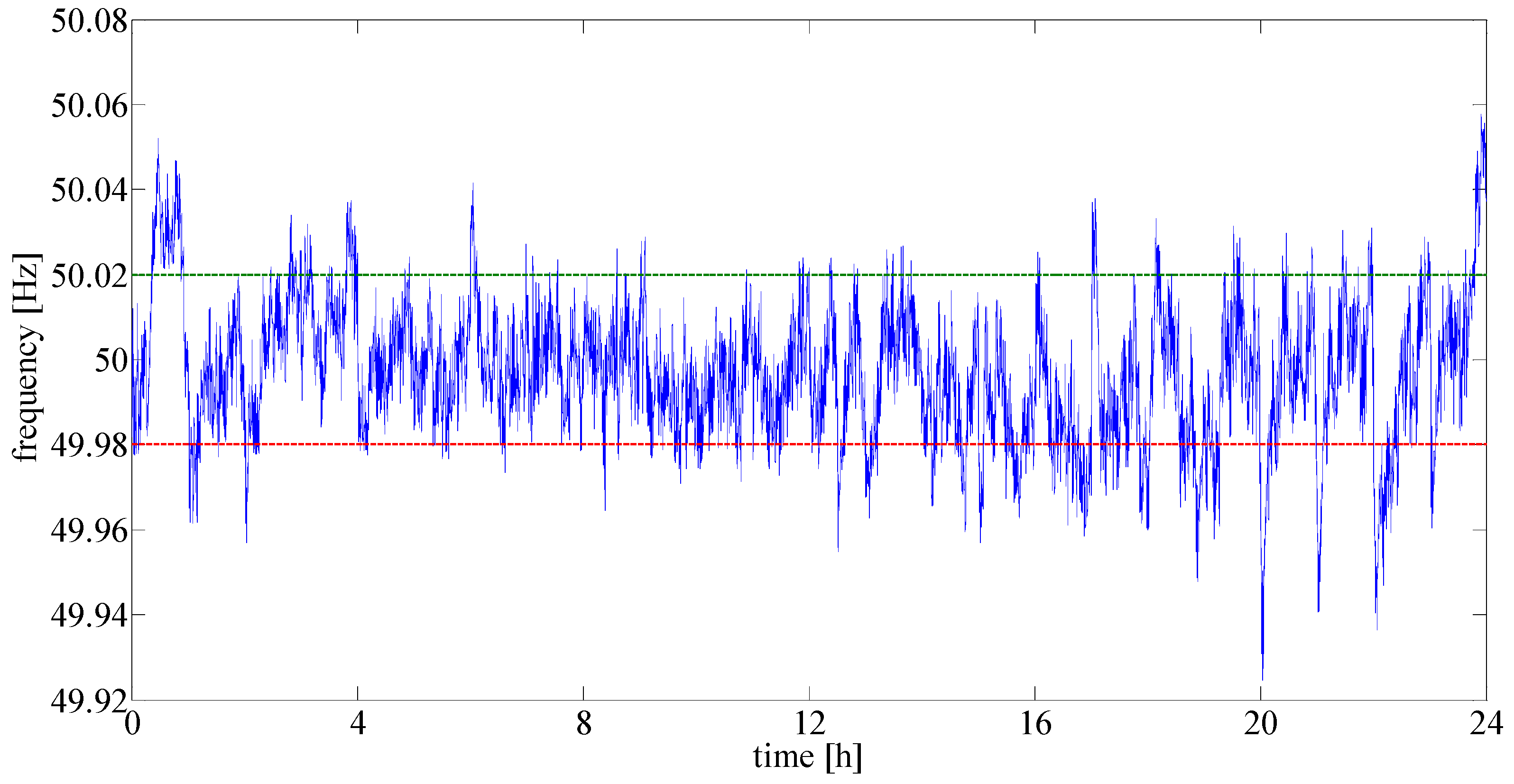
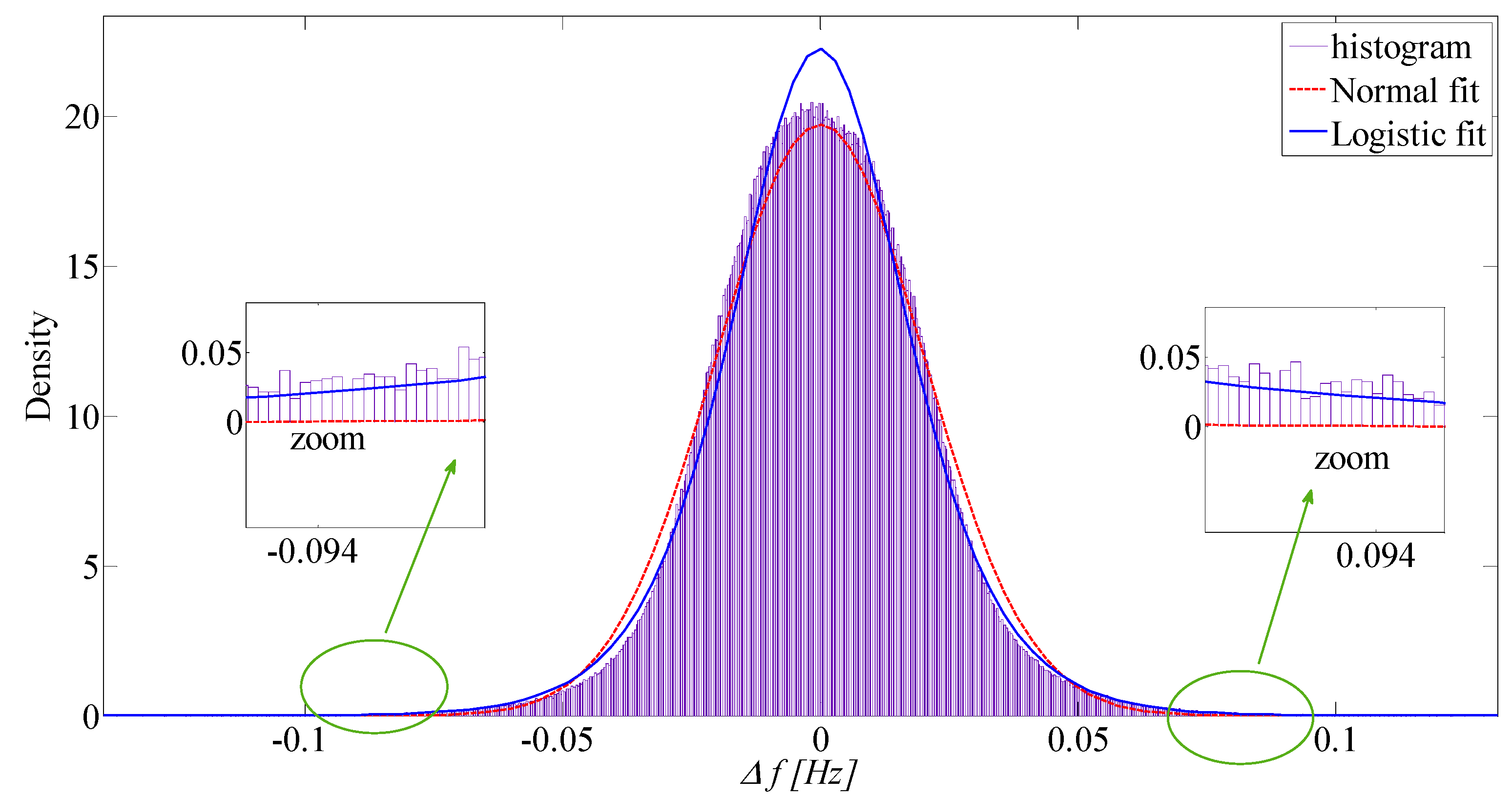

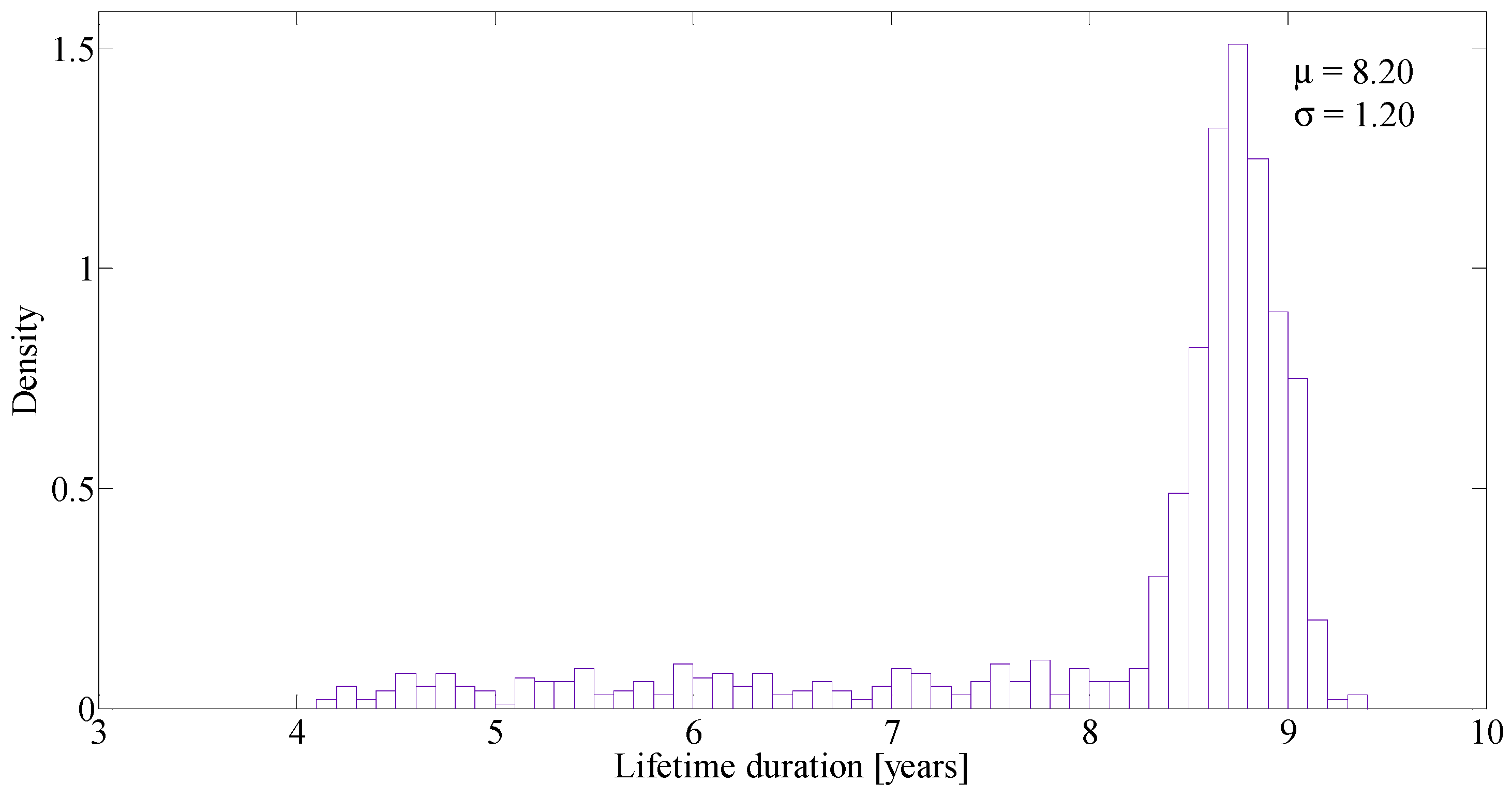
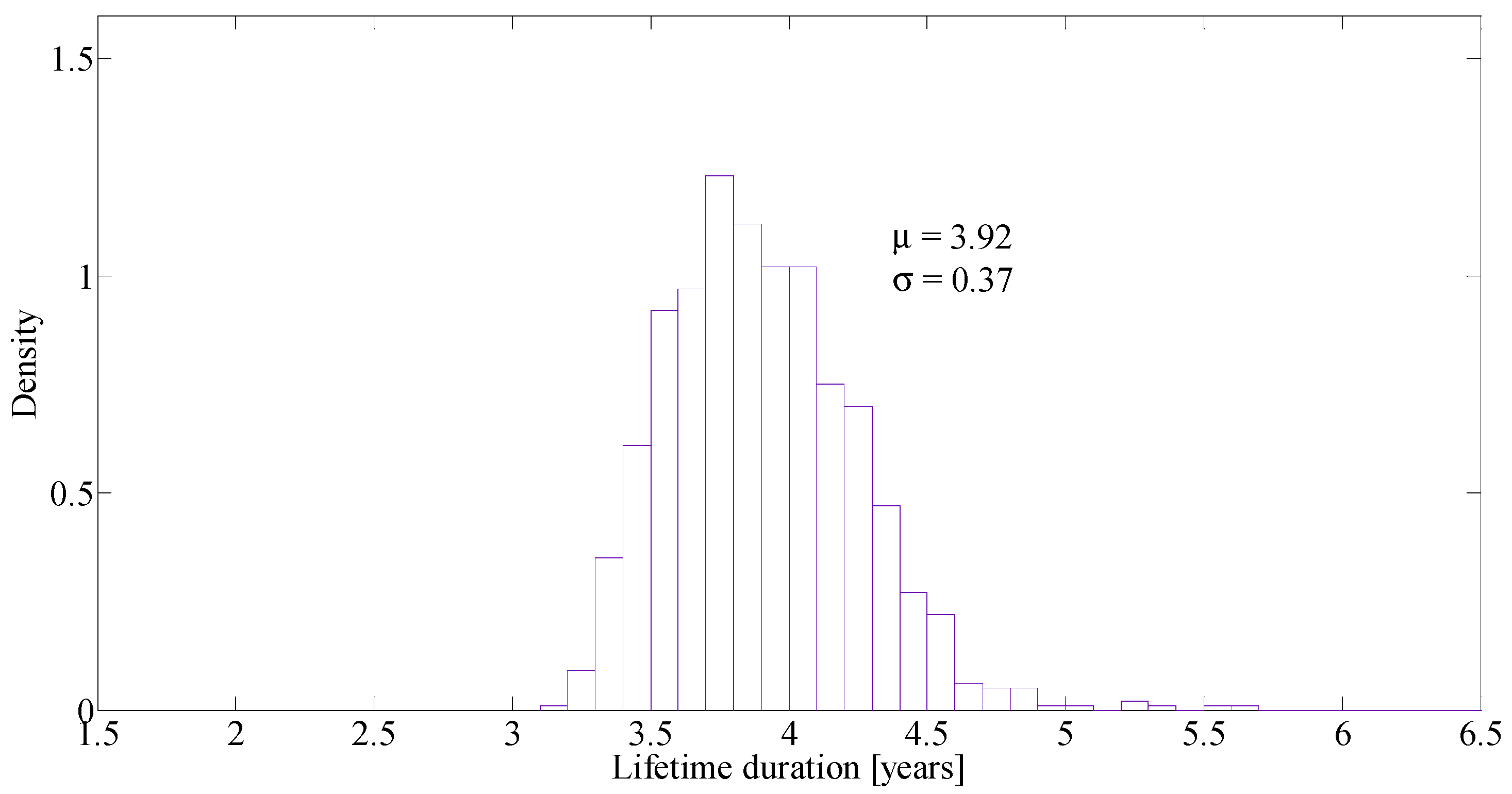
| Fitting Distribution | Mean | Variance | Log Likelihood |
|---|---|---|---|
| Normal | ≅0 | 0.00040936 | 6.92523 × 106 |
| Logistic | ≅0 | 0.00041542 | 6.9568 × 106 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrenacci, N.; Chiodo, E.; Lauria, D.; Mottola, F. Life Cycle Estimation of Battery Energy Storage Systems for Primary Frequency Regulation. Energies 2018, 11, 3320. https://doi.org/10.3390/en11123320
Andrenacci N, Chiodo E, Lauria D, Mottola F. Life Cycle Estimation of Battery Energy Storage Systems for Primary Frequency Regulation. Energies. 2018; 11(12):3320. https://doi.org/10.3390/en11123320
Chicago/Turabian StyleAndrenacci, Natascia, Elio Chiodo, Davide Lauria, and Fabio Mottola. 2018. "Life Cycle Estimation of Battery Energy Storage Systems for Primary Frequency Regulation" Energies 11, no. 12: 3320. https://doi.org/10.3390/en11123320
APA StyleAndrenacci, N., Chiodo, E., Lauria, D., & Mottola, F. (2018). Life Cycle Estimation of Battery Energy Storage Systems for Primary Frequency Regulation. Energies, 11(12), 3320. https://doi.org/10.3390/en11123320








