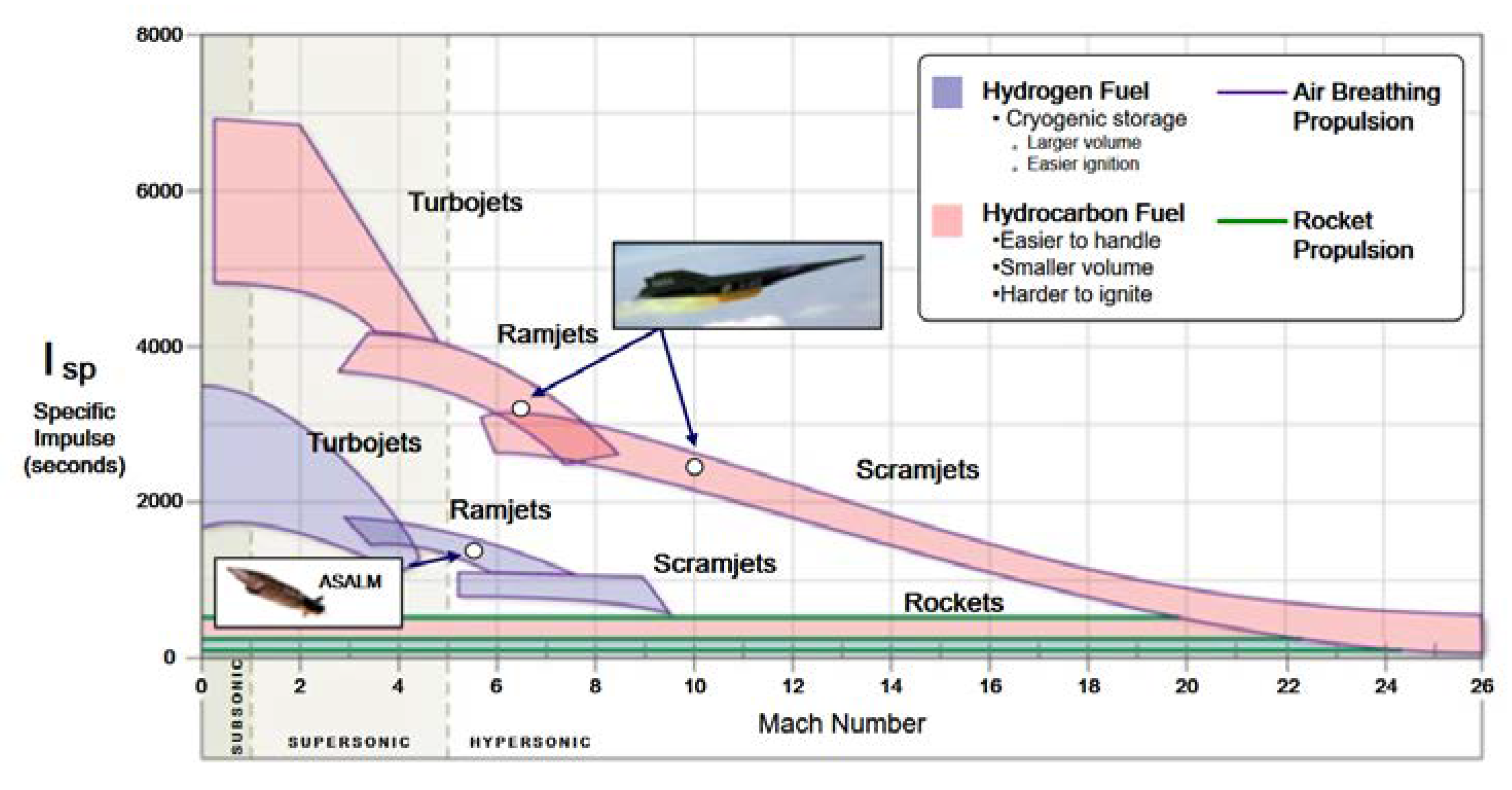
Figure 1.
Operation envelopes of air breathing engines.
Figure 1.
Operation envelopes of air breathing engines.
Figure 2.
2D geometries of (a) nozzle, (b) scramjet engine, and (c) aircraft and scramjet engine integration.
Figure 2.
2D geometries of (a) nozzle, (b) scramjet engine, and (c) aircraft and scramjet engine integration.
Figure 3.
3D geometries of (a) nozzle, (b) scramjet engine, and (c) aircraft and scramjet engine integration.
Figure 3.
3D geometries of (a) nozzle, (b) scramjet engine, and (c) aircraft and scramjet engine integration.
Figure 4.
Sections of 2D mesh for the nozzle (top left), scramjet engine (top right), and integrated aircraft and scramjet engine (bottom).
Figure 4.
Sections of 2D mesh for the nozzle (top left), scramjet engine (top right), and integrated aircraft and scramjet engine (bottom).
Figure 5.
3D mesh for the nozzle (top), scramjet engine (middle), and integrated aircraft and scramjet engine (bottom).
Figure 5.
3D mesh for the nozzle (top), scramjet engine (middle), and integrated aircraft and scramjet engine (bottom).
Figure 6.
Comparison of static pressure contours between Huang et al. [
10] (
left) and the present analysis (
right).
Figure 6.
Comparison of static pressure contours between Huang et al. [
10] (
left) and the present analysis (
right).
Figure 7.
Comparison of Mach number contours between Huang et al. [
10] (
left) and the present analysis (
right).
Figure 7.
Comparison of Mach number contours between Huang et al. [
10] (
left) and the present analysis (
right).
Figure 8.
Comparison of pressure distribution in the nozzle.
Figure 8.
Comparison of pressure distribution in the nozzle.
Figure 9.
Static pressure distribution of SERN DP351 for 80,000 ft. (top) and 100,000 ft. (bottom).
Figure 9.
Static pressure distribution of SERN DP351 for 80,000 ft. (top) and 100,000 ft. (bottom).
Figure 10.
Contours of Mach number for DP 351 at BCC 1.1 (top) and BCC 3.2 (bottom).
Figure 10.
Contours of Mach number for DP 351 at BCC 1.1 (top) and BCC 3.2 (bottom).
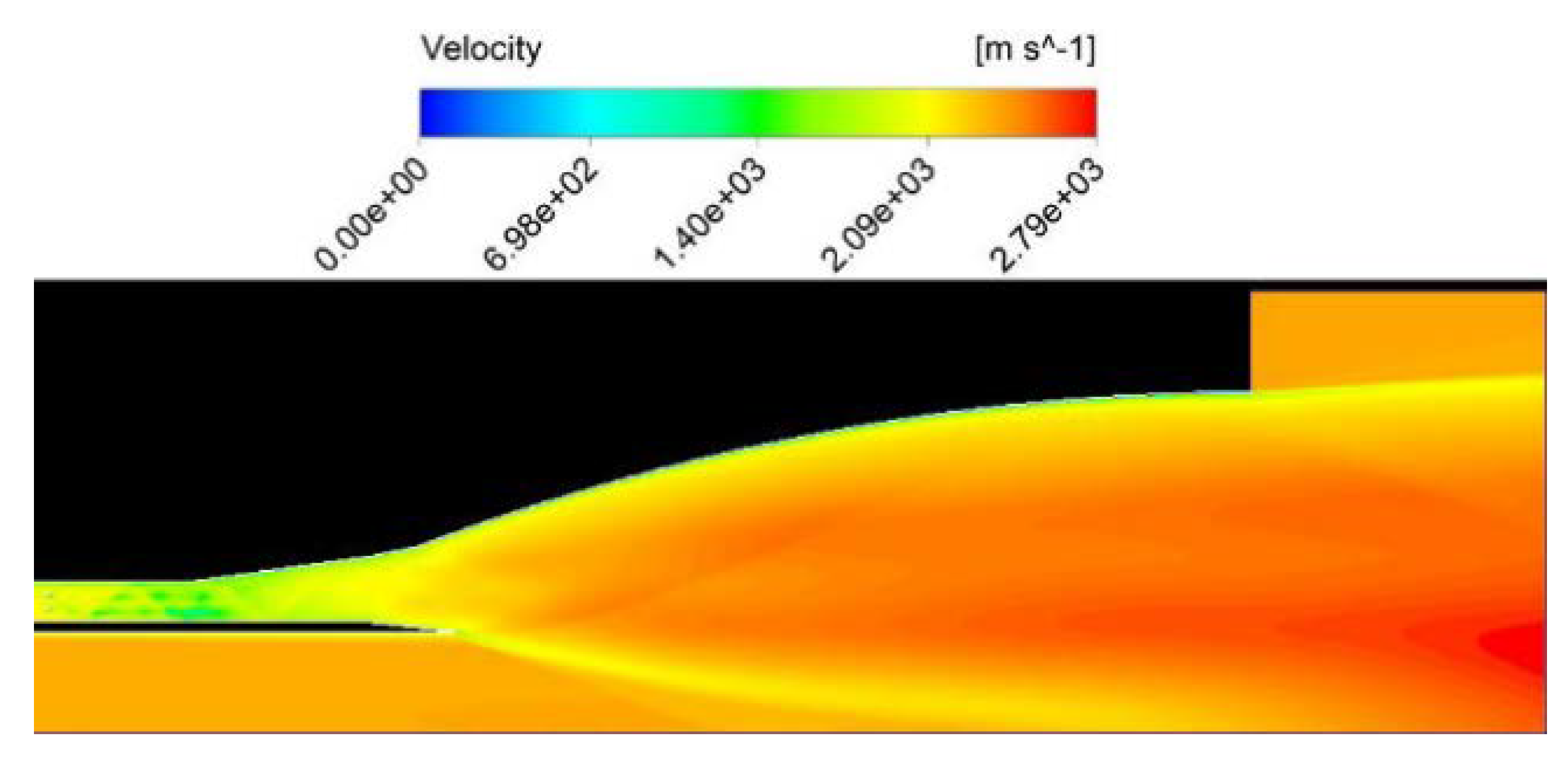
Figure 11.
Contours of velocity for DP 464 (top) and DP 102 (bottom).
Figure 11.
Contours of velocity for DP 464 (top) and DP 102 (bottom).
Figure 12.
Mach number (left) and pressure contours (right) for DP279 (top), DP690 (middle), and DP487 (bottom).
Figure 12.
Mach number (left) and pressure contours (right) for DP279 (top), DP690 (middle), and DP487 (bottom).
Figure 13.
Pressure contours for DP471, DP640, DP52, and DP205 (clockwise from top left).
Figure 13.
Pressure contours for DP471, DP640, DP52, and DP205 (clockwise from top left).
Figure 14.
SERN geometries achieving best performance parameters for BCC 3.1.
Figure 14.
SERN geometries achieving best performance parameters for BCC 3.1.
Figure 15.
Static pressure of DP102 and DP456 along the nozzle inlet centerline.
Figure 15.
Static pressure of DP102 and DP456 along the nozzle inlet centerline.
Figure 16.
Density contours of DP102 (top) and DP456 (bottom) illustrating shock structures.
Figure 16.
Density contours of DP102 (top) and DP456 (bottom) illustrating shock structures.
Figure 17.
Mach number contours for DP102 (top) and DP456 (bottom) depicting the kernel region.
Figure 17.
Mach number contours for DP102 (top) and DP456 (bottom) depicting the kernel region.
Figure 18.
Mach number profiles for different cases at distances (from top to bottom) of: 0 m, 1 m, 2 m, and 3 m from the nozzle inlet.
Figure 18.
Mach number profiles for different cases at distances (from top to bottom) of: 0 m, 1 m, 2 m, and 3 m from the nozzle inlet.
Figure 19.
Mach number (top) and pressure contours (bottom) of DP102 for cold flow (left) and hot flow (right).
Figure 19.
Mach number (top) and pressure contours (bottom) of DP102 for cold flow (left) and hot flow (right).
Figure 20.
Temperature (top) and velocity contours (bottom) of DP102 for cold flow (left) and hot flow (right).
Figure 20.
Temperature (top) and velocity contours (bottom) of DP102 for cold flow (left) and hot flow (right).
Figure 21.
Pressure and velocity contours for SERN DP456.
Figure 21.
Pressure and velocity contours for SERN DP456.
Figure 22.
Velocity contour of SERN DP456 with combustion at 10 m downstream of the SERN exit.
Figure 22.
Velocity contour of SERN DP456 with combustion at 10 m downstream of the SERN exit.
Figure 23.
Pressure variation along the scramjet for different flow types.
Figure 23.
Pressure variation along the scramjet for different flow types.
Figure 24.
Mach number contours for SERN DP456 with small (top) and large (bottom) side fence.
Figure 24.
Mach number contours for SERN DP456 with small (top) and large (bottom) side fence.
Figure 25.
Mach streamlines for SERN DP456 with small (left) and large (right) side fence.
Figure 25.
Mach streamlines for SERN DP456 with small (left) and large (right) side fence.
Figure 26.
Mach contours and streamlines for SERN DP456 with the large side fence configuration at a 4.29° angle.
Figure 26.
Mach contours and streamlines for SERN DP456 with the large side fence configuration at a 4.29° angle.
Figure 27.
Velocity and density streamlines of the scramjet engine.
Figure 27.
Velocity and density streamlines of the scramjet engine.
Figure 28.
Mach number contours of the scramjet engine with planes positioned from the nozzle inlet onwards.
Figure 28.
Mach number contours of the scramjet engine with planes positioned from the nozzle inlet onwards.
Figure 29.
Velocity streamlines and displaying the effect on the SERN performance at Mach 4.5.
Figure 29.
Velocity streamlines and displaying the effect on the SERN performance at Mach 4.5.
Figure 30.
Mach streamlines, contours, and volume of the proposed aircraft at Mach 8.
Figure 30.
Mach streamlines, contours, and volume of the proposed aircraft at Mach 8.
Table 1.
2D nozzle geometric parameters with corresponding values investigated.
Table 1.
2D nozzle geometric parameters with corresponding values investigated.
| Geometrical Parameters | Parameter ID | Range |
|---|
| Nozzle inlet height (m) | P1 | 1, 1.5, 2 |
| Nozzle outlet height (m) | P2 | 5.3, 7.3, 9.3 |
| Expansion ramp contour radius (m) | P3 | 50–5000 (conical) |
| Initial expansion ramp length (m) | P4 | 1.6, 3.2 |
| Initial expansion ramp angle (degree) | P5 | 10, 30 |
| Nozzle and after body length (m) | P6 | 30, 40 |
| Cowl length (m) | P7 | 3 |
| Cowl thickness (m) | P8 | 0.3 |
| Cowl ramp angle (degree) | P9 | 5.72, 33 |
Table 2.
2D mesh statistics.
Table 2.
2D mesh statistics.
| Parameters | Nozzle Only | Scramjet | Integrated Scramjet |
|---|
| Elements | 93,919–151,956 | 360,702 | 453,185 |
| Average skewness | 0.432 | 0.617 | 0.138 |
| Average orthogonal quality | 0.895 | 0.830 | 0.973 |
Table 3.
3D mesh statistics.
Table 3.
3D mesh statistics.
| Parameters | Nozzle Only | Scramjet | Integrated Scramjet Engine |
|---|
| Elements | 3,325,405 | 4,524,968 | 5,591,991 |
| Average skewness | 0.259 | 0.234 | 0.215 |
| Average orthogonal quality | 0.858 | 0.821 | 0.866 |
Table 4.
Boundary conditions for computational analysis.
Table 4.
Boundary conditions for computational analysis.
| Boundary Conditions | Altitude, 80,000 ft | Altitude, 90,000 ft | Altitude, 100,000 ft |
|---|
| Freestream pressure | 2761 | 1730 | 1216 |
| Freestream temperature | 221 | 224 | 224 |
| Freestream Mach number | 5 | 6.5 | 8 |
Table 5.
Input parameters for the nozzle inlet conditions.
Table 5.
Input parameters for the nozzle inlet conditions.
| Boundary Conditions (BCC) | BCC 1.1 | BCC 1.2 | BCC 2.1 | BCC 2.2 | BCC 3.1 | BCC 3.2 |
|---|
| 80,000 ft | 80,000 ft | 90,000 ft | 90,000 ft | 100,000 ft | 100,000 ft |
|---|
| NI pressure | 471,112 | 425,000 | 425,000 | 365,000 | 365,000 | 335,000 |
| NI temperature | 2972 | 3030 | 3030 | 3033 | 3033 | 3048 |
| NI Mach number | 2 | 2.4 | 2.4 | 2.7 | 2.7 | 3 |
| FS (freestream) pressure | 2761 | 2761 | 1730 | 1730 | 1216 | 1216 |
| FS temperature | 221 | 221 | 224 | 224 | 224 | 224 |
| FS Mach number | 5 | 5 | 6.5 | 6.5 | 8 | 8 |
Table 6.
SERN geometries for different design points (DPs).
Table 6.
SERN geometries for different design points (DPs).
| DP | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | Pexit | Expansion |
|---|
| 351 | 1 m | 9.3 m | 5000 m | 3.2 m | 10° | 30 m | 3 m | 0.3 m | 5.72° | 2695 | Over |
| 470 | 1.5 m | 9.3 m | 5000 m | 3.2 m | 10° | 40 m | 3 m | 0.3 m | 33° | 2835 | Under |
| 1524 | 1.5 m | 9.3 m | 5000 m | 3.2 m | 10° | 30 m | 3 m | 0.3 m | 5.72° | 2846 | Under |
Table 7.
SERN geometries which yield maximum thrust at 30 m and 40 m expansion ramp length for BCC 3.2.
Table 7.
SERN geometries which yield maximum thrust at 30 m and 40 m expansion ramp length for BCC 3.2.
| DP | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | Axial Thrust |
|---|
| 102 | 2 m | 9.3 m | 65 m | 1.6 m | 10° | 30 | 3 | 0.3 m | 33° | 5,668,441 N |
| 544 | 2 m | 9.3 m | 125 m | 1.6 m | 10° | 40 | 3 | 0.3 m | 5.72° | 5,063,079 N |
Table 8.
Maximum axial thrust for varying nozzle area ratios of SERN.
Table 8.
Maximum axial thrust for varying nozzle area ratios of SERN.
| DP | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | Area Ratio | Axial Thrust (N) |
|---|
| 102 | 2 m | 9.3 m | 65 m | 1.6 m | 10° | 30 | 3 | 0.3 | 33 | 4.65 | 5,668,441 |
| 456 | 2 m | 7.3 m | 90 m | 1.6 m | 10° | 30 | 3 | 0.3 | 5.72 | 3.65 | 5,144,993 |
| 623 | 1.5 m | 7.3 m | 90 m | 1.6 m | 10° | 30 | 3 | 0.3 | 5.72 | 4.87 | 4,333,759 |
| 86 | 1.5 m | 9.3 m | 60 m | 1.6 m | 10° | 30 | 3 | 0.3 | 33 | 6.2 | 3,990,316 |
| 68 | 1 m | 9.3 m | 57.5 m | 1.6 m | 10° | 30 | 3 | 0.3 | 33 | 9.3 | 2,833,642 |
Table 9.
SERN geometries for best performance.
Table 9.
SERN geometries for best performance.
| DP | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 |
|---|
| 102 | 2 m | 9.3 m | 65 m | 1.6 m | 10° | 30 | 3 | 0.3 | 33 |
| 471 | 1 m | 9.3 m | 5000 m | 3.2 m | 10° | 40 | 3 | 0.3 | 5.72 |
| 633 | 1.5 m | 9.3 m | 75 m | 1.6 m | 30° | 30 | 3 | 0.3 | 5.72 |
| 487 | 1.5 m | 7.3 m | 200 m | 3.2 m | 10° | 40 | 3 | 0.3 | 5.72 |
| 456 | 2 m | 7.3 m | 90 m | 1.6 m | 10° | 30 | 3 | 0.3 | 5.72 |
Table 10.
SERN DP102 overall performance at each BCC.
Table 10.
SERN DP102 overall performance at each BCC.
| Nozzle Inlet Conditions | BCC 1.1 | BCC 1.2 and 2.1 | BCC 2.2 and 3.1 | BCC 3.2 |
|---|
| Axial thrust (N) | 4,084,299 | 4,918,431 | 5,144,993 | 5,668,440 |
| Estimated net thrust | N/A | N/A | 4,874,588 | 5,263,095 |
| Nozzle divergence coeff. | 0.934 | 0.934 | 0.934 | 0.934 |
| Lift coeff. | −0.107 | −0.153 | −0.200 | −0.228 |
| Drag coefficient | 0.139 | 0.155 | 0.166 | 0.173 |
| Moment coefficient | 0.112 | 0.069 | 0.021 | −0.0102 |
| Exit velocity | 2929 | 3245 | 3519 | 3809 |
| Exit pressure | 21,061 | 22,069 | 20,723 | 20,509 |
| Nozzle expansion | under | under | under | Under |
Table 11.
Performance comparison of different nozzle inlet conditions at 10,000 ft. and Mach 8.
Table 11.
Performance comparison of different nozzle inlet conditions at 10,000 ft. and Mach 8.
| Nozzle Inlet Conditions | Uniform DP102 | Uniform DP456 | Cold DP102 | Cold DP456 | Hot DP102 | Hot DP456 | Hot DP456-2 |
|---|
| Axial thrust (N) | 5,144,993 | 4,829,270 | 2,117,356 | 1,992,168 | 2,316,858 | 2,085,313 | 2,098,602 |
| Estimated Net Thrust | 4,874,588 | 4,467,074 | 1,826,559 | 1,732,003 | 2,067,173 | 1,836,564 | 1,873,415 |
| Exit velocity (m/s) | 3518 | 3474 | 2223 | 2423 | 2523 | 2482 | 2500 |
| Exit Pressure | 20,722 | 20,098 | 838 | 558 | 1826 | 2122 | 2083 |
Table 12.
Performance comparison of different nozzle conditions at 100,00 ft. and Mach 8.
Table 12.
Performance comparison of different nozzle conditions at 100,00 ft. and Mach 8.
| Nozzle Inlet Conditions | 2D DP456 | 3D Small Fence
0° Fence Angle | 3D Large Fence
0° Fence Angle | 3D Large Fence
4.29° Fence Angle |
|---|
| Axial thrust (N) | 4,829,270 | 7,533,145 | 13,321,487 | 14,741,256 |
| Estimated net Thrust (N) | 4,467,074 | 6,179,926 | 12,269,893 | 13,775,863 |
| Exit velocity (m/s) | 3474 | 2587 | 2502 | 2468 |
| Exit pressure (Pa) | 20,098 | 4732 | 11,848 | 13,893 |