Acoustic Wave-Based Method of Locating Tubing Leakage for Offshore Gas Wells
Abstract
:1. Introduction
2. Theory and Methods
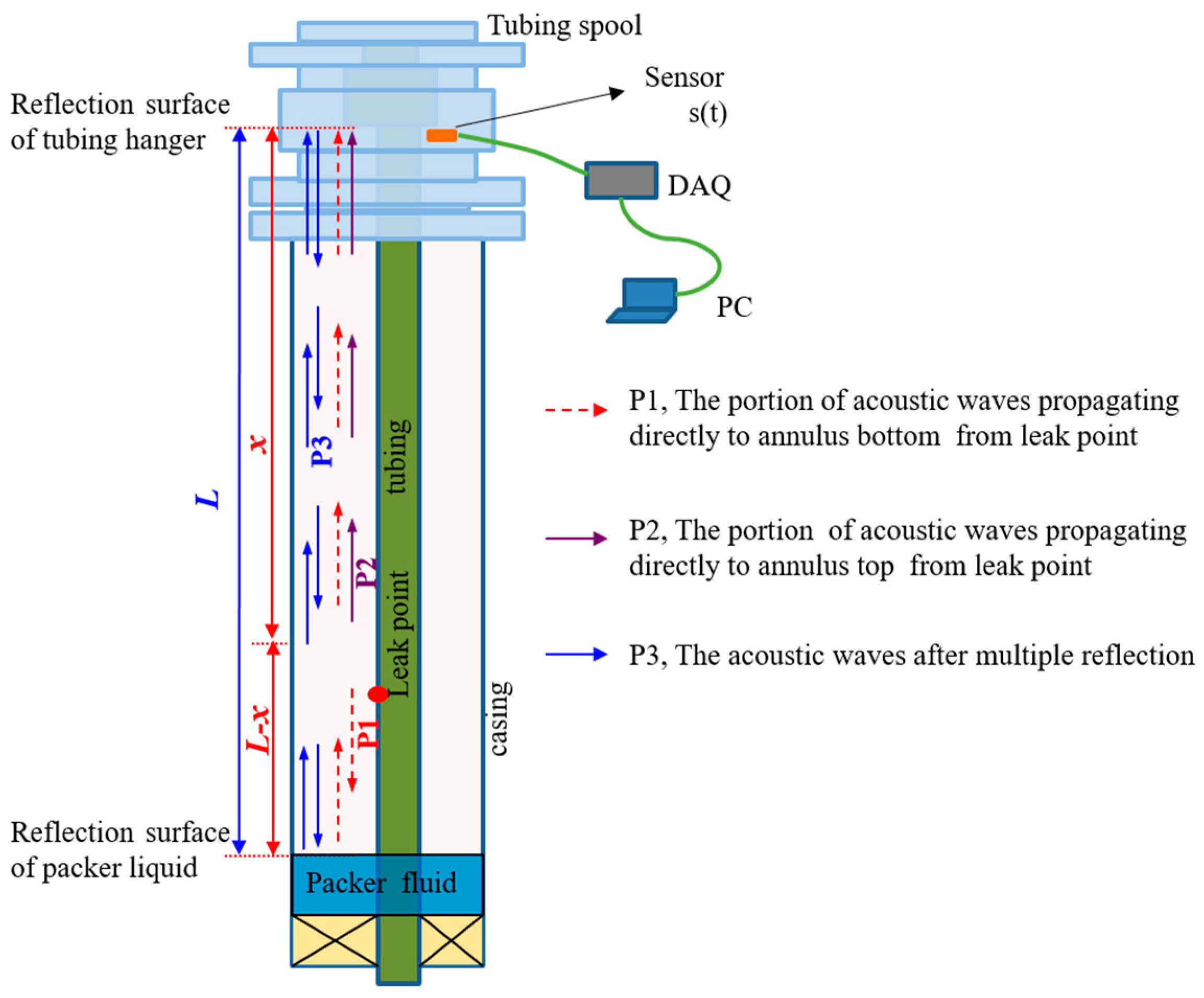
2.1. Principles
2.2. Acoustic Velocity in the Annulus
2.2.1. Temperature Distribution in Annulus
2.2.2. Pressure Distribution in the Annulus
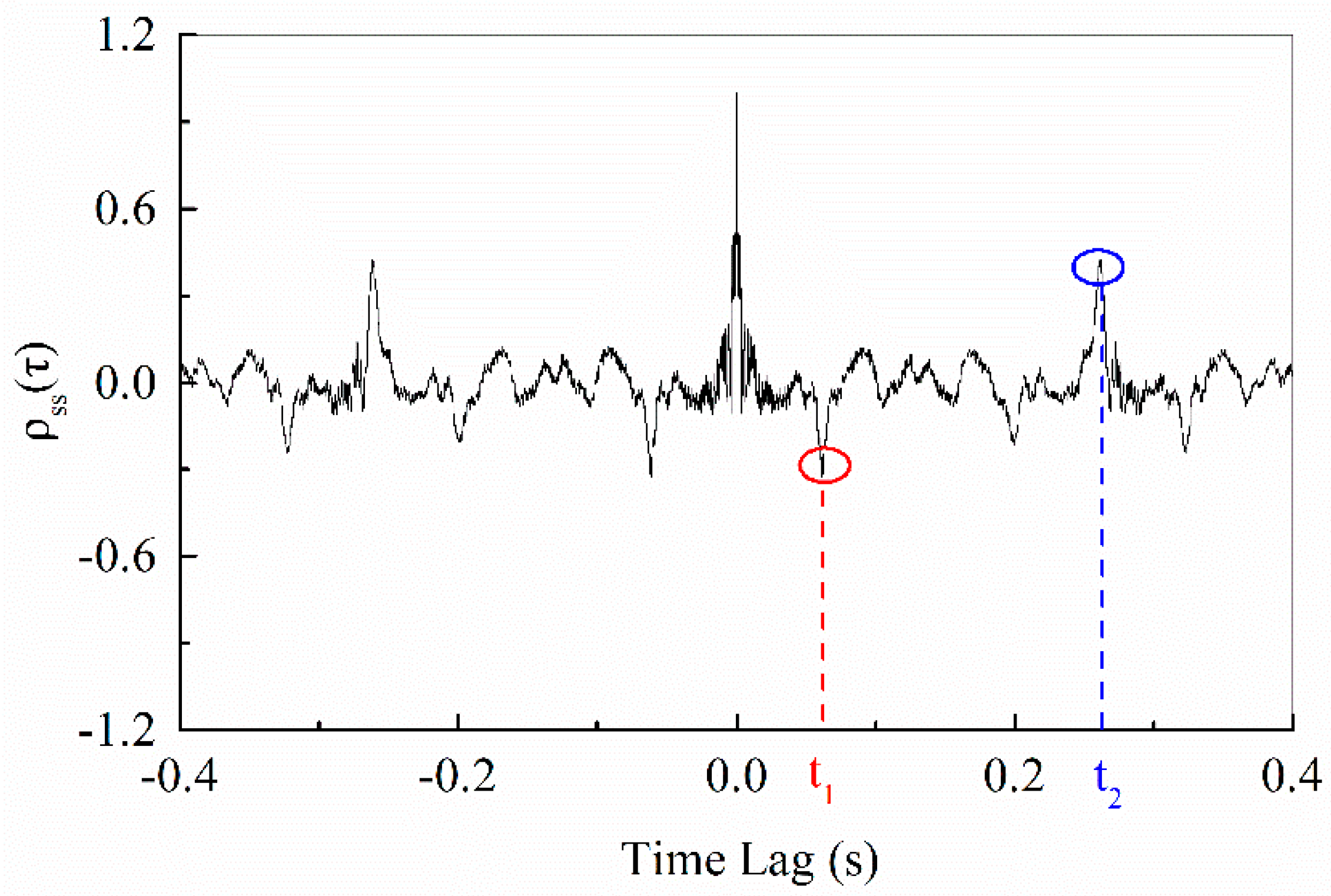
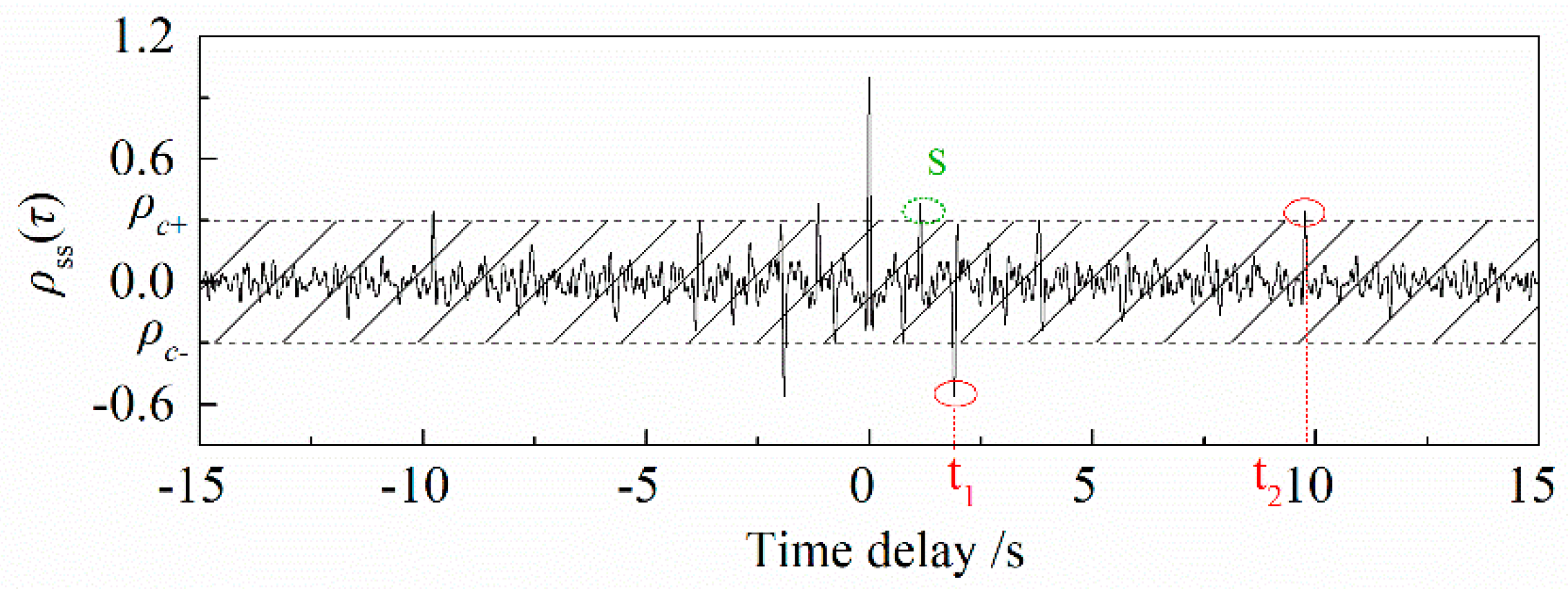
2.3. Extraction of Characteristic Time
2.4. Model for Locating Downhole Tubing Leakage
3. Laboratory Experiments
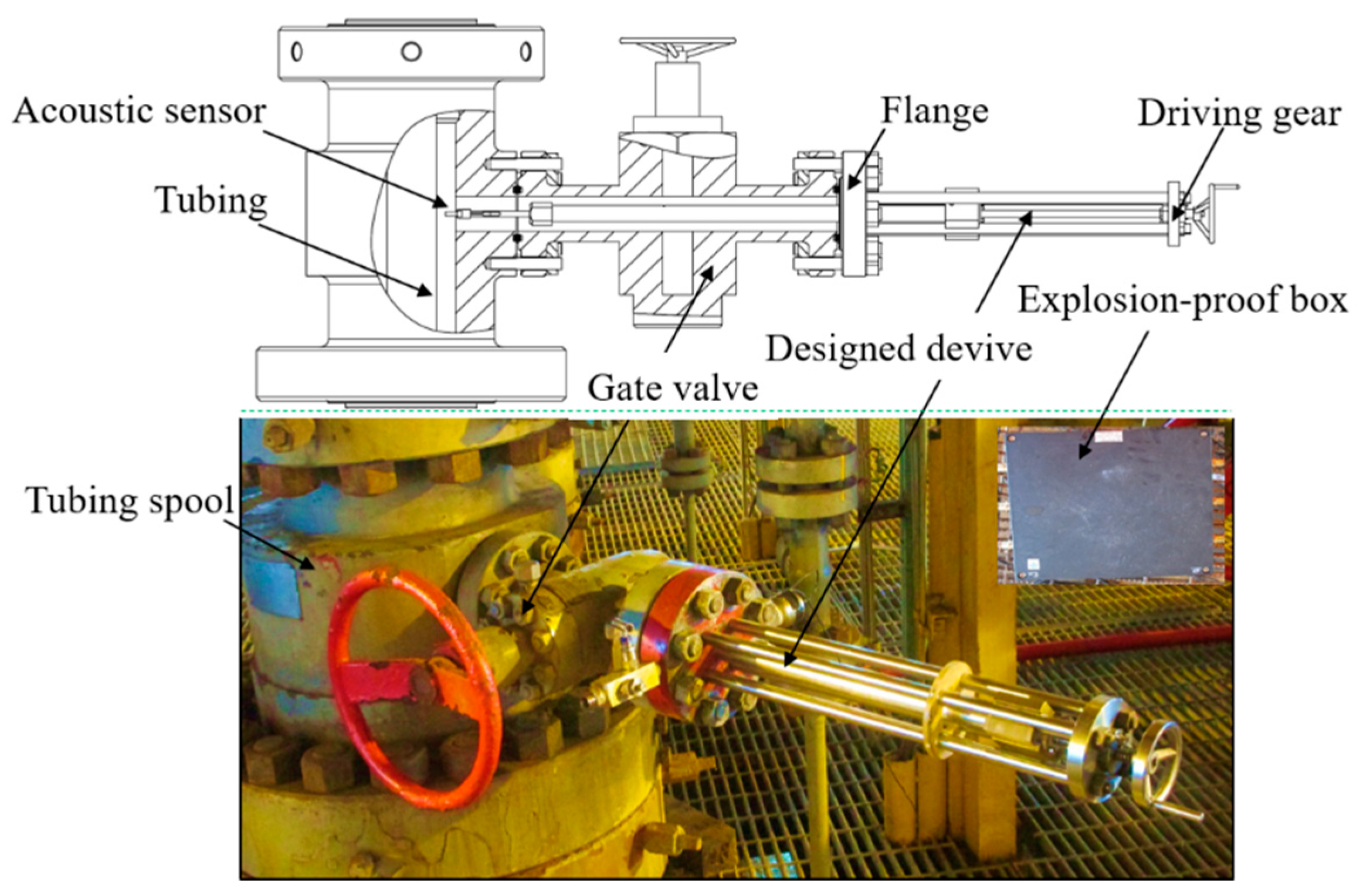
3.1. Experimental System
3.2. Experimental Design
3.3. Experimental Results and Discussion
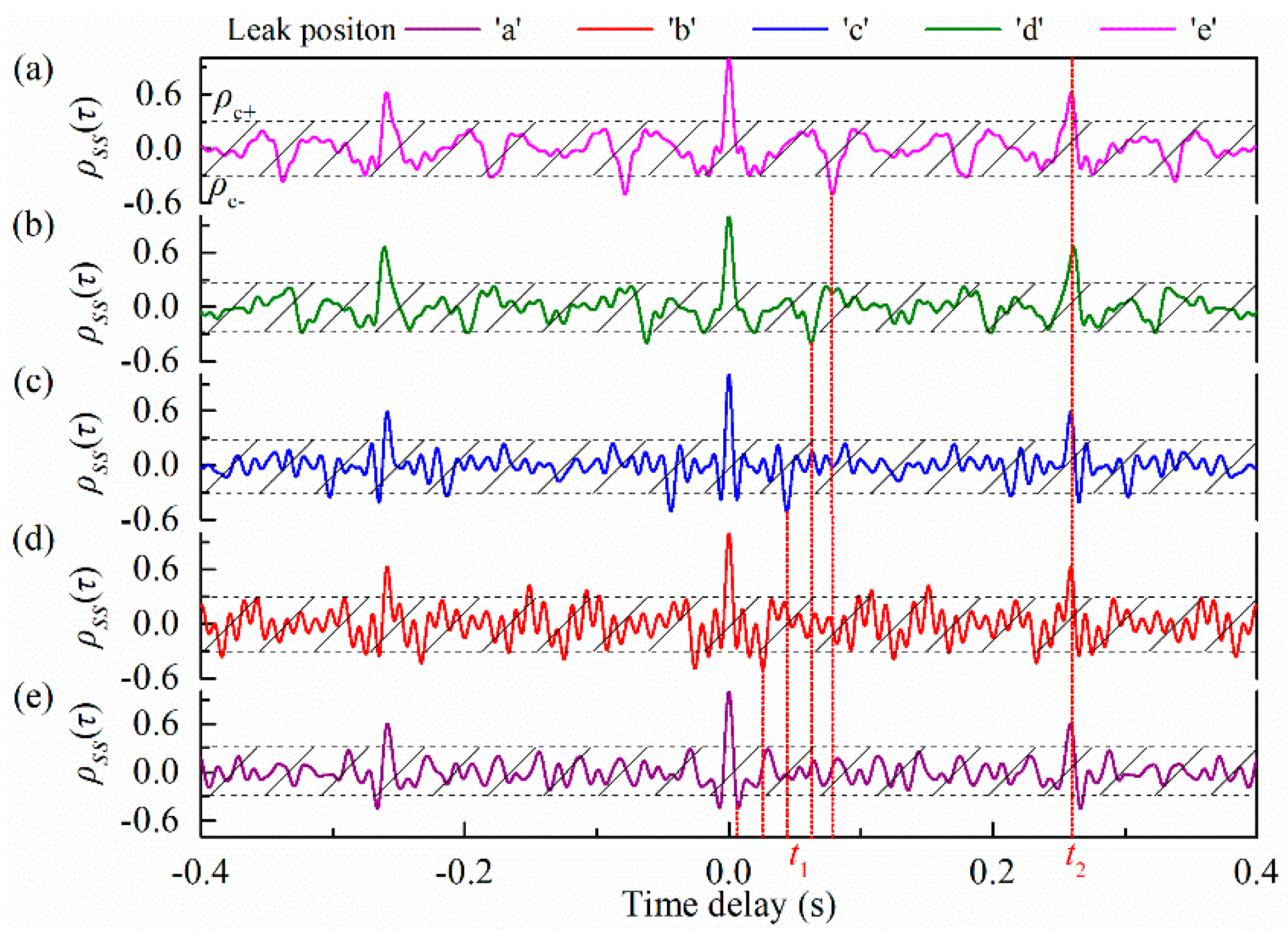
3.3.1. Leak Localization for Different Positions
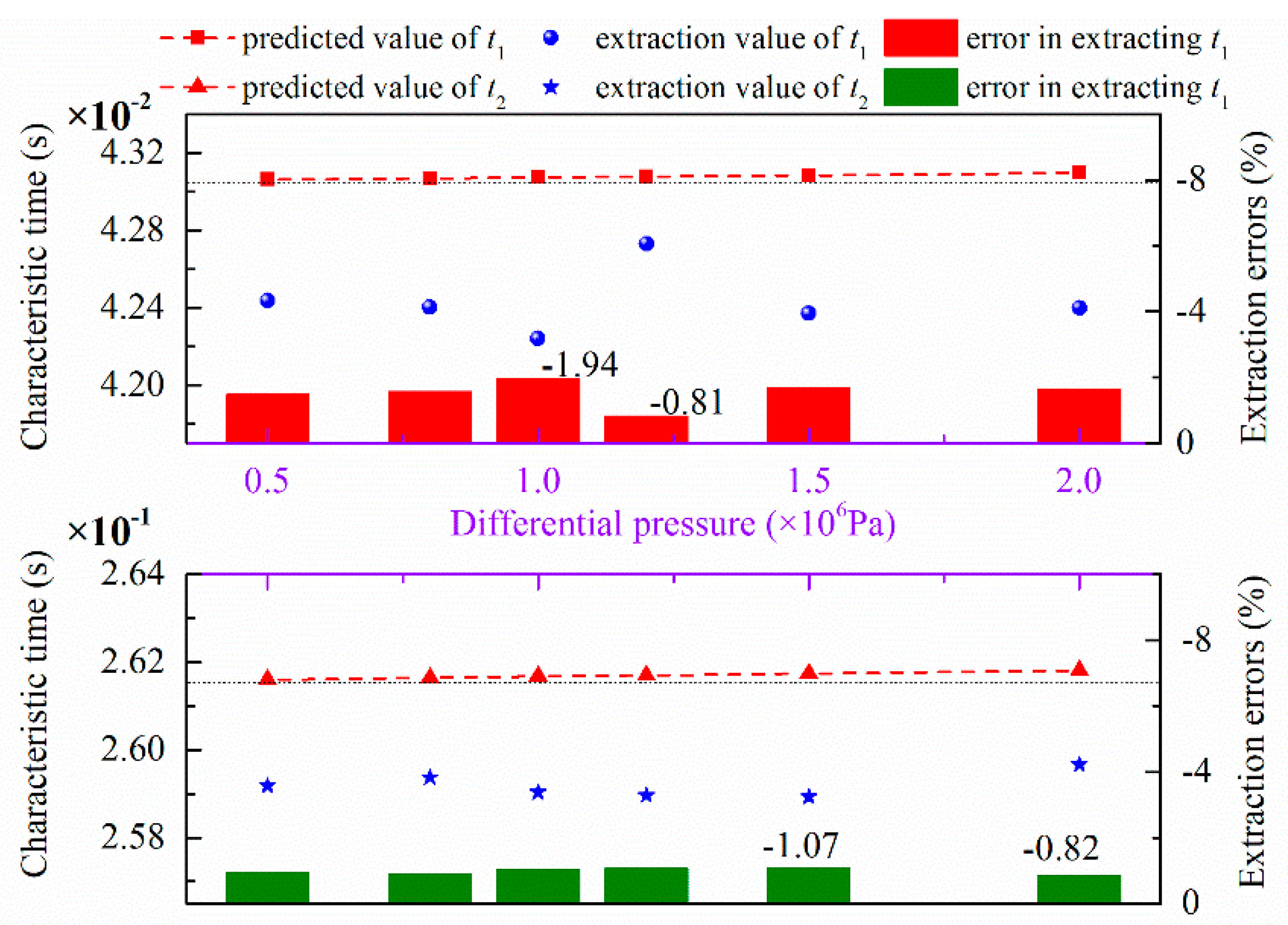
3.3.2. Leak Localization for Different Differential Pressures
3.3.3. Leak Localization for Different Orifice Diameters
4. Field Application
4.1. Description of Field Test
4.2. Field Results and Discussion
5. Conclusions
- The leakage acoustic waves of downhole tubing can be measured by an installed acoustic sensor in the annulus top, and the downhole leakage can be detected at the ground.
- The position of tubing leakage is located by autocorrelation analysis of the acoustic signals in the annulus. The localization model is developed. The fundamental steps and equations for this method are concluded.
- Though errors exist, the proposed model is able to locate the tubing leakage effectively. In the laboratory experiments, leaks as small as 0.5 mm in diameter could be located. The errors generated in the localization process were kept at very low levels. The absolute localization errors were on the order of cm, and the relative errors were within 1%. The errors are mainly determined by characteristic time and annular acoustic velocity.
- Field application demonstrated that the proposed method performs well in locating the depth of downhole leakage and the liquid level in the annulus. Therefore, the merits of the methods are concluded.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Degeare, J. Repaire of Csing Failures and Leaks. In The Guide to Oilwell Fishing Operations, 2nd ed.; Gulf Professional Publishing: Oxford, UK, 2015; Chapter 18; pp. 133–140. ISBN 978-0-12-420004-3. [Google Scholar]
- Bourgoyne, A.T.; Scott, S.L.; Regg, J.B. Sustained casing pressure in offshore producing wells. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 1999; p. 11029. [Google Scholar]
- Chen, P.; Gao, D.; Wang, Z.; Huang, W. Study on aggressively working casing string in extended-reach well. J. Pet. Sci. Eng. 2017, 157, 604–616. [Google Scholar] [CrossRef]
- Bennett, R.; Paul, D.S., Jr.; Gustafson, T.D.; Gillette, I.E. Measuring low flows in devonian shale gas wells with a tracer-gas flowmeter. SPE Form. Eval. 1991, 6, 269–272. [Google Scholar] [CrossRef]
- Johns, J.E.; Blount, C.G.; Dethlefs, J.C.; Loveland, M.J.; Mcconnell, M.L.; Schwartz, G.L.; Julian, J.Y. Applied ultrasonic technology in wellbore-leak detection and case histories in Alaska north slope wells. SPE Prod. Oper. 2009, 24, 225–232. [Google Scholar] [CrossRef]
- Michel, C.M. Methods of detecting and locating tubing and packer leaks in the western operating area of the prudhoe bay field. SPE Prod. Facil. 1995, 10, 124–128. [Google Scholar] [CrossRef]
- Al-Hussain, A.M.; Hossain, M.E.; Abdulraheem, A.; Gajbhiye, R. An integrated approach for downhole leak detection. In Proceedings of the SPE Saudi Arabia Section Annual Technical Symposium and Exhibition, AI-Khobar, Saudi Arabia, 21–23 April 2015; p. 77996. [Google Scholar]
- Bateman, R.M. Well and Field Monitoring. In Cased-Hole Log Analysis and Reservoir Performance Monitoring, 2nd ed.; Springer: New York, NY, USA, 2015; Chapter 14; pp. 244–260. ISBN 978-1-4939-2068-6. [Google Scholar]
- Hill, F.; Bond, A.; Biery, M.; Jagannathan, S.; Walters, D.; Lu, Y. Methodology and array technology for finding and describing leaks in a well. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, UAE, 26–28 September 2016; p. 181497. [Google Scholar]
- Julian, J.Y.; King, G.E.; Cismoski, D.A.; Younger, R.O.; Brown, D.L.; Brown, G.A.; Richards, K.M.; Meyer, C.A.; Sierra, J.R.; Leckband, W.T.; et al. Downhole leak determination using fiber-optic distributed-temperature surveys at Prudhoe Bay, Alaska. In Proceedings of the SPE Annual Technical Conference and Exhibition, Anaheim, CA, USA, 11–14 November 2007; p. 107070. [Google Scholar]
- Zhu, H.; Lin, Y.; Zeng, D.; Zhang, D.; Chen, H.; Wang, W. Mechanism and prediction analysis of sustained casing pressure in “A” annulus of CO2 injection well. J. Nat. Gas Sci. Eng. 2012, 92–93, 1–10. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, L.; Fan, J.; Zhang, X.; Liu, D.; Wang, D. A leakage diagnosis testing model for gas wells with sustained casing pressure from offshore platform. J. Nat. Gas Sci. Eng. 2018, 55, 276–287. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, L.; Fan, J.; Zhang, X.; Zhou, Y.; Wang, D. Prediction analysis of downhole tubing leakage location for offshore gas production wells. Measurement 2018, 127, 546–553. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, J.; Liu, S.; Wen, M.; Lv, N.; Liang, Z. Diagnostic testing of gas wells with sustained casing pressure by application of He tracer. In Proceedings of the twenty-seventh International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017; pp. 400–404. [Google Scholar]
- Ding, X.; Hu, Z.; Ge, L. Research on tubing leak detection and location technology of horizontal well based on negative pressure wave technology in intelligent well. J. Appl. Sci. Eng. 2015, 2, 226–229. [Google Scholar]
- Taylor, C.; Rowlan, L.; McCoy, J. Acoustic techniques to monitor and troubleshoot gas-lift wells. In Proceedings of the SPE Western North American and Rocky Mountain Joint Regional Meeting, Denver, CO, USA, 16–18 April 2014; p. 169536. [Google Scholar]
- Murvay, P.S.; Silea, I. A survey on gas leak detection and localization techniques. J. Loss Prev. Process. Ind. 2012, 25, 966–973. [Google Scholar] [CrossRef]
- Watanabe, K.; Himmelblau, D.M. Detection and location of a leak in a gas-transport pipeline by a new acoustic method. AIChE J. 1986, 32, 1690–1701. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Brennan, M.J.; Liu, Y.; Almeida, F.C.L.; Joseph, P.F. Improving the shape of the cross-correlation function for leak detection in a plastic water distribution pipe using acoustic signals. Appl. Acoust. 2017, 127, 24–33. [Google Scholar] [CrossRef] [Green Version]
- Hunaidi, O.; Chu, W.T. Acoustical characteristics of leak signals in plastic water distribution pipes. Appl. Acoust. 1999, 58, 235–254. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.W.; Li, Y.X.; Yan, Y.K.; Fu, J.T.; Zhang, Y.Q. A new leak location method based on leakage acoustic waves for oil and gas pipelines. J. Loss Prev. Process. Ind. 2015, 35, 236–246. [Google Scholar] [CrossRef]
- Hang, L.J.; He, C.F.; Wu, B. Novel distributed optical fiber acoustic sensor array for leak detection. Opt. Eng. 2008, 47, 525–534. [Google Scholar] [CrossRef]
- Yuan, W.; Pang, B.; Bo, J.; Qian, X. Fiber-optic sensor for acoustic localization. J. Light Technol. 2014, 32, 1892–1898. [Google Scholar] [CrossRef]
- Zhang, X.M.; Fan, J.C.; Wu, S.N.; Liu, D. A novel acoustic liquid level determination method for coal seam gas wells based on autocorrelation analysis. Energies 2017, 10, 1961. [Google Scholar] [CrossRef]
- Farraj, A.K.; Miller, S.L.; Qaraqe, K.A. Channel characterization for acoustic downhole communication systems. In Proceedings of the SPE annual Technical Conference and Exhibition, Antonio, TX, USA, 8–10 October 2012; p. 158939. [Google Scholar]
- Liu, D.; Fan, J.; Liang, Z.; Lv, N. Research on detecting and locating tubing leakage of offshore gas wells based on acoustic method. In Proceedings of the 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017; pp. 392–399. [Google Scholar]
- Speed of Sound in Natural Gas and Other Related Hydrocarbon Gases; AGA Report No. 10; AGA XQ0310; American Gas Association: Washington, DC, USA, 2003; pp. 12–17.
- Coquelet, C.; Chapoy, A.; Richon, D. Development of a new alpha function for the Peng–Robinson equation of state: Comparative study of alpha function models for pure gases (natural gas components) and water-gas systems. Int. J. Thermophys. 2004, 25, 133–158. [Google Scholar] [CrossRef]
- Izgec, B. Transient Fluid and Heat Flow Modeling in Coupled Wellbore/Reservoir Systems. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, May 2008. [Google Scholar]
- Lin, J.; Xu, H.L.; Shi, T.H.; Zou, A.Q.; Mu, A.L.; Guo, J.H. Downhole multistage choke technology to reduce sustained casing pressure in a HPHT gas well. J. Nat. Gas Sci. Eng. 2015, 26, 992–998. [Google Scholar] [CrossRef]
- Sagar, R.; Doty, D.R.; Schmidt, Z. Predicting temperature profiles in a flowing well. SPE Prod. Eng. 1991, 6, 441–448. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. Wellbore heat-transfer modeling and applications. J. Pet. Sci. Eng. 2012, 86–87, 127–136. [Google Scholar] [CrossRef]
- Xu, R. Analysis of Diagnostic Testing of Sustained Casing Pressure in Wells. Ph.D. Thesis, Louisiana State University, Baton Rouge, LA, USA, December 2002. [Google Scholar]
- Hasan, A.R.; Kabir, C.S. Heat transfer during two-phase flow in wellbores: Part I—Formation temperature. In Proceedings of the 66th Annual Technical Conference and Exhibition of the Society of Petroleum Engineers, Dallas, TX, USA, 6–9 October 1991; pp. 469–478. [Google Scholar]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef] [Green Version]
- Heilbronner, R.P. The autocorrelation function: An image processing tool for fabric analysis. Tectonophysics 1992, 212, 351–370. [Google Scholar] [CrossRef]
- Gao, Y.; Brennan, M.J.; Joseph, P.F.; Muggleton, J.M.; Hunaidi, O. A model of the correlation function of leak noise in buried plastic pipes. J. Sound Vib. 2004, 277, 133–148. [Google Scholar] [CrossRef]
- Zhang, M.; Wen, S.P. Applied Numerical Analysis, 4th ed.; Petroleum Industry Press: Beijing, China, 2012; pp. 211–228. ISBN 978-7-5021-9201-3. [Google Scholar]














| Experiments | Variable | Leak Position | Orifice Diameter (mm) | Differential Pressure (MPa) |
|---|---|---|---|---|
| Part 1 | Leak depth | a, b, c, d, e | 1.5 | 2.0 |
| Part 2 | Orifice diameter | c | 0.5, 0.8, 1.0, 1.2, 1.5 | 2.0 |
| Part 3 | Differential pressure | c | 1.5 | 0.5, 0.8, 1.0, 1.2, 1.5, 2.0 |
| Leakage Position | Orifice Diameter (mm) | Differential Pressure (106 Pa) | Annular Length | Distance between Leakage Point and Acoustic Sensor | ||
|---|---|---|---|---|---|---|
| Calculated Value (m) | Relative Errors (%) | Calculated Value (m) | Relative Errors (%) | |||
| a | 1.5 | 2.0 | 46.422 | −1.02 | 45.293 | −0.97 |
| b | 46.365 | −1.14 | 41.760 | −0.90 | ||
| c | 46.516 | −0.82 | 38.920 | −0.55 | ||
| d | 46.725 | −0.37 | 35.686 | −0.33 | ||
| e | 46.403 | −1.06 | 32.432 | −0.87 | ||
| c | 1.5 | 2.0 | 46.516 | −0.82 | 38.920 | −0.55 |
| 1.5 | 46.398 | −1.07 | 38.806 | −0.80 | ||
| 1.2 | 46.409 | −1.05 | 38.749 | −0.92 | ||
| 1.0 | 46.426 | −1.01 | 38.856 | −0.69 | ||
| 0.8 | 46.493 | −0.87 | 38.892 | −0.61 | ||
| 0.5 | 46.467 | −0.92 | 38.859 | −0.68 | ||
| c | 1.5 | 2.0 | 46.528 | −0.79 | 38.758 | −0.90 |
| 1.2 | 46.689 | −0.45 | 38.919 | −0.56 | ||
| 1.0 | 46.582 | −0.68 | 38.689 | −1.05 | ||
| 0.8 | 46.575 | −0.69 | 38.782 | −0.85 | ||
| 0.5 | 46.154 | −1.59 | 38.255 | −1.97 | ||
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Diameter of tubing (mm) | Ф73.02 × 5.51 | Depth of packer (m) | 3394.01 |
| Diameter of production casing (mm) | Ф244.48 × 13.58 | Depth of subsurface safety valve (m) | 238.23 |
| Diameter of surface casing (m) | Ф339.73 × 12.19 | Wellhead temperature (K) | 329.75 |
| Sea level (m) | 46.5 | Annulus top temperature (K) | 318.85 |
| Depth of water (m) | 106.16 | Wellhead pressure (MPa) | 5.383 |
| Formation temperature (K) | 398.65 | Annulus top pressure (MPa) | 1.4 |
| Geothermal gradient (K [100 m]−1) | 2.6 | Gas specific gravity | 0.644 |
| Depth of perforation (m) | 3416.71 |
| Time Difference (s) | Depth of S (m) | Liquid Level (m) | Leakage Depth (m) | ||
|---|---|---|---|---|---|
| t1 | t2 | tS | |||
| 1.90433 | 9.76267 | 1.14167 | 240.57 | 2207.98 | 1779.80 |
| Locating Position | True Depth (m) | Localization Depth (m) | Absolute Error (m) | Relative Error (%) | |
|---|---|---|---|---|---|
| Laboratory experiments 1 | Leak position | 45.75 | 45.293 | −0.457 | −0.97 |
| Annulus length (liquid level) | 46.9 | 46.422 | −0.478 | −1.02 | |
| Field test | Subsurface safety valve | 238.23 | 240.57 | 2.34 | 0.98 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Fan, J.; Wu, S. Acoustic Wave-Based Method of Locating Tubing Leakage for Offshore Gas Wells. Energies 2018, 11, 3454. https://doi.org/10.3390/en11123454
Liu D, Fan J, Wu S. Acoustic Wave-Based Method of Locating Tubing Leakage for Offshore Gas Wells. Energies. 2018; 11(12):3454. https://doi.org/10.3390/en11123454
Chicago/Turabian StyleLiu, Di, Jianchun Fan, and Shengnan Wu. 2018. "Acoustic Wave-Based Method of Locating Tubing Leakage for Offshore Gas Wells" Energies 11, no. 12: 3454. https://doi.org/10.3390/en11123454
APA StyleLiu, D., Fan, J., & Wu, S. (2018). Acoustic Wave-Based Method of Locating Tubing Leakage for Offshore Gas Wells. Energies, 11(12), 3454. https://doi.org/10.3390/en11123454




