An Accurate Method for Delay Margin Computation for Power System Stability
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Proposed Method
- (i)
- is stable,
- (ii)
- + is stable, and
- (iii)
2.2. The Single-Machine-Infinite-Bus Power System with AVR and PSS
| The generator angle | |
| The generator speed with the base speed | |
| E’q | The generator voltage behind the transient reactance |
| Efd | The exciter output voltage, and Efd0 is the reference |
| The time constant and the gain of the exciter | |
| The mechanical power | |
| The generator damping factor | |
| The moment of inertia | |
| The open-loop time constant of the armature winding | |
| The infinite bus voltage | |
| The generator terminal voltage | |
| The transmission line reactance | |
| The transient reactance | |
| The synchronous reactance | |
| The time constants of the Lead-lag compensator | |
| The time constant of the washout filter | |
| The gain of the power system stabilizer |
3. Results
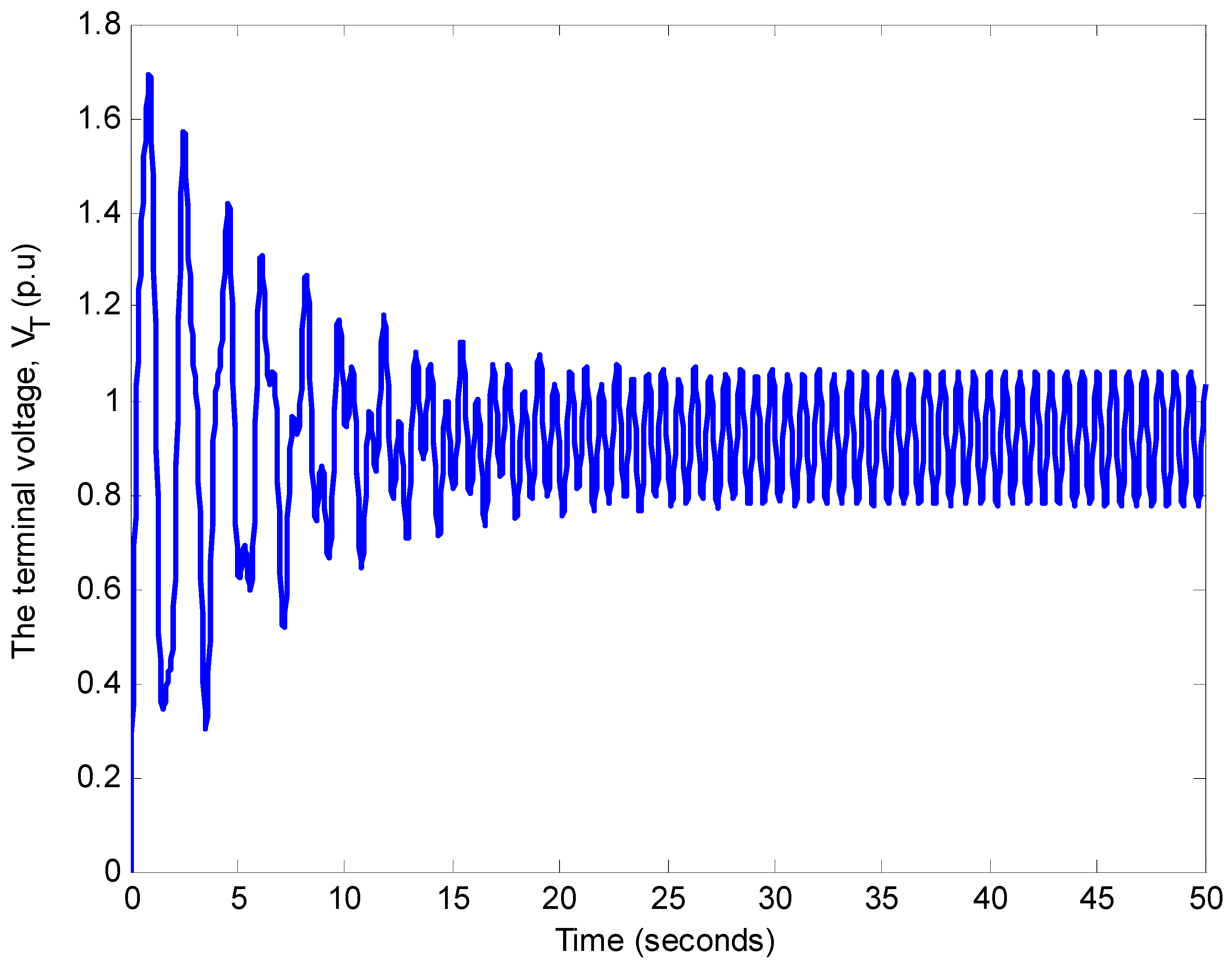
4. Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| The generator angle | |
| The generator speed with the base speed | |
| E’q | The generator voltage behind the transient reactance |
| Efd | The exciter output voltage, and Efd0 is the reference |
| The gain of the exciter and the time constant | |
| Constants | |
| The mechanical power | |
| The generator damping factor | |
| The moment of inertia | |
| The open-loop time constant of the armature winding | |
| The infinite bus voltage | |
| The generator terminal voltage | |
| The Power System Stabilizer (PSS) signal | |
| Vref | The reference terminal voltage |
| The washout filter voltage | |
| The direct axis voltage | |
| Vq | The quadrature axis voltage |
| The transmission line resistance | |
| The windings resistance | |
| The transmission line reactance | |
| The transient reactance | |
| The synchronous reactance | |
| The time constants of the Lead-lag compensator | |
| The time constant of the washout filter | |
| The gain of the power system stabilizer | |
| Id | The direct axis current |
| Iq | The quadrature axis current |
Appendix A
References
- Mak, K.H.; Holland, B.L. Migrating electrical power network SCADA systems to TCP/IP and Ethernet networking. Power Eng. J. 2002, 16, 305–311. [Google Scholar]
- Naduvathuparambil, B.; Valenti, M.C.; Feliachi, A. Communication delays in wide area measurement systems. In Proceedings of the Thirty-Fourth Southeastern Symposium on System Theory (Cat. No.02EX540), Huntsville, AL, USA, 19 March 2002; pp. 118–122. [Google Scholar] [Green Version]
- Holbert, K.E.; Heydt, G.I.; Hui, N. Use of satellite technologies for power system measurements, command, and control. Proc. IEEE 2005, 93, 947–955. [Google Scholar] [CrossRef]
- Li, M.; Chen, Y. A Wide-Area Dynamic Damping Controller Based on Robust H∞ Control for Wide-Area Power Systems With Random Delay and Packet Dropout. IEEE Trans. Power Syst. 2018, 33, 4026–4037. [Google Scholar] [CrossRef]
- Khalil, A.; Wang, J. Stabilization of load frequency control system under networked environment. In Proceedings of the 2015 21st International Conference on Automation and Computing (ICAC), Glasgow, UK, 11–12 September 2015; pp. 1–6. [Google Scholar]
- Khalil, A.; Wang, J.; Mohammed, O. Robust stabilization of load frequency control system under networked environment. Int. J. Autom. Comput. 2017, 14, 93–105. [Google Scholar] [CrossRef]
- Wu, H.; Tsakalis, K.S.; Heydt, G.T. Evaluation of time delay effects to wide-area power system stabilizer design. IEEE Trans. Power Syst. 2004, 19, 1935–1941. [Google Scholar] [CrossRef]
- Kamwa, I.; Grondin, R.; Hebert, Y. Wide-area measurement based stabilizing control of large power systems-a decentralized/hierarchical approach. IEEE Trans. Power Syst. 2001, 16, 136–153. [Google Scholar] [CrossRef]
- Chaudhuri, B.; Majumder, R.; Pal, B.C. Wide-area measurement-based stabilizing control of power system considering signal transmission delay. IEEE Trans. Power Syst. 2004, 19, 1971–1979. [Google Scholar] [CrossRef]
- Bhowmik, S.; Tomsovic, K.; Bose, A. Communication Models for Third Party Load Frequency Control. IEEE Trans. Power Syst. 2004, 19, 543–548. [Google Scholar] [CrossRef] [Green Version]
- Ramakrishnan, K. Delay-dependent stability criterion for delayed load frequency control systems. In Proceedings of the 2016 IEEE Annual India Conference (INDICON), Bangalore, India, 16–18 December 2016; pp. 1–6. [Google Scholar]
- Ramakrishnan, K.; Ray, G. Improved results on delay dependent stability of LFC systems with multiple time delays. J. Control Autom. Electr. Syst. 2015, 2015, 235–240. [Google Scholar] [CrossRef]
- Jiang, L.; Yao, W.; Wu, Q.H.; Wen, J.Y.; Cheng, S.J. Delay-Dependent Stability for Load Frequency Control with Constant and Time-Varying Delays. IEEE Trans. Power Syst. 2012, 27, 932–941. [Google Scholar] [CrossRef]
- Zhang, C.K.; Jiang, L.; Wu, Q.H.; He, Y.; Wu, M. Delay-Dependent Robust Load Frequency Control for Time Delay Power Systems. IEEE Trans. Power Syst. 2013, 28, 2192–2201. [Google Scholar] [CrossRef]
- Zhang, C.K.; Jiang, L.; Wu, Q.H.; He, Y.; Wu, M. Further Results on Delay-Dependent Stability of Multi-Area Load Frequency Control. IEEE Trans. Power Syst. 2013, 28, 4465–4474. [Google Scholar] [CrossRef]
- Xiaofeng, Y.; Tomsovic, K. Application of linear matrix inequalities for load frequency control with communication delays. IEEE Trans. Power Syst. 2004, 19, 1508–1515. [Google Scholar]
- Sönmez, Ş.; Ayasun, S.; Nwankpa, C.O. An Exact Method for Computing Delay Margin for Stability of Load Frequency Control Systems with Constant Communication Delays. IEEE Trans. Power Syst. 2016, 31, 370–377. [Google Scholar] [CrossRef]
- Jia, H.J.; Na, G.Y.; Lee, S.; Zhang, P. Study on the impact of time delay to power system small signal stability. In Proceedings of the MELECON 2006—2006 IEEE Mediterranean Electrotechnical Conference, Malaga, Spain, 16–19 May 2006; pp. 1011–1014. [Google Scholar]
- Jia, H.; Cao, X.; Yu, X.; Zhang, P. A Simple Approach to Determine Power System Delay Margin. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–7. [Google Scholar]
- Jia, H.; Yu, X.; Yu, Y.; Wang, C. Power system small signal stability region with time delay. Electr. Power Energy Syst. 2008, 30, 16–22. [Google Scholar] [CrossRef]
- Ayasun, S. Computation of time delay margin for power system small-signal stability. Eur. Trans. Electr. Power 2009, 2009, 949–968. [Google Scholar] [CrossRef]
- Yu, X.; Jia, H.; Wang, C. CTDAE & CTODE models and their applications to power system stability analysis with time delays. Sci. China Technol. Sci. 2013, 56, 1213–1223. [Google Scholar]
- Jiang, Y.; Jiang, T.; Jia, H.; Dong, C.Y. A novel LMI criterion for power system stability with multiple time-delays. Sci. China Technol. Sci. 2014, 57, 1392–1400. [Google Scholar] [CrossRef]
- Dong, C.; Jia, H.; Jiang, T.; Bai, L.; Hu, Q.; Wang, L.; Jiang, Y. Effective method to determine time-delay stability margin and its application to power systems. Iet Gener. Transm. Distrib. 2017, 11, 1661–1670. [Google Scholar] [CrossRef]
- Sonmez, S.; Ayasun, S. Effect of load increase and power system stabilizer on stability delay margin of a generator excitation control system. Turkish J. Electr. Eng. Comput. Sci. 2016, 24, 5183–5194. [Google Scholar] [CrossRef]
- Chen, J. On Computing the Maximal Delay Intervals for Stability of Linear Delay Systems. IEEE Trans. Autom. Control 1995, 40, 1087–1093. [Google Scholar] [CrossRef]
- Gu, K.; Kharitonov, V.L.; Chen, J. Stability of Time-Delay Systems; Springer: Berlin, Germany, 2003. [Google Scholar]
- Chen, J.; Latchman, H.A. Frequency Sweeping Tests for Stability Independent of Delay. IEEE Trans. Autom. Control 1995, 40, 1640–1645. [Google Scholar] [CrossRef]
- Chen, J.; Gu, G.; Nett, C.N. A New Method for Computing Delay Margins for Stability of Linear Delay Systems. In Proceedings of the 1994 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994; pp. 433–437. [Google Scholar]
- Shahgholian, G.; Faiz, J. The effect of power system stabilizer on small-signal stability in single-machine-innite-bus. Int. J. Electr. Power Eng. 2010, 2010, 45–53. [Google Scholar] [CrossRef]
- Sauer, P.W.; Pai, M.A. Power System Dynamics and Stability, 1st ed.; Stipes Publishing: Singapore, 2002. [Google Scholar]
- de Mello, F.P.; Laskowski, T.F. Concepts of power system dynamic stability. IEEE Trans. Power Appar. Syst. 1975, 94, 827–833. [Google Scholar] [CrossRef]
- Heffron, W.G.; Phillips, R.A. Effect of a Modern Amplidyne Voltage Regulator on Underexcited Operation of Large Turbine Generators. Transactions of the American Institute of Electrical Engineers. Part III Power Appar. Syst. 1952, 71, 692–697. [Google Scholar] [CrossRef]
- Demello, F.P.; Concordia, C. Concepts of synchronous machine stability as affected by excitation control. IEEE Trans. Power Appar. Syst. Pas 1969, 88, 316–329. [Google Scholar] [CrossRef]
- Ji, W.; Venkatasubramanian, V. Hard-limit induced chaos in a fundamental power system model. Electr. Power Energy Syst. 1996, 18, 279–295. [Google Scholar] [CrossRef]






















| M | D | ||||
|---|---|---|---|---|---|
| 6.4 | 0.0 | 2.5 | 0.39 | 9.6 | 0.5 |
| 2.1 | 5 | 1.05 | 377.0 | 0.0 | |
| 0.0 | 0.5 | 0.1 | 2.0 | 100 | 0.05 |
| The parameter | Method | 1 | 2 | 3 |
|---|---|---|---|---|
| ωc (rad/s) | The proposed method | 2.5141 | 11.0472 | 13.1185 |
| The method in Ref. [25] | 2.5140 | 11.0473 | 13.1187 | |
| τ (s) | The proposed method | 0.4958 | 0.3320 | 0.0786 |
| The method in Ref. [25] | 0.4958 | 0.3320 | 0.0786 |
| Method | τ1 (s) | τ2 (s) | τ3 (s) | |
|---|---|---|---|---|
| KPSS = 0 | The proposed method | 0.1854 | 0.4635 | 0.3984 |
| The method in Ref. [25] | 0.1788 | 0.4579 | 0.3678 | |
| KPSS = 5 | The proposed method | 0.1632 | 0.3774 | 0.4262 |
| The method in Ref. [25] | 0.1632 | 0.3774 | 0.4262 | |
| KPSS = 10 | The proposed method | 0.1289 | 0.3539 | 0.4508 |
| The method in Ref. [25] | 0.1289 | 0.3539 | 0.4508 | |
| KPSS = 15 | The proposed method | 0.1010 | 0.3407 | 0.4738 |
| The method in Ref. [25] | 0.1010 | 0.3407 | 0.4738 | |
| KPSS = 20 | The proposed method | 0.0786 | 0.3320 | 0.4958 |
| The method in Ref. [25] | 0.0786 | 0.3320 | 0.4958 | |
| KPSS = 25 | The proposed method | 0.0600 | 0.3258 | 0.5171 |
| The method in Ref. [25] | 0.0600 | 0.3258 | 0.5171 | |
| KPSS = 30 | The proposed method | 0.0439 | 0.3214 | 0.5378 |
| The method in Ref. [25] | 0.0439 | 0.3214 | 0.5378 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalil, A.; Swee Peng, A. An Accurate Method for Delay Margin Computation for Power System Stability. Energies 2018, 11, 3466. https://doi.org/10.3390/en11123466
Khalil A, Swee Peng A. An Accurate Method for Delay Margin Computation for Power System Stability. Energies. 2018; 11(12):3466. https://doi.org/10.3390/en11123466
Chicago/Turabian StyleKhalil, Ashraf, and Ang Swee Peng. 2018. "An Accurate Method for Delay Margin Computation for Power System Stability" Energies 11, no. 12: 3466. https://doi.org/10.3390/en11123466





