Determination of the Structural Characteristics of Microalgal Cells Walls under the Influence of Turbulent Mixing Energy in Open Raceway Ponds
Abstract
:1. Introduction
2. Materials and Methods
2.1. Geometries of the Raceway Pond and Microalgal Cells
2.2. Numerical Modeling
2.2.1. Fluid Flow
2.2.2. Microalgal Cell Wall Structure
3. Numerical Simulation and Mesh Generation
4. Results and Discussion
4.1. Experimental Comparison
4.2. Effects of Microalgal Cell Locations
4.3. Effects of Aspect Ratio
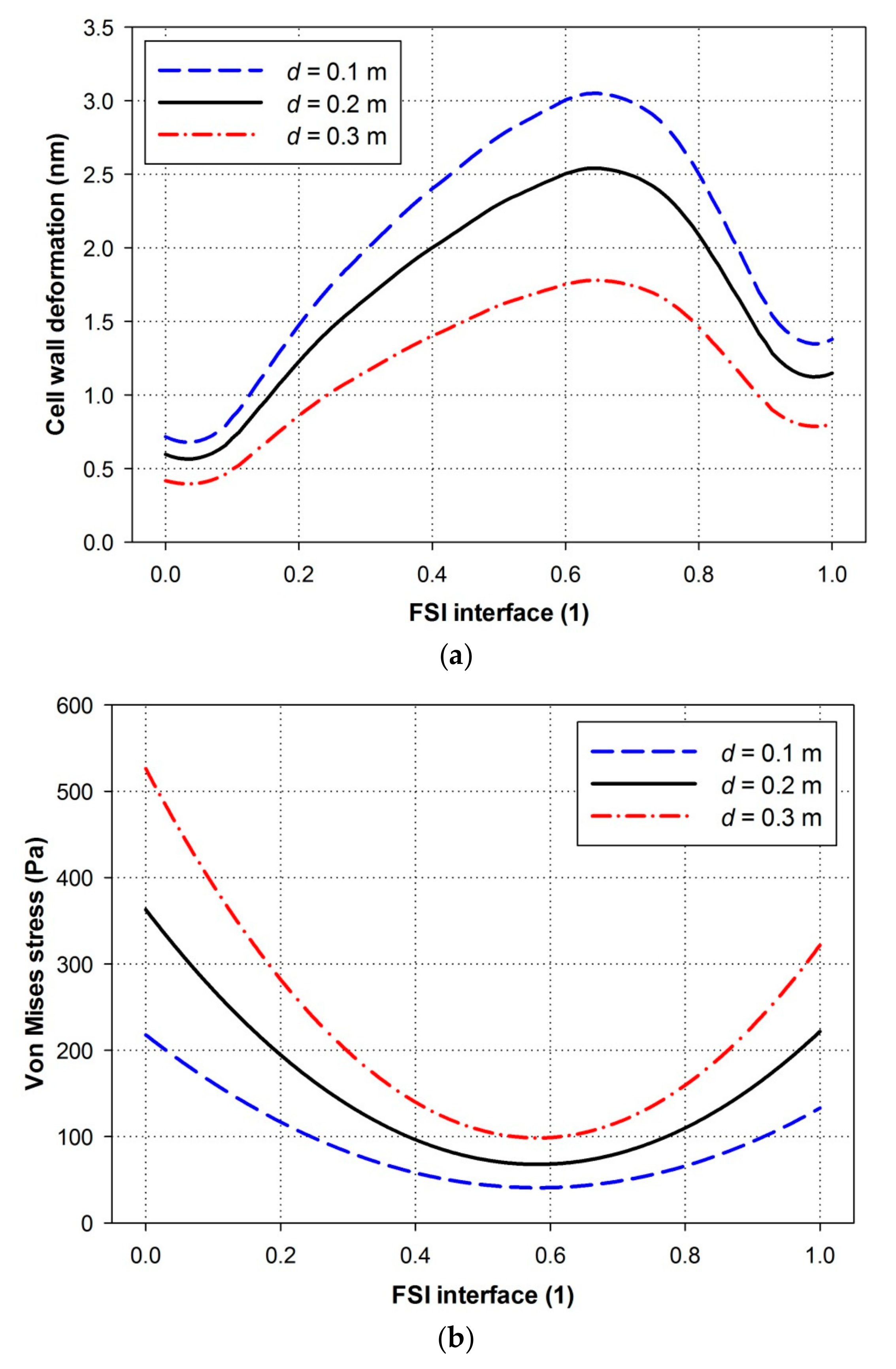
4.4. Effects of Water Depths
4.5. Effects of Paddle Wheel Rotational Speeds
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Borowitzka, M.A. Commercial production of microalgae: Ponds, tanks, tubes and fermenters. J. Biotechnol. 1999, 70, 313–321. [Google Scholar] [CrossRef]
- Grobbelaar, J.U.; Kroon, B.M.A.; Burger-Wiersma, T.; Mur, L.R. Influence of medium frequency light/dark cycles of equal duration on the photosynthesis and respiration of Chlorella pyrenoidosa. Hydrobiologia 1992, 238, 53–62. [Google Scholar] [CrossRef]
- Marshall, J.S.; Huang, Y. Simulation of light-limited algae growth in homogeneous turbulence. Chem. Eng. Sci. 2010, 65, 3865–3875. [Google Scholar] [CrossRef]
- Schapira, M.; Seuront, L.; Gentilhomme, V. Effects of small-scale turbulence on Phaeocystis globosa (Prymnesiophyceae) growth and life cycle. J. Exp. Mar. Biol. Ecol. 2006, 335, 27–38. [Google Scholar] [CrossRef]
- Silva, H.J.; Cortifas, T.; Ertola, R.J. Effect of hydrodynamic stress on dunaliella growth. J. Chem. Technol. Biotechnol. 2007, 40, 41–49. [Google Scholar] [CrossRef]
- Blersch, D.M.; Kangas, P.C.; Mulbry, W.W. Turbulence and nutrient interactions that control benthic algal production in an engineered cultivation raceway. Algal Res. 2013, 2, 107–112. [Google Scholar] [CrossRef]
- Barbosa, M.J.; Albrecht, M.; Wijffels, R.H. Hydrodynamic stress and lethal events in sparged microalgae cultures. Biotechnol. Bioeng. 2003, 83, 112–120. [Google Scholar] [CrossRef] [PubMed]
- Baldyga, J.; Pohorecki, R. Influence of turbulent mechanical stresses on microorganisms. Appl. Mech. Rev. 1998, 51, 121–140. [Google Scholar] [CrossRef]
- Ogbonna, J.C.; Yada, H.; Tanaka, H. Effect of cell movement by random mixing between the surface and bottom of photobioreactors on algal productivity. J. Ferment. Bioeng. 1995, 79, 152–157. [Google Scholar] [CrossRef]
- Weissman, J.C.; Goebel, R.P.; Benemann, J.R. Photobioreactor design: Mixing, carbon utilization, and oxygen accumulation. Biotechnol. Bioeng. 1988, 31, 336–344. [Google Scholar] [CrossRef] [PubMed]
- Bosca, C.; Dauta, A.; Marvalin, O. Intensive outdoor algal cultures: How mixing enhances the photosynthetic production rate. Bioresour. Technol. 1991, 38, 185–188. [Google Scholar] [CrossRef]
- Chisti, Y. Biodiesel from microalgae. Biotechnol. Adv. 2007, 25, 294–306. [Google Scholar] [CrossRef] [PubMed]
- Mendoza, J.L.; Granados, M.R.; de Godos, I.; Acién, F.G.; Molina, E.; Heaven, S.; Banks, C.J. Oxygen transfer and evolution in microalgal culture in open raceways. Bioresour. Technol. 2013, 137, 188–195. [Google Scholar] [CrossRef] [PubMed]
- Drapcho, C. The partitioned aquaculture system: Impact of design and environmental parameters on algal productivity and photosynthetic oxygen production. Aquac. Eng. 2000, 21, 151–168. [Google Scholar] [CrossRef]
- Grobbelaar, J.U. The influence of light/dark cycles in mixed algal cultures on their productivity. Bioresour. Technol. 1991, 38, 189–194. [Google Scholar] [CrossRef]
- Thomas, W.H.; Gibson, C.H. Effects of small-scale turbulence on microalgae. J. Appl. Phycol. 1990, 2, 71–77. [Google Scholar] [CrossRef]
- Camacho, F.G.; Gómez, A.C.; Sobczuk, T.M.; Grima, E.M. Effects of mechanical and hydrodynamic stress in agitated, sparged cultures of Porphyridium cruentum. Process Biochem. 2000, 35, 1045–1050. [Google Scholar] [CrossRef]
- Berdalet, E.; Peters, F.; Koumandou, V.L.; Roldan, C.; Guadayol, O.; Estrada, M. Species-specific physiological response of dinoflagellates to quantified small-scale turbulence. J. Phycol. 2007, 43, 965–977. [Google Scholar] [CrossRef]
- Hondzo, M.; Lyn, D. Quantified small-scale turbulence inhibits the growth of a green alga. Freshw. Biol. 1999, 41, 51–61. [Google Scholar] [CrossRef]
- Al-Homoud, A.; Hondzo, M. Energy dissipation estimates in oscillating grid setup: LDV and PIV measurements. Environ. Fluid Mech. 2007, 7, 143–158. [Google Scholar] [CrossRef]
- Hadiyanto, H.; Elmore, S.; Van Gerven, T.; Stankiewicz, A. Hydrodynamic evaluations in high rate algae pond (HRAP) design. Chem. Eng. J. 2013, 217, 231–239. [Google Scholar] [CrossRef]
- Munns, R.; Greenway, H.; Setter, T.L.; Kuo, J. Turgor pressure, volumetric elastic modulus, osmotic volume and ultrastructure of chlorella emersonii grown at high and low external NaCl. J. Exp. Bot. 1983, 34, 144–155. [Google Scholar] [CrossRef]
- Secomb, T.W.; Hsu, R.; Pries, A.R. Blood Flow and Red Blood Cell Deformation in Nonuniform Capillaries: Effects of the Endothelial Surface Layer. Microcirculation 2002, 9, 189–196. [Google Scholar] [CrossRef] [PubMed]
- Ali, H.; Cheema, T.A.; Yoon, H.-S.; Do, Y.; Park, C.W. Numerical prediction of algae cell mixing feature in raceway ponds using particle tracing methods. Biotechnol. Bioeng. 2015, 112, 297–307. [Google Scholar] [CrossRef] [PubMed]
- Mendoza, J.L.; Granados, M.R.; de Godos, I.; Acién, F.G.; Molina, E.; Banks, C.; Heaven, S. Fluid-dynamic characterization of real-scale raceway reactors for microalgae production. Biomass Bioenergy 2013, 54, 267–275. [Google Scholar] [CrossRef]
- Duarte, F.; Gormaz, R.; Natesan, S. Arbitrary Lagrangian-Eulerian method for Navier-Stokes equations with moving boundaries. Comput. Methods Appl. Mech. Eng. 2004, 193, 4819–4836. [Google Scholar] [CrossRef]
- Clair, G.; Ghidaglia, J.-M.; Perlat, J.-P. A multi-dimensional finite volume cell-centered direct ALE solver for hydrodynamics. J. Comput. Phys. 2016, 326, 312–333. [Google Scholar] [CrossRef]
- Ali, H.; Cheema, T.A.; Park, C.W. Effect of Paddle-Wheel Pulsating Velocity on the Hydrodynamic Performance of High-Rate Algal Ponds. J. Energy Eng. 2015, 141, 4014039. [Google Scholar] [CrossRef]
- Ali, H.; Cheema, T.A.; Park, C.W. Numerical prediction of heat transfer characteristics based on monthly temperature gradient in algal open raceway ponds. Int. J. Heat Mass Transf. 2017, 106, 7–17. [Google Scholar] [CrossRef]
- Ali, H.; Park, C.W. Numerical multiphase modeling of CO2 absorption and desorption in microalgal raceway ponds to improve their carbonation efficiency. Energy 2017, 127, 358–371. [Google Scholar] [CrossRef]
- Williams, P.J.L.B.; Laurens, L.M.L. Microalgae as biodiesel & biomass feedstocks: Review & analysis of the biochemistry, energetics & economics. Energy Environ. Sci. 2010, 3, 554. [Google Scholar] [CrossRef]
- Wijaya, F.B.; Mohapatra, A.R.; Sepehrirahnama, S.; Lim, K.M. Coupled acoustic-shell model for experimental study of cell stiffness under acoustophoresis. Microfluid. Nanofluid. 2016, 20, 69. [Google Scholar] [CrossRef]
- Jia, F.; Ben Amar, M.; Billoud, B.; Charrier, B. Morphoelasticity in the development of brown alga Ectocarpus siliculosus: From cell rounding to branching. J. R. Soc. Interface 2017, 14. [Google Scholar] [CrossRef] [PubMed]
- Lucci, F.; Ferrante, A.; Elghobashi, S. Is Stokes number an appropriate indicator for turbulence modulation by particles of Taylor-length-scale size? Phys. Fluids 2011, 23, 25101. [Google Scholar] [CrossRef]
- Auel, C.; Albayrak, I.; Boes, R.M. Turbulence Characteristics in Supercritical Open Channel Flows: Effects of Froude Number and Aspect Ratio. J. Hydraul. Eng. 2014, 140, 4014004. [Google Scholar] [CrossRef]
- Wolff, K.; Marenduzzo, D.; Cates, M.E. Cytoplasmic streaming in plant cells: The role of wall slip. J. R. Soc. Interface 2012, 9, 1398–1408. [Google Scholar] [CrossRef] [PubMed]
- Papoutsakis, E.T. Fluid-mechanical damage of animal cells in bioreactors. Trends Biotechnol. 1991, 9, 427–437. [Google Scholar] [CrossRef]
- Stenson, J.D.; Thomas, C.R.; Hartley, P. Modelling the mechanical properties of yeast cells. Chem. Eng. Sci. 2009, 64, 1892–1903. [Google Scholar] [CrossRef]
- Simionato, D.; Basso, S.; Giacometti, G.M.; Morosinotto, T. Optimization of light use efficiency for biofuel production in algae. Biophys. Chem. 2013, 182, 71–78. [Google Scholar] [CrossRef] [PubMed]











| Microalgal Cell | Diameter (µm) | Thickness (µm) | Density (kg/m3) | Viscosity (Pa·s) | Elastic Modulus (MPa) |
|---|---|---|---|---|---|
| Cytoplasm | 6.93 | − | 864 | 0.0052 | − |
| Cell wall | − | 0.285 | 1060 | − | 8.5 |
| Geometries | Elements | Fine | Extra-Fine | Extremely-Fine |
|---|---|---|---|---|
| Paddle wheel | Domain | 4334 | 21,670 | 108,350 |
| Boundary | 561 | 2805 | 14,025 | |
| Raceway pond and microalgal cells | Domain | 111,429 | 557,145 | 2,785,725 |
| Boundary | 33,360 | 166,800 | 834,000 | |
| Edge | 6480 | 32,400 | 162,000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, H.; Cheema, T.A.; Park, C.W. Determination of the Structural Characteristics of Microalgal Cells Walls under the Influence of Turbulent Mixing Energy in Open Raceway Ponds. Energies 2018, 11, 388. https://doi.org/10.3390/en11020388
Ali H, Cheema TA, Park CW. Determination of the Structural Characteristics of Microalgal Cells Walls under the Influence of Turbulent Mixing Energy in Open Raceway Ponds. Energies. 2018; 11(2):388. https://doi.org/10.3390/en11020388
Chicago/Turabian StyleAli, Haider, Taqi Ahmad Cheema, and Cheol Woo Park. 2018. "Determination of the Structural Characteristics of Microalgal Cells Walls under the Influence of Turbulent Mixing Energy in Open Raceway Ponds" Energies 11, no. 2: 388. https://doi.org/10.3390/en11020388
APA StyleAli, H., Cheema, T. A., & Park, C. W. (2018). Determination of the Structural Characteristics of Microalgal Cells Walls under the Influence of Turbulent Mixing Energy in Open Raceway Ponds. Energies, 11(2), 388. https://doi.org/10.3390/en11020388






