A Non-Probabilistic Solution for Uncertainty and Sensitivity Analysis on Techno-Economic Assessments of Biodiesel Production with Interval Uncertainties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Several Important Concepts in the TEA for a Biodiesel Production
2.2. NPRI for Measuring Economically Feasible Extent of Biodiesel Production
2.2.1. NPRI for Problems with Interval Parameters
2.2.2. NPRI for Economically Feasible Degree in the TEA of Biodiesel Production
2.3. Evaluation Procedure of the NPRI
2.4. SA of NPRI for Economical Feasibility of Biodiesel Production with Regards to Uncertain Interval Parameter
3. Results and Discussion
3.1. Evaluation of NPRI for Biodiesel Production
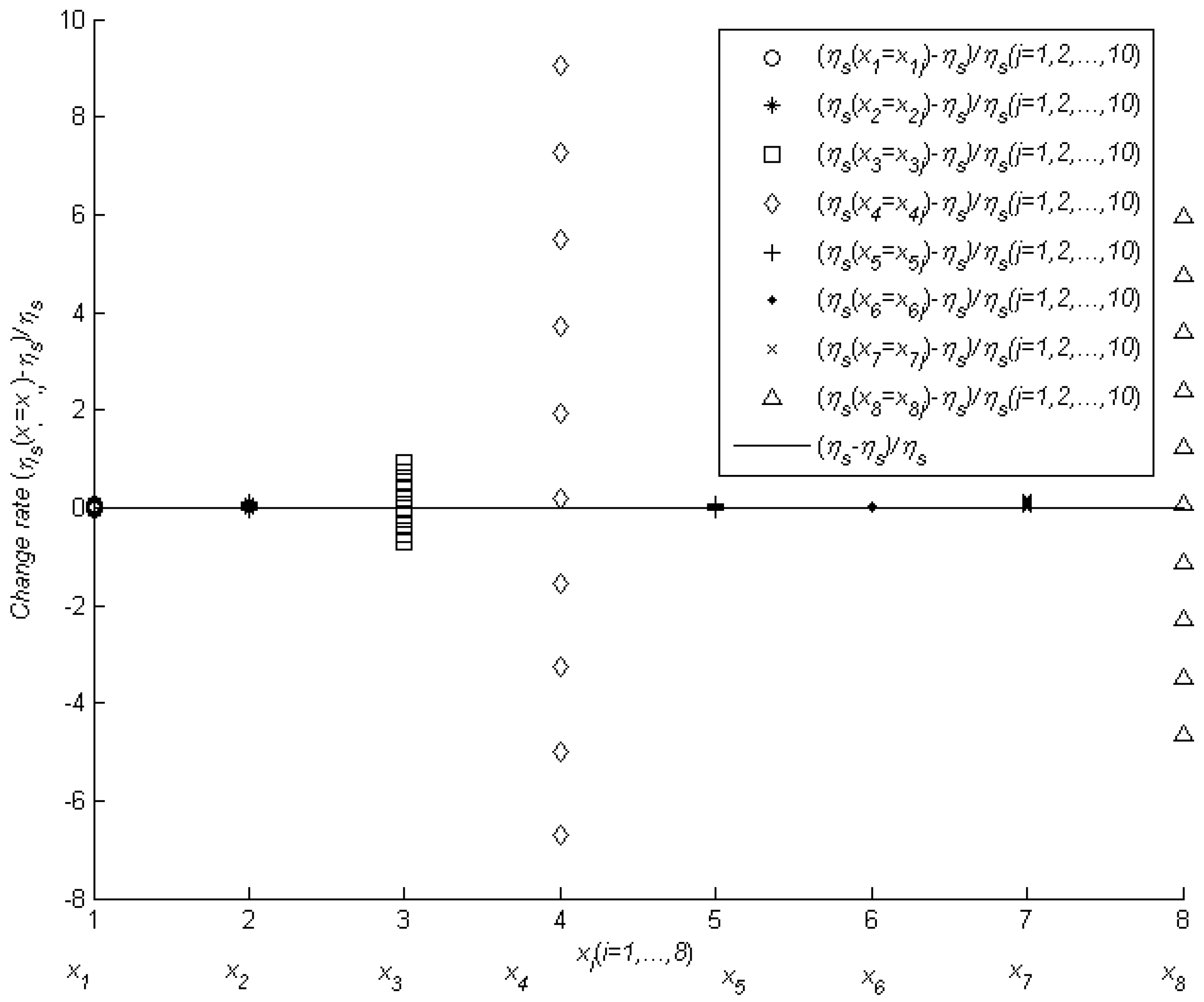
3.2. Evaluation of Sensitivity Analysis for Biodiesel Production with Respect to Interval Parameter
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| biodiesel price | |
| byproduct credit | |
| byproduct credit of the ith year | |
| capital cost | |
| conversion efficiency from feedstock to biodiesel | |
| depreciation rate | |
| feedstock cost | |
| feedstock cost of the ith year | |
| feedstock price | |
| annual total feedstock consumption | |
| glycerol conversion factor | |
| glycerol price | |
| life cycle cost | |
| maintenance cost | |
| maintenance cost of the ith year | |
| maintenance rate | |
| NPRI | non-probabilistic reliability index |
| operating cost | |
| operating cost of the ith year | |
| operating rate or operating cost of per-ton crude-palm-oil-derived biodiesel production | |
| production capacity | |
| payback period of the biodiesel production | |
| allowable upper limit of payback period | |
| worth factor in the year n | |
| replacement cost | |
| interest rate | |
| SA | sensitivity analysis |
| salvage value | |
| annual total taxation | |
| annual total biodiesel sales | |
| techno-economic assessments | |
| total profit | |
| tax rate | |
| UA | uncertainty analysis |
| density of the biodiesel |
References
- Höök, M.; Tang, X. Depletion of fossil fuels and anthropogenic climate change—A review. Energy Policy 2013, 52, 797–809. [Google Scholar] [CrossRef]
- Höök, M. Energy, Climate and Society. 2013. Available online: http://cemusstudent.se/wp-content/uploads/2012/02/Week-49-Energy-Climate-and-Society-Mikael-Höök.pdf (accessed on 3 January 2018).
- Yan, Y.J.; Li, X.; Wang, G.L.; Gui, X.H.; Li, G.L.; Su, F.; Wang, X.F.; Liu, T. Biotechnological preparation of biodiesel and its high-valued derivatives: A review. Appl. Energy 2014, 113, 1614–1631. [Google Scholar] [CrossRef]
- Capellán-Pérez, I.; Mediavilla, M.; Castro, C.; Carpintero, O.; Miguel, L.J. Fossil fuel depletion and socio-economic scenarios: An integrated approach. Energy 2014, 77, 641–666. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable energy resources: Current status, future prospects and their enabling technology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- Mohr, S.H.; Wang, J.; Ellem, G.; Ward, J.; Giurco, D. Projection of world fossil fuels by country. Fuel 2015, 141, 120–135. [Google Scholar] [CrossRef]
- Abas, N.; Kalair, A.; Khan, N. Review of fossil fuels and future energy technologies. Futures 2015, 69, 31–49. [Google Scholar] [CrossRef]
- Nicoletti, G.; Arcuri, N.; Nicoletti, G.; Bruno, R. A technical and environmental comparison between hydrogen and some fossil fuels. Energy Convers. Manag. 2015, 89, 205–213. [Google Scholar] [CrossRef]
- Day, C.; Day, G. Climate change, fossil fuel prices and depletion: The rationale for a falling export tax. Econ. Model. 2017, 63, 153–160. [Google Scholar] [CrossRef]
- Mahmudul, H.M.; Hagos, F.Y.; Mamat, R.; Adam, A.A.; Ishak, W.F.W.; Alenezi, R. Production, characterization and performance of biodiesel as an alternative fuel in diesel engines—A review. Renew. Sustain. Energy Rev. 2017, 72, 497–509. [Google Scholar] [CrossRef]
- No, S.Y. Application of straight vegetable oil from triglyceride based biomass to IC engines—A review. Renew. Sustain. Energy Rev. 2017, 69, 80–97. [Google Scholar] [CrossRef]
- Othman, M.F.; Adam, A.; Najafi, G.; Mamat, R. Green fuel as alternative fuel for diesel engine: A review. Renew. Sustain. Energy Rev. 2017, 80, 694–709. [Google Scholar] [CrossRef]
- Efe, S.; Ceviz, M.A.; Temur, H. Comparative engine characteristics of biodiesels from hazelnut, corn, soybean, canola and sunflower oils on DI diesel engine. Renew. Energy 2018, 119, 142–151. [Google Scholar] [CrossRef]
- Ruhul, A.M.; Kalam, M.A.; Masjuki, H.H.; Shahir, S.A.; Alabdulkarem, A.; Teoh, Y.H.; How, H.G.; Reham, S.S. Evaluating combustion, performance and emission characteristics of Millettia pinnata and Croton megalocarpus biodiesel blends in a diesel engine. Energy 2017, 141, 2362–2376. [Google Scholar] [CrossRef]
- Silva, M.A.V.D.; Ferreira, B.L.G.; Marques, L.G.D.C.; Murta, A.L.S.; Freitas, M.A.V.D. Comparative study of NOx emissions of biodiesel-diesel blends from soybean, palm and waste frying oils using methyl and ethyl transesterification routes. Fuel 2017, 194, 144–156. [Google Scholar] [CrossRef]
- Ding, H.; Ye, W.; Wang, Y.Q.; Wang, X.Q.; Li, L.J.; Liu, D.; Gui, J.Z.; Song, C.F.; Ji, N. Process intensification of transesterification for biodiesel production from palm oil: Microwave irradiation on transesterification reaction catalyzed by acidic imidazolium ionic liquids. Energy 2018, 144, 957–967. [Google Scholar] [CrossRef]
- Zou, C.J.; Zhao, P.W.; Shi, L.H.; Huang, S.B.; Luo, P.Y. Biodiesel fuel production from waste cooking oil by the inclusion complex of heteropoly acid with bridged bis-cyclodextrin. Bioresour. Technol. 2013, 146, 785–788. [Google Scholar] [CrossRef] [PubMed]
- Ali, C.H.; Qureshi, A.S.; Mbadinga, S.M.; Liu, J.F.; Yang, S.Z.; Mu, B.Z. Biodiesel production from waste cooking oil using onsite produced purified lipase from Pseudomonas aeruginosa FW_SH-1: Central composite design approach. Renew. Energy 2017, 109, 93–100. [Google Scholar] [CrossRef]
- Tangy, A.; Pulidindi, I.N.; Perkas, N.; Gedanken, A. Continuous flow through a microwave oven for the large-scale production of biodiesel from waste cooking oil. Bioresour. Technol. 2017, 224, 333–341. [Google Scholar] [CrossRef] [PubMed]
- Allesina, G.; Pedrazzi, S.; Tebianian, S.; Tartarini, P. Biodiesel and electrical power production through vegetable oil extraction and byproducts gasification: Modeling of the system. Bioresour. Technol. 2014, 170, 278–285. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.X.; Yuan, H.R.; Wang, Y.Z.; Shan, R. Transesterification of vegetable oil on low cost and efficient meat and bone meal biochar catalysts. Energy Convers. Manag. 2017, 150, 214–221. [Google Scholar] [CrossRef]
- Tang, S.K.; Zhao, H.; Song, Z.Y.; Olubajo, O. Glymes as benign co-solvents for CaO-catalyzed transesterification of soybean oil to biodiesel. Bioresour. Technol. 2013, 139, 107–112. [Google Scholar] [CrossRef] [PubMed]
- Celante, D.; Schenkel, J.V.D.; Castilhos, F. Biodiesel production from soybean oil and dimethyl carbonate catalyzed by potassium methoxide. Fuel 2018, 212, 101–107. [Google Scholar] [CrossRef]
- Luna, M.D.G.D.; Cuasay, J.L.; Tolosa, N.C.; Chung, T.W. Transesterification of soybean oil using a novel heterogeneous base catalyst: Synthesis and characterization of Na-pumice catalyst, optimization of transesterification conditions, studies on reaction kinetics and catalyst reusability. Fuel 2017, 209, 246–253. [Google Scholar] [CrossRef]
- Li, K.; Fan, Y.L.; Zeng, L.P.; Han, X.T.; Yan, Y.J. Burkholderia cepacia lipase immobilized on heterofunctional magnetic nanoparticles and its application in biodiesel synthesis. Sci. Rep. 2017, 7, 16473. [Google Scholar] [CrossRef] [PubMed]
- Nisar, J.; Razaq, R.; Farooq, M.; Iqbal, M.; Khan, R.A.; Sayed, M.; Shah, A.; Rahman, I. Enhanced biodiesel production from Jatropha oil using calcined waste animal bones as catalyst. Renew. Energy 2017, 101, 111–119. [Google Scholar] [CrossRef]
- Quinn, J.C.; Davis, R. The potentials and challenges of algae based biofuels: A review of the techno-economic, life cycle, and resource assessment modeling. Bioresour. Technol. 2015, 184, 444–452. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, R.P.; Borroto, Y.S.; Espinosa, E.A.M.; Verhelst, S. Assessment of diesel engine performance when fueled with biodiesel from algae and microalgae: An overview. Renew. Sustain. Energy Rev. 2017, 69, 833–842. [Google Scholar] [CrossRef]
- Taparia, T.; Mvss, M.; Mehrotra, R.; Shukla, P.; Mehrotra, S. Developments and challenges in biodiesel production from microalgae: A review. Biotechnol. Appl. Biochem. 2015, 63, 715–726. [Google Scholar] [CrossRef] [PubMed]
- Piligaev, A.V.; Sorokina, K.N.; Samoylova, Y.V.; Parmon, V.N. Lipid production by microalga Micractinium sp. IC-76 in a flat panel photobioreactor and its transesterification with cross-linked enzyme aggregates of Burkholderia cepacia lipase. Energy Convers. Manag. 2018, 156, 1–9. [Google Scholar] [CrossRef]
- Probst, K.V.; Schulte, L.R.; Durrent, T.P.; Rezac, M.E.; Vadlani, P.V. Oleaginous yeast: A value-added platform for renewable oils. Crit. Rev. Biotechnol. 2016, 36, 942–955. [Google Scholar] [CrossRef] [PubMed]
- Sitepu, I.R.; Garay, L.A.; Sestric, R.; Levin, D.; Block, D.E.; German, J.B.; Mills, K.L.B. Oleaginous yeasts for biodiesel: Current and future trends in biology and production. Biotechnol. Adv. 2014, 32, 1336–1360. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Pei, Z.J.; Wang, D.H. Organic solvent pretreatment of lignocellulosic biomass for biofuels and biochemicals: A review. Bioresour. Technol. 2016, 199, 21–33. [Google Scholar] [CrossRef] [PubMed]
- Lam, S.S.; Mahari, W.A.W.; Jusoh, A.; Chong, C.T.; Lee, C.L.; Chase, H.A. Pyrolysis using microwave absorbents as reaction bed: An improved approach to transform used frying oil into biofuel product with desirable properties. J. Clean. Prod. 2017, 147, 263–272. [Google Scholar] [CrossRef]
- Malhotra, R.; Ali, A. Lithium-doped ceria supported SBA−15 as mesoporous solid reusable and heterogeneous catalyst for biodiesel production via simultaneous esterification and transesterification of waste cottonseed oil. Renew. Energy 2018, 119, 32–44. [Google Scholar] [CrossRef]
- Abdullah, S.H.Y.S.; Hanapi, N.H.M.; Azid, A.; Umar, R.; Juahir, H.; Khatoon, H.; Endut, A. A review of biomass-derived heterogeneous catalyst for a sustainable biodiesel production. Renew. Sustain. Energy Rev. 2017, 70, 1040–1051. [Google Scholar] [CrossRef]
- Singh, V.; Sharma, Y.C. Low cost guinea fowl bone derived recyclable heterogeneous catalyst for microwave assisted transesterification of Annona squamosa L. seed oil. Energy Convers. Manag. 2017, 138, 627–637. [Google Scholar] [CrossRef]
- Vinod, B.M.; Madhu, M.K.; Amba, P.R.G. Butanol and pentanol: The promising biofuels for CI engines—A review. Renew. Sustain. Energy Rev. 2017, 78, 1068–1088. [Google Scholar]
- Singh, L.K.; Chaudhary, G. Advances in Biofeedstocks and Biofuels; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Sotoft, L.F.; Rong, B.G.; Christensen, K.V.; Norddahl, B. Process simulation and economical evaluation of enzymatic biodiesel production plant. Bioresour. Technol. 2010, 101, 5266–5274. [Google Scholar] [CrossRef] [PubMed]
- Haas, M.J.; McAloon, A.J.; Yee, W.C.; Foglia, T.A. A process model to estimate biodiesel production costs. Bioresour. Technol. 2006, 97, 671–678. [Google Scholar] [CrossRef] [PubMed]
- Ong, H.C.; Mahlia, T.M.I.; Masjuki, H.H.; Honnery, D. Life cycle cost and sensitivity analysis of palm biodiesel production. Fuel 2012, 98, 131–139. [Google Scholar] [CrossRef]
- Xin, C.H.; Addy, M.M.; Zhao, J.Y.; Cheng, Y.L.; Cheng, S.B.; Mu, D.Y.; Liu, Y.H. Comprehensive techno-economic analysis of wastewater-based algal biofuel production: A case study. Bioresour. Technol. 2016, 211, 584–593. [Google Scholar] [CrossRef] [PubMed]
- Kern, J.D.; Hise, A.M.; Characklis, G.W.; Gerlach, R.; Viamajala, S.; Gardner, R.D. Using life cycle assessment and techno-economic analysis in a real options framework to inform the design of algal biofuel production facilities. Bioresour. Technol. 2017, 225, 418–428. [Google Scholar] [CrossRef] [PubMed]
- Thomassen, G.; Dael, M.V.; Lemmens, B.; Passel, S.V. A review of the sustainability of algal-based biorefineries: Towards an integrated assessment framework. Renew. Sustain. Energy Rev. 2017, 68, 876–887. [Google Scholar] [CrossRef]
- Dutta, S.; Neto, F.; Coelho, M.C. Microalgae biofuels: A comparative study on techno-economic analysis & life-cycle assessment. Algal Res. 2016, 20, 44–52. [Google Scholar]
- Hpffman, J.; Pate, R.C.; Drennen, T.; Quinn, J.C. Techno-economic assessment of open microalgae production systems. Algal Res. 2017, 23, 51–57. [Google Scholar] [CrossRef]
- Xin, C.H.; Addy, M.M.; Zhao, J.Y.; Cheng, Y.L.; Ma, Y.W.; Liu, S.Y.; Mu, D.Y.; Liu, Y.H.; Chen, P.; Ruan, R. Waste-to-biofuel integrated system and its comprehensive techno-economic assessment in wastewater treatment plants. Bioresour. Technol. 2018, 250, 523–531. [Google Scholar] [CrossRef] [PubMed]
- Mandegari, M.A.; Farzad, S.; Görgens, J.F. Recent trends on techno-economic assessment (TEA) of sugarcane biorefineries. Biofuel Res. J. 2017, 4, 704–712. [Google Scholar] [CrossRef]
- Tao, L.; Milbrandt, A.; Zhang, Y.N.; Wang, W.C. Techno-economic and resource analysis of hydroprocessed renewable jet fuel. Biotechnol. Biofuels 2017, 10, 261. [Google Scholar] [CrossRef] [PubMed]
- Patel, M.; Zhang, X.L.; Kumar, A. Techno-economic and life cycle assessment on lignocellulosic biomass thermochemical conversion technologies: A review. Renew. Sustain. Energy Rev. 2015, 53, 1486–1499. [Google Scholar] [CrossRef]
- Busse, S.; Brümmer, B.; Ihle, R. Price formation in the German biodiesel supply chain: A Markov-switching vector error-correction modeling approach. Agric. Econ. 2012, 43, 545–560. [Google Scholar] [CrossRef]
- Mankiw, N.G. Principles of Economics, 6th ed.; South-Western Cengage Learning: Mason, OH, USA, 2011. [Google Scholar]
- Borgonovo, E.; Peccati, L. Uncertainty and Global Sensitivity Analysis in the Evaluation of Investment Projects. Int. J. Prod. 2006, 104, 62–73. [Google Scholar] [CrossRef]
- Brownbridge, G.; Azadi, P.; Smallbone, A.; Bhave, A.; Taylor, B.; Kraft, M. The future viability of algae-derived biodiesel under economic and technical uncertainties. Bioresour. Technol. 2014, 151, 166–173. [Google Scholar] [CrossRef] [PubMed]
- López, P.P.; Montazeri, M.; Feijoo, G.; Moreira, M.T.; Eckelman, M.J. Integrating uncertainties to the combined environmental and economic assessment of algal biorefineries: A Monte Carlo approach. Sci. Total Environ. 2018, 626, 762–775. [Google Scholar] [CrossRef] [PubMed]
- Abubakar, U.; Sriramula, S.; Renton, N.C. Stochastic techno-economic considertations in biodiesel production. Sustain. Energy Technol. Assess. 2015, 9, 1–11. [Google Scholar]
- Tang, Z.C.; Lu, Z.Z.; Liu, Z.W.; Xiao, N.C. Uncertainty analysis and global sensitivity analysis of techno-economic assessments for biodiesel production. Bioresour. Technol. 2015, 175, 502–508. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.J.; Tang, Z.C. A novel perspective for techno-economic assessments and effects of parameters on techno-economic assessments for biodiesel production under economic and technical uncertainties. RSC Adv. 2017, 7, 9402–9411. [Google Scholar] [CrossRef]
- Sajid, Z.; Zhang, Y.; Khan, F. Process design and probabilistic economic risk analysis of biodiesel production. Sustain. Prod. Consum. 2016, 5, 1–15. [Google Scholar] [CrossRef]
- Liew, W.H.; Hassim, M.H.; Ng, D.K.S. Sustainability assessment framework for chemical production pathway: Uncertainty analysis. J. Environ. Chem. Eng. 2016, 4, 4878–4889. [Google Scholar] [CrossRef]
- Batan, L.Y.; Graff, G.D.; Bradley, T.H. Techno-economic and Monte Carlo probabilistic analysis of microalgae biofuel production system. Bioresour. Technol. 2016, 219, 45–52. [Google Scholar] [CrossRef] [PubMed]
- Ochoa, M.P.; Estrada, V.; Maggio, J.D.; Hoch, P.M. Dynamic global sensitivity analysis in bioreactor networks for bioethanol production. Bioresour. Technol. 2016, 200, 666–679. [Google Scholar] [CrossRef] [PubMed]
- Yao, G.L.; Staples, M.D.; Malina, R.; Tyner, W.E. Stochastic techno-economic analysis of alcohol-to-jet fuel production. Biotechnol. Biofuels 2017, 10, 18. [Google Scholar] [CrossRef] [PubMed]
- Garay, A.G.; Miquel, M.G.; Gosalbez, G.G. High-Value Propylene Glycol from Low-Value Biodiesel Glycerol: A Techno-Economic and Environmental Assessment under Uncertainty. ACS Sustain. Chem. Eng. 2017, 5, 5723–5732. [Google Scholar] [CrossRef]
- Trading Economics. Malaysia Interest Rate 1996–2014. 2014. Available online: http://zh.tradingeconomics.com/malaysia/bank-lending-rate (accessed on 3 January 2018).
- Hitchcock, G. The Economics of Biofuel Production and Use. 2014. Available online: http://www.sts-technology.com/docs/Economics-of-biofuel-production-and-use.ppt (accessed on 3 January 2018).
- Duncan, J. Costs of Biodiesel Production. 2003. Available online: http://www.globalbioenergy.org/uploads/media/0305_Duncan_-_Cost-of-biodiesel-production.pdf (accessed on 3 January 2018).
- Nagi, J.; Ahmed, S.K.; Nagi, F. Palm Biodiesel an Alternative Green Renewable Energy for the Energy Demands of the Future. In Proceedings of the International Conference on Construction and Building Technology, Kuala Lumpur, Malaysia, 16–20 June 2008; pp. 79–94. [Google Scholar]
- Nanda, M.R.; Yuan, Z.; Qin, W.; Poirier, M.A.; Chunbao, X. Purification of Crude Glycerol using Acidification: Effects of Acid Types and Product Characterization. Austin J. Chem. Eng. 2014, 1, 1–7. [Google Scholar]
- FarmdocDAILY. Recent Trends in Biodiesel Prices and Production Profits. 2013. Available online: http://farmdocdaily.illinois.edu/2013/09/recent-trends-in-biodiesel.html (accessed on 3 January 2018).
- Cremona, C.; Gao, Y. The possibilistic reliability theory: Theoretical aspects and applications. Struct. Saf. 1997, 19, 173–201. [Google Scholar] [CrossRef]
- Guo, S.X.; Lu, Z.Z.; Feng, Y.S. A non-probabilistic model of structural reliability based on interval analysis. Chin. J. Comput. Mech. 2001, 18, 56–60. [Google Scholar]
- Guo, S.X.; Li, Y. Non-probabilistic reliability method and reliability-based optimal LQR design for vibration control of structures with uncertain-but-bounded parameters. Acta Mech. Sin. 2013, 29, 864–874. [Google Scholar] [CrossRef]
- Kang, Z.; Luo, Y. Non-probabilistic reliability-based topology optimization ofgeometrically nonlinear structures using convex models. Comput. Methods Appl. Mech. Eng. 2009, 198, 3228–3238. [Google Scholar] [CrossRef]
- Ben-Haim, Y.; Elishakoff, I. Convex Models of Uncertainty in Applied Mechanics; Elsevier Press: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Ben-Haim, Y. A non-probabilistic measure of reliability of linear systems based on expansion of convex models. Struct. Saf. 1995, 17, 91–109. [Google Scholar] [CrossRef]
- Ben-Haim, Y. Robust Reliability in the Mechanics Sciences; Springer: Berlin, Germany, 1996. [Google Scholar]
- Ben-Haim, Y. Robust reliability of structures. Adv. Appl. Mech. 1997, 33, 1–41. [Google Scholar]
- Elishakoff, I. Essay on uncertainties in elastic and viscoelastic structures: From A. M. Freudenthal’s criticisms to modern convex modeling. Comput. Struct. 1995, 56, 871–895. [Google Scholar] [CrossRef]
- Elishakoff, I. Are Probabilistic and Anti-Optimization Approaches Compatible? Whys and Hows in Uncertainty Modelling: Probability, Fuzziness and Antioptimization; Springer: New York, NY, USA, 1999. [Google Scholar]





| Uncertain Parameters | Variation Intervals [, ] |
|---|---|
| Capital cost (CC: ) [42] | [$9 million, $15 million] |
| Interest rate (r: ) [66] | [4.44%, 13.53%] |
| Operating rate (OR: ) [42,67,68] | [$37.5/t, $225/t] |
| Feedstock price (FP: ) [42] | [$200/t, $1200/t] |
| Glycerol price (GP: ) [70] | [$0.08/kg, $0.2/kg] |
| Maintenance rate (MR: ) [41,42] | [1%, 2%] |
| Biodiesel conversion efficiency (CE: ) [69] | [96%, 99%] |
| Biodiesel price (BP: ) [71] | [$0.66/L, $1.58/L] |
| Parameters | ||
|---|---|---|
| Capital cost (CC: ) | 4.454 × 10−3 | 3.680 × 10−2 |
| Interest rate (r: ) | 5.231 × 10−3 | 4.322 × 10−2 |
| Operating rate (OR: ) | 4.961 × 10−2 | 4.099 × 10−1 |
| Feedstock price (FP: ) | 4.858 × 10−1 | 4.013 × 100 |
| Glycerol price (GP: ) | 2.865 × 10−3 | 2.367 × 10−2 |
| Maintenance rate (MR: ) | 6.643 × 10−4 | 5.488 × 10−3 |
| Biodiesel conversion efficiency (CE: ) | 9.302 × 10−3 | 7.685 × 10−2 |
| Biodiesel price (BP: ) | 3.257 × 10−1 | 2.691 × 100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Z.-C.; Xia, Y.; Xue, Q.; Liu, J. A Non-Probabilistic Solution for Uncertainty and Sensitivity Analysis on Techno-Economic Assessments of Biodiesel Production with Interval Uncertainties. Energies 2018, 11, 588. https://doi.org/10.3390/en11030588
Tang Z-C, Xia Y, Xue Q, Liu J. A Non-Probabilistic Solution for Uncertainty and Sensitivity Analysis on Techno-Economic Assessments of Biodiesel Production with Interval Uncertainties. Energies. 2018; 11(3):588. https://doi.org/10.3390/en11030588
Chicago/Turabian StyleTang, Zhang-Chun, Yanjun Xia, Qi Xue, and Jie Liu. 2018. "A Non-Probabilistic Solution for Uncertainty and Sensitivity Analysis on Techno-Economic Assessments of Biodiesel Production with Interval Uncertainties" Energies 11, no. 3: 588. https://doi.org/10.3390/en11030588
APA StyleTang, Z.-C., Xia, Y., Xue, Q., & Liu, J. (2018). A Non-Probabilistic Solution for Uncertainty and Sensitivity Analysis on Techno-Economic Assessments of Biodiesel Production with Interval Uncertainties. Energies, 11(3), 588. https://doi.org/10.3390/en11030588






