Numerical Study on Heat Transfer to an Arc Absorber Designed for a Waste Heat Recovery System around a Cement Kiln
Abstract
:1. Introduction
2. Problem Statement and Computational Domain
3. Numerical Study and Mesh Independency
4. Results and Discussions
4.1. Verification of the Numerical Study with Available Results
4.1.1. Natural Convection
4.1.2. Forced Convection
4.1.3. Convection for a Rotating Circular Cylinder
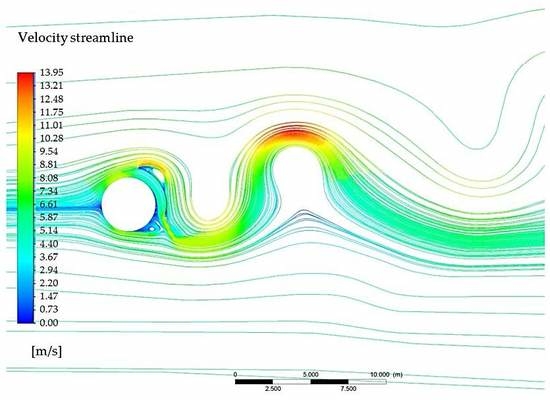
4.2. Numerical Analysis with the Absorber
5. Supporting Study
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zdravkovich, M.M. Flow around Circular Cylinder, Volume I: Fundamentals; Oxford University Press: New York, NY, USA, 1997; ISBN 9780198563969. [Google Scholar]
- Williamson, C.H.K. Vortex Dynamics in the Wake of a Cylinder. In Fluid Vortices. Fluid Mechanics and Its Applications; Green, S.I., Ed.; Springer: Dordrecht, The Netherlands, 1995; pp. 155–234. ISBN 9789401102490. [Google Scholar]
- Schmidt, E.; Wenner, K. Heat Transfer Over the Circumference of a Heated Cylinder in Transverse Flow; NACA TM1050; University of North Texas: Denton, TX, USA, 1941. [Google Scholar]
- Sarma, T.S.; Sukhatme, S.P. Local heat transfer from a horizontal cylinder to air in cross flow: Influence of free convection and free stream turbulence. Int. J. Heat Mass Transf. 1977, 20, 51–56. [Google Scholar] [CrossRef]
- Jain, P.C.; Goel, B.S. A numerical study of unsteady laminar forced convection from a circular cylinder. J. Heat Transf. 1976, 98, 303–307. [Google Scholar] [CrossRef]
- Eckert, E.R.G.; Soehngen, E. Distribution of heat transfer coefficients around circular cylinder in cross flow at Reynolds number 20 to 500. J. Heat Transf. 1952, 74, 343–347. [Google Scholar]
- Scholten, J.W.; Murray, D.B. Unsteady heat transfer and velocity of a cylinder in cross flow—I. low free stream turbulence. Int. J. Heat Mass Transf. 1998, 41, 1139–1148. [Google Scholar] [CrossRef]
- Scholten, J.W.; Murray, D.B. Unsteady heat transfer and velocity of a cylinder in cross flow—II. high free stream turbulence. Int. J. Heat Mass Transf. 1998, 41, 1149–1156. [Google Scholar] [CrossRef]
- Sczepanik, K.; Ooi, A.; Aye, L.; Rosengarten, G. A Numerical Study of Heat Transfer from a Cylinder in Cross Flow. In Proceedings of the 15th Australasian Fluid Mechanics Conference, The University of Sydney, Sydney, Australia, 13–17 December 2004. [Google Scholar]
- Sak, C.; Liu, R.; Ting, D.S.K.; Rankin, G.W. The role of turbulence length scale and turbulence intensity on forced convection from a heated horizontal circular cylinder. Exp. Therm. Fluid Sci. 2007, 31, 279–289. [Google Scholar] [CrossRef]
- Nakamura, H.; Igarashi, T. Variation of Nusselt number with flow regimes behind a circular cylinder for Reynolds numbers from 70 to 30,000. Int. J. Heat Mass Transf. 2004, 47, 5169–5173. [Google Scholar] [CrossRef]
- Nakamura, H.; Igarashi, T. Unsteady heat transfer from a circular cylinder for Reynolds numbers from 3000 to 15,000. Int. J. Heat Fluid Flow 2004, 25, 741–748. [Google Scholar] [CrossRef]
- Van Meel, D.A. A method for the determination of local convective heat transfer from a cylinder placed normal to an air stream. Int. J. Heat Mass Transf. 1962, 5, 715–722. [Google Scholar] [CrossRef]
- Zhukauskas, A.; Ziugzda, J. Heat Transfer of a Cylinder in Cross Flow, 1st ed.; Hemisphere Publishing Corporation: Washington, DC, USA, 1985; ISBN 0891163654. [Google Scholar]
- Chun, W.; Boehm, R.F. Calculation of forced flow and heat transfer around cylinder. Numer. Heat Transf. Part A Appl. 1989, 15, 101–122. [Google Scholar] [CrossRef]
- Churchill, S.W.; Bernstein, M. A correlating equation for forced convection from gases and liquids to a circular cylinder in cross flow. J. Heat Transf. 1977, 99, 300–306. [Google Scholar] [CrossRef]
- Sanitjai, S.; Goldstein, R.J. Forced convection heat transfer from a circular cylinder in cross flow to air and liquids. Int. J. Heat Mass Transf. 2004, 47, 4795–4805. [Google Scholar] [CrossRef]
- Acharya, S.; Dash, K.D. Natural convection heat transfer from a short or long, solid or hollow horizontal cylinder suspended in air or placed on ground. J. Heat Transf. 2017, 139, 072501. [Google Scholar] [CrossRef]
- Acharya, S.; Agrawal, S.; Dash, K.D. Numerical analysis of natural convection heat transfer from a vertical hollow cylinder suspended in air. J. Heat Transf. 2018, 140, 052501-1-12. [Google Scholar] [CrossRef]
- Wang, Y.; Shu, G.; Yu, G.; Tian, H.; Ma, X.; Chen, T. Numerical analysis of forced convection of high-temperature exhaust gas around a metal-foam wrapped cylinder. Int. J. Heat Mass Transf. 2018, 119, 742–751. [Google Scholar] [CrossRef]
- Yoon, H.S.; Kim, H.J.; Wei, D.J. Forced convection heat transfer from the helically twisted elliptic cylinder inspired by a daffodil stem. Int. J. Heat Mass Transf. 2018, 119, 105–116. [Google Scholar] [CrossRef]
- Elsherbiny, S.M.; Teamah, M.A.; Moussa, A.R. Natural convection heat transfer from an isothermal horizontal square cylinder. Alex. Eng. J. 2017, 56, 181–187. [Google Scholar] [CrossRef]
- Hossain, M.A.; Kutubuddin, M.; Pop, I. Radiation-conduction interaction on mixed convection from a horizontal circular cylinder. Heat Mass Transf. 1999, 35, 307–314. [Google Scholar] [CrossRef]
- Molla, M.M.; Saha, S.C.; Khan, M.A.I.; Hossain, M.A. Radiation effects on natural convection laminar flow from a horizontal circular cylinder. Desalin. Water Treat. 2011, 30, 89–97. [Google Scholar] [CrossRef] [Green Version]
- Pachpute, S.; Premachandran, B.; Talukdar, P. A numerical study of combined forced convection and gas radiation from a circular cylinder in cross flow. Heat Transf. Eng. 2015, 36, 135–151. [Google Scholar] [CrossRef]
- Zainuddin, N.; Hashim, I.; Saleh, H.; Roslan, R. Effects of radiation on free convection from a heated horizontal circular cylinder in the presence of heat generation. Sains Malasiana 2016, 45, 315–321. [Google Scholar]
- Nguyen, H.D.; Paik, S.; Douglass, R.W. Unsteady mixed convection about a rotating circular cylinder with small fluctuations in the free-stream velocity. Int. J. Heat Mass Transf. 1996, 39, 511–525. [Google Scholar] [CrossRef]
- Ozerdem, B. Measurement of convective heat transfer coefficient for a horizontal cylinder rotating in quiescent air. Int. J. Heat Mass Transf. 2000, 27, 389–395. [Google Scholar] [CrossRef]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: New York, NY, USA, 2007; ISBN 9780471457282. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson: San Antonio, TX, USA, 2007; ISBN 9780471457282. [Google Scholar]
- ANSYS Workbench User’s Guide, Release 17.2; ANSYS Inc.: Canonsburg, PA, USA, August 2016.
- ANSYS DesignModeler User’s Guide, Release 17.2; ANSYS Inc.: Canonsburg, PA, USA, August 2016.
- ANSYS Fluent Meshing User’s Guide, Release 17.2; ANSYS Inc.: Canonsburg, PA, USA, August 2016.
- ANSYS Fluent in ANSYS Workbench User’s Guide, Release 17.2; ANSYS Inc.: Canonsburg, PA, USA, August 2016.
- ANSYS CFD-Post User’s Guide, Release 17.2; ANSYS Inc.: Canonsburg, PA, USA, August 2016.
- Microsoft Excel; Microsoft Corporation: Redmond, WA, USA, 2010.
- ANSYS Fluent Theory Guide, Release 17.2; ANSYS Inc.: Canonsburg, PA, USA, August 2016.
- Rapti, A.S. Spectral optical atmospheric thickness dependence on the specific humidity in the presence of continental and maritime air masses. Atmos. Res. 2005, 78, 13–32. [Google Scholar] [CrossRef]
- Morgan, V. Heat transfer by natural convection from a horizontal isothermal circular cylinder in air. Heat Transf. Eng. 1997, 18, 25–33. [Google Scholar] [CrossRef]
- Bharti, R.P.; Chhabra, R.P.; Eswaran, V. Steady forced convection heat transfer from a heated circular cylinder to power-law fluids. Int. J. Heat Mass Transf. 2007, 50, 977–990. [Google Scholar] [CrossRef]










| Grid Number | Total Number of Elements | Total Heat Loss from the Kiln (W) |
|---|---|---|
| 1 | 41,857 | 257,769.9 |
| 2 | 69,765 | 243,857.4 |
| 3 | 106,566 | 235,050.9 |
| 4 | 156,722 | 230,442.2 |
| 5 | 227,247 | 228,773.9 |
| 6 | 324,961 | 228,119.8 |
| Laminar Model | Turbulent Model (k-ω-sst) | Reference [39] | |
|---|---|---|---|
| Ra = 100 | 1.9623 | 1.9814 | From 1.64 to 2.28 |
| Ra = 100,000 | 8.0876 | 10.0607 | From 7.23 to 10.1 |
| Nur [-] | Nuc [-] | Nutotal [-] | Difference Percentage | ||
|---|---|---|---|---|---|
| Analytical solution | 2693.4491 | 1779.8081 | 4473.2572 | --- | |
| Numerical solution | Unsteady model | 2693.1123 | 935.5977 | 3628.71 | 18.88% |
| Steady-state model | 2693.1123 | 851.1966 | 3544.3089 | 20.77% |
| Radiation [W] | Convection [W] | Total Heat Loss [W] | Nur [-] | Nuc [-] | Nutot [-] | ||
|---|---|---|---|---|---|---|---|
| Numerical solution | Unsteady model | 183,256 | 47,186.2 | 230,442.2 | 2704.76 | 696.44 | 3401.20 |
| Radiation [W] | Convection [W] | Tave [K] | Nur [-] | Nuc [-] | Nutot [-] | ||
|---|---|---|---|---|---|---|---|
| Numerical solution | Unsteady model | 199,733.9 | 46,122.8 | 789.28 | 2858.20 | 660.02 | 3518.22 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirhosseini, M.; Rezaniakolaei, A.; Rosendahl, L. Numerical Study on Heat Transfer to an Arc Absorber Designed for a Waste Heat Recovery System around a Cement Kiln. Energies 2018, 11, 671. https://doi.org/10.3390/en11030671
Mirhosseini M, Rezaniakolaei A, Rosendahl L. Numerical Study on Heat Transfer to an Arc Absorber Designed for a Waste Heat Recovery System around a Cement Kiln. Energies. 2018; 11(3):671. https://doi.org/10.3390/en11030671
Chicago/Turabian StyleMirhosseini, Mojtaba, Alireza Rezaniakolaei, and Lasse Rosendahl. 2018. "Numerical Study on Heat Transfer to an Arc Absorber Designed for a Waste Heat Recovery System around a Cement Kiln" Energies 11, no. 3: 671. https://doi.org/10.3390/en11030671
APA StyleMirhosseini, M., Rezaniakolaei, A., & Rosendahl, L. (2018). Numerical Study on Heat Transfer to an Arc Absorber Designed for a Waste Heat Recovery System around a Cement Kiln. Energies, 11(3), 671. https://doi.org/10.3390/en11030671