Performance and Accuracy Investigation of the Two-Step Algorithm for Power System State and Line Temperature Estimation

Abstract

Data concerning actual temperatures of line conductors constitutes essential information for the power system operator. The temperature of the power lines can be used to improve the accuracy of the power system model, thereby increasing the accuracy of the state estimation. This article presents a two-step algorithm for the power system state and line temperature estimation. In its second stage, the proposed method searches for a line temperatures vector, which corrects the uncertain power system base model and allows for further minimization of an objective function. As a result, a more accurate estimation is obtained along with a more precise model of the estimated system. The derived model can then be used for more accurate optimization. The presented method enhances standard procedures of power system state estimation, and its advantage is that it does not require direct measurements performed by phasor measurement units or measurements of line conductor temperatures and weather conditions realized by dynamic line rating systems. The results of simulations made on various test models have been examined, confirming the convergence of the procedure to the point at which the average temperature of the line wires together with the voltage values and phase angles are achieved. The algorithm’s performance and improvement method have also been presented. An advantage of the investigated approach is the possibility to calculate the temperature of line wires with the use of primary measurements in the power system. The presented and examined method, however, is sensitive to the measuring device errors. Additionally, an analysis of the method’s errors and ways of reducing them has been performed.

1. Introduction

Modern power systems should have the possibility of flexible power transmission, which is directly related to the more extensive use of Overhead Transmission Line (OTL) capabilities, especially when it comes to high penetration of renewable energy sources [1,2]. The factor limiting the load of the line is the temperature and sag of the conductors. This depends on many factors, including, among others, the type of conductor, load current, and atmospheric weather conditions [3,4,5,6]. Currently, one of the methods for a more efficient use of the transmission capacity of Overhead Transmission Lines (OTLs) is the installation of precise and cost-intensive Dynamic Line Rating (DLR) systems [7,8,9,10,11,12,13,14]. The aim of the presented method is to estimate the temperature of the line wires, in the absence of weather measurements along the line and with a lack of Dynamic Line Rating (DLR) devices installed in the analyzed system. The method presented in the article enables, in a simplified way, the estimation of the system state and temperature of conductors on the basis of primary measurements of active and reactive powers along with bus voltages. Determining the temperature of the conductors is an element of identifying new parameters of the power system base model, i.e. temperature, resistance, and reactances of the lines. The more accurate corrected model of the power system allows for better, more precise optimization and the obtained solution is closer to the actual optimum. In addition, achieving estimated temperatures of line wires, and thus new parameters of the system model may constitute an element of optimization technique proposed in [15], according to which it is possible to achieve the strict optimum of a non-linear system only if its approximate model is available. A solution that allows for the calculation of the actual average temperature of Overhead Transmission Line (OTL) conductors can be the extension of the power system State Estimation (SE) method [16,17]. The SE of an electric power system is a reasonably well recognized problem and it is often referred to as on-line modeling [18,19,20]. There are many modifications of SE procedure that improve performance [21], the accuracy of results [22] or robustness to the power system model parameter errors [23,24,25,26]. One of the many sources of model parameter errors are the actual OTLs’ operation temperatures [16,27,28,29,30,31,32]. In [16], the authors proposed a two-stage estimation, where at the second stage OTL resistances are updated according to available measurements and actual weather parameters. In [17], the authors proposed a similar algorithm, but they incorporated into the measurement vector four groups of data, where the first group is bus voltage magnitude and branch power, the second group contains measurements from installed Phasor Measurement Units (PMUs), the subsequent group contains the current magnitude measurements, and the last group is comprised of weather-related environment data.

In the present article, a two-step power system state and line temperature estimation is proposed that uses only classical measurements such as active and reactive power, bus voltage and current, without any additional measurements such as ambient parameters from weather stations, conductor temperatures from DLR, voltage and current magnitudes with its angles from PMUs or Wide Area Measurement System (WAMs) [22]. The proposed method assumes a well-identified power system topology, and the absence of bad data measurement values [18]. The accuracy of the temperature estimation method mainly depends on measuring apparatus classes. This approach allows us to determine the OTLs without additional measured values, but it increases the demand for computing power. In this case, the Graphical Processing Unit (GPU) can be used to speed up the estimation calculations. The article analyzes the accuracy of estimating temperature of OTL wires as a function of the measuring instrument classes, along with the estimation times as a function of the size of the power system. A modified listing of MATPOWER [33] code is also presented, one that uses a GPU for performance improvement.

In this paper, the author contributes to analyzing and solving the problem of uncertain power system line temperatures’ estimation, which leads to the more accurate state estimation. The main contributions of this paper are summarized as follows.

• The inaccuracy of the power system model results mainly from the actual temperatures of the operating conductors of the power line, which in the case of accurate measurements causes errors in the estimation of the state. Therefore, a two-stage method for estimating the power system state and line temperatures was proposed. The advantage of the presented algorithm is that it does not require any additional measurement data such as the measurement of current in a line conductor, weather information along the line from DLR systems or PMUs, which can be augmented in measurement function h and measurement Jacobian $\mathbf{H}$ as proposed in [17].
• A case study based on the IEEE 39 bus New England test system was presented, in which the power line temperatures have been calculated. Based on the achieved results, the two-step algorithm for power system state and line temperature estimation was applied, in order to better understand the algorithm structure and its operation.
• The performance and accuracy of the presented method have been been examined using different test system cases.
• The speed improvement of the presented algorithm estimating a larger power system model has been examined using graphical processing units. The example of modified MATPOWER code for using graphical processing units has been shown.
• The accuracy of the presented method has been examined as a function of instrument transformers classes.

The remaining part of this paper is organized as follows: in Section 2, the classical state estimation procedure is presented. In Section 3, a two-step algorithm for power system state and line temperature estimation is presented, encompassing both theory and implementation. Section 4 is focused on a practical examination of the presented method, its operation, performance and accuracy. Finally, the article is concluded with Section 5.

2. Power System State Estimation

The present-day development of computer technologies makes it possible to perform real-time SE of large and advanced power systems. SE determines the most probable vector of complex voltages using a system model and measured values of bus voltages, active and reactive power of the generation, transmission and loads [18,20,34,35,36]. Additionally, the SE can use current measurements, but their application sometimes causes problems of a mathematical nature [18,19,37], especially when line current is very small. The calculated most probable vector of phase angles and nodal voltages of the estimated system with its model constitutes a basis for the determining of all dependent variables, i.e. power flows and line currents together in metered and non-metered parts of the network. The measured values of the active and reactive power as well as of the voltage and current are characterized by measurement uncertainty [18,37]. That uncertainty mainly follows from the errors of the measuring devices installed in the system. Measurement uncertainty can also result from the resolution of analog-to-digital converters used for signal processing and transmitting the measurement values to Supervisory Control and Data Acquisition (SCADA) computers. Instrument transformers are the source of the greatest measurement errors, but their operating uncertainty is well defined by their classes. Power system SE is most often realized using the iterative Weighted Least Squares (WLS) method. That process takes into consideration the uncertainty of all measured values using the covariance matrix. In an ideal case, when the measured values and the model parameters are not encumbered with any errors, the iterative SE algorithm converges to a strictly optimal point, where the deviation between the estimated and measured values defined as (1) is equal to zero $\epsilon =0$

$$z_i-h_i(\mathbf{x})=\epsilon$$

(1)

where $z_i$-i-th measurement in the PS, $h_i(\mathbf{x})$—measurement function which is the static model of PS, $\mathbf{x}$—vector of the PS state consisting of voltage magnitudes and angles, $\epsilon$—deviation between the i-th measurement and the model value. Errors of both the measured values and of the model affect the estimation quality defined by the value of $\epsilon$. The State Estimation (SE) uses a static model of the power system, where line resistance values are calculated on the basis of line length and conductor per-length resistances provided by the manufacturer, usually given for the temperature of 20 ${}^{°}$C. Differences between actual parameters of an operating power line and parameters of a static power system model as a rule pertain to resistance and reactance values and are related to temperature changes in the conductors [16,27,28,29,30,31,32]. Those temperature variations result from the heating effect produced by the current flow and the cooling influence of weather conditions [3,4,38,39].

The theory of the power system State Estimation (SE) [18,20,34,35,36,37] assumes that measured values are characterized by the uncertainty ${\sigma }_i$ which is defined by Equations (2)–(4) and stands for a standard deviation of the measurement $z_i$. The measurement uncertainty ${\sigma }_i$ is the statistically recognized error, consistent with the Gaussian distribution where the function $\mathsf{\Phi }(u)$ assumes the form:

$$\mathsf{\Phi }(u)=\frac{1}{\sqrt{2\pi }}·e^{-\frac{u^2}{2}}$$

(2)

defined by:

$$f(z)=\frac{1}{\sqrt{2\pi }\sigma }·e^{-\frac{1}{2}·(\frac{z-\mu }{\sigma })}$$

(3)

The function f(z) varies depending on the parameters $\mu$ and $\sigma$, and, furthermore, its shape can become standardized with the application of the transformation

$$u=\frac{z-\mu }{\sigma }$$

(4)

where: z—random variable, $\mu$—mean or expected value of variable $z=E(z)$, $\sigma$—standard deviation of the variable z.

It is worth noting that the measurement function h is a static model of a power system, where the parameters of its elements such as lines, transformers or shunts can carry an unknown level of uncertainty [18,24]. The SE can be considered as an optimization procedure searching for such a power system’s state vector $\mathbf{x}$ that makes it possible to obtain the minimum value of the objective function defined as Equation (5):

$$J=\sum _{i=1}^N{\mathbf{W}}_{ii}{[z_i-h_i(\mathbf{x})]}^2; \mathrm{and} {\mathbf{W}}_{ii}=\frac{1}{{\sigma }_i^2}$$

(5)

where: J—objective function, ${\mathbf{W}}_{ii}$—diagonal weight matrix, while the ${\sigma }_i$—covariance of the i-th measurement. The minimum determination of the function J can be verified using the basic first order optimality condition (6):

$$g(x)=\frac{\partial J(x)}{\partial x}=0$$

(6)

By expanding $g(x)$ (6) into the Taylor series around $x^{(k)}$ and neglecting further terms of the series, a basis for iterative calculations is defined (7):

$$g(x^{(k)})+\frac{\partial g(x^{(k)})}{\partial x}(x-x^{(k)})=0$$

(7)

The Gauss-Newton method [18,37] can be applied to obtain a solution for the state vector $\mathbf{x}$ that minimizes the J function. By transforming Equations (5) and (7) to the differential form, the following formulas can be obtained, respectively:

$$\mathbf{G}({\mathbf{x}}^{(k)})\Delta {\mathbf{x}}^{(k+1)}={\mathbf{H}}^T({\mathbf{x}}^{(k)})·\mathbf{W}·[\mathbf{z}-h({\mathbf{x}}^{(k)})]$$

(8)

$$\mathbf{G}(\mathbf{x})=\frac{{\partial }^{2}J(x)}{\partial x^2}={\mathbf{H}}^T(\mathbf{x})·\mathbf{W}·\mathbf{H}(\mathbf{x})$$

(9)

where: $\mathbf{G}({\mathbf{x}}^{(k)})$—gain matrix, $\Delta {\mathbf{x}}^{(k+1)}$—solution change in the k-th iteration whereas ${\mathbf{x}}^{(k+1)}={\mathbf{x}}^{(k)}+\Delta {\mathbf{x}}^{(k+1)}$, $\mathbf{H}(\mathbf{x})$—Jacobian determinant of the measurement function is defined as Equation (10):

$$\mathbf{H}(\mathbf{x})=\frac{\partial h_i(x)}{\partial x}$$

(10)

The SE solution, defined by the vector $\mathbf{x}$, can be calculated by solving the $\mathbf{G}({\mathbf{x}}^{(k)})$ for $\Delta {\mathbf{x}}^{(k+1)}$ and performing iteration until the condition $\Delta {\mathbf{x}}^{(k+1)}<\epsilon$ is fulfilled. Newton’s iteration converges to an ideal solution, that is where $J=0$, when both the model and the measured values applied to the SE were achieved by solving the task of power system load flow. State estimation of large power systems is computationally demanding because of frequent inversion of the sparse and large matrix $\mathbf{H}(\mathbf{x})$. The efficiency of $\mathbf{H}(\mathbf{x})$ processing can be improved using GPUs.

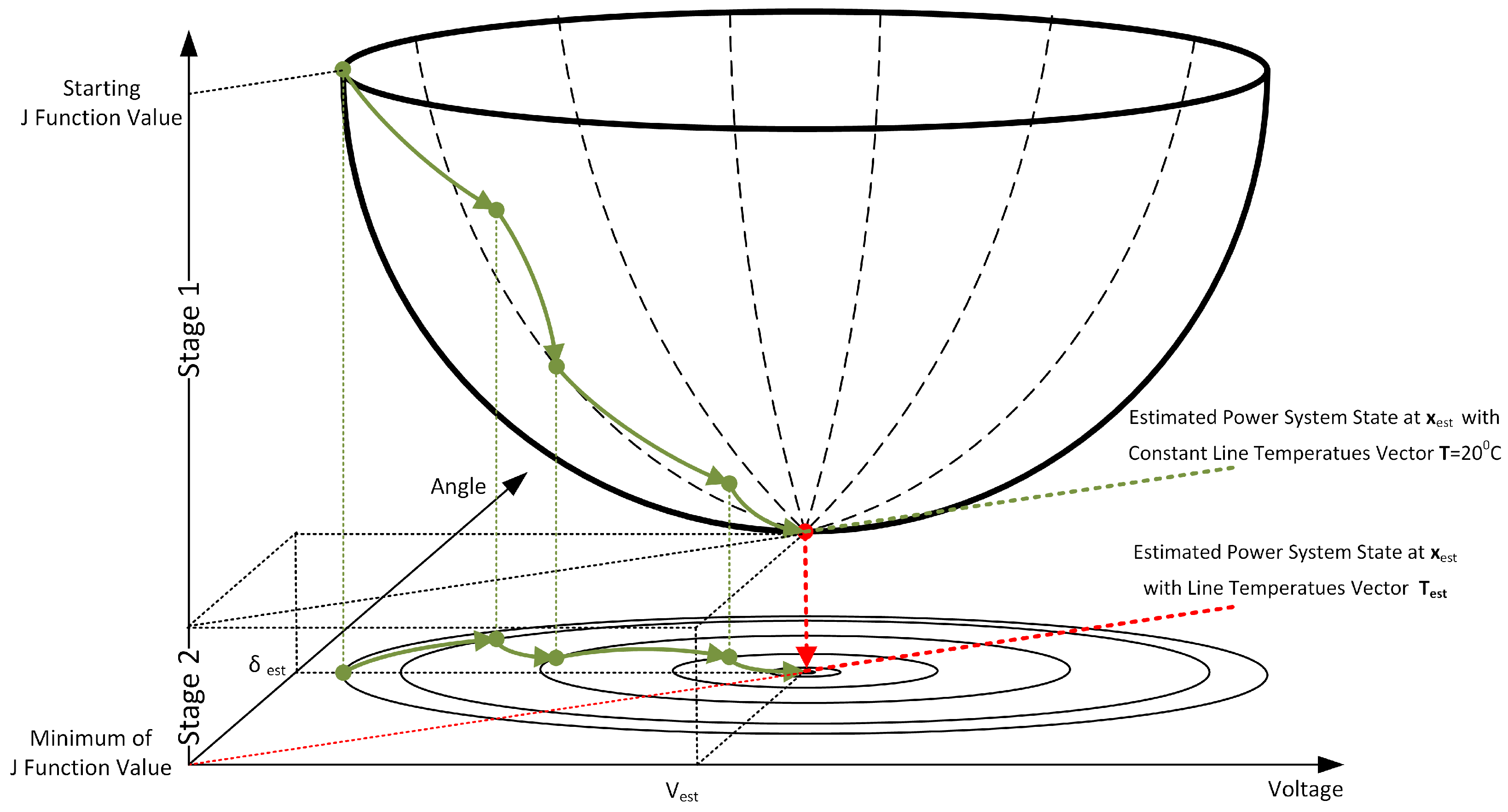
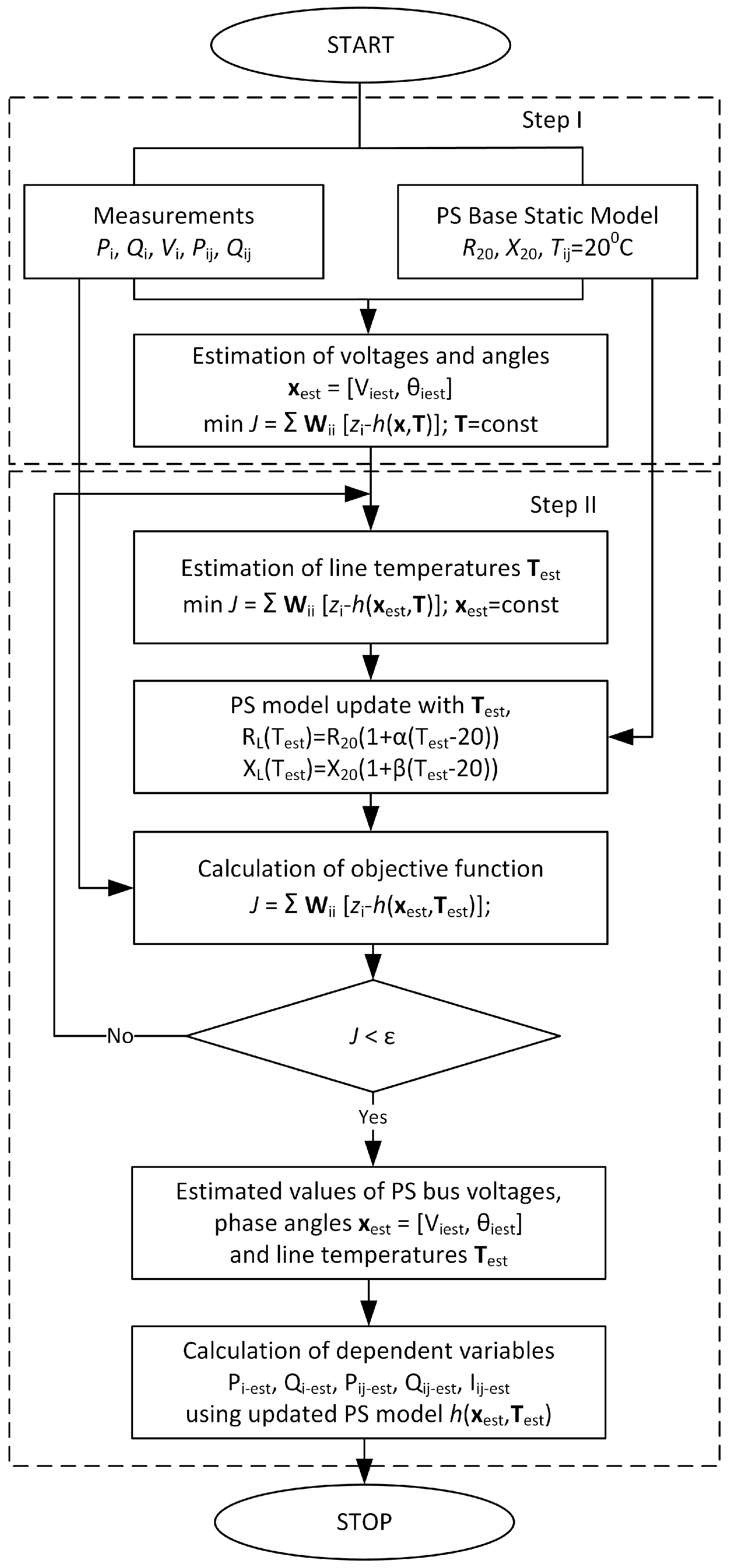
3. The Concept of the Two-Step Method for Power System State and Line Temperature Estimation

In practical applications of the power system state estimators, the measured values and the static parameters of the power system model contain inaccuracies. These mainly result from the errors in determining the conductor length in the power line, inaccurate manufacturer data concerning conductor resistance as well as resistance vs. temperature dependence [18]. Additionally, the unsteady cooling effect of variable weather conditions along the line route means that the modeled resistance of a line in the power system model does not reflect its actual resistance [25,29,30,31,38]. Furthermore, the variable temperature of the conductors in the line spans brings about variations of the conductor length in spans. This in turn causes changes in the total reactance of the line [30,40], which in some circumstances can be neglected [32,39]. In such a case, the error part of Equation (5) assumes the form where the measurement function depends both on the vector of state variables $\mathbf{x}$ and on the vector of model parameters $\mathbf{p}$. In a typical State Estimation (SE), the vector of the model parameters $\mathbf{p}$ remains constant:

$$z_i-h_i(\mathbf{x},\mathbf{p})=\epsilon$$

(11)

where: $z_i$—i-th measurement in the power system (PS), $h_i(\mathbf{x},\mathbf{p})$—measurement function, $\mathbf{x}$—vector of the PS state, $\mathbf{p}$—parameters of the PS model, $\epsilon$—deviation between the i-th measurement and the model value or absolute accuracy [18].

In practice, measurement values acquired by the SCADA systems which constitute the basis for the estimation, are never ideally synchronized and are encumbered with measurement errors. Assuming that the measurements are realized in the steady state condition, the question of non-synchronous measurements can be neglected. In such a case, it can be stated that a static model of a power system is encumbered with errors following the modeling inaccuracies and from the actual operating conditions. As described above, the classical SE [18] assumes that the system model is well recognized and does not need any adjustments, which can eventually yield incorrect estimation results, even if the applied measured quantities are accurate [30,41].

The state of the power system and selected model parameters, e.g., line temperature or resistance, can be estimated in a two-stage process, where the objective function assumes the form:

$$J=\sum _{i=1}^N{\mathbf{W}}_{ii}{[z_i-h_i(\mathbf{x},\mathbf{p})]}^2$$

(12)

and in the first stage the classical power system SE takes place, whose aim is to minimize J (12) incorporating the $\mathbf{p}=const$ condition. The solution of the first estimation stage produces a ${\mathbf{x}}_{est}$ vector. In the second stage, the objective function J gets the form:

$$J=\sum _{i=1}^N{\mathbf{W}}_{ii}{[z_i-h_i({\mathbf{x}}_{est},\mathbf{p})]}^2$$

(13)

and is further minimized where for the searched vector $\mathbf{p}$, the ${\mathbf{x}}_{est}$ is calculated minimizing J. In the second stage, the model parameter vector is finally achieved ${\mathbf{p}}_{est}$ if the minimum condition of the J function is met. At the end of the presented procedure the power system state vector ${\mathbf{x}}_{est}$ and model parameter vector ${\mathbf{p}}_{est}$ is obtained. In such a situation, it can be assumed that the model parameter vector $\mathbf{p}$ is equal to the vector $\mathbf{T}$, which stands for temperatures of lines in the power system. The Equation (13) assumes the final form:

$$J=\sum _{i=1}^N{\mathbf{W}}_{ii}{[z_i-h_i({\mathbf{x}}_{est},\mathbf{T})]}^2$$

(14)

where, analogously, the minimization of J as a function of $\mathbf{T}$ leads to the estimation of the vector of line temperatures ${\mathbf{T}}_{est}$ and ${\mathbf{x}}_{est}$. The illustrative example of the two-stage method for power system state and line temperature estimation has been presented in Figure 1.

3.1. Incorporation of Estimated Line Temperatures into Power System Model

In the models of an electric power system that are used for the load-flow and estimation calculations, a power line is usually modeled in the form of a $\pi$ quadripole (Figure 2), where the line resistance $R_L(T)$ and reactance $X_L(T)$ are lumped parameters. In the present article, it has been assumed that the parameters $R_L(T)$ and $X_L(T)$ vary with conductor temperature. The base values of $R_L$ and $X_L$ are calculated using the well-known dependences [18,19,20] and are determined on the basis of the actual length of the line and its per-unit length parameters. Conductors resistance per length unit is given by their manufacturer and it is usually specified for the temperature of 20 ${}^{°}$C [41], while the per-unit length reactance is determined as a function of the pole geometry, voltage levels and other acknowledged parameters [19,20,31]. The temperature of the conductors affects conductor resistance while thermal expansion affects their length, which implies changes in total line reactance. In such a case, it can be stated that the line reactance $X_L$ becomes temperature-dependent $X_L(T)$, as shown in Figure 2 [16,30].

In the case of a 110 kV line, the total line conductance G and susceptance B (Figure 2) can be considered to be constant at low humidity of the atmospheric air and in some cases can be neglected. Furthermore, it has been assumed that the values B and G are constant. Following [30,38,39], equivalent resistance and reactance of an overhead transmission line can be written as follows:

$$R_L(T)=R_{20}(1+\alpha (T-T_0))$$

(15)

and

$$X_L(T)=X_{20}(1+\beta (T-T_0))$$

(16)

where: $R_{20}$, $X_{20}$—equivalent line resistance and reactance calculated for the temperature of 20 ${}^{°}$C, respectively; $\alpha$—temperature coefficient of the conductor resistance changes dependent on the conductor type assumed that $\alpha$ = 0.00403 for ASCR 7/26; $\beta$—temperature coefficient of the line reactance change, considering the line expansion effect, according to [30], it has been assumed that $\alpha =\beta$, T—actual temperature of the conductor, $T_0=20{}^{°}$C—base temperature used to determine $R_{20}$ and $X_{20}$. In the case of the High Temperature Low Sag (HTLS) conductors, the assumption that $\alpha =\beta$ is invalid and should be corrected [31]. The temperature of the overhead line conductors according to [3,4,31] depends on the conductor design, geometry and the applied materials, which mainly translates into conductor resistance given by the manufacturer as the $R_{20}$ parameter. Resistance also depends on the atmospheric conditions such as air temperature, wind direction and speed, along with solar radiation.

3.2. Implementation of the Two-Step Algorithm of Power System State and Line Temperature Estimation

According to the theory of power system SE [18,19,34,35,36], the iterative Newton-Raphson procedure applied to minimize objective function (5) leads to a strictly optimal solution of ${\mathbf{x}}_{est}$, where the objective function (5) $J=0$, when there are no errors in either the model or the measured values. In an ideal case, the model and measurement values are taken from the load flow solution. In practice, however, both the measured values and the model of the estimating system contain errors. In such a situation, the SE usually yields the result where the objective function (14) $J>0$. The calculated state vector ${\mathbf{x}}_{est}$ is a suboptimal solution with respect to the real state of the power system (e.g., power line conductor temperatures are different than 20 ${}^{°}$C) [41]. The estimation quality can be intensified by the application of a more accurate measuring apparatus coupled with the accuracy improvement of the power system static model. The impact of the power system model accuracy on the results of the power system SE has been analyzed in [16,18,41]. Assuming that accurate and error-free measurements in the power system are available, and in order to meet the $J=0$ condition, it is necessary to update the base model with line conductor temperatures. At the same time, conductor temperature influences the mechanical condition of the lines, such as the sag which translates into total line reactance [30,40,42,43]. In such a case, in order to improve the estimation quality and thereby determine the most probable state of the power system together with the estimation of the actual line conductor temperatures, a two-step algorithm for the state and temperature estimation of the power system model can be applied. The method theoretically presented in Section 3 can be implemented as shown in Figure 3, where $P_i$, $Q_i$—total active/reactive power of the generation and loads in the i-th node of the network , $V_i$—voltage in the i-th node of the network, $P_{ij}, Q_{ij}$—measured power flows in the network branches between the i-th and the j-th nodes. The steady-state condition of the observed power system is assumed, which implies that thermodynamic heating of the conductors and their sagging proceeds slowly.

The realization of the proposed estimation algorithm (Figure 3) is being processed in two stages, as presented schematically in Figure 1. In the first stage, classical estimation of the power system is performed based on the available system model and the measurement data, according to (14). The base system model is where the resistance $R_{20}$ and reactance $X_{20}$ parameters of all the power lines are determined for the temperature of 20 ${}^{°}$C, as [18,20,37,44] argue.

The second stage of the algorithm realization (Figure 3) includes the iterative Newton-Raphson procedure loop, searching for a vector $\mathbf{T}$ composed of the temperature values of individual power lines to be used to adjust the R and X parameters in the model. It starts from the vector $\mathbf{T}$, where all temperature values are equal to 20 ${}^{°}$C and then performs a sequential estimation-optimization procedure to find such a vector $\mathbf{T}$ for which the J indicator is minimal. Next, the objective function J’s value is analyzed to check whether the condition $J<\epsilon$ is met. If the condition $J<\epsilon$ is not met, it means that the power system model parameters should be corrected with new power line temperature values different from 20 ${}^{°}$C in order to minimize J (trying to minimize J more). The determined temperature of the power system lines is the average line temperatures $T_{avg}$ determined on the basis of the values of electrical quantities measured at the line ends. Furthermore, it can be observed that such an approach makes it possible to estimate the line conductor operating temperature without performing any additional meteorological measurements along the line, such as conductor temperature resulting from weather conditions and the current flow [10,17,45], which directly affects the measured electrical quantities. One disadvantage of this approach is that it does not offer any information on the temperature of individual sections of a power line, whose cooling by the wind can vary due to their varied position with respect to wind direction [3,4].

4. Test System Simulation and State with the Line Temperatures Estimation

For the purpose of method testing, the IEEE 39-Bus New England Test System, has been used [33]. The length of all lines had been estimated on the basis of specific resistance for 795 kcmil 26/7 Drake ACSR conductor connected as two-bundle, resulting line resistance 0.03585 $\mathsf{\Omega }$/km at temperature $T_{ref}=20{}^{°}$C. For specific weather conditions used for calculation of conductor temperatures in summer and winter case, the author refers to data presented in Appendix A and in

Table A1. Power Lines’ Parameters and Conductor Temperatures of IEEE 39 Test Case [32].

From Bus	To Bus	Line Length	Summer Case	Winter Case	Line Resistance	Line Reactance
		km	(${\mathit{T}}_{\mathit{c}}{}^{°}$C)	(${\mathit{T}}_{\mathit{c}}{}^{°}$C)	${\mathit{T}}_{\mathit{c}}=20{}^{°}$C	${\mathit{T}}_{\mathit{c}}=20{}^{°}$C
1	2	116.206	43.991	−9.768	4.166	48.919
1	39	33.194	43.991	−9.768	1.19	29.756
2	3	43.152	62.503	−6.852	1.547	17.973
2	25	232.413	47.015	−9.278	8.332	10.236
3	4	43.152	48.738	−8.998	1.547	25.352
3	18	36.513	42.912	−9.948	1.309	15.830
4	5	26.555	43.059	−9.926	0.952	15.235
4	14	26.555	48.046	−9.119	0.952	15.354
5	6	6.639	45.576	−9.52	0.238	3.095
5	8	26.555	47.77	−9.16	0.952	13.331
6	7	19.916	50.7	−8.695	0.714	10.950
6	11	23.236	60.716	−7.137	0.833	9.760
7	8	13.278	43.293	−9.885	0.476	5.475
8	9	76.374	44.541	−9.684	2.738	43.206
9	39	33.194	44.172	−9.744	1.19	29.756
10	11	13.278	59.993	−7.246	0.476	5.118
10	13	13.278	44.698	−9.663	0.476	5.118
13	14	29.874	44.085	−9.759	1.071	12.022
14	15	59.749	43.712	−9.815	2.142	25.828
15	16	29.874	57.385	−7.637	1.071	11.188
16	17	23.236	45.084	−9.588	0.833	10.593
16	19	53.110	62.316	−6.885	1.904	23.210
16	21	26.555	51.01	−8.644	0.952	16.068
16	24	9.958	43.465	−9.855	0.357	7.022
17	18	23.236	45.84	−9.476	0.833	9.760
17	27	43.152	42.768	−9.973	1.547	20.591
21	22	26.555	70.323	−5.688	0.952	16.664
22	23	19.916	42.768	−9.971	0.714	11.426
23	24	73.054	51.471	−8.572	2.619	41.659
25	26	106.248	43.282	−9.892	3.809	38.445
26	27	46.471	48.877	−9.001	1.666	17.497
26	28	142.762	43.944	−9.777	5.118	56.418
26	29	189.233	44.982	−9.608	6.784	74.391
28	29	46.471	50.298	−8.757	1.666	17.973

. The power flow calculations using Electro-Thermal Overhead Line (ET-OHL) model have been performed as in [32]. Next, from the power flow results, the values of active and reactive powers along with bus voltages (P, Q, V) have been used for the power system state and line temperature estimation method. As described in Section 3.2, these values represent the actual measurements acquired by SCADA from Remote Terminal Units (RTUs) and Intelligent Electronic Devices (IEDs). At the first stage of the presented method, the classical SE uses actual measurements with power system base model, containing line resistances calculated for $T_c=20{}^{°}$C, as presented in Table A1. The first step of the presented estimation method leads to the J = 94,693.7034 value, assuming that ${\sigma }_i=0.001$ for every single measurement available. The IEEE 39 Bus New England Test System state estimation results compared to the available measurements, after the first step of the processing method, have been presented in

Table A2. Comparison of Measurements and their Estimations of IEEE 39 Test System for the Summer Case after the First Step of the Presented Method using Base Model Calculated for $20{}^{°}$C.

From	To	Meas. ${\mathit{P}}_{\mathit{From}}$	Est. ${\mathit{P}}_{\mathit{From}}$	Meas. ${\mathit{P}}_{\mathit{To}}$	Est. ${\mathit{P}}_{\mathit{To}}$	Meas. ${\mathit{Q}}_{\mathit{From}}$	Est. ${\mathit{Q}}_{\mathit{From}}$	Meas. ${\mathit{Q}}_{\mathit{To}}$	Est. ${\mathit{Q}}_{\mathit{To}}$
Bus	Bus	p.u.	p.u.	p.u.	p.u.	p.u.	p.u.	p.u.	p.u.
1	2	−1.7623	−1.7168	1.7733	1.7264	−0.3657	−0.3563	−0.2658	−0.2851
1	39	0.7863	0.7581	−0.7855	−0.7575	−0.0763	−0.0812	−0.7082	−0.7007
2	3	3.1477	3.1794	−3.1325	−3.1660	0.8935	0.8939	−0.9937	−1.0135
2	25	−2.4210	−2.4340	2.4687	2.4779	0.8656	0.8668	−0.9688	−0.9730
2	30	−2.5000	−2.5000	2.5000	2.5000	−1.4932	−1.4923	1.6400	1.6405
3	4	0.3562	0.3436	−0.3540	−0.3417	1.0830	1.0816	−1.2751	−1.2769
3	18	−0.4437	−0.4075	0.4439	0.4076	−0.1133	−0.1054	−0.1098	−0.1171
4	5	−1.9747	−2.0160	1.9782	2.0193	−0.1024	−0.1082	0.0228	0.0260
4	14	−2.6712	−2.6383	2.6777	2.6440	−0.4625	−0.4642	0.4282	0.4170
5	6	−5.3730	−5.3785	5.3794	5.3843	−0.5029	−0.5071	0.5424	0.5390
5	8	3.3948	3.3807	−3.3844	−3.3714	0.4801	0.4696	−0.4800	−0.4858
6	7	4.5132	4.5354	−4.4990	−4.5227	0.8362	0.8309	−0.7321	−0.7490
6	11	−3.1658	−3.2026	3.1739	3.2098	−0.3715	−0.3848	0.3262	0.3281
6	31	−6.7268	−6.7268	6.7268	6.7268	−1.0071	−1.0078	2.3198	2.3205
7	8	2.1610	2.1723	−2.1590	−2.1704	−0.1079	−0.1069	0.0549	0.0518
8	9	0.3233	0.3656	−0.3196	−0.3622	−1.3408	−1.3329	1.0064	0.9944
9	39	0.2546	0.2827	−0.2545	−0.2825	−0.3404	−0.3279	−0.9390	−0.9437
10	11	3.2164	3.2358	−3.2115	−3.2315	0.7360	0.7376	−0.7578	−0.7659
10	13	3.2836	3.2637	−3.2788	−3.2595	0.4746	0.4674	−0.4989	−0.4965
10	32	−6.5000	−6.4998	6.5000	6.4998	−1.2106	−1.2089	2.1814	2.1823
12	11	−0.0373	−0.0445	0.0376	0.0448	−0.4235	−0.4270	0.4315	0.4351
12	13	−0.0480	−0.0408	0.0484	0.0411	−0.4565	−0.4530	0.4658	0.4622
13	14	3.2305	3.1857	−3.2204	−3.1767	0.0331	0.0181	−0.0957	−0.0930
14	15	0.5427	0.5038	−0.5421	−0.5033	−0.3325	−0.3406	−0.0328	−0.0258
15	16	−2.6579	−2.6752	2.6671	2.6833	−1.4972	−1.5059	1.4154	1.4133
16	17	2.2627	2.2471	−2.2589	−2.2437	−0.4464	−0.4522	0.3529	0.3548
16	19	−4.5075	−4.5124	4.5437	4.5436	−0.5257	−0.5552	0.6387	0.6101
16	21	−3.2138	−3.2616	3.2227	3.2697	0.1921	0.1813	−0.3116	−0.3113
16	24	−0.4986	−0.4782	0.4989	0.4785	−0.9583	−0.9564	0.8927	0.8906
17	18	2.0269	2.0044	−2.0239	−2.0018	0.0857	0.0791	−0.1902	−0.1867
17	27	0.2319	0.2490	−0.2318	−0.2488	−0.4386	−0.4327	0.0977	0.0939
19	20	1.7473	1.7473	−1.7452	−1.7451	−0.1076	−0.1074	0.1507	0.1510
19	33	−6.2910	−6.2905	6.3200	6.3198	−0.5312	−0.5268	1.1194	1.1216
20	34	−5.0548	−5.0544	5.0800	5.0799	−1.1807	−1.1771	1.6838	1.6856
21	22	−5.9627	−6.0169	5.9955	6.0449	−0.8384	−0.8921	1.1366	1.1079
22	23	0.5045	0.4715	−0.5042	−0.4712	0.4259	0.4162	−0.6230	−0.6118
22	35	−6.5000	−6.4997	6.5000	6.4997	−1.5626	−1.5579	2.1725	2.1747
23	24	3.6148	3.4951	−3.5849	−3.4701	0.0564	−0.0051	0.0293	0.0165
23	36	−5.5856	−5.5850	5.6000	5.5995	−0.2794	−0.2740	1.0604	1.0631
25	26	0.6747	0.6433	−0.6732	−0.6420	−0.1637	−0.1729	−0.4119	−0.3988
25	37	−5.3834	−5.3829	5.4000	5.3997	0.6605	0.6655	−0.0197	−0.0171
26	27	2.5887	2.5739	−2.5782	−2.5646	0.7017	0.6927	−0.8527	−0.8532
26	28	−1.4001	−1.4061	1.4087	1.4141	−0.2137	−0.2125	−0.5525	−0.5521
26	29	−1.9054	−1.8993	1.9266	1.9186	−0.2460	−0.2515	−0.6567	−0.6610
28	29	−3.4687	−3.4718	3.4861	3.4875	0.2765	0.2685	−0.3629	−0.3709
29	38	−8.2476	−8.2468	8.3000	8.2996	0.7506	0.7571	0.2704	0.2737

,

Table A3. Comparison of Measurements and their Estimations of IEEE 39 Test System for the Summer Case after the First Step of the Presented Method using Base Model Calculated for $20{}^{°}$C.

Bus	Measured V	Estimated V	Bus	Measured V	Estimated V	Bus	Measured V	Estimated V
	p.u.	p.u.		p.u.	p.u.		p.u.	p.u.
1	1.0393	1.0354	14	1.0079	1.0073	27	1.0352	1.0317
2	1.0481	1.0428	15	1.0104	1.0098	28	1.0492	1.0442
3	1.0274	1.0248	16	1.0285	1.0256	29	1.0493	1.0442
4	0.9991	0.9995	17	1.0306	1.0276	30	1.0499	1.0448
5	1.0017	1.0020	18	1.0279	1.0252	31	0.9820	0.9820
6	1.0044	1.0044	19	1.0496	1.0437	32	0.9841	0.9828
7	0.9932	0.9944	20	0.9907	0.9852	33	0.9972	0.9918
8	0.9927	0.9939	21	1.0276	1.0249	34	1.0123	1.0069
9	1.0383	1.0350	22	1.0492	1.0432	35	1.0494	1.0436
10	1.0154	1.0140	23	1.0437	1.0381	36	1.0636	1.0582
11	1.0103	1.0095	24	1.0345	1.0311	37	1.0275	1.0214
12	0.9976	0.9966	25	1.0578	1.0516	38	1.0265	1.0216
13	1.0117	1.0107	26	1.0514	1.0461	39	1.0300	1.0271

and

Table A4. Comparison of Measurements and their Estimations of IEEE 39 Test System Generators for the Summer Case after First Step of the Presented Method using Base Model Calculated for $20{}^{°}$C.

Bus	Measured ${\mathit{P}}_{\mathit{Gen}}$	Estimated ${\mathit{P}}_{\mathit{Gen}}$	Measured ${\mathit{Q}}_{\mathit{Gen}}$	Estimated ${\mathit{Q}}_{\mathit{Gen}}$
	p.u.	p.u.	p.u.	p.u.
30	250.0000	249.9972	164.0020	164.0519
31	681.8818	681.8766	236.5753	236.6509
32	650.0000	649.9837	218.1425	218.2277
33	632.0000	631.9840	111.9433	112.1604
34	508.0000	507.9868	168.3800	168.5595
35	650.0000	649.9733	217.2478	217.4728
36	560.0000	559.9549	106.0431	106.3141
37	540.0000	539.9658	−1.9722	−1.7094
38	830.0000	829.9622	27.0394	27.3742
39	1000.0000	1000.0021	85.2824	85.5680

, where $P_{From}, Q_{From}$ – stands for active and reactive powers at the beginning of the line, analogously $P_{To}, Q_{To}$ – stands for active and reactive powers at the end of line as well as $P_{Gen}, Q_{Gen}$ – which are the active and reactive powers produced by generators. The following second stage of the presented methods uses previously measured values. At the second stage, we perform further minimization of the J function, searching for line temperature vector $\mathbf{T}$. The upper and lower bounds for every element of vector $\mathbf{T}$ have been set to $-40{}^{°}$C and $250{}^{°}$C, respectively. The line temperature estimation results and values of the objective function J after 10, 20, 50, 100, 134 iteration have been presented in

Table A5. Estimated Line Temperatures and Objective Function Values j of IEEE 39 Test System for Summer Case performed at the second stage of presented method.

F. Bus	T. Bus	Line Temp.	Iter. 1 Line Temp.	Iter. 10 Estimated Line Temp.	Iter. 20 Estimated Line Temp.	Iter. 50 Estimated Line Temp.	Iter. 100 Estimated Line Temp.	Iter. 134 Estimated Line Temp.
1	2	43.991	20	14.625	33.445	43.051	44.022	43.9909
1	39	43.991	20	17.459	19.269	36.558	44.227	43.9905
2	3	62.503	20	32.562	45.176	61.917	62.487	62.5029
2	25	47.015	20	22.477	23.162	45.581	47.022	47.0149
3	4	48.738	20	20.384	27.938	48.730	48.868	48.7378
3	18	42.912	20	19.044	21.168	28.442	36.045	42.9134
4	5	43.059	20	21.794	25.524	43.339	43.070	43.0587
4	14	48.046	20	20.324	23.780	47.934	47.995	48.0457
5	6	45.576	20	22.403	27.878	44.888	45.554	45.5758
5	8	47.77	20	23.647	38.265	48.195	47.776	47.7697
6	7	50.7	20	25.736	40.611	50.876	50.700	50.6997
6	11	60.716	20	26.207	37.559	60.395	60.654	60.7157
7	8	43.293	20	20.211	24.453	43.211	43.285	43.2927
8	9	44.541	20	17.570	26.175	41.429	44.694	44.5408
9	39	44.172	20	21.439	20.205	19.412	44.900	44.1716
10	11	59.993	20	27.715	31.951	60.957	59.970	59.9927
10	13	44.698	20	13.863	17.236	45.640	44.677	44.6977
13	14	44.085	20	17.871	29.703	43.872	44.088	44.0847
14	15	43.712	20	18.441	21.827	43.472	45.327	43.7113
15	16	57.385	20	25.390	37.607	57.552	57.240	57.3850
16	17	45.084	20	17.350	21.965	46.028	45.291	45.0838
16	19	62.316	20	35.958	58.923	62.336	62.318	62.3160
16	21	51.01	20	23.561	55.300	50.920	51.015	51.0099
16	24	43.465	20	17.616	43.561	45.301	43.582	43.4644
17	18	45.84	20	16.529	21.828	50.047	46.451	45.8397
17	27	42.768	20	19.614	18.483	40.271	41.448	42.7681
21	22	70.323	20	53.461	71.710	70.344	70.326	70.3230
22	23	42.768	20	17.981	41.226	40.889	42.644	42.7686
23	24	51.471	20	31.756	53.886	51.502	51.478	51.4709
25	26	43.282	20	18.976	23.207	39.777	44.348	43.2816
26	27	48.877	20	17.963	32.390	49.235	48.930	48.8769
26	28	43.944	20	20.540	23.285	43.769	43.872	43.9438
26	29	44.982	20	20.608	29.907	44.914	44.931	44.9819
28	29	50.298	20	22.630	42.332	50.363	50.272	50.2980
		J	94,693.7	4456.05	713.72	1.286	0.0152	$9.0\times {10}^{-8}$

and in Figure 4.

4.1. Algorithm Performance Testing and Timing Results

The testing of the two-step algorithm presented in Figure 3 for its performance and convergence has been performed based on the available power system test models IEEE 9, 14, 30, 39, 57, 118 and 300, with the application of the MATPOWER (version 6.0, PSERC, Tempe, AZ, USA) [33]. For performance testing of the presented method, the lines’ resistances and reactances of used test systems have been calculated for $80{}^{°}$C.

The proposed method makes it possible to determine average temperatures of power lines, but with the increasing number of nodes and power lines the procedure realization time gets significantly longer. The notable elongation of temperature estimation time results from several features. The growing complexity of the power system model entails an increased number of iterations in a single system state estimation and calculation of objective function J. The growing number of lines increases the number of elements in the temperature vector $\mathbf{T}$, and thus the number of estimations per one change of the $\mathbf{T}$ vector increases exponentially. The state and line temperatures estimation needs to be performed as soon as possible for the purpose of the usability of results. During the simulation tests, it turned out that the three most computationally costly operations in the estimation process are: (1) Jacobian calculation $\mathbf{J}={\mathbf{H}}^{\prime }·{\mathbf{R}}_{inv}·\mathbf{H}$, where $\mathbf{H}$-measurement Jacobian, ${\mathbf{R}}_{inv}$-covariance matrix; (2) Calculation $\mathbf{F}={\mathbf{H}}^{\prime }·{\mathbf{R}}_{inv}·(\mathbf{z}-{\mathbf{z}}_{est})$; (3) Calculation of step change $d\mathbf{x}=\mathbf{J}/\mathbf{F}$. In order to speed up the estimation calculations, the above matrix operations have been implemented to perform using the GPU. An example of a modified MATPOWER^®software code for performing Graphical Processing Unit (GPU) calculations is shown in Algorithm 1.

The simulations and estimations have been performed using a benchmark machine Fujitsu PRIMERGY TX300^® Server (version S6, Fujitsu Technology Solutions GmbH, Munchen, Germany) equipped with two Intel Xeon^®E5-2690v2 3.0 GHz processors (acting as 20-core CPU) (Intel, Santa Clara, CA, USA) and 192 GB RAM (Fujitsu Technology Solutions GmbH, Munchen, Germany), operating under Microsoft Windows 2012 R2 with and without the Graphical Processing Unit (GPU) (NVIDIA Tesla K40, Santa Clara, CA, USA) support for estimation purposes. The results have been presented in

Table 1. Time of the two-step algorithm realization depending on the power system size.

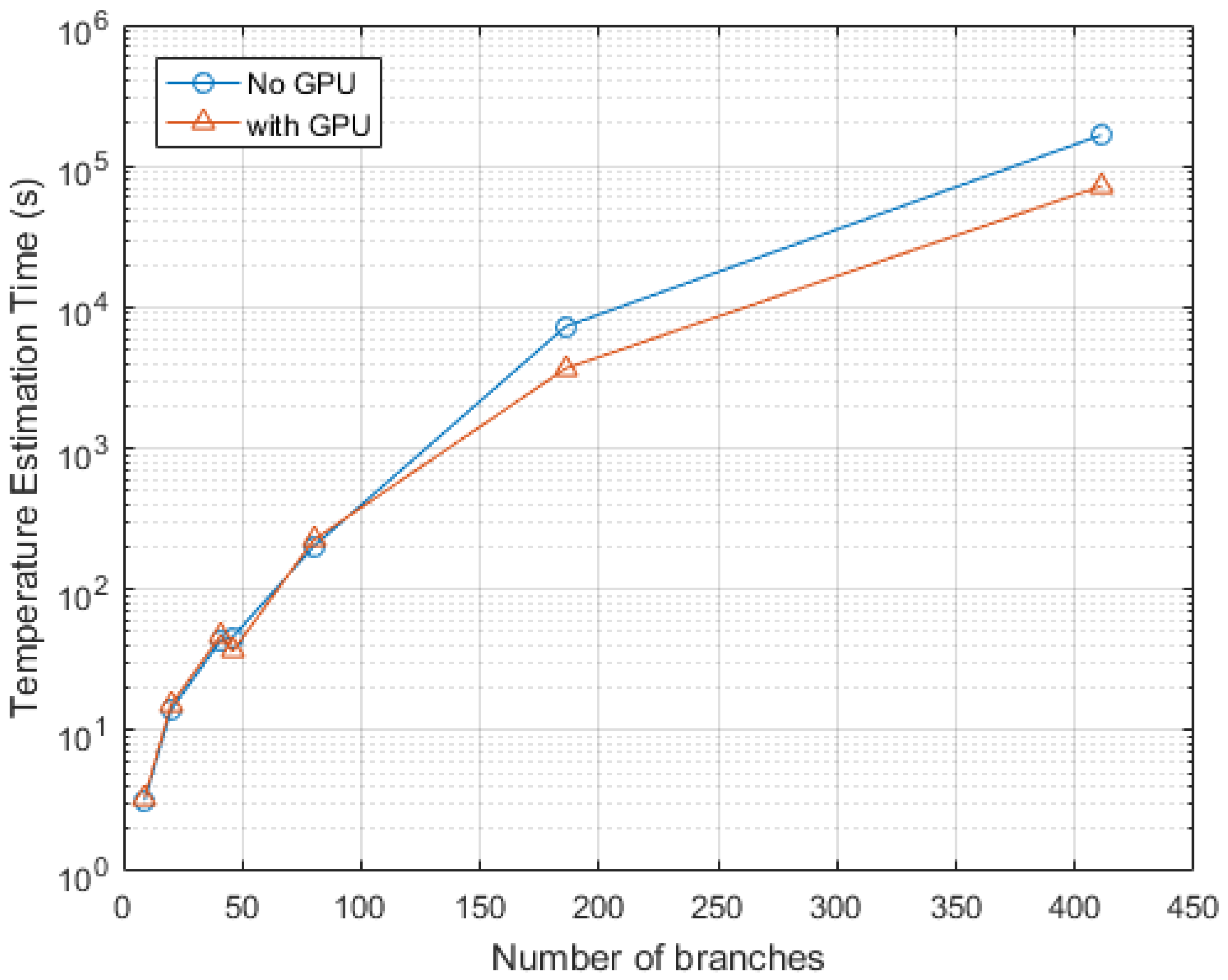
IEEE Test Case	Number of Branches	Mean Single Estimation Time (s)	Line Temperatures Estimation Time (s)	Mean Single Estimation Time (s) Graphical Processing Unit (GPU) Supported	Line Temperatures Estimation Time (s) Graphical Processing Unit (GPU) Supported
9	9	0.050	3.19	0.0087	3.35
14	20	0.051	13.89	0.0115	15.09
30	41	0.031	43.46	0.0172	47.28
39	46	0.095	45.82	0.0269	36.27
57	80	0.056	201.04	0.0757	223.69
118	186	0.186	7308	0.6721	3684
300	411	4.231	165,680	2.6332	72,028

and Figure 5. All the tested cases have shown the algorithm’s convergence to a strictly optimal point using the complete and correct set of measured data, which is a set of values obtained from the load-flow solution. In the case of small systems, transferring the matrixes ${\mathbf{R}}_{inv}$ and $\mathbf{H}$ many times from RAM to GPU and vice versa ($d\mathbf{x}$), as shown in Algorithm 1, effects in a more extended total temperature estimation time. The performance improvement is noticeable in the case of larger systems, where ${\mathbf{R}}_{inv}$ and $\mathbf{H}$ have a larger dimension and computing of $\mathbf{J}$, $\mathbf{F}$ and $d\mathbf{x}$ is faster on GPU than on CPU.

Algorithm 1: Modified code of MATPOWER [33] State Estimation (SE) function doSE.m for performance improvement using Graphical Processing Unit (GPU).

...

% --compute inverse R matrix on GPU

R_inv = gpuArray(diag(1./sigma_square));

...

--construct H matrix on GPU

H = gpuArray(H);

%--compute update step on GPU

J = H’*R_inv*H;

%--evaluate F(x) on GPU

F = H’*R_inv*(z-z_est);

%--compute dx on GPU

dx = (J / F);

%--get matrix from GPU

dx = gather(dx);

It is worth noting that the presented method can be used to analyze operating system state and line average temperatures ex-post, due to the long calculation time for large systems as shown in Table 1. Similar calculation times can be found for power systems optimization with the application of heuristic methods. In [17] the Authors proposed state and line temperature estimation method that finished calculations of IEEE 57 bus test system in 3.29 seconds in single estimation, while the presented technique needs 201.04 seconds. It is inducted by the fact that presented method runs as two iterative steps. The second step, which is a classical state estimation occurs many times because it does not include any additional measurements incorporated into measurement function h and measurement Jacobian $\mathbf{H}$ as in [17].

4.2. Temperature Estimation Error Analysis Using Complete and Incomplete Sets of the Noise-Containing Measured Data

The convergence, errors and sensitivity of the algorithm have been analyzed for the case of an incomplete and noise-containing set of measurement data with the application of a modified IEEE 9 bus test system presented in (Figure 6) where all line temperatures have been assumed as $80{}^{°}$C. The relative error and mean relative error of the presented method have been calculated according to Equation (17).

$$er{r}_{i,\%}=\frac{T_{i,est}-80{}^{°}\mathrm{C}}{80{}^{°}\mathrm{C}}\times 100$$

(17)

The algorithm testing has been performed for two different cases. The first one assumes the availability of a complete set of measurement data in the test system, which means that the measured values of the bus voltage V in all the nodes as well as the measured values of active P and reactive power Q in each line and at generator circuit breaker cubicle are available. Noise has been added to the measured values obtained from the load-flow solution in accordance with the statistically assumed normal error distribution $\sigma$ following from the instrument transformer classes (0.1, 0.2 and 0.5) [18,20,37]. In the test system, ten thousand samples have been produced. For each of the measurement sets, the two-step algorithm for the system state and line temperature estimation has been realized. The testing objective has been to check the procedure’s operation in the conditions where measurement errors occur that simulate the real system operating conditions. In general, the accuracy of the method is conditioned by the accuracy of the deployed measuring apparatus. Preliminary analysis of the gathered results shows that the discussed method of the estimation of line conductor temperature is very sensitive to measurement errors. Even small errors produced by the measuring apparatus can cause considerable temperature value deviations from the real values. Thus, single measurements (singular snapshots of the system) can yield unreliable results.

The accuracy of the method can be significantly improved by averaging measured or estimated values over an adequate time interval, e.g., over one minute at a varied sampling frequency, that is the frequency of taking snapshots. The time constant for the heating of power line conductors varies between 5–15 min depending on the actual weather conditions [3,4]. Therefore, the averaging interval of 1 min has been assumed.

Table 2. Mean relative error of the line temperature estimation method resulting from various classes of the applied measuring apparatus and obtained for a complete set of noise-containing measurement data.

Instrument Transformer Classes	Maximal Mean Relative Error
0.1	0.69%
0.2	0.42%
0.5	1.05%

,

Table 3. Maximal relative error of the line temperature estimation method for a complete set of noise-containing data.

Class	Sampling	Sampling	Sampling	Sampling
	$\mathit{\tau }$ = 30 s	$\mathit{\tau }$ = 10 s	$\mathit{\tau }$ = 5 s	$\mathit{\tau }$ = 2 s
0.1	14.97%	6.64%	4.30%	2.11%
0.2	28.45%	8.82%	8.11%	4.34%
0.5	52.54%	21.81%	20.72%	10.20%

and

Table 4. Mean relative error of the line temperature estimation method for a complete set of noise-containing data.

Class	Sampling	Sampling	Sampling	Sampling
	$\mathit{\tau }$ = 30 s	$\mathit{\tau }$ = 10 s	$\mathit{\tau }$ = 5 s	$\mathit{\tau }$ = 2 s
0.1	4.32%	2.02%	1.14%	0.53%
0.2	8.29%	4.25%	2.86%	2.44%
0.5	20.73%	10.15%	5.41%	2.55%

present data on the method accuracy obtained for the case using a complete measurement data set of the test system shown in Figure 6. An analysis of the results makes it possible to assess the accuracy of the system’s state and line conductor temperature estimation in the case when a complete measurement data set is available.

The results of the algorithm’s application show that the discussed temperature estimation method is very sensitive to the measurement errors of the active P and reactive Q power. Even small measurement errors can yield high mean errors in the estimated line conductor temperature values, even up to 52.5% in the case of single snapshots.

We also tested the method’s accuracy for an incomplete set of the measured values. Figure 6 presents the measurement data that are available in the test system, for which the observability condition is met. In the case of a complete dataset, 57 values of P, Q and U are available, while the incomplete case offers 34 values, which makes almost 60% (exactly 59.65%) of the measurement data available in the complete case.

Table 5. Maximal relative error of the line temperature estimation method for an incomplete set of noise-containing data.

Class	Sampling	Sampling	Sampling	Sampling
	$\mathit{\tau }$ = 30 s	$\mathit{\tau }$ = 10 s	$\mathit{\tau }$ = 5 s	$\mathit{\tau }$ = 2 s
0.1	53.45%	26.25%	19.27%	12.85%
0.2	106.47%	52.70%	38.92%	12.85%
0.5	198.69%	74.59%	65.47%	19.68%

and

Table 6. Mean relative error of the line temperature estimation method for an incomplete set of noise-containing data.

Class	Sampling	Sampling	Sampling	Sampling
	$\mathit{\tau }$ = 30 s	$\mathit{\tau }$ = 10 s	$\mathit{\tau }$ = 5 s	$\mathit{\tau }$ = 2 s
0.1	15.91%	11.54%	9.48%	3.21%
0.2	31.84%	17.67%	10.74%	3.31%
0.5	60.12%	30.92%	16.32%	4.92%

present the results of conductor temperature estimation as a function of the deployed instrument transformer classes and sampling frequencies at the 1-min averaging interval for the case of a limited availability of the measurement data. However, in the case of multiple sequence measurements and estimations performed and followed by the determination of an average line temperature value, the mean error of temperature determination is reduced to below 5% (with the application of the 0.5 class measuring apparatus), which for the power line design temperature values yields the limiting values given below in

Table 7. Maximal absolute error for standard design temperatures of power lines at the sampling rate of 30 samples/min.

Line Design Temperature	Method Limiting Relative Error (Class 0.1–0.5)	Estimated Temperature Maximal Error
40	12.85–19.68%	5.14–7.87 ${}^{°}$C
60		7.71–11.80 ${}^{°}$C
80		10.28–15.74 ${}^{°}$C

and mean values listed in

Table 8. Mean absolute error for standard design temperatures of power lines at the sampling rate of 30 samples/min.

Line Design Temperature	Method Limiting Relative Error (Class 0.1–0.5)	Estimated Temperature Maximal Error
40	3.21–4.92%	1.28–1.97 ${}^{°}$C
60		1.93–2.95 ${}^{°}$C
80		2.57–3.94 ${}^{°}$C

.

5. Conclusions

Based on the performed testing of the two-step power system state and line temperature estimation algorithm and the gathered results, the following conclusions can be drawn. State estimation of an electric power system is performed based on measurement data encumbered with errors. A power system model that is used for the estimation purposes also deviates from real parameters, because of the applied simplifications and modeling errors. However, the main source of parameter deviations are operating factors, such as heating of line conductors, which affects the resistance and reactance of power lines. The power line monitoring is mainly realized in specific spots, which in the case of vast power systems does not work well as weather conditions may vary along long power lines. The advantages of the proposed method are as follows: the convergence of the algorithm to a strict optimum and the fact that the measurements of meteorological quantities are not needed. Furthermore, it means that the presented calculation procedure that is based only on measured electrical quantities available in the power system yields the actual state of all the voltages and angles in the system as well as the actual temperature of the lines. The estimated temperatures of line conductors can constitute important information for the system operator. Knowing average values of line conductor temperatures, it is also possible to determine the mechanical state of the lines. In other words, with the known design conditions, distances and spans, it is possible to estimate sags and stresses for the obtained conductor temperature value, which will be the objective of further research.