Influence of Fracture Heterogeneity Using Linear Congruential Generator (LCG) on the Thermal Front Propagation in a Single Geothermal Fracture-Rock Matrix System

Abstract

An implicit finite difference numerical model has been developed to investigate the influence of fracture heterogeneity on the propagation of thermal front in a single horizontal fracture-matrix system. Instead of depending on a complex and data-demanding geostatistical method for a precise representation of fracture aperture, a statistical linear congruential generator (LCG) method was applied in the present study to replicate the unpredictable nature of fracture aperture morphology. The results have been compared with the parallel plate model and simple sinusoidal model. Finally, sensitivity analysis of fracture aperture size and fluid flow rate has been carried out to identify the conditions at which fracture heterogeneity is critical. The results indicate that LCG-aperture enhances the heat transfer between fracture and hot rock matrix compared to the parallel and sinusoidal fractures. Further, the temperature profiles in hot rock indicate that there was a greater loss of heat for the case of LCG-aperture (25% loss) compared to sinusoidal (16%) and parallel plate (8%) apertures. It was found that heterogeneity does not play a major role at small fracture aperture size (≤50 μm) and at low flow rates. However, as fracture aperture size increases, the heterogeneity plays a vital part even at low flow rates.

1. Introduction

Events and factors like the Paris agreement [1], rapid commercialisation, the decline in fossil fuel production, and increasing production costs have put a focus on alternative energy sources. According to EU’s energy and climate goals, the European Union countries have already agreed on a new renewable energy target of at least 27% by 2030 [2]. At present, there is an enormous dependency on conventional methods for energy needs, and it will take the combination of multiple alternative energy methods to replace the existing conventional sources. Geothermal energy from hot rocks is one of the alternative energy sources, which shows great potential.

The enhanced geothermal system (EGS) is a way of producing electricity from hot dry rocks. The method to generate electricity from EGS is by drilling a well into a hot low permeability rock (<500 K). High-pressure water (cold) is injected through the well, fracturing the hot rock, and the water circulates through the hot rock and gets heated. The hot water is extracted at the production well, which may be used to generate energy. In EGS, the primary heat transmission from the hot rock to the circulating fluid transpires at the intersection of low-permeability hot rock and high-permeability fracture, consisting of circulating fluid. Therefore, it is critical to understand and model the heat transfer and propagation of the thermal front in a fracture-matrix system for better estimation of heat transfer process.

A considerable number of numerical, theoretical, and analytical studies have been previously carried out on the heat transport in a single fractured porous media [3,4,5,6,7,8]. A majority of the studies use the conventional parallel plate theory, where the wall roughness and heterogeneity (spatial variation) of the fracture aperture walls are ignored. This may have a significant influence on the circulating fluid velocity, and hence heat transfer, from the porous rocks to the circulating fluid. Hakami and Barton [9] and Keller and Bonner [10], through their investigations (experimental and field), observed that fractures tend to have a complex geometry such that the aperture size fluctuates along fracture length, and they may even contact at some places. Gale [11] and Raven and Gale [12], from their experimental studies, showed that for both natural and artificial (man-made) fractures, the permeability data diverged significantly from the parallel plate concept. Further, Mourzenko et al. [13] related the effective permeability of channels (fractures) to varying local aperture (fracture aperture). Therefore, it may be concluded that permeability of fracture, fluid flow in fracture, and hence the heat transfer to the fluid, may be sensitive to the geometric heterogeneity of fracture aperture.

Some studies have been carried out that have taken the heterogeneity of the fracture into consideration [14,15,16,17,18], however, these studies are focused on contamination transport (mass transport) and not on thermal front propagation. From these numerical and analytical studies, two ways of inclusion of fracture heterogeneity were identified. The first is by using a complex geostatistical model, which requires an enormous amount of data, as carried out by James and Chrysikopoulos [18] and Chrysikopoulos and Abdel-Salam [17]. The second is by using a simple mathematic function to represent the fracture heterogeneity, as carried out by Natarajan and Kumar [14]. The authors have previously attempted to analyse the effect of fracture heterogeneity on the propagation of the thermal front in a single fracture-matrix system by using simple sinusoidal and logarithmic functions to represent the fracture aperture [19]. 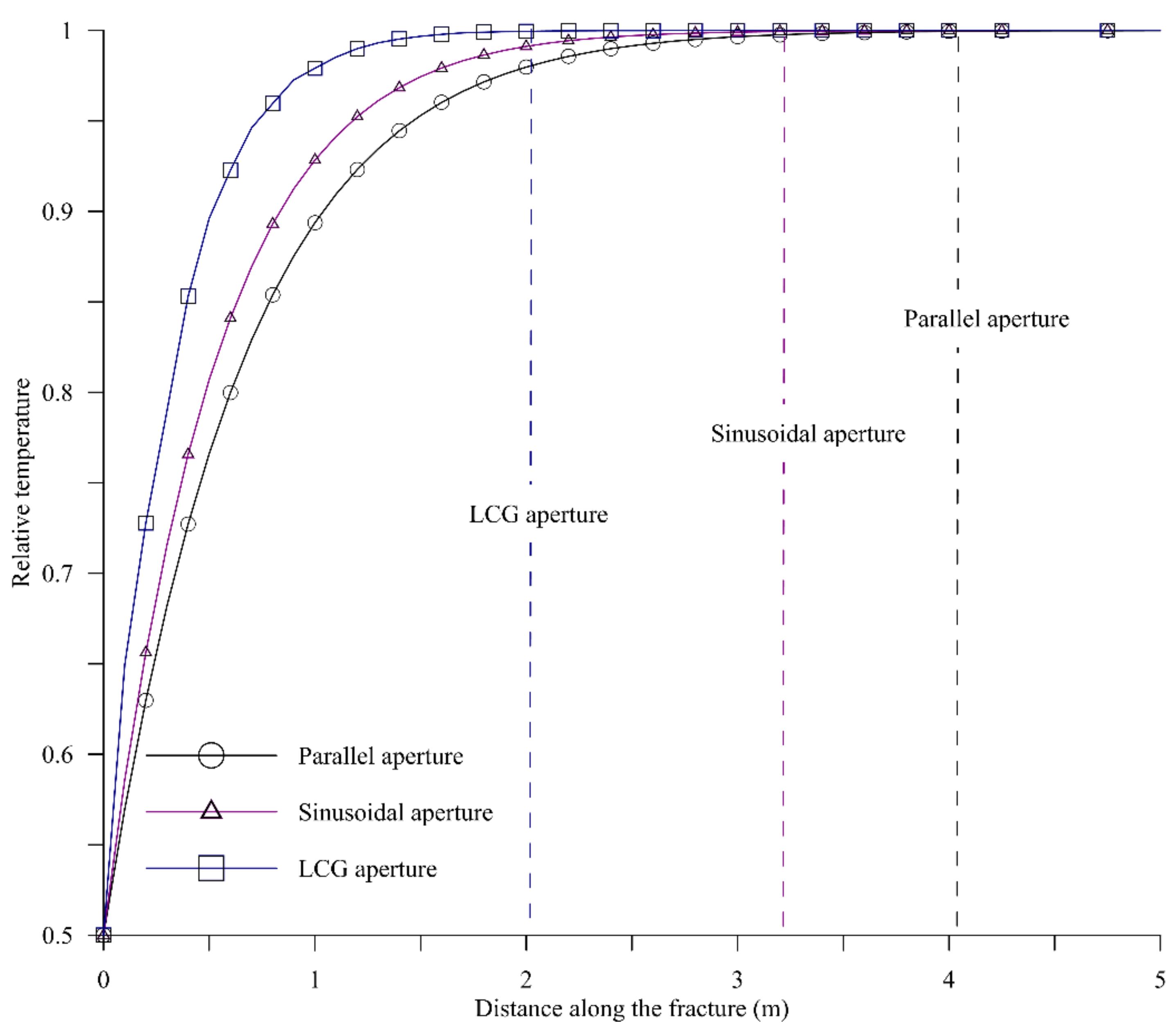Figure 1, obtained from the data presented by Bagalkot and Kumar [19], shows the spatial distribution of thermal fronts in the fracture for parallel plate and variable aperture models (sinusoidal variation and logarithmic variation) for averaged fracture apertures of b = 150 μm. From Figure 1, two observations may be made. First, there is a considerable difference in temperature profile between the parallel plate model and the variable aperture model represented by sinusoidal and logarithmic functions. Second, it may be observed there is a substantial difference in temperature profile among different variable apertures. The sinusoidal aperture underestimates the thermal equilibrium point (point along the fracture where fluid attains the temperature of rock matrix) in the logarithmic model by approximately 35%. These two observations raised the following questions. Are simple mathematical functions the right tools to represent the aperture variations? If not, are there better ways to represent the heterogeneity of fracture in a numerical model? Answering these questions was the motivation and objective of the present study.

Although simple mathematical functions as fracture aperture may indicate the importance of the inclusion of fracture heterogeneity, they may be the right tool to represent fracture aperture. The focus of this study was to come up with a better option that may better represent the actual fracture aperture. In this regard, the present study applied statistical algorithm LCG (linear congruential generator) to model the heterogeneity of the fracture aperture. By using LCG, it may be possible to generate fracture aperture that does not repeat, as in the case of sinusoidal or logarithmic models, while not being as complex to implement as that of the geostatistical model. The present article may be considered as the next step of Bagalkot and Kumar [19], with a better, simpler, and possibly a more accurate representation of heterogeneity of fracture aperture.

The objective of the present study was to investigate the effect of fracture heterogeneity on the propagation of thermal front in a single fracture-matrix system. Instead of using a simple mathematical function or a complex geostatistical model, an LCG algorithm was applied to generate the heterogeneity of fracture aperture. Further, a comparison was made between fracture by LCG and with the parallel plate and sinusoidal models. Sensitivity analysis on the fracture spacing and inlet flow rate of circulating fluid has been done, as they control the thermal front in the fracture.

2. Brief Theory and Physical System

In an EGS, the cold fluid (water) under high pressure is injected into a reservoir consisting of dry hot rocks through an injection well. The high-pressure water circulates through the hot rocks through high-permeability fractures. The interaction of cold water with hot rocks raises the temperature of the circulating water and the hot water is extracted from the production well. Depending on whether the geothermal system is liquid dominated (water) or vapour dominated (steam/steam and water), the extracted fluid at the production site may be water or steam or a combination of both. Figure 2 shows a bisection of a horizontal section of a single horizontal fracture-rock matrix system for three types of fracture aperture variations (parallel, sinusoidal, and LCG-aperture). Figure 2A represents the sinusoidal variation of fracture aperture taken from Bagalkot and Kumar [19]; the sinusoidal mathematical function was based on the self-similarity concept presented by Feder [20]. Figure 2B shows the variation of the fracture aperture obtained from the LCG. In Figure 2, b_L(x), b_s(x), and b_P represent fracture apertures due to LCG, sinusoidal, and the parallel plate models, respectively. Apart from LCG and sinusoidal aperture variation, Figure 2 also shows the difference between the LCG and sinusoidal model with average fracture aperture (b) of the parallel plate model (represented by a red dashed line). In Figure 2, B represents the half fracture spacing, and L_f is the fracture length. Each fracture may be considered symmetrical, as the fracture-rock matrix geometry repeats, and it would be sufficient to consider just one-half for the analysis [21].

In the present study, the principal thermal transport mechanisms involved thermal advection, conduction, and dispersion in the fracture, while within the rock matrix conduction was dominant. At the fracture-matrix, interface a conduction thermal transport was considered. For the present study, a one-dimensional transport was assumed within the fracture, occurring along the fracture, while within the rock matrix the transport was one-dimensional and transverse to the flow in the fracture. In both fracture and rock matrix, the fluid flow was horizontal. The fracture aperture was smaller compared to the length of the fracture (b <<< L_f) [21]. Due to significant lower permeability in rock matrix compared to fracture, the convection within the rock matrix was assumed non-existent [7]. Further, it was assumed that thermal dispersion is analogous to the dispersion of solutes [19]. An equilibrium in pressure exists between fracture and matrix, and the specific heat capacities are independent of temperature [6]. Finally, the circulating fluid was assumed to have a single phase (water), with enthalpy being constant [5,6]. The single-phase assumptions are justified for liquid-dominated geothermal systems, which are more common than the vapour-dominated geothermal systems (multiphase) [22]. Geometric variations (aperture width) of fracture aperture was considered as fracture heterogeneity and moving forward in the present study, the term “heterogeneity” imply geometrical variations.

3. Mathematical Formulation

Fractured porous media is a complex geological structure, as rock properties (permeability and porosity) change drastically across these two regions. The variations in the rock properties cause changes in the fluid properties and hence the physics. Fractures are high-permeability zones, whereas the surrounding rock matrix is a low-permeability zone. Therefore, the fracture forms a discontinuity in the porous rock matrix. This acts as a challenge when representing a fractured porous media numerically, as a single mathematical equation would be insufficient and incorrect to represent the thermal propagation in the fractured porous media. To overcome this challenge, the thermal transport in the single horizontal fracture-matrix system may be described by two coupled PDEs (partial differential equations). One equation represents the thermal transport in the fracture and the other within the rock matrix. The two PDEs are coupled, and coupling is given by the continuity of thermal fluxes between these regions, along the fracture-matrix interface.

The thermal transport in the fracture was adopted from [19], with the modification made to include the heterogeneity of fracture aperture (LCG model) given by Equation (1).

$$\frac{\partial T_f}{\partial t}=-\frac{Q}{A\left(x\right)}\frac{\partial T_f}{\partial x}+D_f\frac{{\partial }^2{T}_f}{\partial x^2}+D_L\left(x\right)\frac{{\partial }^2{T}_f}{\partial x^2}+\frac{{\lambda }_m\left(T\right)}{{\rho }_w{C}_{w}b\left(x\right)}\frac{\partial T_f}{\partial y}|y=b\left(x\right)$$

(1)

In Equation (1), D_f (m²/day) is the thermal conduction coefficient of circulating fluid in fracture; D_L(x) (m²/day) is the longitudinal thermal dispersion coefficient; T_f is the relative temperature of fluid in fracture (K); T_m is relative temperature of fluid in rock matrix (K); t is the time; Q(x) (m³/day) is the flow rate of the fluid through fracture and A(x) is the cross-sectional area; λ_m is matrix thermal conductivity; ρ_w (kg/m³) is the fluid density in fracture; and C_w (J/kg·K) is specific heat capacity of circulating fluid in fracture.

Equation (2) represents the thermal transport with in the rock matrix.

$$\frac{\partial T_m}{\partial t}=\frac{{\lambda }_m\left(T\right)}{{\rho }_m\times C_m}\frac{{\partial }^2{T}_m}{\partial y^2}$$

(2)

where λ_m(T) represents the fluid thermal conductivity in the rock matrix, and ρ_m(T) and C_m(T) are, respectively, density and specific heat of rock matrix as a function of temperature. Empirical relation was applied in the model to take into account the variation of thermal conductivity of fluid in rock matrix (λ_m(T)) with temperature as represented by Equation (3) [23].

$${\lambda }_m\left(T\right)=\frac{A}{350+T}+N$$

(3)

where A and N are coefficients whose value is a function of rock type, λ_m(T) is in W/mK, and T in °C. A = 807 and N = 0.64 for granite, granodiorite, and quartz porphyry [24]. Further, similar to Bagalkot and Kumar [19], in the present article the rock properties like rock density (ρ_m(T)) and rock specific heat capacity (C_m(T)) are calculated as a function of temperature as described in Equations (4) and (5). Equations (4) and (5) are empirical relations obtained by Somerton [25].

$${\rho }_m\left(T\right)=\frac{2650}{1+\left(T-20\right)0.5\times {10}^{-0.4}}$$

(4)

$$C_m\left(T\right)=1234.257-454.546\left(e^{-0.0039}\right)$$

(5)

In Equations (4) and (5), ρ_m(T) is in Kg/m³ and C_m(T) in J/kg·K with T in °C.

A detailed explanation of the initial and boundary conditions for solving the Equations (1) and (2) may be found in Bagalkot and Kumar [19].

3.1. Implementation of Fracture Heterogeneity

Equation 1 gives a clear perspective on the influence of fracture spacing (aperture width) on the thermal front propagation. In Equation (1), the terms which are represented as a function of space (f(x), for example D_f(x)) indicate direct relation with the fracture aperture. It may be observed that the advection (first term on RHS (Right hand side) of Equation (1)), the thermal dispersion (third term on RHS of Equation (1)), and, most importantly, the heat transfer at the interface (last term on RHS of Equation (1)) are all dependent on fracture aperture. Hence, fluctuating the fracture aperture would alter these phenomena and hence estimation of heat transfer in a fracture-matrix system, cementing the need to consider the heterogeneity of fracture aperture. In the present study, a novel and simple statistical LCG was applied to replicate the actual heterogeneity of fracture aperture as closely as possible to reality, as represented by Equation (6). Previously, the authors have applied LCG model for analysing the colloidal transport in the fractured reservoir [26]. For the remainder of the article, the fracture aperture generated by LCG algorithm will be termed as LCG-aperture.

$$b{\left(x\right)}_{n+1}=\left(a\times b{\left(x\right)}_n+\Delta b\left(x\right)\right)\mathrm{mod}m$$

(6)

where a is the multiplier, ∆b is the increment from one value to the next, and m is the modulus. Limits are assigned to Equation (6) so that it generates a number whose average equals that of parallel plate model (example: if for parallel plate the fracture aperture is b = 50 µm, then limits are assigned to Equation (6) so that the average of all the generated values is equal to b(x)_avg = 50 µm). The output from the Equation (6) would be similar to aperture variation shown in Figure 2B. The mathematical function for generating sinusoidal fracture aperture in variable aperture was obtained from Bagalkot and Kumar [19]. The expression of this sinusoidal variation is given by Equation (7).

$$b\left(x\right)=Am\times \exp \left(m\times x\right)\times \left(1+\sin \left(n\times \pi \times x\right)+a\right)$$

(7)

where Am is the maximum aperture width. Variables m, a, n, and d are constants.

Table 1. Maximum, minimum, and average half fracture spacing values for different types of fracture.

Aperture Variation Profile	Max Half Fracture Aperture (μm)	Min Half Fracture Aperture (μm)	Avg Half Fracture Spacing (μm)
Sinusoidal variation	90	60	74.6
Parallel plate model	75	75	75
LCG-aperture	89	55	76

shows the extremities (maximum and minimum) and the average fracture aperture thickness value for different fracture apertures. It may be observed that the fracture aperture thickness for the parallel plate is constant, which may be due to the absence of heterogeneity. It may be seen from Table 1 that the average fracture aperture among the various profiles is approximately 75 μm. For a reliable comparison among fracture types, the value of apertures for sinusoidal and LCG models was chosen such that the average fracture aperture is equivalent to that of the parallel plate.

3.2. Effective Heat Transfer Factor

In Bagalkot and Kumar [19], a novel non-dimensional parameter called “effective heat transfer factor” (EHF) was introduced to efficiently and easily estimate the degree of heat transfer to the circulating fluid from rock matrix. Equation (8) represents the numerical expression of EHF.

$$\mathrm{EHF}=\frac{\left(L_f-L_s\right)}{L_f}$$

(8)

where L_s (m) is the distance from the fracture inlet at which the temperature of the circulating fluid reaches that of hot rock. The value of EHF ranges between 0 and 1. EHF = 0 (L_s = L_f) would indicate the condition where there is minimum or negligible heat transfer from the hot rocks to circulating fluid. EHF = 1 (L_s <<< L_f) shows that the circulating fluid attains the temperature of rock instantaneously, indicating infinite conduction (highly unlikely).

3.3. Numerical Model and Verification

A fully implicit FDM (finite difference method) discretisation has been applied in the present numerical study. The first term on the RHS of Equation (1) describes the convection, and an implicit first-order forward difference (upwind) is applied to discretise it. Dispersion and conduction phenomena are respectively represented by the second and third terms on the RHS of Equation (1), and implicit second-order central discretisation is applied to them. A first-order implicit forward difference is used to discretise the coupling term (last term on the RHS of Equation (1)). A two-point backwards finite difference is used to discretise all the temporal terms. The conduction term in Equation (2) is discretised by a second-order implicit central difference. Iterations were carried out at every time-step to satisfy the continuity at the fracture-matrix interface. A uniform grid spacing was adopted along the length of the fracture (x-axis), and a geometrically increasing (variable) grid space was applied to the rock matrix orthogonal to the flow in fracture (y-axis). The grid size of the rock matrix increases geometrically, with the size of the first grid equal to half of the fracture aperture (y₁ = B). A smaller grid size is used in the first grid and grid near the fracture-matrix interface, which represents the interface of the fracture-matrix to capture the mass flux transfer occurring at the interface effectively. The article Bagalkot and Kumar [19] may be referred to for the detailed explanation of the numerical method and the verification of the model. The values of the parameters used in the present study have been tabulated in

Table 2. Values of the parameters used for validation of the numerical model for parallel fracture aperture.

Parameters	Values
Grid size in fracture ∆x, (m)	0.01
Time step ∆t, (days)	0.05
Total simulation time (days), T	100
Fluid thermal conduction coefficient in fracture Df (m2/day)	[19]
Longitudinal thermal dispersion coefficient in fracture DL (m2/day)	[19]
Density of fluid ρw (kg/m3)	1000
Density of rock matrix ρm (kg/m3)	2600
Rock thermal conductivity λm (W/m/K)	2
Thermal conductivity of fluid in fracture λf (W/m/K)	0.5
Specific heat (water) Cw (J/kg/K)	5000
Specific heat of rock matrix Cm (J/kg/K)	800
Avg half fracture aperture b (μm)	75
Fluid velocity V (m/day)	[19]
Fracture length Lf (m)	10
Half fracture spacing H (m)	0.3

.

4. Results and Discussion

Figure 3 shows the thermal front propagation in the fracture for parallel plate model, sinusoidal model, and LCG-aperture at average half fracture aperture of b = 75 μm, keeping the rest of the parameters the same as in Table 2. Without going into the analysis of Figure 3, the observations clearly indicate “fracture heterogeneity is critical”; simply by altering fracture aperture, a significant difference in thermal front propagation was observed in the fracture. From deeper analysis, two important observations may be made from Figure 2. First, there is a noteworthy difference in the profile of relative temperature in the fracture for different fracture apertures (parallel, sinusoidal, and LCG-aperture). Second, the point of thermal equilibrium (the point at which the circulating fluid attains the temperature of the rock matrix) changes significantly depending on the type of fracture aperture. It may be observed that the for all the fracture types, the temperature profile is logarithmic in nature, however, compared to parallel and sinusoidal fractures, the LCG-aperture profile is more logarithmic, indicating a possibility of greater heat transfer for the LCG-aperture. It may further be observed that the circulating fluid attains thermal equilibrium faster for LCG-aperture, followed closely by sinusoidal and at last for parallel. The vertical line in Figure 3 indicates the point of the fracture where the circulating fluid achieved the temperature of the rock matrix (thermal equilibrium). For LCG-aperture, the thermal equilibrium is achieved approximately 50% before the parallel aperture, and around 30% before the sinusoidal aperture. Hence, both LCG and sinusoidal models—which take heterogeneity into account—perform better than parallel aperture. This is primarily due to the absence of fracture heterogeneity in the parallel aperture. The heterogeneity (undulations of fracture wall) of fracture wall enhances the surface area, which may lead to a greater and faster heat transfer at the fracture-rock interface. Therefore, the fluid attains equilibrium faster for LCG and sinusoidal models than for parallel plate model. Further, the presence of the undulations (heterogeneity) would alter the velocity of the circulating fluid, which ultimately would affect the convection (represented by the first term on RHS of Equation (1)) and thermal dispersion (third term on RHS of Equation (1)). A similar theory of surface area may be attributed to the better performance of LCG over sinusoidal model. From the data obtained from a numerical model, the LCG-aperture shows approximately 15–20% greater surface area compared to the sinusoidal aperture for the same average fracture aperture. This indicates that the LCG-aperture, which is more near reality, would actually lead to a greater heat transfer than the simple sinusoidal variation.

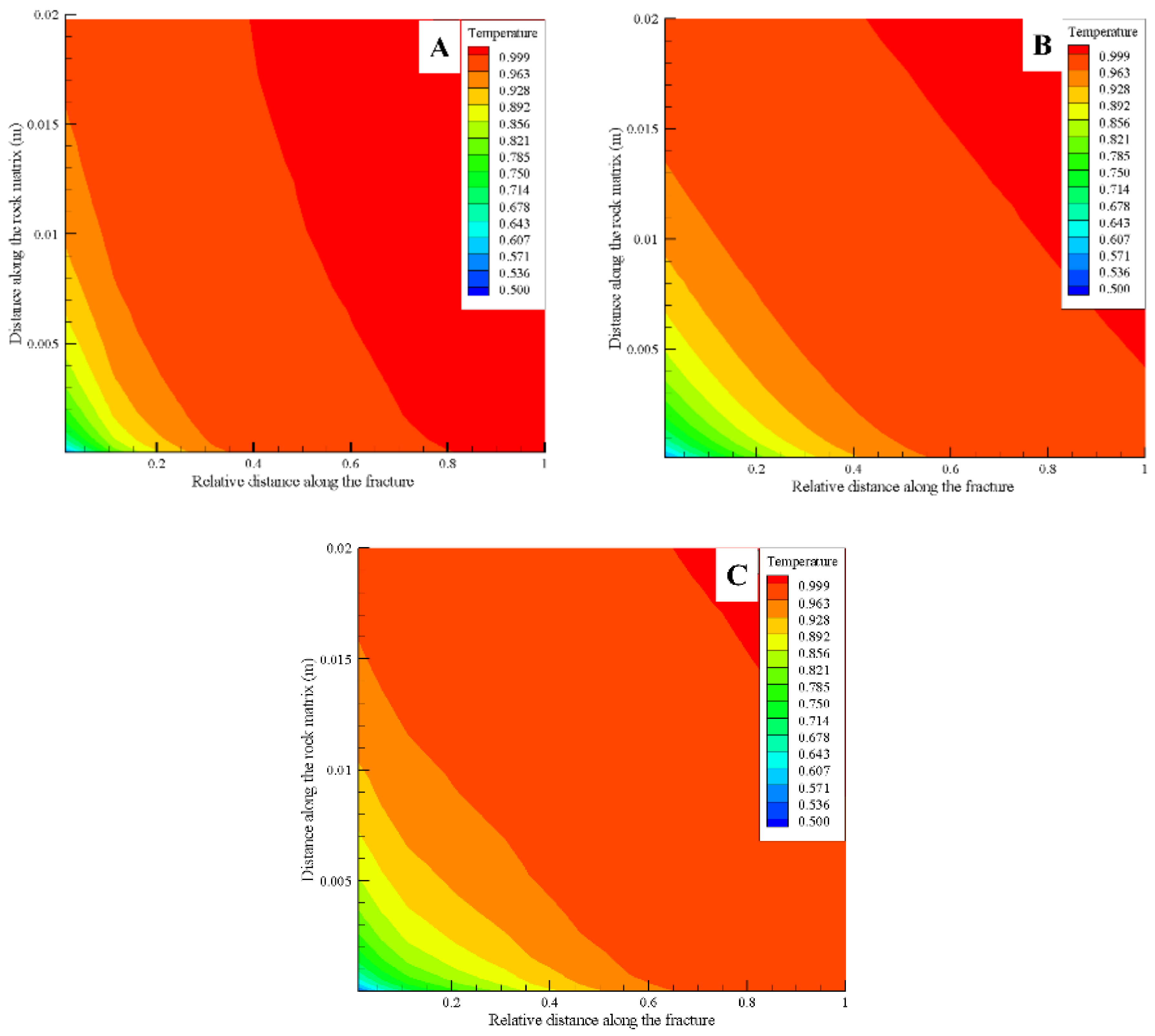
From Figure 3 it may be said that in the fracture, the efficiency of the heat transfer to the circulating fluid may be measured by calculating the equilibrium point from the fracture inlet, while within the rock matrix the efficiency may be measured by the seeing the change in the temperature distribution within the rock matrix. Figure 4A–C represent the contours of the temperature profile within the rock matrix after 100 days of circulation of a fluid for parallel, sinusoidal, and LCG fractures, respectively. The greater the area of hot rock with temperatures near to its original temperature, the lower will be the heat transfer to the circulating fluid in the fracture. Looking at Figure 4, it may be said that for the parallel plate model a large region of the hot rock matrix has retained its original temperature (Figure 4A) compared to the sinusoidal model (Figure 4B) and LCG-aperture (Figure 4C). For the parallel fracture (Figure 4A), approximately 92% of the region of hot rock matrix has retained its original temperature, showing minimal temperature loss (less than 7%), compared to approximately 84% for sinusoidal and 76% for the LCG-aperture. Thus, maximum heat transfer occurs when fracture aperture is represented by LCG model, minimum heat transfer when represented by parallel, while intermediate heat transfer is observed for sinusoidal representation. The additional heat transfer may be credited to the undulations or the heterogeneity in the LCG and sinusoidal models, which is absent in parallel fracture. The coupling term in the Equation (1) (fourth term in RHS) that represents the heat flux transfer between the hot rock matrix and circulating fluid in fracture is dependent on fracture aperture variation (heterogeneity). The undulations (heterogeneity) alter the coupling term, while the parallel plate model, due its homogenous assumption of fracture aperture, weakens the coupling term, thus causing an underestimation in the heat transfer from the rock matrix to the circulating fluid. Further, the results in Figure 4 coincide with the theory present in Figure 3: that the heterogeneity in fracture aperture enhances the heat transfer, leading to circulating fluid reaching thermal equilibrium faster for a case with LCG and sinusoidal compared to parallel. Figure 4 also indicates that the heat transfer is greater for LCG-aperture (Figure 4C) compared to the sinusoidal aperture (Figure 4B), which may be credited to the better representation of heterogeneity by LCG than sinusoidal and hence a greater heat transfer. The result in Figure 4 has a major significance, as it indicates that ignoring heterogeneity (parallel plate) or modest representation of heterogeneity (sinusoidal) would lead to underestimation of heat transfer to the circulating fluid in fracture from the surrounding hot rock. Error at the single fracture-matrix scale would possibly lead to gross error in estimating heat transfer at large scale. Further, the result also indicates that the fracture model represented by LCG algorithm is a better and more realistic option than the sinusoidal or simple mathematical forms.

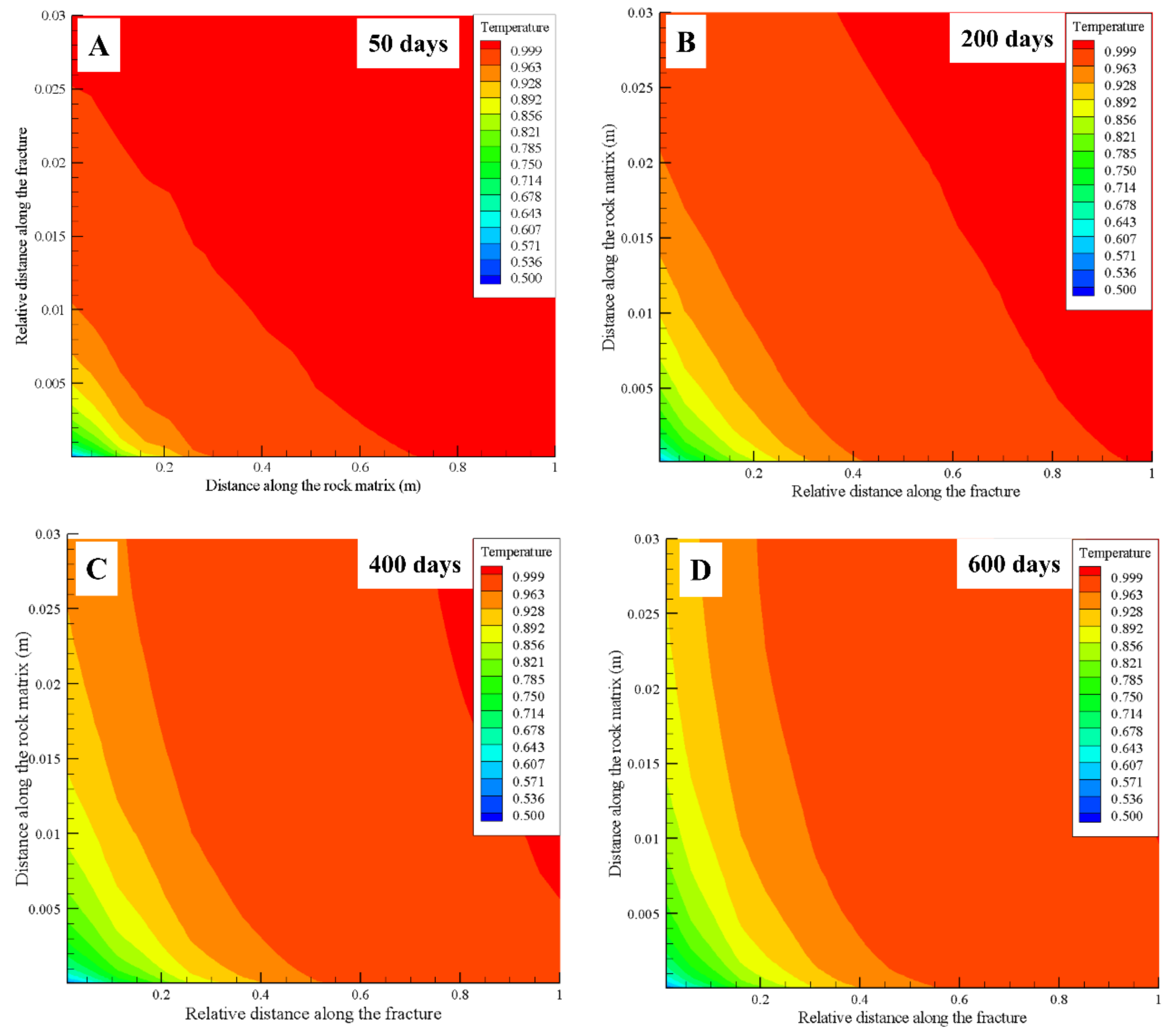
Figure 5A–D represents the transition of temperature profile within hot rock matrix with time at 50, 200, 400, and 600 days respectively for the LCG-aperture. It may be observed that as time progresses the region with initial temperature reduces from 5% at 50 days to 55% at 600 days. As time progresses, more and more circulating fluid is transported into the rock matrix from the fracture aperture, and this fluid carries the heat from the rock matrix to the surface. Thus, as observed, with the progress of time, the region which has retained the original temperature reduces.

As described in Section 3.2, the EHF is an indicator of the degree of heat transfer to the circulating fluid from the hot rock. The greater the value of EHF, the greater will be the heat transfer and vice versa.

Table 3. L_s (distance from the fracture inlet at which the temperature of the circulating fluid reaches that of hot rock) and effective heat transfer factor (EHF) values for different fracture aperture sizes and fluid flow rates.

Influence of Aperture Size (bavg)
Fracture aperture type	bavg = 50 μm		bavg = 100 μm		bavg = 150 μm
	Thermal Equilibrium Point (Ls) (m)	EHF	Thermal Equilibrium Point (Ls) (m)	EHF	Thermal Equilibrium Point (Ls) (m)	EHF
Parallel	1.4	0.86	5.40	0.46	9.75	0.303
Sinusoidal	1.2	0.88	4.25	0.575	6.50	0.535
LCG	1.0	0.90	2.60	0.74	5.25	0.625
Influence of Inlet Flow Rate (Q)
Fracture aperture type	Q = 7.5 × 10−6 m3/day		Q = 37.5 × 10−6 m3/day		Q = 75 × 10−6 m3/day
	Thermal Equilibrium Point (Ls) (m)	EHF	Thermal Equilibrium Point (Ls) (m)	EHF	Thermal Equilibrium Point (Ls) (m)	EHF
Parallel	0.61	0.939	2.9	0.71	5.62	0.438
Sinusoidal	0.51	0.949	2.4	0.76	4.75	0.525
LCG	0.47	0.953	1.9	0.81	3.30	0.67

represents the sensitivity analysis of fracture size and circulating fluid flow rate in terms of EHF (Equation (7)) and thermal equilibrium point (L_s, obtained from the numerical model) for parallel, sinusoidal, and LCG aperture types. The first part of Table 3 shows the EHF and L_s values for three half fracture values, from low (b_avg = 50 μm) to high (b_avg = 150 μm). The results from the first part of Table 3 indicate that regardless of the type of fracture, increasing the aperture size decreases the magnitude of EHF, indicating a reduction in heat transfer to the circulating fluid, hence, the observed increase in the point of thermal equilibrium (L_s) (equilibrium achieved farther away from the fracture inlet). When comparing the EHF values for different aperture sizes among the different types of fracture, two important observations becomes known. First, for small aperture size the fracture heterogeneity has minimal impact on the heat transfer, as the EHF values for all the types of fracture are similar and higher, although EHF for LCG-aperture is marginally higher than in sinusoidal and parallel models. Second, as the aperture size increases, the impact of the heterogeneity becomes dominant. Additional heat transfer (EHF) of approximately 108% at b_avg = 150 μm from a minimal 4.6% at b_avg = 50 μm is observed for LCG-aperture compared to the parallel aperture. A similar observation may also be made between LCG-aperture and sinusoidal aperture, but at a lower scale (2.2% at b_avg = 50 μm to 18% at b_avg = 150 μm). Therefore, it may be concluded that for small aperture sizes (b_avg ≤ 50 μm), the heterogeneity of the fracture may not be influential on the heat transfer and may be neglected from the analysis. However, for medium or large fracture sizes (b_avg > 50 μm), neglecting the heterogeneity would lead to major error of the estimation of the heat transfer to the circulating fluid.

The second part of Table 3 shows the EHF and L_s values for three values of inlet flow rate of the circulating fluid, from low (Q = 7.5 × 10⁻⁶ m³/day) to high (Q = 75 × 10⁻⁶ m³/day) at a fixed fracture size of b_avg = 75 μm. Regardless of the fracture type, increasing the flow rate of the fluid in fracture would decrease the magnitude of the EHF, indicating a decrease in the heat transfer. Increasing the flow rate would make the fracture convection term dominant (first term on RHS of Equation (1)), which would make the fluid move faster through the fracture, giving less residence time for the fluid to extract heat from the hot rocks. Similar to sensitivity analysis of fracture size, two important observations may be made when comparing the EHF values for different flow rates. First, at small flow rates (Q = 7.5 × 10⁻⁶ m³/day) the fracture heterogeneity has minimal impact on the heat transfer, as EHF values for all the types of fracture are similar and higher, with EHF values for LCG-aperture marginally higher than sinusoidal and parallel types. Second, with the increment in the flow rate (Q) the impact of heterogeneity becomes dominant, with greater loss in heat transfer (lower magnitudes of EHF) observed for the parallel plate and sinusoidal models compared to LCG. Further, lower values of EHF may also be observed from Table 3 for sinusoidal compared to LCG-aperture, indicating lower heat transfer for the sinusoidal case compared to LCG. Therefore, it may be concluded that as long as flow rate is kept low, especially for small aperture size, the impact of fracture heterogeneity will be low, and it may not be necessary to include heterogeneity in the analysis. However, as the flow rate increases, even for a small aperture size, the influence of heterogeneity becomes dominant and should not be neglected while estimating the heat transfer to the circulating fluid.

5. Summary and Conclusions

A fully implicit finite difference model has been developed to investigate the influence of fracture heterogeneity on the thermal transport (front propagation) in a single horizontal fracture-matrix system, with a focus on heterogeneity obtained by the LCG. The model results have been compared with the parallel plate and sinusoidal models and, subsequently, the significance of a more accurate and simple method of fracture heterogeneity representation has been emphasized, especially by implementation of LCG-aperture. Finally, sensitivity analysis of fracture aperture size and fluid flow rate has been carried out to identify the conditions at which considering fracture heterogeneity is critical.

The proposed inclusion of fracture heterogeneity using an LCG-aperture shows a significantly dissimilar thermal front compared to the parallel plate model, and comparable difference to the sinusoidal model. The more realistic fracture heterogeneity by the LCG model enhances the heat transfer between fracture and hot rock matrix and thereby the fluid within the fracture attains the temperature of rock matrix earlier, as compared to the parallel and sinusoidal fractures. Further, the results suggest that parallel plate model underestimates the thermal front propagation along the fracture. The LCG-aperture, which is a close representation of the heterogeneity, shows a higher heat transfer to the circulating fluid compared to the simple sinusoidal aperture.

The results of the sensitivity analysis of fracture size indicated that for small aperture sizes (b_avg ≤ 50 μm), the heterogeneity of the fracture may not be influential on the heat transfer and may be neglected from the analysis. However, for medium or large fracture sizes (b_avg > 50 μm), neglecting the heterogeneity would lead to major error. Further, the results of the sensitivity analysis of fracture fluid flow rate indicated that for low flow rate, especially for small aperture size, the impact of fracture heterogeneity will be lower, and it may not be necessary to include heterogeneity in the analysis. However, as the flow rate increases, even for small aperture size, the influence of heterogeneity becomes dominant and should not be neglected.