Energy Management for Smart Multi-Energy Complementary Micro-Grid in the Presence of Demand Response
Abstract
:1. Introduction
2. Smart Microgrid DR Model
2.1. Customer Response Behavior Model
2.2. Customer Satisfaction Model
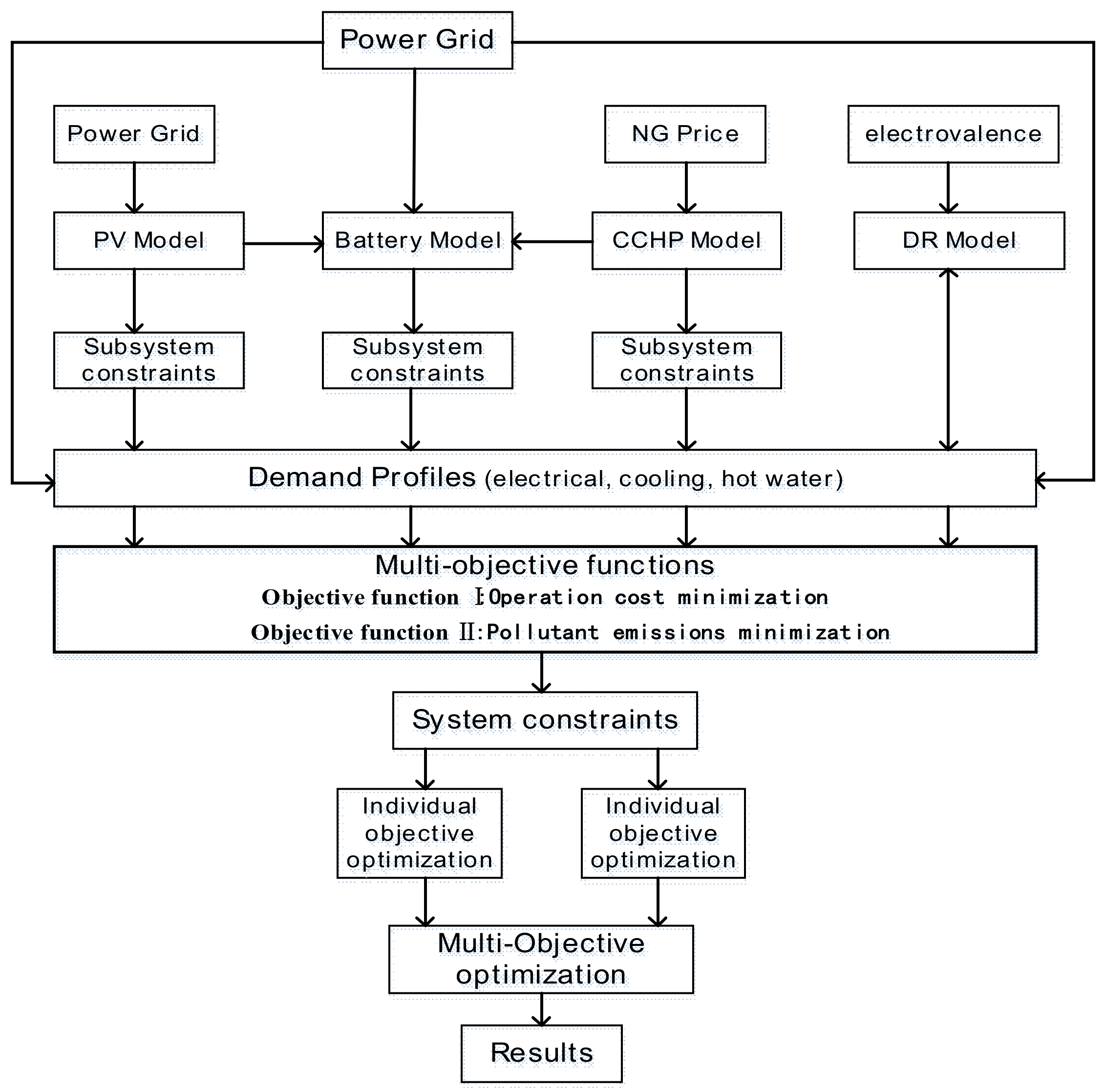
3. Microgrid Operation Optimization Model
3.1. Objective Function Optimization
3.2. Constraints
3.2.1. PV Output Constraint
3.2.2. CCHP Output Constraint
3.2.3. Power Balance
3.2.4. EES Constraints
3.2.5. Power Purchase Cost Constraint
3.2.6. Customer Satisfaction Constraints
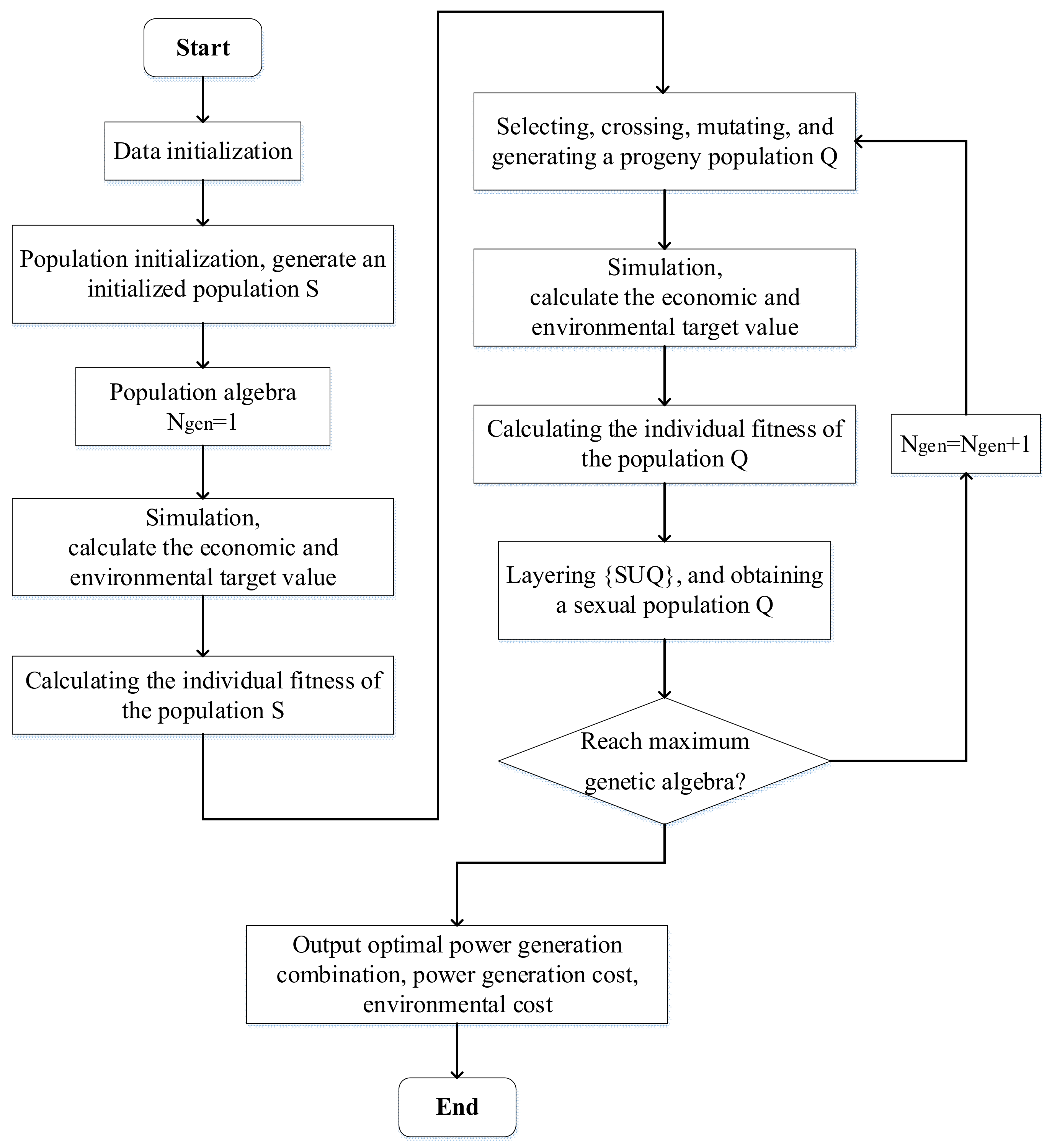
3.3. Model Solution Method and Operating Strategy
3.3.1. Operating Strategy
3.3.2. Model Solution Method
4. Case Study
4.1. Parameters
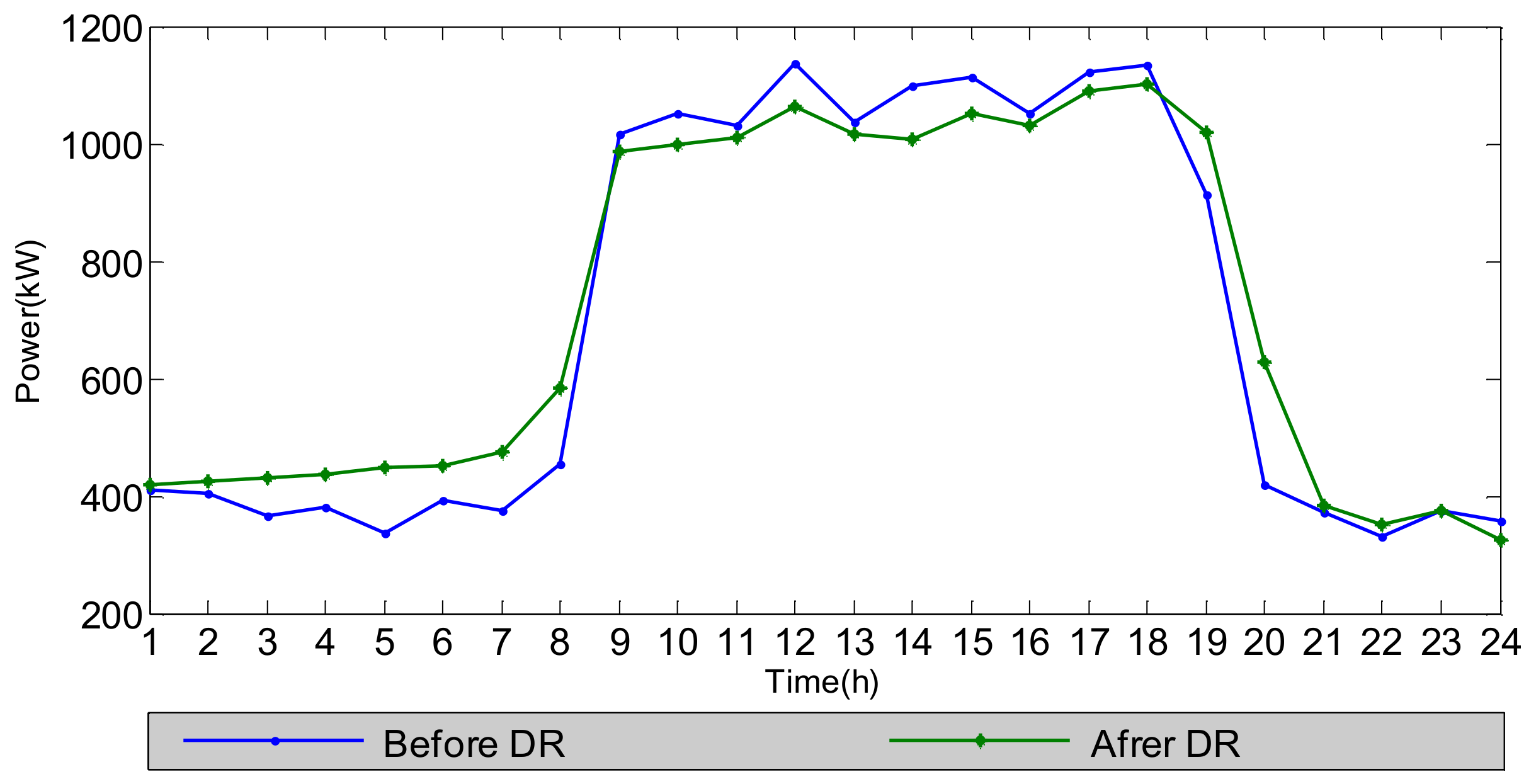
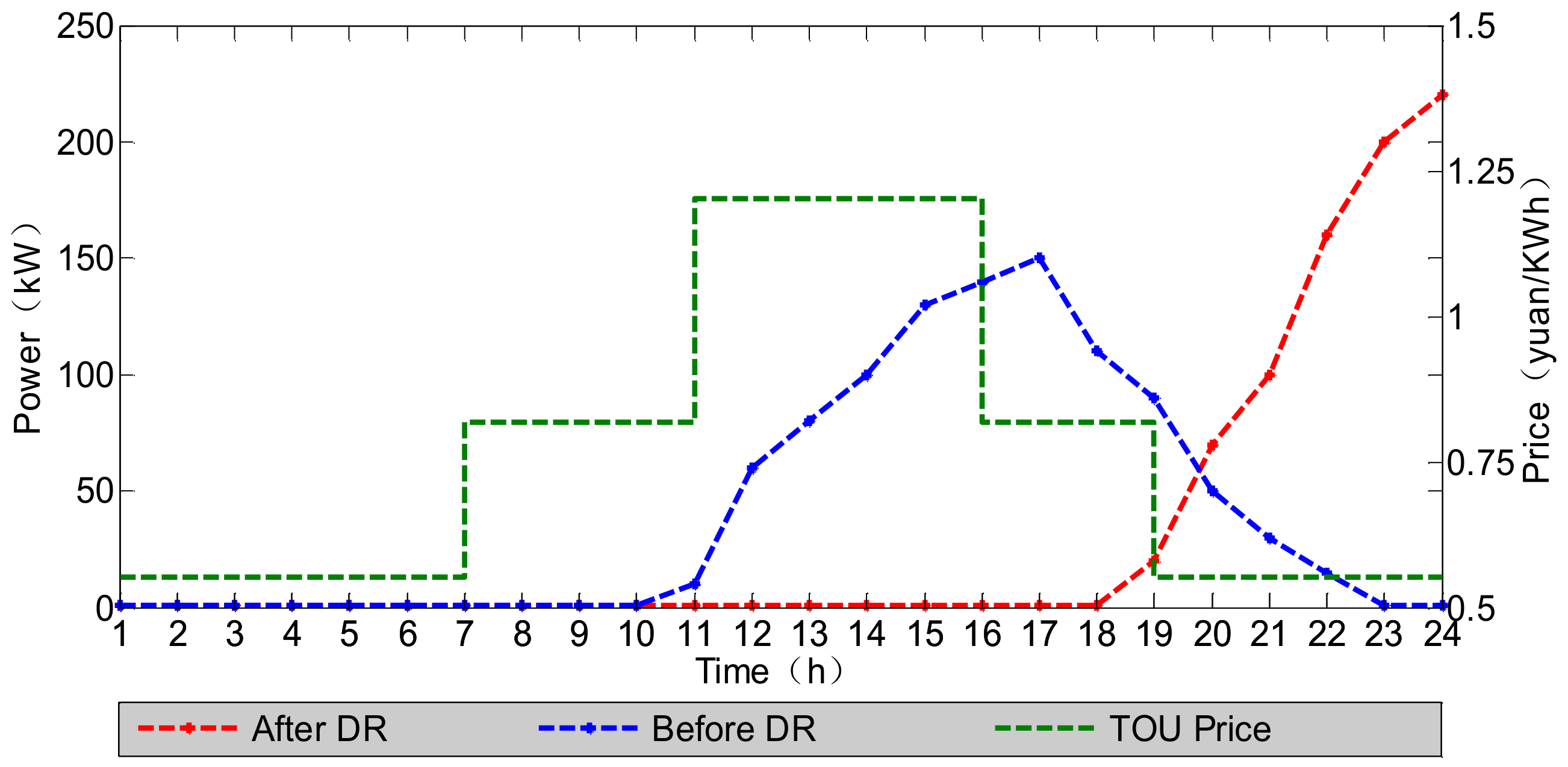
4.2. DR Study Results
4.3. Operation Optimization
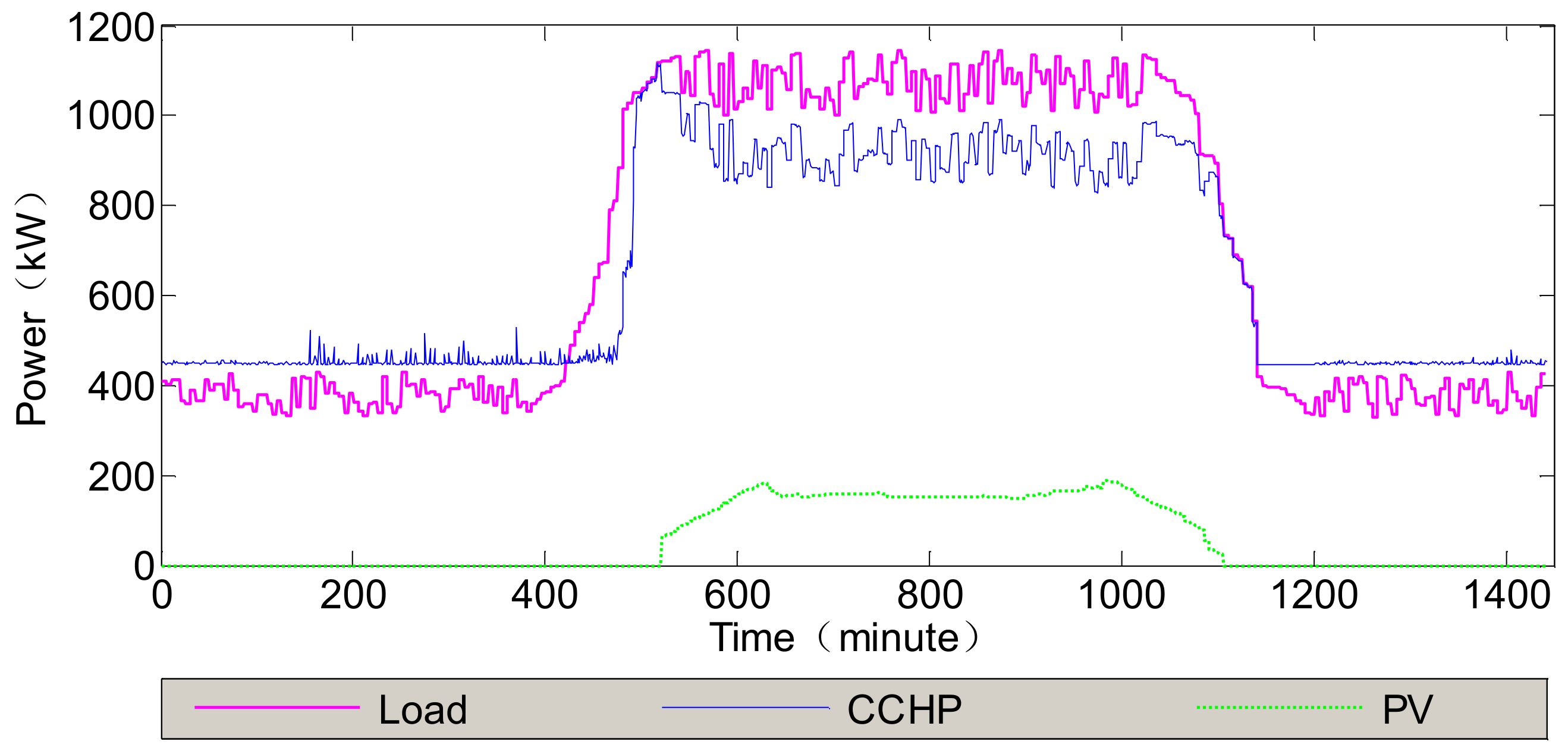
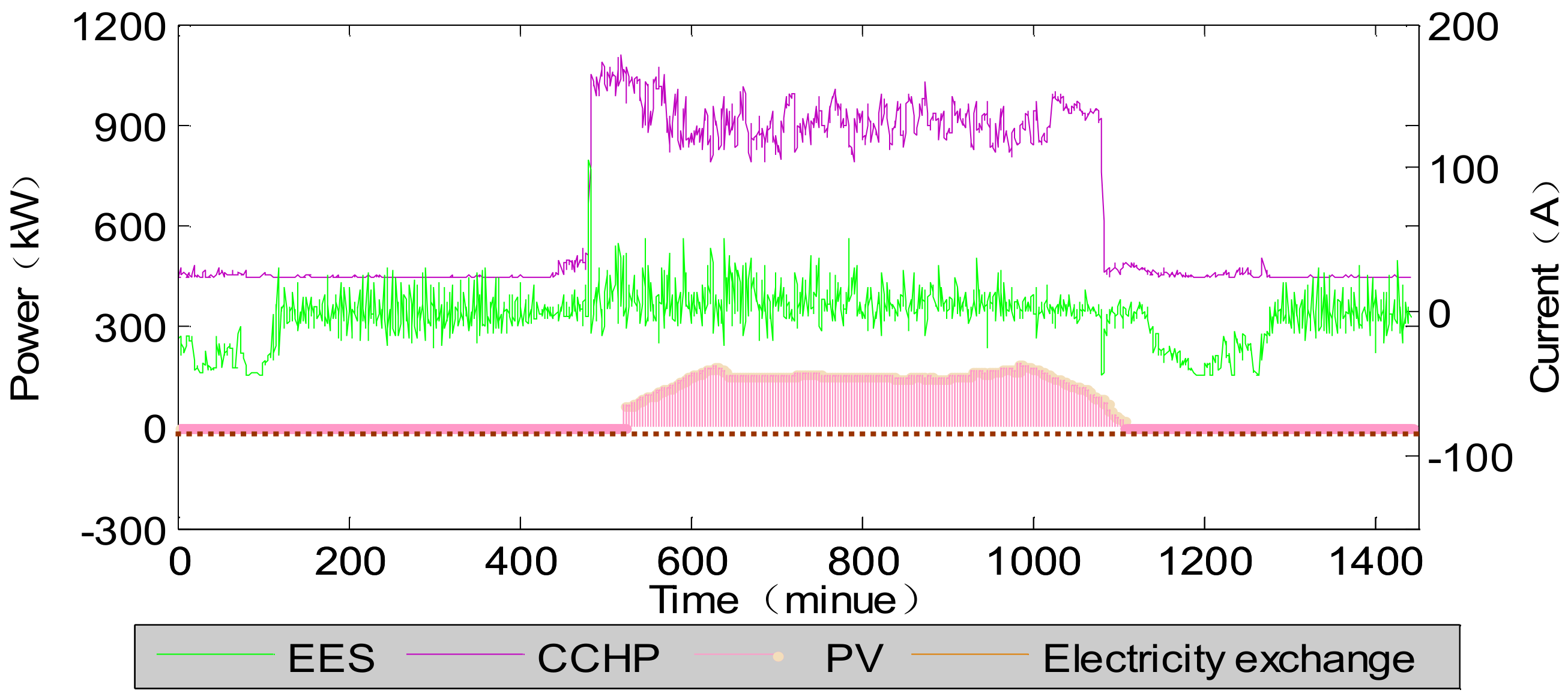
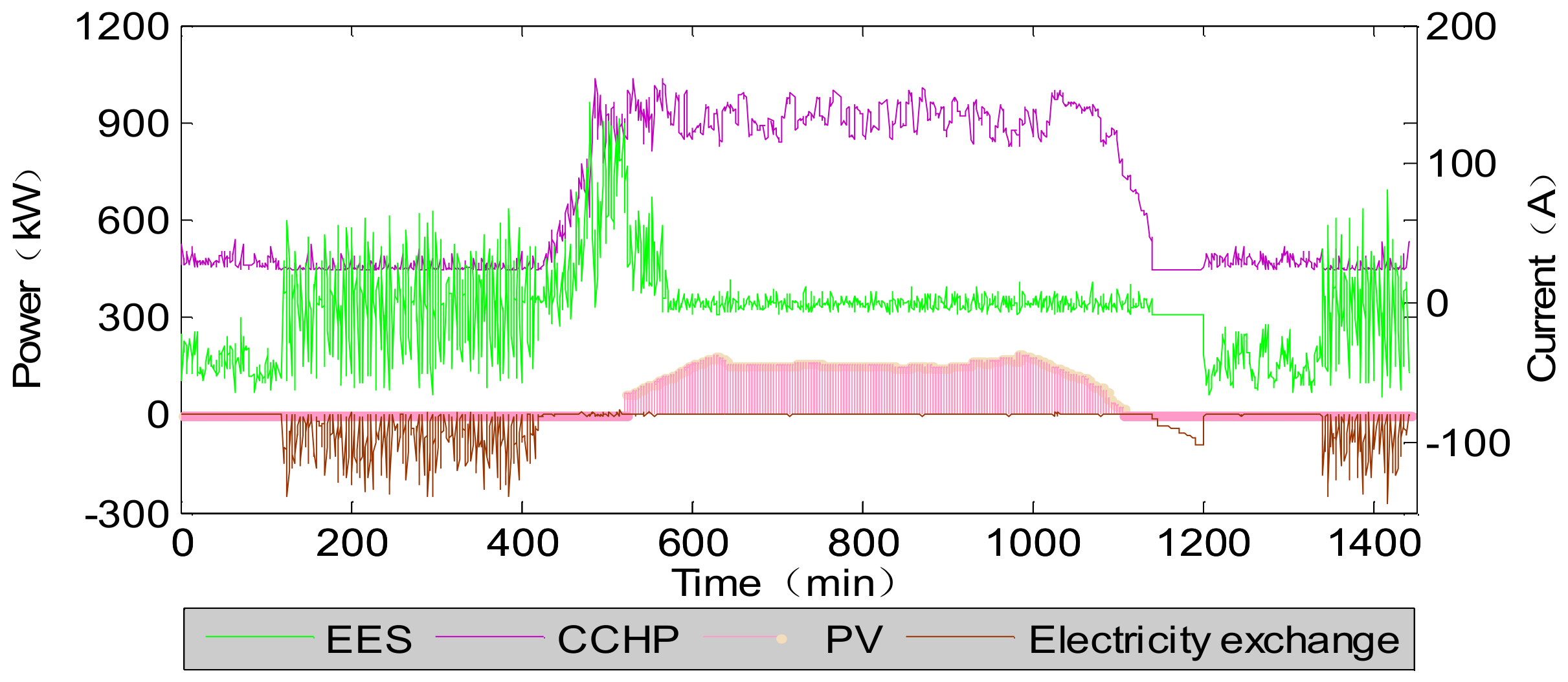
4.3.1. Scene Analysis
4.3.2. Optimization Results
4.3.3. Optimization Process Analysis
4.3.4. Optimization Result Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| the operation cost of system | |
| System gas price, yuan/m3 | |
| I | PV current |
| the equivalent parallel impedance | |
| curve fitting parameter | |
| the current generated by the light and the reflected missing current | |
| the actual depth of discharge | |
| actual capacity | |
| the coefficients of the relationship between electricity and electricity prices | |
| the amount of power and its change | |
| Electricity satisfaction | |
| the output power of the CCHP, kW | |
| the electricity cost of the microgrid during the Scheduling period, yuan/kWh | |
| the power generation efficiency of the CCHP | |
| the heat loss coefficient of the CCHP | |
| the energy exchange power, kW | |
| the core load power in the system/kW | |
| the load lost in the distribution network/kW | |
| the upper limit of the remaining capacity/kW | |
| the maximum value of charging power at time t, kW | |
| maximum value of discharge power at time t, kW | |
| the minimum value of satisfaction with electricity expenditure | |
| the maximum power of DG | |
| the Generation cost, yuan/kW | |
| the equivalent series impedance | |
| the electronic charge | |
| boltzmann constant | |
| the cycle number of stored energy under rated discharge depth and rated discharge current | |
| the actual discharge current ampere hours in the unit of time | |
| the initial investment cost of energy storage | |
| the elastic coefficient of the electricity price | |
| the price and its variation | |
| Electricity expenses satisfaction | |
| the output of DG during the Scheduling period, kw | |
| the operation cost of energy storage, yuan/kWh | |
| the purchase price, yuan/kWh | |
| is the selling price of microgrid in scheduling time, yuan/kWh | |
| the output power of PV system/kW | |
| the power of the adjustable load in the microgrid/kW | |
| the total load involved in demand response scheduling in the system/kW | |
| the power of EES at time t/kW | |
| the total power load of the system | |
| the time period corresponding to the fixed electricity price and the peak-to-valley electricity price | |
| the minimum value of satisfaction with electricity mode |
References
- Zhu, X. Research and Application of Key Technology Based on PCS Intelligent Micro-Grid System; Anhui University: Hefei, China, 2015. [Google Scholar]
- Guo, S.; Zhao, H.; Zhao, H. The Most Economical Mode of Power Supply for Remote and Less Developed Areas in China: Power Grid Extension or Micro-Grid? Sustainability 2017, 9, 910. [Google Scholar] [CrossRef]
- Ming, N.; Wei, H.; Guo, J.; Su, L. Research on Economic Operation of Grid-Connected Micro-grid. Power Syst. Technol. 2010, 34, 38–42. [Google Scholar]
- Hossain, E.; Perez, R.; Padmanaban, S.; Mihet-Popa, L.; Blaabjerg, F.; Ramachandaramurthy, V.K. Sliding Mode Controller and Lyapunov Redesign Controller to Improve Microgrid Stability: A Comparative Analysis with CPL Power Variation. Energies 2017, 10, 1959. [Google Scholar] [CrossRef]
- Yuan, Y.; Li, Z.; Feng, Y.; Zuo, W. Development purposes, orientations and prospects of Micro-grid in China. Auto. Electr. Power Syst. 2010, 34, 59–63. (In Chinese) [Google Scholar]
- Okewu, E.; Misra, S.; Maskeliūnas, R.; Damaševičius, R.; Fernandez-Sanz, L. Optimizing Green Computing Awareness for Environmental Sustainability and Economic Security as a Stochastic Optimization Problem. Sustainability 2017, 9, 1857. [Google Scholar] [CrossRef]
- Zhang, J.; Su, L.; Chen, Y.; Jing, S.U.; Wang, L. Energ management of Micro-grid and its control strategy. Power Syst. Technol. 2011, 35, 24–28. (In Chinese) [Google Scholar]
- Zhao, Z.; Lee, W.C.; Shin, Y.; Song, K.B. An Optimal Power Scheduling Method Applied in Home Energy Management System Based on Demand Response. ETRI J. 2013, 4, 1391–1400. [Google Scholar] [CrossRef]
- Jin, M.; Feng, W.; Liu, P.; Marnay, C.; Spanos, C. MOD-DR: Micro-grid optimal dispatch with demand response. Appl. Energy 2017, 187, 758–776. [Google Scholar] [CrossRef]
- Brearley, B.J.; Prabu, R.R. A review on issues and approaches for Micro-grid protection. Renew. Sustain. Energy Rev. 2017, 67, 988–997. [Google Scholar] [CrossRef]
- Meghwani, A.; Srivastava, S.; Chakrabarti, S. A Non-Unit Protection Scheme for DC Micro-grid Based on Local Measurements. IEEE Trans. Power Deliv. 2017, 32, 172–181. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, L.; Ren, H.; Liu, X. Search Improvement Process-Chaotic Optimization-Particle Swarm Optimization-Elite Retention Strategy and Improved Combined Cooling-Heating-Power Strategy Based Two-Time Scale Multi-Objective Optimization Model for Stand-Alone Microgrid Operation. Energies 2017, 10, 1936. [Google Scholar] [CrossRef]
- Okoye, C.O.; Oranekwu-Okoye, B.C. Economic feasibility of solar PV system for rural electrification in Sub-Sahara Africa. Renew. Sustain. Energy Rev. 2018, 82, 2537–2547. [Google Scholar] [CrossRef]
- Igualada, L.; Corchero, C.; Cruz-Zambrano, M.; Heredia, F.J. Optimal Energy Management for a Residential Microgrid Including a Vehicle-to-Grid System. Available online: https://upcommons.upc.edu/handle/2117/20642 (accessed on 25 March 2018).
- Li, W.T.; Yuen, C.; Hassan, N.U.; Tushar, W.; Wen, C.K.; Wood, K.L.; Hu, K.; Liu, X. Demand Response Management for Residential Smart Grid: From Theory to Practice. Available online: http://xueshu.baidu.com/s?wd=paperuri%3A%28c31a841b8e868b2ef596e1524f3b5937%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fieeexplore.ieee.org%2Fdocument%2F7336481%2F&ie=utf-8&sc_us=15685181391879326455 (accessed on 25 March 2018).
- Saffari, M.; Gracia, A.D.; Fernández, C.; Belusko, M.; Boer, D.; Cabeza, L.F. Optimized demand side management (DSM) of peak electricity demand by coupling low temperature thermal energy storage (TES) and solar PV. Appl. Energy 2018, 211, 604–616. [Google Scholar] [CrossRef]
- Wang, P.; Wang, W.; Meng, N.; Liu, H.; Feng, H.; Xu, D. Optimal sizing of DC micro-grids based on comprehensive evaluation of operating modes and operating targets. Power Syst. Technol. 2016, 40, 741–748. [Google Scholar]
- Xin, A.I.; Xiao, L. Chance constrained model for wind power usage based on demand response. J. North China Electr. Power Univ. 2011, 3, 4. [Google Scholar]
- Zhang, D.; Tong, Y.; Jin, X.; Liang, J. Optimal energy storage configuration of Micro-grid considering demand response. Power Electr. 2016, 50, 107–109. [Google Scholar]
- Yu, Y.; Wen, X.; Zhao, J.; Xu, Z.; Li, J. Co-Planning of Demand Response and Distributed Generators in an Active Distribution Network. Energies 2018, 11, 354. [Google Scholar] [CrossRef]
- Pan, Z.; Gao, C. Economic dispatch of electric vehicles based on demand response. Electr. Power Constr. 2015, 36, 139–145. (In Chinese) [Google Scholar]
- Li, Y.; Luo, Q.; Song, Y.Q.; Xu, J.; Cai, L.; Gu, J. Study on tiered level determination of TOU & tiered pricing for residential electricity based on demand response. Power Syst. Prot. Control 2012, 40, 65–74. (In Chinese) [Google Scholar]
- Fan, W.; Zhou, N.; Liu, N.; Lin, X.; Zhang, J.; Lei, J. Multi-objective optimization operation method of user -side Micro-grid based on demand response. Power Syst. Clean Energy 2016, 32, 17–23. [Google Scholar] [CrossRef]
- Gao, C.; Li, Q.; Li, H.; Zhai, H.; Zhang, L. Integration method and operation mechanism of demand response resources based on load aggregator business. Auto. Electr. Power Syst. 2013, 37, 78–86. [Google Scholar]
- Lu, X.; Sun, K.; Huang, L.; Xiao, X.; Guerrero, J.M. The improved droop control method of distributed energy storage system in islanding AC Micro-grid. Electr. Power Syst. Auto. 2013, 37, 80–185. [Google Scholar] [CrossRef]
- Abdelaziz, M.M.A.; Farag, H.E.; El-Saadany, E.F. Optimum Reconfiguration of Droop-Controlled Islanded Micro-grids. IEEE Trans. Power Syst. 2016, 31, 2144–2153. [Google Scholar] [CrossRef]
- Paterakis, N.G.; Erdinç, O.; Catalão, J.P.S. An overview of Demand Response: Key-elements and international experience. Renew. Sustain. Energy Rev. 2017, 69, 871–891. [Google Scholar] [CrossRef]
- Mengelkamp, E.; Gärttner, J.; Rock, K.; Kessler, S.; Orsini, L.; Weinhardt, C. Designing micro-grid energy markets. Appl. Energy 2018, 210, 870–880. [Google Scholar] [CrossRef]
- Zhou, N.; Fan, W.; Liu, N.; Zhang, J.; Lei, J. Battery storage multi-objective optimization for capacity configuration of PV-based Micro-grid considering demand response. Power Syst. Technol. 2016, 40, 1709–1716. [Google Scholar]
- Alamaniotis, M.; Tsoukalas, L.H. Integration of Price Anticipation and Self-Elasticity for Purchase Decisions and Planning in Price Directed Electricity Markets; IET: Stevenage, UK, 2016. [Google Scholar]
- Chen, C.; Hu, B.; Xie, K.; Wan, L.; Xiang, B. A peak-valley TOU price model considering power system reliability and power purchase risk. Power Syst. Technol. 2014, 38, 2141–2148. [Google Scholar]
- Bie, Z.; Hu, G.; Xie, H.; Gengfeng, L. Optimal dispatch for wind power integrated systems considering demand response. Autom. Electr. Power Syst. 2014, 38, 115–120. [Google Scholar] [CrossRef]
- Khierkhah, A.S.; Nobari, A.; Hajipour, V. A Pareto-based approach to optimise aggregate production planning problem considering reliable supplier selection. Int. J. Serv. Oper. Manag. 2018, 29, 59. [Google Scholar] [CrossRef]
- Sun, Y.; Lin, F.; Xu, H. Multi-objective Optimization of Resource Scheduling in Fog Computing Using an Improved NSGA-II. Wirel. Pers. Commun. 2018, 1, 1–17. [Google Scholar] [CrossRef]
- Liu, W.; Niu, S.; Xu, H. Optimal Planning of Battery Energy Storage Considering Reliability Benefit and Operation Strategy in Active Distribution System. Available online: https://www.researchgate.net/publication/301664508_Optimal_planning_of_battery_energy_storage_considering_reliability_benefit_and_operation_strategy_in_active_distribution_system (accessed on 25 March 2018).
- Chen, X.; Yin, J.; Wang, W.; Wu, L.; Tang, F. Approaches to diminish large unsprung mass negative effects of wheel side drive electric vehicles. J. Adv. Mech. Des. Syst. Manuf. 2016, 10, JAMDSM0064. [Google Scholar] [CrossRef]





| Time Windows | Price (Yuan/kWh) | ||
|---|---|---|---|
| Low Price | Medium Price | High Price | |
| 0:00~6:00 18:00~24:00 | 6:00~10:00 15:00~18:00 | 10:00~15:00 | |
| Purchase | 0.5522 | 0.8185 | 1.2035 |
| Sell | 0.65 | 0.65 | 0.65 |
| Time | Low Price | Medium Price | High Price |
|---|---|---|---|
| (6.5,65) | (5.0,60) | (4.0,58) |
| Situations | Peak of Load/kW | Valley of Load/kW | Peak-Valley Difference of Load/kW | ||
|---|---|---|---|---|---|
| Before DR | 1136.93 | 330.31 | 806.62 | 1 | 0 |
| After DR | 1100.19 | 326.15 | 774.04 | 0.97 | 0.75 |
| Scenarios | Optimization Result/Yuan | NSGA-II | |
|---|---|---|---|
| Scene 1: TOU price | Generation cost | optimal value | 46.980 |
| Average value | 47.206 | ||
| Environmental cost | optimal value | 1.246 | |
| Average value | 1.255 | ||
| Scene 2: fixed price | Generation cost | optimal value | 45.450 |
| Average value | 47.268 | ||
| Environmental cost | optimal value | 1.538 | |
| Average value | 1.541 | ||
| Scene 3: isolated grid mode | Generation cost | optimal value | 50.4 |
| Average value | 51.685 | ||
| Environmental cost | optimal value | 1.325 | |
| Average value | 1.336 | ||
| Optimized time records/s | Average value | 19.675 | |
| Cost/Yuan | Generation Cost/Yuan | Environmental Cost/Yuan | Operation Cost/Yuan | ||||
|---|---|---|---|---|---|---|---|
| CCHP | PV | EES | Electricity Exchange | ||||
| Purchase | Sell | ||||||
| Scene 1 | 12,600 | 1120 | 800 | 0 | 0 | 381.3 | 14,901.3 |
| Scene 2 | 12,260 | 1120 | 770 | 250 | −870 | 359.9 | 13,889.9 |
| Scene 3 | 12,510 | 1120 | 820 | 240 | −1600 | 443.7 | 13,533.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Huang, Y.; Wang, Y.; Yu, H.; Li, R.; Song, S. Energy Management for Smart Multi-Energy Complementary Micro-Grid in the Presence of Demand Response. Energies 2018, 11, 974. https://doi.org/10.3390/en11040974
Wang Y, Huang Y, Wang Y, Yu H, Li R, Song S. Energy Management for Smart Multi-Energy Complementary Micro-Grid in the Presence of Demand Response. Energies. 2018; 11(4):974. https://doi.org/10.3390/en11040974
Chicago/Turabian StyleWang, Yongli, Yujing Huang, Yudong Wang, Haiyang Yu, Ruiwen Li, and Shanshan Song. 2018. "Energy Management for Smart Multi-Energy Complementary Micro-Grid in the Presence of Demand Response" Energies 11, no. 4: 974. https://doi.org/10.3390/en11040974
APA StyleWang, Y., Huang, Y., Wang, Y., Yu, H., Li, R., & Song, S. (2018). Energy Management for Smart Multi-Energy Complementary Micro-Grid in the Presence of Demand Response. Energies, 11(4), 974. https://doi.org/10.3390/en11040974






