Modelling of Biomass Concentration, Multi-Wavelength Absorption and Discrimination Method for Seven Important Marine Microalgae Species
Abstract
:1. Introduction
2. Materials and Methods
2.1. Microalgal Culture
2.2. Software
2.2.1. Growth Modelling
2.2.2. Relationship between OD Measurements and Cell Concentration
2.2.3. Effect of the Wavelength on Optical Density
2.2.4. Microalgae Type Prediction from OD Measurements
3. Results and Discussion
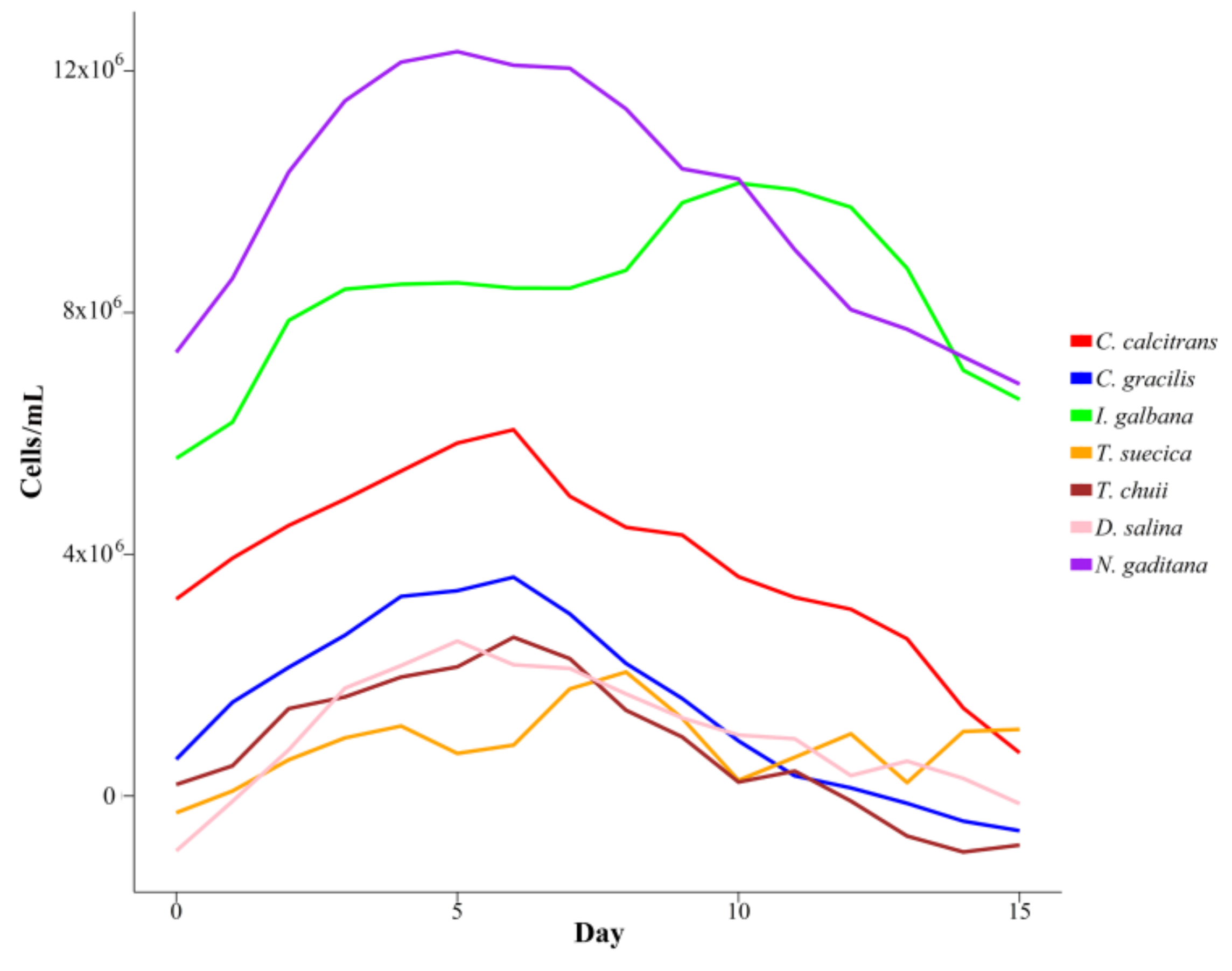
3.1. Growth Performance
3.2. Explaining Cell Concentration from OD Measurements
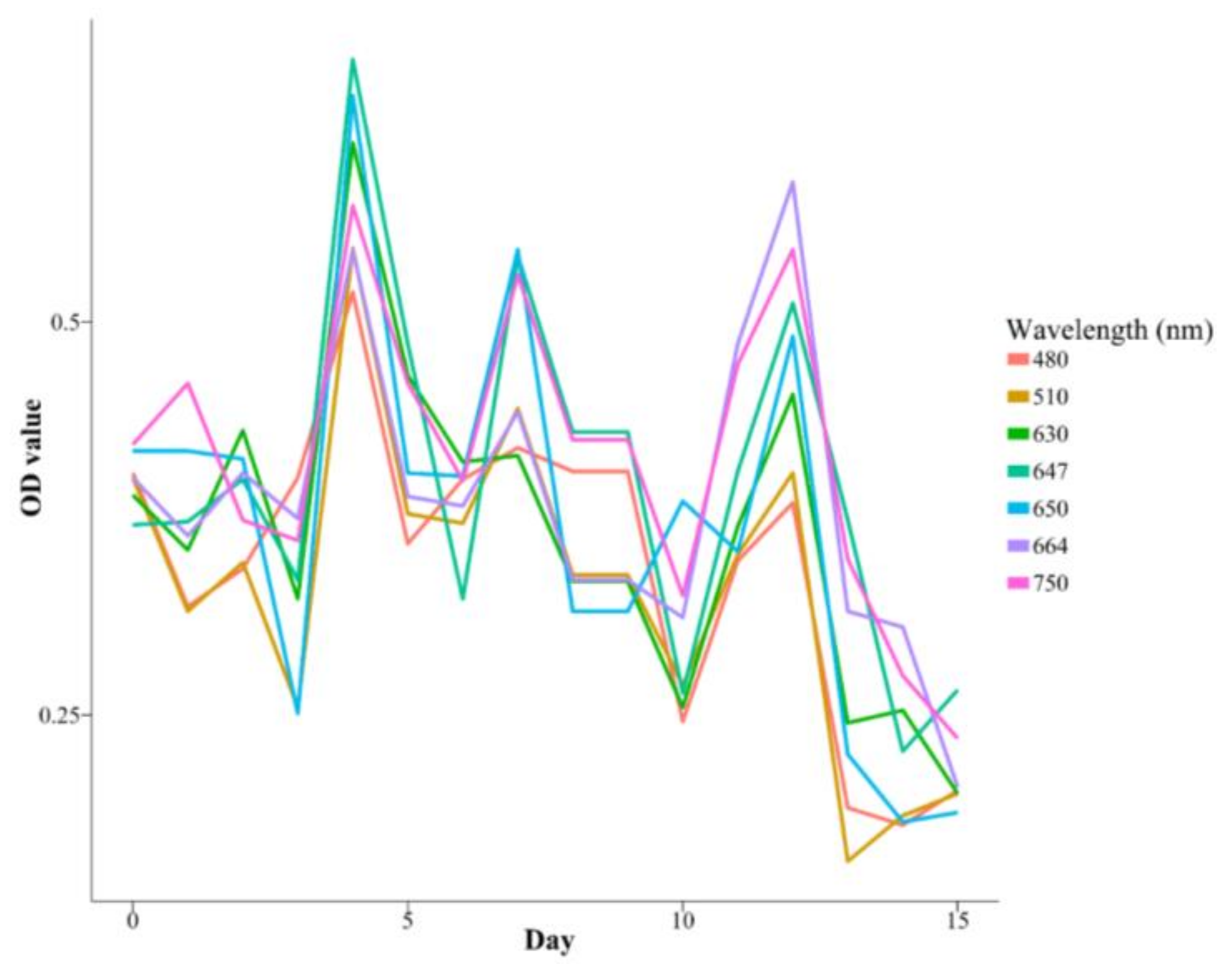
3.3. Intra-Experiment OD Measurements
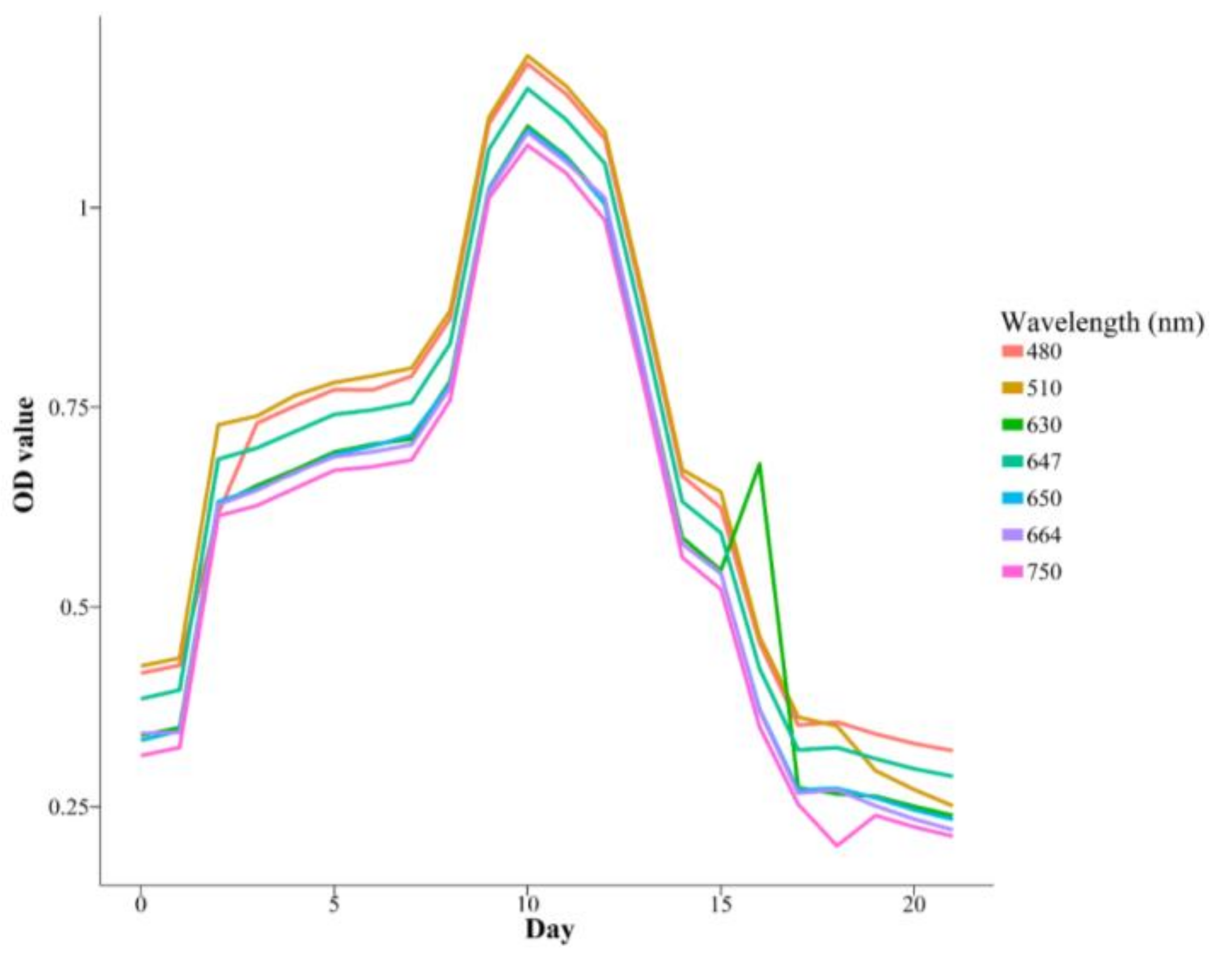
3.4. Inter-Experiment OD Measurements
3.5. Classification Algorithm Performance
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Odjadjare, E.C.; Mutanda, T.; Olaniran, A.O. Potential biotechnological application of microalgae: A critical review. Crit. Rev. Biotechnol. 2015, 37, 37–52. [Google Scholar] [CrossRef] [PubMed]
- Doan, T.T.Y.; Sivaloganathan, B.; Obbard, J.P. Screening of marine microalgae for biodiesel feedstock. Biomass Bioenergy 2011, 35, 2534–2544. [Google Scholar] [CrossRef]
- Mata, T.M.; Martins, A.A.; Caetano, N.S. Microalgae for biodiesel production and other applications: A review. Renew. Sustain. Energy Rev. 2010, 14, 217–232. [Google Scholar] [CrossRef]
- Sung, M.-G.; Lee, B.; Kim, C.W.; Nam, K.; Chang, Y.K. Enhancement of lipid productivity by adopting multi-stage continuous cultivation strategy in Nannochloropsis gaditana. Bioresour. Technol. 2017, 229, 20–25. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M.; Klemm, M.; Nelles, M. Hydrothermal Disintegration and Extraction of Different Microalgae Species. Energies 2018, 11, 450. [Google Scholar] [CrossRef]
- Chen, G.; Chen, J.; He, Q.; Zhang, Y.; Peng, Z.; Fan, Z.; Bian, F.; Yu, J.; Qin, S. Functional Expression of the Arachis hypogaea L. Acyl-ACP Thioesterases AhFatA and AhFatB Enhances Fatty Acid Production in Synechocystis sp. PCC6803. Energies 2017, 10, 2093. [Google Scholar] [CrossRef]
- Du, H.; Ahmed, F.; Lin, B.; Li, Z.; Huang, Y.; Sun, G.; Ding, H.; Wang, C.; Meng, C.; Gao, Z. The effects of plant growth regulators on cell growth, protein, carotenoid, PUFAs and lipid production of chlorella pyrenoidosa ZF strain. Energies 2017, 10, 1696. [Google Scholar] [CrossRef]
- Richmond, A.; Hu, Q. Handbook of Microalgal Culture: Applied Phycology and Biotechnology, 2nd ed.; Wiley-Blackwell: Oxford, UK, 2013. [Google Scholar]
- Razzak, S.A.; Ali, S.A.M.; Hossain, M.M.; DeLasa, H. Biological CO2 fixation with production of microalgae in wastewater—A review. Renew. Sustain. Energy Rev. 2017, 76, 379–390. [Google Scholar] [CrossRef]
- Lage, S.; Gojkovic, Z.; Funk, C.; Gentili, F. Algal Biomass from Wastewater and Flue Gases as a Source of Bioenergy. Energies 2018, 11, 664. [Google Scholar] [CrossRef]
- Smith, L.L.; Fox, J.M.; Treece, G.D. Intensive algal culture techniques. In Handbook of Mariculture Techniques, Crustacean Aquaculture; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Toro, J.E. The growth rate of two species of microalgae used in shellfish hatcheries cultured under two light regimes. Aquac. Res. 1989, 20, 249–254. [Google Scholar] [CrossRef]
- Helm, M.M.; Bourne, N. Hatchery Culture of Bivalves: A Practical Manual. FAO Fisheries and Aquaculture Department; Food and Agriculture Organization of the United Nations: Rome, Italy, 2004. [Google Scholar]
- De Angelis, R.; Melino, S.; Prosposito, P.; Casalboni, M.; Lamastra, F.R.; Nanni, F.; Bruno, L.; Congestri, R. The diatom Staurosirella pinnata for photoactive material production. PLoS ONE 2016, 11, e0165571. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.M.; Kang, S.W.; Kwon, O.N.; Chung, D.; Pan, C.H. Fucoxanthin as a major carotenoid in Isochrysis aff. galbana: Characterization of extraction for commercial application. J. Korean Soc. Appl. Biol. Chem. 2012, 55, 477–483. [Google Scholar] [CrossRef]
- Raposo, M.F.; De Morais, A.M.; De Morais, R.M. Carotenoids from marine microalgae: A valuable natural source for the prevention of chronic diseases. Mar. Drugs 2015, 13, 5128–5155. [Google Scholar] [CrossRef] [PubMed]
- Miyashita, K.; Nishikawa, S.; Beppu, F.; Tsukui, T.; Abe, M.; Hosokawa, M. The allenic carotenoid fucoxanthin, a novel marine nutraceutical from brown seaweeds. J. Sci. Food Agric. 2011, 91, 1166–1174. [Google Scholar] [CrossRef] [PubMed]
- Helmersson, J.; Arnlöv, J.; Larsson, A.; Basu, S. Low dietary intake of beta-carotene, alpha-tocopherol and ascorbic acid is associated with increased inflammatory and oxidative stress status in a Swedish cohort. Br. J. Nutr. 2009, 101, 1775–1782. [Google Scholar] [CrossRef] [PubMed]
- Blanco-Pascual, N.; Gómez-Guillén, M.C.; Montero, M.P. Integral Mastocarpus stellatus use for antioxidant edible film development. Food Hydrocoll. 2014, 40, 128–137. [Google Scholar] [CrossRef]
- Metting, B.; Pyne, J.W. Biologically active compounds from microalgae. Enzym. Microb. Technol. 1986, 8, 386–394. [Google Scholar] [CrossRef]
- Widowati, I.; Zainuri, M.; Kusumaningrum, H.P.; Susilowati, R.; Hardivillier, Y.; Leignel, V.; Bourgougnon, N.; Mouget, J.-L. Antioxidant activity of three microalgae Dunaliella salina, Tetraselmis chuii and Isochrysis galbana clone Tahiti This. J. Phys. Conf. Ser. 2017, 55, 012067. [Google Scholar] [CrossRef]
- Natrah, F.M.I.; Yusoff, F.M.; Shariff, M.; Abas, F.; Mariana, N.S. Screening of Malaysian indigenous microalgae for antioxidant properties and nutritional value. J. Appl. Phycol. 2007, 19, 711–718. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, T. Toshiyuki Life Cycle Analysis of Endosymbiotic Algae in an Endosymbiotic Situation with Paramecium bursaria Using Capillary Flow Cytometry. Energies 2017, 10, 1413. [Google Scholar] [CrossRef]
- Toennies, G.; Gallant, D.L. The relation between photometric turbidity and bacterial concentration. Growth 1949, 13, 7–20. [Google Scholar] [PubMed]
- Lee, C.; Lim, H. New device for continuously monitoring the optical density of concentrated microbial cultures. Biotechnol. Bioeng. 1980, 22, 639–642. [Google Scholar] [CrossRef]
- Griffiths, M.J.; Garcin, C.; van Hille, R.P.; Harrison, S.T.L. Interference by pigment in the estimation of microalgal biomass concentration by optical density. J. Microbiol. Methods 2011, 85, 119–123. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, L.H.R.; Arenzon, A.; Raya-Rodriguez, M.T.; Fontoura, N.F. Algal density assessed by spectrophotometry: A calibration curve for the unicellular algae Pseudokirchneriella subcapitata. J. Environ. Chem. Ecotoxicol. 2011, 3, 225–228. [Google Scholar]
- Santos-Ballardo, D.U.; Rossi, S.; Hernández, V.; Gómez, R.V.; del Carmen Rendón-Unceta, M.; Caro-Corrales, J.; Valdez-Ortiz, A. A simple spectrophotometric method for biomass measurement of important microalgae species in aquaculture. Aquaculture 2015, 448, 87–92. [Google Scholar] [CrossRef]
- Pearl, R.; Slobodkin, L. The Growth of Populations. Q. Rev. Biol. 1976, 51, 6–24. [Google Scholar] [CrossRef]
- Kacena, M.A.; Merrell, G.A.; Manfredi, B.; Smith, E.E.; Klaus, D.M.; Todd, P. Bacterial growth in space flight: Logistic growth curve parameters for Escherichia coli and Bacillus subtilis. Appl. Microbiol. Biotechnol. 1999, 51, 229–234. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, B.R.; Chakraborty, R.; Chaudhuri, U.R. Validity of modified Gompertz and Logistic models in predicting cell growth of Pediococcus acidilactici H during the production of bacteriocin pediocin AcH. J. Food Eng. 2007, 80, 1171–1175. [Google Scholar] [CrossRef]
- Zwietering, M.H.; Jongenburger, I.; Rombouts, F.M.; van ’t Riet, K. Modeling of the bacterial growth curve. Appl. Environ. Microbiol. 1990, 56, 1875–1881. [Google Scholar] [PubMed]
- MacIntyre, H.L.; Lawrenz, E.; Richardson, T.L. Taxonomic Discrimination of Phytoplankton by Spectral Fluorescence. In Chlorophyll a Fluorescence in Aquatic Sciences: Methods and Applications; Springer Netherlands: Dordrecht, The Netherlands, 2010; pp. 129–169. [Google Scholar]
- Coltelli, P.; Barsanti, L.; Evangelista, V.; Frassanito, A.M.; Passarelli, V.; Gualtieri, P. Automatic and real time recognition of microalgae by means of pigment signature and shape. Environ. Sci. Process. Impacts 2013, 15, 1397–1410. [Google Scholar] [CrossRef] [PubMed]
- Promdaen, S.; Wattuya, P.; Sanevas, N. Automated Microalgae Image Classification. Procedia Comput. Sci. 2014, 29, 1981–1992. [Google Scholar] [CrossRef]
- Millie, D.F.; Schofield, O.M.E.; Kirkpatrick, G.J.; Johnsen, G.; Evens, T.J. Using absorbance and fluorescence spectra to discriminate microalgae. Eur. J. Phycol. 2002, 37, 313–322. [Google Scholar] [CrossRef]
- Giordano, M.; Ratti, S.; Domenighini, A.; Vogt, F. Spectroscopic classification of 14 different microalga species: First steps towards spectroscopic measurement of phytoplankton biodiversity. Plant Ecol. Divers. 2009, 2, 155–164. [Google Scholar] [CrossRef]
- Guillard, R.R.; Ryther, J.H. Studies of marine planktonic diatoms. I. Cyclotella nana Hustedt, and Detonula confervacea (Cleve) Gran. Can. J. Microbiol. 1962, 8, 229–239. [Google Scholar] [CrossRef] [PubMed]
- Rice, E.W.; Baird, R.B.; Eaton, A.D.; Clesceri, L.S. (Eds.) Standards Methods for the Examination of Water and Wastewater, 22nd ed.; American Public Health Association, American Water Works Association, Water Environment Federation: Washington, DC, USA, 2016. [Google Scholar]
- Sasaki, K.; Marquez, F.J.; Nishio, N.; Nagai, S. Promotive effect of 5-aminolevulinic acid on the growth and photosynthesis of Spirulina platensis. J. Ferment. Bioeng. 1995, 79, 453–457. [Google Scholar] [CrossRef]
- Katoh, T.; Nagashima, U.; Mimuro, M. Fluorescence properties of the allenic carotenoid fucoxanthin: Implication for energy transfer in photosynthetic pigment systems. Photosynth. Res. 1991, 27, 221–226. [Google Scholar] [CrossRef] [PubMed]
- Rakhimberdieva, M.G.; Vavilin, D.V.; Vermaas, W.F.J.; Elanskaya, I.V.; Karapetyan, N. V Phycobilin/chlorophyll excitation equilibration upon carotenoid-induced non-photochemical fluorescence quenching in phycobilisomes of the cyanobacterium Synechocystis sp. PCC 6803. Biochim. Biophys. Acta 2007, 1767, 757–765. [Google Scholar] [CrossRef] [PubMed]
- Team, R.C. R Language Definition; R Foundation for Statistical Computing: Vienna, Austria, 2000. [Google Scholar]
- Buchanan, R.L.; Whiting, R.C.; Damert, W.C. When is simple good enough: A comparison of the Gompertz, Baranyi, and three-phase linear models for fitting bacterial growth curves. Food Microbiol. 1997, 14, 313–326. [Google Scholar] [CrossRef]
- Bates, D.M.; Watts, D.G. (Eds.) Nonlinear Regression Analysis and Its Applications; Wiley Series in Probability and Statistics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1988. [Google Scholar]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: The forecast package for R. J. Stat. Softw. 2007, 27. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S-PLUS; Springer: New York, NY, USA, 1999; ISBN 9781475731217. [Google Scholar]
- Montero, P.; Vilar, J.A.; Montero, P.; Vilar, J.A. TSclust: An R Package for Time Series Clustering. J. Stat. Softw. 2014, 62. [Google Scholar] [CrossRef]
- Chang, W.; Cheng, J.; Allaire, J.J.; Xie, Y.; McPherson, J. Shiny: Web Application Framework for R. 2017. Available online: https://rdrr.io/cran/shiny/ (accessed on 27 April 2018).
- Microalgae Classifier Based on Absorbance (Optical Density) Data. Available online: https://albriz.shinyapps.io/microalgaeclassification/ (accessed on 25 March 2018).
- Al-Hasan, R.H.; Ghannoum, M.A.; Sallal, A.-K.; Abu-Elten, K.H.; Radwan, S.S. Correlative Changes of Growth, Pigmentation and Lipid Composition of Dunaliella salina in Response to Halostress. Microbiology 1987, 133, 2607–2616. [Google Scholar] [CrossRef]
- Cho, K.; Lee, C.H.; Ko, K.; Lee, Y.J.; Kim, K.N.; Kim, M.K.; Chung, Y.H.; Kim, D.; Yeo, I.K.; Oda, T. Use of phenol-induced oxidative stress acclimation to stimulate cell growth and biodiesel production by the oceanic microalga Dunaliella salina. Algal Res. 2016, 17, 61–66. [Google Scholar] [CrossRef]
- Cho, K.; Hur, S.P.; Lee, C.H.; Ko, K.; Lee, Y.J.; Kim, K.N.; Kim, M.S.; Chung, Y.H.; Kim, D.; Oda, T. Bioflocculation of the oceanic microalga Dunaliella salina by the bloom-forming dinoflagellate Heterocapsa circularisquama, and its effect on biodiesel properties of the biomass. Bioresour. Technol. 2016, 202, 257–261. [Google Scholar] [CrossRef] [PubMed]
- Patil, V.; Källqvist, T.; Olsen, E.; Vogt, G.; Gislerød, H.R. Fatty acid composition of 12 microalgae for possible use in aquaculture feed. Aquac. Int. 2007, 15, 1–9. [Google Scholar] [CrossRef]

| Species | K | r | a | Days |
|---|---|---|---|---|
| C. calcitrans | 7,105,495 ± 102,350 | 0.39 ± 0.17 | 1.45 ± 0.32 | 6.0 ± 2.24 |
| C. gracilis | 3,403,165 ± 533,786 | 0.28 ± 0.08 | 1.58 ± 0.24 | 6.4 ± 1.09 |
| I. galbana | 14,033,908 ± 3,057,825 | 0.37 ± 0.18 | 2.01 ± 0.32 | 9.6 ± 1.98 |
| T. suecica | 1,781,854 ± 427,530 | 0.26 ± 0.15 | 1.69 ± 0.62 | 6.6 ± 2.49 |
| T. chuii | 1,980,891 ± 452,539 | 0.46 ± 0.41 | 2.55 ± 1.88 | 4.4 ± 0.52 |
| D. salina | 2,051,137 ± 433,004 | 0.41 ± 0.18 | 3.71 ± 1.29 | 5.8 ± 1.95 |
| N. gaditana | 17,729,210 ± 1,525,530 | 0.49 ± 0.16 | 1.49 ± 0.57 | 6.2 ± 1.71 |
| nm | 480 | 510 | 630 | 647 | 650 | 664 | 750 |
|---|---|---|---|---|---|---|---|
| 480 | 1 | 0.96 ± 0.05 | 0.96 ± 0.06 | 0.95 ± 0.07 | 0.95 ± 0.07 | 0.94 ± 0.08 | 0.92 ± 0.09 |
| 510 | 0.96 ± 0.05 | 1 | 0.96 ± 0.07 | 0.95 ± 0.06 | 0.96 ± 0.05 | 0.95 ± 0.07 | 0.92 ± 0.08 |
| 630 | 0.96 ± 0.06 | 0.96 ± 0.07 | 1 | 0.96 ± 0.06 | 0.96 ± 0.06 | 0.97 ± 0.05 | 0.94 ± 0.08 |
| 647 | 0.95 ± 0.07 | 0.950.06 | 0.96 ± 0.06 | 1 | 0.96 ± 0.06 | 0.96 ± 0.05 | 0.95 ± 0.07 |
| 650 | 0.95 ± 0.06 | 0.96 ± 0.05 | 0.96 ± 0.06 | 0.96 ± 0.06 | 1 | 0.97 ± 0.06 | 0.94 ± 0.08 |
| 664 | 0.94 ± 0.08 | 0.95 ± 0.07 | 0.97 ± 0.05 | 0.96 ± 0.05 | 0.96 ± 0.06 | 1 | 0.95 ± 0.09 |
| 750 | 0.92 ± 0.09 | 0.92 ± 0.09 | 0.94 ± 0.08 | 0.95 ± 0.07 | 0.94 ± 0.08 | 0.95 ± 0.09 | 1 |
| Species | Replicate 1 | Replicate 2 | Replicate 3 | Replicate 4 | Replicate 5 |
|---|---|---|---|---|---|
| C. calcitrans | 0.98 ± 0.02 | 0.99 ± 0.00 | 0.99 ± 0.00 | 0.99 ± 0.00 | 0.99 ± 0.00 |
| C. gracilis | 0.99 ± 0.00 | 0.99 ± 0.00 | 0.99 ± 0.00 | 0.99 ± 0.00 | 0.99 ± 0.00 |
| I. galbana | 0.99 ± 0.01 | 0.97 ± 0.04 | 0.99 ± 0.00 | 0.99 ± 0.00 | 0.99 ± 0.01 |
| T. suecica | 0.95 ± 0.03 | 0.89 ± 0.05 | 0.96 ± 0.02 | 0.92 ± 0.06 | 0.93 ± 0.04 |
| T. chuii | 0.89 ± 0.05 | 0.83 ± 0.06 | 0.86 ± 0.07 | 0.95 ± 0.04 | 0.92 ± 0.06 |
| D. salina | 0.91 ± 0.05 | 0.89 ± 0.09 | 0.93 ± 0.05 | 0.96 ± 0.02 | 0.93 ± 0.07 |
| N. gaditana | 0.98 ± 0.01 | 0.90 ± 0.13 | 0.91 ± 0.09 | 0.93 ± 0.09 | 0.91 ± 0.10 |
| Species | 480 nm | 510 nm | 630 nm | 647 nm | 650 nm | 664 nm | 750 nm | Mean ± SD |
|---|---|---|---|---|---|---|---|---|
| C. calcitrans | 0.99 ± 0.01 | 0.96 ± 0.0 | 0.99 ± 0.01 | 0.99 ± 0.01 | 0.98 ± 0.01 | 0.98 ± 0.01 | 0.98 ± 0.01 | 0.98 ± 0.01 |
| C. gracilis | 0.84 ± 0.10 | 0.84 ± 0.10 | 0.84 ± 0.10 | 0.84 ± 0.10 | 0.83 ± 0.11 | 0.84 ± 0.09 | 0.84 ± 0.10 | 0.84 ± 0.09 |
| I. galbana | 0.97 ± 0.02 | 0.97 ± 0.03 | 0.96 ± 0.02 | 0.97 ± 0.02 | 0.97 ± 0.03 | 0.97 ± 0.02 | 0.96 ± 0.02 | 0.97 ± 0.02 |
| T. suecica | 0.15 ± 0.27 | 0.17 ± 0.30 | 0.17 ± 0.23 | 0.14 ± 0.32 | 0.15 ± 0.22 | 0.25 ± 0.21 | 0.21 ± 0.25 | 0.18 ± 0.21 |
| T. chuii | 0.44 ± 0.14 | 0.49 ± 0.15 | 0.46 ± 0.18 | 0.47 ± 0.15 | 0.40 ± 0.18 | 0.38 ± 0.27 | 0.47 ± 0.23 | 0.45 ± 0.27 |
| D. salina | 0.58 ± 0.17 | 0.61 ± 0.21 | 0.57 ± 0.23 | 0.61 ± 0.21 | 0.56 ± 0.16 | 0.60 ± 0.22 | 0.61 ± 0.17 | 0.59 ± 0.22 |
| N. gaditana | 0.65 ± 0.23 | 0.61 ± 0.23 | 0.65 ± 0.20 | 0.68 ± 0.20 | 0.66 ± 0.214 | 0.57 ± 0.19 | 0.48 ± 0.24 | 0.62 ± 0.19 |
| Species | C. calcitrans | C. gracilis | I. galbana | T. suecica | T. chuii | D. salina | N. gaditana |
|---|---|---|---|---|---|---|---|
| C. calcitrans | 97.43 | 2.57 | - | - | - | - | - |
| C. gracilis | - | 96.95 | - | - | 2.16 | - | - |
| I.galbana | - | - | 98.04 | - | - | 1.96 | - |
| T. suecica | - | - | - | 98.69 | 1.31 | - | - |
| T. chuii | - | 0.77 | - | 5.14 | 86.90 | - | 7.19 |
| D. salina | - | - | - | - | 1.70 | 97.28 | 1.02 |
| N. gaditana | - | 2.91 | - | 3.44 | 6.47 | 0.63 | 86.54 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chirivella-Martorell, J.; Briz-Redón, Á.; Serrano-Aroca, Á. Modelling of Biomass Concentration, Multi-Wavelength Absorption and Discrimination Method for Seven Important Marine Microalgae Species. Energies 2018, 11, 1089. https://doi.org/10.3390/en11051089
Chirivella-Martorell J, Briz-Redón Á, Serrano-Aroca Á. Modelling of Biomass Concentration, Multi-Wavelength Absorption and Discrimination Method for Seven Important Marine Microalgae Species. Energies. 2018; 11(5):1089. https://doi.org/10.3390/en11051089
Chicago/Turabian StyleChirivella-Martorell, Jerónimo, Álvaro Briz-Redón, and Ángel Serrano-Aroca. 2018. "Modelling of Biomass Concentration, Multi-Wavelength Absorption and Discrimination Method for Seven Important Marine Microalgae Species" Energies 11, no. 5: 1089. https://doi.org/10.3390/en11051089
APA StyleChirivella-Martorell, J., Briz-Redón, Á., & Serrano-Aroca, Á. (2018). Modelling of Biomass Concentration, Multi-Wavelength Absorption and Discrimination Method for Seven Important Marine Microalgae Species. Energies, 11(5), 1089. https://doi.org/10.3390/en11051089






