Analysis of Capacitance to Ground Formulas for Different High-Voltage Electrodes

Abstract

Stray capacitance can seriously affect the behavior of high-voltage devices, including voltage dividers, insulator strings, modular power supplies, or measuring instruments, among others. Therefore its effects must be considered when designing high-voltage projects and tests. Due to the difficulty in measuring the effects of stray capacitance, there is a lack of available experimental data. Therefore, for engineers and researchers there is a need to revise and update the available information, as well as to have useful and reliable data to estimate the stray capacitance in the initial designs. Although there are some analytical formulas to calculate the capacitance of some simple geometries, they have a limited scope. However, since such formulas can deal with different geometries and operating conditions, it is necessary to assess their consistency and applicability. This work calculates the stray capacitance to ground for geometries commonly found in high-voltage laboratories and facilities, including wires or rods of different lengths, spheres and circular rings, the latter ones being commonly applied as corona protections. This is carried out by comparing the results provided by the available analytical formulas with those obtained from finite element method (FEM) simulation, since field simulation methods allow solving such problem. The results of this work prove the suitability and flexibility of the FEM approach, because FEM models can deal with wider range of electrodes, configurations and operating conditions.

1. Introduction

The calculation of capacitance formulas has received little attention compared to the analysis of inductance calculation formulas [1,2]. Nearby surfaces separated by an insulating medium such as air, subjected to different electric potentials, induce a stray or parasitic capacitance, and therefore this configuration acts as a capacitor. High voltages and high frequencies tend to amplify the effects of the unwanted stray capacitance. The analysis of stray capacitance effects is of interest in different disciplines, including electrical engineering, high-voltage applications, radio engineering or physical sciences, among others [3].

Different studies prove that the stray capacitance produces an uneven voltage distribution across each insulator unit in a high-voltage insulator string [4,5]. The effect of the stray capacitance is to reduce the efficacy of each additional insulator unit due to the non-linear voltage distribution [6]. This is because the capacitive current and the corresponding voltage drop across each insulator unit are greater in the insulator units closer to the conductors, due to the effect of the distributed stray capacitances to ground [7]. The string elements closer to the line are subjected to a higher electrical stress than those closer to the tower. Grading rings can be used at both ends of the string to homogenize the voltage drop across each insulator unit [8]. A similar effect occurs in high-voltage switching mode power supplies composed of several modules in series, since in [9] it is proved that the stray capacitance to ground has a significant impact on the individual voltage of each module. In other high-voltage applications, including high-voltage transformers [10] or high-voltage motors, parasitic capacitances have a key role to predict the frequency behavior of such machines.

Accurate methods to calculate the capacitance are based on the calculation of the electrostatic field generated by the system of charged objects under consideration [3]. The capacitance of basic isolated geometries, such as very long horizontal cylindrical conductors, coaxial cylindrical conductors, concentric spheres, or spheres well above ground, can be easily deduced theoretically. However, such formulas have very restricted practical use. The calculation of the capacitance of conductive objects which are close to ground leads to challenging mathematical problems, even for simple geometries. Therefore, analytical solutions for capacitance only exist for a limited number of electrode geometries and configurations, which have almost no practical applications [11], and often only contemplate the stray capacitance to ground, thus disregarding the effects of nearby grounded electrodes, structures or walls [3].

As a consequence, computational methods are increasingly being applied to solve such problem, although most of the published works deal with very particular problems, such as insulator strings [4,5,7], transformer windings [10] or voltage dividers [12], among others. FEM is perhaps the most applied computational technique to calculate the effects of capacitance, since it allows dealing with complex three-dimensional geometries, as reflected in several works [13,14,15,16,17,18,19].

Since stray capacitances are not easily measurable, because of the low immunity to noise of the small signal to be acquired [20], results provided by numerical methods are a good alternative during the design stage of high-voltage devices and instruments. Therefore, the capacitance between energized electrodes or between electrodes and ground is a factor to be considered when designing and planning high-voltage projects and tests [11].

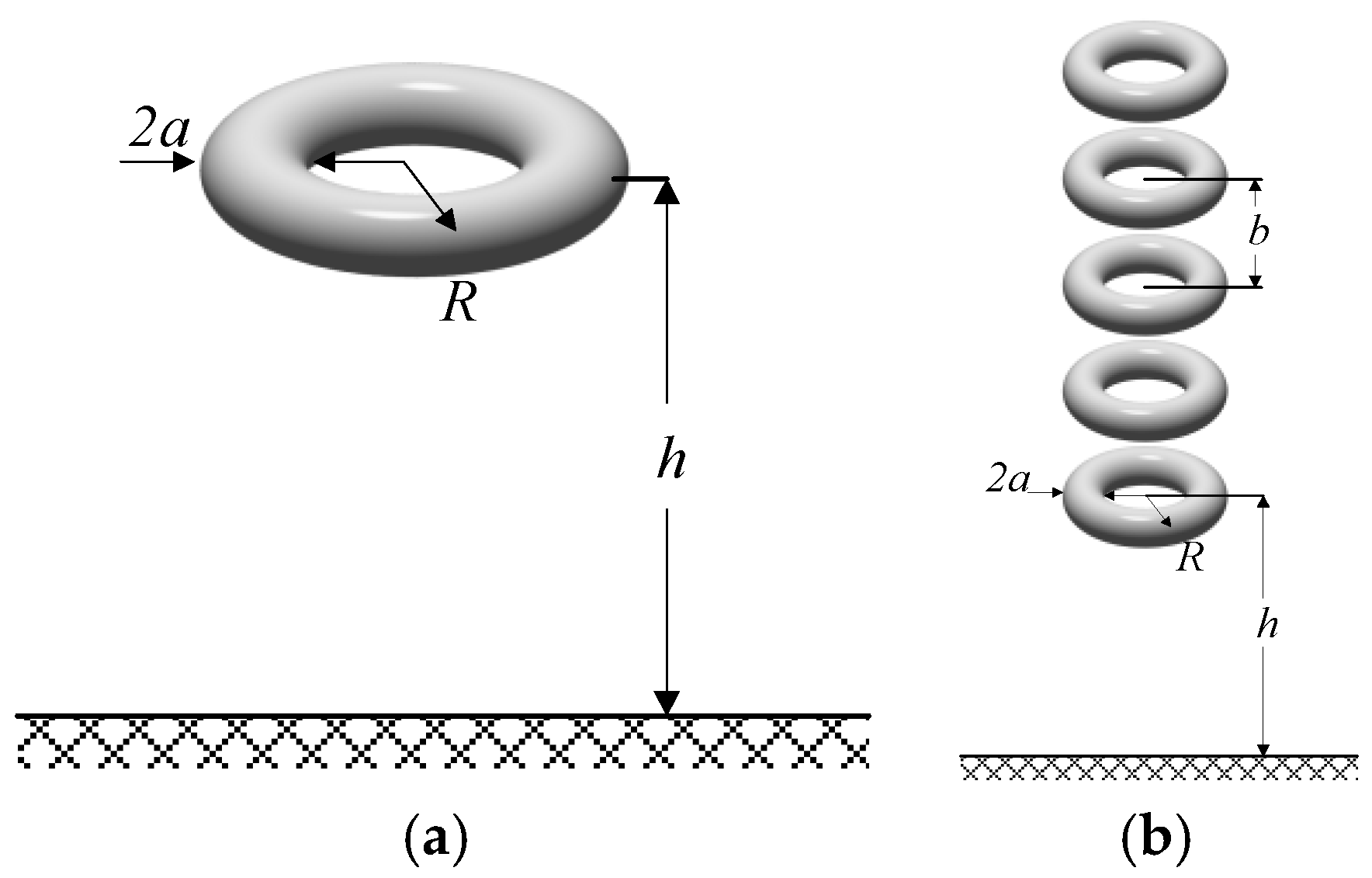
Most works analyze specific problems related to the unwanted effects of stray capacitance, such as in transformer windings [10], motor windings [21] or insulator strings [7], among others. However, there are no recent works providing a systematic account of the problems to calculate the stray capacitance to ground for geometries found in high-voltage laboratories and high-voltage installations such as substations. These geometries include wires, rods, spheres, and circular rings, the latter ones being commonly applied as corona protections. The stray capacitances due to these high-voltage electrodes can have a non-negligible impact on the measurement results and behavior of the devices involved.

This paper is focused to review and analyze the accuracy of different formulas found in the technical literature to calculate the stray capacitance to ground of various high-voltage electrodes. To this end, due to the lack of available experimental data because of experimental difficulties related to the small signal to be acquired and noise immunity, the results provided by the formulas are compared with the results provided by FEM simulations. It is noted that regardless the impact of the stray capacitance in high-voltage applications, at our knowledge, there are no published technical works assessing the accuracy of such formulas; thus this work contributes in this area. Results presented prove that FEM models offer flexibility, simplicity and accuracy to analyze the effects of stray capacitance in high-voltage systems with different geometries.

2. The FEM Approach to Analyze the Stray Capacitance

The stray capacitance to ground is directly related to the distribution of the electric field around high-voltage electrodes [22]. It is a recognized fact that the effects of stray capacitance can be determined by means of FEM-based approaches [12,23].

The capacitance can be calculated from the ratio C = Q/U, defined by the charge Q stored in the system and the electric potential U, supposing that the system under analysis is far from other charged bodies [3]. Therefore, the stray capacitance concept arises between any two charged bodies subjected to different electric potentials, and can be important in high-frequency and high-voltage applications.

For low-frequency applications, the capacitance can be calculated by analyzing the energy related to the electrostatic field, thus disregarding the displacement current. To evaluate the capacitance of a given geometry, it is necessary to calculate the electric potential on the surface of the analyzed conductor. Next, the outer electric potential and the electric field are calculated within all points surrounding the conducting electrodes, by applying the potential as boundary condition [14,24]. Finally, the capacitance of the analyzed system is calculated by applying:

$$C=2·W_E/U^2$$

(1)

W_E being the stored electrostatic energy.

The next paragraphs detail the process to follow for determining the stored electrostatic energy.

From the Gauss law that relates the distribution of the electric charge density (C/m³) to the electric field $\overrightarrow{E}$ (V/m),

$$\overrightarrow{\nabla }\cdot \left(\epsilon ·\overrightarrow{E}\right)=\rho$$

(2)

and the relationship between the electric field and the electric potential U, $\overrightarrow{E}=-\overrightarrow{\nabla }\cdot U$, the Poisson’s equation for electrostatics arises [25],

$${\nabla }^{2}U=-\rho /\epsilon$$

(3)

Equation (3) allows solving for the electric potential and field in all points of the domain [26]. Next, the energy density in any point of the air domain is calculated as:

$$u_E(x,y,z)=\frac{1}{2}\cdot {\epsilon }_o\cdot E{(x,y,z)}^2{(\mathrm{J}/\mathrm{m}}^3)$$

(4)

The electrostatic energy stored in the domain can be calculated by integrating the energy density over the volume of the domain outside the conductive high-voltage electrode [14,27]:

$$W_E=\frac{1}{2}{\displaystyle {\iiint }_v{\epsilon }_o·E{(x,y,z)}^{2}dxdydz}\left(\mathrm{J}\right)$$

(5)

Finally, the capacitance is calculated by applying Equation (1) [24]. Therefore, the capacitance is calculated from the electrostatic energy stored in the air because of the incitation of U.

Figure 1 shows the surface meshes applied to some of the geometries analyzed in this paper, including cylindrical conductors, circular rings and spheres.

Figure 2 shows the blocks and meshes types applied in the simulations. Whereas a sufficiently large outer block was used to set the boundary conditions, a much smaller inner block was used in order to apply a much finer tetrahedral mesh to ensure improved accuracy.

Both three-dimensional (3D) and two-dimensional (2D) FEM simulations were carried out to simulate all geometries analyzed in this work. Whereas 3D-FEM simulations were applied to wires of finite length, circular rings and spheres, 2D-FEM simulations were applied to analyze wires of infinite length. Parametric simulations were carried out to automatically change the value of different parameters, such as the height about ground level or the curvature radius of the different analyzed geometries.

Simulations conducted in this work were performed by means of the Comsol Multiphysics package using the electrostatics module. They consist of approximately 0.5–9.5 million tetrahedral elements, 66–590 thousand triangular elements, 0.5–73 thousand edge elements, and 22–96 vertex elements, depending on the specific geometry analyzed.

3. The Analyzed Geometries

This section analyzes the accuracy of formulas to calculate the capacitance between different electrode geometries and an infinite ground plane, some of them being based on the method of images.

3.1. Finite-Length Straight Round Wire Which Is Parallel to the Ground Plane

Figure 3 shows the layout of a straight conductor of round section which is parallel to a conducting plane.

According to [3], the capacitance of a straight conductor of round section which is parallel to a conducting plane can be approximated as:

$$C=\frac{2\mathsf{\pi }\epsilon l}{\ln (2h/a)-2.303D_1(0.5l/h)} \left(\mathrm{F}\right)$$

(6)

being the permittivity of air, 8.85 × 10⁻¹² F/m, l the length of the conductor, h the height above ground and D₁ a coefficient depending on l/(2h), which is obtained by interpolating the values given in

Table 1. Values of coefficient D₁ as a function of l/(2h).

l/(2h)	D1	l/(2h)	D1	l/(2h)	D1
10.00	0.042	0.85	0.379	0.40	0.617
5.00	0.082	0.80	0.396	0.35	0.664
2.50	0.157	0.75	0.414	0.30	0.721
2.00	0.191	0.70	0.435	0.25	0.790
1.25	0.283	0.65	0.457	0.20	0.874
1.11	0.310	0.60	0.482	0.15	0.990
1.00	0.336	0.55	0.510	0.10	1.155
0.95	0.350	0.50	0.541	0.05	1.445
0.90	0.364	0.45	0.576	0.00	0.000

.

Table 2. Capacitance of a straight round wire of finite length which is parallel to a conducting plane.

Radius	Equation (6) (pF)	FEM (pF)
a (m)	l = 1 m, h = 1 m
0.01	13.728	14.014
0.02	16.561	16.981
0.03	18.834	19.314
0.04	20.867	21.356
0.05	22.773	23.230
0.06	24.609	24.982
0.07	26.410	26.654
0.08	28.198	28.262
0.09	29.988	29.824
0.10	31.793	31.346
a (m)	l = 10 m, h = 1 m
0.01	108.881	109.590
0.02	125.970	127.056
0.03	138.705	140.094
0.04	149.422	151.092
0.05	158.948	160.880
0.06	167.683	169.852
0.07	175.540	178.252
0.08	183.604	186.216
0.09	191.029	193.844
0.10	198.200	201.200
a (m)	l = 1 m, h = 5 m
0.01	13.097	13.360
0.02	15.651	16.031
0.03	17.666	18.095
0.04	19.442	19.876
0.05	21.086	21.490
0.06	22.651	22.980
0.07	24.168	24.388
0.08	25.657	25.726
0.09	27.130	27.016
0.10	28.600	28.256
a (m)	l = 10 m, h = 5 m
0.01	90.696	91.464
0.02	102.251	103.384
0.03	110.484	111.916
0.04	117.179	118.880
0.05	122.958	124.906
0.06	128.121	130.292
0.07	132.837	135.222
0.08	137.212	139.796
0.09	141.317	144.090
0.10	145.203	148.152

compares the capacitance of a finite-length straight round wire, which is parallel to the ground plane, provided by Equation (6) with those obtained by means of FEM simulations.

Data presented in Table 2 show a good agreement between the results provided by Equation (6) and those from FEM simulations.

3.2. Finite-Length Straight Wire of Round Section Which Is Perpendicular to the Ground Plane

According to [3], the capacitance of a straight conductor of round section which is perpendicular to a conducting plane, (see Figure 4) can be approximated as:

$$C=\frac{2\mathsf{\pi }\epsilon l}{\ln (l/a)-2.303D_2}$$

(7)

D₂ being a coefficient, which is calculated by interpolation of the values given in

Table 3. Values of coefficient D₂ as a function of h/l.

h/l	D2	h/l	D2	h/l	D2
10.00	0.144	0.80	0.219	0.15	0.323
5.00	0.153	0.70	0.227	0.10	0.345
2.50	0.170	0.60	0.236	0.08	0.356
2.00	0.177	0.50	0.247	0.06	0.369
1.25	0.196	0.40	0.261	0.04	0.384
1.11	0.202	0.30	0.280	0.02	0.403
1.00	0.207	0.25	0.291	-	-
0.90	0.2125	0.20	0.305	-	-

, as a function of h/l.

Table 4. Capacitance of a straight round wire of finite length which is perpendicular to a conducting plane.

Radius	Equation (7) (pF/m)	FEM (pF/m)
a (m)	l = 1 m, h = 1 m
0.01	13.475	14.014
0.02	16.194	16.981
0.03	18.362	19.314
0.04	20.288	21.356
0.05	22.085	23.230
0.06	23.808	24.982
0.07	25.490	26.654
0.08	27.151	28.262
0.09	28.807	29.824
0.10	30.469	31.346
a (m)	l = 10 m, h = 1 m
0.01	91.004	92.004
0.02	102.642	104.146
0.03	110.941	112.882
0.04	117.693	120.036
0.05	123.524	126.246
0.06	128.735	131.818
0.07	133.497	136.924
0.08	137.917	141.682
0.09	142.065	146.158
0.10	145.993	150.408
a (m)	l = 1 m, h = 5 m
0.01	13.081	13.346
0.02	15.629	16.010
0.03	17.638	18.085
0.04	19.408	19.881
0.05	21.046	21.506
0.06	22.605	23.012
0.07	24.116	24.434
0.08	25.597	25.786
0.09	27.064	27.094
0.10	28.526	28.354
a (m)	l = 10 m, h = 5 m
0.01	87.763	88.516
0.02	98.538	99.650
0.03	106.163	107.574
0.04	112.329	114.008
0.05	117.629	119.552
0.06	122.346	124.498
0.07	126.639	129.004
0.08	130.609	133.176
0.09	134.323	137.080
0.10	137.829	140.770

compares the capacitance of a finite-length straight round wire, which is perpendicular to the ground plane, provided by Equation (7) with those obtained by means of FEM simulations.

Results presented in Table 4 show a good match between the data provided by Equation (7), with the data obtained from FEM simulations, especially when the height h of the conductor above the ground plane increases.

3.3. Infinite-Length Straight Circular Wire Which Is Parallel to a Conducting Plane

By applying the images method, the capacitance per unit length of a round straight conductor of infinite-length, which is parallel to a conducting plane, as shown in Figure 5, can be calculated as [3]:

$$C/l=\frac{2\mathsf{\pi }\epsilon }{\mathrm{acosh}(h/a)} (\mathrm{F}/\mathrm{m})$$

(8)

where a is the radius of the conductor, and h is the distance between its center and the ground plane.

In [28], an equivalent formula is proposed:

$$C/l=\frac{2\mathsf{\pi }\epsilon }{\ln \left(\frac{h+\sqrt{h^2-a^2}}{a}\right)} (\mathrm{F}/\mathrm{m})$$

(9)

Figure 5 shows an infinite straight conductor of radius a, which is parallel to the ground plane:

Table 5. Capacitance of a straight round wire of infinite length which is parallel to a conducting plane.

Radius	Equation (8) = Equation (9) (pF/m)	FEM (pF/m)
a (m)	l = ∞ m, h = 1 m
0.01	10.500	10.499
0.02	12.081	12.079
0.03	13.247	13.246
0.04	14.222	14.220
0.05	15.084	15.082
0.06	15.869	15.867
0.07	16.601	16.599
0.08	17.292	17.289
0.09	17.951	17.949
0.10	18.586	18.583
a (m)	l = ∞ m, h = 5 m
0.01	8.054	8.035
0.02	8.952	8.928
0.03	9.577	9.550
0.04	10.076	10.046
0.05	10.500	10.468
0.06	10.874	10.840
0.07	11.212	11.175
0.08	11.522	11.483
0.09	11.810	11.770
0.10	12.081	12.038

summarizes the results attained by means of Equations (8), (9) and FEM simulations for different values of the radius a, and the height h. It shows an excellent agreement between the results provided by Equations (8), (9) and FEM simulations.

3.4. Infinite-Length Straight Wire of Square Section Which Is Parallel to a Conducting Plane

By applying the method of the mirror images, the capacitance per unit length of an infinite-length straight conductor of square section, which is parallel to a conducting plane, can be calculated as [3]:

$$C/l=\frac{4\mathsf{\pi }\epsilon }{\ln \left(x^2-\frac{2x}{x-1}\right)} (\mathrm{F}/\mathrm{m})$$

(10)

where x = 3.39 h/a, a being the side length of the square, and h the distance between the geometrical center of the wire and the ground plane.

Figure 6 shows the layout of the analyzed conductor.

Table 6. Capacitance of a straight wire of infinite length and square section which is parallel to a conducting plane.

Side Length	Equation (10) (pF/m)	FEM (pF/m)
a (m)	l = ∞ m, h = 1 m
0.01	9.549	9.546
0.02	10.839	10.825
0.03	11.768	11.740
0.04	12.531	12.485
0.05	13.194	13.128
0.06	13.791	13.702
0.07	14.340	14.225
0.08	14.851	14.710
0.09	15.334	15.163
0.10	15.793	15.591
a (m)	l = ∞ m, h = 5 m
0.01	7.482	7.469
0.02	8.251	8.234
0.03	8.779	8.758
0.04	9.197	9.172
0.05	9.549	9.520
0.06	9.858	9.825
0.07	10.134	10.098
0.08	10.387	10.347
0.09	10.621	10.577
0.10	10.839	10.791

shows the results attained by applying Equation (10) and FEM for different values of the side length a, and the height h.

3.5. Sphere Over a Conducting Plane

Spheres are frequently applied as corona protections in high-voltage applications, although their stray capacitance can affect the behavior of sensitive high-voltage devices.

Figure 7 shows the layout of a sphere, where r is its radius, and h the distance between the lowest point of the sphere and the ground plane.

By applying the method of the images, the capacitance of a conductive sphere of radius r placed at a height h above a ground plane is given by [29]:

$$C=4\mathsf{\pi }\epsilon r{\displaystyle \sum _{i=0}^{\infty }\frac{2\cdot \sin \mathrm{h}({\eta }_0)}{e^{(1+2i){\eta }_0}-1}}$$

(11)

where ${\eta }_0=\mathrm{acos}\mathrm{h}(1+h/r)$.

A simplified expression for this arrangement is given in [29] as:

$$C=4\mathsf{\pi }\epsilon r[1+0.5\log (1+r/h)]$$

(12)

An equivalent formulation to Equation (11) was proposed by Snow [28]:

$$C=8\mathsf{\pi }\epsilon r\sqrt{h{\ast }^2-r^2}{\displaystyle \sum _{n=0}^{\infty }\frac{e^{-(n+0.5)\gamma }}{1-e^{-(n+0.5)\gamma }}}$$

(13)

being defined as:

$$\gamma =2\ln \left(\frac{h\ast +\sqrt{h{\ast }^2-r^2}}{r}\right)$$

(14)

and h* = h + r.

Table 7. Capacitance of a sphere over a conducting plane.

Radius	Equation (11) = Equation (13) (pF)	Equation (12) (pF)	FEM (pF)
r (m)	h = 1 m
0.01	1.118	1.115	1.118
0.02	2.247	2.235	2.248
0.03	3.387	3.359	3.388
0.04	4.538	4.489	4.539
0.05	5.699	5.622	5.701
0.06	6.870	6.760	6.873
0.07	8.052	7.903	8.055
0.08	9.244	9.050	9.247
0.09	10.445	10.210	10.449
0.10	11.656	11.357	11.662
r (m)	h = 5 m
0.01	1.114	1.113	1.114
0.02	2.230	2.227	2.230
0.03	3.348	3.342	3.349
0.04	4.468	4.458	4.470
0.05	5.591	5.575	5.593
0.06	6.716	6.693	6.718
0.07	7.843	7.812	7.847
0.08	8.972	8.932	8.976
0.09	10.103	10.053	10.108
0.10	11.237	11.174	11.242
r (m)	h = 1 m
0.1	11.656	11.357	11.662
0.2	24.277	23.134	24.294
0.3	37.741	35.281	37.778
0.4	51.950	47.758	51.992
0.5	66.823	60.531	66.880
0.6	82.297	73.572	82.366
0.7	98.315	86.860	98.412
0.8	114.832	100.373	114.942
0.9	131.809	114.096	131.920
1.0	149.213	128.012	149.333
r (m)	h = 5 m
0.1	11.237	11.174	11.242
0.2	22.689	22.443	22.708
0.3	34.352	33.802	34.388
0.4	46.218	45.250	46.266
0.5	58.282	56.784	58.340
0.6	70.538	68.402	70.600
0.7	82.982	80.102	83.040
0.8	95.608	91.881	95.666
0.9	108.411	103.738	108.448
1.0	121.386	115.670	121.418

shows the results obtained by applying Equations (11)–(13) and FEM, for different values of the radius r and the height h.

Results presented in Table 7 show an excellent match between Equations (11), (13) and FEM results, although a greater difference when applying Equation (13), as expected.

3.6. Circular Ring or Toroid Which Plane Is Parallel to a Conducting Plane

Toroidal rings are commonly used as corona protections in high-voltage applications. However, the rings introduce a non-negligible capacitance in the system, whose impact cannot be neglected depending on the application.

Figure 8 shows a toroid of round section which is parallel to a conducting plane and different toroids lying in parallel planes.

By applying the images method, the capacitance of a circular ring or toroid, which is parallel to a conducting plane, can be calculated as [3]:

$$C=\frac{4{\mathsf{\pi }}^2\epsilon R}{\ln (8R/a)-K(k^2)\cdot k} \left[\mathrm{F}\right]$$

(15)

where a and R are, respectively, the minor and major radiuses, h is the distance between the geometrical center of the toroid and the ground plane, $k^2=\frac{R^2}{R^2+h^2}$ and K is the complete elliptic integral of first kind with modulus k², which can be computed by means of the ellipke function of MATLAB (2017, The MathWorks Ltd., Natick, MA, USA).

Table 8. Capacitance of a toroid which is parallel to a conducting plane for different configurations.

Inner Radius	Equation (15) (pF)	FEM (pF)
a (m)	R = 0.25 m, h = 1 m
0.01	17.792	17.835
0.02	20.716	20.840
0.03	22.919	23.166
0.04	24.789	25.204
0.05	26.464	27.084
0.06	28.011	28.872
0.07	29.467	30.592
0.08	30.856	32.290
0.09	32.195	33.962
0.10	33.495	35.626
a (m)	R = 0.25 m, h = 5 m
0.01	16.741	16.779
0.02	19.305	19.412
0.03	21.204	21.418
0.04	22.796	23.150
0.05	24.204	24.726
0.06	25.493	26.210
0.07	26.692	27.618
0.08	27.827	28.994
0.09	28.911	30.340
0.10	29.955	31.660
a (m)	R = 0.10 m, h = 1 m
0.005	7.107	7.128
0.010	8.273	8.338
0.015	9.151	9.283
0.020	9.896	10.115
0.025	10.563	10.886
0.030	11.179	11.622
0.035	11.759	12.338
0.040	12.312	13.040
0.045	12.845	13.731
0.050	13.362	14.418
Mean difference	-	3.7%
a (m)	R = 0.10 m, h = 5 m
0.005	6.930	6.950
0.010	8.034	8.095
0.015	8.860	8.983
0.020	9.557	9.759
0.025	10.178	10.474
0.030	10.749	11.157
0.035	11.284	11.814
0.040	11.792	12.455
0.045	12.280	13.086
0.050	12.752	13.709

summarizes the results obtained by applying Equation (15) and FEM, for different values of the radiuses a, R and the height h. It shows a good agreement between the results of both systems.

FEM allows the simple simulation of several concentric corona rings sharing the same vertical axis as shown in Figure 8b. This configuration common applied in high-voltage generators, voltage dividers, or capacitors, among others. However, there are no analytical formulas to deal with this geometry.

Table 9. Capacitance of a row of five circular rings which are parallel to a conducting plane.

a (m)	R = 0.10 m, h = 5 m, b = 3a
0.005	11.547
0.010	14.945
0.015	18.036
0.020	20.914
0.025	23.654
0.030	26.294
0.035	28.862
0.040	31.370
0.045	33.836
0.050	36.266

presents the results obtained by means of FEM simulations, when dealing with a row of five circular rings which are placed as shown in Figure 8b.

3.7. n Parallel Round Wires of Finite Length Lying in a Plane Parallel to the Ground Plane

According to [3], the capacitance of n parallel round conductors of finite length lying in the same plane, which is parallel to the ground plane, can be calculated as:

$$C=\frac{2\mathsf{\pi }\epsilon nl}{\ln (2h/a)+(n-1)\ln (2h/b)-2.303n[D_1(0.5l/h)+B_n]}$$

(16)

a being the radius of the conductors, l the length of any conductor, h the distance between the center of any conductor and the ground plane, b the distance between the centers of two adjacent conductors, and B_n a coefficient, which is calculated as:

$$B_n=\frac{2}{n^2}[\log (n-1)+2\log (n-2)+3\log (n-3)+\dots (n-2)\log 2]$$

(17)

The values of D₁ (0.5l/h) are given in Table 1. It is noted that Equation (16) is not a general formula, since it is only valid when b ≤ l/(n−1).

When the distance d_k (k = 1, 2, …, n−1) between any two wires is inferior than the mean height above the ground plane, that is, d_k << h, [3] suggests to apply:

$$C=\frac{2\mathsf{\pi }\epsilon nl}{2.303F_1}$$

(18)

F₁ being calculated as:

$$F_1=\log (2h/a)+{\displaystyle \sum _{k=1}^{n-1}[\log (2h/d_k)+0.434(d_k/l)]}-n{D}_1$$

(19)

Figure 9 shows the layout of the n parallel round wires of finite length, lying in a plane parallel to the ground plane.

Table 10. Capacitance of n round straight wires of finite length lying in a plane which is parallel to the ground plane.

Radius	Equation (16) (pF/m)	Equation (18) (pF/m)	FEM (pF/m)
a (m)	n = 9, l = 1 m, b = 3·a, h = 1 m
0.01	25.486	27.567	26.768
0.02	37.344	38.507	37.170
0.03	51.310	47.995	46.584
0.04	69.840	56.118	55.654
0.05	97.018 *	62.642 *	64.592
0.06	142.245 *	67.377 *	73.482
0.07	234.783 *	70.292 *	82.390
0.08	537.921 *	71.522 *	91.328
0.09	−3873.668 *	71.327 *	100.334
0.10	−464.680 *	70.019 *	109.402
a (m)	n = 9, l = 1 m, b = 3·a, h = 10 m
0.01	23.146	24.845	24.214
0.02	32.526	33.396	32.454
0.03	42.633	40.307	39.500
0.04	54.690	45.885	45.958
0.05	70.057 *	50.156	52.060
0.06	90.936 *	53.147	57.908
0.07	121.568 *	54.944	63.576
0.08	171.655 *	55.693	69.110
0.09	269.653 *	55.574	74.528
0.10	551.085 *	54.777	79.860
a (m)	n = 9, l = 10 m, b = 3·a, h = 1 m
0.01	171.708	187.492	179.876
0.02	218.441	243.370	230.580
0.03	259.804	293.982	274.540
0.04	300.125	344.125	315.860
0.05	341.199	395.835 *	355.940
0.06	384.154	450.434 *	395.400
0.07	429.917	509.035 *	434.560
0.08	479.385	572.740 *	473.660
0.09	533.535	642.756 *	512.800
0.10	593.505	720.493 *	552.120
a [m]	n = 9, l = 10 m, b = 3·a, h = 10 m
0.01	124.029	132.046	129.028
0.02	146.699	157.517	153.758
0.03	164.261	177.270	172.856
0.04	179.509	194.345	189.294
0.05	193.436	209.826	204.120
0.06	206.529	224.233	217.880
0.07	219.065	237.865	230.820
0.08	231.223	250.906	243.180
0.09	243.125	263.480	255.060
0.10	254.860	275.672	266.540

* Does not fulfill the requirements of the formula.

summarizes the results obtained by applying Equations (16), (18) and FEM, for different values of the radius a, the length l, and the height h.

According to the results summarized in Table 10, FEM results are more general results. FEM simulations avoid the inherent limitations and applicability of Formulas Equations (16) and (18), since they are not general, and only provide accurate results when fulfilling some constraints.

3.8. n Identical Straight Wires of Finite Length Parallel to the Ground Plane and Arranged on the Surface of a Circular Cylinder

According to [3], the capacitance of n identical straight wires of finite length parallel to the ground plane, and arranged on the surface of a circular cylinder, is given by Equation (18). It is noted that the coefficients D₁ (0.5l/h) and d_k (distance between the centers of any two wires) included in Equation (19) are obtained from Table 1, and by applying $d_k=2R\sin (k\mathsf{\pi }/n)$ with k = 1, 2, 3, …, n−1, respectively. It is known that Equation (18) is not accurate when the distance d_k (k = 1, 2, …, n−1) between any two wires is inferior than the height of any conductor above the ground plane, that is, d_k << h.

Figure 10 shows n straight round conductors of finite length (radius a, length l) parallel to the ground plane, which are placed on the surface of a circular cylinder of radius R whose center is placed at a height h above the ground plane.

Table 11. Capacitance of n infinitely long parallel wires of round section lying in a plane parallel to a conducting plane.

Radius	Equation (18) (pF)	Equation FEM (pF)
a (m)	n = 8, l = 1 m, R = 0.5 m, h = 1 m
0.01	55.753	65.468
0.02	61.055	73.360
0.03	64.652	78.964
0.04	67.472	83.520
0.05	69.835	87.470
0.06	71.892	91.030
0.07	73.729	94.322
0.08	75.397	97.424
0.09	76.932	100.390
0.10	78.360	103.254
a (m)	n = 8, l = 1 m, R = 0.5 m, h = 10 m
0.01	45.641	51.538
0.02	49.134	56.286
0.03	51.436	59.506
0.04	53.206	62.032
0.05	54.664	64.156
0.06	55.917	66.018
0.07	57.021	67.694
0.08	58.014	69.232
0.09	58.919	70.668
0.10	59.752	72.020
a (m)	n = 8, l = 10 m, R = 0.5 m, h = 1 m
0.01	373.467	391.420
0.02	396.536	420.140
0.03	411.400	440.020
0.04	422.642	456.240
0.05	431.793	470.540
0.06	439.570	483.760
0.07	446.367	496.380
0.08	452.427	508.620
0.09	457.911	520.680
0.10	462.930	532.660
a (m)	n = 8, l = 10 m, R = 0.5 m, h = 10 m
0.01	203.369	209.640
0.02	210.022	217.680
0.03	214.120	222.900
0.04	217.126	226.940
0.05	219.516	230.340
0.06	221.508	233.380
0.07	223.221	236.140
0.08	224.726	238.720
0.09	226.071	241.140
0.10	227.288	243.480

summarizes the results obtained by applying Equation (20) and FEM, for different values of the radius a, the length l, and the height h.

Results summarized in Table 11 prove that the accuracy of Equation (18) lowers when reducing the height of the conductors above the ground plane.

4. Discussion

This section summarizes the results attained in this work. As deduced from Section 3, FEM simulations offer more flexibility, generalization capability, and the possibility to deal with more complex geometries than analytical formulas for calculating the stray capacitance of high-voltage electrodes to ground. Although analytical formulas only are available for some simple geometries, they can be effectively applied to determine the straight capacitance to ground of high-voltage electrodes with simple geometries.

Table 12. Single straight wires. Comparative results between analytical formulas and FEM simulations.

Geometry Analyzed	Mean Difference	Maximum Difference
Finite-length straight round wire which is parallel to the ground plane: Equation (6) vs. FEM
a = 0.01–0.1 m, l = 1 m, h = 1 m	1.6%	2.5%
a = 0.01–0.1 m, l = 10 m, h = 1 m	1.2%	1.5%
a = 0.01–0.1 m, l = 1 m, h = 5 m	1.5%	2.4%
a = 0.01–0.1 m, l = 10 m, h = 5 m	1.6%	2.0%
Finite-length straight wire of round section which is perpendicular to the ground plane: Equation (7) vs. FEM
a = 0.01–0.1 m, l = 1 m, h = 1 m	4.3%	5.0%
a = 0.01–0.1 m, l = 10 m, h = 1 m	2.2%	2.9%
a = 0.01–0.1 m, l = 1 m, h = 5 m	1.6%	2.5%
a = 0.01–0.1 m, l = 10 m, h = 5 m	1.6%	2.0%
Infinite-length straight circular wire which is parallel to a conducting plane: Equation (8) = Equation (9) vs. FEM
a = 0.01–0.1 m, h = 1 m	<0.1%	<0.1%
a = 0.01–0.1 m, h= 5 m	0.3%	0.4%
Infinite-length straight wire of square section which is parallel to a conducting plane: Equation (10) vs. FEM
a = 0.01–0.1 m, h = 1 m	0.6%	1.3%
a = 0.01–0.1 m, h= 5 m	0.3%	0.4%

,

Table 13. Spheres and circular rings. Comparative results between analytical formulas and FEM simulations.

Geometry Analyzed	Mean Difference	Maximum Difference
Sphere over a conducting plane: Equation (11) = Equation (13); Equation (12) vs. FEM
r = 0.01–0.1 m, h = 1 m	<0.1%; 1.4%	<0.1%; 2.6%
r = 0.01–0.1 m, h = 5 m	<0.1%; 0.3%	<0.1%; 0.6%
r = 0.1–1.0 m, h = 1 m	<0.1%; 9.4%	<0.1%; 14.2%
r = 0.1–1.0 m, h = 5 m	<0.1%; 2.7%	0.1%; 4.7%
Circular ring or toroid which plane is parallel to a conducting plane: Equation (15) vs. FEM
a = 0.01–0.1 m, R = 0.25, h = 1 m	2.9%	6.4%
a = 0.01–0.1 m, R = 0.25, h = 5 m	2.5%	5.7%
a = 0.005–0.05 m, R = 0.10, h = 1 m	3.7%	7.9%
a = 0.005–0.05 m, R = 0.10, h = 5 m	3.6%	7.5%

and

Table 14. Multiple wires. Comparative results between analytical formulas and FEM simulations.

Geometry Analyzed	Mean Difference	Maximum Difference
n parallel round wires of finite length lying in a plane parallel to the ground plane: Equation (18) vs. FEM *
a = 0.01–0.1 m, n = 9, l = 1 m, b = 3a, h = 1 m	16.4%	56.2%
a = 0.01–0.1 m, n = 9, l = 1 m, b = 3a, h = 10 m	14.0%	45.8%
a = 0.01–0.1 m, n = 9, l = 10 m, b = 3a, h = 1 m	8.1%	8.6%
a = 0.01–0.1 m, n = 9, l = 10 m, b = 3a, h = 10 m	5.1%	5.5%
n identical straight wires of finite length parallel to the ground plane and arranged on the surface of a circular cylinder: Equation (18) vs. FEM
a = 0.01–0.1 m, n = 8, l = 1 m, R = 0.5 m, h = 1 m	25.5%	31.8%
a = 0.01–0.1 m, n = 8, l = 1 m, R = 0.5 m, h = 10 m	17.4%	20.5%
a = 0.01–0.1 m, n = 8, l = 10 m, R = 0.5 m, h = 1 m	9.7%	15.1%
a = 0.01–0.1 m, n = 8, l = 10 m, R = 0.5 m, h = 10 m	5.1%	7.1%

* Some of the input parameters are out of the applicability limits of the formula.

summarize the main results attained in this work.

Results summarized in Table 12 clearly show a very good agreement between the results provided by analytical formulas and FEM simulation for wires of infinite length, whereas in the case of straight wires of finite length, maximum differences around 1–5% are found.

Results presented in Table 13 clearly show that in the case of spheres, analytical and FEM results are almost the same, whereas in the case of circular rings, maximum differences around 5–8% are found.

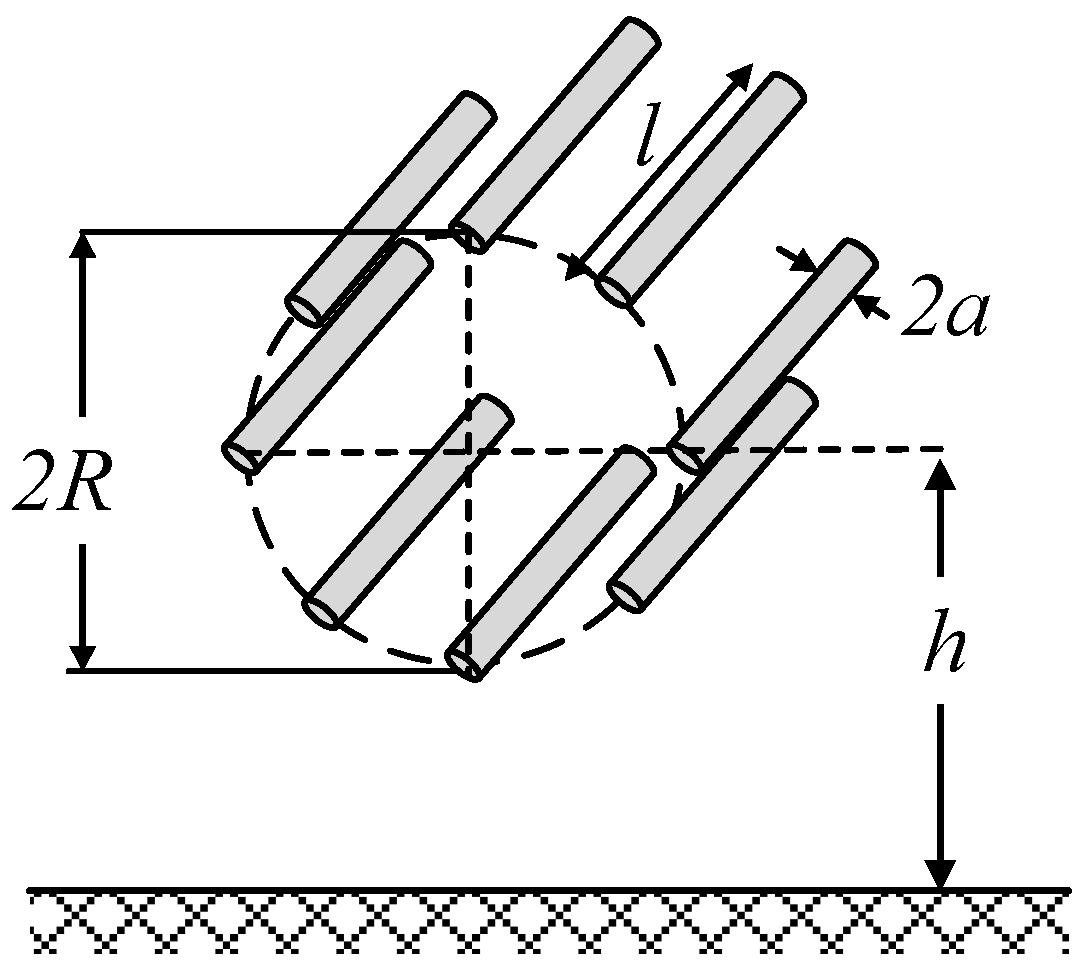
When dealing with multi-wire configurations, the differences are much higher than in the geometries above, since differences around 5–56% can be found. In addition, for some geometries, the analytical formulas available for multi-wire geometries cannot be applied, since some of the input parameters are out of the applicability limits of such formulas.

5. Conclusions

This work has analyzed the behavior of several approximate and exact formulas to calculate the capacitance to ground of high-voltage electrodes with different geometries. Due to experimental difficulties involved, there is a lack of experimental data, so it is necessary to develop numerical methods to infer the value of the capacitance when designing high-voltage tests and projects. The analyzed geometries found in high-voltage applications include different combinations of wires and rods, spheres and circular rings, the latter two being commonly applied as corona protections in high-voltage projects. The results provided by the analyzed formulas have been compared against the results provided by FEM simulations, since FEM simulations are internationally recognized as a valid means of obtaining accurate and reliable data. The analysis performed in this work has proved the inherent limitations of the analyzed formulas. It has been proved that although in some configurations the results are very accurate (single straight wires or single sphere configurations), while in other cases important differences arise, especially when dealing with multi-wire configurations. The stray capacitance of a multi-toroid geometry has been also analyzed, which cannot be calculated by means of analytical formulas. Therefore, this work has proven that analytical formulas can only deal with a narrow number of geometries, and has also proven the enhanced performance and flexibility of FEM simulations, due to their suitability, flexibility, and the wider range of geometries that FEM simulations allow to be evaluated.